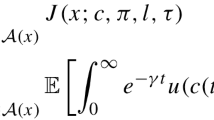1 Introduction

A well-known result in macroeconomic theory is that, in a representative-agent model with complete markets and unproductive public expenditure, no agents would choose redistributive capital income taxation, independently of their initial or long-run net worth levels [13, 23, 24]. More recent studies (e.g., [10, 15, 17, 22]), however, highlight that in the presence of uninsurable idiosyncratic risk capital taxes may be welfare improving and may have very different effects in the short and the long run.

A common assumption of these papers is that investing in firm capital carries no idiosyncratic risk, neglecting that entrepreneurial equity represents a very concentrated risk for a sizable fraction of households [29] and that there has been a steady decline in small- and medium-sized firms going public over the last 20 years [19]. Consequently, they overlook a crucial effect of capital income taxes, which impact agents’ net worth distribution by affecting their consumption-saving decisions jointly with their risk-bearing capacity.Footnote 1 With this in mind, this paper advances previous literature by investigating the role of fiscal policies in redistributing net worth and risk in a heterogeneous-agent economy with uninsurable capital and labour endowment risks.

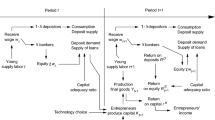
Based on the seminal work of [1], we work in continuous time. The model features a unit mass of infinitely-lived, risk-averse entrepreneurs, their firms, and the government. Each entrepreneur consumes and uses capital to constitute a firm which operates in a perfectly competitive market for production factors and buys government-issued risk-free bonds. Entrepreneurs are self-employed in their firms and supply labour inelastically. In summary, they own the non-tradable ownership of one firm (i.e., there are no equity markets) and thus fully carry her capital depreciation risk. Accordingly, one can interpret each entrepreneur-firm couple as a small-sized enterprise.

On top of capital risk, entrepreneurs’ decisions are subject to borrowing constraints and uninsurable labour-endowment shocks as in [8]. Similarly to [3], the government collects taxes on financial and labour incomes and issues bonds to finance unproductive public expenditure.

We characterize the model’s competitive equilibrium as a forward-backward PDE system and derive a numerical approximation of its long-term (stationary) solution. Then, we investigate the effects of introducing capital risk by comparing the model’s outcome with that of a benchmark economy with no capital risk, à la [17]. We highlight two main results.

First, uninsurable capital depreciation shocks reduce aggregate capital accumulation and, in turn, output and wages relative to the benchmark economy. The reason is that capital risk discourages investments in firms, generating an “inside equity" risk premium. Notably, this is the opposite of what happens when introducing labour income shocks without risky capital, which increases the aggregate capital by fostering agents’ precautionary motives (see [2]).Footnote 2 The reason is that, differently from labour, entrepreneurs can mitigate capital risk exposures by lowering consumption and reducing the risk by choosing an appropriate capital-bond allocation.

Second, capital depreciation risk increases inequality in the long run, fattening the tails of entrepreneurs’ net worth distribution and increasing the share of financially constrained individuals. The result is due to the following.

Low-net-worth entrepreneurs have a higher propensity to consume and derive most of their income from wages. Accordingly, in line with the classical households finance literature (see, e.g., [14]), they seek higher expected returns and allocate a large portion of their savings to capital, earning a positive risk premium.Footnote 3 This preference stems from wages being independent of capital depreciation, thereby providing a “natural" hedge against its risks. Quite the opposite, high-net-worth entrepreneurs’ income depends primarily on financial assets. Coherently, they act in a “financially sophisticated" manner and allocate a larger share of their financial net worth in risk-free bonds to hedge against capital depreciation shocks. These behaviours foster economic inequality by mitigating net worth volatility across high-net-worth entrepreneurs and fostering it among low-net-worth ones, enabling the former to accumulate larger endowments with a higher probability, making the right tail of the net worth distribution fatter. At the same time, lower wages due to lower capital accumulation augment inequality because low-net-worth entrepreneurs become financially constrained more frequently.

Next, the paper explores the impact of different fiscal policies, redistributing taxes between risky capital and bonds or financial and labour income. The former policy involves the following two dynamics.

First, lowering taxes on risky assets promotes capital accumulation, leading to lower rental rates and higher wages. Second, the consequent decrease in safe asset demand exerts upward pressure on risk-free rates, decreasing the nominal risk premium. Despite these effects, net risk premiums increase due to the relatively lower tax rates on capital than bonds. Since low-net-worth entrepreneurs hold more capital than bonds and rely more on wages than financial assets income, the policy reduces the share of financially constrained individuals and, in turn, net worth inequality.

Similarly, redistributing taxes from financial to human capital fosters aggregate capital accumulation, output and, in turn, wages. At the same time, it reduces net worth inequality. The reason is that, despite raising taxes on labour income, the policy augments real wages more than proportionally. Notably, the distributional effects of reducing human capital taxation are much larger than the ones involving only financial assets.

The third part of the paper analyses the long-run welfare effects of different tax policies, in the same spirit of [17]. We find that reducing risky capital taxes at the expense of bonds can produce welfare gains across all entrepreneurs. Such gains accrue more to low-net-worth entrepreneurs. Quite the opposite, the benefits of shifting tax revenues from financial to labour income accrue primarily to high-net-worth entrepreneurs.

Finally, we compare the short and long-run effects of fiscal policies. Our simulations show that, although macroeconomic aggregates reach their long-run levels quickly, high-net-worth entrepreneurs always benefit the most in the short run. This occurs because low-net-worth entrepreneurs need time to build up their net worth after the policy changes, experiencing the advantages of higher wages and risk premiums.

The paper proceeds as follows. Section 2 reviews the most closely related studies. Section 3 describes the model and the algorithm employed in its numerical solution. Section 4 compares the model’s competitive equilibrium with a benchmark economy without capital risk and analyzes the effects of fiscal policies on macroeconomic aggregates, inequality, and welfare. Section 5 concludes.

2 Related literature

From a broad perspective, we relate to several studies on the effects of fiscal policy in incomplete-market economies (e.g., [10, 15, 17, 22], among others). [22] studies taxes in Aiyagari-type economies ([2]) and finds that income tax cuts provide a more significant boost to consumption and a smaller investment stimulus when asset markets are incomplete. In a similar framework [17] show that reducing capital taxes entail substantial re-distributional effects, whose sign and magnitude have large differences in the short and long run. [15] find similar results in an OLG model where households face idiosyncratic, uninsurable income and productivity shocks, showing that capital tax rates are largely positive (about 25 per cent).

More recent contributions show that a uniform flat tax on capital and labour income combined with a lump-sum transfer is nearly optimal when entrepreneurs face income and productivity shocks [10] and that capital taxes can provide redistribution benefits in the short run [18], whereas increasing labour taxes in the medium to long run can mitigate the intertemporal distortion. [26] explore similar issues in a two-period OLG model, showing that the optimal time-invariant tax on capital increases with income risk. While we do not deal with optimal taxation, our paper differentiates from these works by studying the effects of tax policies in a context where entrepreneurs are subject to idiosyncratic capital risk, i.e., considering their portfolio choice of investing in risky capital or risk-free bonds.

We thus connect to the literature on capital market risk and wealth inequality (e.g., [7, 21]).Footnote 4

[7] proves that the stationary wealth distribution in Bewley economies with idiosyncratic capital income risk is heavy-tailed. [21] studies the impact of the heterogeneous exposure to aggregate risk on inequality and its relation with asset prices. Unlike these studies, we focus on the interaction between capital risk and fiscal policy and how they jointly affect wealth inequality. Moreover, we consider the role of public debt.

Finally, from a technical standpoint, the model’s structure and solution build on [1] and exhibit several similarities with the mathematical theory of mean-field games introduced by [27].Footnote 5 Our model, much like other heterogeneous agent economies, deviates from the classical MFG models (see, for instance [12]) because the interaction between individual agents’ decisions and their distribution occurs (indirectly) via market prices rather than (directly) through their utility.

3 Baseline model

Time is continuous and indexed as \(t\in [0,\infty )\). The economy features three types of agents: a unit mass of ex-ante identical entrepreneurs, their firms, and the government.

Firms produce output using labour and capital and have no endowment of their own. Each entrepreneur uses capital to finance a firm, invests in risk-free bonds, and supplies labour to earn a competitive wage. As in [2, 8], entrepreneurs face uninsurable labour endowment shocks and borrowing constraints, generating a non-trivial net worth distribution. Similarly to [7], investing in firm capital is also a source of idiosyncratic risk, which cannot be diversified. In other words, each entrepreneur is self-employed in one firm, constituting an autonomous productive entity (or “enterprise") and carrying her entire business risk. This assumption has its empirical foundation in the work of [29], showing that a significant fraction of households invests more than two-thirds of their holdings in a single (private) company.

The government raises taxes on capital and labour income and issues riskless bonds to finance its exogenous public expenditure. We now review each actor in greater detail.

3.1 Firms

The production sector comprises a unit mass of identical and competitive firms. Firms have no endowment. They use capital \(k_t\) and labour \(l_t\), both supplied by their entrepreneurs, to generate output \(y_t\) utilizing the following Cobb-Douglas technology:

$$\begin{aligned} y_{t}=A k_{t}^{\alpha }l_{t}^{1-\alpha }. \end{aligned}$$
(1)

A and \(\alpha \) parametrize the economy’s Total Factor Productivity (TFP) and capital share, respectively. Firms choose capital and labour solving a standard profit-maximization problem

$$\begin{aligned} \max _{k_{t},l_{t}}\left\{ y_{t}-R_{t}k_{t}-w_{t}l_{t}\right\} , \end{aligned}$$
(2)

where \(R_t\) and \(w_t\) denote the rental rate of capital and labour cost (wages). The problem’s FOCs are

$$\begin{aligned}{} & {} k_{t}:\alpha A\left( \frac{k_{t}}{l_{t}}\right) ^{\alpha -1}=R_{t}, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} l_{t}:\left( 1-\alpha \right) A\left( \frac{k_{t}}{l_{t}}\right) ^{\alpha }=w_{t}. \end{aligned}$$
(4)

Firms can trade both production factors in competitive markets. As a result, optimal capital rental rates and wages are homogeneous across firms, such that marginal revenues equal marginal costs and Eqs. (3) and (4) hold in the aggregate. Accordingly, all firms break even and earn no profits in equilibrium.

3.2 Entrepreneurs

There is a unit mass of ex-ante identical entrepreneurs. Each entrepreneur has a stochastic labour \(Z_t\) and net worth endowment \(n_t\in \mathbb {R}^{+}\backslash \!\left\{ 0\right\} \) and owns one firm. Entrepreneurs maximize the inter-temporal utility of their consumption

$$\begin{aligned} u(c_t)={\left\{ \begin{array}{ll} {\frac{c_t^{1-\gamma }-1}{1-\gamma }}, &{} \text {if }\gamma \ne 1,\\ {\ln c_t,} &{} {\text {if }}\gamma =1, \end{array}\right. } \end{aligned}$$

where \(\gamma > 0\) is the relative risk aversion coefficient. Being subject to labour and net worth shocks, their future consumption is uncertain.

Labour endowment and supply Entrepreneurs’ labour endowment \(Z_t\) follows a 2-state continuous-time Markov chain with (normalized) state space \(\left\{ 1,z<1\right\} \). The transitions \(1 \rightarrow z\) and \(z \rightarrow 1\) occur with intensity \(\lambda _1\) and \(\lambda _z\). The duration in each state is thus exponentially distributed with mean \(1/\lambda _1\) and \(1/\lambda _z\).

Entrepreneurs are self-employed, as in [4]. They supply labour inelastically to their firm at the instantaneous wage \(w_t\). Conditional on their labour endowment, they earn \(w_t Z_t\). The government taxes these earnings at the constant rate \(\tau _l\).

Net worth endowment Entrepreneurs allocate their net worth between capital \(k_{t}\ge 0\) and bonds \(b_{t}\ge 0\), such that \(k_t+b_t=n_t\). By holding capital, entrepreneurs constitute firms, earning returns at the rate \(R_t\) (see Eq. (3)).

Holding capital entails risk because it depreciates at the stochastic rate \(d\Delta _t=-\delta dt+\sigma dW_{t}\), where \(\delta \) and \(\sigma \) are positive constants and \(W_t\) is a standard Brownian motion.Footnote 6 Accordingly, individual capital holdings obey the following Stochastic Differential Equation (SDE):

$$\begin{aligned} dk_{t}=k_{t}\left( R_{t}dt+d\Delta _t\right) . \end{aligned}$$
(5)

Conversely, bonds are risk free and yield deterministic returns

$$\begin{aligned} db_t=b_t r_t dt, \end{aligned}$$
(6)

where \(r_t\) is an endogenous object that we will determine in equilibrium. The government taxes capital and bond earnings at the constant rates \(\tau _k\) and \(\tau _b\), respectively.

State variables and admissible controls By using Eqs. (5) and (6), the dynamics of \(Z_t\), and imposing the balance sheet condition \(n_t=k_t+b_t\), entrepreneurs’ net worth-labour endowment couple (n, Z) obeys the following SDE system:

$$\begin{aligned} {\left\{ \begin{array}{ll} dn_{t}=\underbrace{\left[ \left( 1-\tau _{b}\right) n_{t}r_{t}+k_{t}\left( R_{t}-\delta -r_{t}\right) +w_{t}Z_{t}\left( 1-\tau _{l}\right) -c_{t}\right] }_{:=\mu (c_t,k_t;n_t,Z_t)}dt +\underbrace{k_{t}\left( 1-\tau _{k}\right) \sigma }_{:=\sigma (c_t,k_t;n_t,Z_t)}dW_{t},\\ dZ_{t}=\left( 1-z\right) \mathbb {I}_{Z_{t}=z}dJ_{t}^{z}+\left( z-1\right) \mathbb {I}_{Z_{t}=1}dJ_{t}^{1}, \end{array}\right. } \end{aligned}$$
(7)

where \(J_{t}^{z}\) and \(J_{t}^{1}\) are Poisson processes with intensity \(\lambda _1\) and \(\lambda _{z}\), and \(\mathbb {I}\) is the indicator function. As usual, the system is defined on a probability space \(\left( \Omega ,\mathcal {F}=\mathcal {\mathcal {W\otimes Z}},\mathbb {P}\right) \), equipped with the canonical filtration \(\mathbb {F}=(\mathcal {F}_{t})_{t\ge 0}\), and \(\mathcal {W}\) and \(\mathcal {Z}\) are \(\sigma \)-algebras generated by the capital and labour endowment processes.

The entrepreneurs control their consumption \(c_t\) and capital allocation \(k_t\), influencing the drift and diffusion of their net worth process in Eq. (7). The controls are progressively measurable (with respect to \(\mathbb {F}\)) processes valued within the following admissible set:

$$\begin{aligned} A(n_t,Z_t):=\left\{ (c_t,k_t):\Omega \times [0,\infty )\rightarrow \mathbb {R}^{2},c_{t}\ge 0, n_t\ge k_{t}\ge 0, \forall t\ge 0\right\} . \end{aligned}$$

Notice that throughout the paper, we impose the no-borrowing constraint \(n_t \ge 0\) on the agents’ net worth. This assumption, coupled with \(n_t \ge k_t \ge 0\), implies that agents cannot short-sell bonds, i.e., \(b_t = n_t-k_t \ge 0\).

Objective function Let \(\rho >0\) be the entrepreneurs’ subjective discount rate and \((n_t^s,Z_t^s)\) the unique strong solution to the SDE system in Eq. (7) starting from (n, Z) at \(t=0\). We define the entrepreneurs’ gain function as

$$\begin{aligned} V(n,Z,c,k):=\mathbb {E}\left[ \int _{0}^{\theta }e^{-\rho t}u(c_t)dt+e^{-\rho \theta }\bar{V}(n_{\theta }^{s},Z_\theta ^s)\left| \mathcal {F}_{0}\right. \right] , \end{aligned}$$
(8)

for all \((n,Z)\in \mathbb {R}^{+}\backslash \!\left\{ 0\right\} \times \left\{ 1,z\right\} \) and \((c,k)\in A\), where \(\theta :=\inf \left\{ t\ge 0:Z_t \ne Z\right\} \) is the stopping time at which the labour endowment process “jumps" from its initial state Z to \(\bar{Z}\) (i.e., \(Z_\theta :Z=z\rightarrow \bar{Z}=1\) or \(Z_\theta :Z=1\rightarrow \bar{Z}=z\)), and \(\bar{V}(n,\bar{Z})\) is the correspondent gain function. The entrepreneurs’ value function is then

$$\begin{aligned} v(n,Z)=\sup _{(c,k)\in A(n,Z)}V(n,Z,c,k). \end{aligned}$$
(9)

Given the problem in Eq. (9), we look for an optimal Markovian control in the form \((\hat{c}(n_t^s,Z_t^s),\hat{k}(n_t^s,Z_t^s))\) for some measurable functions in A such that \(v(n;Z)=V(n,Z,\hat{c},\hat{k})\), where \((n_t^s,Z_t^s)\) denotes a unique strong solution to Eq. (7).

Proposition 1

(HJBE and optimal Markovian controls) Let w be a measurable function in \( C^{2}(\mathbb {R}^{+}\backslash \!\left\{ 0\right\} \times \left\{ 1,z\right\} )\), and satisfying a quadratic growth condition; that is, there exists some constant Q such that

$$\begin{aligned} w(n,Z)\le Q\left( 1+|n|^2 \right) ,\forall (n,Z)\in \mathbb {R}^{+}\backslash \!\left\{ 0\right\} \times \left\{ 1,z\right\} . \end{aligned}$$

Suppose that, for \((c,k)\in A\)

$$\begin{aligned}{} & {} 0\ge \sup _{(c,k)\in A}\left\{ u(c)+\lambda _{Z}\bar{w}(n,\bar{Z})+\mathcal {L}^{(c,k)}w(n,Z)\right\} -\left( \rho +\lambda _{Z}\right) w(n,Z) \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \lim _{T\rightarrow \infty }\mathbb {E}\left[ e^{-\left( \rho +\lambda _{Z}\right) T}w(n_{T}^{s},Z_{T}^{s})\right] \ge 0, \end{aligned}$$
(11)

where \(\bar{w}(n,\bar{Z})\) denotes the complementary function when labour endowment \(\bar{Z}=z\) if \(Z=1\) and vice versa, \(\lambda _{\bar{Z}}\) is the associated transition intensity, and \(\mathcal {L}^{(c,k)}\) is the infinitesimal generator of the (controlled) process in Eq. (7). Then, \(w\ge v\) on \(\in \mathbb {R}^{+}\backslash \!\left\{ 0\right\} \times Z\in \left\{ 1,z\right\} \).

Next, suppose that for all \(n\in \mathbb {R}^{+}\backslash \! \left\{ 0\right\} \) and \(Z\in \left\{ 1,z\right\} \) there exist a couple of measurable functions \((\hat{c}(n,Z),\hat{k}(n,Z)) \in A\) such that

$$\begin{aligned} \left( \rho +\lambda _{Z}\right) w(n,Z)-u(\hat{c})-\lambda _{Z}\bar{w}(n,\bar{Z}) -\mathcal {L}^{(\hat{c},\hat{k})}w(n,Z)=0, \end{aligned}$$

Suppose further that \(\mu (\hat{c},\hat{k};n,Z):A\times \mathbb {R}^{+}\backslash \! \left\{ 0\right\} \times \left\{ 1,z\right\} \rightarrow \mathbb {R},\sigma (\hat{c},\hat{k};n,Z):A\times \mathbb {R}^{+}\backslash \! \left\{ 0\right\} \times \left\{ 1,z\right\} \rightarrow \mathbb {R}\) are measurable functions satisfying

$$\begin{aligned} \left| \mu (\hat{c},\hat{k};n,Z)\right| +\left| \sigma (\hat{c},\hat{k};n,Z)\right| \le P\left( 1+\left| n\right| \right) \end{aligned}$$

for \((\hat{c},\hat{k})\in A,n\in \mathbb {R}^{+}\backslash \! \left\{ 0\right\} \), \(Z\in \left\{ 1,z\right\} \), and some constant P, and such that

$$\begin{aligned} \left| \mu (\hat{c},\hat{k};n,Z)-\mu (\hat{c},\hat{k};m,Z)\right| +\left| \sigma (\hat{c},\hat{k};n,Z)-(\hat{c},\hat{k};m,Z)\right| \le D\left( n-m\right) \end{aligned}$$

for some constant D, guaranteeing that Eq. (7) admits a unique strong solution \((n_t^s,Z_t^s)\), which satisfies

$$\begin{aligned} \lim _{T\rightarrow \infty }\mathbb {E}\left[ e^{-\left( \rho +\lambda _{Z}\right) T}w(n_{T}^{s},Z_{T}^{s})\right] \le 0, \end{aligned}$$

for a given initial condition \((n_0=n,Z_0=Z)\) (see [31] Theorem 5.2.1). Then, the following holds.

  1. 1.

    The value function of an entrepreneur with net worth n and labour endowment Z, denoted by v(n, Z), equals w(n, Z) and satisfies the Hamilton-Jacobi-Bellman Equation (HJBE)

    $$\begin{aligned} \left( \rho +\lambda _{Z}\right) v(n,Z)=\max _{(c,k)\in A}\left\{ u(c)+\lambda _{Z}\bar{v}(n,\bar{Z})+\mathcal {L}^{(c,k)}v(n,Z)\right\} . \end{aligned}$$
    (12)
  2. 2.

    The following measurable processes in A are optimal Markovian controls for the problem in Eq. (9):

    $$\begin{aligned}{} & {} \hat{c}(n_{t}^{s},Z_{t}^{s})=\frac{\partial v(n_{t}^{s},Z_{t}^{s})}{\partial n}^{-\frac{1}{\gamma }}, \end{aligned}$$
    (13)
    $$\begin{aligned}{} & {} \hat{k}(n_{t}^{s},Z_{t}^{s})=\min \left\{ -\frac{\frac{\partial v(n_{t}^{s},Z_{t}^{s})}{\partial n}}{\frac{\partial ^{2}v(n_{t}^{s},Z_{t}^{s})}{\partial n^2}}\frac{\left( 1-\tau _{k}\right) \left( R_{t}-\delta \right) -\left( 1-\tau _{b}\right) r_{t}}{\sigma ^{2}},n_{t}^{s}\right\} . \end{aligned}$$
    (14)

Proof

A sketch derivation of the HJBE and the correspondent Verification Theorem appear in Appendix A.1. \(\square \)

An important detail is that entrepreneurs’ borrowing constraint \(n\ge 0\) does not appear in the optimal policies described in Proposition (1). As we discuss in Sect. 3.5, we will enforce the constraint by imposing appropriate boundary conditions for solving the HJBE in Eq. (12). The constraint will be such that the FOCs hold at \(n=0\) and in the interior.

3.3 Government

The government uses tax revenues \(T_t\) and raises debt \(B_t\) to finance an exogenous constant public spending level G. Accordingly, the stock of public debt obeys the following law of motion:

$$\begin{aligned} dB_{t}=r_{t}B_{t}dt+\underbrace{\left( G-T_{t}\right) dt}_{\text {Primary deficit}}. \end{aligned}$$
(15)

where

$$\begin{aligned} T_{t}=K_{t}(R_{t}-\delta )\tau _{k}+L_{t}w_{t}\tau _{l}+B_{t}r_{t}\tau _{b}. \end{aligned}$$
(16)

Public debt grows because it pays the instantaneous interest rate \(r_t\) on its outstanding amount; it then also increases or decreases depending on the sign of the primary deficit, i.e., tax revenues \(T_t\) minus public expenditure G.

3.4 Equilibrium and aggregation

We now define the model’s competitive equilibrium and characterize its steady state. For this purpose, let \(\pi (t,n,Z)\) and \(\bar{\pi }(t,n,\bar{Z})\) denote the time-t density functions of the net worth for entrepreneurs with labour endowment Z and \(\bar{Z}\), respectively.

Definition 1

(Competitive equilibrium) A competitive equilibrium is a set of aggregates \((K_t,B_t)\), factor prices \((R_{t},w_{t})\), risk-free rate \((r_t)\), consumption and asset allocation policies \((\hat{c}(n,Z),\hat{k}(n,Z),\hat{b}(n,Z))\), and net worth distributions \((\pi (t,n,Z))\) such that: (i) firms solve the problem in Eq. (2); (ii) entrepreneurs solve the problem in Eq. (9); (iii) public debt evolves as in Eq. (15); (iv) all markets (capital, bonds, and labour) clear.

The equilibrium level of the risk-free rate \(r_t\) at time t is such that the aggregate net worth of the entrepreneurs equals their total capital and bond holdings, that is,

$$\begin{aligned}{} & {} \underbrace{\sum _{Z}\int _{0}^{\infty }n\pi (t,n,Z)dn}_{=N_t} =\underbrace{\sum _{Z}\int _{0}^{\infty }\hat{k}(n,Z)\pi (t,n,Z)dn}_{=K_{t}}\nonumber \\{} & {} \quad +\underbrace{\sum _{Z}\int _{0}^{\infty }\left( n-\hat{k}(n,Z)\right) \pi (t,n,Z)dn}_{=B_{t}}. \end{aligned}$$
(17)

Similarly, as we show in Appendix A.3, the aggregate labour supply satisfies

$$\begin{aligned} \sum _{Z}\int _{0}^{\infty }Z\pi (t,n,Z)dn=\sum _{Z}Z\frac{\lambda _{Z}}{\lambda _{Z}+\lambda _{\bar{Z}}}=L, \text { } \forall t\ge 0. \end{aligned}$$
(18)

Steady state In the steady state, the public debt level is such that Eq. (15) equals zero:

$$\begin{aligned} B=\frac{w\tau _{l}L+(R-\delta )\tau _{k}K-G}{(1-\tau _b)r}, \end{aligned}$$
(19)

where B, w R, K, r (without time subscripts) denote the steady-state levels of debt, wage, return on capital, aggregate capital, and interest rate.

Equipped with this equation, we can now characterize the system of Fokker–Plank (FP) Equations, whose solution pins down entrepreneurs’ net worth stationary distribution, denoted as \(\lim _{t\rightarrow \infty }\pi (t,n,Z):=\pi (n,Z)\). The following proposition summarizes the result.

Proposition 2

(Stationary density) The stationary net worth distribution of an entrepreneur with labour and net worth endowment (n, Z) satisfies the following FP equation:

$$\begin{aligned} \mathbb {\mathcal {L}}^{*}\pi (n,Z)+\lambda _{\bar{Z}}\bar{\pi }(n,\bar{Z})-\lambda _{Z}\pi (n,Z)=0 \end{aligned}$$
(20)

where \(\bar{\pi }(n,\bar{Z})\) is the density of an entrepreneur with the same net worth and net worth endowment \(\bar{Z}\), and \(\mathcal {L}^{*}\) is the so-called “adjoint" operator:

$$\begin{aligned} \mathbb {\mathcal {L}}^{*}\pi= & {} -\frac{\partial }{\partial n}\left[ \pi \left( nr+wZ\left( 1-\tau _{l}\right) -\hat{c}+\hat{k}\left( \left( 1-\tau _{k}\right) \left( R-\delta \right) -\left( 1-\tau _{b}\right) r\right) \right) \right] \\{} & {} +\frac{1}{2}\frac{\partial ^{2}}{\partial n^{2}}\left( \pi \hat{k}^{2}\sigma ^{2}\right) , \end{aligned}$$

inputting the steady-state risk-free rate and factor prices, r, w, and R.

Proof

See appendix A.2. \(\square \)

Propositions 1 and 2 and Definition 1 characterize the competitive equilibrium’s steady state as a forward-backward PDE system, consisting of two HJBEs (Eq. (12)) and two FPEs (Eq. (20), which interact through the market clearing conditions in Eqs. (17)−(19). Factor prices (i.e., R and w) are given by the firms’ optimal strategies in Eqs. (3) and (4).

We highlight that the equilibrium characterization has similarities with those of the so-called Mean-Field Games (MFGs) introduced by [27]. In particular, as in MFGs, the equilibrium is the solution to a fixed-point problem in which entrepreneurs’ optimal strategies (and the corresponding prices) are such that the distribution of their future individual states matches that of the overall population. An essential difference with the MFG literature is that the coupling between HJBE and FP equations does not occur through the entrepreneurs’ utility (or cost) function but through the market clearing condition.

Another aspect that we would like to stress is that, as explained in [1] (see Online Appendix C.5), the existence and uniqueness results developed in the MFGs literature do not apply to the backwards-forward system describing the competitive equilibrium in our model. More specifically, this happens because the Hamiltonian operator implicit in Eq. (12),

$$\begin{aligned}{} & {} H(n,Z,v,\bar{v},p,M)\\{} & {} \quad =\sup _{(c,k)\in A}\left\{ \begin{array}{l} u(c)+\lambda _Z \bar{v}-\left( \rho +\lambda _{Z}\right) v+\frac{Mk^{2}\sigma ^{2}}{2}+\\ +p\left\{ nr+wZ\left( 1-\tau _{l}\right) -c+k\left[ \left( 1-\tau _{k}\right) \left( R-\delta \right) -\left( 1-\tau _{b}\right) r\right] \right\} \end{array}\right\} \end{aligned}$$

is not additively separable in p and \(\pi \). This happens because, in equilibrium, r, w, R are all functions of the entrepreneurs’ net worth distribution. A comprehensive discussion of the existence and uniqueness of mean-field games solutions can be found in [12].

3.5 Calibration and numerical solution of the equilibrium

Being unable to characterize the equilibrium further analytically, we resort to numerical methods. In this section, we calibrate the model’s parameters and present a sketch of the algorithm adopted to approximate its solution.

We summarize the system whose solution we seek to approximate in the following remark.

Remark 1

(Equilibrium system) The solution of the following system characterizes the steady-state competitive equilibrium of the economy:

$$\begin{aligned} {\left\{ \begin{array}{ll} u(c)+\mathcal {L}^{(c,k)}v(n)+\lambda _{Z}\left( \bar{v}-v\right) -\rho v=0,\\ u(\bar{c})+\mathcal {L}^{(\bar{c},\bar{k})}\bar{v}(n)+\lambda _{\bar{Z}}\left( v-\bar{v}\right) -\rho \bar{v}=0,\\ c=\left( \partial v/\partial n\right) ^{-1/\gamma },\\ \bar{c}=\left( \partial \bar{v}/\partial n\right) ^{-1/\gamma },\\ k=\min \left\{ -\left( \frac{\partial v}{\partial n}/\frac{\partial ^{2}v}{\partial n^{2}}\right) \left( \left( 1-\tau _{k}\right) \left( R-\delta \right) -\left( 1-\tau _{b}\right) r\right) /\sigma ^{2},n\right\} ,\\ \bar{k}=\min \left\{ -\left( \frac{\partial \bar{v}}{\partial n}/ \frac{\partial ^{2}\bar{v}}{\partial n^{2}}\right) \left( \left( 1-\tau _{k}\right) \left( R-\delta \right) -\left( 1-\tau _{b}\right) r\right) /\sigma ^{2},n\right\} ,\\ \mathbb {\mathcal {L}}^{*}\pi +\lambda _{Z}\left( \bar{\pi }-\pi \right) =0,\\ \mathbb {\mathcal {L}}^{*}\bar{\pi }+\lambda _{\bar{Z}}\left( \pi -\bar{\pi }\right) =0,\\ \int _{0}^{\infty }n\left( \pi +\bar{\pi }\right) dn=K+\frac{w\tau _{l}L+(R-\delta )\tau _{k}K-G}{(1-\tau _{b})r},\\ Z\lambda _{\bar{Z}}+\bar{Z}\bar{\lambda }_{Z}=L\left( \lambda _{Z}+\lambda _{\bar{Z}}\right) ,\\ K=\int _{0}^{\infty }\left( k\pi +\bar{\pi }\bar{k}\right) dn,\\ R=\alpha A\left( K/L\right) ^{\alpha -1},\\ w=\left( 1-\alpha \right) A\left( K/L\right) ^{\alpha }. \end{array}\right. } \end{aligned}$$
(21)

equipped with the boundary conditions detailed below.

Boundary conditions and numerical algorithm As a first step to solve the model, we approximate numerically the solution(s) of the entrepreneurs’ HJBE(s). These are second order non-linear ODEs, each requiring two boundary conditions.

Our algorithm applies an implicit upwind scheme (details appear in [11]) over a uniformly-spaced grid \(\left[ n_{1},n_{2},...,n_m,...,n_{M-1},n_{M}\right] \) to find \(\nu (n_{m},Z)\approx v(n,Z)\), imposing boundary conditions at \(n_{1}=0\) and \(n_{M}=\infty \). We approximate \(n_{M}=\infty \) by using a large but finite constant.

To obtain the first set of boundary conditions, we use the fact that when entrepreneurs’ net worth is large, their labour income becomes negligible relative to their net worth. Accordingly, when \(n\rightarrow n_{M}\), entrepreneurs’ value function can be written as \(v(n,Z)=v_{0}+v_{1}\log n_{M}\), for some unknown constants \(v_{0}\) and \(v_{1}\), implying that

$$\begin{aligned} \frac{\partial v}{\partial n}(n_{M},Z)=v_{1}(n_M)^{-1} \text { for } Z\in \left\{ 1,z\right\} . \end{aligned}$$
(22)

By substituting Eq. (22) in Eq. (14) and rearranging, one gets that

$$\begin{aligned} \frac{\partial ^{2}v}{\partial n^{2}}(n_M,Z)=-\frac{1}{n_M}\frac{\partial v}{\partial n}(n_M,Z). \end{aligned}$$
(23)

Imposing that \(n\le n_M\) to the drift of Eq. (7) we get that

$$\begin{aligned} c(n_{M},z)\ge rn_{M}(1-\tau _{b})+n_{M}\frac{\left[ \left( R-\delta \right) (1-\tau _{k})-(1-\tau _{b})r\right] ^{2}}{\sigma ^{2}}+Zwl(1-\tau _{l}). \end{aligned}$$
(24)

Substituting Eq. (24) in Eq. (13) and rearranging delivers the boundary conditions

$$\begin{aligned} \frac{\partial v}{\partial n}(n_{M},Z)=\left( rn_{M}(1-\tau _{b})+n_{M}\frac{\left[ \left( R-\delta \right) (1-\tau _{k}) -(1-\tau _{b})r\right] ^{2}}{\sigma ^{2}}\right) ^{-1}, \text { for } Z\in \left\{ 1,z\right\} . \end{aligned}$$

We find the remaining boundary conditions by using that, when \(n=0\), then \(k=0\) and \(c(0,Z)\le Zw\), which implies

$$\begin{aligned} \frac{\partial v}{\partial n}(0,Z)=c(0,Z)^{-1}=\left( Zw\right) ^{-1} \text { for } Z\in \left\{ 1,z\right\} . \end{aligned}$$
(25)

Having found the numerical solution to the HJBEs, that of the associated FPs come “for free". To derive it, we use an initial guess and apply the adjoint operator obtained by transposing the matrix containing the numerical solution of the HJBE (see [1] for details). As discussed in the same paper, the finite-difference up-wind scheme satisfies the so-called [5] conditions under which the numerical approximation of each PDE converges to its (unique) viscosity solution.

In practice, we compute the equilibrium’s approximation by implementing the steps summarized in Algorithm 1.

Algorithm 1
figure a

(Equilibrium approximation)

Full size image

Parametrization The baseline parameterization appears in Table 1. The subjective discount rate \(\rho =0.04\), the capital share \(\alpha =0.36\), the capital depreciation rate \(\delta =0.025\), and the relative risk aversion \(\gamma =1\) are set to standard values in the macroeconomic literature. Total factor productivity A is normalized to one. Tax rates \(\tau _k=\tau _b=0.23\) and \(\tau _l=0.34\) take values in line with the averages across OECD countries. Consistently with [25], the idiosyncratic volatility of capital depreciation equals \(\sigma =0.2\).

Table 1 Model calibration
Full size table

We set the labour-endowment transition rates \(\lambda _1=0.04\) and \(\lambda _z=0.12\) getting a 75% share of the population in the state \(Z=1\) and an auto-correlation of 0.84. In line with [17], we set the low-state income-shock parameter to \(z=0.65\) to generate a variability of the labour endowment process of 15 per cent. These parameters imply a (constant) aggregate labour supply of \(L=0.913\). Finally, we set the public expenditure level to match the 2022 US debt-to-GDP ratio in the steady state (around 130%).

4 Numerical results

In this section, we first compare the numerical solution of the baseline model, with the parameters in Table 1, with that of a benchmark economy with no capital risk, as in [17], and the same debt-to-GDP level.Footnote 7 Then, we investigate the effect of changing the tax mix between capital, bonds, and labour on entrepreneurs’ net worth distribution and welfare. Finally, we discuss the impact of the different tax policies in the short and long run.

4.1 Capital risk, allocations, and net worth distribution

Our first observation when comparing baseline and benchmark models is that, in the aggregate, introducing capital risk reduces capital accumulation and, in turn, the economy’s output. The result is evident from Table 2, which reports the key macroeconomic aggregates of the two economies’ steady states.

Table 2 Macroeconomic aggregates (Panel A) and sub-aggregates (Panel B) in the benchmark and the baseline models with capital risk
Full size table

The outcome materializes because idiosyncratic capital risk discourages capital investments in favour of bonds. Since labour supply is fixed, lower capital levels depress wages, making entrepreneurs relatively poorer. This result starkly contrasts with what happens when introducing labour income risk, which always increases the aggregate capital stock by fostering agents’ precautionary motive (see for instance [28]).

In the model with capital risk, the opposite happens because entrepreneurs can mitigate their exposure to additional idiosyncratic (capital) risk by lowering consumption and reducing the risk of their financial assets holdings. In line with these intuitions, our simulation shows that safe asset demand grows in relative terms (see Table 4, Panel B) and, as a consequence, its return lowers (from 5.15 to 4.05%). Risky capital entails a rental rate of \(R=8.76\%\) and, as a result, a positive risk premium \(R-\delta -r\) of about 2%, which is a crucial determinant of entrepreneurs’ asset allocation strategies. Due to these outcomes, output and, thus, wages also decrease.

Our second (and main) result is that introducing capital risk increases net worth inequality relative to the benchmark economy. Coherently, the stationary net worth distribution displays a fatter right tail and a larger share of financially constrained entrepreneurs. To display this phenomenon, Table 3 reports different quantiles (\(q_j\)) of the entrepreneurs’ net worth distribution, the Gini coefficient, and the share of financially constrained entrepreneurs, conditional (\(\mathcal {G}_Z\) and \(\Pi _Z\)) and unconditional (\(\mathcal {G}\) and \(\Pi \)) on Z. Indeed, in the presence of capital risk, the share of constrained entrepreneurs increases to 1.60%, up from 0.65% in the benchmark. Likewise, the Gini coefficient grows from 0.37 to 0.64. Accordingly, the lower quantiles decrease while the upper quantiles sharply increase.

To understand why this happens, we analyse the heterogeneous response of consumption and asset allocation policies at the different net worth levels. The four panels of Fig. 1 compare the numerical approximation of the entrepreneurs’ optimal consumption functions (solid lines) and their consumption as a share of average income, denoted as I(n, Z), (dotted lines) in the benchmark and in the baseline models.Footnote 8 The shaded areas report the associated net worth stationary densities. Blue and red lines describe policies and distributions of entrepreneurs whose labour endowment Z equals 1 and z, respectively.

Table 3 Summary statistics of the stationary net worth distribution in the benchmark and baseline model economy for different levels of capital risk \(\sigma \)
Full size table
Fig. 1
figure 1

Numerical approximations of entrepreneurs’ optimal consumption levels and consumption-to-income ratios (lines) and net worth distributions (shaded areas) in the baseline model with capital risk (dark, solid) and in the benchmark model (light, dotted). Blue and red lines depict optimal policies when Z equals 1 and z, respectively

Full size image
Fig. 2
figure 2

Numerical approximations of entrepreneurs’ labour income as a share of net worth and instantaneous total (i.e., financial plus labour) income (solid lines) and net worth distributions (shaded areas) in the baseline model with capital risk. Blue and red lines depict labour income shares when Z equals 1 and z, respectively

Full size image

Analysing the figure, we notice that capital risk hinders absolute consumption level for low-net-worth entrepreneurs but increases it among higher-net-worth ones, independently of their labour endowment. This pattern takes place for the following reasons.

As shown in Fig. 2, which plots real wages as a share of total income, low-net-worth entrepreneurs earn most of their income from labour. Capital risk depresses wages, fostering their precautionary motives and thus curbing their consumption. Quite the opposite, high-net-worth entrepreneurs earn their income primarily from holding financial assets. Therefore, they benefit from the increase in the average financial return relative to the benchmark case, which allows them to increase consumption in absolute terms while reducing it as a share of their income. As mentioned above, these forces make the overall economy poorer (i.e., lower aggregate capital K and bonds B) and net worth more unevenly distributed across agents.

Fig. 3
figure 3

Numerical approximations of entrepreneurs’ capital and bond holdings levels and shares (lines) and net worth distributions (shaded areas) in the baseline model. Blue and red lines depict optimal holdings when entrepreneurs’ labour endowment Z equals 1 and z, respectively

Full size image

A key feature worth stressing is that including capital risk in the model entails an asset allocation decision for the entrepreneurs on top of their consumption-saving strategies. Figure 3 displays the cross-section of optimal allocations between risky capital and risk-less bonds for high- and low-labour endowment entrepreneurs. Notably, their asset allocation depends crucially on their net worth levels. More specifically, capital holdings levels increase monotonically with entrepreneurs’ net worth (Panel (a)). However, the same does not hold in relative terms (Panel (b)). In other words, low-net-worth enterprises allocate a more significant share (if not all) of their net worth into capital. Conversely, high-net worth entrepreneurs tilt their holdings towards riskless bonds (see Panels (c) and (d)); the more, the higher their net worth (and labour) endowment.

This perhaps counter-intuitive pattern is in line with classical household finance models (see, e.g., [14]). It depends crucially on the fact that, as already pointed out, low-net-worth entrepreneurs earn much of their income from labour, and that labour endowment and capital shocks are independent. Since smaller entrepreneurs have a higher propensity to consume and capital earns a positive premium over bonds, they are willing to invest their whole net worth into risky assets to earn (in expectation) higher returns on their savings \((\hat{k}(n,Z)+\hat{b}(n,Z))\). Although risky, capital allows them to diversify labour income shocks since capital depreciation and wage fluctuations are uncorrelated. Moreover, their financial wealth is a relatively small share of their total one (i.e., financial net worth, n, plus human capital, H(Z)).Footnote 9

To further rationalize this last point, Fig. 4 shows that, indeed, entrepreneurs’ capital holdings relative to total wealth are increasing in n. This result can be shown to hold for most parametric combinations.

Fig. 4
figure 4

Numerical approximations of capital-to-total net worth holdings (lines) and net worth distributions (shaded areas) in the baseline model. Blue and red lines depict optimal holdings when entrepreneurs’ labour endowment Z equals 1 and z, respectively

Full size image

Another relevant aspect is that low-net-worth entrepreneurs have a particularly volatile financial endowment due to their asset allocation, which helps us explain why the share of financially constrained entrepreneurs increases with capital risk. Conversely, when entrepreneurs have a higher net worth, their marginal utility of consumption decreases. Moreover, they start investing in bonds above a certain wealth threshold level, which depends on the parameters of the labour endowment process. They do this to hedge their net worth fluctuations due to financial holdings because they constitute a large share of their overall wealth.

In other words, wealthy entrepreneurs are more “financially sophisticated" because they depend less on their future wages. A lower consumption share and a less volatile financial income generate higher capital accumulation for higher-income individuals. Consequently, the distribution of wealth in the presence of capital risk exhibits fatter tails.

The considerations about the increased inequality in distribution carry over to the net worth distribution within high- or low-labour-income entrepreneurs. However, it is worth noting that the distribution of overall wealth across types is almost unaffected by capital risk.

Capital risk level: comparative statics To further explore the effect of introducing capital risk, Tables 3 and 4 compare macroeconomic aggregates and relevant distribution statistics in the steady state for different levels of capital risk \(\sigma \).

Fig. 5
figure 5

Numerical approximations of entrepreneurs’ optimal consumption (lines) and net worth distributions (shaded areas) in the model with capital risk for higher (solid) and lower (dotted) levels of \(\sigma \). Blue and red lines depict optimal policies when Z equals 1 and z, respectively

Full size image
Fig. 6
figure 6

Numerical approximations of entrepreneurs’ optimal capital and bond holdings (lines) and net worth distributions (shaded areas) in the model with capital risk for high (solid) and low (dotted) capital risk levels. Blue and red lines depict optimal policies when Z equals and z

Full size image
Table 4 Macroeconomic aggregates (Panel A) and sub-aggregates (Panel B) in the benchmark and the baseline models for different levels of \(\sigma \)
Full size table

Coherently with our main result, lower capital risk levels mitigate wealth inequality while fostering capital accumulation and wages, thereby reducing entrepreneurs’ hedging motives and, in turn, the risk-free interest rate. Indeed, capital holdings increase in the aggregate and as a share of financial net worth across all the percentiles of the net worth distribution. Figure 6, which compares the numerical approximation of entrepreneurs’ optimal asset allocations across net worth levels for \(\sigma =0.15\) and 0.2, visualizes the outcome in the cross-section. As a result of these forces, as intuition suggests, risk premiums are overall decreasing with \(\sigma \).Footnote 10

Reductions in the risk premium bear essential implications on the net worth distribution because high-net-worth entrepreneurs accumulate less net worth in relative terms. Consequently, the overall distribution becomes less concentrated, and the median entrepreneur’s wealth increases by about 45%, moving from \(\sigma =0.25\) to \(\sigma =0.15\) (see Table 3). In particular, when \(\sigma \) decreases, capital holdings are less concentrated across (financial) net worth levels. Accordingly, a larger share of entrepreneurs holds their whole net worth in risky capital, a share that decreases only for high(er) net worth percentiles. High-income earners hold more capital but less overall savings as capital risk decreases.

When looking at the cross-section of entrepreneurs’ consumption levels, reported in Fig. 5, Panels (a) and (c), lower capital risk mitigates precautionary motifs among low-net-worth individuals, who consume more in levels and as a share of their income. However, wealthier individuals consume less in relative terms. The mechanisms explaining these results are those discussed when comparing baseline and benchmark models with no capital risk. Due to these effects, reducing capital risk boosts output and government debt in the aggregate.

A compelling non-monotonicity result is that the percentage of financially constrained entrepreneurs increases relatively to the baseline when \(\sigma =0.20\) but decreases when \(\sigma =0.25\). This outcome is due to the following forces. First, higher levels of \(\sigma \) reduce aggregate capital accumulation and thus wages, making low-net-worth entrepreneurs more exposed to financial assets’ fluctuations and, in turn, more willing to buy bonds and less to consume. Lower consumption rates (wages) affect the share of financially-constrained entrepreneurs positively (negatively). Second, higher \(\sigma \)s increase entrepreneurs’ net-worth volatility, especially among low-net-worth ones. At the same time, increasing \(\sigma \) generates higher risk premiums by raising expected returns on risky assets and reducing those on bonds, which reduces the share of financially constrained enterprises. The overall effect of changing \(\sigma \) depends non-trivially on which of these different effects dominate.

4.2 Fiscal policy

We now explore how fiscal policy affects the competitive equilibrium in the long run. In particular, we numerically evaluate the effects of changing the tax mix between financial assets (i.e., capital vs. bonds) and labour income and financial assets. In a first simulation, we let the tax rate on risky capital \(\tau _k\) (plus/minus three percentage points) vary and keep the labour tax rate \(\tau _l\) fixed, adjusting \(\tau _b\) to hold tax revenues T constant. We then evaluate a second policy, which changes \(\tau _l\) by the same magnitude while adjusting the tax rate across all financial assets \(\tau _k=\tau _b\) to keep T constant.

Capital vs bond taxes The aggregate effect of changing the financial asset tax mix is relatively straightforward. Panel A of Table 5 reports the macroeconomic aggregates for different tax mixes. Lowering (increasing) risky capital taxes fosters (curbs) capital accumulation, thereby reducing (increasing) its rental rate and fostering (decreasing) wages. At the same time, a lower (higher) demand for safe assets pushes up (down) the risk-free rate. As a result of these forces, following a decrease in capital taxes, the “raw" risk premium \((R-\delta -r)\) decreases (increases) by about 0.81 (0.54) percentage points (see Table 4). However, the tax-adjusted risk premium \(((R-\delta )(1-\tau _k)-r(1-\tau _b))\) increases (decrease) by 0.04 (0.15) percentage points.

The other significant effect of redistributing taxes from risky capital to risk-free bonds (or vice versa) is to reduce (increase) net worth inequality, as shown in Table 6 (Panel A), reporting summary statistics of the net worth distribution. The mechanism behind this result is two-fold.

First, the policy reduces the mass of financially constrained entrepreneurs because labour wages increase. Indeed, the consumption-to-income ratios across the whole population are lower, as Fig. 7, Part (A), Panels (b) and (d) portrays.Footnote 11 Second, higher tax-adjusted risk premiums encourage capital investment across a larger share of entrepreneurs and curb their hedging demand for bonds (see Fig. 7, Part B, Panels (c) and (d)). However, tax adjustments penalise net worth accumulation for high net-worth individuals who invest heavily in bonds, leading to a thinner right tail of the distribution.

Fig. 7
figure 7

Numerical approximations of entrepreneurs’ optimal consumption (Part (A)) and capital holdings (Part (B)) (solid lines) and net worth distributions (shaded areas) in the baseline model with capital risk for different financial asset tax policies. Blue and red lines depict strategies of entrepreneurs with labour endowment Z and 1 and z, respectively

Full size image
Table 5 Macroeconomic aggregates for different mixes of capital vs bonds taxes (Panel A) and human vs financial capital taxes (Panel B)
Full size table

Human vs financial capital taxes Similarly to the previous policy, substituting capital with labour income taxes has a positive effect on net worth and capital accumulation and, in turn, output (see Fig. 8, Part (B), and Table 5, Panel B). The reason is that, by redistributing taxes from capital to labour (and vice versa), the latter yields higher (lower) returns (Table 5, Panel (B), Columns 5 and 6). Indeed, both gross and net wages increase. Coherently, the gross return on risky capital decreases (increases) with labour taxes. In this case, the net tax-adjusted risk premium lowers (from 1.70 to 1.21%), and investing in risky capital becomes relatively less attractive. At the same time, however, the net tax-adjusted risky capital returns remain unchanged at 4.80%.

In summary, Fig. 8 shows that these forces drive entrepreneurs to invest less (more) in capital and to behave more (less) carefully, reducing their consumption-to-income ratios across the whole net worth distribution. Notice that consumption increases for all agents but for the poorest. Since the stock of risk-less debt changes only slightly in equilibrium (2.63 to 2.58), while savings increase, the stock of risky capital going to firms increases by almost 15%.

The combined effect of higher wages and more diversified asset allocations leads to an overall decrease in the Gini coefficient of about three percentage points (see Table 6, Panel B). Notably, the distributional effects of the policy redistributing taxes from financial to human capital are much larger than the ones involving only financial assets.

Fig. 8
figure 8

Numerical approximations of entrepreneurs’ optimal consumption (Panel (A)) and capital holdings (Panel (B)) (solid lines) and net worth distributions (shaded areas) in the baseline model for different human vs financial capital taxes. Blue and red lines depict strategies of entrepreneurs with labour endowment Z and 1 and z, respectively

Full size image
Table 6 Summary statistics of the stationary net worth distribution for different mixes of capital vs bonds taxes (Panel A) and human vs financial capital taxes (Panel B)
Full size table

4.3 Welfare

Long-run We now investigate the long-run welfare effects of the tax policies introduced in Sect. 4.2. To do that, we follow [30] and compute entrepreneurs’ consumption-equivalent welfare gains/losses in the steady-state. In other words, we compute the additional consumption share \(\Omega \) that an entrepreneur should get to obtain the same value she obtains after the policy p; that is,

$$\begin{aligned}{} & {} \mathbb {E}_{0}\left[ \int _{0}^{\infty }e^{-\rho t}\frac{\left( \hat{c}_{t}\left( 1+\Omega \right) \right) ^{1-\gamma }}{1-\gamma }dt\right] =\left( 1+\Omega \right) ^{1-\gamma }\underbrace{\mathbb {E}_{0}\left[ \int _{0}^{\infty }e^{-\rho t}\frac{\hat{c}_{t}^{1-\gamma }}{1-\gamma }dt\right] }_{=v(n,Z)}\\{} & {} \quad =\underbrace{\mathbb {E}_{0}^{p}\left[ \int _{0}^{\infty }e^{-\rho t}\frac{\left( \hat{c}_{t}^{p}\right) ^{1-\gamma }}{1-\gamma }dt\right] }_{=v^{p}(n,Z)}, \end{aligned}$$

and thus

$$\begin{aligned} \Omega (n,Z)=\left( \frac{v^{p}(n,Z)}{v(n,Z)}\right) ^{\frac{1}{1-\gamma }}-1, \end{aligned}$$

where v(n, Z) and \(v^p(n,Z)\) denote the value functions (see Eq. (9)) of an entrepreneur with net worth n and labour endowment Z before and after the implementation of the \(p-\)policy.Footnote 12

To further simplify exposition, we aggregate welfare gains/losses across entrepreneurs with different labour endowment by using their net worth densities, and simply reportFootnote 13:

$$\begin{aligned} {\text {Consumption-equivalent welfare (\%)}}:=\sum _{Z} \Omega \left( n,Z\right) \frac{\pi \left( n,Z\right) }{\pi \left( n,Z\right) +\bar{\pi }\left( n,\bar{Z}\right) }. \end{aligned}$$
(26)

We display the outcome of our analysis in Fig. 9. The solid blue lines depict long-run consumption-equivalent welfare gains/losses (in percentage points) of different fiscal policies across net worth levels. Blue and red shaded areas highlight gains (blue) and losses (red) in the associated stationary density mass. We begin the discussion by focusing on the effects of taxing risky capital vs risk-free bonds (Panels (a) and (b)).

Fig. 9
figure 9

Solid blue lines depict consumption-equivalent welfare gains (in \(\%\)) of the different fiscal policies analyzed in Sect. 4 in the long run for the different net worth levels. Blue and red shaded areas denote gains (blue) and losses (red) in the associated stationary density mass. Red dashed lines highlight the zero thresholds telling welfare gain from losses

Full size image

Our simulations show that reducing risky capital taxes at the expense of bonds produces absolute welfare gains across all entrepreneurs (Panel (a)). Conversely, the effects of the complementary policy differ substantially, generating moderate benefits for high-net-worth enterprises and significant losses among low-net-worth ones (Panel (b)). This happens because low-net-worth entrepreneurs allocate most of their financial net worth to capital, and wealthier ones allocate an increasingly high share of their holdings in bonds, which gives them a tax advantage under this second policy.

Panels (c) and (d) of Fig. 9 display the welfare effect of financing tax cuts on capital (labour) by raising taxes on labour (capital). Lowering capital taxes generates more significant welfare gains (1 to 5 per cent of equivalent consumption units) relative to the previous policy across most individuals, except for the poorest ones. Lowering labour taxes has smaller (about 0.5 percentage points maximum) but more uneven outcomes, with positive (negative) effects across high- and low-net-worth entrepreneurs. Interestingly, both policies affect agents non-linearly, benefiting (hurting) the extreme net worth levels the most. Finally, it is worth noticing that policies that reduce risky capital taxes reduce the mass of poorer agents and increase the mass of higher net-worth entrepreneurs. In contrast, the opposite policies have more nuanced effects, increasing the mass of small and medium-to-high net-worth entrepreneurs at the expense of highly wealthy ones.

Short vs long run So far, our analysis has examined how fiscal policies affect the economy in its steady state, i.e., in the long run. However, as highlighted by [17], the conclusions drawn from this approach may be misleading.

For this reason, we complement the long-run perspective provided in the previous section by evaluating policies in the short run. In practice, we consider the general equilibrium effect of tax changes by holding the wealth distribution constant, computing variations in individual entrepreneurs’ strategies, and letting prices adjust accordingly. The idea is that while agents can immediately change their behaviour, the wealth distribution takes time before adjusting.

Fig. 10
figure 10

Consumption-equivalent welfare gains (in \(\%\)) of capital vs bonds (Panel (a)) and human vs capital taxes (Panel (b)) in the short (dotted red) and long run (solid blue) for different net worth levels

Full size image
Table 7 Macroeconomic aggregates in the short and long run for different mixes of capital vs bonds taxes (Panel A) and human vs financial capital taxes (Panel B)
Full size table

We focus on the two policies which reduce risky capital taxation. Table 7 reports the macroeconomic aggregates in the short run, comparing them with the baseline ones (i.e., before the policy) and with the long-run (i.e., in the steady state).

When we focus on the policy that shifts the tax burden from capital to bonds, our simulation shows that the aggregates adjust close to their long-run ones very quickly (see Table 7, Panel A). However, relative welfare gains accrue in a very different manner in the short and in the long run, benefiting high- or low-net-worth entrepreneurs, respectively (Fig. 10, Panel (a)). The following two forces can explain the result.

First, high-n enterprises benefit immediately because tax-adjusted risk premiums shrink while bond returns, in which they allocate relatively more, increase in the short and long run. Second, low-n entrepreneurs initially benefit less because it takes time to accumulate net worth, moving to the right of the distribution, allowing them to enjoy higher bond returns and milder precautionary motives.

The effects of the fiscal policy decreasing taxes on financial income and increasing taxes on wages are in stark contrast with the previous policy (see Fig. 10). Notably, macroeconomic aggregates feature substantially different (and non-monotonic) responses in the short and long run (see Table 7, Panel B). In particular, government bond supply, risk-free rates, and debt-to-GDP ratios shrink in the short but rise in the long run. Conversely, wages, capital stock, and returns increase monotonically but only gradually.

As a result of these dynamics, welfare gains (losses) accrue more to high (low) net-worth individuals in the short run than in the long run. This happens because, while expected financial returns for low-net-worth individuals decrease both in the short and the long run, real wages initially decrease by 2.5% but then recover in the long run, increasing in equilibrium after the policy, even though just slightly. Moreover, tax-adjusted risk premiums benefit wealthier enterprises, growing by about 0.24 percentage points before gradually reducing by roughly the same amount below their initial level in the long run.

5 Conclusions

We have developed and solved numerically a continuous-time model of a production economy where entrepreneurs face leverage constraints, uninsurable labour endowment and capital depreciation risk.

We show that capital risk curbs aggregate capital accumulation and, in turn, output and wages while increasing wealth inequality. The reason is that entrepreneurs with limited net worth, relying on wages, aim for higher returns through capital investment, leveraging a natural hedge against depreciation risks. In contrast, high-net-worth entrepreneurs, whose income depends on financial asset income, adopt sophisticated strategies, allocating a more significant share to risk-free bonds to hedge against capital risk. These contrasting approaches contribute to economic inequality by stabilizing net worth for the affluent and increasing volatility for those with less wealth and lower wages, subject to tighter financial constraints.

We then analyze the effect of fiscal policy on entrepreneurs’ inequality and welfare in the presence of capital risk. Reducing taxes on risky assets diminishes the proportion of financially constrained individuals and mitigates net worth inequality by increasing real wages and risk premiums. The welfare gains from this policy are immediate for high-net-worth individuals and long-term for low-net-worth individuals, as the former requires time to accumulate additional net worth. Shifting taxes from financial to human capital benefits high-net-worth entrepreneurs while impairing low-net-worth individuals’ consumption but generates more significant wealth inequality reductions.

While the joint presence of uninsurable capital risk and government debt is novel in the literature, our study has some limitations, which we acknowledge. First, we do not allow entrepreneurs to choose their labour supply endogenously (as, for example, in [28]), which may have significant policy implications. Second, our welfare analysis focuses on a “static" comparison between its short- and long-run effects. Since our results hint at non-monotone adjustments between steady states, an interesting extension would be to characterize the full transition dynamics, taking the whole path while evaluating welfare gains and losses. Third, we do not consider the role of aggregate capital risk as, for instance, in [21]. We leave these extensions to future research.