Modelling the industrial production of electric and gas utilities through the $CIR^3$ model

Abstract

This work aims to extend previous research on how a trifactorial stochastic model, which we call $CIR^3$, can be turned into a forecasting tool for energy time series. In particular, in this work, we intend to predict changes in the industrial production of electric and gas utilities. The model accounts for several stylized facts such as the mean reversion of both the process and its volatility to a short-run mean, non-normality, autocorrelation, cluster volatility and fat tails. In addition to that, we provide two theoretical results which are of particular importance in modelling and simulations. The first is the proof of existence and uniqueness of the solution to the SDEs system that describes the model. The second theoretical result is to convert, by the means of Lamperti transformations, the correlated system into an uncorrelated one. The forecasting performance is tested against an ARIMA-GARCH and a nonlinear regression model (NRM).

1 Introduction

Further to previous research [13], in this article, we illustrate a stochastic model to forecast changes in the industrial production (and then market demand) of electric and gas utilities. The examined time series is highly irregular and difficult to predict, with maximum volatility reaching up to 800%, as shown in Fig. 1 and Table 1. Therefore, we have considered a three-factor model [16, 17] and extended it to fit the current case, incorporating a number of changes described in this paper.

In his work, Chen suggested a bond pricing formula ”under a non-trivial, three-factor model of interest rates” [16] where the future short rate ”depends on (1) the current short rate, (2) the short-term mean of the short rate, and (3) the current volatility of the short rate”. In addition, Chen assumed that ”both the short-term mean and the volatility are stochastic”. The rationale of his model lies in the observation that ”short rates should be better modelled as reverting to a short-run mean, rather than to a long-run constant mean”. Similarly, Chen observed that short-rate volatility is not constant and mean reverting as well.

Stochastic models, such as the one proposed by Chen, are designed to replicate short-term interest rates $r_t$, along with their mean $\theta _t$ and volatility $v_t$, for pricing purposes. However, in the case under consideration, our objective is to forecast changes in industrial production. Therefore, we replace interest rates with the production of electric and gas utilities, denoted by $S_t$, and we use $\theta _t$ and $v_t$ to represent its short-term mean and volatility, respectively. Furthermore, we link the processes $S_t$, $\theta _t$, and $v_t$ together through correlations, which is a crucial novelty in our approach. Finally, our approach differs from the literature cited because we do not model the short-term mean $\theta _t$ as a Cox–Ingersoll–Ross process [19] due to the stochastic volatility coefficient that depends on $v_t$.

Our first achievement is an existence and uniqueness result for the solution of the system of stochastic differential equations (SDEs) describing our three-factor model (see Theorem 4.1 and Corollary 4.2 below). To our knowledge, this issue has never been discussed before. Our system of SDEs does not satisfy the classical local Lipschitz condition hence we can not apply well known results of the (global) existence and uniqueness of the solution. For this reason, we first discuss existence in a weak sense (see, for instance, Chapter 4 in [36] or Chapter 5 in [25]), where the probability space and Brownian motions are not fixed a priori but they are part of the solution itself. For the unidimensional CIR model where mean and volatility coefficients are positive constants, the well-known Feller’s condition implies that a CIR process starting from a positive initial point stays strictly positive (see, Section 6.3.1 in [37]). This implies that in our model the volatility $v_t$ is a non-explosive strictly positive process under Feller’s condition. While, even if starting from positive initial points $S_t$ and $\theta _t$, due to their unbounded stochastic volatility $v_t$, hit zero almost surely. Nevertheless, we prove that our model is well defined in a local sense, that is, in terms of a unique weak solution until $\tau = \tau ^S \wedge \tau ^\theta$, where $\tau ^S$ and $\tau ^\theta$ denote the first hitting times of zero for $S_t$ and $\theta _t$, respectively.

Finally, by Theorem 1.1, Chapter 4 in [36] or Corollary 3.2.3, Chapter 5 in [58], (local) weak existence and pathwise uniqueness of a (strict positive) solution implies also (local) strong existence.

As well as in [13], by using the Lamperti transformation, which applies thanks to the strict positivity of $(S_t, \theta _t,v_t)$, we show how the correlated process $S_t$ can be turned into an uncorrelated auxiliary process $X_t$, which is important for simulations and forecasting. We give a rigorous proof of equivalence between the two systems of SDEs related to the dynamics of the triples $(S_t, \theta _t, v_t)$ and $(X_t, \theta _t, v_t)$.

Last but not least, we show that the proposed model accounts for several stylized facts such as the mean reversion of both the process and its volatility to a short-run mean, non-normality, cluster volatility and fat tails. This is because, by design, both the process and its mean are reverting, the volatility is time-dependent and the processes are correlated. A discussion on the choice of the model is provided and specific analysis is carried out on the time series of the industrial production of electric and gas utilities. Subsequently, the implementation shows that the proposed model provides the best fit for the data.

This paper is organized as follows. Section 2 provides the rationale for our quest on model selection and a brief account of the relevant literature. Section 3 shows the time series we are considering and its main statistical characteristics. In Section 4 the three-factor model is presented and the main results are provided (i.e. existence and uniqueness result and the presentation of the Lamperti transformations that lead to the new dynamics of the auxiliary process). Section 5 illustrates a numerical implementation in the following order: calibration, in-sample simulation, out-of-sample forecasts. The last Section contains the concluding remark.

2 Literature and model selection

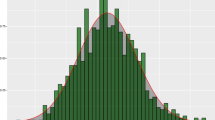
The reason why we thought of a three-factor model is that, as for the interest rates, the time series considered seems to adapt to some characteristics that are well explained by this model. Namely, the level of industrial production of electric and gas utilities, $S_t$, reverts to its mean $\theta _t$ which, in turn, is time-varying and reverting to a constant long-term mean. The distribution of $S_t$ is highly non-normal, displays fat tails (see Fig. 2), its volatility depends on time and seems to be mean reverting as well, as the interest rate’s volatility [44]. In other models volatility is represented either as an Ornstein–Uhlenbeck (OU) process [11, 54, 61] or as a log-normal process [11]. However, in the first case, volatility can take undesirable negative values (except for non-Gaussian Ornstein–Uhlenbeck (OU) processes [5]) and in the second, volatility has no mean reversion [16]. The Chen model, instead, simulates volatility with a square root process, with the advantage that it excludes negative values and allows mean reversion. Furthermore, the model can be designed in such a way as to correlate processes with each other and, as a by-product, this allows for autocorrelation. For reference, on autocorrelation for an OU process see [9] and on autocorrelation for geometric Brownian motion see [57].

As detailed in Sect. 3, both $S_t$ and $v_t$ are mean reverting. Consequently, another class of models that we have considered is the so-called autoregressive integrated moving average (ARIMA) adopted for example by Chavez et al. [15] to simulate and predict future energy production and consumption in Asturias. Other examples of the use of ARIMA models for forecasting can be found in Shi et al. [59] for short-term wind power generation, in Jiang et al. [38] for China’s coal future consumption, in Mahia et al. [46] for industrial electricity consumption in Guangdong, etc. However, since we obtained unsatisfactory results in our simulations, we supplemented the classical ARIMA with a generalized autoregressive conditional heteroskedasticity (GARCH) to model clustering in volatility. Among those who tested the class of ARIMA-GARCH model, we mention Soares et al. [60] who modelled the hourly electricity load in the area covered by an electric utility located in southeastern Brazil. Gupta et al. [29] that implemented the ARIMA-GARCH for wind power prediction. Hussin et al. [35] who used the model for forecasting wind speed. Yotto et al. [64] that employed the ARIMA-GARCH for estimating and forecasting electricity load. Mohammadi et al. [50] who examined ”the usefulness of several ARIMA-GARCH models for modelling and forecasting the conditional mean and volatility of weekly crude oil spot prices” and Diallo et al. [22] who estimated the spread between Hungarian (HUPX) and German (EEX) day-ahead power prices. The latter, in their analysis, found out that NGARCH, TGARCH, EGARCH, GJR GARCH perform similarly in terms of RMSE and MAE. In addition, they claim that all models perform better than ”the simple ARIMA model” [22]. Finally, Bufalo and Orlando [13] have recently used the ARIMA-GARCH as a benchmark against the $CIR^3$ to predict the production of energy material. Thus, for the above mentioned reasons, we find the ARIMA-GARCH a popular and suitable reference model.

In our model’s selection, we also considered the following nonlinear regression model (NRM)

$$\begin{aligned} y = c_1 + c_2 e^{-c_3 x}. \end{aligned}$$

(1)

Eq. (1) is consistent with the expectations of the Ornstein–Uhlenbeck process and, in general, with the expectations coming from multifactor Hull–White model (e.g. G2++ by Brigo and Mercurio [11]), which are widely used in finance [20, 27, 52]. Nonlinear mean reversion in financial time series has been reported by many (e.g. see [4, 18, 28]). Among those that used nonlinear models for energy, we mention Bilgili et al. [7], Kumru et al. [40] and Noskov et al. [51]. To run a robust estimation we adopted the iteratively re-weighted least squares algorithm by Holland [33]. The algorithm recalculates the weights based on the residual from the previous iteration and progressively downweights outliers so that iterations continue until the weights converge.

In summary, drawing inspiration from the literature, ARIMA-GARCH and NRM are the two models used as benchmarks to test the performance of the proposed approach.

3 Data

Figure 1 displays the monthly percent change (i.e., the month-to-month variation in the industrial production) of electric and gas utilities, as classified by the North American Industry Classification System (NAICS) and represented by the IPUTIL index. The data was retrieved from the Federal Reserve Economic Data (FRED) [8]. As a side note, we would like to emphasize that while we model the IPUTIL time series level (i.e. $S_t$), the results displayed are in terms of percent change. This approach is chosen because percent changes are more challenging to model and may hold financial significance, as what matters most are the variations rather than the absolute levels.

Fig. 1

Board of Governors of the Federal Reserve System (US), Industrial Production: Electric and Gas Utilities (NAICS = 2211,2) [IPUTIL] [8]. Percent change. Monthly data from 1939-02-01 to 2020-11-01. Shaded grey areas correspond to recessions and the yellow strip to the right highlights the COVID-19 pandemic

3.1 Statistical characteristics

Regarding the model’s selection mentioned in Sect. 2, as shown in Fig. 2 and Table 1, not only the time series we are considering is very volatile, but its statistical characteristics are quite different from those of the Gaussian distribution.

Fig. 2

Q–Q plot of changes in Industrial Production: Electric and Gas Utilities (IPUTIL) along with a fitted polynomial curve (Polyfit) shows how the data deviates from a Gaussian distribution

Table 1 First four central moments for Industrial Production: Electric and Gas Utilities [IPUTIL] (changes)

3.2 Mean reversion and stationarity

Mean reversion contrasts with random walk behavior, which is used to support the efficient market hypothesis in theoretical studies in finance [10, 12, 26]. However, studies have found mixed or mean-reverting processes in both developed and emerging markets [2, 34, 55]. Mean reversion is used for modeling electricity and natural gas prices [1] because ”most energy and commodity markets exhibit mean-reversion” [56]. As mentioned by Hoque et al. [34], since the pioneering work of Lo and MacKinlay [45], variance ratio (VR) tests have been widely used econometric tools for testing the random walk hypothesis (RWH). The VR test on both the levels and the volatility of the IPUTIL rejects the random walk hypothesis with p-values of $2.33\times 10^{-9}$ and $3.20\times 10^{-19}$, respectively.

Mean reversion is also linked to the absence of a unit root and to stationarity. For assessing that, a number of tests have been developed in the literature such as Augmented Dickey–Fuller, KPSS, Pierre–Perron, and DFGLS tests. Table 2 does not confirm the presence of stationarity in data. Notice that, unlike the other tests, for the KPSS test the null hypothesis is that the time series is trend stationary therefore h = 0 means that there is no statistical indication of a unit root.

Table 2 Rejection decision h and p-value from the Augmented Dickey–Fuller (ADF) test, KPSS test, Philips–Perron (PP) test, Dickey–Fuller-GLS (DFGLS) test for unit roots

3.3 Autocorrelation

Figure 3 plots the sample autocorrelation function (ACF) and sample partial autocorrelation function (PACF) of the IPUTIL index (changes). By a visual inspection, there is autocorrelation at lag 1 and 2. The Ljung–Box Q-test (LBQ) confirms the presence of autocorrelation with a p-value of 5.8953 $\times 10^{-13}$.

Fig. 3

Sample autocorrelation function (ACF) and sample partial autocorrelation function (PACF) of IPUTIL

As a comparison Fig. 4 displays the ACF and PACF of a CIR process. Notice the autocorrelation at lag 1 but the absence of autocorrelation at lag 2. For that reason, we need a more advanced model such as the one proposed in Sect. 4.

Fig. 4

Sample autocorrelation function (ACF) and sample partial autocorrelation function (PACF) of a simulated CIR process. Parameters: $\mu =0.1; \sigma =0.05; k=0.85$

As one can see from Fig. 5, the $CIR^3$ model exhibits a significant autocorrelation both at lag 1 and 2 (with a LBQ p-value around 5.1507$\times 10^{-13}$), and a partial autocorrelation at lag 11 according to the original time series.

Fig. 5

Sample autocorrelation function (ACF) and sample partial autocorrelation function (PACF) of a simulated $CIR^3$ process

3.4 Cluster volatility

Lastly, we check whether the difference between the mean and the realizations display heteroscedasticity (cluster volatility). According to Engle’s ARCH [24] the null hypothesis of no heteroscedasticity should be rejected with a p-value of 5.9 $\times 10^{-13}$.

4 A three-factor stochastic model

Let us denote by $\{S_t\}_{t \ge 0}$ the stochastic process modelling the level of industrial production of electric and gas utilities. In addition, the correlated processes referring to the volatility and the short-run mean of $\{S_t\}_{t \ge 0}$ are, respectively, $\{v_t\}_{t \ge 0}$ and $\{\theta _t\}_{t \ge 0}$.

Let $k_v, \eta , \gamma , k_\theta , \zeta , \beta , k$ and $\alpha$ be positive constants. We consider the following system of SDEs

$$\begin{aligned} {\left\{ \begin{array}{ll} dS_t=k(\theta _t-S_t)dt+\alpha \sqrt{|v_t|}\sqrt{|S_t|}\,dW^{(1)}_t, \\ d\theta _t=k_{\theta }(\zeta -\theta _t)dt+\alpha \beta \sqrt{|v_t|} \sqrt{|\theta _t|}\,dW^{(2)}_t, \\ dv_t=k_v(\eta -v_t)dt+\gamma \sqrt{|v_t|}\,dW^{(3)}_t, \end{array}\right. } \end{aligned}$$

(2)

with the initial condition $(S_0,\theta _0,v_0)\in (0, + \infty )^3$. Here $\{W^{(i)}_t\}_{t\ge 0}$, $i =1,2,3$, are three standard correlated Brownian motions such that

$$\begin{aligned} dW^{(1)}_tdW^{(2)}_t=\rho _{\theta }dt, \qquad dW^{(1)}_tdW^{(3)}_t=\rho _vdt, \qquad dW^{(2)}_tdW^{(3)}_t=0, \end{aligned}$$

(3)

$\rho _{\theta }, \rho _v \in (-1,1)$. Moreover, the correlation coefficients satisfy the following relation

$$\begin{aligned} \rho ^2_{\theta }+\rho ^2_v< 1. \end{aligned}$$

System (2) represents a three-factor type model that we call $CIR^3$. In our framework, each dynamic process follows a square-root process, and, differently from the model in [16], the variance of the processes $S_t$ is proportional to the variance of the process itself, i.e., $v_t$, as often suggested by financial literature (see, [3, 30, 32, 43, 62, 63]). The same holds true for the mean process $\theta _t$.

By introducing the stochastic process

$$\begin{aligned} W^*_t=\frac{W^{(1)}_t-\rho _{\theta }W^{(2)}_t-\rho _{v}W^{(3)}_t}{\sqrt{1-\rho _{\theta }^2-\rho _v^2}}, \end{aligned}$$

(4)

which is a standard Brownian motion, independent both from $W^{(2)}_t$ and $W^{(3)}_t$, the system (2) reads as

$$\begin{aligned} {\left\{ \begin{array}{ll} dS_t=k(\theta _t-S_t)dt+\alpha \sqrt{|v_t|}\sqrt{|S_t|} \big ( \sqrt{1-\rho _{\theta }^2-\rho _v^2} dW^*_t + \rho _{\theta } dW^{(2)}_t + \rho _v dW^{(3)}_t\big )\\ d\theta _t=k_{\theta }(\zeta -\theta _t)dt+\alpha \beta \sqrt{|v_t|} \sqrt{|\theta _t|}\,dW^{(2)}_t, \\ dv_t=k_v(\eta -v_t)dt+\gamma \sqrt{|v_t|}\,dW^{(3)}_t, \end{array}\right. } \end{aligned}$$

(5)

with $(S_0,\theta _0,v_0)\in (0, + \infty )^3$ and $\{ W^*_t, W^{(2)}_t, W^{(3)}_t\}_{t \ge 0}$ a three-dimensional standard Brownian motion.

Assumption 4.1

We assume Feller’s condition

$$\begin{aligned} 2k_v\eta \ge \gamma ^2. \end{aligned}$$

We will work with the weak solution to system (5) according to the following definition. We say that $(\Omega ,\mathcal{F}, {\mathbb P};\textbf{F} = (\mathcal{F}_t)_{t\ge 0}, \textbf{W}, S, \theta , v)$ is a solution of system (5) if:

• $(\Omega ,\mathcal{F}, {\mathbb P};\textbf{F})$ is a filtered probability, $\textbf{W} = \{W^*_t, W^{(2)}_t, W^{(3)}_t\}_{t \ge 0}$ is a 3-dimensional standard $\textbf{F}$-Brownian motion, and $\{S_t, \theta _t, v_t \}_{t \ge 0}$ is an ${\mathbb R}^3$-valued process with continuous sample paths.

• $\{S_t, \theta _t, v_t \}_{t \ge 0}$ satisfies the initial condition $(S_0,\theta _0,v_0)\in (0, + \infty )^3$.

• System (5) holds a.s.

We first prove pathwise uniqueness and weak existence of a local solution to system (5) with state-space $(0, + \infty )^3$.

Theorem 4.1

Under Assumption 4.1, system (5) admits a weak solution $\{ S_t, \theta _t, v_t \}_{t \ge 0}$ with state-space $[0, + \infty )^2 \times (0, + \infty )$. Pathwise uniqueness of the solution to system (5) holds over the stochastic interval $[0, \tau = \tau ^S \wedge \tau ^\theta ]$, where

$$\begin{aligned} \tau ^S = \inf \{ t \ge 0: S_t =0 \}, \quad \tau ^\theta = \inf \{ t \ge 0: \theta _t =0 \} \end{aligned}$$

(6)

are the hitting time of zero for $S_t$ and $\theta _t$, respectively. The random time $\tau$ is such that ${\mathbb P}(\tau >0) = 1$ and for all $t <\tau$ the process $(S_t, \theta _t, v_t)$ takes values in $(0, + \infty )^3$.

Proof

Step (i) Weak existence of a global solution

The coefficient matrix of the diffusion term $\Sigma (S,\theta , v)$ and the drift $b(S, \theta , v)$ associated to system (5) are given by

$$\begin{aligned} \Sigma (S,\theta , v) = \begin{pmatrix} \alpha \sqrt{1-\rho _{\theta }^2-\rho _v^2}\sqrt{|v|}\sqrt{|S|} &{} \alpha \rho _{\theta } \sqrt{|v|}\sqrt{|S|} &{} \alpha \rho _{v} \sqrt{|v|}\sqrt{|S|} \\ 0 &{} \alpha \beta \sqrt{|v|}\sqrt{|\theta |} &{} 0 \\ 0 &{} 0 &{} \gamma \sqrt{|v|} \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} b(S, \theta , v) = \big (k(\theta - S), k_\theta (\zeta - \theta ), k_v(\eta - v) \big )^{T}, \end{aligned}$$

respectively. Note that $\Sigma (S,\theta , v)$ and $b(S, \theta , v)$ are continuous functions and satisfy growth conditions. In fact,

$$\begin{aligned} |\Sigma (S, \theta , v)|^2 = {{\,\textrm{trace}\,}}(\Sigma (S, \theta , v)\Sigma ^T(S, \theta , v)) = (\alpha ^2 |vS| + \alpha ^2 \beta ^2 |v\theta | + \gamma ^2 |v|) \end{aligned}$$

and by the inequality $ab \le \frac{1}{2} (a^2 + b^2)$, $a, b \in {\mathbb R}$, follows the sublinear growth condition

$$\begin{aligned} |\Sigma (S, \theta , v)|^2 \le K (1 + |S|^2 + |\theta |^2 + |v|^2), \end{aligned}$$

(7)

for some constant $K>0$. Moreover, let $x = (S,\theta , v) \in {\mathbb R}^3$, we have

$$\begin{aligned} x \cdot b(x) = S k(\theta -S) + \theta k_\theta (\zeta - \theta ) + v k_v (\eta - v) \le k S \theta + \zeta k_\theta \theta + k_v \eta v \end{aligned}$$

and again by $ab \le \frac{1}{2} (a^2 + b^2)$, $a, b \in {\mathbb R}$, we get the inequality

$$\begin{aligned} x \cdot b(x) \le K (1 + |x|^2), \quad x = (S,\theta , v) \in {\mathbb R}^3 \end{aligned}$$

(8)

for some constant $K>0$. Let us observe that b also satisfies the sublinear growth condition

$$\begin{aligned} |b(x)|^2 \le K (1 + |x|^2) \quad x = (S,\theta , v) \in {\mathbb R}^3 \end{aligned}$$

(9)

for some constant $K>0$.

Thanks to Eqs. (7) and (8) we can apply Theorem 3.10, in [25] (or Theorems 2.3 and 2.4, Chapter 6, in [36]), since $\Sigma$ and b are continuous and satisfy the sublinear growth conditions (7) and (9)). Thus there exists a weak solution $\{ S_t, \theta _t, v_t \}_{t \ge 0}$ to system (5) for any initial condition $(S_0,\theta _0,v_0)\in {\mathbb R}^3$, which does not explode in finite time. Let us note that continuity of $\Sigma (S,\theta , v)$ and $b(S, \theta , v)$ ensures existence of a weak solution (see Theorems 2.3, Chapter 6, in [36]) but this solution could explode (i.e. it could tend to infinity in finite time) and so we need an additional condition, as sublinear growth, which implies that the solution does not explode (see Theorems 2.4, Chapter 6, in [36]).

Summarizing, we have proved that there exist a filtered probability space $(\Omega ,\mathcal {F}, {\mathbb P}, \textbf{F} = (\mathcal {F}_t)_{t\ge 0})$, a three-dimensional $\textbf{F}$-Brownian motion $\{ W^*_t, W^{(2)}_t, W^{(3)}_t\}_{t \ge 0}$, and an $\textbf{F}$-adapted process with sample paths in $C_{{\mathbb R}^3}[0, + \infty )$, $\{ S_t, \theta _t, v_t \}_{t \ge 0}$, such that (5) holds ${\mathbb P}$-a.s. Moreover, we have that for all $t\ge 0$

$$\begin{aligned} {\mathbb E}[ S^2_t + \theta ^2_t + v^2_t] < + \infty . \end{aligned}$$

(10)

Step (ii) Nonnegativity of the global solution.

At this point, we are going to show that if the process starts from a strictly positive initial condition $(S_0,\theta _0,v_0)\in (0, + \infty )^3$ then $\{ S_t, \theta _t, v_t \}_{t \ge 0}$ takes values in $[0, + \infty )^2 \times (0, + \infty )$. Under the Assumption 4.1, for any initial condition $v_0 >0$, it is known that there exists a unique strong solution to the third equation in System (5), the so-called CIR-process, which is strictly positive (see, for instance, Section 6.3.1 in [37]). Hence we get that the process $\{v_t \}_{t \ge 0}$ is strictly positive. We can now prove by comparison result that for any initial conditions $S_0 >0$ and $\theta _0>0$, both the processes $\{S_t\}_{t \ge 0}$ and $\{\theta _t\}_{t \ge 0}$ take values in $[0, + \infty )$.

We first prove that for all $t\ge 0$, $\theta _{t} \ge 0$, ${\mathbb P}-a.s.$. Let us consider, on the probability space $(\Omega ,\mathcal {F}, {\mathbb P}, \textbf{F} = (\mathcal {F}_t)_{t\ge 0})$ where the processes $\{\theta _t\}_{t\ge 0}$ and $\{v_t\}_{t\ge 0}$ are defined, the following SDE

$$\begin{aligned} d\theta ^1_t= - k_{\theta }\theta ^1_tdt+\alpha \beta \sqrt{v_t} \sqrt{|\theta ^1_t|}\,dW^{(2)}_t, \quad \theta ^1_0 =0 \end{aligned}$$

(11)

and note that for any $t\ge 0$, $\theta ^1_t=0$ solves Eq. (11). We can proceed as in the proof of Theorem 1.1, Chapter 6 in [36] with

$$\begin{aligned} b_1(x) = - k_{\theta } x, \quad b_2(x) = k_{\theta }(\zeta -x), \quad \sigma (t, \omega , x)= \alpha \beta \sqrt{v_t(\omega )} \sqrt{|x|}, \quad x \in \mathbb {R}, \omega \in \Omega . \end{aligned}$$

Note that, for all $x\in \mathbb {R}$ $b_1(x) < b_2(x)$, $b_1$ is Lipschitz continuous, i.e.

$$\begin{aligned}|b_1(x) - b_1(x')| \le k_{\theta }|x - x'|, \quad \forall x, x' \in \mathbb {R},\end{aligned}$$

and $\sigma$ satisfies

$$\begin{aligned} |\sigma (t, \omega , x) - \sigma (t, \omega , x') | \le \sqrt{v_t(\omega )} \rho (|x - x'|), \quad x, x' \in \mathbb {R}, \quad (t,\omega ) \in [0,+\infty ) \times \Omega , \end{aligned}$$

where $\rho (x) = \alpha \beta \sqrt{x}$ is a strictly increasing function defined on $[0, + \infty )$ such that $\rho (0)=0$ and satisfying Eq. (1.1) in Chapter 6 of [36].

We can not apply directly Theorem 1.1, Chapter 6 in [36] because the diffusion coefficient depends on the process $\{v_t\}_{t\ge 0}$, which is an unbounded process. Therefore, we use a localization argument and define for all $N\in \mathbb {N}$

$$\begin{aligned} \eta _N =\inf \{ t \ge 0: v_t >N\}. \end{aligned}$$

The sequence of stopping times $\{\eta _N\}_{N \in \mathbb {N}}$ is non-decreasing and such that $\eta _N \rightarrow +\infty$ as $N \rightarrow + \infty$ (since the process $\{v_t\}_{t\ge 0}$ does not explode in a finite time).

We can now consider the non-decreasing sequence of continuous functions $\{\varphi _n(x)\}_{n \in \mathbb {N}}$ as defined in the proof of Theorem 1.1, Chapter 6 of [36], which satisfy $\varphi _n \in C^2(\mathbb {R})$, $\varphi _n(x)=0$ for $x\le 0$, $0 \le \varphi '_n(x) \le 1$ and $\varphi _n(x) \rightarrow (x)_+ =$ $\max \{x,0\}$ as $n \rightarrow +\infty$.

We apply Itô’s rule and by similar computations as in that proof, we get that

$$\begin{aligned} \varphi _n(\theta ^1_{t \wedge \eta _N} - \theta _{t \wedge \eta _N}) = I_1(n,{t \wedge \eta _N}) + I_2(n,{t \wedge \eta _N}) + I_3(n,{t \wedge \eta _N}), \end{aligned}$$

where

$$\begin{aligned}{} & {} I_1(n,{t \wedge \eta _N}) = \int _0^{t \wedge \eta _N}\varphi '_n(\theta ^1_s - \theta _s)[\sigma (s, \theta ^1_s) - \sigma (s, \theta _s)] dW^{(2)}_s\\{} & {} I_2(n,{t \wedge \eta _N}) = \int _0^{t \wedge \eta _N} \varphi ''_n(\theta ^1_s - \theta _s) (b_1(\theta ^1_s) - b_2(\theta _s)) ds\\{} & {} I_3(n,t \wedge \eta _N) = \dfrac{1}{2} \int _0^{t \wedge \eta _N}\varphi ''_n(\theta ^1_s - \theta _s) \rho ^2(|\theta ^1_s - \theta _s|) v^2_s ds. \end{aligned}$$

It is clear that ${\mathbb E}[I_1(n,{t \wedge \eta _N} )] =0$ and since

$$\begin{aligned} {\mathbb E}[I_3(n,t \wedge \eta _N )] \le \dfrac{N^2}{2} {\mathbb E}\Big [ \int _0^{t \wedge \eta _N} \varphi ''_n(\theta ^1_s - \theta _s) \rho ^2(|\theta ^1_s - \theta _s|) ds \Big ] \end{aligned}$$

we can proceed as in the proof of Theorem 1.1, Chapter 6 of [36] obtaining

$$\begin{aligned} {\mathbb E}[I_3(n,{t \wedge \eta _N} )]\le {N^2 t \over n}. \end{aligned}$$

Observing that for all $t \ge 0$

$$\begin{aligned} b_1(\theta ^1_t) - b_2(\theta _t) = b_1(\theta ^1_t) - b_1(\theta _t) + b_1(\theta _t) -b_2(\theta _t) \le b_1(\theta ^1_t) - b_1(\theta _t) \end{aligned}$$

and again as in the proof of Theorem 1.1, Chapter 6 of [36] we get that

$$\begin{aligned} I_2(n,{t \wedge \eta _N} ) \le \int _0^{t \wedge \eta _N}\!\!\varphi ''_n(\theta ^1_s - \theta _s) (b_1(\theta ^1_s) - b_1(\theta _s)) ds \le \int _0^{t \wedge \eta _N} \!\! k_{\theta } (\theta ^1_s - \theta _s)_+ ds. \end{aligned}$$

Hence

$$\begin{aligned} {\mathbb E}[\varphi _n(\theta ^1_{t \wedge \eta _N} - \theta _{t \wedge \eta _N})] \le {N^2 t \over n} + {\mathbb E}\Big [\int _0^{t \wedge \eta _N} \!\! k_{\theta } (\theta ^1_s - \theta _s)_+ ds \Big ] \end{aligned}$$

and by letting $n \rightarrow +\infty$, we obtain

$$\begin{aligned} {\mathbb E}[(\theta ^1_{t \wedge \eta _N} - \theta _{t \wedge \eta _N})_+] \le k_{\theta } \int _0^{t} {\mathbb E}[(\theta ^1_{s \wedge \eta _N}- \theta _{s\wedge \eta _N})_+] ds. \end{aligned}$$

By Gronwall’s Lemma we deduce that for all $t\ge 0$, $N \in \mathbb {N}$, ${\mathbb E}[(\theta ^1_{t \wedge \eta _N} - \theta _{t \wedge \eta _N})_+] =0$, which in turn implies that

$$\begin{aligned} \theta ^1_{t \wedge \eta _N} \le \theta _{t \wedge \eta _N}, {\mathbb P}-a.s. \quad \forall t \ge 0, N \in \mathbb {N}. \end{aligned}$$

Finally, letting $N \rightarrow + \infty$ and recalling that for all $t \ge 0$, $\theta ^1_{t}=0$, we obtain

$$\begin{aligned} \theta _{t} \ge 0, \quad {\mathbb P}-a.s. \quad \forall t \ge 0. \end{aligned}$$

Similarly, we can prove that, for any $t\ge 0$, $S_{t} \ge 0$, ${\mathbb P}-a.s.$ Let us consider, on the probability space $(\Omega ,\mathcal {F}, {\mathbb P}, \textbf{F} = (\mathcal {F}_t)_{t\ge 0})$ where the processes $\{\theta _t\}_{t\ge 0}$, $\{v_t\}_{t\ge 0}$ and $\{S_t\}_{t\ge 0}$ are defined, the following SDE

$$\begin{aligned} dS^1_t= - k S^1_tdt+\alpha \beta \sqrt{v_t} \sqrt{|S^1_t|}\,dW^{(1)}_t, \quad S^1_0 =0 \end{aligned}$$

(12)

and note that $S^1_t=0, \forall t \ge 0$ solves Eq. (12). We now take

$$\begin{aligned} b_1(x) = - k x, \quad b_2(t, \omega , x) = k (\theta _t(\omega ) - x), \quad x \in \mathbb {R}, \quad (t, \omega ) \in [0, + \infty )\times \Omega \end{aligned}$$

and $\sigma (t, \omega , x)$ as before. Note that for all $x \in \mathbb {R}$ and $(t, \omega ) \in [0, + \infty )\times \Omega$,

$$\begin{aligned} b_1(x) \le b_2(t, \omega , x)\quad {\mathbb P}-a.s. \end{aligned}$$

(because, for all $t\ge 0$, $\theta _{t} \ge 0, {\mathbb P}-a.s.$ and $k>0$) and $b_1$ is Lipschitz continuous with Lipschitz constant equals to k. Finally, observing that for all $(t, \omega ) \in [0, + \infty )\times \Omega$

$$\begin{aligned} b_1(x') - b_2(t, \omega , x) = b_1(x') - b_1(x) + b_1(x) -b_2(t, \omega , x) \le b_1(x') - b_1(x), \quad x,x' \in \mathbb {R} \end{aligned}$$

we can perform the same computations as before.

Step (iii) Pathwise uniqueness of a strict positive local solution

We want to show that starting from $(S_0,\theta _0,v_0)\in (0, + \infty )^3$ the process $\{ S_t, \theta _t, v_t \}_{t \ge 0}$ is the unique solution (in pathwise sense) until one of the processes $\{ S_t\}_{t \ge 0}$ or $\{ \theta \}_{t \ge 0}$ reaches zero. Note that $\Sigma (S,\theta , v)$ is not Lipschitz-continuous in $[0, +\infty )^2 \times (0, + \infty )$ but, it is in the open set $U_N = ({1 \over N}, N)^3$, for any $N >0$. In fact,

$$\begin{aligned}{} & {} |\Sigma (S, \theta , v) - \Sigma (S', \theta ', v')|^2 = \sum _{i,j=1}^3 |\Sigma _{ij}(S, \theta , v) - \Sigma _{ij}(S', \theta ', v')|^2 \\{} & {} \quad =\alpha ^2 |\sqrt{vS}- \sqrt{v'S'}|^2 + \alpha ^2 \beta ^2 |\sqrt{\theta S}- \sqrt{\theta 'S'}|^2 + \gamma ^2 |\sqrt{v}- \sqrt{v'}|^2. \end{aligned}$$

By Lagrange’s Theorem, for all $x,x' \in (a,b)$, $0<a<b$, there exists $\bar{x} \in (a,b)$ such that

$$\begin{aligned} |\sqrt{x}- \sqrt{x'}| = {1\over 2 \sqrt{\bar{x}}} |x-x'| \end{aligned}$$

hence

$$\begin{aligned} |\sqrt{x}- \sqrt{x'}| \le {1\over 2 \sqrt{a}} |x-x'|. \end{aligned}$$

It is clear that for all $x,x', y, y' \in ({1 \over N}, N)$,

$$\begin{aligned} |xy- x'y'|^2 \le N^2 \{ |x-x'|^2 + |y-y'|^2\}. \end{aligned}$$

By applying the above inequalities we get that for all $(S, \theta , v), (S', \theta ', v') \in U_N$

$$\begin{aligned} |\Sigma (S, \theta , v) - \Sigma (S', \theta ', v')|^2 \le K_N ( |S - S'|^2 + |\theta - \theta '|^2 + |v - v'|^2) \end{aligned}$$

for some constant $K_N>0$. Then, we can apply Theorem 3.7 in [25], and we get that pathwise uniqueness holds over the stochastic interval $[0, \tau _N]$ where

$$\begin{aligned} \tau _N = \inf \{ t \ge 0: (S_t, \theta _t, v_t) \notin U_N\}. \end{aligned}$$

(13)

Note that $U_N \subset U_{N+1}$, so $\tau _N$ is an increasing sequence of stopping times with $\tau _N \rightarrow \tau$ as $N \rightarrow +\infty$ due to the fact that $\{S_t\}_{t\ge 0}$, $\{\theta _t\}_{t\ge 0}$, and $\{v_t\}_{t\ge 0}$ do not explode and $v_t > 0$ for all $t \ge 0$. Therefore, by taking the limit as $N \rightarrow +\infty$, we obtain pathwise uniqueness on $[0, \tau ]$.

Finally, from continuity of trajectories of $\{ S_t, \theta _t \}_{t \ge 0}$ since $S_0>0$ and $\theta _0>0$ we get that ${\mathbb P}(\tau > 0)=1$ and this concludes the proof.

Ultimately, (local) weak existence and pathwise uniqueness of the solution to system (5) imply (local) strong existence.

Corollary 4.2

Let consider any initial condition $(s_0, \theta _0, v_0) \in (0, + \infty )^3$. The system (5) admits a unique strong solution $(S_t, \theta _t, v_t)$ taking values in $(0, + \infty )^3$, for all $t<\tau$, where

$$\begin{aligned} \tau = \tau ^S \wedge \tau ^\theta = \inf \{ t \ge 0: S_t =0 \ {\text{ o }r} \ \theta _t =0\}. \end{aligned}$$

Proof

The assertion directly comes from Theorem 4.1 and [39, Corollary 3.23, Chapter 5] (or [36, Theorem 1.1, Chapter 4]).

Thanks to the strict positivity of $(S_t,\theta _t,v_t)$ for all $t < \tau$, we can apply a suitable Lamperti transformation that converts the correlated system (5) into an uncorrelated one, as described in (19) below. This transformation will be useful in Sect. 5 for numerical purposes. We first provide a preliminary result.

Lemma 4.1

For any $t\le \tau$, define

$$\begin{aligned} X_t= 2\sqrt{S_t} - \frac{2\rho _{\theta }}{\beta }\sqrt{\theta _t} - \frac{\rho _v \alpha }{\gamma }v_t. \end{aligned}$$

(14)

Then $X_t$ solves for $t < \tau$

$$\begin{aligned} dX_t=\biggl (\frac{2 k\theta _t}{X_t + c_t} -\frac{k}{2} (X_t +c_t) -\sum _{u=0}^2 c_{u,t}\biggr )dt+\alpha \sqrt{v_t}\sqrt{1-\rho _{\theta }^2-\rho _v^2}\,dW^*_t, \end{aligned}$$

(15)

where

$$\begin{aligned} c_t= c(\theta _t,v_t) = \frac{2\rho _{\theta }}{\beta }\sqrt{\theta _t}+\frac{\rho _v \alpha }{\gamma }v_t, \end{aligned}$$

(16)

and

$$\begin{aligned} c_{0,t}=\frac{\alpha ^2 v_t}{2 (X_t + c_t)}, \qquad c_{1,t}=\rho _{\theta }\biggl (\frac{k_{\theta }(\zeta -\theta _t)}{\beta \sqrt{\theta _t}}-\frac{\beta \alpha ^2 v_t}{4\sqrt{\theta _t}}\biggr ), \qquad c_{2,t}= \frac{\rho _v \alpha k_v(\eta -v_t)}{\gamma }.\nonumber \\ \end{aligned}$$

(17)

Proof

By virtue of Itô’s formula we have that for any $t < \tau = \tau ^S \wedge \tau ^\theta$

$$\begin{aligned} dX_t = \frac{1}{\sqrt{S_t} }dS_t - \frac{\rho _\theta }{\beta \sqrt{\theta _t}} d\theta _t - \frac{\rho _\gamma \alpha }{\gamma }dv_t - \frac{\alpha ^2 }{4 \sqrt{S_t} } v_t dt + \frac{\rho _\theta \alpha ^2 \beta }{4 \sqrt{\theta _t} } v_t dt \end{aligned}$$

(18)

By substituting the expressions of $dS_t$, $d\theta _t$ and $dv_t$ in Eq. (18) and observing that

$$\begin{aligned} \sqrt{S_t} = \frac{X_t + c_t}{2} >0 \end{aligned}$$

we obtain Eq. (15).

Based on Lemma 4.1, we introduce the following system of SDEs

$$\begin{aligned} \small {\left\{ \begin{array}{ll} dX_t=\biggl (\frac{2 k\theta _t}{X_t + c_t}- \frac{k}{2} (X_t +c_t) -\sum _{u=0}^2 c_{u,t}\biggr )dt+\alpha \sqrt{v_t}\sqrt{1-\rho _{\theta }^2-\rho _v^2}\,dW^*_t \\ d\theta _t=k_{\theta }(\zeta -\theta _t)dt+\alpha \beta \sqrt{v_t} \sqrt{\theta _t}\,dW^{(2)}_t \\ dv_t=k_v(\eta -v_t)dt+\gamma \sqrt{v_t}\,dW^{(3)}_t, \end{array}\right. } \end{aligned}$$

(19)

where $c_t$, and $c_{i,t}$, $i=0, 1,2$ are defined in Eqs. (16) and (17).

Note that the drift in the dynamics of $X_t$ in system (19) explodes if $\theta _t$ or $X_t + c(\theta _t, v_t)$ hits zero. As a consequence of Theorem 4.1 and Corollary 4.2 we will prove that system (19) admits a unique strong solution over the random interval $[0, \tau ^X \wedge \tau ^\theta )$, where

$$\begin{aligned} \tau ^X = \inf \{ t \ge 0: X_t + c(\theta _t, v_t) \le 0\} \end{aligned}$$

(20)

Theorem 4.3

Let us consider any deterministic initial condition, $(x_0, \theta _0, v_0) \in \mathbb {R} \times (0, + \infty )^2$, such that $x_0 + c(\theta _0, v_0)>0$. Then there exists a unique strong solution to system (19) over the random time interval $[0, \tau ^X \wedge \tau ^\theta )$.

Proof

Step (i) Existence of a strong local solution.

From Theorem 4.1 and Lemma 4.1 we get existence of a solution to system (19) over the random time interval $[0, \tau = \tau ^S \wedge \tau ^\theta$). By construction, for all $t < \tau = \tau ^S \wedge \tau ^\theta$, $X_t + c(\theta _t, v_t) =2 \sqrt{S_t} >0$ and $X_{\tau ^S} \ + c(\theta _{\tau ^S}, v_{\tau ^S}) = 2 \sqrt{S_{\tau ^S}} =0.$ This implies that $\tau ^X =\tau ^S$, and hence the solution is defined on the random time interval $[0, \tau = \tau ^X \wedge \tau ^\theta$).

Step (ii) Pathwise uniqueness of the local solution

Let $(\widetilde{X}_t, \widetilde{\theta }_t, \widetilde{v}_t )$ be a solution to (19), for any $t < \tau ^{\widetilde{X}} \wedge \tau ^{\widetilde{\theta }}$, starting from any deterministic initial condition $(x_0, \theta _0, v_0) \in \mathbb {R} \times (0, + \infty )^2$ satisfying $x_0 + c(\theta _0, v_0)>0$. Let us introduce, on the same probability space where $(\widetilde{X}_t, \widetilde{\theta }_t, \widetilde{v}_t )$ is defined, and, for any $t < \tau ^{\widetilde{X}} \wedge \tau ^{\widetilde{\theta }}$ the process

$$\begin{aligned} \widetilde{S}_t = \biggl (\frac{\widetilde{X}_t+c(\widetilde{\theta }_t, \widetilde{v}_t)}{2} \biggr )^2. \end{aligned}$$

From Itô’s formula we get that for any $t < \tau ^{\widetilde{X}} \wedge \tau ^{\widetilde{\theta }}$ the triple $(\widetilde{S}_t, \widetilde{\theta }_t, \widetilde{v}_t )$ solves system (5), with initial condition

$$\begin{aligned} (s_0, \theta _0, v_0) \in (0, + \infty )^3, \quad s_0= \biggl (\frac{x_0+c(\theta _0, v_0)}{2} \biggr )^2 \end{aligned}$$

By construction, for any $t < \tau ^{\widetilde{X}} \wedge \tau ^{\widetilde{\theta }}$, $\widetilde{S}_t >0$ and $\widetilde{S}_{\tau ^{\widetilde{X}} } =0$. Thus, we have that $\tau ^{\widetilde{S}} =\tau ^{\widetilde{X}}$. By strong uniqueness of a strict positive solution (see Corollary 4.2), we get that $(\widetilde{S}_t, \widetilde{\theta }_t, \widetilde{v}_t )$ and $(S_t, \theta _t, v_t)$ coincides for any $t < \tau ^{\widetilde{S}} \wedge \tau ^{\widetilde{\theta }} = \tau ^{ S} \wedge \tau ^{\theta }$.

System (19) is equivalent to (5). In particular, from the solution to (19) we can derive by a simple transformation, see (21) below, the solution of our original system (5).

Corollary 4.4

Let us consider any deterministic initial condition, $(x_0, \theta _0, v_0) \in \mathbb {R} \times (0, + \infty )^2$, such that $x_0 + c(\theta _0, v_0)>0$. Let $(X_t, \theta _t, v_t)$ be the unique strong solution to system (19) over the random time interval $[0, \tau ^X \wedge \tau ^\theta )$. Then $(S_t, \theta _t, v_t)$, where

$$\begin{aligned} S_t = \biggl (\frac{X_t+c(\theta _t,v_t)}{2} \biggr )^2, \end{aligned}$$

(21)

and $c(\theta _t,v_t)$ given in (16), is the unique strong solution to system (5) over the random time interval $[0, \tau ^S \wedge \tau ^\theta )$.

Proof

The proof follows directly from Step (ii) in the proof of Theorem 4.3.

As just said the main advantage given by the process $X_t$ is to provide a fast and independent simulation of the process $S_t$. Indeed, we can first simulate the pair $(\theta _t,v_t)$, and next the process $X_t$, whose stochastic component $W^*_t$ is uncorrelated with those of $\theta _t$ and $v_t$. Finally, the dynamics of $S_t$ can be obtained by the transformation (21).

Remark 4.1

Note that in our model $S_t$ or $\theta _t$ have unbounded stochastic volatility due to the presence of $v_t$. It is known, see for instance Section 6.3.1 in [37], that a CIR process hits zero almost surely if Feller’s condition is not fulfilled, i.e. the volatility is not sufficiently small. This implies that $S_t$ or $\theta _t$ reaches zero almost surely, that is, ${\mathbb P}(\tau ^S< + \infty ) = {\mathbb P}(\tau ^\theta < + \infty )=1$. However, even if existence and uniqueness of solution to systems (5) and (19) are only in local sense, and we do not have a lower bound for the random time $\tau$, we observe that ${\mathbb E}[\tau ^S]={\mathbb E}[\tau ^{\theta }]=+\infty$. This property is observed only through numerical inspection, and its formal treatment will be the subject of future research. Specifically, to test this numerically, we simulated the process together with 10,000 randomly bootstrapped realizations. In no iteration did we find $S_t$ or $\theta _t$ to be zero.

We conclude the Section with a remark which will be useful in the next sections.

Remark 4.2

It is easy to verify that

$$\begin{aligned}{} & {} {\mathbb E}[\theta _t|\mathcal{F}_s] ={\mathbb E}^{\theta }[\theta _t|\theta _s]=\zeta +(\theta _s-\zeta )e^{-k_{\theta }(t-s)},\quad \forall t >s, \end{aligned}$$

(22)

$$\begin{aligned}{} & {} {\mathbb E}[v_t|\mathcal{F}_s]={\mathbb E}^v[v_t|v_s]=\eta +(v_s-\eta )e^{-k_{v}(t-s)}, \quad \forall t >s. \end{aligned}$$

(23)

Indeed the processes $\int _0^t e^{k_\theta s}\sqrt{v_s \theta _s}\, dW^{(2)}_s$, and $\int _0^t e^{k_v s}\sqrt{v_s}\, dW^{(3)}_s$, $t \ge 0$, thanks to Eq. (10) turn to be $\textbf{F}$-martingales.

5 Results

In this section, we apply our model to the change in the industrial production of electric and gas utilities already mentioned. Other models used as a benchmark are the ARIMA-GARCH and the non-linear regression model (NRM) specified in Eq. (1). Note that, with reference to the model (2), let $(s_1,\ldots ,s_n)$ be the observations of $S_t$, and $(\Theta _1,\ldots ,\Theta _n)$ those of the mean process $\theta _t$, taken as the exponential weighted moving average (EWMA) of $(s_1,\ldots ,s_n)$. Moreover, the observations $(\nu _1,\ldots ,\nu _n)$ of the volatility process $v_t$ are given by the so-called pointwise volatility

$$\begin{aligned} \nu _u=|s_u-\Theta _u| \qquad (1\le u\le n). \end{aligned}$$

Once again, the results displayed are in terms of percent change because, economically, the focus is on the variations rather than absolute levels.

5.1 Parameters calibration

In order to estimate $S_t,\theta _t$, and $v_t$ the involved parameters $k, k_{\theta }, k_{v},\eta ,\zeta ,\alpha ,\beta ,\gamma$ and the correlations $\rho _{\theta },\rho _v$ in Eq. (2) need to be calibrated to the market prices. To estimate the correlation $\rho _{\theta }$ we use the Spearman correlation between the realizations of $S_t$ and $\theta _t$; analogously for $\rho _v$.

Among many approaches existing in the literature to estimate the parameters of the square-root models (see, for instance, [41] and references therein), we consider the estimating function approach for ergodic diffusion models introduced in Bibby et al. [6]. This method proved to be very useful in obtaining optimal estimators for the parameters of discretely sampled diffusion-type models whose likelihood function is usually not explicitly known. In [6, Example 5.4] the authors constructed an approximately optimal estimating function for the square-root model, from which they derived the following explicit estimators of the three parameters based on a sample of n observed market prices. For example, with regard to the process $v_t$, the parameters $k_v,\eta ,\gamma$ on a sample $(\nu _1,\dots ,\nu _n)$ are given by

$$\begin{aligned} \hat{k}_v&=-\ln \left( \frac{(n-1)\sum _{u=2}^n \nu _u/\nu _{u-1} - (\sum _{u=2}^n \nu _{u}) (\sum _{u=2}^n \nu ^{-1}_{u-1})}{(n-1)^{2}-(\sum _{u=2}^n \nu _{u-1})(\sum _{u=2}^n \nu ^{-1}_{u-1})}\right) ,\nonumber \\ \hat{\eta }&=\frac{1}{(n-1)}\sum _{u=2}^n \nu _{u}+\frac{e^{-\hat{k}_{v}}}{(n-1)(1-e^{-\hat{k}_{v}})}(\nu _{n}-\nu _{1}),\\ \hat{\gamma }&=\sqrt{\frac{\sum _{u=2}^n \nu ^{-1}_{u-1}(\nu _{u}-\nu _{u-1}e^{-\hat{k}_{v}}-\hat{\eta }(1-e^{-\hat{k}_{v}}))^{2}}{\sum _{u=2}^n \nu ^{-1}_{u-1}((\hat{\eta }/2-\nu _{u-1})e^{-2\hat{k}_{v}}-(\hat{\eta }-\nu _{u-1})e^{-\hat{k}_{v}}+\hat{\eta }/2)/\hat{k}_{v}}}.\nonumber \end{aligned}$$

(24)

These estimators exist provided that the argument of the logarithm in the first equation is strictly positive (the authors observed that this happens with a probability tending to one as $n\rightarrow \infty$, see Example 5.4 in [6].

Analogously, given the observations $(\Theta _1,\ldots ,\Theta _n)$, we may compute

$$\begin{aligned} \hat{k}_{\theta }&=-\ln \left( \frac{(n-1)\sum _{u=2}^n \Theta _u/\Theta _{u-1} - (\sum _{u=2}^n \Theta _{u}) (\sum _{u=2}^n \Theta ^{-1}_{u-1})}{(n-1)^{2}-(\sum _{u=2}^n \Theta _{u-1})(\sum _{u=2}^n \Theta ^{-1}_{u-1})}\right) ,\nonumber \\ \hat{\zeta }&=\frac{1}{(n-1)}\sum _{u=2}^n \Theta _{u}+\frac{e^{-\hat{k}_{\theta }}}{(n-1)(1-e^{-\hat{k}_{\theta }})}(\Theta _{n}-\Theta _{1}),\\ \widehat{(\alpha \beta )}&=\sqrt{\frac{\sum _{u=2}^n \Theta ^{-1}_{u-1}(\Theta _{u}-\Theta _{u-1}e^{-\hat{k}_{\theta }}-\hat{\zeta }(1-e^{-\hat{k}_{\theta }}))^{2}}{\sum _{u=2}^n \Theta ^{-1}_{u-1}((\hat{\zeta }/2-\Theta _{u-1})e^{-2\hat{k}_{\theta }}-(\hat{\zeta }-\Theta _{u-1})e^{-\hat{k}_{\theta }}+\hat{\zeta }/2) \hat{v}/\hat{k}_{\theta }}},\nonumber \end{aligned}$$

(25)

where $\hat{v}$ is computed through the average (in [1, n]) of the discretization scheme described in Sect. 5.3, once the related parameters are estimated by Eq. (24). Similarly to $\hat{v}$, we obtain $\hat{\theta }$. Finally, given the observations $(s_1,\ldots ,s_n)$, we take

$$\begin{aligned} \hat{k}&=-\ln \left( \frac{(n-1)\sum _{u=2}^n s_u/s_{u-1} - (\sum _{u=2}^n s_{u}) (\sum _{u=2}^n s^{-1}_{u-1})}{(n-1)^{2}-(\sum _{u=2}^n s_{u-1})(\sum _{u=2}^n s^{-1}_{u-1})}\right) ,\\ \hat{\alpha }&=\sqrt{\frac{\sum _{u=2}^n s^{-1}_{u-1}(s_{u}-s_{u-1}e^{-\hat{k}}-\hat{\theta }(1-e^{-\hat{k}}))^{2}}{\sum _{u=2}^n s^{-1}_{u-1}((\hat{\theta }/2-s_{u-1})e^{-2\hat{k}}-(\hat{\theta }-s_{u-1})e^{-\hat{k}}+\hat{\theta }/2) \hat{v}/ \hat{k}}}, \end{aligned}$$

and from $\hat{\alpha }$ we derive $\hat{\beta }=\frac{\widehat{(\alpha \beta )}}{\hat{\alpha }}$.

5.2 Accuracy statistics

5.2.1 Normalized root mean square error (NRMSE)

The root mean squared error (RMSE) is a measure of the closeness between the observed data and the simulated values from a given model. So, it represents the accuracy of the model in terms of goodness of fit. It is defined by

$$\begin{aligned} \text {RMSE} =\sqrt{\frac{1}{n}\sum _{u=1}^n e^2_u}, \end{aligned}$$

(26)

where $e_u$ denotes the residuals between the observed data and their simulations, over n times. Hence, a value near 0 indicates a perfect fit to the data, and values lower than 1 represent a good result. Note that the RMSE depends on the scale of observed data, thus it is sensitive to the outliers; consequently, larger errors have a disproportionately large effect. To solve this issue, we adopt the so-called normalized root mean squared error (NRMSE)

$$\begin{aligned} \text {NRMSE}= \dfrac{\text {RMSE} }{s_{\max } -s_{\min }}, \end{aligned}$$

(27)

where $s_{\max }$ denotes the maximum value and $s_{\min }$ is the minimum value of the observed sample data.

5.2.2 Mean absolute percentage error (MAPE)

The mean absolute percentage error (MAPE) is a measure of prediction accuracy of a forecasting method. It is defined as

$$\begin{aligned} \text {MAPE} =\frac{1}{n}\sum _{u=1}^n \biggl | \frac{e_u}{s_u}\biggr |, \end{aligned}$$

(28)

where $e_u$ denotes the residuals between the observed data $s_u$ and their previsions. Table 3 suggests the accuracy levels of the MAPE criterion.

Table 3 MAPE accuracy levels (indicative)

5.3 In-sample simulation

As mentioned, for simulations, the pointwise volatility of $S_t$ is used as a proxy for the latent variable $v_t$, while the trend of $S_t$, represented by the EWMA, is captured by the latent variable $\theta _t$.

To simulate the processes $v_t, \theta _t$ we apply the strong convergent Milstein discretization ([49]) to the second and third SDE of Eq. (2). Brigo and Mercurio in [11, Section 22.7] showed that the Milstein scheme converges in a much better way than other numerical algorithms for the square-root process. Here the Lévy area terms are expressed by means of the square of the increments of the Brownian motion, as for instance discussed in [21].

Hence, for any $1\le u\le (n-1)$,¹ we compute

$$\begin{aligned} \hat{v}_{u+1} = \hat{v}_u + \hat{k}_v(\hat{\eta } - \hat{v}_u)\, \Delta + \hat{\gamma }\sqrt{\hat{v}_u \Delta }\; \varepsilon ^{(3)}_{u+1} + \frac{\hat{\gamma }^2}{4}\, [(\sqrt{\Delta }\; \varepsilon ^{(3)}_{u+1})^{2} - \Delta ], \end{aligned}$$

(29)

and

$$\begin{aligned} \hat{\theta }_{u+1} = \hat{\theta }_u + \hat{k}_{\theta }(\hat{\zeta } - \hat{\theta }_u)\, \Delta + \widehat{\alpha \beta } \sqrt{\hat{v}_{u}}\sqrt{\hat{\theta }_u \Delta }\; \varepsilon ^{(2)}_{u+1} + \frac{(\widehat{\alpha \beta } \sqrt{\hat{v}_{u}})^2}{4}\, [(\sqrt{\Delta }\; \varepsilon ^{(2)}_{u+1})^{2} - \Delta ],\qquad \end{aligned}$$

(30)

respectively, where $\Delta$ is the time step and $(\varepsilon ^{(i)}_u)_{u\ge 1}$ $(i=1,2,3)$ are i.i.d. (standard) normal random variables.

Once calibrated the model parameters, we simulate the auxiliary process $X_t$ (see Eq. (15))

$$\begin{aligned} \hat{X}_{u+1} = \hat{X}_u+\omega (\hat{X}_u,\hat{\theta }_{u},\hat{v}_u) \Delta +\hat{\alpha }\sqrt{\hat{v}_u \Delta }\sqrt{1-\hat{\rho }_{\theta }^2-\hat{\rho }_v^2}\,\varepsilon ^{(1)}_{u+1}, \end{aligned}$$

(31)

where

$$\begin{aligned} \omega (x,\theta ,v) = \frac{ 2 k \hat{\theta }}{x + \hat{c}(\theta ,v) }- \frac{k}{2} (x + \hat{c}(\theta ,v) )-\sum _{u=0}^2 \hat{c}_{u}(x, \theta , v) \end{aligned}$$

where

$$\begin{aligned} \hat{c}(\theta ,v) = \frac{2 \hat{\rho }_{\theta }}{\hat{\beta }}\sqrt{\theta } + \frac{\hat{\rho }_v \hat{\alpha }}{\hat{\gamma }} v, \qquad \hat{c}_{0}(x,\theta ,v)=\frac{\hat{\alpha }^2 v}{ 2(x + \hat{c}(\theta ,v))} \end{aligned}$$

(32)

and

$$\begin{aligned} \hat{c}_{1} (x,\theta ,v)= \hat{\rho }_{\theta }\biggl (\frac{\hat{k}_{\theta }(\hat{\zeta }-\theta )}{\hat{\beta }\sqrt{\theta }}- \frac{\hat{\beta }\hat{\alpha }^2 v}{4\sqrt{\theta }}\biggr ), \qquad \hat{c}_{2}(x,\theta ,v)= \frac{\hat{\rho }_v \hat{\alpha }\hat{k}_v(\hat{\eta }- v)}{\hat{\gamma }}. \end{aligned}$$

(33)

Next, we obtain by Eq. (21) in Corollary 4.4

$$\begin{aligned} \hat{S}_{u+1}= \frac{1}{4} \biggl (\hat{X}_{u+1}+ \hat{c}( \hat{\theta }_{u+1}, \hat{v}_{u+1} )\biggr )^2. \end{aligned}$$

Figure 6 and Table 4 display the results of our simulations on the entire dataset of the proposed model versus the considered benchmarks mentioned in the literature review. The fitted values are obtained by averaging 100,000 simulations. In particular, we simulate the changes of $S_t$, jointly with their pointwise volatility and their trend (see Fig. 1 and Sect. 5).

As shown, our approach can provide an accurate fit for the considered time series. Observe that the numerical investigation confirms that $\hat{X}_{u+1} + \hat{c}(\hat{\theta }_{u+1}, \hat{v}_{u+1}) >0$ (for any $1\le u\le (n-1)$) as a consequence of the equivalence between systems (5) and (19).

Fig. 6

Real data (changes) versus simulated data via the $CIR^3$ model Eq. (2). The top left graph shows the volatility, while the top right graph shows the trend (i.e., the EWMA). The bottom graph in the center displays the changes of real data. In-sample results

Table 4 Real data (changes) versus simulations

5.3.1 Partitioning and regime changes in data

One may wonder if, because of the extended time period under consideration, data can be more simply explained by a classical ARIMA which models both the moving average and autoregressive components (see Sect. 3.3), coupled with a GARCH process to take into account volatility clustering (see Sect. 3.4). To check this, we divided the dataset using the Lavielle method [42], which identifies the optimal segmentation of a time series by minimizing a contrast function that quantifies the difference between the original and segmented series. Figure 7 visually depicts the dataset partitioned into three segments, while Table 5 presents the model performance results. The proposed model outperforms an ARIMA-GARCH model in all three segments.

Fig. 7

Real data (changes) versus simulated data via the $CIR^3$ model Eq. (2). The top left graph shows the volatility, while the top right graph shows the trend (i.e., the EWMA). The bottom graph in the center displays the changes of real data. In-sample results. The vertical green bars highlight the different intervals identified by Lavielle’s algorithm [42]

Table 5 Real data (changes) versus simulations in each subsample

Fig. 8

Real trend (changes). Actual versus forecasted trend (1 month) obtained through the $CIR^3$ model Eq. (2), ARIMA-GARCH model and NRM model. Out of sample results

Fig. 9

Real data (changes) versus $CIR^3$ Eq. (2) forecasts (1 month). Out of sample results

5.4 Forecasting

To predict changes in the industrial production of electric and gas utilities through our model in system (2), we use the expectations (22), (23) for $\theta _t$ and $v_t$, respectively. In addition, as the distribution of $X_t$ is unknown, we take the Monte Carlo approximation, i.e.

$$\begin{aligned} \hat{X}_{u+z}=\frac{1}{N}\sum _{r=1}^{N} \hat{X}_{u+z,r} \qquad (z\ge 1), \end{aligned}$$

(34)

where, for each iteration r, $\hat{X}_{u+z,r}$ is computed as in Eq. (31), and N =100,000.

Figures 8 and 9 show how close the $CIR^3$ model is to both real data and the selected benchmarks. Table 6 summarizes the results in terms of MAPE and NMRSE thus confirming, once again, that $CIR^3$ forecasts are quite accurate. Here we are interested in forecasting the next data point in terms of process and trend while, for longer horizons, we check how far the estimate goes. Note that it makes sense to add the MAPE to the error analysis as, in this instance, we are dealing with forecasts.

Table 6 MAPE and NRMSE obtained over the horizon of 1, 3 and 6 months

Comparison of competing predictions Given an actual series and two competing predictions, the Diebold and Mariano test [23] calculates a measure of the predictive accuracy of those models. The null hypothesis is that the two methods have the same forecast accuracy. Similarly, the Harvey, Leybourne and Newbold test [31], checks the hypothesis of equal accuracy in forecast performance of two sources of predictions. Table 7 demonstrates that the forecasts of the three models are statistically different.

Receiver operating characteristic (ROC) analysis Having confirmed that the models provide statistically different forecasts. Next is to complement the accuracy of forecasts presented in Table 6 with the receiver operating characteristic (ROC) analysis. The ROC curve plots the true positive rate (TPR) against the false positive rate (FPR) at various threshold settings. The TPR, also said sensitivity, indicates probability of detection. The FPR, also called sensitivity, indicates the probability of a false alarm. In general, the closer the plot is to the top and left-hand borders, the more accurate the test is. Red circles indicate coordinates in terms of 1-specificity (x-axis) and sensitivity (y-axis) of the optimal threshold. This means that the closer the red dot is to the origin, the better. For more details and applications see [14, 47, 53, 65]. Figure 10 and Table 8 confirm that the best model is the $CIR^3$. Note that, for sake of space, we show only the results over 1-month horizon but similar results have been obtained over the 3 and 6-month horizon.

Table 7 p-value from the Diebold–Mariano (DM) test and the Harvey–Leybourne–Newbold (HLN) test for assessing the different nature of two series of predictions

Fig. 10

ROC curves for the three different models (1-month horizon). Red circles indicate coordinates in terms of 1-specificity (x-axis) and sensitivity (y-axis) of the optimal threshold. Top chart $CIR^3$, bottom left chart ARIMA-GARCH, bottom right chart NRM model

Table 8 Quantitative parameters of the ROC (1-month horizon)

6 Conclusions

In this article, we have shown how a three-factor stochastic model, which we call $CIR^3$, can be used to predict changes in the industrial production of electric and gas utilities. To this end, we introduce a model described by a system of SDEs (which accounts for several stylized facts including mean reversion to a stochastic level, stochastic volatility, and correlations/autocorrelations) and discuss the existence and uniqueness of the solution. Next, since the process $S_t$ is correlated with its mean and volatility, by means of Lamperti transformations we obtained an uncorrelated auxiliary process $X_t$ useful for simulation. Numerical simulations show that the proposed model has an edge over the benchmarks considered.