Arbitrage-free Nelson–Siegel model for multiple yield curves

Abstract

We propose an affine term structure model that allows for tenor-dependence of yield curves and thus for different risk categories in interbank rates, an important feature of post-crisis interest rate markets. The model has a Nelson–Siegel factor loading structure and thus economically well interpretable parameters. We show that the model is tractable in terms of estimation and provides good in-sample fit and out-of-sample forecasting performance. The proposed model is arbitrage-free across maturities and tenors, and thus perfectly suited for risk management and pricing purposes. We apply our framework to the pricing of caplets in order to illustrate its practical applicability and its suitability for stress testing.

1 Introduction

The global financial crisis of 2007/2008 has triggered some structural changes in interest rate markets that invalidated the classical notion of a single yield curve. In particular, in post-crisis interest rate markets, yields vary not only with respect to maturity but depend also on the length of the tenor structure of the interest rate derivative from which they are calculated. Thus, nowadays interest rate markets are characterized by multiple (tenor dependent) term structures that reflect different risk categories. This has important implications for pricing, portfolio allocation, risk management and monetary policy.

In this paper, we construct an affine term structure model that (1) allows for tenor-dependent yield curves, (2) is free of arbitrage across maturities and tenors, (3) is computationally tractable with (4) economically interpretable parameters, and (5) provides superior in-sample fit and out-of-sample forecasting performance within the Nelson–Siegel class of models. The model is suitable also for negative interest rate environments and allows for semi-closed pricing formulas for various interest rate derivatives.

Our paper relates to a large literature on term structure models. The models introduced in [28, 30] are heavily used by various central banks to fit daily yield curves (see e.g. [1, 9]). They are flexible enough to describe various different shapes of interest rate term structures and the dynamic extension of the Nelson–Siegel model introduced in [6] has been shown to be highly tractable and at the same time provides accurate forecasting results. While the Nelson–Siegel parameters (as well as the Svensson parameters) have convenient economic interpretations as level, slope and curvature factors, the model is not arbitrage-free and hence not suitable for pricing purposes and of limited use for risk management. Affine arbitrage-free term-structure models have been introduced e.g. in [5, 8] in the single curve setting. However, as shown in [7] the canonical affine models typically provide poor forecasting performance. This shortcoming is overcome in [2] who introduce an arbitrage-free affine specification of the Nelson–Siegel model in the single curve setting.

The financial crisis of 2007/2008, however, has invalidated the classical notion of a single yield curve. Reference [20] points out the importance of taking different risk categories in interbank rates into account. In the past years, affine short rate models in the multiple curve setting have been introduced in [14, 16, 19, 25,26,27] among others. Affine Libor models for tenor dependent yields have been developed in [17, 18]. Reference [4] provides a very general framework to model multiple yield curves through affine processes which comprises short rate models, Libor market models and Heath–Jarrow–Morton (HJM) models of tenor dependent yield curves. In particular, their approach relies on a general numéraire process and the modelling of multiplicative spreads between tenor dependent interbank rates and Overnight Indexed Swap (OIS) rates as first suggested in [3].

Our approach builds on the idea developed in [2] and combines it with the general affine model introduced in [4] in order to develop an affine arbitrage-free multiple curve version of the Nelson–Siegel model. The proposed model inherits advantages from both the affine models as well as the parsimonious Nelson–Siegel class of models: it can be estimated through standard techniques (Kalman filter) and presents good in- and out-of-sample performances. Since it is free of arbitrage across maturities and tenors and has parameters with a sound economic interpretation, the model is well suited for derivative pricing and tailor-made for scenario generation, stress testing and other risk management purposes. We illustrate this by applying our model to the pricing of caplets and by analysing the impact of level, slope and curvature shifts in the discount curve and the multiplicative log spreads on the caplet price.

The remainder of the paper is structured as follows. In Sect. 2 we specify the financial market setting of our model. Section 3 summarizes the general affine multiple curve model introduced in [4] adapted to our market setting. The specification of the arbitrage-free multiple curve Nelson–Siegel model is then derived in Sect. 4. Estimation and forecasting results are provided in Sect. 5 while Sect. 6 discusses the pricing of interest rate derivatives in the proposed model. Section 7 concludes.

2 Financial market instruments

We consider a financial market in which Xibor rates are quoted for a finite and generic set of tenors ${\mathscr {D}}=\{\delta _1,\ldots ,\delta _m\}$ with $\delta _1<\cdots <\delta _m$ for some $m\in \mathbb {N}$ and we denote by $L_t^{k}(t,t+\delta _{\mathrm{k}})$ the (spot) Xibor rate prevailing at time t for the time interval $[t,t+\delta _{\mathrm{k}}]$. The tenor $\delta _{k}$ is typically equal to 1 week (1W) or several months (1M, 2M, 3M, 6M, or 12M). We assume that forward rate agreements with Xibor rates of different tenors as reference rate are traded in the market.

Definition 1

A forward rate agreement (FRA) with tenor $\delta _{k}$, settlement date T and strike K, is a contract stating that the fixed interest rate K will apply to a certain nominal value N, which we assume to be normalized to one, over the specified future period $[T,T+\delta _{k}]$. The payoff at maturity $T+\delta _{k}$ is then given by

$$\begin{aligned} \delta _{k} (L_T^{k}(T,T+\delta _{k})- K). \end{aligned}$$

The interest rate K which ensures that the FRA for period $[T,T+\delta _{k}]$ has value zero at time t is referred to as FRA rate and will be denoted by $L^{k}_t(T,T+\delta _{k})$ in the sequel.

In addition, we assume that overnight indexed swaps are traded in the market. The EONIA rate is the reference rate for overnight borrowing in the interbank market in the Eurozone and represents the underlying of overnight indexed swaps in the Eurozone.

Definition 2

An overnight indexed swap (OIS) is a contract where an investor agrees to pay a predetermined fixed rate K on a notional N at some predetermined equidistant future dates $\{T_0,\ldots , T_n\}$ with tenor $\delta =T_i-T_{i-1}$ to the other party. In return, the investor receives interest rate payments at a floating interest rate on the same notional principal. The floating rate in an OIS is indexed to an overnight rate (such as the EONIA in the Eurozone) and is given by simply compounding the consecutive overnight rates between the dates $T_i$ and $T_i+\delta$. In the following, we again normalize the notional N to one. The fixed rate K such that the OIS contract for the time period $[T_0,T_n]$ has zero value at time $t\le T_0$ is called the time t forward swap rate and will be denoted by $K_t^{\mathrm{OIS}}(T_0,T_n)$.

Applying appropriate bootstrapping techniques (see e.g. [15]) to the quoted OIS forward swap rates, we can extract the term structure $T\mapsto P^{d}(t,T)$ of OIS zero-coupon bond prices $P^{d}(t,T)$ at time t and we define the simple compounded OIS spot rate at time t for the time period $[t,t+\delta ]$ as

$$\begin{aligned} L_t^{d}(t,t+\delta ):= \frac{1}{\delta }\left( \frac{1}{P^{d}(t,t+\delta )}-1\right) . \end{aligned}$$

From the bootstrapped OIS zero-coupon bond prices, we can extract the simple compounded forward OIS rate $L_t^d(T,T+\delta )$ at time t for the time period $[T,T+\delta ]$ which is defined via

$$\begin{aligned} 1+\delta L_t^{d}(T,T+\delta ):= \frac{P^{d}(t,T)}{P^d(t,T+\delta )}. \end{aligned}$$

The OIS rates will be considered as risk-free. This is motivated by the wide dissemination of collateral agreements to reduce the counterparty risk associated with OTC-traded derivatives.¹ Collateralisation is based on discounting at an overnight rate and reflects a funding and hedging mechanism. As a consequence, prices of OTC-traded derivatives quoted in the interbank market can be considered free of credit and liquidity risk.

We then have the following definition of a multiple curve financial market (compare [4, 13]).

Definition 3

For a fixed time horizon $\mathbb {T}<\infty$ we consider a financial market consisting of the following basic traded assets

• 1. OIS zero-coupon bonds for all maturities $T\in [0,\mathbb {T}]$, and

• 2. FRA contracts for all maturities $T\in [0,\mathbb {T}]$ and for all tenors ${\delta _1,\ldots , \delta _m}$.

The risk-free term structure can be derived from the OIS bonds. The tenor-dependent (risky) yield curves reflect different levels of credit and liquidity risk in the interbank market and can be extracted from quoted FRA and swap rates of corresponding tenors. Since the fair swap rate $S_t^k$ at time $t\le T_1$ of a swap with tenor $\delta _k$ and cashflow dates $T_1,\ldots ,T_n$ can be represented through the relation

$$\begin{aligned} S_t^k=\frac{\sum _{j=1}^n L^k_t(T_{j-1},T_{j-1}+\delta _k)}{\sum _{j=1}^n \delta _k P^d(t,T_j)}+K \end{aligned}$$

as a function of FRA rates for some fixed strike rate $K\in \mathbb {R}$ and tenor length $\delta _k$, it suffices to assume that FRA contracts for all maturities and tenors are traded in the market.

3 Continuous-time affine model for tenor-dependent term structures

Next, we set up the continuous time affine model for multiple yield curves. Therefore, we first fix the dynamics of the risk-free short rate. Afterwards, we specify the dynamics of the spreads between tenor-dependent (risky) yields and the risk-free yields in order to obtain the risky term structures.

In the first step, we follow the classical approach of [8] in modelling the term structure of risk-free interest rates as an affine function of underlying latent factors. We suppose that prices are discounted at the OIS rate, i.e., the numéraire $B=(B_t)_{0\le t\le \mathbb {T}}$ is given by the OIS bank account

$$\begin{aligned} B_t=\exp \left( \int _0^t r^{d}_sds\right) , \end{aligned}$$

for $t\in [0,\mathbb {T}],$ where $r^{d}_t$ denotes the overnight short rate at time t. Further, we denote by $\mathbb {Q}$ the associated (spot) martingale measure such that prices of traded assets can be calculated as conditional expectations of B-discounted payoffs under $\mathbb {Q}$. We consider the probability space $(\Omega ,{\mathscr {F}},\mathbb {Q})$ with filtration $({\mathscr {F}}_t)_{t\ge 0}$ generated by a standard Brownian motion $(W_t)_{t\ge 0}$ on $\mathbb {R}^{n}$ under $\mathbb {Q}$. We model the short-rate $r^d$ as an affine function of a state variable $X_t$ that follows an affine process² on some open subset $M\subset \mathbb {R}^n$. More specifically, we assume that $X_t$ satisfies the stochastic differential equation

$$\begin{aligned} dX_t=K(t) [\theta (t)-X_t]dt+\Sigma (t)D(X_t,t) dW_t \end{aligned}$$

under $\mathbb {Q}$, where $\theta :[0,T]\rightarrow \mathbb {R}^n$ and $K:[0,T]\rightarrow \mathbb {R}^{n\times n}$ are bounded, continuous functions. Moreover, the matrix $\Sigma :[0,T]\rightarrow \mathbb {R}^{n\times n}$ is assumed to be a bounded, continuous function and $D:\mathbb {R}^n\times [0,T]\rightarrow \mathbb {R}^{n\times n}$ has diagonal structure,

$$\begin{aligned} D(X_t,t)= & {} \mathrm{diag}\left( \sqrt{\gamma ^1(t)+\vartheta _1^1(t) X_t^1+\cdots +\vartheta ^1_n(t)X_t^n},\ldots ,\right. \left. \sqrt{\gamma ^n(t)+\vartheta _1^n(t) X_t^1+\cdots +\vartheta ^n_n(t)X_t^n}\right) \end{aligned}$$

for $\gamma =(\gamma ^1,\ldots ,\gamma ^n):[0,T]\rightarrow \mathbb {R}^n$ and $\vartheta =(\vartheta _i^j)_{i,j=1,\ldots ,n}:[0,T]\rightarrow \mathbb {R}^{n\times n}$ bounded and continuous functions. We assume that the overnight (discount) short rate $(r_t^{d})_{t\ge 0}$ is an affine function of the state variable, i.e.,

$$\begin{aligned} r_t^{d}=\rho _0^{d}(t)+(\rho _1^{d})^\top X_t, \end{aligned}$$

for a bounded and continuous function $\rho _0^{d}:[0,\mathbb {T}]\rightarrow \mathbb {R}$ and a vector $\rho _1^{d}\in \mathbb {R}^n.$

In the second step, in order to introduce tenor-dependent term structures, we follow [4] and model the multiplicative spot spreads

$$\begin{aligned} S^k(t,t):= \frac{1+\delta _{k} L_t^{k}(t,t+\delta _{k})}{1+\delta _{ k} L_t^{d}(t,t+\delta _{k})}=(1+\delta _{k} L_t^{k}(t,t+\delta _{k})) P^{d}(t,t+\delta _{k}) \end{aligned}$$

between Xibor rates and simple compounded OIS spot rates for each tenor k as exponentially affine in $X_t$. Therefore, we assume that

$$\begin{aligned} \log S^{k}(t,t)= \rho _0^{k}(t)+(\rho _1^{k})^\top X_t \end{aligned}$$

for a bounded and continuous function $\rho _0^{k}:[0,\mathbb {T}]\rightarrow \mathbb {R}$ and a vector $\rho _1^{k}\in \mathbb {R}^n.$ Note that the spot spreads can be directly calculated from the quoted Xibor and OIS rates. Moreover, we define the multiplicative forward spreads $S^{k}(t,T)$ for $0\le t\le T\le \mathbb {T}$ and tenor k by

$$\begin{aligned} S^{k}(t,T):=\frac{1+\delta _{k} L_t^{k}(T,T+\delta _{k})}{1+\delta _{k} L_t^{d}(T,T+\delta _{k})}=(1+\delta _{k} L_t^{k}(T,T+\delta _{k}))\frac{P^{d}(t,T+\delta _{k})}{P^{d}(t,T)}. \end{aligned}$$

(1)

The T-forward measure equivalent to the pricing measure $\mathbb {Q}$ is defined via the Radon-Nikodym derivative

$$\begin{aligned} \frac{d\mathbb {Q}_T}{d\mathbb {Q}}\Big |_{{\mathscr {F}}_t}= \frac{P^d(t,T)}{P^d(0,T)\cdot B_t} \end{aligned}$$

with $P^d(t,T)=\mathbb {E}^{\mathbb {Q}}[B_t/B_T|{\mathscr {F}}_t]$ the time t price of a discount (OIS) bond with maturity T. As shown in [4, Prop. 2.5], the fair FRA rate for tenor $\delta _{k}$ can then be expressed as conditional expectation of the (spot) Xibor rate of tenor $\delta _{k}$, i.e.,

$$\begin{aligned} L_t^{k}(T,T+\delta _{k})=\mathbb {E}^{\mathbb {Q}_{T+\delta _{k}}}[L_T^{k}(T,T+\delta _{k})|{\mathscr {F}}_t], \end{aligned}$$

for all $0\le t\le T\le \mathbb {T}.$ Similarly, the multiplicative (forward) spread satisfies

$$\begin{aligned} S^{k}(t,T)=\mathbb {E}^{\mathbb {Q}_T}[S^{k}(T,T)|{\mathscr {F}}_t], \end{aligned}$$

for all $0\le t\le T\le \mathbb {T}.$ It can be shown that X generates exponentially affine discount bond prices $P^{d}(t,T)$ and forward spreads $S^{k}(t,T)$. More explicitly, by applying Prop. 3.16 in [4], the discount bond prices and forward multiplicative spreads for tenor k are given by

$$\begin{aligned} P^{d}(t,T)= & {} \mathbb {E}^{\mathbb {Q}}\left[ \exp \left( -\int _t^T r^{d}_udu\right) |{\mathscr {F}}_t\right] =\mathbb {E}^{\mathbb {Q}}\left[ \exp \left( -\int _t^T \rho _0^{d}(u) du- \int _t^T (\rho _1^{d})^\top X_udu\right) |{\mathscr {F}}_t\right] \nonumber \\= & {} \exp \left( {\mathscr {A}}^{d}(t,T)+{\mathscr {B}}^{d}(T-t)^\top X_t\right) \end{aligned}$$

(2)

$$\begin{aligned} S^k(t,T)= & {} \mathbb {E}^{\mathbb {Q}_T}\left[ S^{k}(T,T)|{\mathscr {F}}_t\right] = \mathbb {E}^{\mathbb {Q}}\left[ S^{k}(T,T) \frac{d\mathbb {Q}_T}{d\mathbb {Q}}\Big |_{{\mathscr {F}}_t}\right] / \left( \frac{d\mathbb {Q}_T}{d\mathbb {Q}}\Big |_{{\mathscr {F}}_t}\right) \nonumber \\= & {} \frac{B_t}{P^d(t,T)}\mathbb {E}^{\mathbb {Q}}\left[ S^{k}(T,T) \frac{P^d(T,T)}{ B_T}|{\mathscr {F}}_t\right] \nonumber \\= & {} \frac{1}{P^d(t,T)}\mathbb {E}^{\mathbb {Q}}\left[ \exp \left( \rho _0^{k}(T)+ (\rho _1^{k})^{\top } X_T-\int _t^T \rho _0^{d}(u) du-\int _t^T (\rho _1^{d} )^\top X_udu \right) |{\mathscr {F}}_t\right] \nonumber \\= & {} \exp \left( {\mathscr {A}}^k(t,T)+{\mathscr {B}}^k(T-t)^\top X_t\right) \end{aligned}$$

(3)

for all $0\le t\le T\le \mathbb {T}$ and all $k=1,\ldots ,m$, where

$$\begin{aligned} {\mathscr {A}}^{d}(t,T)= & {} -\int _t^T \rho _0^{d}(u) du+\phi (T-t,0,-\rho _1^{\mathrm{d}})\\ {\mathscr {B}}^{d}(T-t)= & {} \psi (T-t,0,-\rho _1^{d})\\ {\mathscr {A}}^{k}(t,T)= & {} \rho _0^{k}(T)+\phi (T-t,\rho _1^{k},-\rho _1^{d})-\phi (T-t,0,-\rho _1^{d})\\ {\mathscr {B}}^{k}(T-t)= & {} \psi (T-t,\rho _1^{k},-\rho _1^{d})-\psi (T-t,0,-\rho _1^{d}), \end{aligned}$$

with $\phi$ and $\psi$ denoting the characteristic exponents of the process $Y=(X,\int _0^{\cdot } X_sds)$, which are given as solutions to the system of ordinary differential equations (ODEs)

$$\begin{aligned} \begin{array}{ccl} \frac{d}{dt}\phi (T-t,u,v)&{}=&{} - \psi (T-t,u,v)^\top K(t)\theta (t)\\ &{}&{} -\frac{1}{2}\sum _{j=1}^n \left( \Sigma ^\top (t) \psi (T-t,u,v)\psi (T-t,u,v)^\top \Sigma (t)\right) _{jj}\gamma ^j(t)\\ \frac{d}{dt}\psi (T-t,u,v)&{}=&{} K(t)^\top \psi (T-t,u,v) \\ &{}&{}-\frac{1}{2}\sum _{j=1}^n \left( \Sigma ^\top (t) \psi (T-t,u,v) \psi (T-t,u,v)^\top \Sigma (t)\right) _{jj}\vartheta ^j(t)-v \end{array} \end{aligned}$$

(4)

with boundary conditions $\phi (0,u,v)=0$ and $\psi (0,u,v)=u$. We refer to “Appendix A” for the derivation of these ODEs.

4 Arbitrage-free dynamic tenor-dependent Nelson–Siegel model

As a special case of the affine multiple term structure model outlined above, we develop in this section an arbitrage-free tenor-dependent Nelson–Siegel model. For simplicity of notation, we consider a model for only two term structures here, the discount curve and a risky curve of tenor k. Therefore, we consider unobservable state variables $X_t=(X_t^{1},\ldots , X^{6}_t)\in \mathbb {R}^6$ where the first three factors correspond to level, slope and curvature factors of the overnight (discount) curve, and the remaining variables influence the level, slope and curvature of the tenor-dependent term structure for tenor k through their impact on the multiplicative spreads. Following [2] we suppose that the overnight (discount) short rate is of the form

$$\begin{aligned} r_t^{d}=X_t^{1}+X_t^{2}, \end{aligned}$$

i.e., $r_t^d$ is determined by the sum of the level and slope factors for the discount curve and the parameters $\rho _0^{d}\equiv 0$ and $\rho _1^{d}=(1,1,0,0,0,0)^\top$ in the notation of Sect. 3. Further, we assume that the state variables have the following $\mathbb {Q}$-dynamics

$$\begin{aligned} dX_t =K\left[ \theta -X_t\right] dt+\Sigma \, dW_t, \end{aligned}$$

with $\theta =(\theta _1,\ldots ,\theta _6)$ and matrix $K\in \mathbb {R}^{6\times 6}$ of triangular form

for $\lambda _d,\lambda _k>0.$ In the following we will denote the upper left $3\times 3$ submatrix of K by $K^{d}$ and the lower right $3\times 3$ submatrix by $K^{k}$. Further, suppose that $\Sigma \in \mathbb {R}^{6\times 6}$ has triangular form

Hence, the first three factors $(X_t^1,X_t^2,X_t^3)$, which influence the discount curve, are independent of the last three factors $(X_t^4,X_t^5,X_t^6)$, which affect the tenor spreads, and vice versa. In analogy to [2] and by application of Eq. (2), we can express the risk-free zero-coupon bond prices in this model as follows

$$\begin{aligned} P^{d}(t,T)= \mathbb {E}^{\mathbb {Q}}_t\left[ \exp \left( -\int _t^T r_u^{d}du\right) \right] = \exp \left( {\mathscr {A}}^{d}(t,T)+{\mathscr {B}}^{d}(T-t)X_t\right) , \end{aligned}$$

where we have

$$\begin{aligned} \frac{d}{dt} {\mathscr {A}}^{d}(t,T)= & {} \displaystyle \rho _0^{d}+\frac{d}{dt} \phi (T-t,0,-\rho _1^{d})\\= & {} \displaystyle - \psi (T-t,0,-\rho _1^{d})^\top K\theta -\frac{1}{2}\sum _{j=1}^6\left( \Sigma ^\top \psi (T-t,0,-\rho _1^{d})\psi (T-t,0,-\rho _1^{d})^\top \Sigma \right) _{jj}, \end{aligned}$$

because $\rho _0^{d}\equiv 0$ and $\gamma _j\equiv 1$ in this setting, and

$$\begin{aligned} \frac{d}{dt} {\mathscr {B}}^{d}(T-t)= \frac{d}{dt} \psi (T-t,0,-\rho _1^{d})=K^\top \psi (T-t,0,-\rho _1^{d})+ \rho _1^{d}, \end{aligned}$$

as $\vartheta ^j\equiv 0$ in this setting. The latter equation can be rewritten as

$$\begin{aligned} \frac{d}{dt} \psi (T-t,0,-\rho _1^{d})=\left( \begin{array}{c} 1\\ 1\\ 0\\ 0\\ 0\\ 0 \end{array}\right) +\left( \begin{array}{c} 0\\ \lambda _d\, \psi _2(T-t,0,-\rho _1^{d})\\ -\lambda _d\, \psi _2(T-t,0,-\rho _1^{d})+\lambda _d\, \psi _3(T-t,0,-\rho _1^{d})\\ 0\\ \lambda _k\, \psi _5(T-t,0,-\rho _1^{d})\\ -\lambda _k\, \psi _5(T-t,0,-\rho _1^{d})+\lambda _k\, \psi _6(T-t,0,-\rho _1^{d})\\ \end{array}\right) \end{aligned}$$

Due to the boundary condition $\psi (0,u,v)=u$ we obtain that the fifth and sixth component of the vector $\psi (T-t,0,-\rho _1^{d})$ are equal to zero and we have

$$\begin{aligned} \psi _i(T-t,0,-\rho _1^d)=0\quad \text{ for }\quad i=4,5,6. \end{aligned}$$

(5)

Thus, due to the special choice of the matrices K and $\Sigma$, we can rewrite the discount bond price as

$$\begin{aligned} P^{d}(t,T)=\exp \left( \sum _{i=1}^3 \psi _i^d(t,T)\, X_t^i +{\mathscr {A}}^{d}(t,T)\right) , \end{aligned}$$

where the functions $\psi ^d(t,T)=(\psi _1^d(t,T),\psi _2^d(t,T),\psi _3^d(t,T))$ with $\psi _i^d(t,T)=\psi _i(T-t,0,-\rho _1^d)$, for $i=1,2,3$, are solutions to the system of Riccati equations

$$\begin{aligned} \left( \begin{array}{c} \frac{d}{dt}\psi _1^d(t,T)\\ \frac{d}{dt}\psi _2^d(t,T)\\ \frac{d}{dt} \psi _3^d(t,T) \end{array} \right) = \left( \begin{array}{ccc} 1\\ 1\\ 0 \end{array}\right) + \left( \begin{array}{ccc} 0&{}0&{}0\\ 0&{}\lambda _d&{}0\\ 0&{}-\lambda _d&{}\lambda _d \end{array}\right) \left( \begin{array}{c} \psi _1^d(t,T)\\ \psi _2^d(t,T)\\ \psi _3^d(t,T) \end{array}\right) \end{aligned}$$

and the function ${\mathscr {A}}^{d}$ solves

$$\begin{aligned} \frac{d{\mathscr {A}}^{\mathrm{d}}(t,T)}{dt}=-\psi ^{\mathrm{d}}(t,T)^\top K^{\mathrm{d}}\theta ^{\mathrm{d}}-\frac{1}{2}\sum _{i=1}^3 ((\Sigma ^\mathrm{d})^\top \psi ^{\mathrm{d}}(t,T)\psi ^{\mathrm{d}}(t,T)^\top \Sigma ^\mathrm{d})_{j,j} \end{aligned}$$

where $\theta ^\mathrm{d}=(\theta ^{d}_1,\theta ^{d}_2,\theta ^{d}_3)^\top$. Hence, the discount bond prices are determined solely by the first three latent factors. The boundary conditions are $\psi _1^d(T,T)=\psi _2^d(T,T)=\psi _3^d(T,T)={\mathscr {A}}^{d}(T,T)=0.$ Similarly to [2], we obtain that the solutions to the ODEs are equal to the Nelson–Siegel factor loadings

$$\begin{aligned} \psi _1^d(t,T)= & {} -(T-t)\\ \psi _2^d(t,T)= & {} -\frac{1-e^{-\lambda _d(T-t)}}{\lambda _d} \\ \psi _3^d(t,T)= & {} (T-t)e^{-\lambda _d(T-t)}-\frac{1-e^{-\lambda _d(T-t)}}{\lambda _d} \end{aligned}$$

and ${\mathscr {A}}^{d}$ is given by

$$\begin{aligned} {\mathscr {A}}^d(t,T)= & {} (K^{d} \theta ^{d})_2 \int _t^T \psi _2^d(s,T) ds+(K^{d}\theta ^{d})_3 \int _t^T \psi _3^d(s,T) ds\\&+\frac{1}{2}\sum _{j=1}^3 \int _t^T ((\Sigma ^{ d})^\top \psi ^d(s,T)\psi ^{d}(s,T)^\top \Sigma ^{d})_{j,j} ds. \end{aligned}$$

Therefore, the risk-free (discount) yields $y^{d}_t(\tau )$ at time t for time-to-maturity $\tau =T-t>0$ are described by a function of the form

$$\begin{aligned} y^{d}_t(\tau )= & {} \displaystyle -\frac{1}{T-t}\log P^{\mathrm{d}}(t,T)\nonumber \\= & {} \displaystyle X_t^1+\frac{1-e^{-\lambda _d\tau }}{\lambda _d \tau } X_t^{2}+\left[ \frac{1-e^{-\lambda _d \tau }}{\lambda _d \tau }-e^{-\lambda _d \tau }\right] X_t^{3}-\frac{{\mathscr {A}}^{d}(t,t+\tau )}{\tau } \end{aligned}$$

(6)

Thus, factor loadings agree with those in the Nelson–Siegel model but there is an additional "yield-adjustment term" $-{\mathscr {A}}^{d}(t,T)/(T-t)$ which depends on the maturity of the bond. As has been shown in [2], by taking this additional term into account, the classical dynamic Nelson–Siegel model developed in [6] can be turned into an arbitrage-free term structure model. In other words, the yield-adjustment-term ensures absence of arbitrage across maturities in our model.

Next, we turn to the term structure of interest rates for tenor k. Therefore, we assume that the multiplicative spot spread for tenor k is of the form

$$\begin{aligned} \log S^{k}(t,t)=X_t^4+X_t^5, \end{aligned}$$

i.e. $\rho _0^{k}=0$ and $\rho _1^{k}=(0,0,0,1,1,0)^\top$ in the notation of Sect. 3. We obtain from Eq. (3) that the tenor-dependent multiplicative forward spreads satisfy

$$\begin{aligned} S^{k}(t,T)=\exp \left( {\mathscr {A}}^{k}(t,T)+{\mathscr {B}}^{k}(T-t) X_t \right) \end{aligned}$$

with

$$\begin{aligned}&\frac{d}{dt} {\mathscr {A}}^{k}(t,T)=\displaystyle \frac{d}{dt} \phi (T-t,\rho _1^{k},-\rho _1^{d})-\frac{d}{dt}\phi (T-t,0,-\rho _1^{d})\\&\quad =\displaystyle -\psi (T-t,\rho _1^{k},-\rho _1^{d})^\top K\theta -\frac{1}{2}\sum _{j=1}^6 \left( \Sigma ^\top \psi (T-t,\rho _1^{k},-\rho _1^{d})\psi (T-t,\rho _1^{k},-\rho _1^{d})^\top \Sigma \right) _{jj} \\&\qquad \displaystyle +\psi (T-t,0,-\rho _1^{d})^\top K\theta +\frac{1}{2}\sum _{j=1}^6 \left( \Sigma ^\top \psi (T-t,0,-\rho _1^{d})\psi (T-t,0,-\rho _1^{d})^\top \Sigma \right) _{jj} \end{aligned}$$

since $\rho _0^{k}\equiv 0$ and $\gamma _j\equiv 1$ in this setting. Moreover, we have

$$\begin{aligned} \frac{d}{dt} {\mathscr {B}}^{k}(T-t)= & {} \displaystyle \frac{d}{dt}\psi (T-t,\rho _1^{k},-\rho _1^{d})-\frac{d}{dt}\psi (T-t,0,-\rho _1^{d})\\= & {} \displaystyle K^\top \psi (T-t,\rho _1^{k},-\rho _1^{d}) +\rho _1^{d} - K^\top \psi (T-t,0,-\rho _1^{d})-\rho _1^{d} \end{aligned}$$

as $\vartheta ^j\equiv 0$. The latter equation implies that

$$\begin{aligned} \frac{d}{dt}{\mathscr {B}}^{k}(T-t)= \left( \begin{array}{c} 0\\ 0\\ 0\\ 0\\ \lambda _k\, \psi _5(T-t,\rho _1^{k},-\rho _1^{d})\\ -\lambda _k\, \psi _5(T-t,\rho _1^{k},-\rho _1^{d})+\lambda _k\, \psi _6(T-t,\rho _1^{k},-\rho _1^{d}) \\ \end{array} \right) \end{aligned}$$

where we use the fact that $\psi _i(T-t,0,-\rho _1^{d})=0$ for $i=4,5,6$ (compare Eq. (5)) and the fact that we have $\psi _i(T-t,\rho _1^{k},-\rho _1^{d})=\psi _i(T-t,0,-\rho _1^{d})$ for the first three components $i=1,2,3$, as implied by the boundary condition $\psi (0,u,v)=u$ for $u=\rho _1^{k}=(0,0,0,1,1,0)^\top$. Hence, we can express the multiplicative forward spreads as

$$\begin{aligned} S^{k}(t,T)= & {} \displaystyle \exp \left( \sum _{i=1}^3 \psi _i^k(t,T) X_t^{3+i}+{\mathscr {A}}^{k}(t,T)\right) \end{aligned}$$

(7)

where the functions $\psi ^k(t,T)=(\psi ^k_1(t,T),\psi _2^k(t,T),\psi _3^k(t,T))$ with $\psi _i^k(t,T)=\psi _{3+i}(T-t,\rho _1^k,-\rho _1^d)$ for $i=1,2,3$, are solutions to the system of Riccati equations

$$\begin{aligned} \left( \begin{array}{c} \frac{d}{dt}\psi _1^k(t,T) \\ \frac{d}{dt}\psi _2^k(t,T) \\ \frac{d}{dt}\psi _3^k(t,T) \end{array} \right) = \left( \begin{array}{ccc} 0&{}0&{}0\\ 0&{}\lambda _k&{}0\\ 0&{}-\lambda _k&{}\lambda _k \end{array}\right) \left( \begin{array}{c} \psi _1^k(t,T) \\ \psi _2^k(t,T) \\ \psi _3^k(t,T) \end{array}\right) \end{aligned}$$

and the function ${\mathscr {A}}^{k}$ solves

$$\begin{aligned} \frac{d{\mathscr {A}}^{k}(t,T)}{dt}=-\psi ^{k}(t,T)^\top K^{k}\theta ^{k}-\frac{1}{2}\sum _{i=1}^3 ((\Sigma ^{k})^\top \psi ^{k}(t,T)\psi ^{k}(t,T)^\top \Sigma ^{k})_{j,j} \end{aligned}$$

where $\theta ^{k}=(\theta _4,\theta _5,\theta _6)^\top .$ Hence, the multiplicative forward spreads are solely determined by the last three latent factors. The boundary conditions are given by $\psi ^k(T,T)=(1,1,0)$ and ${\mathscr {A}}^{k}(T,T)=0$. The solution of this system of equations is given by

$$\begin{aligned} \begin{array}{ccl} \psi ^k_1(t,T)&{}=&{} 1\\ \psi ^{k}_2(t,T)&{}=&{}\displaystyle e^{-\lambda _k(T-t)}\\ \psi ^{k}_3(t,T)&{}=&{}\displaystyle (T-t)\lambda _k e^{-\lambda _k(T-t)} \end{array} \end{aligned}$$

and

$$\begin{aligned} \begin{array}{ccl} {\mathscr {A}}^{k}(t,T)&{}=&{} (K^{k}\theta ^{k})_2 \int _t^T \psi _2^{k}(s,T) ds+(K^{k}\theta ^{k})_3 \int _t^T \psi _3^{k}(s,T) ds\\ &{}&{}+\frac{1}{2}\sum _{j=1}^3 \int _t^T ((\Sigma ^{ k})^\top \psi ^{k}(s,T)\psi ^{k}(s,T)^\top \Sigma ^{k})_{j,j} ds. \end{array} \end{aligned}$$

Thus, the bond prices and multiplicative spreads are both exponentially affine in $X_t$ with coefficients that have a similar structure as the Nelson–Siegel factor loadings. We now consider the risky (tenor-dependent) term structure for tenor k. The one-period continuously compounded yields $y^{k}_t(t+\delta _{k})$ can be calculated from the simple compounded spot Xibor rates as follows

$$\begin{aligned} \begin{array}{ccl} y^{k}_t(t+\delta _{k})&{}=&{} \frac{1}{\delta _{k}} \log \left( 1+\delta _{k} L_t^{k}(t,t+\delta _{k}) \right) \\ &{}=&{}\frac{1}{\delta _{k}} \log \left( \frac{S^{k}(t,t)}{P^{d}(t,t+\delta _{k})} \right) \\ &{}=&{} \frac{1}{\delta _{k}} \log S^{k}(t,t))- \frac{1}{\delta _{k}} \log P^{d}(t,t+\delta _{k})=y_t^d(t+\delta _k)+\frac{1}{\delta _{k}} \log S^{k}(t,t)), \end{array} \end{aligned}$$

where we used relation (1). The multi-period yields $y^{k}_t(\tau )$ at time t for tenor k and time-to-maturity $\tau =T-t=N\delta _k$ for some $N\in \mathbb {N}$, are obtained as follows

$$\begin{aligned} \begin{array}{ccl} y^{k}_t(\tau )&{}=&{}-\frac{1}{\tau } \log \left( \prod _{n=0}^{N-1} \left( 1+\delta _{ k} L_t^{k}(t+n\delta _{k},t+(n+1)\delta _{k})\right) ^{-1}\right) \\ &{}=&{} -\frac{1}{\tau } \log \left( \prod _{n=0}^{N-1} \left( \frac{P^{d}(t,t+(n+1)\delta _{k})}{S^{k}(t,t+n\delta _k)P^{d}(t,t+n\delta _{k})}\right) \right) \\ &{}=&{}y^d_t(\tau ) +\frac{1}{\tau } \sum _{n=0}^{N-1} \log S^{k}(t,t+n\delta _{k}), \end{array} \end{aligned}$$

where we again applied relation (1). Since the discount yields are affine in $X_t$ (compare Eq. (6)) and the multiplicative forward spreads are exponentially affine in $X_t$ (compare Eq. (7)), we obtain that the tenor-dependent yields are also affine in $X_t$. Moreover, we observe that the tenor-dependent term structure is also of Nelson–Siegel shape due to the special structure of the discount short rate and the multiplicative spot spreads. As the multiplicative spreads are usually greater than one in the post crisis period, the level, slope and curvature factors for the spreads lead to a positive shift of the overnight (discount) curve so that the risky term structures are strictly larger than the discount curve. The terms ${\mathscr {A}}^k(t,t+n\delta _k)/\tau$ in the expression for the tenor-dependent yields represent “tenor-adjustment terms” which ensure absence of arbitrage across tenors.

5 Numerical results

In this section we illustrate the numerical performances of the proposed model by fitting it to real data. We start by illustrating how the historical time series of yields and tenor dependent multiplicative spreads are built, then we show in-sample and out-of-sample performances in terms of estimation and forecasting. Computations are done using Matlab^®(Version R2019b) in Microsoft Windows 10^®running on a machine equipped with Intel(R) Core(TM) i7-9750HQ CPU @2.60GHz and 16 GB of RAM.

5.1 Data

Our data set consists of daily bootstrapped discount and three month yield curves for maturities up to 10 years. More specifically, we use European market data provided by Bloomberg for the time period from September 2nd, 2005, until May 22nd, 2018. We bootstrap the discount curves from Overnight Indexed Swap (OIS) rates indexed to the EONIA rate with maturities ranging from one week up to 10 years. Further, we construct the risky 3 month yield curves from market quotes of deposit rates for 3 month maturity and swap rates with maturities between 6 months and 10 years. All yields have been bootstrapped following the procedure in [15]. In total we consider 3316 observations for yields and multiplicative spreads of 3 months tenor. From the constructed yield curves we only consider the interest rates with maturities $\tau \in \{0.25,0.5,1,3,5,7,10\}$ (expressed in years) in the in-sample estimation and out-of-sample forecasting. These have been directly bootstrapped from market data and hence do not allow for any arbitrage opportunities that might arise due to interpolation methods. Including interest rates of further maturities has only a minor impact on the results.

5.2 Yield curve fitting

In Sect. 4, we introduced an affine term structure model which is free of arbitrages across tenors and maturities and takes into account correlations between factors. We will refer to this model as correlated arbitrage-free multiple curve Nelson Siegel (AFMCNS) model. We provide a state-space formulation of the AFMCNS model and describe the Kalman filter estimation of the model in “Appendix B”. Parameters can then be estimated by maximizing numerically the log-likelihood function in (14), for which we use the built-in Matlab^® function fmincon.

To evaluate the model’s in- and out-of-sample performances, we consider three sub-models which are closely related to the correlated AFMCNS model for comparison. The first is the independent AFMCNS model, which is equivalent to the correlated one with the obvious exception that the off-diagonal elements in the matrices $K^{\mathbb {P}}$ and $\Sigma$ are equal to 0. The estimation results for the correlated as well as for the independent version of the AFMCNS model are presented below. Second, by forcing the yield and tenor adjustment terms to be equal to 0, we obtain a dynamic Nelson–Siegel model which is not arbitrage-free but adapted for a multiple-curve setting. We refer to this model as MC-DNS model. It can be written in state-space form as

$$\begin{aligned} X_t&= (I - A)\mu + A X_{t-1} + \eta _t \nonumber \\ y_t&= B X_t + \epsilon _t \end{aligned}$$

(8)

where $X_t = \{X^1_t, X^2_t, X^3_t, X^4_t, X^5_t, X^6_t\}$, $y_t = \{y^d_t(\tau _n), \log S^k_t(\tau _n)\}_{n=1}^{7}$, B is the matrix of the Nelson–Siegel factor loading coefficients, and A is a diagonal matrix in the independent MC-DNS and a full matrix in the correlated MC-DNS. Finally,

$$\begin{aligned} \left( \begin{array}{c} \eta _t \\ \epsilon _t \\ \end{array} \right) \sim N\left[ \left( \begin{array}{c} 0 \\ 0 \\ \end{array} \right) , \left( \begin{array}{cc} Q &{} 0 \\ 0 &{} H \end{array} \right) \right] , \end{aligned}$$

(9)

where H is a diagonal matrix and $Q=q q'$ is a diagonal matrix in the independent MC-DNS and a full matrix in the correlated MC-DNS. The Kalman filter for the MC-DNS model is set up following [2, Section 4.1]. Estimation results for the MC-DNS model are reported in Table 1.

Table 1 Parameter estimates of A and $\mu$ as in (8) and matrix $Q=qq'$ as in (9) of the MC-DNS model

Table 2 Parameter estimates of the AFMCNS model with 3 month tenor

5.2.1 AFMCNS model estimation

Table 2 shows the estimation results for the AFMCNS model. For the one-day conditional mean-reversion matrix $\exp \left( -K^{\mathbb {P}} /252\right)$ the elements on the main diagonal are similar in the independent and correlated case, with factors related to the discount yields more persistent than those related to the log-spreads. Off-diagonal elements appear non negligible, especially for those elements corresponding to $\{X_t^i\}_{i=4}^{6}$ for which we find a lot of values higher than 0.01 in absolute value. Concerning the long-run mean $\theta ^{\mathbb {P}}$ there is not much difference between the two models. However, the values are shifted when compared to $\mu$ (in the MC-DNS) which can be explained by the fact that we are adding the adjustment term. In fact, the yield and tenor adjustment terms are negative for all maturities and decreasing in maturity (compare Fig. 1). Since we subtract the adjustment terms in the measurement equation, the mean level in the AFMCNS model is smaller than in the MC-DNS model. Moreover, the tenor adjustment term is much smaller in size compared to the yield adjustment term (roughly by a factor 0.1) which explains why the mean level of the log spreads is less affected than the mean level of the discount yields.

Fig. 1

Yield and tenor adjustments (in basis points) in the independent and correlated AFMCNS models

When converting the volatility matrix $\Sigma$ into a one-day conditional covariance matrix³

$$\begin{aligned} Q = \int _{0}^{1/252} \exp \left( -K^{\mathbb {P}}s\right) \Sigma \Sigma '\exp \left( -(K^{\mathbb {P}})'s\right) ds, \end{aligned}$$

we obtain:

$$\begin{aligned} Q = \begin{bmatrix} \text {9.67E--08} &{} 0&{} 0&{} 0&{} 0&{} 0\\ 0&{} \text {1.80E--07}&{} 0&{} 0&{} 0&{} 0\\ 0&{} 0 &{}\text {1.49E--06}&{} 0&{} 0&{} 0\\ 0&{} 0&{} 0&{} \text {1.07E--08}&{} 0&{} 0\\ 0&{} 0&{} 0&{} 0&{} \text {1.13E--08}&{} 0\\ 0&{} 0&{} 0&{} 0&{} 0&{} \text {1.72E--07}\end{bmatrix} \end{aligned}$$

in case of independence and

$$\begin{aligned} Q = \begin{bmatrix}\text {4.09E--07} &{} -\text {4.26E--07}&{} -\text {6.67E--07}&{} 0&{} 0&{} 0\\ -\text {4.26E--07}&{} \text {4.74E--07}&{} \text {6.68E--07}&{} 0&{} 0&{} 0\\ -\text {6.67E--07}&{} \text {6.68E--07}&{} \text {2.60E--06}&{} 0&{} 0&{} 0\\ 0&{} 0&{} 0&{} \text {1.45E--10}&{} \text {2.36E--10}&{} -\text {1.96E--09}\\ 0&{} 0&{} 0&{} \text {2.36E--10}&{} \text {2.62E--09}&{} -\text {5.58E--09}\\ 0&{} 0&{} 0&{} -\text {1.96E--09}&{} -\text {5.58E--09}&{} \text {3.81E--08}\end{bmatrix} \end{aligned}$$

in the correlated case. We find that factors related to the discount yields are more volatile than those related to the log-spreads. This is comparable in case of the MC-DNS model.⁴ From the covariance estimates, we calculate correlation coefficients between factors

$$\begin{aligned} \begin{bmatrix} 1&{} {-0.9665}&{} {-0.6458} &{} 0 &{}0&{} 0\\ {-0.9665}&{} 1&{} {0.6007}&{} 0&{} 0&{} 0\\ {-0.6458}&{} {0.6007}&{} 1&{} 0&{} 0&{} 0\\ 0&{} 0&{} 0&{} 1&{} {0.3817}&{} {-0.8350}\\ 0&{} 0&{} 0&{} {0.38173}&{} 1&{} {-0.5572}\\ 0&{} 0&{} 0&{} {-0.8350}&{} {-0.5572}&{} 1 \end{bmatrix} \end{aligned}$$

and find that correlations are not negligible. E.g. there is a very strong negative correlation of -0.9665 (resp. -0.8350) between $X_1$ and $X_2$ (resp. between $X_4$ and $X_6$). This indicates that for the discount yields level shifts often go along with slope changes while for the log spreads level shifts mostly go along with curvature changes.

When comparing the log-likelihood values reported in the caption of Table 2, it is evident that the correlated version of the AFMCNS model performs better in-sample than the independent specification. This is not only due to the higher number of parameters, as largely confirmed by the likelihood ratio (LR) test for which we obtain a very high LR of 10755.21, but this is also confirmed by the results in Table 3, where root mean squared errors (RMSEs) are consistently smaller in the correlated case than in the independent factor case. RMSEs and mean errors (ME) displayed in Table 3 are computed from the differences between the historical yields and model estimated yields. Figure 2 shows a plot of these time series. This figure also appreciates the ability of the proposed model to replicate the time series of observed yields. Further, comparing the log-likelihood ratios of the MC-DNS and the AFMCNS models (reported in the captions of Tables 1 and 2) confirms superiority of the AFMCNS model. This is also confirmed by the smaller RMSEs in Table 3.

Table 3 Summary statistics for in-sample model fit

5.3 Forecasting

We evaluate the forecasting performance of our proposed model by comparing six- and twelve-months ahead forecasts of discount and tenor dependent yields with its non-arbitrage free counterpart. For convenience of exposition, we denote $y_t := \{y^d_t(\tau _n), y^k_t(\tau _n)\}_{n=1}^{7}$. Forecasting yields in the AFMCNS model consists of two steps:

• (1) Estimate model parameters over the sample period ending at time T as in Sect. 5.2.

• (2) Compute optimal h months ahead forecasts as

$$\begin{aligned} y^{AF}_{T+h} = \left( \begin{array}{c} E^{\mathbb {P}}_T[X_{T+h}^1] + \frac{1-e^{-\lambda _d \tau }}{\lambda _d} E^{\mathbb {P}}_T[X_{T+h}^2] + \left( \frac{1-e^{-\lambda _d \tau }}{\lambda _d} - e^{-\lambda _d \tau }\right) E[X_{T+h}^3]\\ E[X_{T+h}^4] + e^{-\lambda _k \tau } E^{\mathbb {P}}_T[X_{T+h}^5] + \tau \lambda _k e^{-\lambda _k \tau } E^{\mathbb {P}}_T[X_{T+h}^6] \end{array}\right) - \left( \begin{array}{c} \frac{{\mathscr {A}}^d(\tau )}{\tau }\\ -{\mathscr {A}}^k(\tau )\\ \end{array} \right) \end{aligned}$$

(10)

where $E^{\mathbb {P}}_T[X_{T+h}] = (I - \exp \left( -K^{\mathbb {P}} h)\right) )\theta ^{\mathbb {P}} + \exp \left( -K^{\mathbb {P} }h\right) X_{T}$. We are interested in computing 6 and 12 months ahead forecasts which are typically better achieved using monthly data instead of daily data. Therefore, we split our data set with daily observations in 21 datasets with monthly observations by taking one data point each month. More specifically, we construct historical time series of yields taking every 21st observation. We do so starting from each day of the first month of the dataset. In this way, we get 21 historical time series with monthly observations. Then, on each sub-dataset, we estimate the model on a 6 years (72 months) rolling window and forecast yields using Eq. (10). This produces 73 forecasts for each sub-dataset and in total $73 \times 21 = 1533$ six and twelve months ahead forecasts. In Table 4 we report the root mean squared forecasting errors (RMSFE) for the proposed arbitrage free multiple curve Nelson Siegel model (AFMCNS) and for the multiple curve dynamic Nelson Siegel (MCDNS) model for benchmark comparison. Note that we only consider here the independent versions of those models. In fact, in unreported tests, we obtained superior out of sample performances of those models with respect to their correlated counterparts. This finding is consistent with [2, Table 7]. Results in Table 4 are striking and show that the AFMCNS is better in forecasting than the MCDNS throughout all the various yields and maturities with a RMSFE around 40-60% smaller than the benchmark model for short maturities and 12-40% for higher maturities.

Fig. 2

Historical (black line) yields and yields estimated with the correlated AFMCNS model (grey line) for 7 different maturities ($\tau = \{0.25, 0.5, 1, 3, 5, 7, 10\}$, expressed in years) and tenor k equal to 3 months

Table 4 Out-of-sample forecasting results

6 Derivative pricing

As an application, we illustrate the pricing of derivative instruments under the proposed AFMCNS model. More specifically, we consider the price at time t of a caplet with notional N, reset date T, and settlement date $T+ \delta _k$. Its payoff at the settlement date is given by $N\delta _k(L(T, T+\delta _k) - K )^+$. Following [4] the time t price of the caplet can be derived in semi-closed form. Therefore, we first define

$$\begin{aligned} Y_t\equiv \log \left( \frac{S^k(t,t)}{P^d(t,T+\delta _k)}\right) . \end{aligned}$$

Then Eqs. (2) and (3) imply that

$$\begin{aligned} \begin{array}{ccl} Y_t&{}=&{} {\mathscr {A}}^k(t,t)+{\mathscr {B}}^k(0)^\top X_t-{\mathscr {A}}^d(t,T+\delta _k)-{\mathscr {B}}^d(T+\delta _k-t)^\top X_t\\ &{}=&{} \rho _0^k(t)+\phi (0,\rho _1^k,-\rho _1^d)-\phi (0,0,-\rho _1^d)+\left( \psi (0,\rho _1^k,-\rho ^d_1)-\psi (0,0,-\rho _1^d)\right) ^\top X_t\\ &{}&{} \displaystyle +\int _t^{T+\delta _k} \rho _0^d(u)du-\phi (T+\delta _k-t,0,-\rho _1^d)-\psi (T+\delta _k-t,0,-\rho _1^d)^\top X_t\\ &{}=&{} \displaystyle \rho _0^k(t)+\int _t^{T+\delta _k} \rho _0^d(u)du-\phi (T+\delta _k-t,0,-\rho _1^d)-\psi (T+\delta _k-t,0,-\rho _1^d)^\top X_t+(\rho _1^k)^\top X_t\\ &{}=&{} \displaystyle -\phi (T+\delta _k-t,0,-\rho _1^d)-\psi (T+\delta _k-t,0,-\rho _1^d)^\top X_t+(\rho _1^k)^\top X_t \end{array} \end{aligned}$$

where we used that $\rho _0^d=\rho _0^k\equiv 0$ in our Nelson–Siegel setting as well as $\phi (0,u,v)=0$ and $\psi (0,u,v)=u$. Then, the modified moment generating function of $Y_T$ can be calculated (using Eq. (2) and $\rho _0^d=\rho _0^k\equiv 0$) as

$$\begin{aligned} \begin{array}{ccl} \varphi _{Y_T}(u)&{}\equiv &{}\displaystyle \mathbb {E}^{\mathbb {Q}}\left[ \frac{P^d(T,T+\delta _k)}{B_T} e^{iuY_T}\Big | {\mathscr {F}}_t\right] \\ &{}=&{}\displaystyle \mathbb {E}^{\mathbb {Q}} \left[ e^{iu\left( -\phi (\delta _k,0,-\rho _1^d)-\psi (\delta _k,0,-\rho _1^d)^\top X_T+(\rho _1^k)^\top X_T\right) } \cdot e^{\phi (\delta _k,0,-\rho _1^d)+\psi (\delta _k,0,-\rho _1^d)^\top X_T}\right. \\ &{}&{}\quad \left. \cdot e^{-\int _0^T (\rho _1^d)^\top X_u) du}\Big |{\mathscr {F}}_t\right] \\ &{}=&{}\displaystyle e^{(1-iu) \phi (\delta _k,0,-\rho _1^d)}\cdot \mathbb {E}^{\mathbb {Q}} \left[ e^{(1-iu) \psi (\delta _k,0,-\rho _1^d)^\top X_T +iu (\rho _1^k)^\top X_T}\cdot e^{-\int _t^T (\rho _1^d)^\top X_u du}\right. \\ &{}&{}\quad \left. \cdot e^{-\int _0^t (\rho _1^d)^\top X_u du} \Big |{\mathscr {F}}_t\right] \\ &{}=&{}\displaystyle e^{(1-iu) \phi (\delta _k,0,-\rho _1^d)}\cdot e^{\phi (T-t,(1-iu) \psi (\delta _k,0,-\rho _1^d)+iu \rho _1^k,-\rho _1^d)} \cdot \\ &{}&{}\displaystyle e^{\psi (T-t,(1-iu) \psi (\delta _k,0,-\rho _1^d)+iu \rho _1^k,-\rho _1^d)^\top X_t} \cdot e^{-\int _0^t (\rho _1^d)^\top X_u du} \end{array} \end{aligned}$$

with $\phi (T-t, u, v)$ and $\psi (T-t, u, v)$ given by the solution to the system of ODEs in Eq. (4) adapted to our Nelson–Siegel setting, i.e.

$$\begin{aligned} \begin{array}{ccl} \frac{d}{dt}\phi (T-t,u,v)&{}=&{} - \psi (T-t,u,v)^\top K\theta ^{\mathbb {Q}} -\frac{1}{2}\sum _{j=1}^6 \left( \Sigma ^\top \psi (T-t,u,v)\psi (T-t,u,v)^\top \Sigma \right) _{jj}\\ \frac{d}{dt}\psi (T-t,u,v)&{}=&{} K^\top \psi (T-t,u,v) -v \end{array} \end{aligned}$$

with boundary conditions $\phi (0,u,v)=0$ and $\psi (0,u,v)=u$. This ODE system can be solved analytically and the solution for $\psi (T-t, u, v)$ is given by⁵

$$\begin{aligned} \psi (T-t, u, v) = \begin{bmatrix} v_1 (T-t)+u_1\\ \frac{e^{\lambda _d (t-T)} (\lambda _d u_2-v_2)+v_2}{\lambda _d}\\ \frac{-e^{\lambda _d (t-T)} \left( \lambda _d^2 u_2 (t-T)-\lambda _d (v_2 (t-T)+u_3)+v_2+v_3\right) +v_2+v_3}{\lambda _d}\\ v_4 (T-t)+u_4\\ \frac{e^{\lambda _k (t-T)} (\lambda _k u_5-v_5)+v_5}{\lambda _k}\\ \frac{-e^{\lambda _k (t-T)} \left( \lambda _k^2 u_5 (t-T)-\lambda _k (v_5 (t-T)+u_6)+v_5+v_6\right) +v_5+v_6}{\lambda _k} \end{bmatrix} \end{aligned}$$

where $v_i$ and $u_i$ are $i^\mathrm{th}$ entries of the vectors u and v.

The price of the caplet can then be expressed as

$$\begin{aligned} \begin{array}{ccl} \Pi (t, T, T+ \delta _k, K, N) &{}=&{} \displaystyle N B_t\delta _k \, \mathbb {E}^{\mathbb {Q}}\left[ \frac{1}{B_{T+\delta _k}} \left( L_T(T,T+\delta _k)- K\right) ^+ \Big | {\mathscr {F}}_t\right] \\ &{}=&{}\displaystyle N \, \mathbb {E}^{\mathbb {Q}}\left[ \frac{B_t}{B_T} \left( S^k(T,T)-(1+\delta _k K)P^d(T,T+\delta _k)\right) ^+ \Big | {\mathscr {F}}_t\right] \\ &{}=&{}\displaystyle N \, \mathbb {E}^{\mathbb {Q}}\left[ \frac{B_t}{B_T} P^d(T,T+\delta _k) \left( e^{Y_T}-(1+\delta _k K)\right) ^+\Big | {\mathscr {F}}_t\right] . \end{array} \end{aligned}$$

Using the above modified moment generating function, we thus obtain (compare [4], Proposition 4.2)

$$\begin{aligned}&\Pi (t, T, T+ \delta _k, K, N) \nonumber \\&\quad = N B_t \left( \frac{1}{2}\varphi _{Y_T}(-i) + \frac{1}{\pi }\int _{0}^{\infty } \mathrm {Re}\left( \exp \left( -i u \log (1+\delta _k K)\right) \frac{\varphi _{Y_T}(u-i)}{-u(u-i)}\right) du\right) \end{aligned}$$

(11)

where

$$\begin{aligned} \varphi _{Y_T}(u)&= \exp \left( (1-i u) \phi (\delta _k, 0, -\rho _1^d) +\phi (T-t,(1-iu)\psi (\delta _k,0,-\rho _1^d)+iu\rho _1^k,-\rho _1^d)\right) \times \\&\exp \left( \psi \left( T-t,(1-iu)\psi (\delta _k,0,-\rho _1^d)+iu\rho _1^k,-\rho _1^d\right) ^\top X_t - \left( \rho _1^d\right) ^\top \int _0^t X_sds \right) \end{aligned}$$

This illustrates the applicability of our model to the pricing of caplets, which also holds in a negative interest rate environment. To further confirm the practical relevance of the model for derivative pricing we propose a simple calibration exercise. We build a surface of caplet prices on 15 Sep 2016 using discount bond values and cap implied volatilities, following the procedure outlined in [10]. We end up with market caplet prices for $n_T = 15$ maturities $T=\{2.5, 3, 3.5, 4, 4.5, 5, 5.5, 6, 6.5, 7, 7.5, 8, 8.5, 9, 9.5\}$ years and $n_K = 5$ strikes $K = \{-0.005, -0.0013, 0.0025, 0.01, 0.02\}$. Then, we calibrate the proposed model by solving numerically the following minimization problem:

$$\begin{aligned} \min _{\Theta } \frac{1}{n_T n_K} \sum _{k=1}^{n_k} \sum _{t=1}^{n_T}|\Pi (K_k, T_t)^{mkt}-\Pi (0, T_t, T_t + \delta _k, K_k, 1,\Theta )| \end{aligned}$$

where $\Theta$ is the model parameters vector, $\Pi ^{mkt}$ is the market caplet prices surface and $\Pi (\Theta )$ is the model caplet prices surface (where we have put in evidence the dependence on the model parameters) computed as in (11). Let us consider for this numerical illustration the independent version of the AFMCNS model. We obtain the following estimates for the model parameters: $\lambda ^d = 0.3540$, $\lambda ^k = 0.4680$, $X_0 =\{0.0121, -0.0237,-0.0212,0.0003, -0.0004, 0.0004\}$ and

$$\begin{aligned} \Sigma = \begin{bmatrix} 0.0016 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0.0201 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0.0156 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0&{} 0.0026 &{} 0 &{}0\\ 0 &{} 0 &{} 0&{} 0 &{} 0.0021 &{} 0 \\ 0 &{} 0 &{} 0&{} 0 &{} 0 &{} 0.0031 \end{bmatrix}. \end{aligned}$$

Figure 3 shows the final calibration output. We find that the model is able to replicate correctly observed caplet prices with a mean absolute error (MAE) around 1.10E-04 (and squared pricing error of order $10^{-7}$).

Fig. 3

Model prices against market prices as of 15 September 2016. On the left panel, market prices are represented by blue circles while model prices by red circles. On the right panel, price squared errors are reported. Further notes: $\delta _K = 6/12$, $N=1$

The pricing of swaptions in our framework can in principle be done by adapting the results in [4, Section 4.2] to the proposed AFMCNS model along the same lines to what has been done in the case of caplets. It should be pointed out, however, that the pricing problem is more delicate since the semi-closed formulas in the mentioned paper rely on an approximation of the exercise boundary by an event which is defined in terms of an affine function of the driving process. Finally, for what concerns derivative instruments with more involved payoff structure, we remark that, since $X_t$ evolves according to a multi-dimensional Gaussian Ornstein-Uhlenbeck process, which can be simulated efficiently using for example the Euler scheme or, alternatively, the state transition Eq. (13), interest rate derivatives can be efficiently priced under the proposed model via Monte Carlo simulation. Other analytical or semi-closed pricing formulas for interest rate derivatives in the multiple curve setting are derived e.g. in [12] using continuous-state branching processes with immigration as driving processes or in [11] using time-inhomogeneous Lévy processes to model forward swap rates.

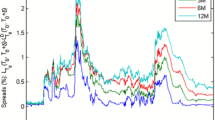
As the proposed model has a Nelson–Siegel factor loading structure, the latent variables have convenient economic interpretations as level, slope and curvature factors. Due to this feature and the fact that the model is free of arbitrage, our approach is tailor-made for risk management purposes. In the sequel, we illustrate such an application by studying the price of the caplet for varying initial state variables $(X^1_t,\ldots , X_t^6)$. Results reported in Fig. 4 show that the caplet price is most severely affected by shifts in the level $X_t^1$ of the discount curve, followed by slope changes $X_t^2$, and finally by curvature shifts $X_t^3$. Corresponding changes in $X_t^4,X_t^5,$ and $X_t^6$ representing shifts in level, slope and curvature of the multiplicative log spreads have a smaller but non-negligible impact on the caplet price. This is particularly interesting when considering the fact that during the global financial crisis, spreads between interbank rates and overnight (discount) rates increased from less than 10bps to levels up to 250bps at the peak of the crisis. In this way, our proposed approach has important implications for risk management as economically meaningful stress scenarios can be easily simulated and due to absence of arbitrage can be used for calculating portfolio values under adverse market situations.

Fig. 4

Price of the Caplets computed from (11) for varying $\{X^i_t\}_{i=1}^{6}$. Model parameters as in Table 2 (independent case) except $\theta ^{\mathbb {Q}}$ which we set equal to 0 in agreement with [2], with $X_t = \{0.0233;-0.0271;-0.0277;0.0002;-0.0003;0.0005\}$. Contract parameters: $N = 1000$, $t=0$, $T=1$, $\delta _k = 3/12$, $K=0.0025$

7 Conclusions

In this paper, we proposed an arbitrage-free affine term structure model for multiple yield curves that has a Nelson–Siegel factor loading structure. Our numerical results document superior in-sample and out-of-sample performance of our approach within the Nelson–Siegel class of models. Due to the sound economic interpretation of the latent variables of our model and the absence of arbitrage, the setting is very well suited for risk management purposes. In particular, it allows to study the sensitivity of a portfolio of interest rate related products with respect to level, slope and curvature shocks to the risk-free yield curve and/or to the tenor spreads. We illustrated this by applying the proposed model to the pricing of caplets. Since the valuation of various interest rate derivatives relies on forward looking interest rates, such as LIBOR, and hence on potential spread adjustments to overnight rates, we believe that our results remain relevant also beyond a discontinuation of LIBOR after 2021.

Appendices

A Derivation of characteristic exponents of Y

To derive explicit expressions for the characteristic exponents $\phi$ and $\psi$ of the process $Y=(X, \int _0^{\cdot } X_sds)$, we first calculate the characteristic exponents of the process X starting in $X_0.$ Therefore, suppose that

$$\begin{aligned} \mathbb {E}\left[ e^{u X_t}\right] =e^{{\tilde{\phi }}(t,u)+{\tilde{\psi }}(t,u)^\top X_0} \end{aligned}$$

(12)

for functions ${\tilde{\phi }}(t,u)$ and ${\tilde{\psi }}(t,u)$. Define the process

$$\begin{aligned} M_t:= f(t,X_t)=\exp ({\tilde{\phi }}(T-t,u)+{\tilde{\psi }}(T-t,u)^\top X_t) \end{aligned}$$

with ${\tilde{\phi }}(0,u)=0$ and ${\tilde{\psi }}(0,u)=u$. Then

$$\begin{aligned} M_T=\exp ({\tilde{\phi }}(0,u)+{\tilde{\psi }}(0,u)^\top X_T)=e^{\langle u,X_T\rangle } \end{aligned}$$

and

$$\begin{aligned} \mathbb {E}[e^{\langle u,X_T\rangle }]=\mathbb {E}[M_T]=M_0 \end{aligned}$$

if M is a martingale. In that case, we then obtain

$$\begin{aligned} \mathbb {E}[e^{\langle u,X_T\rangle }]=e^{{\tilde{\phi }}(T,u)+{\tilde{\psi }}(T,u)^\top X_0} \end{aligned}$$

and (12) indeed gives the correct characteristic function. Thus, we need to prove that $f(t,X_t)$ is a martingale. Denoting the time derivative by $'$ and applying Itô’s formula to $f(t,X_t)$, we obtain

$$\begin{aligned} \begin{array}{ccl} \frac{df(t,X_t)}{f(t,X_t)}&{}=&{} - \left( {\tilde{\phi }}'(T-t,u)+{\tilde{\psi }}'(T-t,u)^\top X_t\right) dt+{\tilde{\psi }}(T-t,u)^\top dX_t\\ &{}&{} +\frac{1}{2}\sum _{j=1}^n \left( \Sigma ^\top (t) {\tilde{\psi }}(T-t,u){\tilde{\psi }}^\top (T-t,u)\Sigma (t)\right) _{jj}(\vartheta ^j(t)^\top X_t+\gamma ^j(t))dt. \end{array} \end{aligned}$$

Hence, $f(t,X_t)$ is a local martingale if

$$\begin{aligned}&{\tilde{\phi }}'(T-t,u)+{\tilde{\psi }}'(T-t,u)^\top X_t ={\tilde{\psi }}(T-t,u)^\top K(t) \left[ \theta (t)-X_t\right] \\&\quad +\frac{1}{2}\sum _{j=1}^n \left( \Sigma ^\top (t) {\tilde{\psi }}(T-t,u){\tilde{\psi }}^\top (T-t,u)\Sigma (t)\right) _{jj}(\vartheta ^j(t)^\top X_t+\gamma ^j(t)), \end{aligned}$$

i.e. if we have

$$\begin{aligned} \begin{array}{ccl} \frac{d}{dt}{\tilde{\phi }}(T-t,u)&{}=&{}- {\tilde{\psi }}(T-t,u)^\top K(t)\theta (t)-\frac{1}{2}\sum _{j=1}^n \left( \Sigma (t)^\top {\tilde{\psi }}(T-t,u){\tilde{\psi }}(T-t,u)^\top \Sigma (t)\right) _{jj}\gamma ^j(t)\\ \frac{d}{dt}{\tilde{\psi }}(T-t,u)&{}=&{} K(t)^\top {\tilde{\psi }}(T-t,u) -\frac{1}{2}\sum _{j=1}^n \left( \Sigma (t)^\top {\tilde{\psi }}(T-t,u){\tilde{\psi }}(T-t,u)^\top \Sigma (t)\right) _{jj}\vartheta ^j(t)^\top \end{array} \end{aligned}$$

with boundary conditions ${\tilde{\phi }}(0,u)=0$ and ${\tilde{\psi }}(0,u)=u$. We define the functional characteristics $({\tilde{F}},{\tilde{R}})$ of X via

$$\begin{aligned} \begin{array}{ccl} \frac{d}{dt}{\tilde{\phi }}(t,u)&{}=&{} {\tilde{F}}({\tilde{\psi }}(t,u)),\quad {\tilde{\phi }} (0,u)=0,\\ \frac{d}{dt}{\tilde{\psi }}(t,u)&{}=&{} {\tilde{R}}({\tilde{\psi }}(t,u)),\quad {\tilde{\psi }} (0,u)=u. \end{array} \end{aligned}$$

We can then apply Theorem 4.10 in [23] to infer the functional characteristics (F, R) of Y as

$$\begin{aligned} F(t,u,v)={\tilde{F}}(t,u)\quad \text{ and }\quad R(t,u,v)= \left( \begin{array}{c} {\tilde{R}}(u)+v\\ 0 \end{array}\right) . \end{aligned}$$

Thus, the characteristic exponents $\phi$ and $\psi$ of the process Y can be written as

$$\begin{aligned} \frac{d}{dt}\phi (T-t,u,v)= & {} - \psi (T-t,u,v)^\top K(t)\theta (t)\\&\quad -\frac{1}{2}\sum _{j=1}^n \left( \Sigma (t)^\top \psi (T-t,u,v)\psi (T-t,u,v)^\top \Sigma (t)\right) _{jj}\gamma ^j(t)\\ \frac{d}{dt}\psi (T-t,u,v)= & {} K(t)^\top \psi (T-t,u,v)\\&-\frac{1}{2}\sum _{j=1}^n \left( \Sigma (t)^\top \psi (T-t,u,v)\psi (T-t,u,v)^\top \Sigma (t)\right) _{jj}\vartheta ^j(t)^\top -v \end{aligned}$$

with boundary conditions $\phi (0,u,v)=0$ and $\psi (0,u,v)=u$ (see also [24], Sec. 3).

B State-space formulation and estimation framework

We fit the parameters of the model under the real-world measure $\mathbb {P}$. The relationship of the process dynamics between the real-world and the risk-neutral measure are characterised by Girsanov’s Theorem. In particular we have

$$\begin{aligned} dW_t = dW^{\mathbb {P}} - b_tdt, \end{aligned}$$

where the risk premium $b_t(\omega )$ is a predictable process of affine form

$$\begin{aligned} b_t = b_0 + B X_t \end{aligned}$$

with $b_0 \in \mathbb {R}^6, B \in \mathbb {R}^{6 \times 6}$. This specification ensures the affine structure of the state variables X under $\mathbb {P}$ (see [7]). Hence, we are able to choose any vector $\theta ^{\mathbb {P}}$ and matrix $K^{\mathbb {P}}$ under $\mathbb {P}$ and still ensure the required $\mathbb {Q}$-dynamics of the model.

Following [2], the state transition equation is given by

$$\begin{aligned} X_t = (I - \exp (- K^\mathbb {P} \Delta t))\theta ^\mathbb {P} + \exp (-K^\mathbb {P} \Delta t) X_{t-1} + \eta _t \end{aligned}$$

(13)

with $X_t=(X_t^1,\ldots ,X_t^6)^{\top }$ and the measurement equation is

$$\begin{aligned} \underbrace{\left( \begin{array}{c} y_t^{d}(\tau _1)\\ y_t^{d}(\tau _2)\\ \vdots \\ y_t^{d}(\tau _N)\\ \log S^{ k}(t,t+\tau _1)\\ \log S^{k}(t,t+\tau _2)\\ \vdots \\ \log S^{k}(t,t+\tau _N)\\ \end{array} \right) }_{\equiv y_t} =&\underbrace{\left( \begin{array}{cccccc} 1&{}\frac{1-e^{-\lambda _d\tau _1}}{\lambda _d\tau _1}&{} \frac{1-e^{-\lambda _d\tau _1}}{\lambda _d\tau _1}-e^{-\lambda _d\tau _1}&{}0&{}0&{}0\\ 1&{}\frac{1-e^{-\lambda _d\tau _2}}{\lambda _d\tau _2}&{} \frac{1-e^{-\lambda _d\tau _2}}{\lambda _d\tau _2}-e^{-\lambda _d\tau _2}&{}0&{}0&{}0\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ 1&{}\frac{1-e^{-\lambda _d\tau _N}}{\lambda _d\tau _N}&{} \frac{1-e^{-\lambda _d\tau _N}}{\lambda _d\tau _N}-e^{-\lambda _d\tau _N}&{}0&{}0&{}0\\ 0&{}0&{}0&{} 1&{} e^{-\lambda _k\tau _1}&{} \tau _1 \lambda _k\ e^{-\lambda _k\tau _1}\\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ 0&{}0&{}0&{} 1 &{} e^{-\lambda _k\tau _N} &{} \tau _N \lambda _ke^{-\lambda _k\tau _N} \end{array} \right) }_{\equiv B} \left( \begin{array}{c} X_t^1\\ X_t^2\\ X_t^3\\ X_t^4\\ X_t^5\\ X_t^6 \end{array} \right) \\&+ \underbrace{\left( \begin{array}{c} -\frac{{\mathscr {A}}^d(\tau _1)}{\tau _1}\\ -\frac{{\mathscr {A}}^d(\tau _2)}{\tau _2}\\ \vdots \\ -\frac{{\mathscr {A}}^d(\tau _N)}{\tau _N}\\ {\mathscr {A}}^k(\tau _1)\\ {\mathscr {A}}^k(\tau _2)\\ \vdots \\ {\mathscr {A}}^k(\tau _N)\\ \end{array} \right) }_{\equiv A} + \left( \begin{array}{c} \epsilon ^{ d}_t(\tau _1)\\ \epsilon _t^{ d}(\tau _2)\\ \vdots \\ \epsilon ^{d}_t(\tau _N)\\ \epsilon ^{k}_t(\tau _1)\\ \epsilon _t^{ k}(\tau _2)\\ \vdots \\ \epsilon ^{ k}_t(\tau _N)\\ \end{array} \right) , \end{aligned}$$

where the transition and measurement errors are assumed to be orthogonal to the initial state and

$$\begin{aligned} \left( \begin{array}{c} \eta _t \\ \epsilon _t \\ \end{array} \right) \sim N\left[ \left( \begin{array}{c} 0 \\ 0 \\ \end{array} \right) , \left( \begin{array}{cc} Q &{} 0 \\ 0 &{} H \end{array} \right) \right] \end{aligned}$$

with diagonal matrix H and

$$\begin{aligned} Q = \int _{0}^{\Delta t} e^{-K^{\mathbb {P}} s} \Sigma \Sigma ' e^{-(K^{\mathbb {P}})' s } ds. \end{aligned}$$

Following [29], we set the mean level $\theta =(\theta _1,\ldots , \theta _6)$ under $\mathbb {Q}$ equal to zero. Therefore we obtain

$$\begin{aligned} \frac{{\mathscr {A}}^d(t,T)}{T-t}&= \frac{1}{2(T-t)}\sum _{j=1}^3 \int _t^T ((\Sigma ^{ d})^\top \psi ^d(s,T)\psi ^{d}(s,T)^\top \Sigma ^{d})_{j,j} ds \\&=\, d_1 \frac{(T-t)^2}{6} + d_2 \Big [ \frac{1}{2 \lambda _d^2} - \frac{1-e^{-\lambda _d(T-t)}}{\lambda _d^3(T-t)} + \frac{1-e^{-2 \lambda _d (T-t)}}{4 \lambda _d^3 (T-t)} \Big ] \\&\quad + d_3 \Big [ \frac{1}{2\lambda _d^2} + \frac{e^{-\lambda _d(T-t)}}{\lambda _d^2} - \frac{(T-t)e^{-2\lambda _d(T-t)}}{4\lambda _d} - \frac{3 e^{-2\lambda _d(T-t)}}{4\lambda _d^2} \\&\quad - \frac{2(1-e^{-\lambda _d(T-t)})}{\lambda _d^3(T-t)} + \frac{5(1-e^{-\lambda _d(T-t)})}{8\lambda _d^3(T-t)} \Big ] \\&\quad + d_4 \Big [\frac{T-t}{2 \lambda _d} + \frac{e^{-\lambda _d(T-t)}}{\lambda _d^2} - \frac{1-e^{-\lambda _d(T-t)}}{\lambda _d^3 (T-t)} \Big ] \\&\quad + d_5 \Big [ \frac{3e^{-\lambda _d(T-t)}}{\lambda _d^2} + \frac{T-t}{2 \lambda _d} + \frac{(T-t)e^{-\lambda _d(T-t)}}{\lambda _d} - \frac{3(1-e^{-\lambda (T-t)})}{\lambda _d^3 (T-t)} \Big ] \\&\quad + d_6 \Big [ \frac{1}{\lambda _d^2} + \frac{e^{-\lambda _d(T-t)}}{\lambda _d^2} - \frac{e^{-2\lambda _d(T-t)}}{2\lambda _d^2} - \frac{3(1-e^{-\lambda _d(T-t)})}{\lambda _d^3(T-t)} + \frac{3(1-e^{-2\lambda _d (T-t)})}{4\lambda _d^3(T-t)} \Big ] \end{aligned}$$

and

$$\begin{aligned} \frac{{\mathscr {A}}^{k}(t,T)}{T-t}&= \frac{1}{2(T-t)}\sum _{j=1}^3 \int _t^T ((\Sigma ^{ k})^\top \psi ^{k}(s,T)\psi ^{k}(s,T)^\top \Sigma ^{k})_{j,j} ds \\&= c_1 \frac{T-t}{2} + c_2 \frac{1-e^{- \lambda _k(T-t)}}{4 \lambda _k}\\&\quad + c_3 \Big [ \frac{1-e^{-2\lambda _k (T-t)}}{8 \lambda _k} - \frac{\lambda _k(T-t)^2 e^{- 2 \lambda _k (T-t)} + (T-t) e^{-2 \lambda _k (T-t)}}{4}\Big ] \\&\quad + c_4 \frac{1-e^{-\lambda _k(T-t)}}{\lambda _k} + c_5 \Big [\frac{1-e^{-\lambda _k(T-t)}}{\lambda _k} - (T-t) e^{- \lambda _k (T-t)} \Big ] \\&\quad + c_6 \Big [ \frac{1-e^{-2 \lambda _k(T-t)}}{4 \lambda _k} - \frac{(T-t)e^{-2\lambda _k (T-t)}}{2} \Big ] \end{aligned}$$

where the coefficients are given by $d_1=\sigma _{11}^2, d_2=\sigma _{21}^2 + \sigma _{22}^2, d_3= \sigma _{31}^2+ \sigma _{32}^2+\sigma _{33}^2, d_4=\sigma _{11}\sigma _{21}, d_5=\sigma _{11}\sigma _{31}, d_6=\sigma _{21}\sigma _{31}+ \sigma _{22}\sigma _{32}$ and $c_1=\sigma _{44}^2, c_2=\sigma _{54}^2 + \sigma _{55}^2, c_3=\sigma _{64}^2 + \sigma _{65}^2 + \sigma _{66}^2, c_4=\sigma _{44}\sigma _{54}, c_5=\sigma _{44}\sigma _{64}, c_6=\sigma _{54}\sigma _{64} + \sigma _{55}\sigma _{65}$.

The Kalman filter can be now set up in analogy to [2]. Therefore, the filter is initialised at the unconditional mean and variance of the state variables under $\mathbb {P}$: $X_0 = \theta ^\mathbb {P}$ and $\Sigma _0 = \int _{0}^{\infty } e^{-K^{\mathbb {P} }s} \Sigma \Sigma ' e^{-(K^{\mathbb {P}})' s} ds$. The prediction step is

$$\begin{aligned} X_{t|t-1} = \Phi _t + \Psi _t X_{t-1}\\ \Sigma _{t | t-1} = \Psi _t \Sigma _{t-1}\Psi _t' + Q \end{aligned}$$

where $\Phi _t = (I - \exp \left( -K^{\mathbb {P} }\Delta t \right) ) \theta ^{\mathbb {P}}$, $\Psi _t = \exp \left( -K^{\mathbb {P}} \Delta t\right)$ where $\Delta t$ is the time between observations, which we set equal to 1/252 (respectively, 1/12) wherever we deal with daily (monthly) data. $X_t$ is updated at time t via

$$\begin{aligned} X_t = X_{t|t-1} + \Sigma _{t|t-1} B' F_t^{-1}v_t,\\ \Sigma _t = \Sigma _{t|t-1} - \Sigma _{t|t-1} B' F_{t}^{-1} B \Sigma _{t|t-1}, \end{aligned}$$

where

$$\begin{aligned} v_t&= y_t - A - B X_{t|t-1}\\ F_t&= B \Sigma _{t|t-1} B ' + H,\\ H&= \text {diag}\left( \sigma ^2_{\epsilon ,d}(\tau _1), \ldots , \sigma ^2_{\epsilon , d}(\tau _N), \sigma ^2_{\epsilon , k}(\tau _1), \ldots , \sigma ^2_{\epsilon , k}(\tau _N)\right) \end{aligned}$$

The Gaussian log-likelihood is then computed according to:

$$\begin{aligned} \log l(y_1, \ldots , y_T) = \sum _{t=1}^{T} - \frac{N}{2} \log (2 \pi ) - \frac{\log \det (F_t)}{2} - \frac{1}{2}v_t' F_t^{-1}v_t \end{aligned}$$

(14)

where N is the number of observed yields and $\det (\cdot )$ denotes the determinant of a square matrix.