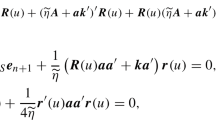Abstract
We study optimal execution with “self-exciting” price impact, where persistent trades not only incur price impact but also increase the execution costs for successive orders. This model is motivated by an equilibrium between fundamental sellers, market makers, and end users. For risk-neutral investors, it leads to faster initial trading compared to the constant execution rate of Bertsimas and Lo [5]. For risk-averse liquidation as in Almgren and Chriss [2, 3] or Huberman and Stanzl [15], self-excitement has a moderating effect: slow liquidation is sped up, whereas fast schedules are slowed down.



Similar content being viewed by others
Notes
Front running becomes optimal in the presence of sufficiently large “preys” in the models of Brunnermeier and Pedersen [6] as well as Carlin, Lobo, and Viswanathan [7]. In the model of Schied and Schöneborn [20], potential predators can be either detrimental or beneficial depending on the model parameters.
Recently, a different kind of “self-excitement” has also started to receive increasing attention, see, e.g., [1] and the references therein. In these models, the orders of other market participants are modeled by a Hawkes process, a counting process whose jump intensities are self-exciting in that they are influenced by the past jumps. Whence, self-excitement is produced by the trades of the other market participants in these models, whereas it is instigated by the large trader in ours.
Since time horizons for liquidation programs are typically short, drifts are usually neglected (but cf. [16]) and it is reasonable to work with more tractable arithmetic Brownian motions rather than their geometric counterparts (but cf. [9]). In the case of a risk-neutral investor, the price process need not be an arithmetic Brownian motion, but can be a general martingale.
This price impact is purely temporary, in that it only affects the current trade but not subsequent ones. Linear permanent price impact can also be accounted for by shifting the unaffected price quote, see [3]. However, like proportional transaction costs, linear permanent impact does not alter optimal execution strategies. Hence, we disregard these two frictions throughout. Nonlinear permanent price impact depending on the cumulated number of shares sold by the large trader is studied by [13].
The linear dependence is assumed for tractability. It allows for closed-form solutions and also can be seen as a first-order approximation for more general small self-excitement mechanisms.
Indeed, assume we start with X shares. Buying shares at a constant rate on the interval \([0,\frac{T}{2}]\) to reach \(X+\frac{\ell _0}{\ell _1}+k\), for some integer k, and selling back these shares at the same speed on \([\frac{T}{2},T]\) yields an expected profit of order \(O(k^3)\) as k grows to infinity, while the standard deviation of the final profit is of order O(k).
To allow for buy orders in our model and rule out price manipulations, we could define the price impact parameter as \(\lambda _t:=\ell _0 + \ell _1 (X-x_t)^+\) when selling (\(\dot{x}_t<0\)) and \(\lambda _t:=\ell _0\) when buying (\(\dot{x}_t > 0\)). This means that, during a substantial liquidation, sales increase the price impact of further sales whereas the price impact of purchases remains constant. In such a model round-trips have a strictly positive expected cost, and optimal strategies are necessarily decreasing.
For convenience, we assume that \(h/\Delta t\) is an integer.
Here, the risk-free rate is set equal to zero, because the time horizons we consider are short.
Adaptive strategies are studied by Almgren and Lorenz [17] for a mean-variance criterion and by Schied and Schöneborn [19] for von Neumann-Morgenstern utilities. Here, we focus on deterministic strategies to obtain tractable solutions also with our more complicated price impact structure in Sect. 4.2. In the risk-neutral case, this entails no loss of generality, cf. Remark 4.2.
The integrand to be minimized pointwise for each \(t\in [0,T]\) is given by \(F\left( t,x,v\right) = (\ell _0+\ell _1 X)v^2 -\ell _1 x v^2 \); its Hessian is \( \left( {\begin{array}{l@{\quad }l} 0 &{}\quad { - 2\ell _{1} v} \\ { - 2\ell _{1} v} &{}\quad {2\left( {\ell _{0} + \ell _{1} \left( {X - x} \right) } \right) } \\ \end{array} } \right) \) . The sum of this matrix’ eigenvalues is positive for \(x\in [0, X]\) and their product negative. Whence the goal functional is not convex.
Indeed, an inspection of the explicit formula shows that this holds uniformly on [0, T], so that the claim for the remainder follows from the dominated convergence theorem.
References
Alfonsi, A., Blanc, P.: Dynamic optimal execution in a mixed-market-impact Hawkes price model. Preprint (2014)
Almgren, R.F., Chriss, N.: Value under liquidation. Risk 12(12), 61–63 (1999)
Almgren, R.F., Chriss, N.: Optimal execution of portfolio transactions. J. Risk 3, 5–40 (2001)
Bacry, E., Iuga, A., Lasnier, M., Lehalle, C.-A.: Market impacts and the life cycle of investors orders. Preprint (2014)
Bertsimas, D., Lo, A.W.: Optimal control of execution costs. J. Financ. Markets 1(1), 1–50 (1998)
Brunnermeier, M.K., Pedersen, L.H.: Predatory trading. J. Financ. 60(4), 1825–1863 (2005)
Carlin, B.I., Lobo, M.S., Viswanathan, S.: Episodic liquidity crises: cooperative and predatory trading. J. Financ. 62(5), 2235–2274 (2007)
Garleanu, N., Pedersen, L.H.: Dynamic portfolio choice with frictions. Preprint (2013)
Gatheral, J., Schied, A.: Optimal trade execution under geometric brownian motion in the Almgren and Chriss framework. Int. J. Theor. Appl. Financ. 14(03), 353–368 (2011)
Gatheral, J., Schied, A.: Dynamical models of market impact and algorithms for order execution. In: Fouque, J.P., Langsam, J. (eds.) Handbook on systemic risk, pp. 579–602. Cambridge University Press, Cambridge (2013)
Gökay, S., Roch, A.F., Soner, H.M.: Liquidity models in continuous and discrete time. In: Di Nunno, J. (ed.) Advanced mathematical methods for finance, pp. 333–365. Springer, Heidelberg (2011)
Gomes, C., Waelbroeck, H.: Is market impact a measure of the information value of trades? Market response to liquidity vs. informed metaorders. Quant. Financ. 15(5), 773–793 (2015)
Guéant, O.: Permanent market impact can be nonlinear. Preprint (2013)
Huberman, G., Stanzl, W.: Price manipulation and quasi-arbitrage. Econometrica 72(4), 1247–1275 (2004)
Huberman, G., Stanzl, W.: Optimal liquidity trading. Rev. Financ. 9(2), 165–200 (2005)
Lorenz, C., Schied, A.: Drift dependence of optimal trade execution strategies under transient price impact. Financ. Stoch. 17(4), 743–770 (2013)
Lorenz, J., Almgren, R.F.: Mean-variance optimal adaptive execution. Appl. Math. Financ. 18(5), 395–422 (2011)
Madhavan, A.: Market microstructure: a survey. J. Financ. Markets 3(3), 205–258 (2000)
Schied, A., Schöneborn, T.: Risk aversion and the dynamics of optimal liquidation strategies in illiquid markets. Financ. Stoch. 13(2), 181–204 (2009)
Schöneborn, T., Schied, A.: Liquidation in the face of adversity: stealth vs. sunshine trading. Preprint (2009)
Acknowledgments
We thank Pierre Collin-Dufresne for fruitful discussions in the initial stages of the project. We are also grateful to two anonymous referees and an anonymous associate editor for numerous constructive comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
Partially supported by the ETH Foundation.
Rights and permissions
About this article
Cite this article
Cayé, T., Muhle-Karbe, J. Liquidation with self-exciting price impact. Math Finan Econ 10, 15–28 (2016). https://doi.org/10.1007/s11579-015-0148-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11579-015-0148-2