Estimating the market risk premium for valuations: arithmetic or geometric mean or something in between?

Abstract

It is well-known that using arithmetic averages of yearly return observations leads to downward biased discount rates estimations. Well-known corrections, however, lead to upward biased results under the presence of negative serial correlation. Using a simulation analysis, we first show that a specific variant of the Cooper estimator, labelled as C4 in this paper, leads to robust estimations even under the presence of both serial correlation and heteroscedasticity. We also show that among the simple estimators, i.e. the arithmetic (AM) or geometric mean (GM) or the mean of both (MoM), the first one tends to perform best unless there is a high degree of negative serial correlation. In that case using the so-called mean of means rule would be better. Secondly, using data from Jordà et al. (Q J Econ 134(3):1225–1298, 2019) we find negative serial correlation and heteroscedasticity in market risk premia to be a widely spread phenomenon. Finally, we use this data to derive presumably least biased market risk premia estimations based on the C4 estimator. For the majority of the countries we find that these estimations are somewhere between the arithmetic and geometric average. When comparing these simple estimators among each other based on the empirical data, we find the arithmetic mean and mean of means to perform almost equally well, while the geometric mean clearly underperforms. Moreover, we found some evidence that the MoM is slightly outperforming the AM under a local CAPM perspective, while the opposite tends to be true under a global CAPM perspective. This leads us the cautious conclusion that the mean of means rule used by practitioners has some empirical rationale when there is evidence for substantial negative serial correlation.

1 Introduction

When estimating the cost of capital based on the CAPM the market risk premium is a necessary and pivotal input parameter. In the so-called historical method a long record of historical observations, in developed countries in some cases more than 100 years, is used. Typically, the market risk premium is then extracted as the arithmetic average of these observations.

However, starting with Blume (1974) there is an ongoing debate on how an unbiased estimation for the market risk premium has to be derived. Interestingly, he showed that even under ideal conditions, i.e. iid-returns, the unbiased estimator for a long-run compounding rate is an appropriately weighted average of the arithmetic and geometric mean return derived from historical return observations. Hereby, the weight on the arithmetic mean is the larger the longer the observation period relative to the compounding period is. A derivation and detailed analysis of an unbiased compounding estimator under the iid lognormal assumption can be found in Jacquier et al. (2003) and Jacquier et al. (2005). One compelling feature of the Blume estimator consists in the fact that the weights are always between 0 and 100%. Hence, by applying this estimator to the market risk premium the estimation used in the compounding problem is never larger than its arithmetic mean and never smaller than its geometric mean.

Unfortunately, this result does not hold anymore if applied to discounting problems, as it is the case in any valuation problem. Actually, Cooper (1996) shows that under the iid assumption the arithmetic mean is downward biased, i.e. valuations are upward biased.¹ Again, he shows that the unbiased estimator can be represented as a weighted average of the arithmetic and the geometric mean. However, the weight on the arithmetic mean is larger than 100%. Given that the geometric mean is smaller than the arithmetic mean, the unbiased estimation for the market risk premium must always be larger than the arithmetic mean of the historical observations, except for the one period discount rate estimation. And this distance is increasing in the length of the discounting period.

Since then a small number of papers dealing with these biases in discount rate estimations have been published. Elsner and Krumholz (2013) give a comprehensive overview and derive a specific version of the Cooper estimator under the assumption of lognormally distributed returns. Breuer et al. (2014) and Breuer et al. (2017) analyze the performance of a specific version of the Cooper estimator relative to their own “truncated” arithmetic mean estimator based on bootstrapped empirical data. While they find biases in present values to be significant overall, only for low growth firms the Cooper estimator does a reasonable job. When looking at high growth firms, using the arithmetic average but ignoring cash flows beyond year 30 or 50, i.e. “truncating” the estimation, leads to the least biased results.² Moreover, it seems that the estimator of Elsner/Krumholz performs relatively well, if the cost of equity is estimated on the basis of a total return approach (cf. Breuer et al. 2017, p. 738).

While this work is closely related to our paper, there is also an important difference. Breuer et al. (2014, 2017) are interested in the valuation bias created at the single firm level. This is, of course, the ultimate question in the context of a valuation problem. Therefore, the bias finally not only depends on a flawed market risk premium estimation, but it is also determined by the level of the risk-free rate, the systematic risk of the company as well as the time pattern of a company’s cash flows. In this respect their work is very insightful, as they show that the bias is most important for firms with high growth rates.

Nevertheless, in this paper we want to focus on the bias at the level of the market risk premium estimation. Therefore, we ignore any additional effects stemming from firm and cash flow characteristics as well as the risk-free term structure. Nevertheless, our results might give some guidance on how to mitigate estimation problems at the level of the market risk premium. This, however, does not rule out that estimation problems might be amplified when applied to specific valuation problems.

Practitioners rarely apply the Cooper estimator when deriving the discount rates or the underlying market risk premium. From a German perspective, one reason might be that there is no official statement by competent institutions, like the FAUB, recommending the usage of the Cooper-estimator. Moreover, as Breuer et al. (2014, p. 592), point out, there are several unknowns when it comes to the practical application of this estimator. In Pratt and Grabowski (2014, p. 156), a well-known handbook for practitioners, it is argued that the bias caused by using the arithmetic average in practical valuation problems tends to be small as most of the value comes from cash flows in the first ten years. Koller et al. (2020), another well-known source for practical valuation, do even not mention the Cooper estimator at all, while they briefly explain the Blume estimator. However, there is no recommendation as to whether, and if so, under which circumstances, this estimator should be used.

While, to the best of our knowledge, there is no survey giving a picture of how practitioners are handling this estimation problem, it seems that they are using simple estimators as the arithmetic or geometric mean. Moreover, it might well be that some of them are using a simplified version of the Blume estimator, as it is the case in Germany with the so-called Mean of the Means, i.e. the simple average of the arithmetic and geometric average; cf. Wagner et al. (2006), or Stehle (2016). From an international perspective, recommendations for using such a rule of thumb are harder to find. However, a cautious indication in this direction can be found in Welch (2017, p. 199). Hence, one might conclude that most valuations are actually upward biased, as the discount rates tend to be downward biased.

This conclusion, however, might be premature. The estimators discussed so far have been derived under the condition of iid returns. In reality, we have to take into account that stock returns and, therefore, also market risk premia, over the long-run might display mean reverting behavior, making them negatively serially correlated; cf. among others Shiller (2014), Spierdijk et al. (2012), Pástor and Stambaugh (2012), Campbell (2003, p. 803), Campbell and Shiller (1988), Poterba and Summers (1988), Shiller (1981). Intuitively it is not so hard to see that negative serial correlation tends to inflate the market risk premium estimation as long as it is based on the arithmetic mean; cf. Wenger (2005), Cooper (1996), and Indro and Lee (1997). Therefore, Cooper (1996) derived an estimator under the assumption of lognormally distributed returns displaying negative serial correlation. This estimator, which in this paper will be labelled C4, leads to smaller discount rates the larger the degree of serial correlation is.³

It should be noted in this regard that when estimating market risk premia two opposite effects have to be taken into account. At the one side, extracting an unbiased discount rate estimation for an N-year discounting period from T one-year historical return observations leads to a correction which increases in N and yields estimations higher than the arithmetic average. However, taking into account negative serial correlation at the other side, causes the unbiased discount rate to decrease in the degree of serial correlation. Therefore, under realistic conditions the net effect on the unbiased estimation is unclear and in general we cannot say whether the unbiased estimation finally is larger or smaller than the arithmetic mean.

This is where this paper wants to make contribution. First, by running a simulation analysis we are comparing different existing estimators, the arithmetic and the geometric mean, the mean of means, the Blume estimator, the Elsner/Krumholz estimator as well as four different variants of the Cooper estimator, including the above mentioned C4 estimator. Our results clearly indicate that under the presence of serial correlation and heteroscedasticity in the market risk premium, the C4 estimator performs best. Interestingly, in this horse race the mean of means estimator arrives second in those cases where there is considerable negative serial correlation. In all other cases, however, it is clearly inferior to many of the other estimators. When taking an agnostic perspective with respect to the empirical properties of market return behavior, i.e. by comparing the rankings of all estimators in 24 different baseline parameter combinations, we again find the C4 estimator to perform best. It is followed by the C2 and C3 estimator, the Blume estimator and the arithmetic mean.

Second, we then apply an empirical analysis to a broad set of countries and regions from a global CAPM perspective. For that purpose, we measure historical market risk premia realizations in three different base currencies. The results indicate that negative serial correlation and heteroscedasticity is a wide-spread phenomenon, even though in some cases we also find positive serial correlation. This is especially true, if we include pre-World War periods and use the Euro/Mark as the base currency.

Third, we use the C4 estimator in order to derive the presumably least biased market risk premia estimations for the countries or regions in our data set. Interestingly, we find that in the majority of the cases this presumably least biased market risk premia estimation is somewhere in between the geometric and the arithmetic average. More precisely, when comparing the arithmetic mean and the mean of means on the basis of their estimation errors, we find that they perform on an almost equal footing, with the mean of means being better in situations of pronounced negative serial correlation. This leads us the cautious conclusion that the so-called mean of means rule proposed among others by Wagner et al. (2006) and Stehle (2016) and used by practitioners might have some empirical rationale.

The rest of paper proceeds as follows. Section 2 is laying down the problem of why arithmetic averages generate biased estimations in the context of a simple example. Section 3 reviews the literature and explains the different estimators that have been developed in the literature. In Sect. 4 the results of the simulation analysis are presented, while Sect. 5 describes the data used for the empirical analysis and discusses the results. Finally, Sect. 6 concludes.

2 Sketching the problem

In order to illustrate the problem, we develop the following simple example. Assume a perfect capital market with one representative stock. The returns of this stock are binomially distributed with the upward return factor being u = 1.2 and the downward return factor d = 0.9. The risk-free rate is assumed to be zero. Hence, it follows that the risk-neutral probability for an upward movement is q_n = 1/3. Assuming the physical probability⁴ of an upward movement being q = 1/2, the expected return of the stock is 5%, which is equal to the arithmetic average of the returns.

Now, in this economy the value of a new project has to be determined. The expected cashflows evolve according to the binomial distribution given above starting from a value of 50 for the last expired period. The distribution of these cash flows is resumed in Fig. 1. According to the fundamental asset pricing theorem the value of this project is equal to the expected present value of future cash flows where the expectation is calculated under the risk-neutral measure and the discount rate is equal to the risk-free rate.⁵ Hence, the value is [(1/3 × 60 + 2/3 × 45)/1 + (1/9 × 72 + 4/9 × 54 + 4/9 × 40.5)/1²] = 100.

Fig. 1

Binomially distributed stock returns and project cash flows

Alternatively, the value of this project could be determined as the expected present value using the physical probability distribution and discounting with the expected return, i.e. the arithmetic average. At this point, because all distributional parameters are perfectly known, this leads to the same value. Noting that the expected cash flow in t = 1 is CF₁ = 52.5 and in t = 2 is CF₂ = 55.125, it follows: 52.5/1.05 + 55.125/1.05² = 100. So, in this world without any estimation problems, valuation using physical probabilities for calculating expected cash flows and arithmetic averages for determining the risk-adjusted discount rate would work well, i.e. would lead to unbiased results.

However, things change once we introduce estimation problems. Assume that the true distributional parameters are not known, and we can only observe random paths of two period return realizations. Hence, in this example we would either observe two upward steps (path A) with an arithmetic average of realized returns of 20%. For the case of one up- and one downward step (path B) the arithmetic average would be 5% and for two downward steps (path C) –10%. The probability that path A or C is observed is 25% each, while for path B the probability is 50%.

Now, if by chance we would have observed path A the project would have been valued at 52.5/1.2 + 55.125/1.2² = 82.03, while if we would have observed path C the value would have been 52.5/0.9 + 55.125/0.9² = 126.39. Only in case of path B being realized we would have inferred the correct value of 100. Hence, the expected project value using the arithmetic average of realized returns as discount rates would be 82.03 × 0.25 + 100 × 0.5 + 126.39 × 0.25 = 102.11. As one can easily see, using the arithmetic average leads to an upward biased project value or, which is the same, to a downward biased discount rate estimation. And if we would have used the geometric average, which in this case would have been 3.92%, overvaluation would have even been worse.

The underlying reason for this result is the fact that present values are a convex function in the discount factors making the absolute valuation error of an underestimation of the true discount rate not being symmetric to the absolute error caused by an overestimation of the same amount. In more formal terms this could be stated as follows. Assume ${\widehat{D}}_{N}$ is the unbiased discount factor over N periods and the expected annualized N-period return estimation is ${\mu }_{N}=E\left[1+{\widetilde{r}}_{N}\right]$, e.g. the arithmetic mean. Then according to Jensen’s inequality Butler and Schachter (1989, p. 15), show that the following holds:

$${\widehat{D}}_{N}=E\left[{\left(\frac{1}{1+{\widetilde{r}}_{N}}\right)}^{N}\right]\ge {\left[\frac{1}{E\left[1+{\widetilde{r}}_{N}\right]}\right]}^{N}={\left[\frac{1}{1+{\mu }_{N}}\right]}^{N}$$

(1)

Hence, using the arithmetic average of observed yearly return realizations and plugging this into an N-period valuation problem causes an upward bias in the resulting value.

3 Unbiased estimators

3.1 The case of iid returns

The observation illustrated by the preceding example was the starting point of the paper of Blume (1974), who developed an unbiased estimator for the interest rate to be used in a compounding problem. He showed that under iid returns the unbiased compounding rate estimation is an appropriately weighted average of the arithmetic and the geometric mean. By extending this analysis to valuation problems, i.e. by analyzing how unbiased discount rates can be estimated, Butler and Schachter (1989) and Cooper (1996) were the first to come up with explicit solutions. Most importantly, under the assumption of iid returns Cooper (1996) derived the following unbiased estimator for the N-period discount factor:

$${\widehat{D}}_{C1,N}=b{A}^{-N}+\left(1-b\right){G}^{-N}\mathrm{ with }\,b=\frac{N+T}{T-1}$$

(2)

Here, N is the length of the discounting period expressed in years, while T ≥ N is the number of yearly return observations on which the discount rate estimation is based upon.⁶ Assuming return observations are expressed as return factors, i.e. 1 + yearly return, A stands for the arithmetic mean and G for the geometric mean of these return factors. Expressing the yearly return observation as ${\widetilde{r}}_{t}$ and having a total of T observations, these two means are defined as follows:

$$A=\frac{1}{T}\sum_{t=1}^{T}\left(1+{\widetilde{r}}_{t}\right)$$

(3)

$$G={\left[\prod_{t=1}^{T}\left(1+{\widetilde{r}}_{t}\right)\right]}^{1/T}$$

(4)

For expositional convenience the unbiased discount factor can be transformed into an unbiased yearly discount rate in the following way:

$${\widehat{R}}_{C1,N}={\left[b{A}^{-N}+\left(1-b\right){G}^{-N} \right]}^{-\frac{1}{N}}-1$$

(5)

Two remarks have to be made here. First, as the weighting factor b is always larger than 1, it must hold that the unbiased yearly discount rate according to (5) is always larger than the arithmetic mean, i.e. ${\widehat{R}}_{C1,N}>A-1$, holds. However, in the special case of N = 1 and T being relatively large, the discount rate is almost equal to the arithmetic average. Second, the unbiased discount rate is a function of the length of the discounting period. This creates the somewhat counterintuitive result that even though returns are drawn from a stationary distribution, yearly discount rates used in valuation problems are not constant.

By adding the assumption that returns are lognormally distributed, i.e. $\mathrm{ln}\left(1+\widetilde{r}\right)\sim \phi \left(\mu ,\sigma \right)$, Cooper (1996) is able to derive the following more specific unbiased estimators⁷:

$${\widehat{D}}_{C2,N}={G}^{-N}{e}^{-\left(T+N\right)\frac{N{\sigma }^{2}}{2T}}$$

(6)

$${\widehat{R}}_{C2,N}=G{e}^{\left(T+N\right)\frac{{\sigma }^{2}}{2T}}-1$$

(7)

Finally, under the assumption of lognormal returns the relationship $A=G{e}^{\frac{1}{2}{\sigma }^{2}}$ holds and this estimator can alternatively be written as:

$${\widehat{D}}_{C3,N}={A}^{-N}{e}^{-\frac{{N}^{2}{\sigma }^{2}}{2T}}$$

(8)

$${\widehat{R}}_{C3,N}={Ae}^{\frac{N{\sigma }^{2}}{2T}}-1$$

(9)

This last equation again clearly points out that using the arithmetic average leads to an upward bias in valuations or to a downward bias in the discount rate.

Finally, it should be mentioned that (Elsner and Krumholz 2013), besides providing a comprehensive overview on different estimators, also analytically develop an unbiased estimator under conditions of iid distributed returns. Their approach is slightly different as they are interested in an unbiased estimation of the cost of capital. However, by assuming that all their assumptions apply to the market risk premium as well, their estimator, which we call EK, can be written as follows:

$${\widehat{D}}_{EK,N}={\left\{{e}^{{\left[{e}^{\left[0.5{\left(ln\left(1+A\right)\right)}^{2}\frac{T}{{\sigma }^{2}}\right]}\sqrt{2\pi \frac{T}{{\sigma }^{2}}}\left(1-\Phi \left[0;-ln\left(1+A\right)\frac{T}{{\sigma }^{2}};\sqrt{\frac{T}{{\sigma }^{2}}}\right]\right)\right]}^{-1}}\right\}}^{-N}$$

(10)

$${\widehat{R}}_{EK,N}={e}^{{\left[{e}^{\left[0.5{\left(ln\left(1+A\right)\right)}^{2}\frac{T}{{\sigma }^{2}}\right]}\sqrt{2\pi \frac{T}{{\sigma }^{2}}}\left(1-\Phi \left[0;-ln\left(1+A\right)\frac{T}{{\sigma }^{2}};\sqrt{\frac{T}{{\sigma }^{2}}}\right]\right)\right]}^{-1}}-1$$

(11)

Here, Φ is the standard normal cumulative distribution function. It should be noted that (Elsner and Krumholz 2013) have developed an unbiased cost of capital estimator for the terminal value calculation. Hence, their estimator gives a discount rate for a perpetual cash flow stream. In our simulations we are interested in estimating discount rates for one-time cash flows accruing after N years. Therefore, comparing this estimator with the others presented above to some extend is unfair. We have decided to include the EK estimator for informational reasons nevertheless. Due to construction, we expect it to work better for longer discounting periods. As a drawback when it comes to simulations it should be mentioned that non existing values may arise for this estimator.

3.2 The case of non-iid returns

While the derivation of unbiased discount rate estimations in the case of iid-returns is clearly understood, it is still an open debate how to adjust these estimations, when it comes to take empirical distributions into account. Most importantly, two stylized facts have to be addressed in this regard. First, starting with Shiller (1981), Poterba and Summers (1988) and Campbell and Shiller (1988) there is plenty of literature pointing out that stock market returns display mean-reverting behavior, especially in the long-run.⁸ Moreover, in a more recent strand of literature it is shown that this empirical behavior of stock returns can be seen as an equilibrium outcome which goes along with time-varying market risk-premia (cf. Campbell and Cochrane 1999; Campbell 2003; Wachter 2006; Santos and Veronesi 2006; Lettau and Wachter 2011; Berkman et al. 2011).

This literature raises fundamental questions on how market risk premia can be inferred from empirical data. Most importantly, if risk premia are time-varying a method based on historical observations might be conceptually flawed. This is why a new strand of literature has evolved trying to infer market risk premia either from analyst expectations (cf. Claus and Thomas 2001; Gebhardt et al. 2001; Fama and French 2002; Easton 2004; Ohlson and Juettner-Nauroth 2005),⁹ bond prices (cf. Campello et al. 2008) or derivatives (cf. Berg and Kaserer 2013; van Binsbergen et al. 2013). However, this literature on the so-called implied market risk premium is beyond the scope of this paper. Therefore, it will not be considered here as an alternative to the historical method.

Coming back to the historical method, it is interesting to note that Cooper (1996) already analyzed the implications of serial correlation on the estimation of discount factors. And in fact, by simply assuming that returns still follow a lognormal distribution, even though with time-varying distributional parameters, i.e. $\mathrm{ln}\left(1+{\widetilde{r}}_{N}\right)\sim \phi \left({\mu }_{N},{\sigma }_{N}\right)$, he derived the following unbiased estimators¹⁰:

$${\widehat{D}}_{C4,N}={G}^{-N}{e}^{-\left(T+N\right)\frac{N{\sigma }_{N}^{2}}{2T}}$$

(12)

$${\widehat{R}}_{C4,N}=G{e}^{\left(T+N\right)\frac{{\sigma }_{N}^{2}}{2T}}-1$$

(13)

Note that these estimators are equivalent to the one in Eqs. (6) and (7) just with the adjustment that the annualized N-period variance ${\sigma }_{N}^{2}$ is used instead of the constant annualized variance ${\sigma }^{2}$.¹¹ As this estimator will play an important role in this paper, we will label it as the C4 estimator.

As a second empirical phenomenon, heteroscedasticity, including fat-tailed distributions, has to be taken into account. However, in the literature so far no unbiased estimators controlling for heteroscedasticity have been developed. It is, therefore, an interesting question to see how sizeable the biases created by heteroscedasticity are.

4 Simulation analysis

4.1 Methods

In this section we run a simulation analysis in order to compare the biases caused by different estimators assuming specific characteristics in the stocks’ return generating process. It should be noted here that we focus on the bias created by the market risk premium estimation only. We ignore any additional problems stemming from the level or the curvature of the risk-free term structure.

Following Campbell et al. (1997, p. 483 n), the return generating process for the market risk premium, defined as$r=\mathrm{ln}\left(1+{\widetilde{r}}_{m}\right)-\mathrm{ln}\left(1+{r}_{f}\right)$, where r_m is the market return and r_f is the risk-free rate, is defined as follows:

$${r}_{t}=\mu +\gamma \left(\mu -{r}_{t-1}\right)+{\sigma }_{t}{\epsilon }_{t}$$

(14)

$${\sigma }_{t}^{2}={\omega }^{2}+\alpha {\sigma }_{t-1}^{2}+\left(\alpha -\beta \right){\sigma }_{t-1}^{2}\left({\varepsilon }_{t}^{2}-1\right)$$

(15)

with $-1\le \gamma <1$, $0\le \alpha <1$, $0\le \beta <\alpha$, and $\epsilon ,\varepsilon \sim N\left(\mathrm{0,1}\right)$

Note, this process captures all of the above-mentioned return characteristics. First, if γ= α= β= 0 we have an iid-distributed market risk premium with an expected continuously compounded return equal to μ and standard deviation ω. Return innovations in this case are only temporary. Second, by setting 0 < γ  < 1 we get a weakly stationary mean-reverting process with a negative autocorrelation coefficient, i.e. ρ_t,t-1 = -γ.¹² This captures the stylized empirical fact of variance ratios below 1, as will be shown in Sect. 5.3. In this case return innovations have a persistent component. Third, by setting 0 ≤ β  < α < 1 we allow for heteroscedasticity leading to market risk premia which display excess kurtosis and fat tails. In this case, also variance innovations have a persistent component. As a special case we will also run some simulations using -1 < γ < 0. In this case returns display positive serial correlation.

In every single run, i.e. for every combination of the parameters mentioned in Eqs. (14) and (15) we randomly draw a yearly return path over T = 100 years. This number is chosen for two reasons. First, it resembles typical historical records available for the estimation of market risk premia. Of course, for some countries, like the US, even longer periods are available, while for others, like emerging markets, periods are much shorter. However, for most industrial countries historical periods in this range are available. Second, for the unbiased as well as the C4 estimator we need return observations over non-overlapping periods. We choose these periods as integer fractions of the simulated historical period T = 100, i.e. we use all periods N for which T/N is an integer. Hence, we simulate discount rate estimations for periods N of 1, 2, 4, 5, 10, 20 and 25 years.¹³ The fact that 100 years could be split-up in 7 such integer fractions is an additional reason for choosing this specific simulation period.

In each of these single runs we generate T = 100 random return drawings based on the return generating process defined in (14) and (15). Then, based on these simulated returns, we calculate the arithmetic (AM) and the geometric mean (GM) according to Eqs. (3) and (4). Also, in each single run we calculate the N-period discount factors based on the estimators introduced in Sect. 3, i.e. the estimator according to Blume (1974), the mean of geometric and arithmetic average (MoM), the Cooper estimator according to Eq. (2) (C1), the Cooper estimator according to Eq. (6) (C2), the Cooper estimator according to Eq. (8) (C3), the Cooper estimator according to Eq. (12) (C4), and the EK estimator according to Eq. (10). Note that for the C4 estimator we estimate the annualized N-period variance ${\sigma }_{N}^{2}$ by using in each single run non-overlapping intervals equal N.

We then repeat each single run 200,000 times ending up with a total of 200,000 estimates.¹⁴ Then, after having completed all runs, the average over all runs for each of these estimators for the N-period discount factors is calculated. And finally, for expositional reasons, each N-period discount factor estimate is then transformed into a yearly discount rate.

We then compare the average outcome of these yearly discount rate estimates over all simulations with the unbiased estimation also resulting from our simulations. This unbiased estimation is calculated in the same way as the “simple estimator” in Blume (1974). This approach has the advantage that we do not need any assumptions about the independence of the one-period returns. In each single run we compute the N-period compounding factor for each discounting period N. Each of these compounding factors is then averaged over all 200,000 runs and, finally, transformed into a yearly discount rate.

Finally, the different estimators have to be compared. Dittmann and Maug (2008) have shown that when it comes to compare valuation methods it makes a difference how error measurement is defined. As we are interested in the first place in the impact of the estimation error on the valuation error, we define the error as the following present value difference:

$$\Delta =ln\left[\frac{{\left(1+u\right)}^{-N}}{{\left(1+x\right)}^{-N}}\right]=N\left[\mathrm{ln}\left(1+x\right)-\mathrm{ln}(1+u)\right]$$

(16)

Here, u stands for the unbiased discount rate estimation, i.e. the average of the unbiased discount rate over all simulation runs, and x stands for the discount rate given by one specific estimator, again averaged over all simulation runs. Hence, assuming that the market risk premium could be directly used as a discount rate, Eq. (16) gives the difference of the logarithm of the present value of a one-time one Euro cash flow accruing in N years calculated with one specific estimator to the unbiased present value. It should be noted that a positive sign indicates that the estimated market risk premium is higher than the unbiased one, leading to an underestimation of the present value.

Now, given that we are looking at estimates for different time horizons N, there might be a bias using this error definition. As we finally look at errors over different discounting periods, errors in the discount rate used for longer periods are amplified because of discounting. Hence, in some sense they are implicitly assigned a higher weight. Therefore, we use also a second error definition, where we basically normalize the error per discounting year. Starting from Eq. (16), this error is defined as:

$$\Delta =\mathrm{ln}\left(1+x\right)-\mathrm{ln}(1+u)$$

(17)

We will rank the estimators according to both error measures. For most estimators, there are no striking differences in the ranking depending on which of the two error measures is used.

4.2 Results

Baseline simulation results are presented in Tables 1 and 2 of this paper. The following parameters were chosen. First, the arithmetic average of the market risk premium is set to 5% in continuous compounding. Empirical numbers calculated in Table 5 in Sect. 5.3 display a median of 5.67% over all cases considered. But of course, there is substantial cross-country variation. Hence, we take a somehow intermediate number. For the structural results of our simulations this should be of minor importance.

Table 1 Simulated estimation errors produced by different estimators in a low volatility environment

Table 2 Simulated estimation errors produced by different estimators in a high volatility environment

Second, long-term return volatility ω is set at 15 or 20%, respectively. In this way, a low and high volatility environment is captured. As can be seen from Table 5 in Sect. 5.3, volatilities calculated in USD or GBP are rarely above 20%, while those calculated in Euro/Mark in almost all cases are above this number. The median over all cases considered in Table 5 is 16%, with 90% of all observations being in the range of 16−25%. By taking into account that realized volatilities in our simulations are in the range of 10−40%, we think that we cover a large spectrum of observed volatility ranges.

Third, the mean reverting coefficient γ is set to be equal −0.2, 0, 0.2, and 0.5. By using these values in our simulation, we get variance ratios, i.e. ratios of one year to N-period annualized volatility, in the range of 35−148% with smaller discounting periods being associated with a smaller range. This is exactly what we would have expected based on Eq. (22) in Sect. 5.3, where the structural relationship between the mean reverting coefficient, the length of the discounting period and the variance ratio is more deeply analyzed.

When comparing this simulation-based range according to Eq. (22) with the empirical range of variance ratios, it can be seen that almost all country/discounting period observations fall into this range. The specific ratios are reported in Table 6. Therefore, we think that with the simulation parameters described above we cover most of the empirically relevant range of mean reverting behavior.

Fourth, the heteroscedasticity parameter α is set to be equal 0 or 0.6 in combination with β = 0.5α. In the latter case this leads to an excess kurtosis in the range of 0.44−0.65. This is in line with the excess kurtosis found for Germany for one specific case in the after-World War II period in Table 5 in Sect. 5.3. However, compared to other countries this number seems to be relatively low. Therefore, we also run a robustness simulation producing a quite higher kurtosis of 0.83−1.50. It should be noted that the median kurtosis in Table 5 is 2.2; however, when only considering the after-World War II periods, the median is 1.5.

Structurally, the following results can be observed. First, in the case of iid-distributed returns all estimators except the geometric average and the mean of means work very well. Of course, by construction the Cooper estimators 1 to 3 generate the best results. This is true independently of whether there is a high or low volatility environment. For the EK estimator we can see that errors are small as well and, due to construction, decreasing in the length of the discounting period. The arithmetic mean and the Blume estimator behave oppositely. They work well for short discounting periods, but errors increase with the length of the discounting period. For the arithmetic mean this is the well-known bias already discussed in the introduction. As the Blume estimator is based on a weighted average of the arithmetic and the geometric mean with weights on the second increasing in the length of the discounting period, it follows from the behavior of the arithmetic mean that this estimator deteriorates with longer discounting periods. For a similar reason also the MoM estimator generates errors increasing in the discounting period.

Second, once we add negative serial correlation estimation errors increase significantly for all estimators except the C4 estimator and, to some extent, also the Blume and MoM estimator. This, by itself, is not surprising given the construction of these estimators. However, it might be interesting to see how stable the C4 estimator performs over different degrees of negative serial correlation and simulated volatility ranges. This, in principle, is also true for positive serial correlation, even though the error produced by the C4 estimator in the high volatility environment becomes somewhat larger.

Third, by adding heteroscedasticity to independently distributed returns, we see that all estimators belonging to the family of Cooper estimators continue to produce small errors as long as simulated volatility is not too high. While this statement also applies to the arithmetic average, it does not apply to the GM as well as MoM estimator.

Fourth, if we combine negative serial correlation with heteroscedasticity errors in most of the cases increase. Only the C4 estimator continues to produce relatively low errors as long as volatility is not too high. Moreover, while the AM estimator deteriorates with an increasing degree of negative serial correlation, the GM estimator improves. As a consequence, also the MoM estimator is positively affected by an increasing degree of negative serial correlation. In fact, for a high degree of negative serial correlation the MoM estimator performs very well and comes close to the C4 estimator. Compared to that the Blume estimator achieves its best results for a medium degree of negative serial correlation and outperforms the MoM estimator in these cases.¹⁵

Fifth, if we combine positive serial correlation with heteroscedasticity errors become very large for all estimators. But again, in this case the C4 estimators clearly outperforms all the others; and also the EK estimator is doing remarkably well in these cases.

In order to get a better structural picture of the different estimators a ranking based on the error measurement according to Eq. (17), i.e. the error in present value terms over one year discounting periods, is summarized in Table 3. In this ranking we simply order the estimators form the best to the worst result and then look at their ranks. Moreover, when we look at the ranking of estimators over different parameter combinations, we calculate their rank sum and rank them accordingly. Corroborating to what we have said before, it can be seen that under an iid environment the C2 estimator generates the best results independently of the volatility level. However, once we introduce serial correlation without any heteroscedasticity, the C4 estimator under all circumstances produces the best results. Interestingly, this also holds true if we allow for heteroscedasticity. In fact, when looking at the rank sum over all 16 parameter combinations we have analyzed here, the C4 estimator is clearly the winner.

Table 3 Ranking of different estimators 

Moreover, as an additional remark it should be pointed out that in all 16 different parameter combinations used for compiling Table 3, one estimator belonging to the Cooper family occupied the first place. This corroborates the statement that this family of estimators performs very well.

According to this overall ranking the GM estimator produces the worst estimates. While the GM estimator produces bad results under most parameter combinations, the Blume estimator works relatively well as long as there is negative serial correlation. However, for none or positive serial correlation it performs badly.

For the MoM estimator it can be said that it produces good results in the case of high negative serial correlation independently of the heteroscedasticity and variance level. However, for all other cases, i.e. low negative or positive serial correlation, the estimator generates flawed results.

Interestingly, these rankings do not change much, if instead of an error term normalized by the length of the discounting period we look at the error in present value terms. In fact, the grey shaded area in Table 3 gives the aggregated rankings based on Eq. (16). There are no striking differences.

Finally, a graphical resume of these results, especially with respect to the C4 and MoM estimator, is given in Fig. 2. Again, it can be seen there that the C4 estimator works remarkably well under all circumstances, while the MoM estimator only does a somehow acceptable job in the case of high negative serial correlation. The AM estimator comes close to the C4 estimator in case of no negative serial correlation.

Fig. 2

Biases of different estimators under high or low volatility, negative serial correlation and heteroscedasticity. This figure is based on a simulation of 200,000 random yearly return realizations according to Eqs. (14) and (15) as described in Sect. 4. Parameters σ, γ and α are varied according to the values given below. The long-term return volatility ω is set at 15 or 20%, for the long-term return we define μ = 0.05–0.5ω². Moreover, we set β = 0.5α. The errors according to Eq. (17) for the N-period discount rate estimations are show. The estimators are: Δ_AM: arithmetic mean; Δ_GM: geometric mean; Δ_MoM: mean of geometric and arithmetic average; Δ_C4: Cooper estimator according to Eq. (12). A Low risk, high negative serial correlation, no heteroscedasticity (σ = 0.15, γ = 0.5, α  = 0). B Low risk, no negative serial correlation, high heteroscedasticity (σ = 0.15, γ = 0, α  = 0.6). C Low risk, high negative serial correlation, high heteroscedasticity (σ = 0.15, γ = 0.5, α = 0.6). D High risk, high negative serial correlation, high heteroscedasticity (σ = 0.20, γ = 0.5, α  = 0.6). E High risk, high negative serial correlation, no heteroscedasticity (σ = 0.20, γ = 0.5, α  = 0). F High risk, no negative serial correlation, high heteroscedasticity (σ = 0.20, γ = 0, α  = 0.6)

From a practitioners’ perspective, these results can be summarized as follows. Under conditions of ambiguity, i.e. it is unclear to what extent market returns are subject to serial correlation and heteroscedasticity, it would be best to work with the C4 estimator, as it outperforms the other estimators over a large range of different parameter combinations. Based on the analysis in the next section, where we show that negative serial correlation is a somewhat pervasive phenomenon, using the C4 estimator is clearly supported. If serial correlation could be ruled out, using the C2 estimator would be recommendable, while if heteroscedasticity could be ruled, the C4 estimator should again be preferred.

However, it has been argued that practitioners prefer to use simple estimators, like the AM, GM or MoM. Of course, this analysis has shown that none of these estimators constitutes a perfect solution, as each of them comes with a risk. In fact, the GM estimator performs badly unless there is a very high degree of negative serial correlation. In the 16 baseline parameter combinations analyzed here, it was always outperformed either by the AM or the MoM estimator.

Results are clearly better for the AM estimator, as it outperforms the GM and MoM estimator in all those circumstances where negative serial correlation is not too high. Hence, using the mean of means―as some practitioners seem to be doing―can only be justified on the basis of empirical evidence pointing to a substantial degree of negative serial correlation. It will be shown in the next section that negative serial correlation is a widely spread, even though not ubiquitous, phenomenon. However, it seems that the empirically measured degree of negative serial correlation is not sufficiently high in order to give the MoM estimator a clear preference over the AM estimator.

Finally, as an additional robustness test we have re-run the simulation by setting the parameters in a way that much higher heteroscedasticity is produced, i.e. we use α = 0.4, β = 0 and α = 0.5, β = 0. In fact, kurtosis in these simulations is in a range of 0.81 to 1.50. Results are reported in Table 4. It can be seen that they are qualitatively unchanged. Again, the C4 estimator overall performs better than any other estimator under consideration.¹⁶ Moreover, it might be worth to mention that the performance of the Blume as well as the AM estimator slightly improve with respect to the base case were kurtosis was clearly lower.

Table 4 Ranking of different estimators in high heteroskedasticity cases

As a final disclaimer it should be mentioned that we have not done an extensive analysis of all possible return generating processes. It might well be that processes can be found where also the C4 estimator leads to significantly biased results. Answering this question must be left to future research.

5 International evidence

5.1 Background

In the preceding section it has been shown that under many circumstances the C4 estimator works best. If we are restricted to use a simple estimator, the choice depends most importantly on whether there exists significant negative serial correlation. In that case the MoM estimator outperforms the AM and GM, while in most other cases the AM estimator seems to work best among these three alternatives. Hence, it is an empirical question which of these estimators are more suitable for a practical valuation problem.

Therefore, in this section we focus on the simultaneous impact of correcting the discount rate estimation for biases stemming from observational problems and serial correlation. The question we are interested in is to empirically infer the relationship between the unbiased market risk premium estimation in the context of valuation problems with its geometric and arithmetic average as well as the mean of means. Of course, in an empirical application we do not know the true unbiased estimation. However, according to our results presented in Sect. 4 we assume that the C4 estimator produces estimations close to the unobserved unbiased estimation.

For our analysis we use an international sample of long historical records on stock- and bond-market returns as provided by Jordà et al. (2019). Because of the international nature of these data we use the global CAPM as an analytical starting point for the analysis. Following the work of Solnik (1974), Grauer et al. (1976), Stulz (1981), Solnik (1982), Adler and Dumas (1983), Dumas and Solnik (1995), and others, we write the securities market line equation in an international context as follows:

$${r}_{i}^{c}={r}_{f}^{c}+{\beta }_{i,w}^{c}\left({r}_{w}^{c}-{r}_{f}^{c}\right)={r}_{f}^{c}+{{\beta }_{i,w}^{c} mrp}_{w}^{c}$$

(18)

Here, c is the currency indicator making clear that all components of the securities market line equation have to be measured in one single currency, i.e. the base currency. This has an important implication: as there is only one risk-free asset in each currency, the risk-free rate ${r}_{f}^{c}$ refers to the domestic government bond issued in the country with the currency c as the legal tender. Hence, depending on the home country of the respective investor, the market risk premium ${mrp}_{w}^{c}$ is measured as the difference of the return of a worldwide equity portfolio expressed in the domestic currency c minus the domestic risk-free rate. The realized market risk premium from the perspective of a German investor reflects the premium he was able to earn by holding the world stock market portfolio above the German government bond. As a consequence, from the perspective of a German investor the historically realized world market risk premium is different than from the perspective of a US-investor or any other investor with a different home currency.

It should be noted that the global CAPM according to Eq. (18) is a simplified version of the international CAPM as developed by the authors given above. In principle, these models show that the covariance risk of exchange rates with asset returns are priced adding an additional factor to the pricing equation given above. However, under specific conditions this risk factor can be ignored, for instance if exchange rates reflect purchasing power parity (cf. Stulz 1981; Dumas and Solnik 1995). Empirically it seems, however, that exchange rate risk might be a priced factor (cf. Dumas and Solnik 1995). We nevertheless stick to the simplified version of a global CAPM given in Eq. (18) as even under a truly international CAPM the world market risk premium is a pricing factor (cf. Adler and Dumas 1983), making its empirical estimation a relevant issue.

Finally, the question whether a global or local CAPM is more appropriate depends on the degree of market integration on an international level. While some markets might be highly integrated, others probably are not. And independently of market integration behavioral restrictions, such as the well-known home bias, might prevent investors from fully exploiting international diversification opportunities. While in reality this might cause the appropriate asset pricing model to some kind of mixture between a global and local CAPM,¹⁷ we use a simpler approach by paying attention either to the global or to the local CAPM perspective. Therefore, we also measure the market risk premium of single countries or regions.

5.2 Data

As our base case we use the data provided by Jordà et al. (2019),¹⁸ which we will refer to as the JST data. This is one of the few databases with a very long historical record of stock- and bond-market returns, exchange rates and also real GDP. In fact, this data set covers the 146 year period from 1870 to 2015. Over this period, we have stock and bond market returns for 16 countries with some years with missing entries.¹⁹ However, for the sake of clarity we conduct our analysis from the perspective of a US, UK, or German investor. Hence, we use the US-Dollar, the British Pound or a combination of Euro/Deutsche Mark/Reichsmark as base currencies. Moreover, we calculated average real GDP weighted returns in order to come up with estimates for the domestic as well as a European and a World market risk premium.²⁰ For all countries and regions we calculate up to 145 yearly market risk premium realizations in three different base currencies according to the following equation:

$${mrp}_{it}^{c}=\mathrm{ln}\left(\frac{{S}_{i,t}^{c}}{{S}_{i,t-1}^{c}}\right)-\mathrm{ln}\left(\frac{{B}_{c,t}}{{B}_{c,t-1}}\right)$$

(19)

Here, c stands for one of the following three currencies: US-Dollar, British Pound or a combination of Euro, Deutsche Mark and its predecessors; i stands for one of the five regions/countries mentioned above. ${S}_{i,t}^{c}$ gives the value of a broad stock market portfolio in country/region i in year t expressed in currency c. ${B}_{c,t}$ gives the value of a portfolio of long-term government bonds at the end of year t issued in the country where c is the domestic currency. Hence, it represents the return of an investment in a portfolio of risk-free bonds issued by the country where the currency c is the legal tender. Because of the global or local CAPM perspective, we do not use all possible currency/country combinations, as this would lead, for instance, to calculate the US market risk premium from the perspective of a German investor. Hence, we combine each currency with the world stock market as well as with those domestic markets, where this currency is the legal tender. The British Pound and the Euro/Mark currency are also combined with the European stock market portfolio.

Because of the special situation during the two World War periods―and also because of a missing data issue―we do all the calculations also for the post-war period from 1957 to 2015 separately. For Germany we also use the online data provided by Richard Stehle.²¹ The data, which will be called the FTS-data, provides yearly total returns of a broadly diversified German stock market portfolio and covers the period 1953 to 2013. We use the data over the period 1957 to 2015 by extending the data for the last remaining three years with the returns of the CDAX. The return on the long-term German government portfolio is proxied by the REXP index.²² However, this index is only available starting from the year 1968. For the missing years we approximate this return by using the yield on German government bonds reported by the Bundesbank and assuming that this represents the yield of a 10-year German government bond and the bond is quoted at par.²³ As this data is only available starting from 1956, we have to restrict the whole FTS data to start from that year.

5.3 Results

The first set of results can be found in Table 5. There we report the statistical distribution of the continuously compounded market risk premium according to Eq. (19) for different combinations of currencies and countries/regions. Not surprisingly, the average returns are clearly impacted by the currency in which they are defined. It should be noted that this might be due to long-term trends in exchange rates as well as persistent differences in the level of the risk-free interest rates.

Table 5 Distribution of the market risk premium relative to different base currencies

In general, it could be said that the differences in average market risk premia are not too pronounced. In fact, leaving two cases aside, namely the World and European market risk premium calculated based on the EUR/Mark, the (arithmetic) average after-World War II risk premia are in a range of 4.63–5.73%.²⁴ However, the World or European market risk premium in EUR/Mar is significantly lower at 3.82%. This might be caused by the huge appreciation of the Deutsche Mark.

When calculating long-term realized market risk premia dispersion is a bit higher, with UK being at the one (4.63%) and Germany (6.86%) at the other end of the range. It should be noted here that for Germany we do not have data for the hyperinflation period 1992–1923 as well as for the World War II collapse period from 1944 to 1948. Moreover, while in most of the cases the volatility of the market risk premium is in the range of 15–20%, it gets somewhat higher (about 22%) for Germany.

As a side remark, it should be pointed out that a direct comparison of the results presented in Table 5 with other sources presenting market risk premia estimations has to be done carefully. As explained in the preceding section, we apply a global CAPM, which means that stock market returns are converted into one base currency (i.e. USD, EUR or GBP); from this return the return on the government bond in that base currency is deducted.²⁵ Only for the market risk premia of Germany, US and UK a direct comparison with other studies is possible, as for these countries stock returns measured in local currency are compared with local risk-free rates.

What is more interesting for our purposes is the fact that regardless of the country, region or base currency we have excess kurtosis, which seems to be more pronounced for pre-war period returns. We also find in 12 out of 15 cases negative skew. This is in line with downside fat tails.

Coming back to the focus of the paper we next investigate the existence of negative serial correlation. For that purpose we calculate the variance ratios of the market risk premium following the approach of Campbell et al. (1997, p. 48 n). It should be noted that under the null hypothesis, i.e. iid returns, variance ratios are not different from 1. In fact, it should not make a difference whether the variance is calculated on the basis of yearly or, let’s say, bi-annual returns. The bi-annual variance should simply be twice the annual variance. However, under the presence of serial correlation this is not true anymore. Therefore, in the presence of negative (positive) serial correlation the variance ratio VR(q), intuitively expressed as the ratio of the annualized variance of q-yearly return observations to the variance of yearly return observations, should be the lower (higher) the higher the degree of negative (positive) serial correlation.

In general, the variance ratio can be approximated by a linear combination of the first q−1 autocorrelation coefficients with arithmetically declining weights (cf. Campbell et al. 1997, p. 54), i.e. for q ≥ 2.

$$VR\left(q\right)\approx 1+2\sum_{k=1}^{q-1}\left(1-\frac{k}{q}\right)\rho \left(k\right)\, with\, \rho \left(k\right)=\frac{Cov\left({r}_{t},{r}_{t+k}\right)}{Var\left({r}_{t}\right)}$$

(20)

In case q = 2 this simplifies to:

$$VR\left(2\right)=1+\rho (1)$$

(21)

Hence, having in mind that VR(2) is the variance ratio of the annualized bi-annual return variance to the yearly return variance, a variance ratio of 0.8 would imply an empirical coefficient of autocorrelation close to −0.2.

Moreover, under an AR(1) process with a one-period autocorrelation coefficient γ, the variance ratio can be written as (cf. Campbell et al. 1997, p. 49):

$$VR\left(q\right)=1+\frac{2}{1-\gamma }\left[\gamma -\frac{{\gamma }^{q}}{q}-\frac{\gamma -{\gamma }^{q}}{q\left(1-\gamma \right)}\right]$$

(22)

We have already discussed in Sect. 4.2 that for our simulations this implies a range of variance ratios from 35 to 148%. Now we can compare this with the empirical results, which are given in Table 6. Note that the variance ratio depends on the length of the time period over which the return is measured. The length of this period measured in years is labelled as q. It should be noted that when using Euro or the Deutsche Mark (and its predecessors) as a base currency, we are restricted to post-World War II periods as we have missing observations in the pre-World War II period.

Table 6 Variance ratios of the global and local market risk premium

Overall, it could be said that the picture in Table 6 is quite consistent. In about 7% of all region/frequency-observations we derive variance ratios above one. Almost all of these cases arise when using the British Pound as a base currency and calculating world-wide market risk premia. Maybe this could be related to the World War experience. In that case it might well be that we would observe similar results, if we were able to calculate Euro/Mark-based variance ratios for periods including the two World Wars. As a side remark, however, it should be noted that having serial correlation in the long run might give way to some serious questions about the rationality of the market equilibrium.²⁶

As a final remark it should be said that we do not report any statistical test for the variance ratios. As has been shown by Campbell et al. (1997, p. 57 n.), there are serious difficulties in making long-horizon inferences based on these variance ratios. If the ratio q/T is not close to zero these tests will have little power. And, moreover, even under the null hypothesis variance ratios tend to be below one. In fact, Richardson and Stock (1989) and Campbell et al. (1997, p. 58), show that expected variance ratios under the null hypothesis converge to

$$E\left[VR\left(q,T\right)\right]={\left(1-\frac{q}{T}\right)}^{2}$$

(23)

Therefore, having q/T-ratios of up to 1/6 the fact that most of the empirical variance ratios are below one should not be overinterpreted. In order to cope with this issue an additional statistic is presented in Table 6. It is called the Mean Ratio and it gives the ratio of the average empirical variance ratio over the respective regions to the expected variance ratio according to Eq. (23). In case of negative serial correlation this ratio should be lower than 1. It can be seen that only in a few cases, i.e. 8 out of 51, this does not hold and ratios are above one. It is interesting to note that most of these cases happen for very long frequencies, i.e. for frequencies beyond 10 years.

To sum up, despite the poor statistical robustness the evidence presented here is broadly in line with the notion that negative serial correlation tends to be an ubiquitous phenomenon.

5.4 Practical implications

The evidence presented so far should not be ignored when it comes to the estimation of discount rates. Starting from this observation we now ask the question whether there is any practical guidance that can be drawn from our results. In this respect, two remarks emerge from our analysis.

First, because serial correlation seems to be a pervasive phenomenon ideally the C4 estimator according to Eq. (12) should be used for estimating discount rates in valuation problems. This is true even in the presence of heteroscedasticity, as we have shown. However, by using this estimator the valuation problem is enlarged by new degrees of freedom, as one needs to have an information about the extent of serial correlation over many different lags. This is not easy to implement, especially also because the analysis presented in this section showed that due to the relatively small number of return observations results are not very robust.

Therefore, as a second remark we address the question whether our analysis would allow for any kind of heuristic rule in order to simplify the problem. For that purpose, we run an additional analysis, where we estimate the presumably least biased market risk premium according to the C4 estimator in Eq. (12). The period specific variance ${\sigma }_{N}^{2}$ is estimated using the variance ratio results presented in Table 6. We then compare these presumably least biased estimates with the well-known AM, GM, and MoM estimators.

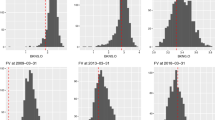
Some first graphical results are presented in Figs. 3 and 4. In the majority of the cases the least biased discount rate estimation is between the geometric and the arithmetic average. This corroborates the intuition that because of negative serial correlation the unbiased discount rate estimators have to be corrected downward. Interestingly, based on the empirical distributions found here, this correction in many cases leads to unbiased estimators below the arithmetic average. At the same time, it can be seen that the unbiased estimator is rarely below the MoM. Hence, form graphical inspection it is unclear, whether the AM or MoM estimator perform better. Of course, both are clearly biased, but which of the two tends to be less biased cannot simply be inferred from graphical inspection.

Fig. 3

Unbiased local market risk premia based on the C4-estimator for Germany, US, and UK. This figure draws the discretely compounded unbiased market risk premia estimated on the basis of the C4 estimator according to Eq. (12); for more details cf. Sect. 3.2. Raw data is from JST or FTS as described in Sect. 5.2 covering the period 1871 to 2015 or 1957 to 2015. GM, AM, and MoM indicate the discretely compounded geometric or arithmetic mean or the mean of both. A Germany (short JST data) with Deutsche Mark (and its predecessors) and Euro as base currency. B Germany (FTS data) with Deutsche Mark and Euro as base currency. C US (JST data) with US-Dollar as base currency. D US (short JST data)) with US-Dollar as base currency. E UK (JST data) with British Pound as base currency. F UK (short JST data) with British Pound as base currency

Fig. 4

Unbiased global market risk premia based on the C4-estimator. This figure draws the discretely compounded unbiased market risk premia estimated on the basis of the C4 estimator according to Eq. (12). Raw data is from JST as described in Sect. 5.2 covering the period 1871 to 2015 or 1957 to 2015. GM, AM, and MoM indicate the discretely compounded geometric or arithmetic mean or the mean of both. A World (short) with Deutsche Mark and Euro as base currency, B Europe (short) with Deutsche Mark and Euro as base currency. C World with US-Dollar as base currency, D Europe (short) with British Pound as base currency. E World with British Pound as base currency, F Europe with British Pound as base currency

Therefore, we perform a more precise analysis by computing the estimation biases based on the measures introduced in Eqs. (16) and (17) in Sect. 4.1. A similar approach has already been used when evaluating the simulation results in Sect. 4.2. By using the currency/region combinations presented in Table 6 and assuming that the C4 estimator according to Eq. (9) produces the least biased results, we can calculate for every discounting period q a weighted or unweighted estimation error based on Eqs. (16) and (17). Further distributional data needed for this exercise is taken from Table 5. Results are reported in Table 7.

Table 7 Estimation errors and rankings of simple estimators

Several results emerge from this exercise. First, it can be seen that in practically all cases the GM produces the most biased results. Secondly, AM and MoM generate significantly smaller biases. Third, the MoM is more likely to outperform the AM, if there is more pronounced negative serial correlation. In fact, those cases were MoM is ranked on the first place are the cases where the variance ratios are strongly declining over time. However, as long as variance ratios stay relatively high, i.e. they are not clearly going below 70–80%, the AM performs better. It is important to emphasize that this result to some extent might also be driven by the length of the time series. In fact, in Panel B and C the MoM estimator outperforms the AM estimator in (almost) all those cases where short time series are used, while in the cases with the long time series the opposite is true.

Fourth, from graphical inspection one gets the impression that the MoM tends to perform better than the AM in those cases where the local CAPM is applied, i.e. Figure 3, while in the global CAPM cases, i.e. Fig. 4, the opposite tends to be true. This might be driven by the different degrees of negative serial correlation we have found in local vs. international markets. For this reason, we have calculated average ranks in Table 7 for the local and global CAPM cases separately. Actually, it can be said that in the local CAPM cases the MoM ranks slightly better than the AM. The average rank over all three Panels in Table 7 is 1.2 as compared to 1.8 for the AM. However, the opposite happens, if the global CAPM is applied. Here the average rank of the MoM is 1.8 as compared to 1.2 for the AM. This result also implies that when doing a ranking over all cases considered in Table 7 the average rank of both estimators is equal. And the question whether the ranking is based on Eq. (16) or (17) is almost irrelevant.

Fifth, as a final remark it should also be said that at least in some cases shown in Figs. 3 and 4 it seems that the MoM gets the better the longer the discounting period is. This is not totally surprising as we have seen that variance ratios tend to decline in the length of the return measurement period. However, it cannot be taken as a general rule. Moreover, when it comes to the practical implementation of these estimators it might not be viable to switch among MoM and AM estimators depending on the length of the discounting period.

To summarize, based on the reasoning presented in this section we should be careful in making any unconditional statement regarding the relative performance of the two estimators. The analysis presented here, however, corroborates the perception that in those cases where we have a noteworthy degree of negative serial correlation the ranking would be tilted towards the MoM. And if variance ratios are decreasing in the length of the time periods, the usage of the MoM estimator would be even more important in cases a company with substantially growing cash flows has to be valued.

6 Conclusion

In this paper we have done a twofold analysis. First, we started from the well-known result of Cooper (1996) that estimating unbiased discount rates in a perfect capital market setting implies to use discount rates that display an increasing premium above the arithmetic average the longer the discounting period is. At the same time, however, it has been shown that a downward correction of these discount rates is warranted in the presence of negative serial correlation. The appropriate estimator has also been developed by Cooper (1996) and was labelled as the C4 estimator in this paper.

Taking into account that besides negative serial correlation also heteroscedasticity is a well-documented phenomenon in capital markets, we were interested in detecting the potential bias of the C4 estimator in the presence of both phenomena. Based on a simulation analysis we have presented some evidence that this estimator seems to work pretty well even under both serially correlated and heteroscedastic stock market returns. In any case, it clearly outperforms all other estimators analyzed in this paper under a wide range of different parameter combinations for the return generating process.

In the second part of the paper we then presented evidence of serial correlation and heteroscedasticity in a worldwide sample of realized market risk premia. By applying the global and local CAPM we provided evidence that negative serial correlation is a wide-spread phenomenon, even though we also found a few currency/region combinations displaying positive serial correlation. However, this only happened when taking the pre-World War II period into account. We have also shown that heteroscedasticity is a wide-spread phenomenon.

Finally, we applied these results to the so called C4 estimator, i.e. an estimator accounting for serial correlation, and found that in the majority of the cases the presumably least biased market risk premia delivered by this estimator is somewhere in between the MoM and the AM, with the AM performing the better the less prevalent negative serial correlation is, the shorter the discounting periods are, and the longer the historical return series are. Hence, using the MoM tends to produce better results for cases with a noteworthy degree of negative serial correlation and for longer discounting periods. However, by comparing the two estimators based on the empirical data collected for this paper we cannot give a clear indication which of the two likely produces less biased results. If ever, we found some evidence that the MoM is slightly outperforming the AM under a local CAPM perspective, while the opposite tends to be true under a global CAPM perspective. Overall, even though there is some rationale for the so-called mean of means rule used by practitioners any recommendation strongly depends on the distributional parameters of the market risk premium.

Of course, the results presented in this paper need further investigation. For instance, in our simulation analysis we restricted ourselves to a relatively small range of return generating processes. Also, we did not account for any firm specific characteristics or different time patterns of cash flows. In order to better understand the robustness of the C4 estimator it should be challenged by a much broader range of different processes and firm specific characteristics. Also, bringing the empirical analysis to a wider range of datasets with higher frequency should be helpful.