Abstract
Despite advances in the field, we still know little about the socio-cognitive processes of team decisions, particularly their emergence from an individual level and transition to a team level. This study investigates team decision processes by using an agent-based model to conceptualize team decisions as an emergent property. It uses a mixed-method research design with a laboratory experiment providing qualitative and quantitative input for the model’s construction, as well as data for an output validation of the model. First, the laboratory experiment generates data about individual and team cognition structures. Then, the agent-based model is used as a computational testbed to contrast several processes of team decision making, representing potential, simplified mechanisms of how a team decision emerges. The increasing overall fit of the simulation and empirical results indicates that the modeled decision processes can at least partly explain the observed team decisions. Overall, we contribute to the current literature by presenting an innovative mixed-method approach that opens and exposes the black box of team decision processes beyond well-known static attributes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Group and team decisions shape the corporate world, for example, through management boards or project teams.Footnote 1 There is broad agreement that groups have the potential to make better decisions than individuals because they can aggregate diverse information, skills, and perspectives while, at the same time, compensate for limitations such as individual biases or mitigate problems of self-interested behavior (DeVilliers et al. 2016; Schulz-Hardt et al. 2002). Teams are a vital element to ensure the flexibility and adaptability of organizations (Delgado et al. 2008). Nevertheless, groups and teams do not always outperform individuals. Group think theory, for example, describes dysfunctional interaction patterns that may result in poor decisions (Janis 1972, 1982; Esser 1998). Uniformity pressure, group homogeneity, or other social and contextual influences can suppress individual contributions or effective group decision making (Schulz-Hardt et al. 2002).
Against this backdrop, social and applied psychology literature investigated determinants of capable group and team decision making, related to social, behavioral, cognitive, and contextual factors (Reader 2017). Previous research also discussed the properties of effective teams. For example, Katzenbach and Smith (2015) described them as teams that have an appropriate number of members with diverse skills and viewpoints, clearly defined goals, specific roles, and rules for members. More recently, team cognition literature studied team processes and team performance (Mesmer-Magnus et al. 2017), going beyond the predominantly static attributes addressed by previous research. In this context, the term “cognition” describes cognitive processes such as learning, planning, reasoning, decision making, and problem solving at the team level. Capable team cognition processes may result in superior team performance, which is described as “collective intelligence” (Woolley et al. 2015). From the analytical perspective of team cognition theory, interactions between team members are central elements of the cognitive processes. Interactive team cognition theory emphasizes team cognition as an activity and not as a property. It describes teams as dynamic cognitive systems in which “cognition emerges through interaction” (Cooke et al. 2013, p. 256).
Several scholars support the implied call for research on the socio-cognitive interaction processes in teams (Grand et al. 2016; Crusius et al. 2012; Woolley et al. 2010; Rousseau et al. 2006). This issue is also of significant managerial relevance, as these processes, including potential path dependencies, determine team performance. Nevertheless, the processes and mechanisms of how cognition at the team level emerges from individual cognition remain, to a large extent, a “black box.” Hence, it is the aim of this study to show how team decision making can be studied as an emergent property using an agent-based model and how this can contribute to a better understanding of team decision processes. In line with this perspective, this study contributes to the exploration of “how and why organizationally relevant outcomes emerge rather than focus only on differences in what has already emerged” (Grand et al. 2016, p. 45).
This study presents a mixed-method approach with the potential to increase our understanding of the underlying socio-cognitive processes of team decision making. We use an agent-based approach to model team decisions as an emergent property, that is, we link individual cognition to team-level decisions. The agent-based model is combined with a laboratory experiment to provide input and output validation of its essential aspects. The experimental setup generates data about individual and team cognition structures and suggests typical decision processes triggered by these structures. Based on this empirical data, we use the agent-based model to analyze the mechanisms of how team decisions emerge from an individual level and advance to a team level. Given the empirical data on team decisions, we test the fit between the simulated results and the observed team decisions, and we assess whether the hypothesized decision processes provide a possible explanation for observed team results (Klingert and Meyer 2012; Smith and Rand 2017). These empirically supported processes can be refined in future and, in turn, be tested in forthcoming setups.
The paper is structured as follows. The first section describes the relevant literature and the use of the two main methods. Thereafter, we present the laboratory experiment and its main results. With these results, we develop the “team cognition matrix” as a measure for the observed cognitive structures. The identified, typical team cognition patterns in our data provide the basis for developing a team decision algorithm that we subsequently implement in an agent-based model. We test several decision submodels in a simulation experiment for a better understanding of the observed team decision processes and evaluate their predictive power. This is followed by a discussion of additional influencing factors and possible model modifications. Finally, we provide a short conclusion and outlook.
2 Related literature and method
This study investigates the processes underlying team cognition and team decision making. Because of increasing task and technological complexity, individuals are unable to meet the resulting cognitive demands. Therefore, these growing cognitive demands require that cognition is a team effort (Cooke 2015). Ideally, each team member should complement the expertise and skills of the other members. Team cognition emerges fairly naturally when people work face-to-face in shared workspaces (Gutwin and Greenberg 2004). But team cognition is complex and more than the mere sum of the individual team members’ cognition; it emerges from the interplay of each team member’s individual cognition and the team processes (Cooke et al. 2013; Hollan et al. 2000; Hauke et al. 2018). In this paper, both teams and groups in general are seen as dynamic systems of interacting individuals, modeled as agents. Team and group results emerge from the interactions of individuals.
Teams have the potential to act intelligently as a collective. The term “intelligence” was originally used to describe an individual’s ability to understand and learn from information, as well as to apply this ability to solve problems. Researchers have since produced a wide range of definitions of intelligence, depending on their approach and method. Terms like “IQ” and mental or cognitive ability are often used interchangeably. A widely used interpretation of intelligence is that of Gottfredson (1997) who defines it as a “very general mental capability that, among other things, involves the ability to reason, plan, solve problems, think abstractly, comprehend complex ideas, learn quickly and learn from experience.” In the 1980s, group intelligence became a research focus. As opposed to individual intelligence, “collective intelligence” or “shared intelligence” emerges from the collaboration and competition of individuals (Szuba 2001) and represents the combined intelligence of a group of individuals.
The emergence of collective intelligence has been the focus of several studies, as a non-linear, “complex feedback loop of individual-environment-individual interactions” (Singh et al. 2013, p. 187). Each individual contributes specific knowledge and skills, which can result in something more than the sum of its parts. Accordingly, Lévy and Bononno (1997) describe collective intelligence as “a form of universally distributed intelligence, constantly enhanced, coordinated in real time, and resulting in the effective mobilization of skills.” Analogous to the general cognitive ability of individuals (called the “g-factor”), Woolley et al. (2010) proposed a collective intelligence factor c that describes how well a group performs on a diverse range of tasks; a factor that can be used to predict future group performance. In turn, this c-factor can be explained via properties such as group diversity, the number of females in a group, and conversational turn-taking. Although these are static properties of groups, the authors regard them as indicators of relevant group cognition processes.
The decision making of groups differs in some respects from that of individuals. Hill (1982) documents that groups, compared to individuals, are more likely to be aggressive and inclined to take risks in choice dilemmas and gambling tasks. They are also less likely to accept responsibility due to dispersed rewards or punishments and are less engaged. The theory of social loafing (Karau and Williams 1993) states that individuals are inclined to put less effort into group work than into individual work, with the result that an increasing number of group members degenerate group outputs.
Hill (1982) documents that group sizes of three to six members are favored as larger groups perform less, and that a large proportion of group discussions is required for decision making. Hill also reviewed three decision strategies: (1) truth wins, where members realize that a particular option is superior, (2) majority rules, where the majority decides on the solution, and (3) where decisions are otherwise made through equiprobability. He found that low-ability groups are more likely to outvote a member who has the correct ranking position. By contrast, in high-ability groups, the best member makes the decision supported by one or more of the others (truth wins).
The ability, gender, and team-mindedness of the participants also affect the success of teamwork. Hill (1982) asserted that the performance of groups with mixed cognitive abilities are generally superior to that of individuals. Male groups improved more in concept attainment tasks, while female groups improved more in information processing tasks. He also observed that groups achieve better results when the members prefer to work as a group rather than as individuals (affiliation preference).
Devine and Philips (2001) investigated the influence of individual cognitive ability on team performance through several meta-analyses of the cognitive score of the best and lowest score, the group mean score, and the standard deviation of scores. They found that whereas the standard deviation was unrelated to performance, the other three scores had moderate positive relationships through best member score r = 0.208, lowest member score r = 0.246, and mean member score r = 0.294 (Devine and Philips 2001).
Another relevant factor is the homogeneity or diversity of a group, for example, in age, gender, culture, or background. Diverse groups have a broader range of skills and information and can, therefore, achieve better results. To explain how a group’s diversity affects its success, Van Knippenberg et al. (2004) developed a framework which incorporated both decision making and social categorization perspectives on work-group diversity and performance. The authors found that the main positive factor was the broader range of information and abilities. Different task demands – for example, complex creative tasks – benefit from increased diversity, while repetitive and routine tasks suffer from it. Diversity is also more likely to be positive if members are motivated and have a high task ability. Still, a greater similarity between members also reduces intergroup bias, which could otherwise hinder teamwork (Van Knippenberg et al. 2004).
As soon as people become part of a group, the members establish a form of conduct among themselves. This conduct can either hinder the decision process by reducing effort, withholding information, and resulting in coordination losses, or it can increase the group’s effectiveness by pooling the members’ efforts, skills, and knowledge (Hackman and Morris 1975). Some studies propose possible ways to improve team cognitive abilities. For example, Willems (2016) claims that team members can improve their cognition when they perform similar tasks, assume similar responsibilities, and interact intensively (Willems 2016). According to Moreland and Myaskovsky (2000), a positive correlation exists between group performance and group members’ familiarity with each other’s abilities and expertise. Moreover, they argue that training, which includes team building, strategy creation, improved situation awareness, stress management, collaboration, and cooperation, has a positive impact on attendees’ cognitive skills (Helmreich 2000).
Engel et al. (2014) examined the relationship between social sensitivity and successful teamwork. They measured the participants’ social sensitivity with the “Reading the Mind in the Eyes” test, which quantifies a person’s ability to assess other people’s emotions by identifying facial expressions. They found that the proportion of women correlates with the collective intelligence of the group (r = 0.23), which in turn was explained by their higher social sensitivity scores. The correlation held even if the meetings were not face-to-face but online, with r = 0.41 (Engel et al. 2014).
Finally, the term “decision dynamics” is often used interchangeably with “opinion” or “consensus dynamics.” It indicates how individuals influence each other’s opinions, leading to either consensus or dissent. Models on opinion dynamics differ in many respects, including linearity and opinion type, as well as regime activation and updating (Deffuant et al. 2000; Hegselmann and Krause 2002; Urbig et al. 2008). Besides, it is also necessary to consider related areas in computer-based decision modeling, such as fuzzy logic (Ji et al. 2007) or the estimation model of group decision making (Klein et al. 2018).
Overall, the literature has identified a substantial number of individual and group attributes, all of which can positively affect team performance. Recent studies also emphasized that teams are dynamic systems, and that team performance emerges from the interactions of the individual team members. Nevertheless, the identified attributes remain mainly static and the exact mechanisms of how team cognition emerges from the individual level remain largely a “black box.”
Against this backdrop, this study uses agent-based modeling to study team cognition processes. Although agent-based modeling has matured and gained ground in different disciplines (Hauke et al. 2017; Wall and Leitner 2020), it still cannot be considered a mainstream method (Klein et al. 2018). A particular advantage of agent-based modeling is “its ability to represent key elements of group dynamics, such as organizational structure and individual heterogeneity” (Smaldino et al. 2015, p. 301). Compared to mainly verbal descriptions, formal modeling can increase precision. In particular, it allows a multiple-level modeling of an organization, especially to capture potentially complex interactions between the levels (Smaldino et al. 2015). Agent-based modeling can also be used to formally specify and test potential mechanisms. In this paper, we use these comparative advantages of agent-based modeling to develop and test implementations of potential socio-cognitive processes, which translate individual assessments into collective decisions. It can be seen as an instance of theory development using agent-based modeling (Lorscheid et al. 2019; Grimm and Railsback 2012; Heine et al. 2005). Our dual intention is to outline the general approach through which agent-based modeling can contribute to this, and to take the first step in this direction.
Our research uses a mixed-method approach. Data generated through a laboratory experiment are used for both the input and output validation of the model. In particular, we use the empirical data at the individual level regarding cognition and team structure and validate the model-generated decisions at the team level with the empirical data. Until recently, only a few papers explored the potential of combining experimental research and agent-based modeling. For example, Smith and Rand (2017) used agent-based modeling to explore the macro implications of their experimental findings in the context of job-search behavior. Klingert and Meyer (2018) used the data of previously published laboratory experiments to develop a micro validation of different trading strategies for an agent-based investigation of different market mechanisms. Both examples used experimental research to increase the validity of agent-based modeling and its conclusions.
3 Laboratory experiment
The core of the laboratory setup is a team building game (Knox 2016). The team task is to rank 15 items (mirror, oil, water, army ration, plastic sheeting, chocolate bar, fishing kit, nylon rope, seat cushion, shark repellent, rum, radio, map, mosquito net, sextant). The scenario of this ranking task is a hypothetical accident at sea. Fire leads to an emergency in which the team has to abandon a sinking ship. The 15 listed items are possible objects to transfer from the sinking ship to a lifeboat. The task is to evaluate the items in terms of their relevance to survival. A handout describes the story line, along with the list and explanation of the items.
Each team consists of three to five participants, which is a suitable team size according to Hill (1982).Footnote 2 The participants were mainly recruited from an Industrial Engineering and Management (M.Sc.) program and an international MBA program, as well as through workshops with international researchers in the field of social simulation (mainly PhD level). As far as possible, attention was paid to the heterogeneity of the team configurations in terms of gender, age, nationality, and educational background. In the first phase of the experiment, each participant is asked to rank all items individually on a ranking chart, within a time limit of ten minutes and without any contact with other participants. In the second phase, after completing the individual ranking, the team convenes to discuss and agree on a joint team ranking, which it notes on another ranking chart. This discussion has a time limit of 20 min.Footnote 3 The team discussions are audio recorded to provide information on the team’s interaction dynamics, such as conversational turn-taking or leadership. Finally, following this team discussion, the game is overFootnote 4 and the individual and team rankings are evaluated.
The experimental setup makes provision for an evaluation of both the individual performance and the team performance. For this, we use an expert evaluation of the items as a benchmark. The individual and team performance measures are identified by calculating how closely the individual and team decisions match the expert opinion. The individual performance score is the sum of the absolute differences between the individual ranking positions and the expert ranking positions. The resulting distances for all 15 items are summed as a score for each individual. The lower the score, the better the performance (and inversely). The team performance score uses the same calculation method by summing the absolute differences between the team ranking positions and the expert ranking.
These measures allow a comparison of individual performance and team performance, regarding the task. To quantify this, we introduce the performance measures “team result,” “team intelligence,” and “team stupidity” (Table 1). These measures were adopted from Cooke and Kernaghan (1987) and extended by us to evaluate the team result. The average of the individual scores provides a benchmark to analyze whether the team interactions result in a gain or a loss in comparison to the individual results. In addition, if the team score is lower than the best individual score, the team succeeded in achieving a better result than all team members individually. In this example, we identify a case of team intelligence. On the contrary, if the team score is higher than the worst individual score, the team performed worse than all individual team members and we identify a case of team stupidity.
Considering the experimental results (Table 2), we observe a wide range of team performances. Of the 26 teams, 23 benefited from the team interaction. These teams have a better score than the average of all individual scores. We identify team intelligence for nine teams. In three of these teams we even see large increases, from − 10 to − 18, in comparison to the best individual score (see team IDs 24, 9, 1). The three worst-performing teams in the data set have a loss in team performance, meaning that the team score was worse than the average score of all individuals. We also analyzed the effects of team size on team performance. In our data set, an increase in the team size from four to five leads to an improvement of average team results from − 10.2 to − 12.5 and reduces average team stupidity from − 24.2 to − 32.6.
4 Team cognition matrix
The individual and team ranking charts of the laboratory experiment explicate the individual and the resulting team-level socio-cognitive structures underlying the decision-making process. These structures provide data for the analysis of the emergent process from different perspectives, such as the relative ranking positions in a team or the distances of ranking positions per item.
For the evaluation of the team structures for each of the 15 ranking items, we developed the team cognition matrix (Fig. 1). This matrix provides an overview of the team’s cognition structure per ranking item. The matrix is quadratic, with n rows and n columns. The order n of the matrix depends on team size g. The matrix elements are absolute distances between ranking positions. We use absolute distances to evaluate the performance, as the direction of deviations is not in focus. Rows and columns with indices from 1,1 to g,g (A) contain distances between two individual ranking positions for all team members and all possible pairwise combinations. The elements in the row and column with the index g + 1 show the distances between the respective individual ranking position and the team decision (B). The elements in the row and column with the index g + 2 contain the distances between the individual ranking positions and the expert ranking (C). The main diagonal has zero values, as these elements are self-referential. The entries in the matrix are filled symmetrically identical over the main diagonal to simplify the analytical process.
Team cognition matrix (TCM) – Overview of the cognitive structure of a single team with team size g, filled for a single ranking item. A distances of individual decisions to other team member decisions, B distances of individual decisions to team decision, and C distances of individual decision to expert decision (performance measure)
Figure 2 shows an example of a team cognition matrix based on the laboratory experiment data set. The left part of the Figure indicates the individual rankings and team ranking for the item “fishing kit” and the team with team-ID 6 (here labeled “A”). The experimental setup specifies 15 ranking items. Consequently, the range of possible distance values in the matrix is the interval of [1,14]. The team, in this example, has four members. Team member A1 ranked the item on position 1. This ranking position leads to the following distances to the other team members: 13 to team member A2, 3 to team member A3, and 4 to team member A4. These values are the first four elements of the first row in the team cognition matrix (the right-hand section of Fig. 2). The next value of this row shows the distance of A1 to the team decision, being four positions away from the team ranking position 5. The expert opinion on the relative relevance of the “fishing kit” is ranking position 7. The last value of the first row shows the distance of the individual ranking by A1 to this benchmark ranking, being six positions away. Accordingly, the matrix contains all distances for all team members. Additionally, the element on ag+1,g+2 shows the distance between the team ranking (here: 5) and the benchmark ranking (here: 7).
Looking at this exemplary team cognition matrix in Fig. 2, we identify two individuals being very close to each other in their ranking positions (A3 and A4), while another team member is far away from the other individual ranking positions (A2). The fourth individual A1 has a small to medium-range distance to A3 and A4. Given these distances, we can identify a general heterogeneity of individual ranking positions for the “fishing kit” in this team.Footnote 5 At the same time, there is a majority with very close ranking positions of 4 and 5, and the team agreed on ranking position 5. This indicates the possible occurrence of a majority decision on this ranking position. The majority and team decision were also closer to the benchmark than the other team member ranking positions. Thus, the better decision prevails in this example.
The matrix structure allows for such an evaluation of emergent results from individual to team levels. We analyze and identify the individual and team cognition structure characteristics, their frequency of occurrence, and their explanatory power. In addition, this model provides a formal link to the team decision submodels in our agent-based model.
5 Measuring team cognition
Along with this structure, we measured and reported team cognition matrices for each team and item in the laboratory experiment, resulting in 390 matrices for 15 items and 26 teams. These matrices provide information on the distances between team member rankings (representing the homogeneity of the cognitive structures), the distances between individual and team rankings (representing the degree of consensus between individual and team rankings), and the distances from the benchmark (representing the individual and team performances). On closer inspection, the analysis reveals four reoccurring team cognition structures: consensus, majority, parties, and compromise (Fig. 3). For the identification of these types, we focus on the individual distances between team member rankings (the areas within the dotted lines).
In the example of case 1 (consensus), all members of team 23 individually ranked “water” as the most relevant item for survival. Consequently, all values are zero; the cognitive structure among the team members is homogeneous. We refer to this case as a “consensus.” The distances between individual rankings and team decisions reveal the degree of agreement between the individual rankings and team ranking. In case 1, these values are zero for all team members. The team agreed on “water” being the most relevant item.
Overall, we observe a consensus pattern (case 1) in 15.1% of all ranking decision scenarios. From this situation, it is potentially easier to come to an agreement when individual positions are close to each other, as reflected in this example. In the laboratory experiment, we frequently observe this situation for the item “water.” Given the qualitative data from observations and audio records, the decision on this item is often the first and most straightforward decision. Regarding the performance, this decision reached individual and team scores of 2, as the expert opinion ranked “water” in position three.
More complicated situations occur if the positions are further apart from one another. Case 2 shows the team cognition structure for team 4 and the item “map.” As evident, there is a majority of three team members with close ranking positions, and one team member with large distances being ten to twelve positions away from the team. Consequently, we call this case a “majority.” We frequently find this majority structure, more specifically in 46.7% of all ranking decisions.Footnote 6 Looking at the distances between individual and team rankings in the empirical example of Fig. 3, we find that the majority determined the team decision.
Case 3 illustrates another typical team cognition structure, with the team members split into two parties. Here, the two team members of each of the two parties have close ranking positions, but the subgroups as such are far away from each other (by six and seven ranking positions). This is a frequently observed structure that we call “party.” In our data set, we identify both successful winning and unsuccessful winning parties. 24.4% of all ranking decisions had a party structure. We often observe that a particular party gets its way and defines the team decision. In this example, Team 17 ranked the item “radio” close to one of the two parties.
Finally, in 13.9% of all ranking items, we identify situations in which the individual ranking positions are scattered to such an extent that no majority or no party split of ratings is formed. This decision structure is called a “compromise.” Case 4 represents such an example for team 23 and the item “mosquito net.” If no majority emerges, teams often find a compromise between individual ranking positions.
6 Agent-based model of team cognition
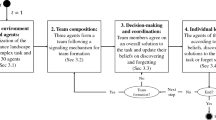
To further explicate the potential link between socio-cognitive structures and subsequent team decisions, we use the identified team cognition patterns to implement potential decision dynamics in a simulation study. By doing so, our aim is to test their predictive power for the emergent team outcome and performance. We apply agent-based simulation (Macal 2016; Smaldino et al. 2015; Secchi 2015) and endow the agents with team decision rules that use the team cognition structures as criteria for the team decision. For the implementation of the simulation model and the analysis of the empirical and simulated data, we use the programming language R.Footnote 7 The data analysis of the laboratory experiment and the simulation output analysis runs through the same code lines in R. This procedure reduces errors and facilitates the validation process.
The simulation provides a computational testbed to investigate team processes and to develop theory in this field via agent-based modeling (Lorscheid et al. 2019; Grimm and Railsback 2012; Heine et al. 2005). As a first step, we use a random decision model to create a benchmark to evaluate the performance of the individuals and the groups in the laboratory experiment (see Sect. 6.1). We also use this model to perform an error variance analysis to determine the number of required simulation runs. In the second step (see Sect. 6.2), we analyze the predictive power of the different implemented team decision models. Finally, as a third step (Sect. 6.3), we discuss potential model refinements, such as the effects of the interdependencies among the items.
6.1 Performance evaluation based on a random model
We start with a random decision model as a benchmark to evaluate the empirical results.Footnote 8 In essence, this model is based on the random drawing of ranking positions per item. The model provides an orientation to the expected values and the range of the performance measures for purely random decisions.
The random model is implemented as follows: First, to rank each item, a random ranking position is drawn from a uniform distribution Ω = [1,15]. Thereafter, a cleaning step is run through every ranking position, starting with the first ranking item, to check for duplicates in ranking positions. To eliminate these duplicates, the algorithm randomly selects one of the duplicate occupancies and sets it at the next ranking position.
This stochastic model has many possible combinations. Therefore, to obtain stable and representative results, the number of repetitive draws via simulation runs is important (Lorscheid et al. 2012). For this reason, we perform an error variance analysis to determine the number of runs for the subsequent simulation model experiments (see Appendix B). Accordingly, we set the number of runs at 5226. This provides a good balance between further decreases of variance and the computational costs of more runs, and avoids the risk to overpower by adding too many runs, which affects the significance of the results (Secchi and Seri 2016).
The random model can be used as a benchmark for both the experimental results and the implemented decision models. In this section, we evaluate the performance at the individual and team levels in the laboratory experiment in comparison to the performance of a random process. To operationalize performance, we again use the distance of the ranking positions relative to the expert ranking position.
First, at the level of individual decisions, we compare key descriptive statistics (mean, median, min, and max) of the performance scores from the laboratory experiment with those of the random model. The median of the score in the random model benchmark is 76, the mean score is 74.86, and the standard deviation 12.56. In the laboratory experiment we have a median score of 60, a mean score of 60.07, and a standard deviation of 14.90 for the rankings at the level of individuals. Thus, the individual rankings improve in comparison to the random benchmark by − 14.79. The maximum possible score and thus the worst score in the random simulation model is 112. The minimum theoretical achievable score is 0. The actual best score for all 15 items observed in the simulated random model is 22,Footnote 9 whereas it is 28 in the laboratory experiment.
Considering the team level results of the laboratory experiment, we find a better performance for teams than at the individual level. The mean of all team scores in the empirical data set of 26 teams is 48.85, the median is 46, and the standard deviation is 12.21. Comparing the median scores, the group almost doubles the overall improvement (− 30) to the individual results (− 16), which indicates the capability of team decisions. In this line, the team decision process leads to better overall results in comparison to the random model by − 26.01 on average.
In addition, we considered the performance of individual items, as they might differ from item to item, for a more nuanced understanding of the underlying processes. The top boxplot A in Fig. 4 shows the distribution of performance of the benchmark simulation model for each item. The items are plotted on the x-axis in the order of the expert ranking, starting with the highest ranked item “mirror” and the least relevant item “sextant” at position 15. Given the ranking structure from 1 to 15 and the operationalization of performance, the individual items are limited differently. Items that lie in the middle range of the expert ranking have a smaller possible deviation to empirical ranking positions than items that lie at the edge. The central item “nylon rope” has a maximum score of 7. By contrast, the items “mirror” or “sextant” have a possible maximum score of 14. Accordingly, the distributions of the scores obtained from the random model are wider at the borders and more restricted in the middle range. The resulting different ranges of scores per item apply equally to the empirical and simulated rankings.
Evaluation of random ranking scores (A) vs. individual random ranking scores (B) vs. team ranking scores (C) using boxplots. Note that in this figure the item abbreviations are the following: mir (mirror), oil (oil), wat (water), arm (army ration), pla (plastic sheeting), cho (chocolate bar), fis (fishing kit), nyl (nylon rope), cus (seat cushion), sha (shark repellent), rum (rum), rad (radio), map (map of the atlantic ocean), mos (mosquito net), and sxt (sextant)
In Fig. 4, the two boxplots B and C depict the performance of the individual and team-level decisions in the laboratory experiments. Table 3 identifies the differences between the three data sets. Here, as well, we mainly find improvements in the score distributions for individual and team rankings, as previously identified through the aggregated statistical measures.
In respect of the box plot B for the individual decisions, there is evidence of a good performance for the items “water” (mean = 2.12, sd = 1.46), “army ration” (mean = 2.32, sd = 1.94), and “nylon rope” (mean = 2.35, sd = 1.77). The narrow distribution indicates a similar initial evaluation of these items among all participants. For the other items, the distribution scale is broader, for example “map” (sd = 3.61), “mirror” (sd = 4.46), and “sextant” (sd = 4.40). For these items, the decisions are based on more diverse ranking positions.
The boxplot for the team decisions (C) confirms that the teams benefit from the collective decision-making process and attain better results than the individual participants. Here, we do find an interesting development for the first two items, “mirror” and “oil.” The individual decisions on these two items do not perform better but slightly worse than the random model (by 0.52 for mirror and by 0.93 for oil).Footnote 10 Irrespective, considering the team decisions for these items, we find evidence of an improvement of the team decision performance relative to the individual performance (−2.14 by for mirror and by −1.45 for oil). This indicates the existence of instances of “truth wins” as identified by Hill (1982), particularly for the item “mirror.” The discussion drew the participants closer to the expert ranking than the individuals were able to do on their own. Overall, in comparison to the random model, a positive effect on team performance is documented for both individual knowledge and the subsequent team processes.
6.2 Comparative analysis of team decision models
This section focuses on the process of team decision making, which in turn leads to the better performances documented in the previous section. Specifically, we address the process of how a team arrives at a collective decision from the individual assessments. Given the complexity and richness of team decision processes (Hill 1982), this is a long-term endeavor. However, our dual intention in this paper is to outline the general approach through which agent-based modeling can contribute to this, and to take the first step in this direction.
As a starting point, we propose team decision models to reproduce the empirical data. To provide a suitable approach for a better understanding of the team decision process, we implement several submodels of team decision making in a simulation experiment and evaluate their predictive power. While a submodel ideally approximates the empirically observed team decisions, it is already useful to see how much the respective decision algorithms are an improvement on simple models. The results of alternative submodels provide additional benchmarks to assess the predictive power of our decision algorithm. This practice of testing different submodels with reference to empirically observed patterns is considered a key element in theory development using agent-based modeling (Lorscheid et al. 2019; Grimm and Railsback 2012; Heine et al. 2005).
Following Lorscheid et al. (2012), Table 4 explicates the design logic of our computational experiments. In the simulation experiments, we analyze three submodels (independent variable) and evaluate their distance from the empirical data. Here, we calculate the empirical distances as absolute distances from the simulated team rank positions to empirical rank positions for each item i and each simulated team t (dependent variable). The decision space (control variable) of the simulated agents is set at 15 ranking positions according to the empirical scenario, the consensus limit to 3 and the number of runs to 5226 (see Appendix B). In the following sections, we consider the individual submodels and assess the predictive power of each, respectively.
6.2.1 Random
As a first submodel, we implement the decision model “Random” as a benchmark. In this model, random teams of random individuals are formed to make random decisions. This submodel provides a benchmark to specify the potential value range, determine the decision scenario, and to evaluate how much randomness we identify in the empirical decisions. For the evaluation, the team decisions of the random model are compared with the empirical team ranking positions.
In this random model, a random generator draws on a uniform distribution of items, ranking their positions from 1 to 15. One might therefore expect uniform distances between all of the items. The first row of Table 5 shows the resulting values of the predictive power of Random. In the mean values, we see fluctuating values in the range of 4.34–6.53. In order to understand these variations, we need to consider the opposite side of the measured distances, namely the empirical ranking positions of the teams (Fig. 5A).
Depending on the dispersion of empirical team decisions, the comparison with random decisions is larger or smaller. The largest distance of the random model to the lab results is for “water” (6.53). For this item we only found a single team decision in the empirical team data: all teams rated “water” as the most relevant item, thereby placing it in position 1. All other items are on ranking positions greater than or equal to 2. Consequently, we observe that this item has a low predictive power in the random model. However, for the item “nylon-rope” or “chocolate bar,” large variations are apparent in the team decisions. Correspondingly, for these items, the deviation of the random model is at a smaller value of 4.34 and 4.48. For the item “oil,” we come close to the theoretically expected value of 4.67.Footnote 11 The mean of all items is higher at 4.96.
The results, as expected, confirm the random model’s low predictive power. Overall, this presents us with a first indication that individual knowledge and cognitive team processes matter; aspects that are addressed by the next submodels.
6.2.2 Zero-intelligence agents representing a simple majority
The second submodel is a Zero Intelligence (ZI) model. The concept of Zero-Intelligence (ZI) Agents (Gode and Sunder 1993) was originally developed for trading scenarios, in which agents without any strategy traded randomly on the market. Surprisingly, in this setting, they produced rather good results. We apply this concept to analyze a team decision without a detailed strategy.
The decision model involves a random selection of a single, individual ranking position from the team for each item. The team compositions correspond with the empirical teams of the laboratory experiment, with the inclusion of the individual knowledge of the team members. The teams consist of the same number of individuals with the same knowledge structure combinations as in the laboratory experiment. Content wise, the model implements a simple type, random majority mode: the probability of selecting a ranking position increases with the number of shared or similar individual positions in the team, as the model randomly draws an individual evaluation of a team member. The restriction that each ranking position can only occur once still holds, implying a subsequent cleaning step that eliminates double entries. In this case, the same randomized cleaning step is applied as described in Sect. 6.1 regarding the random model.
The second row of Table 5 reports the predictive power of the ZI model. Overall, its performance is better than that of the random model, as reflected by a mean empirical distance of 3.22 for all items. In this context it should be noted that we find a different picture for the item “water” than in the random model. Whereas “water” had the least predictive power in the random model, in the ZI model it has the most predictive power with the smallest empirical distance of 0.76. For this item, a simple random majority model already provides a good prediction.
The highest value for distances are evident for the items “map” (4.25), “sextant” (3.95), “mirror” (3.94), and “oil” (3.92). This indicates that the selection of these items did not result from majority decisions but were decided on by means of other discussion processes not included in this model. The teams formed new opinions that are not represented in most of the individual assessments. In the team discussions' observations, we find evidence that these items had been considered for a long time. In a subsequent study, this finding should be further examined with quantified measures on the number of arguments exchanged per item. Overall, the ZI model provides a substantial improvement and therefore insight into the extent to which majorities influence and explain team decisions.
6.2.3 Decision algorithm team cognition matrix (TCM)
The third team decision model is based on the identified patterns of the team cognition matrix (subsequently abbreviated as TCM). This submodel includes more complex, empirically measured structures in the decision process (Sect. 5). As described below, the structures provide a refined algorithm for team decision making.
Overall, the TCM team decision process has three phases: the identification of the team cognition structure per item (phase 1), the decision on a team ranking position per item (phase 2), and the cleaning of the ranking to avoid duplicates (phase 3). The model runs through all of these phases for each item and each team.
In phase 1, the algorithm evaluates if the cognitive structure represents the category “consensus”, “majority”, “party”, or “compromise”. The control variable “consensus limit” supports the identification of the team’s cognition-structure category. The distance between two individual ranking positions must be smaller than or equal to the consensus limit, so that this distance is assessed to be “close enough” to confirm consensus between the two positions. This comparison of distance and consensus limit constitutes the core decision for the structural evaluation of each team cognition matrix in the simulated team decision. In the current simulation experiments, we set the value of the consensus limit at 3.Footnote 12 When all individual, absolute-ranking position distances in a team are smaller than the consensus limit, the program identifies consensus in the team. If this is not the case, the algorithm continues and checks if a majority of team members have close ranking positions below this limit. If so, the algorithm identifies a majority structure for this item. Otherwise, if no majority structure is identified, the program proceeds to check if the team splits into two parties of ranking positions. In this case, the model evaluates a party structure. If the simulation does not find a party structure, it means that none of the three chosen categories matched and then the socio-cognitive structure of the item is assigned to the fourth type; labeled a compromise decision.
In phase 2, the identified category of phase 1 determines the chosen team ranking position of the respective item. If the team exhibits consensus in the individual ranking positions, it agrees on a randomly chosen,Footnote 13 individual ranking position within the consensus range. Otherwise, if the team has a majority, one of the individual rankings from the majority determines the team decision. If there is no majority but a party structure in the team for an item, a randomly chosen party wins, and one of the individual rankings in the winning party defines the team ranking position. This represents a random selection of one of the two parties, which has no further relation to other factors in the current model’s version (additional factors might be individual characteristics such as dominant individuals or spokespersons). We account for this stochasticity by repeating the simulation of team decisions several times. If the cognitive structure belongs to “others,” the team opts for a compromise, being the average of all individual ranking positions for this item. We often observe this heuristic at the end of discussions when the team has not reached an agreement on open items and then jointly agrees on an evaluation positioned in the center.
Phase 3 involves a cleaning step for the TCM decision model to avoid duplicates. In contrast to the previous models, this model includes priorities for ranking positions based on the cognitive structure. Depending on the individual knowledge combination in the team, items are prioritized so that they maintain their rank and not shift due to competing ratings. As observed in the laboratory experiments, teams were more certain about items on which there were more agreement. Accordingly, teams retained these ranking positions, while the ranking positions of the items that produced more controversy were more likely subject to change. Fitting in with this team process, items resulting from a consensus decision (15.1% of all cases) have a higher priority in the TCM model than majority decisions (46.7%), items with majorities have a higher priority than party decisions (24.4%), and compromise decisions (13.9%) have the lowest priority for retaining their ranking positions in the case of duplicates. Items with the same ranking position and the same priority class are selected randomly and are moved.
Panel B (Fig. 5) graphically depicts the resulting team ranking positions of the TCM model. By considering the distributions and comparing them with the empirical ranking positions, we identify many items with the same tendencies regarding high, medium, or low median values. However, we also identify broader distributions in the simulated data set than in the empirical data set; an outcome that is partly driven by the large number of observations in the simulation
According to the empirical data, all teams ranked “water” as their highest priority. Looking at the simulated data, we find a ranking position greater than 1 (at ranking positions between 3 and 6) in 1.9% of all team decisions on “water.” In all of these cases the team decision was a party decision, meaning that this decision was not determined by the majority. A review of the individual empirical data shows that in 25 cases the study’s participants rated the item “water” in lower-ranked positions. As the decision algorithm’s calculation is based on empirical team compositions, some simulated groups followed these individual evaluations.
The comparative analysis (Table 5) shows that both submodels provide an improvement over the random benchmark and that the TCM model has a smaller empirical distance (mean = 2.87) than the ZI model (mean = 3.22). Overall, both models succeed in providing a certain approximation to the team decisions. Considering the improvements for each item, we find that the TCM model has similar or better values than the ZI model. By comparing the ZI and TCM models, we find that the latter is generally up to −0.85 better than the ZI model. We notice an improvement in eleven items. Only four items show no or only a small decrease in the predictive power of the TCM model compared to the ZI model (highest value 0.15). The biggest improvement in predictive power concerns the item “sextant” (− 0.85 from ZI to TCM). Other items with better results for TCM are “army ration” (− 0.82), “map” (− 0.77), and “water” (− 0.68). Collectively, TCM adds complexity to the simple majority model of ZI, referring to potential team processes and these aspects have a positive effect on the predictive power of TCM.
The best result is for the item “water” (−5.77 from Random to ZI and −6.45 from Random to TCM). The empirical data confirms the existence of a broad consensus among all teams and individuals that this item must be ranked high. We notice a similar picture for the item “army ration.” At the lower end, we identify weak predictive power for the item “mirror” (−0.50 from Random to ZI and −0.48 from Random to TCM), and results between −0.7 and −1.0 for the items “chocolate bar,” “oil,” and “plastic sheeting.” For these items, we observe diverse perspectives on the part of the team participants and no knowledge in the individual data, implying that the decision model cannot come to a better conclusion.
Table 6 provides another perspective of TCM's predictive power by listing the frequencies of the respective empirical distances per item. This analysis evaluates how close the simulated group decisions come to the empirical group decisions and for which share of ranking decisions. This comparison is possible for each group in the laboratory experiment because the simulation selects the team decisions for the same team constellations as in the empirical data. We find that in 19% of all ranking decisions, the simulation matches the empirical team decision with a distance of zero. In 66% of the cases the distance remains at a maximum of 3 and in 89% of the cases at a maximum of 6.
Finally, we performed a Kolmogorov–Smirnov test (Fig. 6) for a more detailed look at ranking positions at the item level. In this test, we compared the distributions of the empirical team ranking positions with the simulated team ranking positions per item. The analysis shows that, for some items, a similar distribution of the empirical power can be seen across all ranking positions (see, e.g., “fishing kit,” “nylon rope,” or “seat cushion”). Some items are better predicted by the simulation on some than on other item positions (e.g., “mirror,” “plastic sheeting,” or “chocolate bar”). The smallest deviations between the distributions are reported by the Kolmogorov–Smirnov test for the items “water” (D = 0.02, p = 1), “nylon rope” (D = 0.13, p = 0.81), and “seat cushion” (D = 0.13, p = 0.80). We do not find any evidence of systematic over or underestimation of the model.
Overall, we see the first approximations of the decision models to the empirical data. The predictive power of Random provides a benchmark, as it represents predictions based on random team constellations and random team decisions. It is a “zero model” in respect of which we do not assume any strategies, knowledge, or rationality (Railsback and Grimm 2012). Starting from this benchmark, we continued the research process by extending the model to the ZI and TCM models with improved empirical validity. We contend that they at least partially represent individual knowledge and empirical team dynamics. We assume a certain logic behind the empirical team decisions in the laboratory experiment, which we would like to approximate and understand step by step. The ZI model captures the idea that the more individuals share a similar ranking, the greater the probability that this determines the team decision. The TCM model includes more detailed information on team cognition structures and on the potential decision processes triggered by these structures. A further step in this direction would be to add a “truth wins” component to the models, representing the notion that discussions tend to converge on truth.
We recognize the step-by-step approximation achieved by the ZI and TCM models. In the next section we discuss additional observations derived from the laboratory experiments and indicate how they affect the submodels and ideally increase their predictive power.
6.3 Effects of the cleaning step and other explorations
We forthwith discuss additional factors that influence the decision process, leading to the identification of small variations in a particular submodel, and suggest how the submodels could be extended by future research.
6.3.1 Cleaning step
At the outset, we considered the interdependence of the item positions. Participants in the laboratory experiments faced the task of assigning all 15 ranking positions only once. Therefore, items that were equally rated in importance had to be ranked in sequence. The same process was also implemented in the simulation by a cleaning step. After the first evaluation of the items based on the decision rules of the respective model (Random, ZI, or TCM), the team result was checked for duplicates in the ranking positions. In the Random and ZI model, one of the duplicates was randomly drawn and moved downward by one ranking position (Sect. 6.1). This was repeated for all multiple assignments. The TCM model added priorities based on the teams’ cognitive structure regarding the particular item, as observed in empirical observations.
The effect of this cleaning step on the predictive power of the TCM submodel is indicated in Table 7, based on the comparative before-after change of mean empirical distances in respect of each item. The data indicate the overall smaller effects of this model’s modification, since all values are below + / − 0.4. Regarding a possible interpretation, it should be kept in mind that the items are sequenced along the expert-ranked order. For the most important items, the cleaning step leads away from the empirical results. Based on the priority-based shift of positions, the model’s predictive power improves for less relevant items. The items in the center area exhibit larger shifts in both directions.
According to the observations in the laboratory experiment, the items’ order of discussion – in most cases – started with the individually highest-evaluated items, continued with the items that were individually evaluated as least important, and concluded with the remaining items. Consequently, items at a medium level of priority shifted most in the rankings.
6.3.2 Consensus and majority
Another observation is that consensus and majority are only two of the observed team cognition structures (61.80%). Nevertheless, they constitute the core element of the current TCM model. Therefore, it is worth considering the predictive power of the related decision types (majority and consensus decisions) by contrasting them with the model’s other, lower prioritized types (party and compromise decisions). Figure 7 compares the predictive power of these two decision types by separating the data sets, accordingly.
The graph shows that, in many cases, the distribution of empirical distances for majority and consensus decisions is narrower with smaller variance than that of the other team decision heuristics, for example, the items “oil,” “fishing kit,” or “sextant.” For “oil” we observe a mean empirical distance of 3.26 and a standard deviation of 2.00 for consensus and majority decisions, and a mean of 4.37 and a standard deviation of 3.07 for the other heuristics. For “sextant” we observe a more extreme change, namely a change from consensus and majority decisions (mean = 2.22, sd = 1.83) to party and compromise decisions (mean = 3.98, sd = 3.65). However, there are a few other examples where the situation is different. For the items “chocolate bar” and “rum”Footnote 14 the majority decision appears not to perform better.
We find that, to a certain extent, decision type correlates with predictive power. Table 8 shows the Pearson correlation coefficients between the measures “empirical distance” and “decision type” for all 15 items. Decision type was coded by the values 1 for consensus, 2 for majority, 3 for party decision, and 4 for compromise. In this analysis we find medium correlations for “water” (0.40**), “army ration” (0.38**), and “fishing kit” (0.36**), as well as for “shark repellent” (0.28**), “map” (0.22**), and “sextant” (0.28**). No correlations were found for “plastic sheeting” (0.10), “chocolate bar” (− 0.09), “seat cushion” (−0.06) and “rum” (0.09). This again indicates that there must be additional explanations for the decisions.
6.3.3 Dominant individuals and exchange of arguments
Our analysis, for the most, shows that a focus on consensus and majority decisions leads to a further increase in predictive power. The social process and communication enhance team cognition, which was also reflected in the simulation model. By contrast, we found other cases where the TCM prediction fell short. From the observations of the laboratory experiments’ team dynamics, we learned that the discussions also show irrational behavior that goes beyond our models. Hence, the team dynamics of a particular task must contain more mechanisms than consensus and majority. Based on the laboratory experiments, we therefore identify two additional points on which further analyses and model refinements should focus: the roles that individuals play in the discussion process and the various process paths in the discussion (exchange of arguments).
We observed that dominant speakers can influence team decisions. As they present their arguments with confidence, other team members are impressed and follow their recommendations. However, this self-confidence does not always reflect the state of knowledge. This was obvious in the case of observed team stupidity. After the experiment, when the group was asked who the spokesperson and most influential member was during the discussion, the members identified the person with the weakest individual ranking pattern. Similar processes that go beyond the communication and exchange of arguments and that are based on individual characteristics have the potential effect of weakening predictive power, as they are currently not represented in the simulation models.
In the recorded and transcribed team discussions we identified differences in the group processes, such as the exchange of arguments in respect of ranking positions. To further analyze this, we coded the arguments from the recordings. If a participant argued for a ranking position of an item, it was noted accordingly. The result of this analysis is a table that presents the exchange of arguments, along with information on who argued in what sequence for which item and which position. Another relevant aspect is the point in time when the team decided on a ranking position during this exchange. This was also documented. The resulting sequence is the first deeper look into the discussion process, such as the frequency of argumentation or jumps between the items during the discussion. This analysis also provides an indication of which team member prepared decisions in advance, how often and when, while the other members remained passive and silent. We provide a video illustrating this analysis in the supplementary material; an analysis that can be extended in future research.
Overall, this section illustrates how the combination of laboratory experiments and agent-based modeling can contribute to a better understanding of team decision processes. Given the complexity of the issue, this is a long-term endeavor, with this paper indicating and performing the first steps. Subsequently, other alternative submodels must be developed and tested (Lorscheid et al. 2019; Grimm and Railsback 2012; Heine et al. 2005), which could also incorporate behavior that directs team decisions away from the correct ranking, among others the behavior of dominant individuals. The focus on contrasting alternative theories corresponds with the principles of inductive “strong inference” (Platt 1964). Theoretical development and maturation come into play when repeating the cycle of formulating and testing alternative submodels, which are fostered by the availability of new data and patterns.
7 Conclusion
This paper addressed the socio-cognitive processes of teams and, more specifically, the emergence of decisions at the individual and team levels. We proposed a research process that addresses team decisions as an emergent property, using agent-based modeling that connects individual cognition to team-level decisions. We validated our model with a laboratory experiment using a ranking task. The experiment provided data on the individual and team rankings, as well as quantitative and qualitative data on the dynamics of the team decision. We introduced a team cognition matrix as a measure of the underlying socio-cognitive structure of teams. By applying this concept to the experimental data, we identified four categories of team decision dynamics. These categories formed the basis of the decision algorithm that we implemented in an agent-based simulation model. Through this simulation model, we tested several submodels of team decision making, representing potential, simplified mechanisms of how team cognition emerges from individual cognition. The increasing overall fit of the simulation and the empirical results supports the hypothesis that the modeled decision processes can partly explain the observed team decisions. The combination of the applied methods explicates possible micro processes driving decision making in teams, for example in boards or committees.
Overall, this study has shown that, fundamentally, group decision making has the potential to reveal the correct decision. There is a tendency to reach a true conclusion through the exchange of arguments and communication, recognizable as better group performance. However, there are also processes that lead away from rationality and accurate decision making, involving dominant individuals or a lack of argumentation. We provided a first indication of the influence of these processes on team cognition.
This paper contributes in at least three ways to the current literature on interactive team cognition and collective intelligence. First, it develops a process-oriented model of team decision making. Although the collective intelligence literature emphasizes the importance of processes, these processes are mainly represented by static variables such as team members' social sensitivity or equal shares of conversational turn-taking (e.g., Woolley et al. 2010; Cooke et al. 2000). By contrast, the paper adopts a micro perspective of team cognition and creates a dynamic model using agent-based modeling (Smaldino et al. 2015). In this respect, this article also provides an example and indication of the benefits of combining laboratory experiments and simulation modeling (Klingert and Meyer 2012; Smith and Rand 2017). Using this mixed-method approach, empirical investigations and formal modeling can iteratively inform each other. Overall, this should increase our knowledge of team decision processes and contribute to theory development (Lorscheid et al. 2019; Grimm and Railsback 2012; Heine et al. 2005).
Second, the paper develops and tests a measure of team cognition structures by introducing the concept of a team cognition matrix. This concept can be useful to complement existing measures of team cognition in the collective intelligence literature. An advantage of our proposed measure is that the team cognition matrix is a quantitative representation of the problem's social and cognitive aspects, to be solved by the team members. Besides, this measure is more process oriented, as it is linked to typical decision processes that are triggered by these structures.
Third, this paper identifies four categories of typical team cognition structures. These team cognition structures are empirically accessible and lead to testable hypotheses, which future research can refine. Building on the insights of Hill (1982), the identified team cognition structures and the corresponding decision algorithms also have immediate practical value as teams may exhibit this course of team decision dynamics when anyone observes or participates in team discussions. The categories allow for a critical reflection on both beneficial and dysfunctional team dynamics. The ubiquity of teams and team decisions in firms underscores the potential impact of these results on and their benefits for management.
This paper is the first step in modeling the emergence of team cognition. It provides a basis that can also include other social settings. Our approach shows a way of finding possible explanations for “how and why organizationally relevant outcomes emerge” (Grand et al. 2016, p. 45), and how to identify underlying patterns. Future research should test and refine the hypotheses about the four identified structures and the decision processes they trigger. Alternative and refined process models should also be developed and tested. This includes modeling interdependencies among items and the implementation of rules such as “truth wins.” All of this can help to explain the delta concerning the empirical results that are not currently explained by the decision algorithm. Analyzing communication processes appears to be particularly promising as a next step to refine the model and to increase its predictive power. Additional simulation experiments could potentially reveal further links between cognition patterns and team performance. It is also possible to vary the experimental setting. Similarly, further empirical research outside the laboratory and the analysis of resulting team cognition matrices in different contexts could help to identify common patterns and to produce new data on team decisions and relevant micro-level processes.
Notes
In line with the literature, we consider a team as a specific type of group. Miller (2003) describes a group as a system with dynamic social and work processes throughout the group’s lifetime. A team is considered as a collection of two or more individuals who pursue a common goal and share the responsibility for outcomes (Cooke et al. 2013; Cohen and Bailey 1997; Kozlowski and Ilgen 2006). We use the term “group” when we explicitly refer to the literature on groups.
More details on the data set and the participants are provided in Appendix A. When considering the design of the game and the performance measures used, it should be kept in mind that the purpose of the experiment is not to test specific hypotheses but to generate empirical data for the validation and calibration of the agent-based model.
The time limits for the game rounds are set according to the original rules of the team building game.
Further adaptations could include another individual ranking after the team discussion to analyze the change of individual decisions and to explicate hidden knowledge that was not part of the team ranking.
More details on the distribution of distances and the evaluation measures of distances follow in Sect. 6.
Interestingly, for the item “map,” the majority of team 4 was not correct in comparison to the expert opinion. We identify a team score of 11. The individual with a single opinion, however, was very close to the benchmark with an almost perfect individual score of 1. We find both correct and wrong majority decisions in the data.
The R code and data are available from Iris Lorscheid (2021, May 23). “Team Cognition” (Version 1.0.0). CoMSES Computational Model Library. Retrieved from: https://www.comses.net/codebases/59e2039b-3ebb-413a-bf34-5c8c9f441be2/releases/1.0.0/.
The benchmark model could alternatively be analytically modelled as a stochastic urn model without replacement. In our research process, we start with the random simulation model as benchmark that is then stepwise extended to the decision models. Through this systematic approach, we stepwise extend the external model validity and evaluate the results of these changes.
The reason why the theoretical optimum of 0 was not reached in the simulated model resides in the large number of combinations of 15! – which is significantly larger than the performed 5226 runs.
Since both elements are in the first two positions of the expert ranking, the possible empirical deviations can reach far into the back-ranking positions and thus we empirically identify a worse result than with a random evaluation. In the empirical results, “water” and “army ration” are more to the front and, as a result, they displace the distribution of the ranking positions of “oil” and “mirror” by forcing them to the back.
For the frequency distribution of all possible distances within an equally distributed ranking from 1 to 15, we calculate an expected distance for random draws of 4.67.
The value 3 is a compromise to capture not only equal ranking positions as consensus, but also ranking positions that are close to one another. A sensitivity analysis shows that lower values of the consensus limit tend to weaken the predictive power of several items, while higher values tend to strengthen the predictive power. But there are no consistent effects for all items. This confirms the power of majority decisions as identified by Hill (1982). In a future analysis, we aim to systematically analyze variations of consensus limits to identify varying sizes of majorities that determine decisions made at a team level. This will be another, different team decision submodel, the predictive power of which is to be evaluated in comparison to the other models.
We intend considering alternative selection strategies in future research, such as choosing the individual ranking position that appears most frequently within the consensus range.
Mean values and standard deviation for consensus and majority decisions on “chocolate bar”: mean = 4.27, median = 4, and sd = 2.26, and “rum”: mean = 3.44, median = 3, and sd = 2.39 vs. mean values and standard deviation for compromise and party decisions on “chocolate bar”: mean = 3.36, median = 3, and sd = 2.55, and “rum”: mean = 2.85, median = 3, and sd = 2.13.
References
Cohen SG, Bailey DE (1997) What makes teams work: Group effectiveness research from the shop floor to the executive suite. J Manag 23(3):239–290
Cooke NJ (2015) Team cognition as interaction. Curr Dir Psychol Sci 24(6):415–419. https://doi.org/10.1177/0963721415602474
Cooke RA, Kernaghan JA (1987) Estimating the difference between group versus individual performance on problem-solving tasks. Group Organ Studies 12(3):319–342
Cooke NJ, Salas E, Cannon-Bowers JA, Stout RJ (2000) Measuring team knowledge. Hum Factors 42(1):151–173
Cooke NJ, Gorman JC, Myers CW, Duran JL (2013) Interactive team cognition. Cogn Sci 37(2):255–285. https://doi.org/10.1111/cogs.12009
Crusius J, van Horen F, Mussweiler T (2012) Why process matters: a social cognition perspective on economic behavior. J Econ Psychol 33(3):677–685
Deffuant G, Neau D, Amblard F, Weisbuch G (2000) Mixing beliefs among interacting agents. Adv Complex Syst 3(04):87–98
Delgado PMI, Martínez AMR, Martínez LG (2008) Teams in organizations: a review on team effectiveness. Team Perform Manag Internat J 14(1/2):7–21. https://doi.org/10.1108/13527590810860177
DeVilliers R, Woodside AG, Marshall R (2016) Making tough decisions competently: assessing the value of product portfolio planning methods, devil’s advocacy, group discussion, weighting priorities, and evidenced-based information. J Bus Res 69(8):2849–2862. https://doi.org/10.1016/j.jbusres.2015.12.054
Devine DJ, Philips JL (2001) Do smarter teams do better: a meta-analysis of cognitive ability and team performance. Small Group Res 32(5):507–532
Engel D, Woolley AW, Jing LX, Chabris CF, Malone TW (2014) Reading the mind in the eyes or reading between the lines? Theory of mind predicts collective intelligence equally well online and face-to-face. PLoS ONE 9(12):e115212
Esser JK (1998) Alive and well after 25 years: a review of groupthink research. Organ Behav Hum Decis Process 73(2):116–141. https://doi.org/10.1006/obhd.1998.2758
Gode DK, Sunder S (1993) Allocative efficiency of markets with zero-intelligence traders: market as a partial substitute for individual rationality. J Polit Econ 101(1):119–137
Gottfredson LS (1997) Mainstream science on intelligence: an editorial with 52 signatories, history, and bibliography. Intelligence 24(1):13–23. https://doi.org/10.1016/S0160-2896(97)90011-8
Grand JA, Braun MT, Kuljanin G, Kozlowski SW, Chao GT (2016) The dynamics of team cognition: a process-oriented theory of knowledge emergence in teams. J Appl Psychol 101(10):1353–1385. https://doi.org/10.1037/apl0000136
Grimm V, Railsback SF (2012) Pattern-oriented modelling: a ‘multi-scope’for predictive systems ecology. Philos Trans Royal Soc B: Biol Sci 367(1586):298–310
Gutwin C, Greenberg S (2004) The importance of awareness for team cognition in distributed collaboration.
Hackman JR, Morris CG (1975) Group tasks, group interaction process, and group performance effectiveness: a review and proposed integration. In: advances in experimental social psychology, vol 8. Academic Press, pp 45–99
Hauke J, Lorscheid I, Meyer M (2017) Recent development of social simulation as reflected in JASSS between 2008 and 2014: a citation and co-citation analysis. J Artif Soc Soc Simul 20 (1)
Hauke J, Lorscheid I, Meyer M (2018) Individuals and their interactions in demand planning processes: an agent-based, computational testbed. Int J Prod Res 56(13):4644–4658. https://doi.org/10.1080/00207543.2017.1377356
Hegselmann R, Krause U (2002) Opinion dynamics and bounded confidence models, analysis, and simulation. J Artif Soc Soc Simul 5 (3)
Heine B-O, Meyer M, Strangfeld O (2005) Stylised facts and the contribution of simulation to the economic analysis of budgeting. J Artif Soc Soc Simul 8 (4)
Helmreich RL (2000) On error management: lessons from aviation. The BMJ 320(7237):781–785
Hill GW (1982) Group versus individual performance: are N+1 heads better than one? Psychol Bull 91(3):517–539. https://doi.org/10.1037/0033-2909.91.3.517
Hollan J, Hutchins E, Kirsh D (2000) Distributed cognition: toward a new foundation for human-computer interaction research. ACM Trans Comput Hum Interact 7(2):174–196
Janis IL (1972) Victims of groupthink: a psychological study of foreign-policy decisions and fiascoes. Houghton-Mifflin
Janis IL (1982) Groupthink. Houghton-Mifflin
Ji Y, Massanari RM, Ager J, Yen J, Miller RE, Ying H (2007) A fuzzy logic-based computational recognition-primed decision model. Inf Sci 177(20):4338–4353. https://doi.org/10.1016/j.ins.2007.02.026
Karau SJ, Williams KD (1993) Social loafing: a meta-analytic review and theoretical integration. J Pers Soc Psychol 65(4):681–706
Katzenbach JR, Smith DK (2015) The wisdom of teams: creating the high-performance organization. Harvard Business Review Press
Klein D, Marx J, Fischbach K (2018) Agent-based modeling in social science, history, and philosophy. Historical Soc Res Historische Sozialforschung 43(1):7–27. https://doi.org/10.12759/hsr.43.2018.1.7-27
Klingert F, Meyer M (2012) Effectively combining experimental economics and multi-agent simulation: suggestions for a procedural integration with an example from prediction markets research. Comput Math Organ Theory 18(1):1–28
Klingert F, Meyer M (2018) Comparing prediction market mechanisms: an experiment-based and micro validated multi-agent simulation. J Artif Soc Soc Simul 21(1):7. https://doi.org/10.18564/jasss.3577
Knox G (2016) Lost at sea. A team building game. Insight. http://insight.typepad.co.uk/insight/2009/02/lost-at-sea-a-team-building-game.html. (Accessed 29 Oct 2020)
Kozlowski SWJ, Ilgen DR (2006) Enhancing the effectiveness of work groups and teams. Psychol Sci Pub Interest 7(3):77–124. https://doi.org/10.1111/j.1529-1006.2006.00030.x
Lévy P, Bononno R (1997) Collective intelligence: Mankind’s emerging world in cyberspace. Perseus books
Lorscheid I, Heine B-O, Meyer M (2012) Opening the ‘black box’ of simulations: increased transparency and effective communication through the systematic design of experiments. Comput Math Organ Theory 18(1):22–62
Lorscheid I, Berger U, Grimm V, Meyer M (2019) From cases to general principles: a call for theory development through agent-based modeling. Ecol Model 393:153–156. https://doi.org/10.1016/j.ecolmodel.2018.10.006
Macal CM (2016) Everything you need to know about agent-based modelling and simulation. J Simul 10(2):144–156
Mesmer-Magnus J, Niler AA, Plummer G, Larson LE, DeChurch LA (2017) The cognitive underpinnings of effective teamwork: a continuation. Career Dev Int 22(5):507–519. https://doi.org/10.1108/CDI-08-2017-0140
Miller DL (2003) The stages of group development: a retrospective study of dynamic team processes. Can J Adm Sci 20(2):121–134
Moreland RL, Myaskovsky L (2000) Exploring the performance benefits of group training: transactive memory or improved communication? Organ Behav Hum Decis Process 82(1):117–133
Railsback SF, Grimm V (2012) Agent-based and individual-based modeling: a practical introduction. Princeton University Press
Reader TW (2017) Team decision making. The wiley blackwell handbook of the psychology of team working and collaborative processes. John Wiley & Sons Ltd, pp 271–296
Rousseau V, Aubé C, Savoie A (2006) Teamwork behaviors: a review and an integration of frameworks. Small Group Res 37(5):540–570
Schulz-Hardt S, Jochims M, Frey D (2002) Productive conflict in group decision making: genuine and contrived dissent as strategies to counteract biased information seeking. Organ Behav Hum Decis Process 88(2):563–586. https://doi.org/10.1016/S0749-5978(02)00001-8
Secchi D (2015) A case for agent-based models in organizational behavior and team research. Team Perform Manag Internat J 21(1/2):37–50. https://doi.org/10.1108/TPM-12-2014-0063
Secchi D, Seri R (2016) Controlling for false negatives in agent-based models: a review of power analysis in organizational research. Comput Math Organ Theory 23(1):94–121
Singh V, Singh G, Pande S (2013) Emergence, self-organization and collective intelligence -- modeling the dynamics of complex collectives in social and organizational settings. In: UKSim 15th International Conference on Computer Modelling and Simulation. IEEE, pp 182–189
Smaldino PE, Calanchini J, Pickett CL (2015) Theory development with agent-based models. Organ Psychol Rev 5(4):300–317. https://doi.org/10.1177/2041386614546944
Smith EB, Rand W (2017) Simulating macro-level effects from micro-level observations. Manage Sci 64(11):5405–5421
Szuba T (2001) A formal definition of the phenomenon of collective intelligence and its IQ measure. Futur Gener Comput Syst 17(4):489–500
Urbig D, Lorenz J, Herzberg H (2008) Opinion dynamics: The effect of the number of peers met at once. J Artif Soc Soc Simul 11(2):4
Van Knippenberg D, De Dreu CK, Homan AC (2004) Work group diversity and group performance: an integrative model and research agenda. J Appl Psychol 89(6):1008–1022
Wall F, Leitner S (2020) Agent-based computational economics in management accounting research: opportunities and difficulties. Agent-based computational economics in MAR. J Manag Account Res
Willems J (2016) Building shared mental models of organizational effectiveness in leadership teams through team member exchange quality. Nonprofit Volunt Sect Q 45(3):568–592
Woolley AW, Chabris CF, Pentland A, Hashmi N, Malone TW (2010) Evidence for a collective intelligence factor in the performance of human groups. Science 330(6004):686–688
Woolley AW, Aggarwal I, Malone TW (2015) Collective intelligence and group performance. Curr Dir Psychol Sci 24(6):420–424
Acknowledgements
We thank the participants of several conferences, workshops and research seminars for insightful discussions and supportive comments on this project, such as the attendees of the 2017 and 2018 Social Simulation Conference, the 2018 ESSA@Work Workshop, the VHB annual meeting 2019, the AI-FORA symposium, and the Hamburg Management Accounting Research Seminar. We also thank the editors and three anonymous reviewers for insightful and thoughtful comments that significantly improved the paper. A special thanks goes to Tugba N. Yildiz for her support and contributions during the revision of this article.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
Table 9 provides additional data about our laboratory experiment.
Appendix B
2.1 Error variance analysis
The error variance analysis supports the identification of the number of runs in simulation experiments that is necessary to achieve a stable and representative result from the simulation’s stochastic process (Lorscheid et al. 2012). The standard error serves as a central measure. This measure relates the standard deviation to the square root of the number of observations (N) and therewith corrects the confidence interval for smaller N.
Figure 8 depicts the standard error of the ranking positions when increasing the number of random ranking repetitions. As can be seen, the measure decreases and stabilizes with more repetitions and larger sample sizes. Table 10 indicates the statistics for increasing numbers of repetitions to identify the score’s error variance. We identify a stabilization of variance between 5000 and 7500 runs. More than 5000 simulation runs appear to be a good compromise between further increases in accuracy and the computational costs of more runs. In our simulation, we performed 201 runs for each of the 26 empirical teams, leading to 5226 teams in total performing 78,000 ranking decisions. Regarding the number of runs, we had 5226 runs for the team decisions in the model, with each defining a team ranking across the 15 items (Table 10).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lorscheid, I., Meyer, M. Toward a better understanding of team decision processes: combining laboratory experiments with agent-based modeling. J Bus Econ 91, 1431–1467 (2021). https://doi.org/10.1007/s11573-021-01052-x
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11573-021-01052-x
Keywords
- Agent-based modeling
- Zero-intelligence agents
- Team decision
- Group processes
- Cognition
- Laboratory experiment