1 Introduction

Oscillations are well known as abundant phenomena in science, nature, engineering and social life (Sterman 2000; Jenkins 2013). These oscillations, such as the rhythm of pendulum clocks, the periodic firing of neurons, singing crickets, or business cycles in economics, affect the performance of the respective systems (Luan 2014; Pikovsky et al. 2003). Motivated by the success of oscillators in the modelling, analysis and control of dynamical systems, we developed a related approach for the dynamic description of supply chains. The purpose of this paper is to introduce a generic oscillator model for supply chains, where oscillations not only emerge as solutions by solving flow-oriented equations, but by the original application of oscillator equations.

In a first step inventory and stock oscillations of a specific supply chain echelon are mapped by a nonlinear differential equation (van der Pol equation). Then the case of a Just-in-Sequence (JIS) supply process from the automotive industry is used to model a two-tier supply chain. Therefore two van der Pol oscillators, representing the inventory oscillations of a car manufacturer and its supplier, are coupled together, representing the interactions between the dynamical states of a supply chain. Transactions occurring between the successive stages of a supply chain can be then described as serial interaction between coupled oscillators (Dunbar 2007). Each echelon of the supply chain vibrates according to its specific excitations, induced by supplier-customer relationships. This oscillatory behaviour in supply chains is pervasive and ubiquitous.

The advantage of the oscillator approach in describing supply chain dynamics is based on the fact that any oscillatory state can be reduced to just one variable, which is the phase of the oscillation (phase reduction). Whilst the amplitude of oscillations depends on the kind of swings investigated (e.g. inventory levels, capacity utilisation, order stock) the phase of the oscillation is for all different kinds of supply chain dynamics always the same. Further advantages of using an oscillatory approach for supply chain management are:

  • Oscillatory phenomena are universal and can be understood within a well-established framework based on modern nonlinear dynamics.

  • The oscillatory model can be applied to situations where it is not possible to describe supply chain processes exactly. Equations describing supply chain processes are then solved geometrically with the help of trajectory analysis in phase space.

  • Synchronisation as a major research topic of supply chain management can be well described and understood in an oscillating supply chain context.

  • There is a vast number of existing control strategies for coupled oscillators that can be applied to perform stability and suppress harmful oscillations.

An oscillatory approach allows to support supply chain managers for the planning, operating and controlling of supply chains. Introducing new analytical techniques (like phase maps, Hilbert transform, Arnold tongue representation) can help to gain a more profound understanding of the conditions of supply chain dynamics and especially for the emergence of synchronisation.

The paper is organised as follows. Section 2 discusses already existing oscillatory approaches in operations and supply chain management. Section 3 introduces a first oscillator model, which is then enlarged in Sect. 4 to a more complex nonlinear oscillator model to describe real inventory control processes. Section 5 applies a coupled oscillator model to a real-life automotive supply process. Section 6 provides a brief summary of the investigation, its limitations and perspectives for further research.

2 Literature background

Based on a general definition of oscillation as a repetitive variation, typically in time, of some measure about different states, we already find many hints of oscillatory tendencies in supply chain literature. Oscillatory effects occur in many features of the supply chain, like in demand and supply, inventory levels, capacity and transport utilisation (see Table 1).

Table 1 Examples of oscillatory models generally suitable to model supply chains [following Luan (2014)]
Full size table

Forrester (1961) was one of the very first to investigate variations in time of information feedback control to explain how decisions, delays and predictions can produce unstable operations with production swings and inventory fluctuations. “It is well known that factory production rate often fluctuates more widely than does the actual consumer purchase rate” (Forrester 1961, p. 22). Burbidge (1961) pointed out that stock control systems triggered by pre-determined reorder levels generate extremely variable multi-phase material flows, leading to highly fluctuating inventories (Towill 1997). Shingo (1981) argues that customer order-based production causes unavoidable fluctuations. The adjustment of production capacity amplifies unanticipated changes in demand. This relation is supported by many empirical studies (Flynn et al. 1995; Taylor 1999), which indicated variability in process capability and subsequent product quality as an inherent source of material flow variability. Sterman (1986) argues that there are inherent oscillatory tendencies in the adjustment of production capacity within firms due to the inevitable lags in acquiring factors of production and reacting to changes in demand. He further pointed out that cycles arise from the interaction of the physical delays in production and capacity acquisition with bounded rational decision making by individual producers. Supply chains consist of a stock and flow structure for the acquisition, storage, and transformation of inputs into outputs. Sterman (2000) showed that stock and flow management structure explains the origin of ample oscillations in supply chains. Oscillation requires time delays regulating the state of a system and that decision makers fail to account for these delays. The decision structure includes policies for ordering, scheduling, purchasing and shipping. Time delays in adjusting the appropriate production and inventory levels cause chronical overshoot and undershoot and therefore supply chains are prone to oscillation. A further crucial issue was posed by Burbidge (1984) about the problem of multi-cycle ordering, whereby each item has its own ordering cycle and is considered independently of any other required item. He summarised this effect by the “ordering cycle law” and states that “If the various components made in a factory are ordered and made to different time cycles, they will generate high amplitude and unpredictable variations in both stocks and load as the many contributing component stock cycles drift in and out of phase”. This effect, caused by unsynchronised ordering and production cycles (multi-cycling), is known as the Burbidge Effect, which can be minimised (but not eliminated) by synchronisation of reordering and switchover times (single-cycling). A further cause of excessive oscillations in ordering is repeated batching by time and/or quantity due to Economic Batch Quantity (EBQ)/ Economic Order Quantity (EOQ) policies at each echelon of the supply chain. This order batching effect occurs in different forms within a supply chain. Common examples for batching are order, transport and production batching. Accumulation until reaching a pre-determined threshold causes boom and bust behaviour in material flows. This drives oscillation through the whole supply chain.

Inspired by interconnected oscillators Helbing et al. (2004) and Helbing and Lämmer (2005) investigate a supply chain as a physical transport problem. Alexopoulos et al. (2008) apply an oscillatory model to analyse the dynamic behaviour of manufacturing systems. They are using an analogy between a mechanical system with inertia, damping and stiffness and a manufacturing system. With the help of a system identification technique the response of a manufacturing system is estimated to any given input. Scholz-Reiter et al. (2006) and Scholz-Reiter and Tervo (2006) investigate phase-locking phenomena of a production network with oscillating demand and supply. Donner et al. (2007) study the self-organisation and optimisation of conflicting material flows on complex networks. A decentralised control is used to approach a demand-driven switching between states of the flows. Under rather general conditions, the control approach leads to phase synchronisation and therefore controlled oscillations of material flows at the intersections within a transportation network. Chankov et al. (2014) showed that logistics synchronisation is mainly composed of a temporal and performance-related coupling of the state of individual logistics elements or complete systems.

Most of the oscillatory phenomena in supply chains are summarised and best described by the bullwhip effect. Research on the bullwhip effect in supply chains, has gained interest since the start of the twentieth century, and is well known to economists (Geary et al. 2006). Bullwhip refers to the phenomenon where the variance of demand is amplified from a downstream site to an upstream site as the orders proceed through each stage of a supply chain (Lee et al. 1997). In addition to characterise supply chains dynamics with oscillations some authors already used a wave analogy to describe bullwhip (demand variations) and backlash (supply variations) effects in supply chains. Bullwhip and backlash effects are analogous to amplitude pressure wave propagation (bullwhip) and reflections (backlash) in physical systems such as flow ducts (Shukla et al. 2009) or water flow on beaches (Hines et al. 2000). Klug (2016) also used this analogy to wave theory and described order and supply oscillations as a process of wave propagation and reflection. Here the point of demand (customer) generates an order wave corresponding to order levels. The propagation and amplification of orders upstream in a supply chain is mapped by a linear order wave with increasing amplitude. Reaching the last supply chain stage the order wave is changing in direction and by nature, the incoming order wave is processed and reflected as supply wave. According to the definition of backlash as delivery variation downstream in the supply chain, the reflected wave corresponds to supply fluctuations induced by varying demand.

Though, someone can already find many hints for an oscillatory supply chain model indicated by terms like oscillations, fluctuations, vibrations or swings often used when describing supply chain dynamics, so far no generic oscillatory model of supply chains was proposed. In this context we consider as generic that oscillations not only emerge as solutions by solving flow-oriented equations (e.g. material, transport, information, monetary), but by the original application of oscillator equations (see Sect. 3). Physics and engineering offer a vast set of oscillatory models and approaches that can be applied to supply chain management, which go far back in scientific history. Christian Huygens, most famous for his studies in optics and the construction of telescopes, was probably the first scientist who studied connections between oscillators (Pikovsky et al. 2003). In 1665 he discovered that two pendulum clocks, hung from the same wooden structure, will always oscillate in synchrony.

To map and investigate supply chain dynamics properly, we have to discuss existing types of oscillator models. Oscillators respond to different excitation levels induced either by other oscillators (coupled oscillators) or a dynamically changing external force (one oscillator). Table 1 depicts examples of different oscillatory descriptions, which can be generally applied to investigate real-world supply chains. As usual in supply chain management one can start by modelling a simple one-echelon supply chain to study e.g. inventory oscillations of a warehouse or fluctuations in demand and supply. In a next step two, three and more supply chain echelons (partners) can be modelled with the help of more interacting oscillators. The highest level of complexity is a network structure, allowing to model n to m relationships with n echelons (e.g. suppliers) linked with m echelons (e.g. customers).

Besides the number of supply chain partners mapped, the kind of interaction between these supply chain partners can differ. Depending on the specific supply chain property described by oscillators (e.g. inventory, demand, supply), the coupling and therefore interrelation represents different types of oscillator interactions (e.g. transport, call-off, order).

3 The inventory oscillator

The cooperative behaviour of a supply chain can be described and modelled with oscillators, which correspond to a specific supply chain entity, mapping the repetitive variation in time of a specific property. In this paper, we are going to focus exclusively on inventory and stock related oscillations in supply chain management. This allows for a consistent and therefore more distinct description of the new approach. Depending on the supply chain management focus all further considerations can be easily transferred to other supply chain properties without losing generality.

The inventory system can be described and mapped by a number of state variables ξi (e.g. stock level, rate of stock change or maximum and minimum stock levels). Which state variables are used, depends on the specific case of application. The dynamic behaviour of the inventory system can be then completely described by the time evolution of the state vector p(t). We consider a general N-dimensional (N ≥ 2) system of ordinary differential equations

$$\frac{dp}{{dt}} = \left\{ { \frac{{d\xi_{1} }}{dt} ,\frac{{d\xi_{2} }}{dt} , \ldots ,\frac{{d\xi_{N} }}{dt}} \right\}$$
(1)

and suppose that this inventory system has a stable periodic (with period T0) solution. The behaviour of the inventory system as a whole follows its intrinsic dynamics, mapped by the system variables change over time. A visual representation of the oscillatory dynamic behaviour is a phase space trajectory, mapping the time evolution of the state vector p in phase or state space (see Fig. 1). The multi-dimensional phase space is determined by the number of variables used. Each variable ξn is represented by one dimension in phase space. The system variables span the phase space of the inventory system in which all possible states of a system are represented. A phase space trajectory acts as compact measure to describe the temporal succession of inventory states. One state of the supply chain is represented by a single point on the trajectory in the phase space (state vector). The state vector P in the phase space moving along the cycle represents the oscillations (see Fig. 1). The stable periodic solution is represented as a closed attractive trajectory, called the limit cycle. This graphical representation enables the immediate insight into the dynamic behaviour of inventories in geometric form, without directly representing the variable of time. Finding this geometric form, called phase portrait, without solving the supply chain equations analytically, lies at the heart of a new oscillatory approach. Phase space trajectories are intuitive, scale independent and geometrically oriented, which opens up a broad area of applications, this includes the design, the operation and the control of supply chains in industrial practice (Klu 2016).

Fig. 1
figure 1

Time evolution of the state vector P for a harmonic oscillator with ω0 = 1 and ϕ0 = 0

Full size image

The inventory system in (1) can be described in its simplest form by a harmonic oscillation without damping, describing the relationship between stock acceleration \(\ddot{s}\) (second time derivative of the stock level) and the stock level s itself.

$$\ddot{s} + \omega_{0}^{2} s = 0 { }$$
(2)

The general solution of this homogenous differential equation describes the dynamic inventory evolution with

$$s\left( t \right) = s_{0} \cos (\omega_{0} t + \phi_{0} ).$$
(3a)

and

$$\dot{s}\left( t \right) = - s_{0} \omega_{0} \sin (\omega_{0} t + \phi_{0} ).$$
(3b)

Here ω0 denotes the angular frequency, which is related to the oscillation period ω0 = 2π/T0, characterised by its period T0, the time for a single stock level oscillation. The angular frequency does represent the velocity of stock changes. The intensity of oscillation is determined by its amplitude s0, corresponding to a maximum (positive) or minimum (negative) stock level. The quantity ϕ(t) = ω0 t + ϕ0 is called phase and represents the actual stock level with initial phase ϕ0 as the initial inventory. The phase changes uniformly with

$$\dot{\phi } = \omega_{0}$$
(4)

where ω0 is a constant. Therefore the state vector P is circulating with a constant angular velocity. Figure 1 depicts the phase space of the differential Eq. (2) with the closed, stable limit cycle. This solution is periodic, so that the state vector on the limit cycle returns after each period T0 = 2π/ω0.

The phase unambiguously determines the state of a periodic oscillator. In general the phase does not only determine the state of a single inventory system, but also allows evaluating synchronisation processes (like phase-locking) between two oscillators by comparing phase differences Δϕ. If the time-independent phase difference is small (Δϕ ≈ 0) we observe in-phase synchronization, whilst in the opposite case of Δϕ ≈ π we find anti-phase synchronization (Pikovsky et al. 2003).

4 The oscillating inventory model

After a first general description of inventory dynamics with the help of a linear oscillator model, nonlinear processes are introduced in this section. This enables to map real inventory control processes, where damping and reinforcing of inventory stock levels allow to stay in a predefined inventory corridor, based on a respective management goal.

A very successful and therefore most popular classical example of an oscillation dynamics is the van der Pol equation (1920). If we interpret its dynamical variable s as a stock, the model can be used to describe the dynamical evolution of an inventory system as

$$\ddot{s} - \mu \left( {1 - s^{2} } \right)\dot{s} + \omega_{0}^{2} s = 0$$
(5)

where μ is a positive parameter, coined by van der Pol as relaxation parameter. This nonlinear, homogenous, ordinary differential equation was originally developed to stabilise the frequency of an electronic generator by nonlinear feedback. Van der Pol and Appleton showed that the frequency of a generator can be entrained, or synchronised, by a weak external signal of a slightly different frequency (Appleton and van der Pol 1921). Satisfying the Liénard Theorem Eq. (5) has a unique, stable limit cycle surrounding the origin in the phase space (see Appendix).

The van der Pol oscillator shows interesting dynamics, which correspond well to the needs of inventory control. The oscillator has a negative linear damping (reinforcing) \(- \mu \dot{s}\) as well as an amplitude which is limited by a nonlinear, positive damping term \(\mu s^{2} \dot{s}\). When s is small, the quadratic term s2 is negligible and the system becomes a linear differential equation with a negative damping \(- \mu \dot{s}.\) A negative damping reinforces the oscillatory dynamics and hence produces an amplification of motion (see Fig. 2—left side). On the other hand, when s is large, the term s2 becomes dominant and the damping becomes positive. Now true damping occurs and the motion decays (see Fig. 2—middle). As a consequence a van der Pol oscillator generates self-sustained oscillations with a stable limit cycle (see Fig. 2—right side). The oscillation is periodic but not sinusoidal. The steady-state amplitude of the oscillation is then s0 = 2 where the average damping vanishes over a complete period of the oscillation, so that the oscillation can be maintained at its natural frequency (Jenkins 2013).

Fig. 2
figure 2

Reinforcing dynamics (left side), damping dynamics (middle) and stable limit cycle dynamics (right side)

Full size image

Each inventory stock is an accumulation of items, which is driven by daily stock variations caused by the inflows of production and/or deliveries and the outflows of stock sold and delivered to the customers. Each flow into and out of stock increases or depletes inventory levels s directly, which is related to its natural frequency \(\omega_{0}^{2}\). Besides that, real stock systems are always subject to different perturbations, forcing the required stock levels to over- or undershoot. These daily operational problems correspond to different excitation levels of the oscillator either by other oscillators (coupled oscillators) or a dynamically changing external force. By positive or negative damping a predefined inventory corridor (based on a respective management goal) can be reached. Figure 3 depicts the evolution of the damping term

$$d = - \mu \left( {1 - s^{2} } \right){ }$$
(6)
Fig. 3
figure 3

Different damping terms depending on μ

Full size image

in (5) where \(\mu\) is the control parameter to influence different levels of damping and therefore to represent different inventory control strategies (see Fig. 3). For s =  ± 1 the damping term d is 0 so that no damping occurs. For \(\left| s \right| < 1\) negative damping reinforces the oscillation. For \(\mu \ll 1\) small oscillations build up to the steady state amplitude, while large oscillations decay down to it. Its final state is no damping at all, which leads to a sinusoidal limit cycle like shown in Fig. 1. For \(\left| s \right| > 1\) positive damping occurs, where in the strong nonlinear limit of \(\mu \gg 1\), small displacements grow very quickly, causing them to overshoot s0, whereupon the nonlinear term causes the amplitude to decay back down, until it eventually shoots off in the other direction. This produces a cycle of rapid buildup and slower decay that van der Pol identified as a relaxation oscillation (Jenkins 2012). Finding the optimal relaxation process and therefore the optimal inventory dynamics to control a real supply chain process is the goal of the following.

5 Analysing synchronous supply in the automotive industry

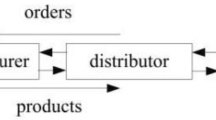
To show how the oscillating inventory model can be applied to a real-life problem, we are going to analyse synchronisation issues in automotive industry, as one of the major concerns in lean management. The application of synchronisation principles in supply chain management is one of the remedies to dampen or eliminate unwanted oscillations. The material flow must be harmonised so that parts move in a coordinated fashion. Synchronisation of the supply chain, especially concerning the inbound delivery, is a critical success factor. Perhaps one of the most significant synchronisation principles becoming widely adopted and practised in car industry is that of JIS supply, where all elements of the supply chain are synchronised. Valuable modules and systems with a high number of variants such as seats, bumper systems or front and rear axles require late configuration and demand that suppliers deliver in sequence to the vehicle manufacture plant. Nowadays JIS is a standard delivery approach in synchronous supply. In this concept, the entire vehicle assembly process is dependent upon the timely delivery of complex modules and systems. Synchronous supply necessitates a logistics integration which can accommodate the time-critical transfer of data and activate the synchronous manufacturing process to deliver zero defect goods, at the right time, at the right place and at the right cost (Bennett and Klug 2012). It enables the supply chain partners to share logistics information such as production-plans and capacities, delivery-orders and stock levels. Transparency of information upstream and downstream maintains the flow of materials in time to the rhythm of the production process.

5.1 Seat supply process of German car manufacturer

Our goal is to analyse a real JIS supply process between a major supplier and a car manufacturer (OEM) with the help of the oscillatory model developed in Sect. 4. The two inventory systems used and described by oscillators are the outbound buffer stock of the supplier (sS) and the inbound buffer stock of the car manufacturer (sM) (see Figs. 4 and 5). Our coupled inventory oscillator model has been mapped according to an existing JIS process of a large car manufacturer based in Southern Germany. The module assembly plant of the 1-Tier supplier of car seats is based in a regional distance of 18 km to the car assembly plant, where on average every 15 min a full truck load (FTL) with 15 seat sets (driver seat, co-driver seat, back-driver seating bench) is delivered. The synchronous supply process is operating on a three-shift model six days a week. The OEM-ordered seat sets are supplied, in accordance with the sequence call-off. A logistic service provider is also integrated into the information process and is provided with collection contracts to schedule collection dates and times. Loading and unloading times have to be synchronised because there are small inventory buffers on the assembly line, which compensate slight delays in inbound delivery.

Fig. 4
figure 4

Coupled oscillator supply model

Full size image
Fig. 5
figure 5

Coupled oscillator model of Just-in-Sequence supply

Full size image

The supply chain dynamics is going to be described by two coupled van der Pol oscillators (Woafo and Kraenkel 2002), where

$$\ddot{s}_{M} - \mu \left( {1 - \alpha s_{M}^{2} } \right)\dot{s}_{M} + \omega_{M}^{2} s_{M} = 0$$
(7a)

is representing the inventory oscillations of the car manufacturer with frequency ωM and where

$$\ddot{s}_{S} - \mu \left( {1 - \alpha s_{S}^{2} } \right)\dot{s}_{S} + \omega_{S}^{2} s_{S} = K\left( {s_{M} - s_{S} } \right)$$
(7b)

is representing the inventory dynamics of the supplier with frequency ωS.

Coupled oscillator models have been successfully applied in many fields of science and technology to describe interacting dynamical systems (Kuramoto 2012; Strogatz 2014). As shown in Sect. 4 the van der Pol oscillator describes the inventory stock dynamics very well, without mapping the microscopic physical movement of material and goods in detail.

The macroscopic oscillator model, used in this paper, does focus on the continuous inventory oscillations of the outbound and inbound buffer of the automotive supply process (see Fig. 4). Continuous material flow modelling does make sense in this paper, as the synchronisation of a supply process is in focus and not the concrete planning of individual entities in the logistics system (e.g. lot sizing or job sequencing). All inventory oscillations are driven by the demanded delivery rate TM, which is related to the cycle time of the car assembly process and according to ω0 = 2π/T0 the angular frequency of the inbound buffer inventory oscillation ωM (see Fig. 4). The parameter α is linked to the amplitude of the oscillation and reflects the delivery batch size. The coupling constant K allows to describe different synchronisation degrees between car manufacturer and supplier. The higher K the better synchronised is the supply process, which is mainly driven by the cycle time overlap between supplier and car manufacturer (see Sect. 5.2). The parameter μ controls the inventory dynamics of the supply chain and relates to the relaxation process describing how the inventory system reacts to stimuli of the supply system (see Sect. 4 and Fig. 3).

With Eqs. (7a) and (7b) we are able to map a unidirectional coupling between the manufacturer and the supplier, based on the fact that in an automotive JIS supply process the car manufacturer fixes the master schedule. The supplier responds immediately on the actual backlog as the difference between sM and sS. Each deviation between demand and supply (positive relates to supply backorders and negative relates to supply excess) can be seen as suboptimal under an economic and especially lean perspective. This model did not take into account time delays in the flow of information and/or materials that exist in reality. To evaluate different synchronisation scenarios (Chankov et al. 2016), over a specific time period T, we introduce the performance indicator “Mean Synchronisation Performance” MSP with

$$MSP = \frac{1}{T}\mathop \smallint \limits_{t = 0}^{T} dt \left| {s_{M} \left( t \right) - s_{S} \left( t \right)} \right| \to _{{}} min!$$
(8)

This quantity-oriented service level indicator measures the proportion of demanded sM and supplied inventory sS over a time period T. The MSP does not only reflect the stockout event (sS (t) < sM (t)) but also the surplus inventory, which is available in the car manufacturer’s buffer stock but not actually used for manufacturing (sS (t) > sM (t)). The supply goal is to minimise MSP and therefore optimise the classical supply chain trade-off between high material availability and low tied-up inventory. This metric evaluates inventories at the same time t and therefore can only evaluate complete in-phase synchronization. Processes that are synchronized with a time delay (so-called lagged synchronization) are therefore not taken into account. Possible extensions of the model, as discussed in the conclusions section (see Sect. 6), inevitably lead to an extension of the target system. An expanded consideration with additional supplier levels, where both upstream and downstream inventory variations have to be taken into account, leads to conflicting optimization goals, which can again trigger instabilities (Donner et al 2010).

The steady-state amplitude of Eq. (5) is s0 = 2 where the average damping vanishes over a complete period of the oscillation (see Sect. 4). To enable a flexible modelling of real inventory processes it is necessary to adapt the oscillator amplitude to maximum and minimum stock levels. The parameter α allows for tuning the relevant seat set inventory related to the actual JIS supply process (see Sect. 5.2 and Table 2).

Table 2 Just-in-Sequence seat supply model parameters
Full size table

5.2 Empirical evaluation of the model parameters

The main parameter of a JIS supply system is the cycle time of the car assembly line. The cycle time is used to synchronise the pace of car assembly with the pace of seat production and delivery. The investigated car manufacturer is using a production levelling system, which is a standard approach in the planning and controlling of the master schedule in car industry (Monden 2011). Besides production levelling, there are slight variations in cycle time between different shifts, based on empirical data. The possible cycle time variations are always fixed to predefined time shifts. In our case there are three different cycle times used at the specific assembly line investigated with 55 s, 60 s and 65 s. The inbound buffer, which is placed adjacent to the assembly line, supplies production compliant with the chosen cycle time. Due to economic order batching, seats are always reordered in fixed “bulk call-offs”, comprising 15 seat sets (driver seat, co-driver seat, back-driver seating bench). Given that the seat supply process operates in batches (from the outbound buffer of the supplier through to the inbound buffer of the car manufacturer), we link all stock variations to the batch size of 15 seat sets. According to the three different cycle times used at the car manufacturer’s assembly line (55 s, 60 s, 65 s), we get three different delivery periods (13.75 min, 15.00 min, 16.25 min) (see Table 2 and Fig. 9). Based on ω0 = 2π/T0 (see Sect. 3) the time for a single stock level oscillation can be used to derive the angular frequency (0.46 min−1, 0.42 min−1, 0.39 min−1), representing the velocity of stock changes. The angular frequency ωM does represent the velocity of inbound stock changes in the assembly plant of the car manufacturer. Assembly demand and its induced stock variations of the inbound buffer trigger the supply process. This process is autonomously defined by the car manufacturer in relation to its levelled master schedule and mapped of Eq. (7a).

The supplier is manufacturing the seat modules on two assembly lines. Both lines can be controlled and linked mainly to the customer pace of production (see Fig. 5). According to the fact that there are high setup costs (mainly in the upholstery) it is not possible for the supplier to work totally flexible in the shift model of the customer cycle time. Therefore it is necessary to build up stock in an outbound buffer, where the produced seat sets of the two assembly lines are being merged. We calculate three different angular frequencies ωS, which represent the velocity of stock changes of the outbound buffer in the assembly plant of the seat supplier. The supply process is on the one hand linked to the production speed of the customer but also in relation to the current supply backlog (see Sect. 5.1). This is described in Eq. (7b) by the backlog parameter (sm(t)—ss(t)) at any time t and in reality guided and controlled by a specific JIS software system, generating the relevant call-offs for the supplier and transmitting transport orders for the carrier.

All JIS transports are going to be performed by a logistic service provider. There is a pool of trucks available to run the shuttle service between the supplier and the manufacturer. On average every 15 min a truck arrives at the JIS-dock next to the car assembly line. To guarantee synchronous supply there are three possible transport cycle times. Transport cycles can be adapted flexibly and are always oriented on the assembly line cycle time of the driving car manufacturer (see Fig. 5). Transport is therefore no bottleneck in the seat supply process. Triggered by different supply and demand cycle times, there are three different coupling constants ranging from 1 (supplier and demand cycle time are to 100% identical) to 0.85 (supplier and demand cycle time are to 85% identical). Depending on the cycle time overlap between supplier and manufacturer a supply backorder (sm(t)—ss(t) > 0) or supply excess (sm(t)—ss(t) < 0) can only be fulfilled in a specific reaction period of time. The coupling constant is also influenced by the transport reliability. Due to the fact that JIS-transports over this small distance of 18 km never drop under an availability rate of less than 85%, we concentrate only on the cycle time overlaps.

For tuning the relevant seat set batch the parameter α is used (see Sect. 5.2 and Table 2). The steady-state amplitude of (5) is s0 = 2, so it is necessary in Eqs. (7a) and (7b) to map the seat batch size of 15 sets per delivery. With a value of α = 0.07 the amplitude grows to s0 = 7.5.

The crucial parameters for analysing the coupling between inventory oscillations—and in our specific case the analyses of synchronisation issues in automotive supply—are the coupling constant K and the relaxation parameter μ. The coupling constant K allows to model the coupling strength between supplier and car manufacturer. The parameter μ relates to the relaxation process describing how the inventory system reacts to stimuli of the supply system. It controls the buildup and decay of inventory levels and therefore controls the inventory dynamics of the supply chain (see Sect. 4 and Fig. 3).

To clarify how an oscillating supply chain model can be applied, we are going to focus on two crucial supply chain management tasks, namely mapping and synchronising supply processes, which do play a major part in inbound-logistics management in the automotive and many other industries, with the following issues:

  • How can we map supply chain dynamics with a compact visual representation, which can be used to plan, control and improve real-life supply processes?

  • What are the boundaries of delivery period fluctuations in a JIS supply process between manufacturer and supplier without losing synchronicity?

5.3 Describing supply chain dynamics and transitions with phase maps

As a first step we perform a visual analysis of different supply chain states with phase maps in accordance with the empirical seat supply process. To illustrate how synchronisation between the two different oscillators in Eqs. (7a) and (7b) operate, we investigate first different coupling levels. By comparing the dynamic evolution of the seat supplier stock sS and car manufacturer stock sM we can span a two-dimensional phase space of the supply process (see Sect. 3). The phase space trajectory, based on the evolution of the state vector with its components sM and sS, is able to map relevant dynamic supply effects like oscillation, amplification, damping and synchronisation simultaneously (Strogatz 2014).

By comparing different frequency ratios ωM/ωS and phase differences Δϕ we can generate idealistic superpositions (harmonic inventory oscillation without relaxation), of sinusoidal functions known as Lissajous figures (Fig. 6).

Fig. 6
figure 6

Phase portraits of harmonic oscillator pairs with different frequency ratios and various phase differences (μ = 0)

Full size image

The first Lissajous figure with an angular frequency ratio between ωM and ωS of 1 and a phase shift of 0, can be seen, from an oscillatory point of view, as a perfect synchronisation level. All further figures map a less perfect synchronisation process due to phase and or frequency mismatches. As one goes to more complicated frequency ratios, the resulting curves tend to become more complex. To illustrate how synchronisation between the two different oscillators in Eqs. (7a) and (7b) o operate, we investigate first different coupling levels. Table 3 depicts different synchronisation levels of the seat supply process (calculated over a period of one shift) for the maximum possible frequency shift of Δω = 0.07 (TM1 = 13.75 min and TS3 = 16.25 min) from maximum coupling (K = 1) to minimum coupling (K = 0).

Table 3 Different synchronisation levels for Δω = 0.07
Full size table

The different inventory phase maps in Table 3 show the loss of synchronisation as a transition from motion with one compact, unidirectional (angle bisector) motion to a non-synchronous motion, where the trajectory never returns to the same state vector after one cycle. The performance indicator Mean Synchronisation Performance (8), as a measure of the proximity of the supplied to the demanded inventory, is therefore ranging from 0.35 to 6.11. However, based on the high level of coupling between the seat supplier and car manufacturer, with a coupling constant K ranging from 0.85 to 0.92 (see Table 2), synchronisation remains in daily operation mainly on a very high level. The high investment in a JIS supply system (electronic data interchange, track and trace system, spare trucks, etc.) guarantees that every deviation of the sequence call-off leads to quick and intense correction processes. A crucial success factor of every JIS supply process in car industry is the strict adherence of the supply sequence by time and quantity (see Sect. 5.1). From a management point of view, the critical issue is to decide about the optimal relaxation parameter μ, which can be later used for the fine tuning of a software based call-off system (see Fig. 9). Table 4 shows a range of actual synchronisation levels with different cycle shifts (calculated over a period of one shift). In general, according to the high level of coupling, the MSP values remain on a low level (ranging from 0.23 to 0.71), compared to the non-synchronous cases of Table 3 (up to 6.11). We start with the case of μ = 0 where the damping term d = 0 (6) and therefore no damping and/or reinforcement of the inventory stock does exist (see Table 4). Although there is a high level of coupling (K = 0.92 and K = 0.85) the trajectory experiences small shifts, which widens the angle bisector, causing additional buffer stock needed to compensate supply and demand deviations. Less coupling causes for all cases a broader phase map with higher MSP values. By increasing the relaxation parameter from μ = 0.0 to μ = 0.2 the supply system is improving, resulting in narrower phase space maps and lower MSP values. This shows the impact of the relaxation process, which guarantees that a disturbed inventory oscillator is going to be forced back on the limit cycle. One can see that a low level of relaxation is enough to stabilise and smooth the seat supply process. For μ > 0.2 the phase space trajectory widens and the MSP values grow. A higher MSP value does mean a deviation between demand and supply, which induces higher levels of outbound and inbound stock. Buffer stock is always generated when the phase space trajectory does deviate from the optimum level of synchronisation, depicted as a thin straight angle bisector of the phase space (see Fig. 7).

Table 4 Synchronisation development of the seat supply process
Full size table
Fig. 7
figure 7

Different synchronisation regions of the phase space

Full size image

Figure 7 summarises different regions of the phase space, which can act as control platform for the seat supply process. An analysis of the stable phase space maps shown in Tables 3 and 4 are linked to three different supply scenarios:

  • A perfect synchronisation of the JIS seat supply process is mapped as a compact and thin, straight lined angle bisector of the phase space (green line). The length of the phase portrait depends on the batch size (amplitude).

  • By losing synchronicity the phase space map extends to a motion where the trajectory never returns to the same state vector after one cycle. Trajectory space and MSP values are growing up to the extreme case of non-correlation between supply and demand (red rectangle) (see also Table 3).

  • Besides of the perfect synchronisation (green line), every deviation between demand and supply is shown in region A and B. In region A (B) demanded inventory sM is higher (lower) than supplied inventory sS. Therefore every state vector in region A or B is a deviation from the optimum level of synchronisation generating stockout events (A) or surplus inventory (B).

Previous results showed that a higher level of relaxation does not necessarily mean a higher level of synchronisation. With the help of a parametric (according to μ) numerical solution of the differential equations in (7a) and (7b) the optimum relaxation parameter for the two possible coupling modes has been calculated (see Fig. 8).

Fig. 8
figure 8

Comparing different relaxation parameters and synchronisation levels

Full size image

The graphical reference of the JIS supply process—shown as phase maps—can act as the quantitative basis for a dynamical continuous control of the JIS supply during its operation by manipulating the system trajectory. Figure 9 depicts how a real-time control system of the seat supply process can be performed with the help of an oscillatory model.

Fig. 9
figure 9

Real time control of the JIS supply process

Full size image

One major supply chain goal is to minimise the total amount of supply backlog during a shift (see Sect. 5.2). An adaptive control mechanism for the automatic cancellation of strange dynamics can be developed, by readjusting the internal parameters of the JIS system. An already implemented track and trace system is generating a large number of status messages during the whole supply process. These fixed points in the material flow can be used to calculate the outbound buffer as well as the inbound buffer stock at any time. Based on the actual stock levels (sS, sM), the optimum damping term d and the demanded coupling constant K, the inventory controller (conducted by the JIS software system) is calculating target values. While comparing the actual phase map (see red trajectory in Fig. 9) with the predefined settings of the target phase map (see blue trajectory in Fig. 9) a deviation can be recognised and evaluated. The main parameter to react to perturbations and variations is a phase change. In an oscillatory context, controlling is achieved by a weak external action to change the neutral phase of the inventory oscillations (Pikovsky et al. 2003). By delaying or accelerating the inventory oscillations of the supplier stock a detuned coupled supply process, which was slightly out of step, can be easily re-synchronised without changing the amplitude (seat batch size). This task is carried out by the car manufacturer’s JIS software system, which is continuously calculating the necessary phase shift to force the actual phase portrait to the optimum limit cycle. For each cycle time a correction of the supplier call-off time and a change of the pick-up time for the transport order is calculated, adapted and transmitted to the supplier and carrier.

5.4 Supply synchronisation between manufacturer and supplier

To investigate inventory synchronisation sets the focus on the coincidence of the phases where the phase difference is bounded. This so-called phase-locking or entrainment happens with the onset of a certain relationship between the manufacturer inventory oscillation phase ϕM and supplier phase ϕS (Rosenblum et al. 2001). Coupled oscillators are able to synchronise even when the initial frequencies are slightly different. This phase synchronisation means that oscillators have a preferred phase-relation to each other and that the oscillators adjust their phase as function of their phase difference (Lowet et al. 2016). The question about phase synchronisation between manufacturer and supplier is extremely important for the planning, management and control of synchronous supply (Scholz-Reiter et al. 2006a). A phase synchronisation is existent if the instantaneous phases of both oscillations are locked, which can be measured by the time evolution of the phase difference. We calculate the phase difference as

$$\Delta \phi_{MS} \left( t \right) = \left| {n\phi_{M} \left( t \right) - m} \right.\left. {\phi_{S} \left( t \right)} \right| \le \varepsilon .$$
(9)

where \({\upalpha } \in {\mathbb{R}}\) is a constant threshold and \(n,m \in {\mathbb{Z}}.\) The variables n and m represent the frequency ratios in which the oscillators can satisfy the condition of phase-locking despite different frequencies ωM and ωS. If the phase difference does not exceed a specific threshold the two oscillations are bounded. JIS supply can only happen between nearby demand and supply frequencies. Therefore a small frequency band with n = m = 1 is in focus of our research, where it is impossible that the coupled oscillators move with an integer multiple between their frequencies.

To identify a possible phase synchronisation we have to extract the phase by transforming the inventory oscillations via a Hilbert transform. This approach from the field of signal processing generates from any arbitrary signal s(t) the instantaneous phase and amplitude via construction of the analytic signal, which is a complex function of time defined as (Pikovsky et al. 2003):

$$\xi \left( t \right) = s\left( t \right) + is_{H} \left( t \right) = A\left( t \right)e^{{i\phi_{S} \left( {\text{t}} \right)}}$$
(10)

The function sH(t) is the Hilbert transform of s(t)

$$s_{H} \left( t \right) = \frac{1}{\pi }{\text{ P}}.{\text{V}}.{ }\mathop \smallint \limits_{ - \infty }^{\infty } \frac{s\left( \tau \right)}{{t - \tau }}d\tau$$
(11)

where P.V. means that the integral is taken in the sense of the Cauchy principal value. The instantaneous phase of s(t) can be calculated from the complex analytical signal sH(t) as:

$$\phi_{S} \left( t \right) = \arg \xi \left( t \right) = \left\{ \begin{gathered} \arctan \left( {\frac{{s_{H} \left( t \right)}}{s\left( t \right)}} \right); \, s\left( t \right) > 0, s_{H} \left( t \right) \ge 0 \hfill \\ \arctan \left( {\frac{{s_{H} \left( t \right)}}{s\left( t \right)}} \right) + \pi ; \, s\left( t \right) < 0, s_{H} \left( t \right) \ge 0 \hfill \\ \arctan \left( {\frac{{s_{H} \left( t \right)}}{s\left( t \right)}} \right) + \pi ; \, s\left( t \right) < 0, s_{H} \left( t \right) < 0 \hfill \\ \arctan \left( {\frac{{s_{H} \left( t \right)}}{s\left( t \right)}} \right) + 2\pi ; \, s\left( t \right) > 0, s_{H} \left( t \right) < 0 \hfill \\ \end{gathered} \right.$$

By calculating the instantaneous phases ϕM and ϕS, representing the actual stock levels sS and sM (see Sect. 3), we can calculate the instantaneous phase difference ΔϕMS at any time t. Whilst the detuning ΔϕMS determines the phase precession frequency (de-synchronisation force), the coupling strength K determines the strength of phase adjustments (synchronisation force) (Lowet et al. 2016). Table 5 depicts phase differences for different possible supply frequency shifts of (Δω = 0.04 or 0.07). For K = 0.92 and K = 0.85 a phase synchronisation over the whole analysing period (based on two shifts, to be able to map a phase slip in the second shift) is established. All different types of synchronisation are bounded according to their high level of coupling constant. The higher the coupling constant the lower the phase difference between supplier and manufacturer inventory oscillation. A maximum phase difference (9) of \(\varepsilon\) = 0.07 (only 1% of the total oscillation period of 2π) does show the high level of phase entrainment. For the supply case with the highest synchronisation level (first case of Table 5 with μ = 0.04), quantified by the lowest MSP value of around 0.18 (in order to allow better comparability with the previous results all MSP values are related to one shift), the supply chain reaches a state of complete synchronisation, where the amplitude is completely (determined by the constant seat set batch size) and the phase is nearly perfectly correlated (ΔϕMS ≤ 0.005).

Table 5 Phase-locking of different synchronisation types
Full size table

The last depiction of Table 5 characterises a non-synchronized supply case with no coupling at all (K = 0.00). The phase difference is gradually increasing and for this reason not bounded.

To map how the level of inventory frequency detuning Δ \({\omega }^{2}\) between the manufacturer (\({{\omega }_{M}}^{2}\)) and supplier (\({{\omega }_{S}}^{2}\)) and the coupling constant K are linked to phase-locking, we apply a graphical analysis. Both parameters depicted in a two-dimensional diagram can map the transition process to phase-locking (see Fig. 10). In this diagram one can observe an inverted triangle that defines the phase-locking region (grey area). According to its tongue-like shape it is referred to as the “Arnold tongue” (Pikovsky et al. 2003). From a supply chain planning point of view it is important to find the synchronisation domain and the right trade-off between the coupling strength K and the detuning values Δω.

Fig. 10
figure 10

Arnold’s tongue of the JIS supply process

Full size image

With the help of the Arnold tongue representation it is possible to find the optimal parameters to the synchronisation threshold and to avoid loss of synchronisation and instability. By comparing different states of synchronisation during time it is also possible to investigate the transient phase between synchronous and non-synchronous supply (area next to the red marked line). Figure 10 includes the two stable solutions of the real seat supply process. Due to its high levels of coupling, combined with low levels of inventory frequency detuning, both solutions are far from the transient phase of losing synchronicity. We can also see that even a weak interaction (K < 0.5) can synchronise when the frequency detuning is low (Δ\({\omega }^{2}\) < 0.25).

6 Conclusions

In this paper we have used a deductive approach by using a predetermined van der Pol oscillator model and applied it to a concrete supply problem. Based on an automotive supply chain in the German car industry, it was shown how the oscillatory approach can be applied to a real-life supply process. According to its reductionist approach only two differential Eqs. (7a) and (7b) are used—describing a pair of coupled oscillators – to map and analyse a JIS seat supply process. Besides the high level of synchronisation of the chosen supply process, the approach can be also applied in a lower synchronised context. Mutual phase synchronisation is independent on the amplitude, it is therefore not necessary for the supply partner to work with aligned batch sizes (like in the seat supply process with a fixed batch size). It is important to stress that besides the deductive approach used in this paper a more general inductive approach can be also applied. In this case not a predetermined oscillator is used, but the empirical captured time series of the investigated parameter. By applying a Fourier analysis each empirical oscillation can be then decomposed into simple sinusoidal oscillations, and therefore build up the basis for the parameterisation of suitable oscillators.

Due to its simplicity, the application depth of the oscillatory approach is limited. However there are advantages in applying an oscillatory model to the planning, operating and controlling of supply chains:

  • The “Oscillating Supply Chain” describes supply chain dynamics mainly based on the phase of the oscillation. This phase reduction approach allows a simple description of complex real-life management problems.

  • Existing control strategies for coupled oscillators can be applied to ensure stability by continuous control of critical supply chain parameters during its operation.

  • The dynamic and continuous measurement of oscillations and their Hilbert transforms, allows to map the transient behaviour of dynamical supply chains, like losing bounded phase states according to its Arnold tongue representation.

There are many possible application areas of an oscillatory supply chain model. The oscillatory mapping (with e.g. phase portraits, Arnold tongue) combined with a decision-relevant cost and performance evaluation, can generate a powerful decision support tool. The general flexibility of a coupled oscillator model, allows to model not only linear supply chains but also more complex supply networks.

The compact graphical representation of the oscillator dynamics, with the help of phase maps, act as a quantitative basis for an adaptive control mechanism during its operation. It was shown that from a management point of view, the critical issue is to decide about the optimal relaxation parameter μ, which can be used for the fine tuning of a software based call-off system (see Fig. 8). By delaying or accelerating the inventory oscillations of the supplier stock a detuned coupled supply process can be re-synchronised. A Hilbert analysis helps to find the boundaries of phase-locking between the inventory oscillation phases, where the instantaneous phases are bounded. Furthermore, parameters of the synchronisation threshold and the transient phases between synchronous and non-synchronous regimes can be investigated, supported by an Arnold tongue representation. The investigations show that an oscillatory model enlarges the classical management approaches to measure and quantify phenomena of inventory dynamics—especially synchronisation—in supply chains.

The oscillatory supply chain model is still preliminary and needs further verification on more sophisticated supply chains. In this paper two deterministic oscillators have been used without time delays and with unidirectional coupling (form the manufacturer to the supplier). These limitations can be reduced by applying one of the many existing oscillatory models already used in science and technology (see Sect. 2). The simple two-echelon supply process, used in this paper, can be easily enlarged to study n-tier supply chains with the help of more interacting and time-delayed oscillators. Random processes can be introduced with stochastic oscillators by adding a random process to the phase Eq. (4). This allows for describing oscillations in the presence of noise, which relates to slight deviations in the daily operation of real supply chains. Another possibility of extension concerns the introduction of upper and lower stock limits to ensure that maximum bounds on storage capacity or minimum bounds on safety stock are maintained in order to ensure security of supply and avoid zero stock or negative stock situations. The unidirectional coupling used in the paper described by Eqs. (7a) and (7b) could be modified by a mutual coupling. This would mean that not only the supplier but also the customer varies their velocity of stock changes, to improve synchronisation in the supply chain. Further possible enlargements are the contemplation of delayed oscillations (caused by information delays) and network structures. Especially the Kuramoto approach (Kuramoto 2012), developed and introduced for the synchronisation of a large number of distributed oscillators (supply chain partners), seems promising to be successfully applied in a supply network context (Chankov et al. 2016, 2018a, b). This approach does not only allow a network description on a phase approximation, but also delivers answers to the problem of synchronisation transition (Kuramoto transition).