1 Introduction

In many work settings, employees face trade-offs between the number of output units produced and the value of each output unit. As an example, consider R&D professionals of a pharmaceutical company who can either produce incremental or radical innovations. While radical innovations tend to be financially rewarding, they also tend to be more risky, more time consuming, and more costly than incremental innovations (Banbury and Mitchell 1995; Cardinal 2001). Hence, R&D professionals have to choose whether to make many rather incremental innovations or few rather radical and more valuable innovations. Similarly, when employees of a hotel reservation center need to maximize the total value of bookings handled, they face a trade-off between the number of bookings handled per hour and the average value of handled bookings (Berger et al. 2013b). That is, when finishing less valuable tasks is relatively easy and fast, while finishing more valuable tasks is relatively difficult and time consuming (Bracha and Fershtman 2013)Footnote 1, employees face volume–value trade-offs.

Employees who intend to maximize the total value of their output (that is, their performance) in the face of such trade-offs can choose between two generic strategies: either they produce few, more valuable units (value strategy); or many, less valuable units of output (volume strategy). As an example, consider researchers who are expected to publish articles in professional journals (in addition to other tasks, such as teaching). How well they fulfil this single task depends on both the number of articles they publish in a given period and the quality of the journals in which the articles are published (Ayaita et al. 2018). In an effort to maximize the total value of their output, researchers can either publish few articles in top-tier journals (value strategy), or more articles in second- or third-tier journals (volume strategy).Footnote 2

Superiors will be indifferent as to which strategy an employee chooses as long as it yields maximum performance in a given period.Footnote 3 But maximizing performance does not require that all employees work on the most valuable tasks. As employees in an organization vary in their abilities, they should choose the task strategy that best fits their respective ability. For some this may mean to focus on value, while for others it will mean to focus on volume. That is because generally, more valuable products are also more difficult to produce, and not every employee is equally capable of producing them in a reasonable amount of time. Quite the contrary, the value of some employees’ total output may be highest when they spend their time on solving many easy problems rather than try to solve few difficult problems (and possibly fail).

In such a situation, management control systems can—through the incentives they provide (Küpper et al. 2013)—fulfil two crucial functions. First, they should motivate employees to exhibit as much effort as possible to maximize their performance. This role of management control systems has often been called decision-influencing as it is meant to overcome control problems and align employee behavior with the goals of the organizations (Demski and Feltham 1976). Second, management control systems should help employees choose the optimal task strategy. This role has often been called decision-facilitating. Put broadly, in order to perform well in presence of a volume–value trade-off, beyond working hard (effort), employees should also choose an adequate task strategy (strategy choice).

An increasingly popular management control system that may be useful in both, motivating high effort and facilitating optimal strategy choice, is the provision of relative performance information, or RPI (Mahlendorf et al. 2014; Newman and Tafkov 2014; Tafkov 2013). Firms frequently rank their employees in order to inform them on how well they perform in comparison to their peers. In recent years, rankings have played a fundamental role in firms’ attempts to improve the productivity of their workforce through the gamification of tasks—i.e., the application of online game aspects to business contexts (Reeves and Read 2013; Werbach and Hunter 2012). For instance, employees can earn points for the completion of tasks, and their respective scores are compared with those of their peers in public performance rankings on virtual leaderboards (Meder et al. 2013: 490).

When employees face volume–value trade-offs, RPI may not only prove helpful in motivating effort but also in facilitating optimal strategy choice. This is because the social comparison involved in competitive contexts, can spur individuals’ desire to learn about their relative strengths and this way help them to improve their task ability (Griffin-Pierson 1990; Ryckman et al. 1997; Tassi and Schneider 1997). If RPI provides employees with valuable information on their relative strengths and the relative advantages of different strategies, it may also help them choose the best strategy. This function requires that the information included in RPI is more comprehensive than just translating performance scores into ranks. For example, RPI can include information on exact performance differences, on chosen task strategies, or on developments over time (Berger et al. 2013b; Charness et al. 2014; Gill et al. 2019: 495; Pedreira et al. 2015). In the following, I will call such detailed information detailed RPI. In contrast, I will call rankings that only include information on ranks, simple RPI.

Despite a growing interest in RPI, almost no research exists on the behavioral effects of RPI when employees face volume–value trade-offs. Hannan et al. (2013, 2019) analyze the effects of rankings on performance when agents can allocate effort among multiple tasks, but do not consider the case where employees face trade-offs between multiple dimensions of one task (volume v. value). Christ et al. (2016), in turn, analyze a multi-dimensional task setting, but do not consider RPI in their study.

Hence, the current study investigates how the exact content of RPI affects its usefulness in improving the performance of employees who face volume–value trade-offs. This paper reports the results of an experimental study in which participants could choose between two difficulty levels when performing a real-effort math task. Difficult problems where more valuable than easy ones in terms of participants’ performance score, so that participants could choose whether to solve fewer, rather difficult and valuable problems (value strategy); or more, rather easy and less valuable problems (volume strategy). Performance was ranked within groups of three participants, and the rankings varied in terms of the information they disclosed. While simple RPI included only the group members’ performance scores, detailed RPI additionally included information on each group member’s task strategy.

In addition to analyzing the effects of simple v. detailed RPI, the current study investigates an important but often ignored factor that may moderate the behavioral consequences of RPI: group composition in terms of team members’ task abilities. Group composition is important in this context because it may influence whether rank information is motivating or frustrating (Berger et al. 2013b; Dutcher et al. 2015; Gill et al. 2019). As will be discussed in more detail in the hypotheses section, I expect that in homogeneous groups, RPI is motivating as it facilitates social comparison. In heterogeneous groups, however, RPI can frustrate low-ranking team members—and simultaneously demotivate high-ranking team members by lowering the competitive pressure on them.

Group composition is also likely to determine how RPI affects performance. In homogeneous teams, detailed RPI can facilitate learning and improve task strategies. This is because members of a homogeneous team are comparable, and information on successful and less successful members’ strategies can be used to learn and infer on one’s own optimal strategy choice (Houston et al. 2002; Stanne et al. 1999). In heterogeneous teams, however, detailed RPI can provide misleading information and hence impair strategy choice. This is because nuanced information on other members’ strategies does not necessarily allow for inferring one’s own strategy.

The remainder of this paper is structured as follows. In the next section I provide more details on the setting considered, and derive hypotheses on the behavioral consequences of different forms of RPI in homogeneous vs heterogeneous teams. Section 3 describes the design of the experimental study. Results are reported in Sect. 4. In Sect. 5, I discuss these results; Sect. 6 draws conclusions.

2 Setting and hypotheses

2.1 Setting

I consider a setting in which agent j works on one task at two difficulty levels \(d \in \left\{ {1,2} \right\}\), each with a different per unit value p. How many units x a given agent can produce in a fixed amount of time depends on his or her ability a and task difficulty d. Each agent’s performance level is determined as follows:

$$s_{j} = \mathop \sum \limits_{t}^{{}} p_{jt} \cdot x_{jt}$$

where \(p_{jt} { := }p\left( {d_{jt} } \right)\), \(x_{jt} { := }x\left( {a_{j} ,d_{jt} } \right)\), and \(d_{jt}\) is the difficulty chosen by agent j in round t.

To illustrate the decision and control problems involved in this setting, consider a numerical example with two agents with different task abilities: low and high. Both agents work on a task at two difficulty levels, each yielding a different value, expressed in terms of “points”: \(p_{1} = 2\),\(p_{2} = 8\). Each agent faces the optimization problem to choose the optimal difficulty level dj*. The optimal level is the one that maximizes points per minute. This level depends on the agent’s ability, which affects the time needed to solve a given problem. Table 1 provides an overview of this example and highlights dj* for each agent (italics).

In this example, an agent with low task ability should choose the volume strategy and try to solve many, easy tasks. In contrast, an agent with high task ability should choose the value strategy and solve fewer but more difficult tasks.

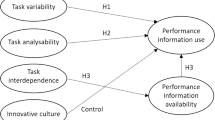
The experiment reported below is designed to analyze how different forms of RPI can help agents choose the right strategy and increase performance. As I will argue in more detail below, RPI in general, and detailed RPI in particular, should be helpful in both respects. It should induce social comparison and thus motivate higher effort—and it should facilitate learning and hence improve strategy choices. In addition to these main effects of RPI, I will also analyze the moderating effects of group composition in terms of the group members’ task abilities. Figure 1 summarizes the effects investigated in this study.

Fig. 1
figure 1

Effects investigated in this study

Full size image

2.2 Hypotheses

2.2.1 Effect of simple RPI on performance

Competition has long been argued to have a motivating and effort-enhancing effect. As Triplett (1898: 533) described it in his early study on the behavioral effects of competition, “…the bodily presence of another contestant participating simultaneously in the race serves to liberate latent energy not ordinarily available”. Findings from social psychology suggest that competitive control systems can motivate employees to exert more effort, if their rank is important to them (Johnson and Johnson 1989). This argument goes back to Festinger’s (1954) theory of social comparison. According to this theory, being ahead in a competition is a way of gaining in social status, which is why individuals have an interest in winning a contest. Importantly, this motivational effect does not presuppose monetary incentives. Studies in the accounting literature showed that the provision of RPI alone can already lead to increased effort and performance (Fisher et al. 2002; Frederickson 1992; Hannan et al. 2008, 2013; Tafkov 2013; Young et al. 1993).

However, this motivational effect of competition does not persist unconditionally, because humans differ in their preferences for competition. For example, various experimental field and laboratory studies have provided considerable evidence for the existence of a gender gap in competitiveness, suggesting that men are generally more competitive and have a higher preference for competitive environments than women (Frick 2011; Healy and Pate 2011; Niederle and Vesterlund 2007). Consequently, some studies showed that competition leads to performance improvements among male, but not among female participants (Gneezy et al. 2003; Gneezy and Rustichini 2004).

Another factor that influences the behavioral effects of RPI is the degree to which competing group members vary in their task ability (Arnold et al. 2018; Cardinaels et al. 2018). In the setting we consider, group composition in terms of task ability is important in mainly two ways. First, group composition can strengthen or weaken the social comparison involved in rankings. Research in social psychology has found that similarity in terms of agents’ attributes is an antecedent of rivalry and the motivation to win a competition (Garcia et al. 2013; Kilduff et al. 2010, 2016). As task ability is a crucial personal attribute in a relative performance evaluation setting, I expect that, if groups are homogeneous, rather than heterogeneous in their task abilities, their members will be more likely to engage in social comparison and competition, leading to increased effort and performance.

Second, group composition may affect the relation between an individual’s effort and the likelihood of moving up or down in a ranking. That is, group composition affects the marginal effect of effort which is important if competition ought to unfold its motivational effects. There is ample evidence that individuals are willing to exert high effort if this allows them to win a competition, or to avoid being last (Dutcher et al. 2015; Gill et al. 2019). But this mechanism requires that participants in a competition have some control over their rank. If groups are homogeneous in terms of task ability, each group member has a reasonable chance to affect his or her rank. High effort is likely to result in higher ranks, while low effort is likely to lead to lower ranks.

In contrast, if groups are heterogeneous, high-ranking members have a reasonable chance of keeping their rank even when not exerting maximal effort. Analogously, low-ranking members may find it frustrating that, even when they try hard, they have no chance of improving their rank, let alone winning the contest. This argument is consistent with recent findings that, if individuals fall far behind the high-ranking rivals, they reduce effort. Apparently, if it becomes less likely to win a contest, people give up and reduce effort and performance (Berger et al. 2013b: 149; Brown et al. 1996; Hannan et al. 2008).

From these findings I conclude that the effort-enhancing effects typically ascribed to competition only persist if groups are homogeneous in terms of task ability. In heterogeneous teams, however, competition risks being frustrating and demotivating. The following hypotheses summarize the arguments on the effects of RPI on effort, conditional on group composition:

H1a:

If teams are homogeneous in terms of task ability, the provision of simple RPI (compared to no RPI) has a positive effect on performance.

H1b:

If teams are heterogeneous in terms of task ability, the provision of simple RPI (compared to no RPI) has a negative effect on performance.

2.2.2 Effects of detailed RPI on performance

After the discussion of how group composition may change the effects of simple RPI on performance, the following arguments go beyond the RPI yes/no dichotomy. More specifically, this study is designed to analyze how the specific content of RPI affects behavior. It is not just important whether employees receive RPI, but also which kind of information they receive. This differentiation is important because firms have begun to use multidimensional rankings that provide information on various kinds of performance characteristics, including scores, speed, and development over time (Charness et al. 2014; Gill et al. 2019: 495; Pedreira et al. 2015). This analysis responds to recent calls from organizational scholars who argue that, from an organizational design perspective, it is important to understand how employees respond to competitive control systems with varying content (Gill et al. 2019: 495).

In the context considered, employees face a volume–value trade-off and need to make a strategic decision. Here, RPI may not only provide information on each employee’s performance level, but also on how each employee achieved that performance level, that is, on their performance strategy. If RPI contains detailed information on strategies, employees may not only learn that they are ahead of or behind others, but also why. But this requires that the information on one member’s strategy choice is useful for other members’ choice. Again, whether that is the case depends on group composition. As I will argue in the following, the social comparison involved in rankings may facilitate learning processes but could also distort strategy choice.

From one perspective, RPI may be useful in providing agents with a clue on their ability relative to those of their peers (Stanne et al. 1999). More nuanced RPI may help employees to better understand their competitive advantages and to find their optimal difficulty level. Specifically, it may help them understand why they are being outperformed by their peers; whether this is because others exhibit higher levels of effort, or because they have higher task abilities, allowing them to successfully choose higher difficulty levels.

Social psychologists have argued that the comparison with others in a contest may motivate people to improve their task ability. The basic argument is that the comparison facilitated through RPI allows agents to assess their own task ability against that of others, which provides them with a clue about how well they could perform. Thus, one motivation following from competition is the desire to improve one’s task ability (Hibbard and Buhrmester 2010; Houston et al. 2002; Tassi and Schneider 1997: 1557). The behavioral consequences of this motivation may include efforts to try harder, to exploit learning opportunities in order to improve task ability, and ultimately to perform better.

From another perspective, RPI may distort employees’ performance strategy (Hannan et al. 2013). This problem is particularly relevant if group members vary in their task abilities. In such a situation, not every strategy is equally beneficial for every group member. However, from observing that other group members perform better at higher difficulty levels, employees may conclude that higher difficulty levels are optimal for themselves. In particular, low-ranking participants may be tempted to mimic high-ranking peers’ value strategy. Such a conclusion could, however, be erroneous because the value strategy is only optimal for group members with higher abilities.

In sum, I expect that the effects of detailed, as opposed to simple, RPI on performance will depend on group composition. This argument is captured in the following two hypotheses:

H2a:

If teams are homogeneous in terms of task ability, performance will be higher under detailed RPI compared to simple RPI.

H2b:

If teams are heterogeneous in terms of task ability, performance will be lower under detailed RPI compared to simple RPI.

3 Experimental design

3.1 Task description

To test the hypotheses outlined above, I conducted a behavioral laboratory experiment. In the experiment, participants perform a real-effort math task. Similar to prior experiments on social comparison and performance, the task consists of solving multiplication problems (Hannan et al. 2013; Knauer et al. 2017; Tafkov 2013). Each problem is at one of two difficulty levels. Solving an easier or a more difficult problem yields 2 or 8 points for participants, respectively. That is, more difficult problems are also more valuable to the participants in terms of their performance score.

In each round, participants choose a difficulty level before performing the task. In terms of task strategy, they can choose whether to solve few, rather difficult and valuable problems; or many, comparatively easy and less valuable problems. The former approach corresponds to a “value strategy”, and the latter to a “volume strategy”.

Given this research design, it is important that the multiplication problems are equally difficult within each level, and that difficult problems are strictly more difficult than easy problems. Each problem requires the multiplication of two integers. Three criteria determine the difficulty level of a multiplication problem: the number of digits of each of the two integers; the number of carry-overs needed to solve the problem; and the number of digits of the solution. Table 2 provides an overview on the two difficulty levels at which participants can solve multiplication problems.

Table 1 A numerical illustration of the problem
Full size table
Table 2 Characteristics of multiplication problems at two difficulty levels
Full size table

I use the results of several pilot studies with students to calibrate the number of points a participant would get for solving one problem. The goal is to ensure that no dominant strategy exists for all participants. For participants with comparably high task ability, the best strategy should be to work on the difficult and valuable problems. For participants with comparatively low task ability, in contrast, it should be better to work on easy and less valuable problems. The values of 2 and 8 points for the two difficulty levels fulfil these criteria and ensure that there is no dominant strategy for the participants.

3.2 Participants and experimental procedures

I use a 1 + 2 × 2 between-subjects experimental design and manipulate performance feedback at three levels: no performance ranking (NoRPI), a simple ranking (SimpleRPI), and a detailed ranking (DetailedRPI). Rankings always refer to groups of three participants. This group size fits the purposes of the experiment because competition and rivalry among group members tend to be higher in smaller groups—an effect that has become known as the “N-effect” (Garcia and Tor 2009). When RPI is present, I manipulate group composition at two levels. In the heterogeneous groups treatments (HetGroups), each participant is randomly assigned to a group of three participants. In the homogeneous groups treatments (HomGroups), participants are matched based on their math problem-solving abilities. Table 3 visualizes the 1 + 2 × 2 design.

Table 3 Tabular summary of this study’s 1 + 2 × 2 factorial design
Full size table

The experiment was conducted at MaXLab, the Magdeburg Experimental Laboratory of Economic Research. The participants in the experiment were 150 students from different academic backgrounds, whom I recruited using the hroot software (Bock et al. 2014). On average, the participants were 21.7 years old and 57.3% of them were male. They were randomly assigned to one of the five experimental groups, so that there were 30 participants in each group. To program and conduct the experiment, I used the software z-Tree (Fischbacher 2007).

The following section describes the experimental setup. Each experimental session consists of three stages. The first two stages are identical across the five treatment groups; differences occur only on the third stage, where I manipulate RPI and group composition. Before each stage, the participants receive specific instructions, which the experimenter reads aloud to make clear that every participant has to perform the same tasks.

First (“lottery stage”), I present to the participants a short lottery task to elicit their risk preferences (Holt and Laury 2002). Participants have to make ten choices between paired lotteries, each involving different risks and different expected pay-offs. The participants’ answers provide a measure of their risk-aversion.

Second (“ability stage”), participants go through two rounds to solve math problems at two different difficulty levels: easy and difficult. All participants receive the same multiplication tasks in the same order. Within each round, they have one minute to familiarize themselves with the task and the new difficulty level, followed by five minutes in which they are incentivized to solve as many problems as possible. Participants see on their screen one multiplication problem at a time. They type their solution into a field next to the problem and press a button. If their solution is incorrect, an error message appears and they have to re-enter their solution. If it is correct, the next problem appears on the screen.

Participants are informed that their performance score s is the product of the value of a given problem and the number of problems they solve. In the ability stage, participants are paid €0.03 for each performance point. The primary purpose of this second stage is to determine participants’ task ability and, as a consequence, their optimal task strategy.

The third part (“treatment stage”) of the experiment is designed to test the effect of different forms of RPI and group composition on task strategy and performance. It involves five rounds of 300 s each. Participants perform the same math task as before. There are, however, several important differences compared to the second part:

  • In the RPI treatments, all participants are grouped in teams of three. According to the procedure described further below, groups are either matched randomly (in the HetGroups treatments) or according to performance scores in the ability stage (in the HomGroups treatments).

  • At the beginning of the ability stage, participants are asked to choose a gender-neutral nickname from a list (except in the NoRPI treatment).

  • In each round, participants can choose the difficulty level on which they would like to solve problems.

  • At the end of each round, the performance scores of all three group members are compared in a performance ranking (SimpleRPI and DetailedRPI treatments).

  • As a compensation for their work, participants receive €1 per round independently of their performance (flat wage).

In the NoRPI, the baseline treatment, participants also perform the same task as before and can choose their preferred difficulty level in each round. In contrast to the RPI treatments, however, they continue to perform individually and receive no rank information. Only their own scores are displayed to them at the end of each round.

After the experiment, all participants are asked to complete a short post-experimental questionnaire including questions on demographics, their math grade in school, and their preferences for the task. At the end of each session, each participant is remunerated in private with cash. Each session lasted approximately 70 min (including preparatory and payment procedures). Each participant receives a €4 show-up fee in addition to his or her variable remuneration; average pay was €14.83.

3.3 Manipulations

In the third part of the experiment, the treatment stage, I manipulate RPI at three levels. In the NoRPI treatment, participants learn their performance score after each round. In the SimpleRPI treatment, within each group of three, they can view a performance ranking indicating performance scores and ranks of the three group members. I do not tie the level of compensation to the participants’ absolute or relative performance, because my intention is to isolate the effects of social comparisons on behavior in the presence of RPI (Hannan et al. 2008, 2013). After each round, the participant with the highest performance score is declared the “winner” of the current round, and a little trophy icon is displayed next to his or her name in the ranking list. This procedure is based on prior studies’ evidence that ranks and symbols alone are able to motivate higher effort (Charness et al. 2014).

The DetailedRPI treatment includes the same information as the SimpleRPI treatment. In addition to the performance scores and ranks, participants in the DetailedRPI treatment receive information on each group member’s task strategy. In every round, the ranking indicates for each group member whether he or she followed a “value strategy” or a “volume strategy”. This way, participants have detailed information not only on how well each group member performed, but also on the strategy they used to achieve their scores.

Group composition is manipulated at two levels. In heterogeneous groups (HetGroups), participants are randomly assigned to a group of three members, which remains constant across the rest of the experiment. Homogeneous groups (HomGroups), in contrast, are formed according to participants’ relative performance during the ability stage (Berger et al. 2013a: 56). All 30 participants are ranked in order of their performance, measured in terms of output s achieved during that stage. Then, the participants with the ranks 1–3 are matched to form group 1; those with the ranks 4–6 form group 2; and all the way down to the participants with the ranks 28–30, who form group 10.Footnote 4 This procedure ensures that within-group variance of participants’ task ability is minimized.

4 Results

4.1 Calibration checks and descriptive statistics

During the ability stage, participants solve math problems for two periods, each at a different difficulty level. Period 1 includes easy problems (difficulty level 1), period 2 includes difficult problems (difficulty level 2). Participants’ task performance during that stage is important to test two features of the experimental design. First, I need to verify that math problems on level 2 are actually more difficult than those on level 1. As summarized in Table 4, participants solve significantly more problems on level 1 than on level 2. Based on these results from the ability stage, I conclude that math problems at difficulty level 2 are in fact more difficult than those at level 1.

Table 4 Descriptive statistics on # of problems solved per difficulty level (on ability stage)
Full size table

Second, the study design should ensure that no single task strategy is optimal for all participants during the treatment stage. For some, the value strategy should be optimal, for others the volume strategy. To determine which strategy would be optimal for each participant during the treatment stage, I compare their scores at each difficulty level during the ability stage. Results indicate that based on their performance during the ability stage, it would be optimal for 66.7% of the participants to choose a volume strategy during the treatment stage. That is, they would perform best if they chose level 1 problems, while the remaining participants should choose level 2 problems.

Although the optimal difficulty levels are not evenly distributed, the parametrization in the experiment leads to the intended effect: no single task strategy is optimal for all participants. Figure 2 contrasts the participants’ optimal task strategies with their actual choices in the five periods of the treatment stage. As the graph illustrates, participants do not always choose their optimal strategies. In 85 cases, they choose the volume strategy although the value strategy would be optimal. Similarly, there are 123 instances in which participants choose the value strategy although the volume strategy would be optimal. Taken together, 27.7% (208 out of 750) of the task strategy choices are not optimal. I will have a closer look at the determinants of participants’ choices in the subsequent section when I discuss the treatment effects.

Fig. 2
figure 2

Distribution of optimal and actual task strategies

Full size image

Finally, some descriptive statistics provide information on the differences between homogeneous and heterogeneous groups. To begin with, the following simple analysis suggests the manipulation actually works. In the ability stage (on which the sorting is based), the average standard deviation of the performance scores within each group is 5.32 for homogeneous groups and 33.23 for heterogeneous groups. That is, participants’ task abilities vary more within heterogeneous groups than within homogeneous groups. The groups do not differ significantly in their task strategies during the performance stage. In 95% of the heterogeneous groups, the most frequently chosen strategy is the volume strategy (easy problems). The corresponding number is 85% for the homogeneous groups—but the difference is not statistically significant (p = 0.30, two-tailed t-test).

4.2 Main hypothesis tests

This section reports the results of my hypothesis tests. I begin by analyzing the performance effects of the main treatments and then go on to explain these effects in terms of participants’ task strategies.

Table 5 summarizes mean performance scores across groups, and mean comparison tests. H1a and H1b posited that the effects of SimpleRPI on performance will depend on whether rank information is provided to heterogeneous or to homogeneous groups. The average performance score in the NoRPI treatment is 61.08 points. Under SimpleRPI in groups with homogeneous task abilities, performance increases to 67.05, but this effect is not statistically significant (p = 0.202, one-tailed t-test), so that H1a is not fully supported. In contrast, under SimpleRPI in groups with heterogeneous task abilities, performance drops to 48.67 (p = 0.040, one-tailed t-test). This result fully supports H1b.

Table 5 Comparison of performance between treatments
Full size table

In the hypothesis section, I argued that the effect of DetailedRPI on performance should depend on group composition. Specifically, I expected that detailed RPI would facilitate optimal strategy choice and enhance performance in homogeneous groups; and that it would distort strategy choice and hamper performance in heterogeneous groups (H2a and H2b). The results presented below do not support these hypotheses. In homogeneous groups, performance is lower under detailed than under simple RPI (58.00 v. 67.05; p = 0.072, one-tailed t-test), and just the contrary is true for heterogeneous teams. Here, performance is higher under detailed than under simple RPI (63.44 v. 48.67; p = 0.018, one-tailed t-test).

In addition to Table 5, Fig. 3 gives a graphical summary of the effects of different forms of RPI on performance. The interaction graph illustrates how the performance effects of RPI depend on team composition. In HetGroups, average performance is higher under DetailedRPI than under SimpleRPI. In HomGroups, quite the contrary, average performance is lower under DetailedRPI than under SimpleRPI.

Fig. 3
figure 3

Interaction effects of team composition and RPI treatment

Full size image

Finally, Table 6 reports results of a GLS estimation which accounts for period effects and serial correlation within subjects. To ease the interpretation of the coefficients, I restrict the analysis to the four treatment groups in which RPI is present. The results basically confirm those of the mean comparison tests above: How performance is affected by simple v. detailed RPI, depends on whether it is provided to heterogeneous or to homogeneous groups. Also, gender, math grade in school, and period all have an influence on performance.Footnote 5

Table 6 Random effects GLS regression of performance on the treatment and control variables
Full size table

4.3 Additional analyses

The following additional analyses are meant to explore potential explanations for the results obtained above. In particular, I am interested in further understanding the performance effects of detailed v. simple RPI. According to my hypotheses, there are two ways to explain differences in performance. One is through varying levels of effort, the other is through different task strategies.

As summarized in Table 7, there are no significant differences in terms of task strategy (i.e., chosen difficulty levels) across treatments. Apparently, the effect of RPI on strategy choice is negligible.

Table 7 Comparison of chosen difficulty levels in treatment stage between treatments
Full size table

However, this result does not allow for conclusions as to the quality of the choices. Because whether a given difficulty level is a good choice depends on each participant’s task ability. To see whether there are differences across treatments in how well participants choose their task strategies, I contrast their optimal strategies with those they actually choose. More technically, I construct a dummy variable taking value 1 if a participant chooses his or her optimal strategy in a given period. Using a Random Effects Probit model, I then regress this dummy variable on the treatment and period variables. Table 8 reports the results of the analysis.

Table 8 Random effects probit regression of optimal strategy choice on treatment variables
Full size table

Results indicate that participants make slightly inferior strategy choices under DetailedRPI although the effect is rather small. Interestingly, this effect does not depend on group composition.

Finally, it is worth asking whether the observed performance differences between detailed v. simple RPI can be attributed to how often participants change their task strategies from one period to the other. More frequent changes could be interpreted as inconsistencies and a reason for inferior performance. Across the five performance periods, however, most of the participants (80.67%) either always apply the same strategy or change it only once. More importantly, the average number of changes does not vary significantly across treatments. The only significant difference is in heterogeneous groups. Here, participants under SimpleRPI change their strategy 0.5 times on average; compared to 0.93 (p = 0.051, one-sided t-test) under DetailedRPI. The best performing group is actually the least consistent—so that the number of strategy changes can hardly explain performance differences across treatments.

5 Discussion

With this study, I set out to investigate experimentally the behavioral effects of different forms of RPI. Specifically, I focused on a work setting in which employees face a volume–value trade-off. In such a setting, RPI can be decision-influencing when it affects employees’ motivation to exert high effort and to perform well in order to win a contest, even if no monetary incentives are tied to winning. RPI can also be decision-facilitating when it helps employees find the right task strategy contingent on their problem-solving abilities.

I hypothesized that the exact behavioral consequences of RPI will depend on its content and on whether it is provided to groups that are homogeneous v. heterogeneous in terms of their members’ task abilities. The first set of hypotheses stated that simple RPI, which only includes information on the group members’ ranks, would enhance performance in homogeneous teams, and lower performance in heterogeneous teams. Indeed, results suggest that performance under simple RPI is highest in homogeneous teams, and lowest in heterogeneous teams. By illuminating the role of group composition in terms of task ability, these results offer a more nuanced view on the generic finding that RPI can be either motivating or frustrating (Berger et al. 2013b; Garcia et al. 2006, 2013).

To be sure, average performance in the HomGroups/Simple RPI group is higher than in the baseline treatment (67.05 v. 61.08), although this difference is not statistically significant (p = 0.202, one-tailed t-test). Of course, this result should not be taken to infer that RPI does not generally affect performance. Previous studies repeatedly found that simple RPI, even without monetary incentives, can spur the desire to win, and enhance effort and performance (Charness et al. 2014; Hannan et al. 2008; Hartmann and Schreck 2018; Kuhnen and Tymula 2012; Tran and Zeckhauser 2012). The failure to replicate this standard result in the current study does not contradict prior results. Previous studies employed rather boring (sorting and decoding) tasks to induce sufficient disutility of effort. In the current experiment, many participants enjoyed the task (see footnote 7), and they greatly varied in their task abilities. This led to high within-group variances, making it more demanding to detect between-group differences. Taken together, it may very well be that the result is more due to a lack of statistical power than to a lack of an actual association between simple RPI and performance in homogeneous groups. It should also be noted that the focus of the current study is not to test the main effects of RPI, but its differential effects contingent on group composition and the level of details contained in RPI.

In line with that goal, the study’s results suggest the effort-enhancing effects of RPI may only exist when teams are homogeneous. Here, rank information is primarily a signal of effort and group members know that they have some control over their rank. Under these conditions, RPI is equally motivating for those who strive to be first in a ranking; and for those who try to avoid being last (Gill et al. 2019).

The informational value and the motivational effects of simple RPI change when teams are heterogeneous and there is considerable uncertainty about each group member’s relative strengths (Arnold et al. 2018). Here, rank information becomes primarily a signal of an individual’s relative ability. As such, RPI can be demotivating for both, those at the top and those at the bottom of the ranking. For top performers, competitive pressure is lower than in homogeneous teams as they know that, given the differences in ability, it takes less effort to defend one’s rank if competitors aren’t of equal ability. Similarly, low-ranking group members understand that it will be very hard, or even impossible, to keep up with their higher-rank competitors. Eventually, they give up in the competition. Taken together, the current study contributes to the literature by offering an explanation for when RPI can be motivating—and when it can be demotivating.

By considering the informational details of RPI and their effects on task strategies and performance, this study’s goal was to add to the very few studies that go beyond analyzing the behavioral effects of simple RPI (e.g., Hannan et al. 2006). I hypothesized that the additional information on task strategy included in detailed RPI would facilitate strategy choice in homogeneous groups, and distort strategy choice in heterogeneous teams. The main argument behind these hypotheses was that in homogeneous teams, information on other group members’ strategies would allow participants to learn the value of a given strategy relative to their abilities (Houston et al. 2002; Stanne et al. 1999), while in heterogeneous teams this information would be misleading because here, it is not possible to infer from other participants’ successful strategies on the value of that strategy for oneself.

However, the results do not lend support to these hypotheses. Quite the contrary, the analysis suggests that more details deprive RPI of its motivational effects when teams are homogeneous; and weakens the demotivating effects when they are heterogeneous. In the sample, detailed RPI has no effect on performance compared to the NoRPI treatment.

In an effort to explore the exact mechanisms through which detailed RPI unfolds its effects in comparison to simple RPI, I found hardly any differences in terms of strategy choices across treatment groups. Choices are slightly inferior under detailed RPI, although the effect is small and independent of group composition. So more detailed information does not improve strategic decision making in either homogeneous or heterogeneous teams in the experiment. I conclude from this result that the differential performance effects of detailed RPI in homogeneous and heterogeneous groups cannot be explained entirely via its effects on strategy choice.Footnote 6

One potential explanation for the surprising effects of detailed RPI is that the additional information on strategy choice might weaken the social comparison involved in rankings. In homogeneous groups, more detailed information may hinder the social comparison that is responsible for enhanced effort. When informed about the strategies that competitors use to achieve their performance scores, participants understand that performance differences are not merely due to different strategies, but that they reflect more profound differences in problem-solving abilities, decreasing the marginal benefit of increased effort. For low-ranking participants, this may mean that they understand how difficult it would be to outperform their competitors and to improve their rank. At the same time, high-ranking participants may be tempted to choose easier problems. The volume strategy may not maximize their performance score, but it would require less effort and still allow them to rank high if their competitors are obviously weaker in their problem-solving abilities.

In heterogeneous groups, more detailed information may hinder the social comparison that is responsible for the potentially demotivating effects of RPI. When low-ranking group members learn that performance differences are indeed due to different problem-solving abilities, they may stop comparing themselves to others and might be less frustrated by the performance differences as expressed in ranks. Similarly, high-ranking group members may stop feeling motivated once they understand that they lead a ranking because their performance is compared to competitors with lower task-solving abilities.

Of course, these arguments are rather speculative and require empirical scrutiny, including the psychometric assessment of rivals’ competitive traits and states (e.g., Harris and Houston 2010; Kilduff et al. 2016; Mudrack et al. 2012). This study’s experimental design, however, does not allow for further analyzing these potential mechanisms because there are no observable measures of the participants’ motivations, and we do not know how exactly participants used the information provided by detailed RPI. Hence, future research should investigate further how and why detailed RPI may strengthen or weaken social comparison and, in turn, performance.

6 Conclusion and implications

This study’s findings have important implications for both, business practice and research. To begin with, it provides evidence that, if the employees who are compared in rankings are similar in their task ability, a simple RPI system can induce social comparison and enhance performance. If, in contrast, employees differ strongly in their task abilities, there may be no, or even negative performance effects of RPI. Given the potentially detrimental effects of competition in organizations (Chowdhury and Gürtler 2015; Dato and Nieken 2014; Hartmann and Schreck 2018; Schreck 2015), it is questionable whether the use of RPI is beneficial under such circumstances at all.

In light of the inconclusive results on the behavioral effects of detailed RPI, this study cannot deliver clear recommendations on how the content of RPI should best be designed. Although I do find that strategy choice is slightly better under simple than under detailed RPI, these differences do not help explain the performance differences observed in the experiment. Also, the results fail to lend support to my hypotheses regarding the differential effects of detailed RPI contingent upon group composition. Taken together, the study cautions against an unreflected use of performance rankings in organizations. The specific work context, in which such rankings are used, and its exact content can determine whether RPI is motivating or demotivating, whether it is performance-enhancing or performance-inhibiting. Such intended and unintended effects of incentive systems are important to consider from a management control perspective—not just because of their economic significance, but also because they may be conflicting with employees’ profound values (Küpper 2011: 327). Hence, care should be taken to analyze the specific conditions of use before implementing performance rankings.

Finally, I would like to point out two features of my study that may limit the generalizability of its results, but that offer opportunities for future research at the same time. First, the specific task I used is well suited to capture differences in problem-solving abilities, and to manipulate two difficulty levels neatly. However, as responses to a post-experimental questionnaire reveal, participants vary greatly in their preferences for the task.Footnote 7 Presumably, these differences lead to a large variance in intrinsic motivation, limiting the extrinsic motivational effects of the rankings (Whitehead and Corbin 1991). Future research could take different real effort tasks to investigate the behavioral effects of different forms of RPI and group compositions. Specifically, they could focus on boring tasks where varying performance levels are less attributable to differences in ability but rather to differences in effort (Charness et al. 2018). Alternatively, differences in intrinsic motivation could be mitigated by a stronger RPI manipulation. For example, by tying monetary incentives to participants’ rank—turning rankings into a relative performance evaluation (RPE) system (Hannan et al. 2008; Matsumura and Shin 2006).

Second, the set of only two strategies available to participants was quite restrictive. This design allows for a focus on the differences between easy and difficult tasks. However, it does not allow for fine-grained differences that may be more suitable to capture the variance in participants’ task abilities. Future research could take this study’s results as a point of departure to investigate how participants respond to a greater set of available strategies.