Estimating the energy of dissipative neural systems

Abstract

There is, at present, a lack of consensus regarding precisely what is meant by the term 'energy' across the sub-disciplines of neuroscience. Definitions range from deficits in the rate of glucose metabolism in consciousness research to regional changes in neuronal activity in cognitive neuroscience. In computational neuroscience virtually all models define the energy of neuronal regions as a quantity that is in a continual process of dissipation to its surroundings. This, however, is at odds with the definition of energy used across all sub-disciplines of physics: a quantity that does not change as a dynamical system evolves in time. Here, we bridge this gap between the dissipative models used in computational neuroscience and the energy-conserving models of physics using a mathematical technique first proposed in the context of fluid dynamics. We go on to derive an expression for the energy of the linear time-invariant (LTI) state space equation. We then use resting-state fMRI data obtained from the human connectome project to show that LTI energy is associated with glucose uptake metabolism. Our hope is that this work paves the way for an increased understanding of energy in the brain, from both a theoretical as well as an experimental perspective.

Introduction

The concept of energy in the brain is understood in various ways across different sub-disciplines of neuroscience. In the study of consciousness, energy is often linked to metabolic activities that support brain function (Magistretti and Allaman 2022). For example, ATP and glucose have been shown to maintain the brain's functional connectivity (Chen and Zhang 2021)—whereas in cognitive neuroscience, the brain's metabolic energy has been linked to different mental states (Galijašević et al. 2021). In clinical neuroscience on the other hand, energy is of relevance to many neurodegenerative (Kirch and Gollo 2021) and neuropsychiatric disorders (Shokri-Kojori et al. 2019; Zhang and Raichle 2010; Raichle 2006) and is also often discussed in terms of deficit as a result of pathology—for example following intracerebral haemorrhage (Rass and Helbok 2019). In computational neuroscience, the Ising model can be used to calculate a measure of energy in terms of the level of correlation between neural regions (Riehl et al. 2017). Spiking neuron models, originating in reservoir computing, define the energy of neural systems in terms of their computational efficiency (Gaurav et al. 2023). In the context of dynamic causal modelling (DCM), ‘free energy’ is defined as the statistical evidence for a particular hypothesis following Bayesian model inversion (Friston 2010). Among these different approaches, a key challenge remains in terms of reaching a cross-disciplinary consensus as to precisely what is meant by 'energy' in the context of the brain.

Such a consensus already exists across the various sub-disciplines of physics, in which a system's total energy is defined as a conserved quantity—i.e., it does not change in time. This idea was first formalized within Hamiltonian mechanics, which allows for a system's equations of motion to be derived under the presupposition that total energy is conserved. However, there are scenarios in which it is advantageous to conceive of a system as being dissipative, meaning that energy is continuously being lost. Let us consider for instance, a ball rolling along the floor with an initial movement ('kinetic') energy (Fig. 1A).

Fig. 1

A A ball rolls along the floor with an initial velocity indicated by the arrow. The floor and surrounding air have a certain temperature, indicated by the thermometer. B As the ball slows down, we find that the temperature of the floor and surrounding air increase slightly, due to the ball's kinetic energy having been transferred to atomic motion in the environment

The ball then gradually slows down in what would appear to be a dissipation of energy. However, upon closer inspection we find that the ball's energy is not actually lost, but rather has been transferred to degrees of freedom that are more difficult to measure. These degrees of freedom take the form of increased motion of the atoms in the floor and surrounding air, leading to an increase in temperature (Fig. 1B). In fact, we find that the ball loses energy at exactly the same rate as the environment absorbs energy and thus the total energy in the combined ball + environment system is conserved.

Virtually every equation of motion in computational neuroscience e.g., the models of Hodgkin and Huxley (1952), Izhikevich (2003), and Wilson and Cowan (1972) describe dissipative processes. As such, these models only capture the energy-dissipating system of interest, but do not take account of the energy-absorbing environment. This focus on purely dissipative dynamics creates a an incompatibility between the models of computational neuroscience and the foundations of Hamiltonian mechanics, which require that energy be conserved.

We can, however, circumvent this incompatibility by ways of a technique that was first formulated by Morse and Feshbach in the 1940's in the context of fluid dynamics (Morse and Feshbach 1954). The 'dodge' (to quote the authors) is that for every dissipative system we can conceive of a mirror system that exists only mathematically and functions so as to absorb energy at the same rate as the original system loses energy. The combined dissipative system + 'undissipative' mirror system conserves energy when considered in unison and can hence be described by Hamiltonian mechanics. Here, we show how this technique can be applied to the linear time-invariant (LTI) equation of motion, as this forms the basis of a large number of dissipative equations used in computational neuroscience.

Similar approaches are gaining popularity in numerical solutions to large-scale dynamical systems e.g., in the application of Lagrangian neural networks (Cranmer, et al. 2003; Sosanya and Greydanus 2022). Other studies consider similar approaches with regard to the associated computational methodology (Gori et al. 2016). Furthermore, the modelling of neural activity within a Lagrangian framework—including a comparison with existing models—was recently laid out by Galinsky and Frank (2021).

Our paper comprises three sections:

In the first section, we describe the Morse and Feshbach mirror system approach using: (a) the simple case of exponential decay, (b) the LTI form with sinusoidal driving input, and (c) the LTI form with an unknown driving input.

In the second section, we establish the relationship between the model parameters of the LTI equation and its associated average energy by using synthetic data generated by the LTI equation itself.

In the third section, we establish the energy associated with regional fMRI timeseries from the human connectome project (HCP) and compare these with known structural, functional, metabolic and electrophysiological Neuromaps (Markello et al. 2022).

Methods

The mirror system Let us begin with a simple dissipative dynamical system tracking the evolution of a dependent variable $x\left(t\right)$ that decays exponentially in time:

$$\dot{x}=-ax,$$

(1)

where $a$ is a positive constant.

In addition, we describe the environment in terms of a mirror system that evolves according to a new variable $\widetilde{x}\left(t\right)$, where this system gains energy at the same rate as the original system in Eq. (1) loses energy, such that:

$$\dot{\widetilde{x}}=a\widetilde{x}$$

(2)

The need for this mirror system approach can be motivated by the limitations of alternative approaches, as outlined in Appendix 1.

We can then cast Eqs. (1) and (2) in the form of the following Lagrangian $\mathcal{L}$:

$$\mathcal{L}=\frac{1}{2}\left(\dot{x}\widetilde{x}-x\dot{\widetilde{x}}\right)+ax\widetilde{x}$$

(3)

which we can verify by recovering the equations of motion via the Euler–Lagrange equations:

$$\begin{gathered} \frac{{\partial {\mathcal{L}}}}{{\partial \tilde{x}}} - \frac{d}{{dt}}\left( {\frac{{\partial {\mathcal{L}}}}{{\partial ~\dot{\tilde{x}}}}} \right) = 0~~~~ \Rightarrow ~~~~\dot{x} = - ax \hfill \\ \frac{{\partial {\mathcal{L}}}}{{\partial x}} - \frac{d}{{dt}}\left( {\frac{{\partial {\mathcal{L}}}}{{\partial \dot{x}}}} \right) = 0~~ \Rightarrow ~~~\dot{\tilde{x}} = a\tilde{x} \hfill \\ \end{gathered}$$

(4)

The energy¹$E$ associated with the Lagrangian in Eq. (3) is then obtained via the Legendre transformation:

$$\begin{aligned} E & = \frac{{\partial {\mathcal{L}}}}{{\partial \dot{\tilde{x}}}}\dot{\tilde{x}} + \frac{{\partial {\mathcal{L}}}}{{\partial \dot{x}}}\dot{x} - {\mathcal{L}} \\ & = - ax\tilde{x} \\ \end{aligned}$$

(5)

The solutions of Eqs. (1) and (2) read:

$$\begin{aligned} x\left( t \right) & = c_{0} e^{ - at} \\ \tilde{x}\left( t \right) & = c_{1} e^{at} \\ \end{aligned}$$

(6)

where ${c}_{0}$ and ${c}_{1}$ are integration constants.

Using Eqs. (5) and (6) we then find that the energy is conserved, as required (Fig. 2)

$$E = - ac_{0} c_{1} \Rightarrow \dot{E} = 0$$

(7)

Fig. 2

For chosen values of $a = - 0.4$, $c_{0} = 2$, $c_{1} = 4$, we show time (arbitrary units) on the horizontal axis and the dependent (dep.) variables on the vertical axis—consisting of the time course of $x\left( t \right)$ (solid black line), the corresponding mirror time course $\tilde{x}\left( t \right)$ (dashed line) from Eq. (6), and the resultant constant energy $E$ (red line) time course from Eq. (7)

Bayesian model inversion We use dynamic causal modelling (DCM) with the statistical parametric mapping (SPM) software to extract estimates of model parameters (Friston et al. 2003) for a given time course. This routine sets all free parameters (such as coupling strengths) to Bayesian priors of zero—providing starting points from which the model inversion then searches for Bayesian posterior values that best explain the underlying data, by using variational Laplace to estimate the variance of states (Roebroeck et al. 2011).

Specifically, we begin by setting the model states in terms of the initial conditions of the dependent variable at $t=0$. We also set the prior means of model parameters to zero and set prior variances of unity, thereby allowing the posteriors of the model parameters to deviate from the prior means. We set up an observation function consisting of the dependent variable and apply an external driving input that is initialized as a randomized time course with mean zero. Furthermore, we set the precisions of observation noise, state noise, and of exogenous causes and run Bayesian model inversion (spm_LAP in spm12) to infer the best fits of the model parameters and external driving input for a given dataset. This routine returns a summary statistic known as the variational free energy, which represents a trade-off between the accuracy and complexity of a given model. In other words, for a given level of accuracy, model evidence is penalized for each additional degree of freedom used, thereby avoiding an potential overfitting problem. Full details of this routine are provided in the accompanying code.

Resting-state fMRI We next use empirical neuroimaging timeseries to obtain estimates of energy across a 100-region brain parcellation (Schaefer atlas) of the cortex (Schaefer et al. 2018).

Regional fMRI blood-oxygen-level-dependent (BOLD) resting-state data were sourced from the 1200-subject release of the Human Connectome Project (HCP) (Essen et al. 2013). The acquisition of these data was performed using a Siemens Skyra 3 Tesla MRI scanner with a 3T imaging capability. The scanning parameters included a repetition time (TR) of 720 ms, an echo time (TE) of 33 ms, a flip angle of 52 degrees, and a voxel size of 2 mm isotropic. The scan covered 72 slices with a matrix size of 104 × 90 and a field of view (FOV) of 208 × 180 mm, employing a multiband acceleration factor of 8. From this dataset, 100 subjects aged between 22 and 35 were selected at random, with three individuals excluded due to missing data.

To mitigate the effects of global movement and respiratory-induced artifacts, we ran the fMRI data through noise reduction via the ICA-FIX based pipeline. FMRIB's ICA-based Xnoiseifier (ICA-FIX) serves as a preprocessing framework aimed at cleaning fMRI data by eliminating components associated with noise. This framework integrates two distinct techniques: independent component analysis (ICA) and FMRIB's Automated Removal of Motion Artefacts (FMRIB-AROMA) (Griffanti et al. 2014). We then used the 100-region Schaefer cortical atlas in MNI152 2 mm standard space to extract the mean regional fMRI signal for each subject.

Neuromaps Finally, we assessed whether our empirical resting-state fMRI-derived regional LTI energy estimates corresponded to any pre-existing regional measures of biologically-based notions of energy. To this end, we used the Neuromaps toolbox to obtain structural, functional, metabolic and electrophysiological maps, parcellated according to the same 100-region Schaefer cortical atlas as used with the resting-state fMRI datasets. These maps include regional cerebral metabolic rate (rCMRGlu), derived from 18-flurodeoxyglucose positron emission tomography (FDG-PET)—frequently used to estimate metabolic energy consumption in vivo. The maps also include regional cerebral blood flow (CBF) derived from MRI arterial spin labelling (ASL), which is tightly coupled to rCMRGlu in the healthy resting brain.

The list of 16 Neuromaps we used is as follows: cerebral blood flow, blood volume, metabolic rate, and metabolic rate of glucose (Vaishnavi et al. 2010); the first three diffusion map embedding gradients of group-averaged functional connectivities (Margulies et al. 2016); MEG timescales, together with alpha, beta, delta, low gamma, high gamma, and theta power distributions (Essen et al. 2013; Shafiei et al. 2022); MRI cortical thicknesses and T1w/T2w ratios (Glasser et al. 2016).

Significance testing To account for the contribution of spatial autocorrelation between maps, we correlated our subject-averaged LTI energy map with $N=\text{10,000}$ spatial null maps for significance testing (Markello and Misic 2021). This allows us to calculate a p-value by assessing where a given correlation strength lies within a sorted list of $\text{10,000}$ correlation strengths, each of which is calculated from maps that have a different spatially randomized (spinpermuted) segmentation. One such significance test was performed for each of the 16 Neuromaps.

As a further test of significance, we repeated all correlations with mean signal values, rather than with mean energy values. This is done in order to assess whether a given result, once spatial autocorrelation is accounted for, is specifically due to the form of the LTI energy expression (see Eq. (15) in Results), as opposed to some more basic property of the time course that can be captured just by its mean value.

Results

All information required for reproducibility is provided in the accompanying MATLAB code (see ‘Code availability'). All figure axes are normalized between zero and unity.

The average energy of a dissipative system with sinusoidal input Beginning with the simple case outlined in Methods in Eqs. (1) through (7), let us increase the complexity of the system + mirror system by adding the effect of a sinusoidal driving input $Acos\left(\omega t\right)$, where $A$ is the amplitude and $\omega$ is the angular frequency. The systems now evolve according to:

$$\begin{aligned} &\dot{x} = - ax + Acos\left( {\omega t} \right) \hfill \\ &\dot{\tilde{x}} = a\tilde{x} - Acos\left( {\omega t} \right) \hfill \\ \end{aligned}$$

(8)

which can be cast in the form of the following Lagrangian and associated Legendre transform-derived energy:

$$\begin{aligned} {\mathcal{L}} & = \frac{1}{2}\left( {\dot{x}\tilde{x} - x\dot{\tilde{x}}} \right) + ax\tilde{x} \\ & \quad - Acos\left( {\omega t} \right)\left( {x + \tilde{x}} \right) \\ E & = - ax\tilde{x} + Acos\left( {\omega t} \right)\left( {x + \tilde{x}} \right) \\ \end{aligned}$$

(9)

Choosing initial conditions of $x\left(0\right)=\widetilde{x}\left(0\right)=0$, the differential equations in Eq. (8) have the following solutions:

$$\begin{aligned} x\left( t \right) & = \frac{A}{{a^{2} + \omega^{2} }}\left( {acos\left( {\omega t} \right) + \omega sin\left( {\omega t} \right) - ae^{ - at} } \right) \\ \tilde{x}\left( t \right) & = \frac{A}{{a^{2} + \omega^{2} }}\left( {acos\left( {\omega t} \right) - \omega sin\left( {\omega t} \right) - ae^{at} } \right) \\ \end{aligned}$$

(10)

which allow us, together with Eq. (9), to write the energy as follows:

$$E = \frac{{aA^{2} }}{{\left( {a^{2} + \omega^{2} } \right)^{2} }}\left( {\left( {\omega^{2} - a^{2} } \right)sin^{2} \left( {\omega t} \right) + 2\omega^{2} cos^{2} \left( {\omega t} \right) - 2\omega^{2} cos\left( {\omega t} \right)cosh\left( {at} \right) + 2a\omega sin\left( {\omega t} \right)sinh\left( {at} \right)} \right)$$

(11)

This allows us to consider the mirror system approach for a more complicated, yet still analytically solvable system. More specifically, we can obtain an expression for the system's average energy (Gray et al. 1996) $\overline{E }$ over one period $\frac{2\pi }{\omega }$ of the driving input:

$$\overline{E }=\frac{\omega }{2\pi }{\int }_{0}^{\frac{2\pi }{\omega }}Edt$$

(12)

which, together with Eq. (11), means that the average energy is given by:

$$\overline{E }=\frac{a{A}^{2}}{\pi {\left({a}^{2}+{\omega }^{2}\right)}^{3}}\left(3\pi {\omega }^{4}-4{\omega }^{3}asinh\left(\frac{2a\pi }{\omega }\right)+2\pi {a}^{2}{\omega }^{2}-\pi {a}^{4}\right)$$

(13)

We calculated the average energy $\overline{E }$ of this system over one cycle of the input using Eq. $\left(13\right)$ and plotted how $\overline{E }$ varies with respect to the driving amplitude $A$ and angular frequency $\omega$ (Fig. 3).

Fig. 3

The amplitude $A$ and angular frequency $\omega$ of the sinusoidal driving input are plotted across the vertical and horizontal axes. The average energy $\overline{E}$ is indicated by the colour bar

Therefore, as an initial sanity check we find that higher amplitudes and frequencies of the driving input result in higher average energies, as expected.

The energy of a dissipative driven system with an unknown input Let us now consider what happens when the form of the external driving input is not known a priori. We describe this unknown input by a function $u\left(t\right)$, such that we extend the original system + mirror system in Eqs. (1) and (2) to the following:

$$\begin{aligned} \dot{x} & = - ax + bu\left( t \right) \\ \dot{\tilde{x}} & = a\tilde{x} - bu\left( t \right) \\ \end{aligned}$$

(14)

where $b$ is an external coupling constant. This is the linear time-invariant (LTI) state space equation as used in control theory. Note that the unknown function $u\left(t\right)$ is taken (but not constrained) to be non-linear and initialized as a randomized time course to model the effect of aberrant neuronal fluctuations driving the system.

The Lagrangian and associated Legendre transform-derived energy for Eq. (14) are given by:

$$\begin{aligned} {\mathcal{L}} & = \frac{1}{2}\left( {x\dot{\tilde{x}} - \tilde{x}\dot{x}} \right) - ax\tilde{x} \\ & \quad + bu\left( {x + \tilde{x}} \right) \\ E & = ax\tilde{x} - bu\left( {x + \tilde{x}} \right) \\ \end{aligned}$$

(15)

see Fig. 4.

Fig. 4

For chosen values of $a = - 0.1$ and $b = 1$, and a sinusoidal driving input $u\left( t \right)$ we show time (arbitrary units) on the horizontal axis and the dependent (dep.) variables on the vertical axis—consisting of the time course of $x\left( t \right)$ (solid black line), the corresponding mirror time course $\tilde{x}\left( t \right)$ (dashed line) from Eq. (14), and the resultant energy $E$ (red line) time course from Eq. (15)

We note that, unlike the example shown in Fig. 2, the energy is no longer conserved due to the time-dependent nature of the driving input.

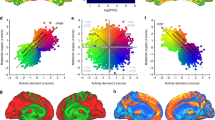
The energy of resting-state fMRI timeseries predicts glucose uptake metabolism We next calculated the region-wise subject-averaged LTI energy derived from resting-state fMRI (Fig. 5A). Upon accounting for spatial autocorrelation between brain maps, we find that these regional LTI energy values are only significantly correlated $\left(p=0.01 , {R}^{2}=0.39\right)$ with the Neuromap of regional metabolic rate of glucose (rCMRGlu) (Fig. 5B).

Fig. 5

A The parcellated average LTI energy ($\overline{E}$), (colour bar) is shown per brain region when averaged across subjects from resting-state fMRI. B The y-axis shows LTI energy ($\overline{E}$) and the x-axis shows the regional metabolic rate of glucose (rCMRGlu) parcellated into the same 100 brain regions as in (A), for an average taken across a different group of subjects

Discussion

We showed that it is possible to extract the energy associated with linear time-invariant (LTI) state space representations using a technique originally described by Morse and Feshbach in the context of fluid dynamics. We first used a ground-truth simulation to show that the average LTI energy over one cycle of an oscillating driving input is proportional to both the amplitude as well as to the frequency of oscillations, as expected.

We went on to show how the LTI energy varies across anatomically delineated regions in the brain using resting-state fMRI timeseries from the Human Connectome Project (HCP). We found that LTI energy related strongly and specifically to the regional cerebral metabolic rate for glucose. This finding aligns with the established view of glucose as a source of energy for the brain in terms of ATP production, neurotransmitter synthesis, and oxidation (Dienel 2019).

In Hamiltonian mechanics and more broadly across the physical sciences, energy is defined as a quantity that does not change as a dynamical system evolves in time. In this sense, all systems are in fact conservative and when we refer to a ‘non-conservative’ process we are not actually making any statement about the system itself, but rather about our inability to take sufficiently accurate measurements. In other words, a non-conservative process is also conservative, but it is one in which energy is transferred into microscopic degrees of freedom where it is difficult to measure—see the rolling ball example in Fig. 1. Herein lies the Morse and Feshbach insight: every equation of motion describing a dissipative system can be considered as just one half of an overall process, with the other half describing an ‘undissipating’ mirror system into which energy is absorbed. The balance between this dissipation/undissipation results in an overall energy conservation that can then be brought into the formal framework of Hamiltonian mechanics.

Morse and Feshbach developed the mirror system technique in the context of fluid mechanics, in which dissipation occurs due to viscous drag. However, given that we apply this technique to neuronal systems, the energy dissipation we estimate is instead a consequence of processes including synaptic activity at small scales and metabolic processes at larger scales. The mathematical expressions we use involve solving equations that describe the time evolution of neural states evolving in tailored phase space representations (Dezhina et al. 2023). The adaptation of the mirror approach to neuroscience allows us to explore the relationships between the energy that can be directly estimated from neuroimaging timeseries and the more commonly adopted measures of neural energy, such as glucose uptake metabolism.

One could of course conceive of alternative approaches with which to describe the energy of dissipative dynamics using Hamiltonian mechanics. For instance, we can look to the arguments applied in statistical mechanics in which one deals with a very large number of degrees of freedom. For example, if all air molecules start off in one corner of a room we would find that the molecules spread out and fill the room and that they do not return to their point of origin in the corner. There is, however, nothing in the laws of physics that prevents this from happening—the probability is just astronomically small. Following the same logic, we could conceive of a model in which a neural system is connected to a reservoir of a large number of surrounding regions. The system is described by a conventional Hamiltonian and the reservoir regions are described by simple harmonic oscillators, where energy can be transferred between regions. We then imagine that the system of interest begins with a certain amount of energy, with no energy in the reservoir. We would then find that energy gradually leaks out from the system into the reservoir and—given a sufficiently large reservoir—this energy does not return to the initial system. This is for the same reason that the air molecules do not return to the corner of the room—as long as there are enough reservoir oscillators, any energy that leaves the system of interest has such a small probability of returning that its dynamics are effectively dissipative. This construct has the benefit of being more 'physical' than the Morse and Feshbach mirror approach, as it is closer to the way in which nature actually creates dissipation. Furthermore, because simple harmonic oscillators are as their name suggests, simple, it may be possible to then 'integrate out' their influence to derive an isolated expression for the dissipative dynamics of the neural system of interest.

Our findings support those of the neural energy theory proposed in the Wang–Zhang (W–Z) model, in which the authors emphasize the coupling of neural information with neural energy (Wang et al. 2023).

It is our hope that future studies will develop non-invasive tools for studying brain energetics and identifying metabolic abnormalities in neurodegenerative and neuropsychiatric disorders. However, there are limitations when making inferences from neuroimaging timeseries by using mathematical techniques that were intended for mechanical oscillators rather than for neural systems. The transmission of neural signals in the mammalian cerebral cortex is metabolically expensive and the encoding of neural signals is closely coupled with biologically complex processes involving both oxygen and glucose production. However, simplified models such as the ones presented here are still valuable in opening new avenues for understanding the energetics of the brain and allowing for conceptual bridges to be built between the physical and biological disciplines. It is our hope that future work will benefit from our approach in more accurately modelling the dissipative, nonlinear, and interconnected processes characterizing neural function.

Appendix I

We next demonstrate two erroneous attempts at using Lagrangian mechanics to derive the energy of the system in Eq. (1).  These attempts illustrate the challenges involved and motivate the need for the mirror system approach.

Attempt 1—order augmentation To arrive at a Lagrangian for Eq. (1) we may find it easier to deal with a second-order differential equation, as these are commonly associated with Lagrangian mechanics. As such, we begin by differentiating Eq. (1) with respect to time:

$$\ddot{x}=-a\dot{x},$$

(16)

which, together with Eq. (1), means that:

$$\ddot{x}={a}^{2}x,$$

(17)

We can cast this in terms of the following Lagrangian $\mathcal{L}$:

$$\mathcal{L}=\frac{1}{2}\left({\dot{x}}^{2}+{a}^{2}{x}^{2}\right).$$

(18)

We can then verify that this is the correct Lagrangian form via the Euler–Lagrange equation:

$$\frac{d}{dt}\left( {\frac{{\partial {\mathcal{L}}}}{{\partial \dot{x}}}} \right) = \frac{{\partial {\mathcal{L}}}}{\partial x} \Rightarrow \ddot{x} = a^{2} x.$$

(19)

i.e., we recover the second-order equation of motion in Eq. (16).

To obtain the energy $E$, we then use the Legendre transform:

$$\begin{aligned} E & = \frac{{\partial {\mathcal{L}}}}{{\partial \dot{x}}}\dot{x} - {\mathcal{L}} \\ & = \frac{1}{2}\left( {\dot{x}^{2} - a^{2} x^{2} } \right) \\ \end{aligned}$$

(20)

However, there is a problem with this expression, as it does not actually apply to the original equation of motion in Eq. (1), other than the trivial case in which $E=0$ at all times. The reason for this is that although every solution of Eq. (1) is also a solution of Eq. $\left(2\right)$, the reverse is not true. In other words, the energy we derive applies only to the second-order equation of motion, but not to the original first-order equation of motion. We can therefore disregard this first attempt as an invalid approach to describing the energy of a dissipative system such as Eq. (1). The problems inherent in this approach are circumvented by the mirror system technique which does not involve order augmentation of the original first-order system.

Attempt 2—complex variables Another approach (Fagerholm et al. 2021) to describing the energy of Eq. (1) is to rewrite the equation of motion using a complex variable $z\left(t\right)$ and to introduce an imaginary unit on the left-hand side:

$$i\dot{z}=-\sqrt{a}z.$$

(21)

The associated Lagrangian is then given by:

$$\mathcal{L}=\frac{i}{2}\left({z}^{*}\dot{z}-z{\dot{z}}^{*}\right)+\sqrt{a}z{z}^{*}$$

(22)

where ${z}^{*}$ is the complex conjugate of $z$. We can verify this Lagrangian form via the Euler–Lagrange equations:

$$\begin{gathered} \frac{d}{dt}\left( {\frac{{\partial {\mathcal{L}}}}{{\partial \dot{z}^{*} }}} \right) = \frac{{\partial {\mathcal{L}}}}{{\partial z^{*} }} \Rightarrow i\dot{z} = - \sqrt a z. \hfill \\ \frac{d}{dt}\left( {\frac{{\partial {\mathcal{L}}}}{{\partial \dot{z}}}} \right) = \frac{{\partial {\mathcal{L}}}}{\partial z} \Rightarrow i\dot{z}^{*} = \sqrt a z^{*} . \hfill \\ \end{gathered}$$

(23)

i.e., we recover the equation of motion in Eq. (21) together with its adjoint.

The energy $E$ is then obtained from Eq. (21) with the Legendre transform:

$$\begin{aligned} E & = \frac{{\partial {\mathcal{L}}}}{{\partial \dot{z}}}\dot{z} + \frac{{\partial {\mathcal{L}}}}{{\partial \dot{z}^{*} }}\dot{z}^{*} - {\mathcal{L}} \\ & = - \sqrt a zz^{*} \\ \end{aligned}$$

(24)

This expression applies to the original equation of motion in Eq. (21) and we might think that we have therefore successfully described the energy of a first-order equation of motion. However, this is not the case.

To see why, let us re-write Eq. (21) by writing out the complex variable in terms of its real and imaginary components according to $z\triangleq x+iy$:

$$i\left(\dot{x}+i\dot{y}\right)=-\sqrt{a}\left(x+iy\right)$$

(25)

for which we can equate the real and imaginary components, such that:

$$\begin{aligned} \dot{y} & = \sqrt a x \\ \dot{x} & = - \sqrt a y \\ \end{aligned}$$

(26)

i.e., beginning with Eq. (21) we obtain two coupled first-order equations that can be re-written as a single second-order system:

$$\dot{y} = \sqrt a x = - \frac{1}{{\sqrt a }}\ddot{x}~~ \Rightarrow ~\ddot{x} = - ax$$

(27)

i.e., we find that the first-order system in Eq. (21) was in fact just the second-order system in Eq. (27) all along, just disguised by virtue of the two degrees of freedom afforded by the use of a complex variable. We therefore face the same issue as in the first attempt at describing the energy of the dissipative system in Eq. (1). The problems inherent in this approach are circumvented by the mirror system technique which does not involve the use of complex variables.