On K-stability of $\mathbb {P}^3$ blown up along a quintic elliptic curve

Abstract

In this note, we study K-stability of smooth Fano threefolds that can be obtained by blowing up the three-dimensional projective space along a smooth elliptic curve of degree five.

Let $C_5$ be a smooth quintic elliptic curve in $\mathbb {P}^3$, and let $\pi :X\rightarrow \mathbb {P}^3$ be the blow up of this curve. Then X is a smooth Fano threefold in the family No 2.17, and every smooth Fano 3-fold in this family can be obtained by blowing up $\mathbb {P}^3$ along a suitable smooth quintic elliptic curve.

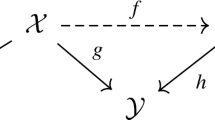
It is well known that there exists the following Sarkisov link:

where Q is a smooth quadric threefold in $\mathbb {P}^4$, and q is the blow up of a smooth quintic elliptic curve $C_5^\prime$. Let $E_{\mathbb {P}^3}$ and $E_Q$ be the exceptional divisors of $\pi$ and q, respectively. If $\ell$ is a general fiber of the natural projection $E_{\mathbb {P}^3}\rightarrow C_5$, then $q(\ell )$ is a secant of the curve $C_5^\prime$ contained in Q. Similarly, if $\ell ^\prime$ is a general fiber of the projection $E_Q\rightarrow C_5^\prime$, then $\pi (\ell ^\prime )$ is a trisecant of the curve $C_5$.

FormalPara Example 1

Let $\mathcal {E}$ be the harmonic elliptic curve, and let $\theta$ be an element in $\textrm{Aut}(\mathcal {E})$ of order 4 that fixes a point $P\in C_5$. Then it follows from [9] that

$$\begin{aligned} \textrm{Aut}\big (\mathcal {E},[5P]\big )\cong \varvec{\mu }_5^2\rtimes \varvec{\mu }_4, \end{aligned}$$

and there exists an $\textrm{Aut}(\mathcal {E},[5P])$-equivariant embedding $\phi :\mathcal {E}\hookrightarrow \mathbb {P}^4$ such that $\phi (\mathcal {E})$ is a smooth quintic elliptic curve. Let G be a subgroup in $\textrm{Aut}(\mathcal {E},[5P])$ such that $G\cong \varvec{\mu }_5\rtimes \varvec{\mu }_4$. Then G fixes a unique point in $\mathbb {P}^4$ that is not contained in the hypersurface spanned by the secants of the quintic curve $\phi (\mathcal {E})$. Let $\psi :\mathbb {P}^4\dasharrow \mathbb {P}^3$ be the projection from this point. Then $\psi \circ \phi (\mathcal {E})$ is a smooth quintic elliptic curve. Let $C_5=\psi \circ \phi (\mathcal {E})$. Then $\textrm{Aut}(X)\cong \varvec{\mu }_5\rtimes \varvec{\mu }_4$, and X is K-stable [2, Section 5.7]

Since being K-stable is an open condition, a general member of the family No 2.17 is K-stable. In fact, all smooth Fano threefolds in the deformation family No 2.17 are expected to be K-stable [2]. To show this it is enough to prove that $\beta (\textbf{F})=A_X(\textbf{F})-S_X(\textbf{F})>0$ for every prime divisor $\textbf{F}$ over the Fano threefold X [7, 10], where $A_X(\textbf{F})$ is the log discrepancy of the divisor $\textbf{F}$, and

$$\begin{aligned} S_X\big (\textbf{F}\big )=\frac{1}{(-K_X)^3}\int \limits _0^{\infty }\textrm{vol}\big (-K_X-u\textbf{F}\big )du. \end{aligned}$$

Unfortunately, we are unable to prove this. Instead, we prove the following weaker result:

FormalPara MainTheorem

Let $\textbf{F}$ be a prime divisor over X such that $\beta (\textbf{F})\leqslant 0$, let Z be its center on X. Then Z is a point in $E_{\mathbb {P}^3}\cap E_Q$.

By [13, Corollary 4.14], the Main Theorem implies the following corollary.

FormalPara Corollary 2

Suppose that $\textrm{Aut}(\mathbb {P}^3,C_5)$ does not fix a point in $C_5$. Then X is K-stable.

Observe that $\textrm{Aut}(X)\cong \textrm{Aut}(\mathbb {P}^3,C_5)$, and all possibilities for the group $\textrm{Aut}(\mathbb {P}^3,C_5)$ can be easily derived from [9]. Namely, if $C_5$ is general, then $\textrm{Aut}(\mathbb {P}^3,C_5)$ is trivial, so Corollary 2 is not applicable. If $\textrm{Aut}(\mathbb {P}^3,C_5)$ is not trivial, then it must be isomorphic to one of the following finite groups:

$$\begin{aligned}\varvec{\mu }_5\rtimes \varvec{\mu }_4, \varvec{\mu }_5\rtimes \varvec{\mu }_2, \varvec{\mu }_6, \varvec{\mu }_5, \varvec{\mu }_4, \varvec{\mu }_2.\end{aligned}$$

Furthermore, if $\textrm{Aut}(\mathbb {P}^3,C_5)$ contains a subgroup isomorphic to $\varvec{\mu }_5$, it acts on $C_5$ by translations. This implies that $\textrm{Aut}(\mathbb {P}^3,C_5)$ does not fix a point in $C_5$ $\iff$ $\textrm{Aut}(\mathbb {P}^3,C_5)$ contains a subgroup isomorphic to $\varvec{\mu }_5$. Therefore, Corollary 2 gives the following generalization of Example 1.

FormalPara Corollary 3

Suppose that $\textrm{Aut}(X)$ contains a subgroup isomorphic to $\varvec{\mu }_5$. Then X is K-stable.

FormalPara Example 4

([9]) Fix $a\in \mathbb {C}$ such that $a\ne 0$ and $a^{10}+11a^5-1\ne 0$. Let $C_5^\prime$ be the quintic elliptic curve in $\mathbb {P}^4$ given by the following system of equations:

$$\begin{aligned} \left\{ \begin{aligned}&x_0^2+ax_2x_3-\frac{x_1x_4}{a}=0,\\&x_1^2+ax_3x_4-\frac{x_2x_0}{a}=0,\\&x_2^2+ax_4x_0-\frac{x_3x_1}{a}=0,\\&x_3^2+ax_0x_1-\frac{x_4x_2}{a}=0,\\&x_4^2+ax_1x_2-\frac{x_0x_3}{a}=0, \end{aligned} \right. \end{aligned}$$

where $[x_0:x_1:x_2:x_3:x_4]$ are coordinates on $\mathbb {P}^4$. Let $\sigma$, $\tau$, $\iota$ be the automorphisms of $\mathbb {P}^4$ given by

$$\begin{aligned} \sigma \big ([x_0:x_1:x_2:x_3:x_4]\big )&=[x_1:x_2:x_3:x_4:x_0],\\ \tau \big ([x_0:x_1:x_2:x_3:x_4]\big )&=[x_0:\omega _5x_1:\omega _5^2x_2:\omega _5^3x_3:\omega _5^4x_4],\\ \iota \big ([x_0:x_1:x_2:x_3:x_4]\big )&=[x_0:x_4:x_3:x_2:x_1], \end{aligned}$$

where $\omega _5$ is a primitive fifth root of unity. Set $G=\langle \sigma ,\tau ,\iota \rangle$. Then $G\cong \varvec{\mu }_5^2\rtimes \varvec{\mu }_2$, and $C_5^\prime$ is G-invariant. Consider the following quadric hypersurface:

$$\begin{aligned} Q=\Big \{x_0^2+ax_2x_3-\frac{x_1x_4}{a}=0\Big \}\subset \mathbb {P}^4. \end{aligned}$$

Observe that Q is smooth, and Q is $\langle \tau ,\iota \rangle$-invariant. Let $q:X\rightarrow Q$ be the blow up of the curve $C_5^\prime$. Then we have $\langle \tau ,\iota \rangle$-equivariant Sarkisov link ($\bigstar$) for an appropriate non-singular quintic elliptic curve $C_5\subset \mathbb {P}^3$. Since $\langle \tau ,\iota \rangle \cong \varvec{\mu }_5\rtimes \varvec{\mu }_2$, X is K-stable by Corollary 3.

Let $\Bbbk$ be a subfield in $\mathbb {C}$ such that $C_5$ is defined over $\Bbbk$. Then the Sarkisov link ($\bigstar$) is also defined over the field $\Bbbk$. Moreover, the Main Theorem and [13, Corollary 4.14] imply the following result.

FormalPara Corollary 5

If the intersection $E_{\mathbb {P}^3}\cap E_Q$ does not have $\Bbbk$-points, then X is K-stable.

FormalPara Corollary 6

If $C_5(\Bbbk )=\varnothing$ or $C_5^\prime (\Bbbk )=\varnothing$, then X is K-stable.

In fact, one can show that $C_5(\Bbbk )=\varnothing$ if and only if $C_5^\prime (\Bbbk )=\varnothing$.

Corollary 6 has many applications. For instance, if $\Bbbk$ is a number field, there are infinitely many smooth quintic genus one curves in $\mathbb {P}^3$ defined over $\Bbbk$ that do not have $\Bbbk$-rational points [3, 4, 11]. Thus, using Corollary 6 and Pfaffian representations of quintic elliptic curves [5], one can construct infinitely many explicit examples of K-stable smooth Fano threefolds in the family No 2.17.

FormalPara Example 7

(T. Fisher) Fix a prime $p\geqslant 2$. Let $C_5^\prime$ be the quintic elliptic curve in $\mathbb {P}^4$ given by

$$\begin{aligned} \left\{ \begin{aligned}&x_0^2+px_1x_4-px_2x_3=0,\\&x_1^2+x_0x_2-px_3x_4=0,\\&x_2^2+x_1x_3-x_0x_4=0,\\&px_3^2+px_2x_4-x_0x_1=0,\\&px_4^2+x_0x_3-x_1x_2=0, \end{aligned} \right. \end{aligned}$$

let Q be the quadric $\{x_0^2+px_1x_4-px_2x_3=0\}$, and let $q:X\rightarrow Q$ be the blow up along the curve $C_5^\prime$, where $[x_0:x_1:x_2:x_3:x_4]$ are the coordinates on $\mathbb {P}^4$. Then ($\bigstar$) exists for an appropriate quintic elliptic curve $C_5\subset \mathbb {P}^3$. We can set $\Bbbk =\mathbb {Q}$. Then $C_5^\prime (\Bbbk )=\varnothing$, so X is K-stable by Corollary 6.

Let us prove the Main Theorem. Let $\textbf{F}$ be a prime divisor over X, and let Z be its center on X. Suppose that Z is not a point in $E_{\mathbb {P}^3}\cap E_Q$. Let us show that $\beta (\textbf{F})>0$.

If Z is a surface, then it follows from [6] that $\beta (\textbf{F})>0$. Thus, we may assume that

• either Z is a point,

• or Z is an irreducible curve.

Let P be any point in Z. Choose an irreducible smooth surface $S\subset X$ such that $P\in S$. Set

$$\begin{aligned} \tau =\textrm{sup}\Big \{u\in \mathbb {Q}_{\geqslant 0}\ \big \vert \ \text {the divisor } -K_X-uS \text { is pseudo-effective}\Big \}. \end{aligned}$$

For $u\in [0,\tau ]$, let P(u) be the positive part of the Zariski decomposition of the divisor $-K_X-uS$, and let N(u) be its negative part. Then $\beta (S)=1-S_X(S)$, where

$$\begin{aligned} S_X(S)=\frac{1}{-K_X^3}\int \limits _{0}^{\infty }\textrm{vol}\big (-K_X-uS\big )du=\frac{1}{24}\int \limits _{0}^{\tau }P(u)^3du. \end{aligned}$$

Let us show how to compute P(u) and N(u). Set $H_{\mathbb {P}^3}=\pi ^*(\mathcal {O}_{\mathbb {P}^3}(1))$ and $H_{Q}=q^*(\mathcal {O}_{Q}(1))$. Then

$$\begin{aligned} H_{\mathbb {P}^3}&\sim 2H_{Q}-E_{Q},&H_{Q}&\sim 3H_{\mathbb {P}^3}-E_{\mathbb {P}^3},\\ E_{\mathbb {P}^3}&\sim 5H_{Q}-3E_{Q},&E_{Q}&\sim 5H_{\mathbb {P}^3}-2E_{\mathbb {P}^3}. \end{aligned}$$

Let us compute P(u) and N(u) in the following cases: $S\in |H_{\mathbb {P}^3}|$, $S\in |H_{Q}|$, and $S=E_{\mathbb {P}^3}$.

FormalPara Example 8

Suppose that $S\in |H_{\mathbb {P}^3}|$. Then $\tau =\frac{3}{2}$, since $-K_{X}-uS\sim _{\mathbb {R}}\frac{3-2u}{2}S+\frac{1}{2}E_{Q}$. Based on that, the positive part of the Zariski decomposition has the following form

$$\begin{aligned} P(u)\sim _{\mathbb {R}} \left\{ \begin{aligned}&(4-u)H_{\mathbb {P}^3}-E_{\mathbb {P}^3} \ \text { for } 0\leqslant u\leqslant 1, \\&(3-2u)H_{Q}\ \text { for } 1\leqslant u\leqslant \frac{3}{2}, \end{aligned} \right. \end{aligned}$$

and the negative part

$$\begin{aligned} N(u)= \left\{ \begin{aligned}&0\ \text { for } 0\leqslant u\leqslant 1, \\&(u-1)E_{Q}\ \text { for } 1\leqslant u\leqslant \frac{3}{2}, \end{aligned} \right. \end{aligned}$$

which gives

$$\begin{aligned} S_{X}(S){} & {} =\frac{1}{24}\int \limits _{0}^{\frac{3}{2}}\big (P(u)\big )^3du=\frac{1}{24}\int \limits _0^{1}24-u^3+12u^2-33udu \\{} & {} \quad \ +\frac{1}{24}\int \limits _{1}^{\frac{3}{2}}2(3-2u)^3du=\frac{23}{48}. \end{aligned}$$

FormalPara Example 9

Suppose that $S\in |H_{Q}|$. Then $-K_{X}-uS\sim _{\mathbb {R}} \frac{4-3u}{3}S+\frac{1}{3}E_{\mathbb {P}^3}$. Then $\tau =\frac{4}{3}$,

$$\begin{aligned} P(u)\sim _{\mathbb {R}} \left\{ \begin{aligned}&(3-u)H_Q-E_Q \ \text { for } 0\leqslant u\leqslant 1, \\&(4-3u)H_{\mathbb {P}^3}\ \text { for } 1\leqslant u\leqslant \frac{4}{3}, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} N(u)= \left\{ \begin{aligned}&0\ \text { for } 0\leqslant u\leqslant 1, \\&(u-1)E_{\mathbb {P}^3}\ \text { for } 1\leqslant u\leqslant \frac{4}{3}, \end{aligned} \right. \end{aligned}$$

which gives

$$\begin{aligned} S_{X}(S)=\frac{1}{24}\int \limits _0^{1}24-2u^3+18u^2-39udu+\frac{1}{24}\int \limits _{1}^{\frac{4}{3}}(4-3u)^3du=\frac{121}{288}. \end{aligned}$$

FormalPara Example 10

Suppose that $S=E_{\mathbb {P}^3}$. Then $-K_{X}-uS\sim _{\mathbb {R}} \frac{3-5u}{5}E_{\mathbb {P}^{3}}+\frac{4}{5}E_{Q}$. Then $\tau =\frac{3}{5}$,

$$\begin{aligned} P(u)\sim _{\mathbb {R}} \left\{ \begin{aligned}&4H_{\mathbb {P}^3}-(1+u)E_{\mathbb {P}^3} \ \text { for } 0\leqslant u\leqslant \frac{1}{3}, \\&(3-5u)H_{Q}\ \text { for } \frac{1}{3}\leqslant u\leqslant \frac{3}{5}, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} N(u)= \left\{ \begin{aligned}&0\ \text { for } 0\leqslant u\leqslant \frac{1}{3}, \\&(3u-1)E_{Q}\ \text { for } \frac{1}{3}\leqslant u\leqslant \frac{3}{5}, \end{aligned} \right. \end{aligned}$$

which gives

$$\begin{aligned} S_{X}(S)=\frac{1}{24}\int \limits _0^{\frac{1}{3}}20u^3-60u+24du+\frac{1}{24}\int \limits _{\frac{1}{3}}^{\frac{3}{5}}2(3-5u)^3du=\frac{227}{1080}. \end{aligned}$$

Now, we choose an irreducible curve $C\subset S$ that contains the point P. For instance, if Z is a curve, and S contains Z, then we can choose $C=Z$. Since $S\not \subset \textrm{Supp}(N(u))$, we can write

$$\begin{aligned} N(u)\big \vert _S=d(u)C+N^\prime (u), \end{aligned}$$

where $N^\prime (u)$ is an effective $\mathbb {R}$-divisor on S such that $C\not \subset \textrm{Supp}(N^\prime (u))$, and $d(u)=\textrm{ord}_C(N(u)\vert _S)$. Now, for every $u\in [0,\tau ]$, we set

$$\begin{aligned} t(u)=\sup \Big \{v\in \mathbb R_{\geqslant 0} \ \big |\ \text {the divisor }P(u)\big |_S-vC \text { is pseudo-effective}\Big \}. \end{aligned}$$

For $v\in [0, t(u)]$, we let P(u, v) be the positive part of the Zariski decomposition of $P(u)|_S-vC$, and we let N(u, v) be its negative part. Following [1, 2], we let

$$\begin{aligned} S\big (W^S_{\bullet ,\bullet };C\big ){} & {} =\frac{3}{(-K_X)^3}\int \limits _0^{\tau }d(u)\Big (P(u)\big \vert _{S}\Big )^2du \\{} & {} \quad \ +\frac{3}{(-K_X)^3}\int \limits _0^\tau \int \limits _0^{\infty }\textrm{vol}\big (P(u)\big \vert _{S}-vC\big )dvdu, \end{aligned}$$

which we can rewrite as

$$\begin{aligned} S\big (W^S_{\bullet ,\bullet };C\big )=\frac{3}{(-K_X)^3}\int \limits _0^{\tau }d(u)\big (P(u,0)\big )^2du+\frac{3}{(-K_X)^3}\int \limits _0^\tau \int \limits _0^{t(u)}\big (P(u,v)\big )^2dvdu. \end{aligned}$$

If Z is a curve, $Z\subset S$ and $C=Z$, then it follows from [1, 2] that

$$\begin{aligned} \frac{A_X(\textbf{F})}{S_X(\textbf{F})}\geqslant \min \Bigg \{\frac{1}{S_X(S)},\frac{1}{S\big (W^S_{\bullet ,\bullet };C\big )}\Bigg \}. \end{aligned}$$

(1)

Hence, if Z is a curve, $Z\subset S$, $C=Z$ and $S(W^S_{\bullet ,\bullet };C)<1$, then $\beta (\textbf{F})>0$, since $S_X(S)<1$ by [6].

FormalPara Lemma 11

Suppose that Z is a curve, $Z\subset E_{\mathbb {P}^3}$, and $\pi (Z)$ is not a point. Then $\beta (\textbf{F})>0$.

FormalPara Proof

Let e be the invariant of the ruled surface $E_{\mathbb {P}^3}$ defined in Proposition 2.8 in [8, Chapter V]. Then $e\geqslant -1$ by [12]. Moreover, there is a section $C_{0}$ of the projection $E_{\mathbb {P}^3}\rightarrow C_5$ such that $C_0^2=-e$. Let $\ell$ be a fiber of this projection. Then $H_{\mathbb {P}^{3}}\vert _{E_{\mathbb {P}^3}}\equiv 5\ell$ and $E_{\mathbb {P}^3}\vert _{E_{\mathbb {P}^3}}\equiv -C_{0} + \lambda \ell$ for some $\lambda \in \mathbb {Z}$. Since

$$\begin{aligned} -20=-c_{1}\big (N_{C_5/\mathbb {P}^{3}}\big )=E_{\mathbb {P}^3}^{3}=(-C_{0}+\lambda \ell )^{2}=-e -2\lambda , \end{aligned}$$

we get $\lambda =\frac{20-e}{2}$. Then e is even, so $e\geqslant 0$. Moreover, since $3H_{\mathbb {P}^3}-E_{\mathbb {P}^3}\sim H_{Q}$ is nef, the divisor

$$\begin{aligned} \big (3H_{\mathbb {P}^{3}}-E_{\mathbb {P}^{3}}\big )\big \vert _{E_{\mathbb {P}^{3}}}\equiv C_{0}+(15-\lambda )\ell \end{aligned}$$

is also nef. Then $0\leqslant \big ( C_{0}+(15-\lambda )\ell \big )\cdot C_{0} = 15 - e - \lambda = 15 - e - \frac{20-e}{2}$, which implies $e\leqslant 10$ and hence we have $e\in \{0,2,4,6,8,10\}$.

Now, we set $S=E_{\mathbb {P}^{3}}$ and $C=Z$. Using (1), we see that to prove that $\beta (\textbf{F})>0$, it is enough to show that $S(W^S_{\bullet ,\bullet };C)<1$. Let us estimate $S(W^S_{\bullet ,\bullet };C)$. It follows from Example 10 that $\tau =\frac{3}{5}$ and

$$\begin{aligned} P(u)\big \vert _{S}\equiv \left\{ \begin{aligned}&(1+u)C_{0}+\bigg (10+\frac{1}{2}e+\frac{1}{2}ue-10u\bigg )\ell \ \text { for } 0\leqslant u \leqslant \frac{1}{3}, \\&(3-5u)C_{0}+\bigg (15+\frac{3}{2}e-25u- \frac{5}{2}ue \bigg )\ell \ \text { for } \frac{1}{3} \leqslant u\leqslant \frac{3}{5}. \end{aligned} \right. \end{aligned}$$

Moreover, if $0\leqslant u \leqslant \frac{1}{3}$, then $N(u)=0$. Furthermore, if $\frac{1}{3} \leqslant u\leqslant \frac{3}{5}$, then

$$\begin{aligned} N(u)\big \vert _{S}=(3u-1)E_Q\big \vert _{S}, \end{aligned}$$

and $E_Q\big \vert _{S}\equiv 2C_0+(5+e)\ell$. But it follows from Proposition 2.20 in [8, Chapter V] that

$$\begin{aligned} Z\equiv aC_{0} + b\ell \end{aligned}$$

for some integers a and b such that $a\geqslant 0$ and $b\geqslant ae$. Since $\pi (Z)$ is not a point, we also have $a\geqslant 1$. This gives $\textrm{ord}_{C}(E_Q\vert _{S})\leqslant 2$. Hence, if $\frac{1}{3} \leqslant u\leqslant \frac{3}{5}$, then $d(u)\leqslant 2(3u-1)$. This gives

$$\begin{aligned} S(W_{\bullet ,\bullet }^{{S}};{C})= & {} \frac{3}{24}\int \limits _{\frac{1}{3}}^{\frac{3}{5}}d(u)\Big (P(u)\big \vert _{S}\Big )^2du+ \frac{3}{24}\int \limits _0^{\frac{3}{5}}\int \limits _0^\infty \textrm{vol}\big (P(u)\big \vert _{{S}}-v{C}\big )dvdu \\{} & {} \leqslant \frac{3}{24}\int \limits _{\frac{1}{3}}^{\frac{3}{5}}2(3u-1)\Big (P(u)\big \vert _{S}\Big )^2du+ \frac{3}{24}\int \limits _0^{\frac{3}{5}}\int \limits _0^\infty \textrm{vol}\big (P(u)\big \vert _{{S}}-v{C}\big )dvdu \\{} & {} =\frac{3}{24}\int \limits _{\frac{1}{3}}^{\frac{3}{5}}2(3u-1)(250u^2-300u+90)du \\{} & {} \quad \ + \frac{3}{24}\int \limits _0^{\frac{3}{5}}\int \limits _0^\infty \textrm{vol}\big (P(u)\big \vert _{{S}}-v{C}\big )dvdu \\{} & {} =\frac{32}{405}+\frac{3}{24}\int \limits _0^{\frac{3}{5}}\int \limits _0^\infty \textrm{vol}\big (P(u)\big \vert _{{S}}-v{C}\big )dvdu\\{} & {} =\frac{32}{405}+\frac{3}{24}\int \limits _0^{\frac{3}{5}}\int \limits _0^\infty \textrm{vol}\big (P(u)\big \vert _{{S}}-v(aC_{0} + b\ell )\big )dvdu. \end{aligned}$$

On the other hand, since $a\geqslant 1$, we have

$$\begin{aligned} \frac{3}{24}\int \limits _0^{\frac{3}{5}}\int \limits _0^\infty \textrm{vol}\big (P(u)\big \vert _{{S}}-v(aC_{0}+b\ell )\big )dvdu\leqslant \frac{3}{24}\int \limits _0^{\frac{3}{5}}\int \limits _0^\infty \textrm{vol}\big (P(u)\big \vert _{{S}}-vC_{0}\big )dvdu, \end{aligned}$$

Therefore, to show that $S(W^S_{\bullet ,\bullet };C)<1$, we may assume that $Z=C_0$. Then

$$\begin{aligned} t(u)=\left\{ \begin{aligned}&1+u\ \text { for } 0\leqslant u\leqslant \frac{1}{3}, \\&3-5u\ \text { for } \frac{1}{3}\leqslant u\leqslant \frac{3}{5}. \end{aligned} \right. \end{aligned}$$

Moreover, if $0 \leqslant u \leqslant \frac{1}{3}$ and $v\in [0,t(u)]$, then

$$\begin{aligned} P(u,v)=(1+u-v)C_{0}+ \bigg (10+\frac{1}{2}e+\frac{1}{2}ue-10u \bigg )\ell \end{aligned}$$

and the negative part N(u, v) is trivial. Similarly, if $\frac{1}{3}\leqslant u \leqslant \frac{3}{5}$ and $v\in [0,t(u)]$, then

$$\begin{aligned} P(u,v)=(3-5u-v)C_{0}+\bigg (15+\frac{3}{2}e-25u- \frac{5}{2}ue \bigg )\ell \end{aligned}$$

and the negative part N(u, v) is trivial. Using the collected data, we compute

$$\begin{aligned}{} & {} \frac{3}{24}\int \limits _0^{\frac{3}{5}}\int \limits _0^\infty \textrm{vol}\big (P(u)\big \vert _{{S}}-vC_{0}\big )dvdu=\frac{3}{24}\int \limits _0^{\frac{3}{5}}\int \limits _0^{t(u)}\big (P(u,v)\big )^2dvdu\\{} & {} \quad =\frac{3}{24}\int \limits _{0}^{\frac{1}{3}}\int \limits _{0}^{u+1}\bigg (20+(e-20)v-20u^2-ev^2+(e+20)vu\bigg )dvdu\\{} & {} \quad +\frac{3}{24}\int \limits _{\frac{1}{3}}^{\frac{3}{5}}\int \limits _{0}^{3-5u}\bigg ( 90-300u+(3e-30)v+250u^2-ev^2 +(-5e+50)vu\bigg )dvdu\\{} & {} \quad =\frac{377e}{25920}+\frac{733}{1296}. \end{aligned}$$

As explained above, this gives

$$\begin{aligned} S(W_{\bullet ,\bullet }^{{S}};{C})\leqslant \frac{32}{405}+\frac{3}{24}\int \limits _0^{\frac{3}{5}}\int \limits _0^\infty \textrm{vol}\big (P(u)\big \vert _{{S}}-vC_{0})\big )dvdu=\frac{377e}{25920} + \frac{4177}{6480}. \end{aligned}$$

Since $e \in \{0,2,4,6,8,10\}$, we conclude that $S(W_{\bullet ,\bullet }^{{S}};{C})<1$. Then $\beta (\textbf{F})>0$ by (1). $\square$

Let $f:\widetilde{S}\rightarrow S$ be the blow up of the point P, and let F be the f-exceptional curve. Write

$$\begin{aligned} f^*\big (N(u)\big \vert _S\big )=\widetilde{d}(u)F+\widetilde{N}^\prime (u), \end{aligned}$$

where $\widetilde{N}^\prime (u)$ is the strict transform of the divisor $N(u)\vert _{S}$ on the surface $\widetilde{S}$, and $\widetilde{d}(u)=\textrm{mult}_P(N(u)\vert _S)$. For every $u\in [0,\tau ]$, we set

$$\begin{aligned} \widetilde{t}(u)=\sup \Big \{v\in \mathbb R_{\geqslant 0} \ \big |\ \text {the divisor }f^*\big (P(u)\big |_S\big )-vF \text { is pseudo-effective}\Big \}. \end{aligned}$$

For $v\in [0,\widetilde{t}(u)]$, we let $\widetilde{P}(u,v)$ be the positive part of the Zariski decomposition of $f^*(P(u)|_S)-vF$, and we let $\widetilde{N}(u,v)$ be its negative part. As above, we let

$$\begin{aligned} S\big (W^S_{\bullet ,\bullet };F\big ){} & {} =\frac{3}{(-K_X)^3}\int \limits _0^{\tau }\widetilde{d}(u)\Big (P(u)\big \vert _{S}\Big )^2du \\{} & {} \quad \ + \frac{3}{(-K_X)^3}\int \limits _0^\tau \int \limits _0^{\infty }\textrm{vol}\big (f^*\big (P(u)\big |_S\big )-vF\big )dvdu, \end{aligned}$$

which we can rewrite as

$$\begin{aligned} S\big (W^S_{\bullet ,\bullet };F\big )=\frac{3}{(-K_X)^3}\int \limits _0^{\tau }\widetilde{d}(u)\big (P(u,0)\big )^2du+ \frac{3}{(-K_X)^3}\int \limits _0^\tau \int \limits _0^{\widetilde{t}(u)}\big (\widetilde{P}(u,v)\big )^2dvdu. \end{aligned}$$

For every point $O\in F$, we let

$$\begin{aligned} F_O\big (W_{\bullet ,\bullet ,\bullet }^{\widetilde{S},F}\big )=\frac{6}{(-K_X)^3} \int \limits _0^\tau \int \limits _0^{\widetilde{t}(u)}\big (\widetilde{P}(u,v)\cdot F\big )\cdot \textrm{ord}_O\big (\widetilde{N}^\prime (u)\big |_F+\widetilde{N}(u,v)\big |_F\big )dvdu, \end{aligned}$$

and

$$\begin{aligned} S\big (W_{\bullet , \bullet ,\bullet }^{\widetilde{S},F};O\big )=\frac{3}{(-K_X)^3}\int \limits _0^\tau \int \limits _0^{\widetilde{t}(u)}\big (\widetilde{P}(u,v)\cdot F\big )^2dvdu+F_O\big (W_{\bullet ,\bullet ,\bullet }^{\widetilde{S},F}\big ). \end{aligned}$$

Then it follows from [1, 2] that

$$\begin{aligned} \frac{A_{X}(\textbf{F})}{S_X(\textbf{F})}\geqslant \min \Bigg \{\frac{1}{S_X({S})},\frac{2}{S\big (W^{S}_{\bullet ,\bullet };F\big )},\inf _{O\in F}\frac{1}{S\big (W_{\bullet , \bullet ,\bullet }^{\widetilde{S},F};O\big )}\Bigg \}. \end{aligned}$$

(2)

In the next two lemmas, we show how to apply this inequality to prove that $\beta (\textbf{F})>0$ under certain generality conditions on the position of the point P.

FormalPara Lemma 12

Let S be a general surface in $|H_{\mathbb {P}^3}|$ such that $P\in S$. Suppose $P\not \in E_{\mathbb {P}^3}$, $-K_S$ is ample, and P is not contained in a $(-1)$-curve in S. Then $\beta (\textbf{F})>0$.

FormalPara Proof

Observe that $\pi (S)$ is a general plane in $\mathbb {P}^3$ that contains $\pi (P)$, and $\pi$ induces a birational morphism $\varpi :S\rightarrow \pi (S)$ that blows up the points $\pi (S)\cap C_5$. Let $\textbf{e}_1$, $\textbf{e}_2$, $\textbf{e}_3$, $\textbf{e}_4$, $\textbf{e}_5$ be the $\varpi$-exceptional curves. Then $E_{\mathbb {P}^3}\big \vert _{S}=\textbf{e}_1+\textbf{e}_2+\textbf{e}_3+\textbf{e}_4+\textbf{e}_5$.

Let $L=H_{\mathbb {P}^3}\vert _{S}$. For $i\in \{1,2,3,4,5\}$, the pencils $|L-\textbf{e}_i|$ and $|2L+\textbf{e}_i-\textbf{e}_1-\textbf{e}_2-\textbf{e}_3-\textbf{e}_4-\textbf{e}_5|$ contain an irreducible curve that passes through the point P. Denote these curves by $\mathscr {Z}_i$ and $\mathscr {Z}_i^\prime$, respectively. Then $\varpi (\mathscr {Z}_i)$ is the line in $\pi (S)$ that passes through $\pi (P)$ and $\varpi (\textbf{e}_i)$, and $\varpi (\mathscr {Z}_i^\prime )$ is the conic that passes through $\pi (P)$ and all points among $\varpi (\textbf{e}_1)$, $\varpi (\textbf{e}_2)$, $\varpi (\textbf{e}_3)$, $\varpi (\textbf{e}_4)$, $\varpi (\textbf{e}_5)$ except for $\varpi (\textbf{e}_i)$. Set

$$\begin{aligned} \mathscr {Z}&=\sum _{i=1}^{5}\mathscr {Z}_i\sim 5L-(\textbf{e}_1+\textbf{e}_2+\textbf{e}_3+\textbf{e}_4+\textbf{e}_5),\\ \mathscr {Z}^\prime&=\sum _{i=1}^{5}\mathscr {Z}_i^\prime \sim 10L-4(\textbf{e}_1+\textbf{e}_2+\textbf{e}_3+\textbf{e}_4+\textbf{e}_5). \end{aligned}$$

Let $\widetilde{\mathscr {Z}}$ and $\widetilde{\mathscr {Z}}^\prime$ be the proper transforms on $\widetilde{S}$ of the curves $\mathscr {Z}$ and $\mathscr {Z}^\prime$, respectively. On the surface $\widetilde{S}$, we have $\widetilde{\mathscr {Z}}\cdot \widetilde{\mathscr {Z}}^\prime =F\cdot \widetilde{\mathscr {Z}}=F\cdot \widetilde{\mathscr {Z}}^\prime =5$ and $\widetilde{\mathscr {Z}}^{2}=(\widetilde{\mathscr {Z}}^\prime )^{2}=-5$. Using Example 8, we get $\tau =\frac{3}{2}$ and

$$\begin{aligned} f^{*}\big (P(u)\big \vert _{S}\big )-vF \sim _{\mathbb {R}}\left\{ \begin{aligned}&\frac{3-2u}{5}\widetilde{\mathscr {Z}}+\frac{1+u}{10}\widetilde{\mathscr {Z}}^\prime +\frac{7-3u-2v}{2}F \ \text { for } 0\leqslant u\leqslant 1, \\&\frac{3-2u}{5}\big (\widetilde{\mathscr {Z}}+\widetilde{\mathscr {Z}}^\prime \big )+(6-4u-v)F\ \text { for } 1\leqslant u\leqslant \frac{3}{2}. \end{aligned} \right. \end{aligned}$$

This gives

$$\begin{aligned} \widetilde{t}(u)=\left\{ \begin{aligned}&\frac{7-3u}{2}\ \text { for } 0\leqslant u\leqslant 1, \\&6-4u\ \text { for } 1\leqslant u\leqslant \frac{3}{2}. \end{aligned} \right. \end{aligned}$$

Furthermore, if $0\leqslant u\leqslant 1$, then

$$\begin{aligned} \widetilde{P}(u,v)= \left\{ \begin{aligned}&\frac{3-2u}{5}\widetilde{\mathscr {Z}}+\frac{1+u}{10}\widetilde{\mathscr {Z}}^\prime +\frac{7-3u-2v}{2}F \ \text { for } 0\leqslant v\leqslant 3-u, \\&\frac{18-7u-5v}{5}\widetilde{\mathscr {Z}}+\frac{1+u}{10}\widetilde{\mathscr {Z}}^\prime +\frac{7-3u-2v}{2}F \ \text { for } 3-u \leqslant v \leqslant \frac{7-3u}{2}, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{N}(u,v)= \left\{ \begin{aligned}&0\ \text { for } 0\leqslant v\leqslant 3-u, \\&(v+u-3)\widetilde{\mathscr {Z}}\ \text { for } 3-u\leqslant v\leqslant \frac{7-3u}{2}, \end{aligned} \right. \end{aligned}$$

which gives

$$\begin{aligned} \big (\widetilde{P}(u,v)\big )^2= \left\{ \begin{aligned}&u^2-v^2-8u+11\ \text { for } 0\leqslant v\leqslant 3-u, \\&2(4-u-v)(7-3u-2v)\ \text { for } 3-u\leqslant v\leqslant \frac{7-3u}{2}, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{P}(u,v)\cdot F= \left\{ \begin{aligned}&v\ \text { for } 0\leqslant v\leqslant 3-u, \\&15-5u-4v\ \text { for } 3-u\leqslant v\leqslant \frac{7-3u}{2}. \end{aligned} \right. \end{aligned}$$

If $1\leqslant u\leqslant \frac{3}{2}$, then $\widetilde{P}(u,v)=\frac{3-2u}{5}(\widetilde{\mathscr {Z}}+\widetilde{\mathscr {Z}}^\prime )+(6-4u-v)F$ and $\widehat{N}(u,v)=0$ for $v\in [0,6-4u]$, so

$$\begin{aligned} \widehat{P}(u,v)^2=(6-4u-v)(6-4u+v) \end{aligned}$$

and $\widetilde{P}(u,v)\cdot F=v$ for every $v\in [0,6-4u]$.

Set $R=E_Q\vert _{S}$. Then R is smooth curve, since S is a general surface in $|H_{\mathbb {P}^3}|$ that passes through P. Let $\widetilde{R}$ be the proper transform of the curve R on the surface $\widetilde{S}$. Then it follows from Example 8 that

$$\begin{aligned} \widetilde{N}^\prime (u)=\left\{ \begin{aligned}&0 \ \text { for } 0\leqslant u\leqslant 1, \\&(u-1)\widetilde{R} \ \text { for } 1\leqslant u\leqslant \frac{3}{2}. \end{aligned} \right. \end{aligned}$$

If $0\leqslant u\leqslant 1$, we have $\widetilde{d}(u)=0$. Similarly, if $1\leqslant u\leqslant \frac{3}{2}$ and R does not contain P, then $\widetilde{d}(u)=0$. Finally, if $1\leqslant u\leqslant \frac{3}{2}$ and $P\in R$, then $\widetilde{d}(u)=(u-1)$.

Using the data collected above, we can compute $S(W^S_{\bullet ,\bullet };F)$. Namely, if $P\in E_{Q}$, then

$$\begin{aligned}{} & {} S\big (W^S_{\bullet ,\bullet };F\big )=\frac{1}{8}\int \limits _1^{\frac{3}{2}}(u-1)(16u^2-48u+36)du+ \frac{1}{8}\int \limits _0^{\frac{3}{2}}\int \limits _0^{\widetilde{t}(u)}\big (\widetilde{P}(u,v)\big )^2dvdu \\{} & {} \quad =\frac{1}{96}+\frac{1}{8}\int \limits _{0}^{1}\int \limits _{0}^{3-u}u^2-v^2-8u+11dvdu \\{} & {} \quad \ +\frac{1}{8}\int \limits _{0}^{1}\int \limits _{3-u}^{\frac{7-3u}{2}}2(4-u-v)(7-3u-2v)dvdu\\{} & {} \quad +\frac{1}{8}\int \limits _{1}^{\frac{3}{2}}\int \limits _{0}^{6-4u}(6-4u-v)(6-4u+v)dvdu=\frac{1}{96}+\frac{655}{384}+\frac{1}{12}=\frac{691}{384}<2. \end{aligned}$$

Similarly, if $P\not \in E_{Q}$, then $S(W^S_{\bullet ,\bullet };F)=\frac{655}{384}+\frac{1}{12}=\frac{229}{128}<2$.

Now, let O be any point in F. Then

$$\begin{aligned} S\big (W_{\bullet , \bullet ,\bullet }^{\widetilde{S},F};O\big )= & {} \frac{1}{8}\int \limits _0^{\frac{3}{2}}\int \limits _0^{\widetilde{t}(u)}\big (\widetilde{P}(u,v)\cdot F\big )^2dvdu+F_O\big (W_{\bullet ,\bullet ,\bullet }^{\widetilde{S},F}\big )\\= & {} \frac{1}{8}\int \limits _{0}^{1}\int \limits _{0}^{3-u}v^{2}dvdu+\frac{1}{8}\int \limits _{0}^{1}\int \limits _{3-u}^{\frac{7-3u}{2}}(15-5u-4v)^2dvdu\\{} & {} \quad \ +\frac{1}{8}\int \limits _{1}^{\frac{3}{2}}\int \limits _{0}^{6-4u}v^2dvdu+F_O\big (W_{\bullet ,\bullet ,\bullet }^{\widetilde{S},F}\big )\\= & {} \frac{163}{192}+F_O\big (W_{\bullet ,\bullet ,\bullet }^{\widetilde{S},F}\big ). \end{aligned}$$

Moreover, if $O\in \widetilde{R}\cap \widetilde{\mathscr {Z}}$, then we compute $F_O(W_{\bullet ,\bullet ,\bullet }^{\widetilde{S},F})$ as follows:

$$\begin{aligned}{} & {} F_O\big (W_{\bullet ,\bullet ,\bullet }^{\widetilde{S},F}\big )= \frac{1}{4}\int \limits _0^{\frac{3}{2}}\int \limits _0^{\widetilde{t}(u)}\big (\widetilde{P}(u,v)\cdot F\big )\cdot \textrm{ord}_O\big (\widetilde{N}^\prime (u)\big |_F\big )dvdu\\{} & {} \quad + \frac{1}{4}\int \limits _0^{\frac{3}{2}}\int \limits _0^{\widetilde{t}(u)}\big (\widetilde{P}(u,v)\cdot F\big )\cdot \textrm{ord}_O\big (\widetilde{N}(u,v)\big |_F\big )dvdu\\{} & {} \quad =\frac{1}{4}\int \limits _1^{\frac{3}{2}}\int \limits _0^{6-4u}\big (\widetilde{P}(u,v)\cdot F\big )(u-1)\big (\widetilde{R}\cdot F\big )_Odvdu\\{} & {} \quad + \frac{1}{4}\int \limits _0^{1}\int \limits _{3-u}^{\frac{7-3u}{2}}\big (\widetilde{P}(u,v)\cdot F\big )(v+u-3)\big (\widetilde{\mathscr {Z}}\cdot F\big )_{O}dvdu\\{} & {} \quad =\frac{1}{4}\int \limits _{1}^{\frac{3}{2}}\int \limits _{0}^{6-4u}v(u-1)dvdu+\frac{1}{4}\int \limits _{0}^{1}\int \limits _{3-u}^{\frac{7-3u}{2}}(15-5u-4v)(v+u-3)dvdu\\{} & {} \quad =\frac{1}{96}+\frac{7}{384}=\frac{11}{384}, \end{aligned}$$

because the curve $\widetilde{R}$ intersects F transversally, and every irreducible component of the curve $\widetilde{\mathscr {Z}}$ also intersects F transversally. Hence, if $O\in \widetilde{R}\cap \widetilde{\mathscr {Z}}$, then $S(W_{\bullet , \bullet ,\bullet }^{\widetilde{S},F};O)=\frac{337}{384}<1$. Similar computations imply that $S(W_{\bullet , \bullet ,\bullet }^{\widetilde{S},F};O)<\frac{337}{384}<1$ if $O\not \in \widetilde{R}$ or $O\not \in \widetilde{\mathscr {Z}}$. Thus, using (2), we see that $\beta (\textbf{F})>0$. $\square$

FormalPara Lemma 13

Let S be a general surface in $|H_{\mathbb {P}^3}|$ such that $P\in S$. Suppose $P\not \in E_{\mathbb {P}^3}$, $-K_S$ is ample, and P is contained in a $(-1)$-curve $B\subset S$ such that $\pi (B)$ is a conic. Then $\beta (\textbf{F})>0$.

FormalPara Proof

Let us use notations introduced in the proof of Lemma 12, and let $\widetilde{B}$ be the proper transform on the surface $\widetilde{S}$ of the curve B. Observe that $\widetilde{B}$ and $\widetilde{Z}$ are disjoint, and $\widetilde{B}^2=-2$ on the surface $\widetilde{S}$. Moreover, it follows from Example 8 that $\tau =\frac{3}{2}$ and

$$\begin{aligned} f^{*}\big (P(u)\big \vert _{S}\big )-vF \sim _{\mathbb {R}}\left\{ \begin{aligned}&\frac{2-u}{3}\widetilde{Z}+\frac{1+u}{3}\widetilde{B}+\frac{11-4u-3v}{3}F \ \text { for } 0\leqslant u\leqslant 1, \\&\frac{3-2u}{3}\big (\widetilde{Z}+2\widetilde{B}\big )+\frac{21-14u-3v}{3}F\ \text { for } 1\leqslant u\leqslant \frac{3}{2}. \end{aligned} \right. \end{aligned}$$

This gives

$$\begin{aligned} \widetilde{t}(u)=\left\{ \begin{aligned}&\frac{11-4u}{3}\ \text { for } 0\leqslant u\leqslant 1, \\&\frac{21-14u}{3}\ \text { for } 1\leqslant u\leqslant \frac{3}{2}. \end{aligned} \right. \end{aligned}$$

Furthermore, if $0\leqslant u\leqslant 1$, then

$$\begin{aligned} \widetilde{P}(u,v)= \left\{ \begin{aligned}&\frac{2-u}{3}\widetilde{Z}+\frac{1+u}{3}\widetilde{B}+\frac{11-4u-3v}{3}F \ \text { for } 0\leqslant v\leqslant 3-2u, \\&\frac{2-u}{3}\widetilde{Z}+\frac{11-4u-3v}{6}\big (\widetilde{B}+2F\big ) \ \text { for } 3-2u \leqslant v \leqslant 3-u,\\&\frac{11-4u-3v}{6}\big (2L+\widetilde{B}+2F\big ) \ \text { for } 3-u \leqslant v \leqslant \frac{11-4u}{3}, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{N}(u,v)= \left\{ \begin{aligned}&0 \ \text { for } 0\leqslant v\leqslant 3-2u, \\&\frac{v+2u-3}{2}\widetilde{B} \ \text { for } 3-2u \leqslant v \leqslant 3-u,\\&\frac{v+2u-3}{2}\widetilde{B}+(v+u-3)\widetilde{Z} \ \text { for } 3-u \leqslant v \leqslant \frac{11-4u}{3}, \end{aligned} \right. \end{aligned}$$

which gives

$$\begin{aligned} \big (\widetilde{P}(u,v)\big )^2= \left\{ \begin{aligned}&u^2-v^2-8u+11 \ \text { for } 0\leqslant v\leqslant 3-2u, \\&\frac{31}{2}-14u-3v+3u^2-\frac{v^2}{2}+2vu \ \text { for } 3-2u \leqslant v \leqslant 3-u,\\&\frac{(11-4u-3v)^2}{2}\ \text { for } 3-u \leqslant v \leqslant \frac{11-4u}{3}, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{P}(u,v)\cdot F= \left\{ \begin{aligned}&v \ \text { for } 0\leqslant v\leqslant 3-2u, \\&\frac{3-2u+v}{2} \ \text { for } 3-2u \leqslant v \leqslant 3-u,\\&\frac{33-12u-9v}{2} \ \text { for } 3-u \leqslant v \leqslant \frac{11-4u}{3}. \end{aligned} \right. \end{aligned}$$

Similarly, if $1\leqslant u\leqslant \frac{3}{2}$, then

$$\begin{aligned} \widetilde{P}(u,v)= \left\{ \begin{aligned}&\frac{3-2u}{3}\big (\widetilde{Z}+2\widetilde{B}\big )+\frac{21-14u-3v}{3}F \ \text { for } 0\leqslant v\leqslant 3-2u, \\&\frac{3-2u}{3}\widetilde{Z}+\frac{21-14u-3v}{6}\big (\widetilde{B}+2F\big ) \ \text { for } 3-2u \leqslant v \leqslant 6-4u,\\&\frac{21-14u-3v}{6}\big (2\widetilde{Z}+\widetilde{B}+2F\big ) \ \text { for } 6-4u \leqslant v \leqslant \frac{21-14u}{3}, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{N}(u,v)= \left\{ \begin{aligned}&0 \ \text { for } 0\leqslant v\leqslant 3-2u, \\&\frac{v+2u-3}{2}\widetilde{B} \ \text { for } 3-2u \leqslant v \leqslant 6-4u,\\&\frac{v+2u-3}{2}\widetilde{B}+(v+4u-6)\widetilde{Z} \ \text { for } 6-4u \leqslant v \leqslant \frac{21-14u}{3}, \end{aligned} \right. \end{aligned}$$

which gives

$$\begin{aligned} \big (\widetilde{P}(u,v)\big )^2= \left\{ \begin{aligned}&(6-4u-v)(6-4u+v) \ \text { for } 0\leqslant v\leqslant 3-2u, \\&\frac{81}{2}-54u-3v+18u^2-\frac{v^2}{2}+2vu \ \text { for } 3-2u \leqslant v \leqslant 6-4u,\\&\frac{(21-14u-3v)^2}{2} \ \text { for } 6-4u \leqslant v \leqslant \frac{21-14u}{3}, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{P}(u,v)\cdot F= \left\{ \begin{aligned}&v \ \text { for } 0\leqslant v\leqslant 3-2u, \\&\frac{3-2u+v}{2} \ \text { for } 3-2u \leqslant v \leqslant 6-4u,\\&\frac{63-42u-9v}{2} \ \text { for } 6-4u \leqslant v \leqslant \frac{21-14u}{3}. \end{aligned} \right. \end{aligned}$$

Thus, as in the proof of Lemma 12, we compute

$$\begin{aligned} S\big (W^S_{\bullet ,\bullet };F\big )= \left\{ \begin{aligned}&\frac{523}{288} \ \text { if } P\in E_{Q}, \\&\frac{65}{36} \ \text { if } P\not \in E_{Q}, \end{aligned} \right. \end{aligned}$$

so that $S(W^S_{\bullet ,\bullet };F)<2$. Similarly, if O is a point in F, then

$$\begin{aligned} S\big (W_{\bullet , \bullet ,\bullet }^{\widetilde{S},F};O\big )= \left\{ \begin{aligned}&\frac{257}{288} \ \text { if } O\in \widetilde{B}\cap \widetilde{R}, \\&\frac{119}{144} \ \text { if } O\in \widetilde{Z}\cap \widetilde{R},\\&\frac{127}{144} \ \text { if } O\in \widetilde{B}\ \text {and}\ O\not \in \widetilde{R}, \\&\frac{235}{288} \ \text { if } O\in \widetilde{Z}\ \text {and}\ O\not \in \widetilde{R},\\&\frac{307}{384} \ \text { if } O\not \in \widetilde{B}\cup \widetilde{Z}\ \text {and}\ O\in \widetilde{R}\\&\frac{101}{128} \ \text { if } O\not \in \widetilde{B}\cup \widetilde{Z}\cup \widetilde{R}. \end{aligned} \right. \end{aligned}$$

Therefore, using (2), we see that $\beta (\textbf{F})>0$. $\square$

On the other hand, we have the following purely geometric result.

FormalPara Lemma 14

Suppose that $P\not \in E_{\mathbb {P}^3}$. Let S be a general surface in $|H_{\mathbb {P}^3}|$ such that S passes through P. Then $-K_{S}$ is ample. Further, if P is contained in a $(-1)$-curve $B\subset S$, then $\pi (B)$ is a smooth conic.

FormalPara Proof

The surface $\pi (S)$ is a general plane in $\mathbb {P}^3$ that contains the point $\pi (P)$. Write

$$\begin{aligned} \pi (S)\cap C_5=P_1\cup P_2\cup P_3\cup P_4\cup P_5, \end{aligned}$$

where $P_1$, $P_2$, $P_3$, $P_4$, $P_5$ are distinct points. Then $\pi$ induces a birational morphism $\varpi :S\rightarrow \pi (S)$, which is a blow up of the intersection points $P_1$, $P_2$, $P_3$, $P_4$, $P_5$. Thus, to prove that $-K_S$ is ample, we must show that at most two points among these five are contained in a line.

If three points among $P_1$, $P_2$, $P_3$, $P_4$, $P_5$ are contained in a line $\ell$, it is a trisecant of the curve $C_5$, the line $\ell$ is contained in $\pi (E_Q)$, and its proper transform on X is a fiber of the projection $E_Q\rightarrow C_5^\prime$. However, the planes containing $\pi (P)$ and a trisecant of the curve $C_5$ form a one-dimensional family. Hence, a general plane in $\mathbb {P}^3$ that passes through $\pi (P)$ does not contain trisecants of the curve $C_5$, so that at most two points among $P_1$, $P_2$, $P_3$, $P_4$, $P_5$ are contained in a line. Thus, $-K_S$ is ample.

Now, we suppose that P is contained in a $(-1)$-curve $B\subset S$. If $\pi (B)$ is not a conic, it must be a secant of the curve $C_5$ that contains $\pi (P)$. Let $\phi :\mathbb {P}^3\dasharrow \mathbb {P}^2$ be the linear projection from $\pi (P)$. Since $\pi (P)\not \in C_5$, $\phi$ induces a birational morphism $C_5\rightarrow \phi (C_5)$, and $\phi (C_5)$ is a singular irreducible curve of degree 5. Moreover, if $\ell$ is a secant of the curve $C_5$ that contains $\pi (P)$, then $\phi (\ell )$ is a singular point of the curve $\phi (C_5)$. Since this curve has finitely many singular points, we conclude that there are finitely many secants of the curve $C_5$ that passes through $\pi (P)$. This shows that $\pi (S)$ does not contain secants of the curve $C_5$ that pass through $\pi (P)$, because $\pi (S)$ is a general plane in $\mathbb {P}^3$ that contains the point $\pi (P)$. So, we conclude that $\pi (B)$ must be a conic. $\square$

Hence, applying Lemmas 11, 12, 13, 14, we obtain

FormalPara Corollary 15

If $\beta (\textbf{F})\leqslant 0$, then Z is a fiber of the projection $E_{\mathbb {P}^3}\rightarrow C_5$.

FormalPara Remark 16

By [13, Corollary 4.14], Corollary 15 implies both Corollaries 2 and Corollaries 5.

To complete the proof of the Main Theorem, we may assume Z is a fiber of the projection $E_{\mathbb {P}^3}\rightarrow C_5$.

Note that $Z\not \subset E_Q$, since $E_Q$ is irrational. Thus, we can choose $P\in Z$ such that $P\not \in E_Q$ either. Now, let S be a general surface in $|H_{Q}|$ such that $P\in S$. Then the surface q(S) is a general hyperplane section of the quadric Q that contains q(P), so $q(S)\cong \mathbb {P}^1\times \mathbb {P}^1$ and $q(S)\cap C_5^\prime =P_1\cup P_2\cup P_3\cup P_4\cup P_5$, where $P_1$, $P_2$, $P_3$, $P_4$, $P_5$ are distinct points in $C_5^\prime$. Then the morphism $q:X\rightarrow Q$ induces a birational morphism $S\rightarrow q(S)$ that blows up the points $P_1$, $P_2$, $P_3$, $P_4$, $P_5$.

FormalPara Lemma 17

The divisor $-K_{S}$ is ample.

FormalPara Proof

Observe that q(S) is a general hyperplane section of the quadric Q that passes through q(P), and it follows from the adjunction formula that $-K_S\sim H_{\mathbb {P}^3}\big \vert _{S}$. Thus, if $-K_S$ is not ample, S contains a fiber $\ell$ of the projection $E_{\mathbb {P}^3}\rightarrow C_5$ such that $q(\ell )$ is a secant line of the curve $C_5^\prime$. On the other hand, hyperplane sections of Q that contain q(P) and a secant line of the curve $C_5^\prime$ form a two-dimensional family. So, we may assume that q(S) is not one of them, which implies that $-K_S$ is ample. $\square$

Since $-K_{S}$ is ample, the morphism $\pi$ induces an isomorphism $S\cong \pi (S)$, and $\pi (S)$ is a smooth cubic surface in $\mathbb {P}^3$ that contains the curve $C_5$. Let us identify S with the smooth cubic surface $\pi (S)$. Using this identification, we see that $C_5=E_{\mathbb {P}^3}\cap S$. Then $P\in C_5$, since $P\in E_{\mathbb {P}^3}$.

Let $L_1$ and $L_2$ be the proper transforms on S of two rulings of the surface $q(S)\cong \mathbb {P}^1\times \mathbb {P}^1$ that pass through the point q(P). Then $L_1$ and $L_2$ are conics in S, because $q(L_1)$ and $q(L_2)$ do not contain any of the points $P_1$, $P_2$, $P_3$, $P_4$, $P_5$, since we assume that q(S) is a general hyperplane section of the quadric Q that contains the point q(P). Moreover, it follows from Example 9 that

$$\begin{aligned} P(u)\big \vert _{S}\sim _{\mathbb {R}} \left\{ \begin{aligned}&-K_S+(1-u)(L_1+L_2) \ \text { for } 0\leqslant u\leqslant 1, \\&(4-3u)(-K_S)\ \text { for } 1\leqslant u\leqslant \frac{4}{3},\\ \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} N(u)\big \vert _{S}=\left\{ \begin{aligned}&0\ \text { for } 0\leqslant u\leqslant 1, \\&(u-1)C_5\ \text { for } 1\leqslant u\leqslant \frac{4}{3},\\ \end{aligned} \right. \end{aligned}$$

Let $T_P$ be the unique curve in the linear system $|-K_S|$ that is singular at P. Then $T_P$ is cut out by the hyperplane in $\mathbb {P}^3$ that is tangent to S at the point P. In particular, the curve $T_P$ is reduced.

FormalPara Lemma 18

We have the following three possible cases:

• $T_P$ is an irreducible cubic curve,

• $T_P=\ell +C_2$, where $\ell$ is a line, $C_2$ is a smooth conic such that $C_2\ne L_1$ and $C_2\ne L_2$,

• $T_P=\ell _1+\ell _2+\ell _3$, where $\ell _1$, $\ell _2$, $\ell _3$ are lines such that $P=\ell _1\cap \ell _2$ and $P\not \in \ell _3$.

FormalPara Proof

A priori, since $T_P$ is a reduced cubic curve, we may have the following cases:

• (1) $T_P$ is an irreducible curve,

• (2) $T_P=\ell +L_1$, where $\ell$ is a line,

• (3) $T_P=\ell +L_2$, where $\ell$ is a line,

• (4) $T_P=\ell +C_2$, where $\ell$ is a line, $C_2$ is a smooth conic such that $C_2\ne L_1$ and $C_2\ne L_2$,

• (5) $T_P=\ell _1+\ell _2+\ell _3$, where $\ell _1$, $\ell _2$, $\ell _3$ are lines such that $P=\ell _1\cap \ell _2$ and $P\not \in \ell _3$,

• (6) $T_P=\ell _1+\ell _2+\ell _3$, where $\ell _1$, $\ell _2$, $\ell _3$ are lines such that $P=\ell _1\cap \ell _2\cap \ell _3$.

If $T_P=\ell _1+\ell _2+\ell _3$ for three lines $\ell _1$, $\ell _2$, $\ell _3$ such that $P=\ell _1\cap \ell _2\cap \ell _3$, then

$$\begin{aligned} 2=-K_S\cdot L_1=\big (\ell _1+\ell _2+\ell _3\big )\cdot L_1\geqslant \sum _{i=1}^3\big (\ell _i\cdot L_1\big )_P\geqslant 3, \end{aligned}$$

which is absurd. Thus, we see that the last case is impossible. To complete the proof, we must show that the second and the third cases are also impossible.

Suppose that $T_P=\ell +L_1$ for some line $\ell$. Then $q(\ell )$ is a twisted cubic curve in Q that contains all intersection points $P_1$, $P_2$, $P_3$, $P_4$, $P_5$. In particular, we see that $E_Q\cap \ell \geqslant 5$. On the other hand, the curve $q(\ell )$ is not contained in the surface $q(E_{\mathbb {P}^3})$, because the only rational curves in the ruled irrational surface $E_{\mathbb {P}^3}$ are fibers of the natural projection $E_{\mathbb {P}^3}\rightarrow C_5$, which are mapped to lines by q. Therefore, since $P\in E_{\mathbb {P}^3}$ by assumption, we have

$$\begin{aligned} 1\leqslant \big (E_{\mathbb {P}^3}\cdot \ell \big )_{P}\leqslant E_{\mathbb {P}^3}\cdot \ell =\big (5H_Q-3E_Q\big )\cdot \ell =15-3E_Q\cdot \ell \leqslant 0, \end{aligned}$$

which is absurd. This shows that the conic $L_1$ cannot be an irreducible component of the curve $T_P$. Similarly, we see $L_2$ is also not an irreducible component of the curve $T_P$. $\square$

From Example 9, we know that $S_X(S)<1$. So, it follows from (2) that $\beta (\textbf{F})>0$ if $S(W^S_{\bullet ,\bullet };F)<2$, and $S(W_{\bullet , \bullet ,\bullet }^{\widetilde{S},F};O)<1$ for every point $O\in F$. Let us check these conditions.

Let $\widetilde{L}_1$, $\widetilde{L}_2$, $\widetilde{T}_P$ be proper transforms on $\widetilde{S}$ of the curves $L_1$, $L_2$, $T_P$. Then

$$\begin{aligned} f^{*}\big (P(u)\big \vert _{S}\big )-vF \sim _{\mathbb {R}}\left\{ \begin{aligned}&\widetilde{T}_P+(1-u)\big (\widetilde{L}_1+\widetilde{L}_2\big )+(4-2u-v)F \ \text { for } 0\leqslant u\leqslant 1, \\&(4-3u)\widetilde{T}_P+(8-6u-v)F\ \text { for } 1\leqslant u\leqslant \frac{4}{3}. \end{aligned} \right. \end{aligned}$$

(3)

Hence, if $0\leqslant u\leqslant 1$, then $\widetilde{t}(u)=4-2u$. Similarly, if $1\leqslant u\leqslant \frac{4}{3}$, then $\widetilde{t}(u)=8-6u$. Moreover, since the curve $C_5=E_{\mathbb {P}^3}\cap S$ is smooth, we have $\widetilde{d}(u)=0$ for $0\leqslant u\leqslant 1$, and $\widetilde{d}(u)=u-1$ for $1\leqslant u\leqslant \frac{4}{3}$. Finally, let $\widetilde{C}_5$ be the proper transform on $\widetilde{S}$ of the curve $C_5$. Then

$$\begin{aligned} \widetilde{N}^\prime (u)=\left\{ \begin{aligned}&0 \ \text { for } 0\leqslant u\leqslant 1, \\&(u-1)\widetilde{C}_5 \ \text { for } 1\leqslant u\leqslant \frac{4}{3}. \end{aligned} \right. \end{aligned}$$

Now, we can compute $S(W^S_{\bullet ,\bullet };F)$ and $S(W_{\bullet , \bullet ,\bullet }^{\widetilde{S},F};O)$ for every point $O\in F$.

FormalPara Lemma 19

If $T_P$ is irreducible, then $S(W^S_{\bullet ,\bullet };F)<2$ and $S(W_{\bullet , \bullet ,\bullet }^{\widetilde{S},F};O)<1$ for every point $O\in F$.

FormalPara Proof

Suppose that the curve $T_P$ is irreducible. Then $\widetilde{S}$ is a smooth del Pezzo surface of degree 2. Note that $\widetilde{L}_1$, $\widetilde{L}_1$, $\widetilde{T}_P$ are disjoint $(-1)$-curves on $\widetilde{S}$. If $0\leqslant u\leqslant \frac{1}{2}$, it follows from (3) that

$$\begin{aligned} \widetilde{P}(u,v)= \left\{ \begin{aligned}&\widetilde{T}_P+(1-u)\big (\widetilde{L}_1+\widetilde{L}_2\big )+(4-2u-v)F\ \text {for}\ 0\leqslant v\leqslant 3-u,\\&\widetilde{T}_P+(4-2u-v)\big (\widetilde{L}_1+\widetilde{L}_2+F\big )\ \text {for}\ 3-u\leqslant v\leqslant \frac{7-4u}{2},\\&(4-2u-v)\big (2\widetilde{T}_P+\widetilde{L}_1+\widetilde{L}_2+F\big )\ \text {for}\ \frac{7-4u}{2}\leqslant v\leqslant 4-2u, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{N}(u,v)= \left\{ \begin{aligned}&0\ \text {for}\ 0\leqslant v\leqslant 3-u,\\&(v+u-3)\big (\widetilde{L}_1+\widetilde{L}_2\big )\ \text {for}\ 3-u\leqslant v\leqslant \frac{7-4u}{2},\\&(v+u-3)\big (\widetilde{L}_1+\widetilde{L}_2\big )+(2v+4u-7)\widetilde{T}_P\ \text {for}\ \frac{7-4u}{2}\leqslant v\leqslant 4-2u, \end{aligned} \right. \end{aligned}$$

which gives

$$\begin{aligned} \big (\widetilde{P}(u,v)\big )^2= \left\{ \begin{aligned}&2u^2-v^2-12u+13\ \text {for}\ 0\leqslant v\leqslant 3-u,\\&4u^2+4uv+v^2-24u-12v+31\ \text {for}\ 3-u\leqslant v\leqslant \frac{7-4u}{2},\\&5(2u+v-4)^2\ \text {for}\ \frac{7-4u}{2}\leqslant v\leqslant 4-2u, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{P}(u,v)\cdot F= \left\{ \begin{aligned}&v\ \text {for}\ 0\leqslant v\leqslant 3-u,\\&6-2u-v\ \text {for}\ 3-u\leqslant v\leqslant \frac{7-4u}{2},\\&20-10u-5v\ \text {for}\ \frac{7-4u}{2}\leqslant v\leqslant 4-2u. \end{aligned} \right. \end{aligned}$$

Likewise, if $\frac{1}{2}\leqslant u\leqslant 1$, then it follows from (3) that

$$\begin{aligned} \widetilde{P}(u,v)= \left\{ \begin{aligned}&\widetilde{T}_P+(1-u)\big (\widetilde{L}_1+\widetilde{L}_2\big )+(4-2u-v)F\ \text {for}\ 0\leqslant v\leqslant \frac{7-4u}{2},\\&(4-2u-v)\big (2\widetilde{T}_P+F\big )+(1-u)\big (\widetilde{L}_1+\widetilde{L}_2\big )\ \text {for}\ \frac{7-4u}{2}\leqslant v\leqslant 3-u,\\&(4-2u-v)\big (2\widetilde{T}_P+\widetilde{L}_1+\widetilde{L}_2+F\big )\ \text {for}\ 3-u\leqslant v\leqslant 4-2u, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{N}(u,v)= \left\{ \begin{aligned}&0\ \text {for}\ 0\leqslant v\leqslant \frac{7-4u}{2},\\&(2v+4u-7)\widetilde{T}_P\ \text {for}\ \frac{7-4u}{2}\leqslant v\leqslant 3-u,\\&(v+u-3)\big (\widetilde{L}_1)+\widetilde{L}_2\big )+(2v+4u-7)\widetilde{T}_P\ \text {for}\ 3-u\leqslant v\leqslant 4-2u, \end{aligned} \right. \end{aligned}$$

which gives

$$\begin{aligned} \big (\widetilde{P}(u,v)\big )^2= \left\{ \begin{aligned}&2u^2-v^2-12u+13\ \text {for}\ 0\leqslant v\leqslant \frac{7-4u}{2},\\&18u^2+16uv+3v^2-68u-28v+62\ \text {for}\ \frac{7-4u}{2}\leqslant v\leqslant 3-u,\\&5(2u+v-4)^2\ \text {for}\ 3-u\leqslant v\leqslant 4-2u, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{P}(u,v)\cdot F= \left\{ \begin{aligned}&v\ \text {for}\ 0\leqslant v\leqslant \frac{7-4u}{2},\\&14-8u-3v\ \text {for}\ \frac{7-4u}{2}\leqslant v\leqslant 3-u,\\&20-10u-5v\ \text {for}\ 3-u\leqslant v\leqslant 4-2u. \end{aligned} \right. \end{aligned}$$

Similarly, if $1\leqslant u\leqslant \frac{4}{3}$, then

$$\begin{aligned} \widetilde{P}(u,v)= \left\{ \begin{aligned}&(4-3u)\widetilde{T}_P+(8-6u-v)F\ \text {for}\ 0\leqslant v\leqslant \frac{12-9u}{2},\\&(8-6u-v)(2\widetilde{T}_P+F)\ \text {for}\ \frac{12-9u}{2}\leqslant v\leqslant 8-6u, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{N}(u,v)= \left\{ \begin{aligned}&0\ \text {for}\ 0\leqslant v\leqslant \frac{12-9u}{2},\\&(2v+9u-12)\widetilde{T}_P\ \text {for}\ \frac{12-9u}{2}\leqslant v\leqslant 8-6u, \end{aligned} \right. \end{aligned}$$

which gives

$$\begin{aligned} \big (\widetilde{P}(u,v)\big )^2= \left\{ \begin{aligned}&27u^2-v^2-72u+48\ \text {for}\ 0\leqslant v\leqslant \frac{12-9u}{2},\\&3(6u+v-8)^2\ \text {for}\ \frac{12-9u}{2}\leqslant v\leqslant 8-6u, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{P}(u,v)\cdot F= \left\{ \begin{aligned}&v\ \text {for}\ 0\leqslant v\leqslant \frac{12-9u}{2},\\&24-18u-3v\ \text {for}\ \frac{12-9u}{2}\leqslant v\leqslant 8-6u. \end{aligned} \right. \end{aligned}$$

As in the proof of Lemma 12, we get $S(W^S_{\bullet ,\bullet };F)=\frac{1103}{576}$. Likewise, if O is a point in F, then

$$\begin{aligned} S\big (W_{\bullet , \bullet ,\bullet }^{\widetilde{S},F};O\big )= \left\{ \begin{aligned}&\frac{131}{144} \ \text { if } O\in \widetilde{T}_P,\ T_P \text { has a node at }P,\ \text {and}\ O\in \widetilde{C}_5,\\&\frac{29}{32} \ \text { if } O\in \widetilde{T}_P,\ T_P \text { has a node at }P,\ \text {and}\ O\not \in \widetilde{C}_5,\\&\frac{277}{288} \ \text { if } O\in \widetilde{T}_P,\ T_P \text { has a cusp at }P,\ \text {and}\ O\in \widetilde{C}_5,\\&\frac{23}{24} \ \text { if } O\in \widetilde{T}_P,\ T_P \text { has a cusp at }P\ \text {and}\ O\not \in \widetilde{C}_5,\\&\frac{1045}{1152} \ \text { if } O\in \widetilde{L}_1\cup \widetilde{L}_2\ \text {and}\ O\in \widetilde{C}_5, \\&\frac{347}{384} \ \text { if } O\in \widetilde{L}_1\cup \widetilde{L}_2\ \text {and}\ O\not \in \widetilde{C}_5, \\&\frac{247}{288} \ \text { if } O\not \in \widetilde{L}_1\cup \widetilde{L}_2\cup \widetilde{T}_P\ \text {and}\ O\in \widetilde{C}_5,\\&\frac{41}{48} \ \text { if } O\not \in \widetilde{L}_1\cup \widetilde{L}_2\cup \widetilde{T}_P\ \text {and}\ O\not \in \widetilde{C}_5. \end{aligned} \right. \end{aligned}$$

The lemma is proved. $\square$

FormalPara Lemma 20

Suppose $T_P=\ell +C_2$, where $\ell$ is a line, $C_2$ is a smooth conic such that $L_1\ne C_2\ne L_2$. Then $S(W^S_{\bullet ,\bullet };F)<2$ and $S(W_{\bullet , \bullet ,\bullet }^{\widetilde{S},F};O)<1$ for every point $O\in F$.

FormalPara Proof

Let $\widetilde{\ell }$ and $\widetilde{C}_2$ be the proper transforms on the surface $\widetilde{S}$ of the curves $\ell$ and $C_2$, respectively. Then $\widetilde{\ell }$ is a $(-2)$-curve, $\widetilde{C}_2$ is a $(-1)$-curve, and the intersection $\widetilde{\ell }\cap \widetilde{C}_2$ consists of a single point. Note also that $\widetilde{\ell }\cap \widetilde{C}_2\in F$ $\iff$ $\ell$ and $C_2$ are tangent at P. If $0\leqslant u\leqslant \frac{2}{3}$, it follows from (3) that

$$\begin{aligned} \widetilde{P}(u,v)= \left\{ \begin{aligned}&\widetilde{\ell }+\widetilde{C}_2+(1-u)\big (\widetilde{L}_1+\widetilde{L}_2\big )+(4-2u-v)F\ \text {for}\ 0\leqslant v\leqslant 3-2u,\\&\frac{5-2u-v}{2}\widetilde{\ell }+\widetilde{C}_2+(1-u)\big (\widetilde{L}_1+\widetilde{L}_2\big )+(4-2u-v)F \ \text {for}\ 3-2u\leqslant v\leqslant 3-u,\\&\frac{5-2u-v}{2}\widetilde{\ell }+\widetilde{C}_2+(4-2u-v)\big (\widetilde{L}_1+\widetilde{L}_2+F\big ) \ \text {for}\ 3-u\leqslant v\leqslant \frac{11-6u}{3},\\&(4-2u-v)\big (2\widetilde{\ell }+3\widetilde{C}_2+\widetilde{L}_1+\widetilde{L}_2+F\big ) \ \text {for}\ \frac{11-6u}{3}\leqslant v\leqslant 4-2u, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{N}(u,v)= \left\{ \begin{aligned}&0\ \text {for}\ 0\leqslant v\leqslant 3-2u,\\&\frac{v+2u-3}{2}\widetilde{\ell } \ \text {for}\ 3-2u\leqslant v\leqslant 3-u,\\&\frac{v+2u-3}{2}\widetilde{\ell }+(v+u-3)\big (\widetilde{L}_1+\widetilde{L}_2\big ) \ \text {for}\ 3-u\leqslant v\leqslant \frac{11-6u}{3},\\&(4u+2v-7)\widetilde{\ell }+(6u+3v-11)\widetilde{C}_2+(v+u-3)\big (\widetilde{L}_1+\widetilde{L}_2\big ) \ \text {for}\ \frac{11-6u}{3}\leqslant v\leqslant 4-2u, \end{aligned} \right. \end{aligned}$$

which gives

$$\begin{aligned} \big (\widetilde{P}(u,v)\big )^2= \left\{ \begin{aligned}&2u^2-v^2-12u+13\ \text {for}\ 0\leqslant v\leqslant 3-2u,\\&\frac{35}{2}-18u-3v+4u^2-\frac{v^2}{2}+2uv \ \text {for}\ 3-2u\leqslant v\leqslant 3-u,\\&\frac{71}{2}-30u-15v+6u^2+\frac{3v^2}{2}+6uv \ \text {for}\ 3-u\leqslant v\leqslant \frac{11-6u}{3},\\&6(4-2u-v)^2 \ \text {for}\ \frac{11-6u}{3}\leqslant v\leqslant 4-2u, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{P}(u,v)\cdot F= \left\{ \begin{aligned}&v\ \text {for}\ 0\leqslant v\leqslant 3-2u,\\&\frac{3-2u+v}{2} \ \text {for}\ 3-2u\leqslant v\leqslant 3-u,\\&\frac{15-6u-3v}{2} \ \text {for}\ 3-u\leqslant v\leqslant \frac{11-6u}{3},\\&24-12u-6v \ \text {for}\ \frac{11-6u}{3}\leqslant v\leqslant 4-2u, \end{aligned} \right. \end{aligned}$$

Likewise, if $\frac{2}{3}\leqslant u\leqslant 1$, then it follows from (3) that

$$\begin{aligned} \widetilde{P}(u,v)= \left\{ \begin{aligned}&\widetilde{\ell }+\widetilde{C}_2+(1-u)\big (\widetilde{L}_1+\widetilde{L}_2\big )+(4-2u-v)F\ \text {for}\ 0\leqslant v\leqslant 3-2u,\\&\frac{5-2u-v}{2}\widetilde{\ell }+\widetilde{C}_2+(1-u)\big (\widetilde{L}_1+\widetilde{L}_2\big )+(4-2u-v)F \\&\quad \text {for}\ 3-2u\leqslant v\leqslant \frac{11-6u}{3},\\&(4-2u-v)\big (2\widetilde{\ell }+3\widetilde{C}_2+F\big )+(1-u)\big (\widetilde{L}_1+\widetilde{L}_2\big )\ \text {for}\ \frac{11-6u}{3}\leqslant v\leqslant 3-u,\\&(4-2u-v)\big (2\widetilde{\ell }+3\widetilde{C}_2+\widetilde{L}_1+\widetilde{L}_2+F\big ) \ \text {for}\ 3-u\leqslant v\leqslant 4-2u, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{N}(u,v)= \left\{ \begin{aligned}&0\ \text {for}\ 0\leqslant v\leqslant 3-2u,\\&\frac{v+2u-3}{2}\widetilde{\ell } \ \text {for}\ 3-2u\leqslant v\leqslant \frac{11-6u}{3},\\&(4u+2v-7)\widetilde{\ell }+(6u+3v-11)\widetilde{C}_2 \ \text {for}\ \frac{11-6u}{3}\leqslant v\leqslant 3-u,\\&(4u+2v-7)\widetilde{\ell }+(6u+3v-11)\widetilde{C}_2+(v+u-3)\big (\widetilde{L}_1+\widetilde{L}_2\big )\\&\quad \text {for}\ 3-u\leqslant v\leqslant 4-2u, \end{aligned} \right. \end{aligned}$$

which gives

$$\begin{aligned} \big (\widetilde{P}(u,v)\big )^2= \left\{ \begin{aligned}&2u^2-v^2-12u+13\ \text {for}\ 0\leqslant v\leqslant 3-2u,\\&\frac{35}{2}-18u-3v+4u^2-\frac{v^2}{2}+2uv \ \text {for}\ 3-2u\leqslant v\leqslant \frac{11-6u}{3},\\&22u^2+20uv+4v^2-84u-36v+78 \ \text {for}\ \frac{11-6u}{3}\leqslant v\leqslant 3-u,\\&6(4-2u-v)^2 \ \text {for}\ 3-u\leqslant v\leqslant 4-2u, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{P}(u,v)\cdot F= \left\{ \begin{aligned}&v\ \text {for}\ 0\leqslant v\leqslant 3-2u,\\&\frac{3-2u+v}{2} \ \text {for}\ 3-2u\leqslant v\leqslant \frac{11-6u}{3},\\&18-10u-4v+18 \ \text {for}\ \frac{11-6u}{3}\leqslant v\leqslant 3-u,\\&24-12u-6v \ \text {for}\ 3-u\leqslant v\leqslant 4-2u, \end{aligned} \right. \end{aligned}$$

Similarly, if $1\leqslant u\leqslant \frac{4}{3}$, then

$$\begin{aligned} \widetilde{P}(u,v)= \left\{ \begin{aligned}&(4-3u)\big (\widetilde{\ell }+\widetilde{C}_2\big )+(8-6u-v)F\ \text {for}\ 0\leqslant v\leqslant 4-3u,\\&\frac{12-9u-v}{2}\widetilde{\ell }+(4-3u)\widetilde{C}_2+(8-6u-v)F \ \text {for}\ 4-3u\leqslant v\leqslant \frac{20-15u}{2},\\&(8-6u-v)\big (2\widetilde{\ell }+3\widetilde{C}_2+F\big ) \ \text {for}\ \frac{20-15u}{2}\leqslant v\leqslant 8-6u, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{N}(u,v)= \left\{ \begin{aligned}&0\ \text {for}\ 0\leqslant v\leqslant 4-3u,\\&\frac{v+3u-4}{2}\widetilde{\ell } \ \text {for}\ 4-3u\leqslant v\leqslant \frac{20-15u}{2},\\&(9u+2v-12)\widetilde{\ell }+(15u+3v-20)\widetilde{C}_2\ \text {for}\ \frac{20-15u}{2}\leqslant v\leqslant 8-6u, \end{aligned} \right. \end{aligned}$$

which gives

$$\begin{aligned} \big (\widetilde{P}(u,v)\big )^2= \left\{ \begin{aligned}&27u^2-v^2-72u+48\ \text {for}\ 0\leqslant v\leqslant 4-3u,\\&56-84u-4v+\frac{63u^2}{2}-\frac{v^2}{2}+3uv \ \text {for}\ 4-3u\leqslant v\leqslant \frac{20-15u}{2},\\&4(6u+v-8)^2\ \text {for}\ \frac{20-15u}{2}\leqslant v\leqslant 8-6u, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{P}(u,v)\cdot F= \left\{ \begin{aligned}&v\ \text {for}\ 0\leqslant v\leqslant 4-3u,\\&\frac{4-3u+v}{2} \ \text {for}\ 4-3u\leqslant v\leqslant \frac{20-15u}{2},\\&32-24u-4v\ \text {for}\ \frac{20-15u}{2}\leqslant v\leqslant 8-6u, \end{aligned} \right. \end{aligned}$$

Now, we can compute

$$\begin{aligned} S\big (W^S_{\bullet ,\bullet };F\big )=\frac{1}{8}\int \limits _1^{\frac{4}{3}}(u-1)(27u^2-72u+48)du+\frac{1}{8}\int \limits _0^{\frac{4}{3}}\int \limits _0^{\widetilde{t}(u)}\big (\widetilde{P}(u,v)\big )^2dvdu=\frac{1661}{864}. \end{aligned}$$

Let O be a point in F. If $O\in \widetilde{\ell }\cap \widetilde{C}_2\cap \widetilde{C}_5$, then $O\not \in \widetilde{L}_1\cup \widetilde{L}_2$, so that

$$\begin{aligned}{} & {} F_O\big (W_{\bullet ,\bullet ,\bullet }^{\widetilde{S},F}\big )= \frac{1}{4}\int \limits _1^{\frac{4}{3}}\int \limits _0^{8-6u}(u-1)\big (\widetilde{P}(u,v)\cdot F\big )dvdu \\{} & {} \quad \ + \frac{1}{4}\int \limits _0^{\frac{4}{3}}\int \limits _0^{\widetilde{t}(u)}\big (\widetilde{P}(u,v)\cdot F\big )\cdot \textrm{ord}_O\big (\widetilde{N}(u,v)\big |_F\big )dvdu\\{} & {} \quad =\frac{1}{576}+\frac{1}{4}\int \limits _0^{\frac{2}{3}}\int \limits _{3-2u}^{\frac{11-6u}{3}}\big (\widetilde{P}(u,v)\cdot F\big )\frac{v+2u-3}{2}dvdu \\{} & {} \quad \ +\frac{1}{4}\int \limits _0^{\frac{2}{3}}\int \limits _{\frac{11-6u}{3}}^{4-2u}\big (\widetilde{P}(u,v)\cdot F\big )\big ((6u+3v-11)+(4u+2v-7)\big )dvdu\\{} & {} \quad +\frac{1}{4}\int \limits _{\frac{2}{3}}^1\int \limits _{3-2u}^{\frac{11-6u}{3}}\big (\widetilde{P}(u,v)\cdot F\big )\frac{v+2u-3}{2}dvdu \\{} & {} \quad \ +\frac{1}{4}\int \limits _0^{\frac{2}{3}}\int \limits _{\frac{11-6u}{3}}^{4-2u}\big (\widetilde{P}(u,v)\cdot F\big )\big ((6u+3v-11)+(4u+2v-7)\big )dvdu\\{} & {} \quad +\frac{1}{4}\int \limits _{1}^{\frac{4}{3}}\int \limits _{4-3u}^{\frac{20-15u}{3}}\big (\widetilde{P}(u,v)\cdot F\big )\frac{v+2u-3}{2}dvdu \\{} & {} \quad \ +\frac{1}{4}\int \limits _{1}^{\frac{4}{3}}\int \limits _{\frac{20-15u}{3}}^{8-6u}\big (\widetilde{P}(u,v)\cdot F\big )\big ((6u+3v-11)+(4u+2v-7)\big )dvdu=\frac{235}{1728}, \end{aligned}$$

so that

$$\begin{aligned} S\big (W_{\bullet , \bullet ,\bullet }^{\widetilde{S},F};O\big )=\frac{1}{8}\int \limits _0^{\frac{4}{3}}\int \limits _0^{\widetilde{t}(u)}\big (\widetilde{P}(u,v)\cdot F\big )^2dvdu+\frac{235}{1728}=\frac{1685}{1728}. \end{aligned}$$

Similarly, if $O\in \widetilde{\ell }\cup \widetilde{C}_2$, then $S(W_{\bullet , \bullet ,\bullet }^{\widetilde{S},F};O)\leqslant \frac{1685}{1728}$. If $O\in \widetilde{L}_1\cup \widetilde{L}_2$, then $O\not \in \widetilde{\ell }\cup \widetilde{C}_2$, and O is contained in exactly one of the curves $\widetilde{L}_1$ or $\widetilde{L}_2$. In this case, we have

$$\begin{aligned} S\big (W_{\bullet , \bullet ,\bullet }^{\widetilde{S},F};O\big )= \left\{ \begin{aligned}&\frac{515}{576} \ \text { if } O\in \widetilde{C}_5,\\&\frac{257}{288} \ \text { if } O\not \in \widetilde{C}_5. \end{aligned} \right. \end{aligned}$$

The lemma is proved. $\square$

FormalPara Lemma 21

Suppose $T_P=\ell _1+\ell _2+\ell _3$, where $\ell _1$, $\ell _2$, $\ell _3$ are lines such that $P=\ell _1\cap \ell _2$ and $P\not \in \ell _3$. Then $S(W^S_{\bullet ,\bullet };F)<2$ and $S(W_{\bullet , \bullet ,\bullet }^{\widetilde{S},F};O)<1$ for every point $O\in F$.

FormalPara Proof

Let $\widetilde{\ell }_1$, $\widetilde{\ell }_2$, $\widetilde{\ell }_3$ be the proper transforms on $\widetilde{S}$ of the lines $\ell _1$, $\ell _2$, $\ell _3$, respectively. If $0\leqslant u\leqslant 1$, then it follows from (3) that

$$\begin{aligned} \widetilde{P}(u,v)= \left\{ \begin{aligned}&\widetilde{\ell }_1+\widetilde{\ell }_2+\widetilde{\ell }_3+(1-u)\big (\widetilde{L}_1+\widetilde{L}_2\big )+(4-2u-v)F \text { for } 0\leqslant v\leqslant 3-2u, \\&\frac{5-2u-v}{2}\big (\widetilde{\ell }_1+\widetilde{\ell }_2\big )+\widetilde{\ell }_3+(1-u)\big (\widetilde{L}_1+\widetilde{L}_2\big )+(4-2u-v)F \\&\quad \text { for } 3-2u \leqslant v\leqslant 3-u,\\&\frac{5-2u-v}{2}\big (\widetilde{\ell }_1+\widetilde{\ell }_2\big )+\widetilde{\ell }_3+(4-2u-v)\big (\widetilde{L}_1+\widetilde{L}_2+F\big ) \\ {}&\quad \text { for } 3-u \leqslant v\leqslant 4-2u, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{N}(u,v)= \left\{ \begin{aligned}&0 \text { for } 0\leqslant v\leqslant 3-2u, \\&\frac{v+2u-3}{2}\big (\widetilde{\ell }_1+\widetilde{\ell }_2\big ) \ \text { for } 3-2u \leqslant v\leqslant 3-u,\\&\frac{v+2u-3}{2}\big (\widetilde{\ell }_1+\widetilde{\ell }_2\big )+(v+u-3)\big (\widetilde{L}_1+\widetilde{L}_2\big ) \ \text { for } 3-u \leqslant v\leqslant 4-2u, \end{aligned} \right. \end{aligned}$$

which gives

$$\begin{aligned} \big (\widetilde{P}(u,v)\big )^2= \left\{ \begin{aligned}&2u^2-v^2-12u+13 \text { for } 0\leqslant v\leqslant 3-2u, \\&6u^2+4uv-24u-6v+22 \ \text { for } 3-2u \leqslant v\leqslant 3-u,\\&8u^2+8uv+2v^2-36u-18v+40 \ \text { for } 3-u \leqslant v\leqslant 4-2u, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{P}(u,v)\cdot F= \left\{ \begin{aligned}&v \text { for } 0\leqslant v\leqslant 3-2u, \\&3-2u\ \text { for } 3-2u \leqslant v\leqslant 3-u,\\&9-4u-2v \ \text { for } 3-u \leqslant v\leqslant 4-2u. \end{aligned} \right. \end{aligned}$$

Similarly, if $1\leqslant u\leqslant \frac{3}{2}$, then

$$\begin{aligned} \widetilde{P}(u,v)= \left\{ \begin{aligned}&(4-3u)\big (\widetilde{\ell }_1+\widetilde{\ell }_2+\widetilde{\ell }_{3}\big )+(8-6u-v)F \ \text { for } 0\leqslant v\leqslant 4-3u, \\&\frac{12-9u-v}{2}\big (\widetilde{\ell }_1+\widetilde{\ell }_2\big )+(4-3u)\widetilde{\ell }_3+(8-6u-v)F \\ {}&\quad \text { for } 4-3u\leqslant v \leqslant 8-6u, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{N}(u,v)= \left\{ \begin{aligned}&0\ \text { for } 0\leqslant v\leqslant 4-3u, \\&\frac{v+3u-4}{2}\big (\widetilde{\ell }_1+\widetilde{\ell }_2\big ) \ \text { for } 4-3u\leqslant v \leqslant 8-6u, \end{aligned} \right. \end{aligned}$$

which gives

$$\begin{aligned} \big (\widetilde{P}(u,v)\big )^2= \left\{ \begin{aligned}&27u^2-v^2-72u+48 \ \text { for } 0\leqslant v\leqslant 4-3u, \\&2(4-3u)(8-6u-v) \ \text { for } 4-3u\leqslant v \leqslant 8-6u, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \widetilde{P}(u,v)\cdot F= \left\{ \begin{aligned}&v\ \text { for } 0\leqslant v\leqslant 4-3u, \\&4-3u\ \text { for } 4-3u\leqslant v \leqslant 8-6u. \end{aligned} \right. \end{aligned}$$

Since $P\in C_5$ and $C_5$ is smooth, we compute $S(W^S_{\bullet ,\bullet };F)=\frac{31}{16}$. Similarly, if O is a point in F, then

$$\begin{aligned} S\big (W_{\bullet , \bullet ,\bullet }^{\widetilde{S},F};O\big )= \left\{ \begin{aligned}&\frac{329}{384} \ \text { if } O\in \widetilde{\ell }_1\cup \widetilde{\ell }_{2},\\&\frac{161}{192} \ \text { if } O\in \widetilde{L}_1\cup \widetilde{L}_2, \\&\frac{155}{192} \ \text { if } O\not \in \widetilde{\ell }_1\cup \widetilde{\ell }_{2}\cup \widetilde{L}_1\cup \widetilde{L}_2. \end{aligned} \right. \end{aligned}$$

The lemma is proved. $\square$

Thus, we see that $S(W^S_{\bullet ,\bullet };F)<2$ and $S(W_{\bullet , \bullet ,\bullet }^{\widetilde{S},F};O)<1$ for every point $O\in F$. Hence, using (2), we conclude that $\beta (\textbf{F})>0$. The Main Theorem is proved.