1 Introduction

The application of mathematics to physics and life sciences allows the formulation of models to interpret the phenomena that are observed by the experimentalists. A wealth of examples can be drawn for instance from mechanics, material sciences, fluid mechanics [4] or human population dynamics [1]. For instance, with the advancement of technology, new materials have appeared that exhibit features that depart from the classical assumptions of Newtonian fluids. They are at the boundary between fluids and soft solids, with a behavior that is plastic and not elastic. Rheology investigates the properties of these soft solids. For their understanding, new reformulations of the classical equations of mathematical physics are required.

In physics in particular, attention has recently been paid to situations in which the energy at a point depends also on the neighboring points, up to a threshold distance which is a function of the range of the molecular forces. Thus a material that has two possible stable states can be set up from these microscopic interactions over a lattice of points. This gives a dynamical system, in which the sum of the lattice interactions represent an approximated integral. In this way nonlocal alternatives of well-known equations such as Phase-Field Klein-Gordon as well as Allen-Cahn, are obtained [5]. For instance, expressing the concentration of a species at a point in a two-element alloy gives rise to the nonlocal version of the Cahn-Hilliard equation [6,7,8].

To give another example, also a nonlocal version of the nonlinear Schrödinger equation, which is based on a convolution, has been investigated. A numerical method has been proposed to ease the computational costs involved in the simulation of the original equation. By means of a suitable reformulation that employs partial differential equation techniques, the original integro-differential equation is reformulated as a system of partial differential equations. The latter can then be numerically integrated by means of an improvement of a finite integration method [13].

Many numerical methods for nonlocal equations have been developed based essentially on techniques related to partial differential equations, see for instance the unconditionally energy stable finite difference convex splitting schemes of [2], one being first order accurate in time and second order accurate in space, the second one instead representing a fully second-order scheme, both solved by efficient nonlinear multigrid methods. Also consider the more recent second order methods presented in [3].

In this paper we would like to address the problem of nonlocal diffusion type equations describing a fourth order scheme for its solution. The main novelty of this investigation consists in the fact that the proposed line method avoids any reformulation of the problem, dealing instead directly with the original integro-differential formulation. To illustrate the method, we consider a relatively simple diffusive equation.

The paper is organized as follows. In the next section we describe the equation under study, the numerical scheme is presented in Sect. 3, the needed quadratures are contained in Sect. 4 and numerical evidence in support of our results concludes the paper.

2 The sample model

We illustrate the numerical method on a simple example. Our starting point is a simple diffusion equation in which nonlocal interactions are considered. Specifically we consider the following nonlinear diffusion equation subject to nonlocal interactions

$$\begin{aligned} \frac{\partial u(x,t)}{\partial t}=\frac{\partial ^2 u(x,t)}{\partial x^2} - u(x,t) \int _{-a}^a \varphi (y-x)u(y,t)\ dy, \qquad a \in {\mathbb {R}}^+, \end{aligned}$$
(1)

where the kernel function \(\varphi (y-x)\) is sufficiently smooth. The initial condition is

$$\begin{aligned} u(x,0)=k(x), \quad k \in C([-a,a]) \end{aligned}$$

while the Dirichlet boundary conditions read

$$\begin{aligned} u(-a,t)=H_-(t), \quad u(a,t)=H_+(t), \quad t>0, \quad H_{\pm } \in C([0,\infty )) . \end{aligned}$$
(2)

In the examples, we will simply take \(H_-=H_+\). For the subsequent illustration of the numerical method it is convenient to set a specific notation for the nonlocal interactions, namely

$$\begin{aligned} J(u,x,t)=\int _{-a}^a \varphi (y-x)u(y,t)\ dy, \qquad a \in {\mathbb {R}}^+ . \end{aligned}$$

3 The method

We propose to use the method of lines, suitably adapted for this task. It can be summarized in the following steps:

  • Collocate (1) in a set of \(n-1\) equispaced internal points \(\{x_i\}_{i=1}^{n-1}\) of the interval \((-a,a)\);

  • Approximate the spatial derivatives \(\frac{\partial ^2 u(x,t)}{\partial x^2}\Big |_{x=x_i}\) by means of finite differences schemes;

  • Approximate the integrals \(J(u,x_i,t)\) with a quadrature formula based on the Generalized Bernstein polynomials;

  • Solve the obtained ordinary differential system by applying the standard Runge-Kutta-Fehlberg (4,5) method.

More in detail, let n denote the number of nodes in the spatial mesh; the nodes and the stepsize are

$$\begin{aligned} x_i=-a+hi, \quad i=0,1,\ldots ,n, \quad \displaystyle h=2a n^{-1}; \end{aligned}$$

equation (1) is collocated at the internal nodes \(x_i\), \(i=1,\ldots ,n-1\):

$$\begin{aligned} \frac{\partial u(x_i,t)}{\partial t}=\frac{\partial ^2 u(x_i,t)}{\partial x^2} - u(x_i,t) J(u,x_i,t), \quad i=1,\ldots ,n-1; \end{aligned}$$
(3)

At the points \(x_0\) and \(x_n\) the boundary conditions (2) are employed. The restriction of the solution at the nodes becomes a function solely of time, denoted by \(u_i(t) = u(x_i,t)\); its second partial derivative in space is discretized by means of the divided central difference scheme of order \(\mathcal {O}(h^4)\) (see for instance [10]):

$$\begin{aligned} \frac{\partial ^2 u(x,t)}{\partial x^2}\bigg |_{x=x_i} \simeq \frac{1}{h^2} \left[ -\frac{1}{12} u_{i-2}(t) + \frac{4}{3} u_{i-1}(t) -\frac{5}{2} u_i(t) \right. \nonumber \\ \left. + \frac{4}{3} u_{i+1}(t)-\frac{1}{12} u_{i+2}(t) \right] , \quad i=2,\ldots ,n-2; \end{aligned}$$
(4)

For nodes involving points that lie outside the mesh, we suitably modify the finite difference formulae, while keeping their accuracy commensurable with the one of (4), namely order \(\mathcal {O}(h^4)\). These meshpoints near the boundary are those with index \(i=1\) and \(i=n-1\); the modified finite difference formulae are:

$$\begin{aligned} \frac{\partial ^2 u(x,t)}{\partial x^2}\bigg |_{x=x_1}\simeq & {} \frac{1}{h^2} \left[ \frac{5}{6} u_0(t) -\frac{15}{12}u_1(t)-\frac{1}{3} u_2(t)+\frac{7}{6} u_3(t) \right. \nonumber \\- & {} \left. \frac{1}{2} u_4(t)+ \frac{1}{12}u_5(t)\right] , \end{aligned}$$
(5)
$$\begin{aligned} \frac{\partial ^2 u(x,t)}{\partial x^2}\bigg |_{x=x_{n-1}}\simeq & {} \frac{1}{h^2} \left[ \frac{1}{12}u_{n-5}(t)-\frac{1}{2} u_{n-4}(t)+\frac{7}{6} u_{n-3}(t)\right. \nonumber \\- & {} \left. \frac{1}{3} u_{n-2}(t) - \frac{15}{12}u_{n-1}(t)+\frac{5}{6} u_{n}(t) \right] ; \end{aligned}$$
(6)

Moreover in (3) we approximate the integrals \(J(u,x_i,t)\) by means of one of the two quadrature formulae that will be illustrated in Sect. 4; both of them are based on the uniform mesh \(x_i\), \(i=0,\ldots ,n\). The choice between these quadratures depends on the nature of the kernel \(\varphi (y-x)\). Hence, denoting by \(J_n(u,x,t)\) the quadrature rule used for the discretization of J, see (16), from the divided difference scheme (4)-(6), we get the following system of ODEs

$$\begin{aligned} \frac{d u_1(t)}{dt}= & {} \frac{1}{h^2} \left[ \frac{5}{6} u_0(t)-\frac{15}{12}u_1(t)-\frac{1}{3} u_2(t) +\frac{7}{6} u_3(t)-\frac{1}{2} u_4(t) \right. \nonumber \\&+ \left. \frac{1}{12}u_5(t)\right] - u_1(t) J_n(u,x_1,t), \nonumber \\ \frac{d u_i(t)}{dt}= & {} \frac{1}{h^2} \left[ -\frac{1}{12} u_{i-2}(t) + \frac{4}{3} u_{i-1}(t)-\frac{5}{2} u_i(t)+ \frac{4}{3} u_{i+1}(t) \right. \nonumber \\&- \left. \frac{1}{12} u_{i+2}(t) \right] - u_i(t) J_n(u,x_i,t), \quad i=2,\ldots ,n-2, \nonumber \\ \frac{d u_{n-1}(t)}{dt}= & {} \frac{1}{h^2} \left[ \frac{1}{12}u_{n-5}(t)-\frac{1}{2} u_{n-4}(t)+\frac{7}{6} u_{n-3}(t)-\frac{1}{3} u_{n-2}(t) \right. \nonumber \\&- \left. \frac{15}{12}u_{n-1}(t)+\frac{5}{6} u_{n}(t) \right] -u_{n-1}(t)J_n(u,x_{n-1},t), \end{aligned}$$
(7)

with initial conditions \(u_i(0)=k(x_i)\), \(i=0,\ldots ,n\). The final discretized system of ordinary differential equations (7) is then solved by means of the Runge-Kutta (4, 5) method, implemented by the "ode45" Matlab integrator.

4 The quadrature formulae

Let us fix x and t. To approximate the integral

$$\begin{aligned} J(u,x,t)=\int _{-a}^a \varphi (y-x)u(y,t)\ dy, \qquad a \in {\mathbb {R}}^+ \end{aligned}$$
(8)

we suggest two possible strategies, according to the nature of the kernel \(\varphi \). The first case deals with very smooth kernels, the second one is reliable in all the cases where the kernel presents some kind of pathologies: weak singularity, high oscillations (see Fig. 1), “near” strong singularity, etc. In such cases the standard rules fail, and product integration rules provide satisfactory results because they integrate exactly the pathology. Each kernel has to be treated with specific approaches based on its very nature, and this entails different ways of implementing the computation. For the pathological case we consider oscillating kernels of the type

$$\begin{aligned} \varphi (y-x)=e^{i\omega (y-x)} \end{aligned}$$

for a “large” oscillation frequency \(\omega \).

Fig. 1
figure 1

For \(x\in [-1,1],\ y\in [0,10]\), graphics of the kernels \(\varphi (y-x)=\sin (5(y-x))\) (left) and \(\varphi (y-x)=\cos (25(y-x))\) (right)

Full size image

Both the rules that we consider are based on the same Generalized Bernstein operator

$$\begin{aligned} B_{n,\ell }=I-(I-B_n)^\ell ,\quad n,\ell \in \mathbb {N}^*:=\mathbb {N}\small {\smallsetminus }\{0\}, \end{aligned}$$

where \(B_n\) is the ordinary Bernstein operator, shifted to the interval \([-a,a]\). Boolean sums based on the Bernstein operator \(B_n\) represent an adequate tool to attain our goal, since they are based on \(n+1\) equally spaced points in \([-a,a]\). Furthermore, unlike the “originating” operator \(B_{n}\), the speed of convergence accelerates as the smoothness of the approximating function increases. To be more precise, first we recall that for \(r\in \mathbb {N}^*,\) with \(1 \le r\le 2\ell \), the \(r-\)th Sobolev-type space is defined as

$$\begin{aligned} W_r([-a,a])=\left\{ f^{(r-1)}\in \mathcal{AC}\mathcal{} : \Vert f^{(r)}\phi ^r\Vert _\infty <\infty \right\} ,\quad \ \Vert f\Vert _{W_r}=\Vert f\Vert _\infty +\Vert f^{(r)}\phi ^r\Vert _\infty , \end{aligned}$$

where \(\displaystyle \Vert f\Vert _{\infty }:=\max _{x\in [-a,a]}|f(x)|\) is the uniform norm, \(\phi (x)=\sqrt{a^2-x^2}\) and \(\mathcal{AC}\mathcal{}\) denotes the space of all locally absolutely continuous functions on \([-a, a]\). Consequently, for each \(f \in W_r([-a,a])\) the error is estimated as \(\Vert f-B_{n,\ell }(f)\Vert _\infty = \mathcal {O}(\sqrt{n^{-r}})\), \(1 \le r\le 2\ell \). In other words, the convergence rate behaves like the square root of the best approximation error for this functional space. Note that \(C^r([-a,a])\subset W_r([-a,a])\). A survey on the Generalized Bernstein polynomials and their applications is contained in [12].

In what follows by writing \(g_x(y)\) we mean that any bivariate function g(x, y) is taken as function just of the variable y. Furthermore, from now on we use \(\mathcal {C}\) in order to denote a positive constant, which may have different values at different occurrences, and we write \(\mathcal {C}\ne \mathcal {C}(n,f,\ldots )\) to mean that \(\mathcal {C}>0\) is independent of \(n,f, \ldots \).

4.1 First case: the “smooth” kernel \(\varphi (y-x)\)

In this case we use the Generalized Bernstein quadrature formula studied in [11] and based on shifted Generalized Bernstein Polynomials:

$$\begin{aligned} \int _{-a}^a f(y)\varphi (y-x) \ dy\simeq & {} \int _{-a}^a B_{n,\ell }(f\varphi _x,y) \ dy= \sum _{j=0}^{n} f(x_j)\varphi (x_j-x)D_j^{(\ell )},\nonumber \\ D_j^{(\ell )}= & {} \frac{2a}{n+1}\sum _{i=0}^n c_{i,j}^{(n,\ell )},\quad x_k:=-a+k\frac{2a}{n}, \end{aligned}$$
(9)

where \(c_{i,j}^{(n,\ell )}\) are the entries of the matrix \(C_{n,\ell }\in {\mathbb {R}}^{(n+1)\times (n+1)}\),

$$\begin{aligned} C_{n,\ell } ={\textbf {I}}+({\textbf {I}}-{\textbf {A}})+\ldots +({\textbf {I}}-{\textbf {A}})^{\ell -1},\quad C_{n,1}={\textbf {I}}, \end{aligned}$$
(10)

and \({\textbf {I}}\) denotes the identity matrix. Furthermore

$$\begin{aligned} \begin{aligned} {\textbf {A}}:=({\textbf {A}}_{i,j}), \qquad {\textbf {A}}_{i,j}:= p_{n,j}(x_i),\quad i,j\in \{0,1,\dots ,n\},\\ p_{n,i}(x):= \left( {\begin{array}{c}n\\ i\end{array}}\right) \left( \frac{a+x}{2a}\right) ^i \left( \frac{a-x}{2a}\right) ^{n-i},\quad \ i=0,1,\dots ,n. \end{aligned} \end{aligned}$$

Letting

$$\begin{aligned} \varepsilon _n(f \varphi _x)=\int _{-a}^a \left[ f(y)\varphi (y-x)- B_{n,\ell }(f\varphi _x,y)\right] \ dy, \end{aligned}$$

under the assumption

$$\begin{aligned} \sup _{x\in [-a,a]} (f \varphi _x)\in W_r([-a,a]), \quad 1 \le r\le 2\ell \end{aligned}$$

and setting

$$\begin{aligned} \mathcal {M}:=\sup _{x\in [-a,a]}\Vert f\varphi _x\Vert _{W_r}, \end{aligned}$$

we have [9]

$$\begin{aligned} \sup _{x\in [-a,a]} |\varepsilon _n(f \varphi _x) |\le \mathcal {C}\left( \frac{a^{r+1}\mathcal {M}}{(\sqrt{n})^r}\right) , \quad \mathcal {C}\ne \mathcal {C}(n,f,\varphi ). \end{aligned}$$
(11)

An analogous estimate was derived in [11] in the classical case on the interval [0, 1].

4.2 Second case: the kernel \(\varphi (y-x)=e^{i\omega (y-x)}\)

By splitting this kernel into its real and imaginary parts, we obtain integrals of the type

$$\begin{aligned} \int _{-a}^a f(y)\kappa (\omega (y-x)) \ dy, \quad \kappa (\omega (y-x)) ={\left\{ \begin{array}{ll} \sin (\omega (y-x)),\\ \cos (\omega (y-x)). \end{array}\right. } \end{aligned}$$
(12)

Hence, by approximating f by \(B_{n,\ell }(f)\) we have

$$\begin{aligned} \int _{-a}^a f(y)\kappa (\omega (y-x)) \ dy\simeq & {} \int _{-a}^a B_{n,\ell }(f,y)\kappa (\omega (y-x))\ dy \nonumber \\= & {} \sum _{j=0}^{n} f(x_j)\sum _{i=0}^n c_{i,j}^{(n,\ell )}\int _{-a}^a p_{n,i}(y) \, \kappa (\omega (y-x)) \, dy \nonumber \\=: & {} \sum _{j=0}^{n} f(x_j)\sum _{i=0}^n c_{i,j}^{(n,\ell )}q_i(x). \end{aligned}$$
(13)

where \(p_{n,i}(y)\) and \(c_{i,j}^{(n,\ell )}\) are defined as in the previous subsection.

For the product rule to work, the integrals \(q_i(y)\) need to be accurately computed. To this end, we use the formula proposed in [9]. For the benefit of the reader, we now briefly recall it. Let \(N=\left\lfloor \omega \frac{a}{\pi }\right\rfloor +1\) and consider the partition \([-a,\ a]=\bigcup _{h=1}^N [t_{h-1}, t_h]\), \(t_h=-a+\frac{2a}{N}h.\) Hence, we have

$$\begin{aligned} q_i(x)= & {} \sum _{h=1}^N \int _{t_{h-1}}^{t_h} \kappa (\omega (y-x)) p_{n,i}(y)dy\\= & {} \frac{a}{N}\sum _{h=1}^N \int _{-1}^1 p_{n,i}\left( \gamma _h^{-1}(z)\right) \kappa \left( \omega \left( \gamma _h^{-1}(z)-x\right) \right) dz, \end{aligned}$$

where for \(h=1,2\dots ,N\) the transformations

$$\begin{aligned} y=\gamma ^{-1}_h(z):= \frac{a}{N}(z+1)+t_{h-1}, \end{aligned}$$
(14)

map \([t_{h-1},\,t_h]\) into \([-1,\,1]\). Then, approximating each integral by the n-th Gauss-Legendre rule,

$$\begin{aligned} \int _{-1}^1 g(y) dy\simeq \sum _{k=1}^n g(z_k) \lambda _k \end{aligned}$$

where \(\{z_k\}_{k=1}^{n}\) represent the zeros of the \(n-\)th Legendre polynomial and \(\{\lambda _k\}_{k=1}^{n}\) the corresponding Christoffel numbers, we have

$$\begin{aligned} q_i(x)= & {} \frac{a}{N}\sum _{h=1}^N \left( \sum _{k=1}^n p_{n,i}\left( \gamma _h^{-1}(z_k)\right) \kappa \left( \omega \left( \gamma _h^{-1}(z_k)-x\right) \right) \lambda _k+\varepsilon _{n}^{i,h}(x)\right) . \end{aligned}$$

Combining the above equation with (13), we obtain the following quadrature rule:

$$\begin{aligned}&\int _{-a}^a f(y)\kappa (\omega (y-x)) \ dy = \sum _{j=0}^{n} f(x_j)P_{j}^{(\ell )}(x)+ R_{n}^{(\ell )}(x), \nonumber \\&P_{j}^{(\ell )}(x)=\frac{a}{N}\sum _{i=0}^n c_{i,j}^{(n,\ell )} \sum _{h=1}^N \left( \sum _{k=1}^n p_{n,i} \left( \gamma _h^{-1}(z_k)\right) \kappa \left( \omega \left( \gamma _h^{-1}(z_k)-x\right) \right) \lambda _k\right) .\nonumber \\ \end{aligned}$$
(15)

For the quadrature error, for any \(f\in W_r([-a,a])\), \(1 \le r \le 2\ell \), and for n sufficiently large, say \(n>n_0\) for a fixed \(n_0\), we have [9]

$$\begin{aligned} \sup _{x\in [-a,a]} |R_{n}^{(\ell )}(x) |\le \mathcal {C}\Vert f\Vert _{W_r} \left[ \frac{a^{r+1} }{(\sqrt{n})^r}+n^{\frac{3}{2}} \Vert C_{n,\ell }\Vert _\infty \left( \frac{a}{N} \cdot \frac{n+\omega }{2n-1}\right) ^{n}\,\right] , \end{aligned}$$

where \(\mathcal {C}\ne \mathcal {C}(n,f)\) and \(\Vert C_{n,\ell }\Vert _\infty \) denotes the infinity norm of the matrix \(C_{n,\ell }\) defined in (10).

4.3 The approximation of J(u, x, t)

In summary, by using the results of the previous two subsections, to calculate (8) we have the following alternatives:

$$\begin{aligned} J(u,x,t)\simeq J_n(u,x,t):= {\left\{ \begin{array}{ll} \sum _{j=0}^{n} u(x_j,t)\varphi (x_j-x)D_j^{(\ell )}, &{} \text { first case }\\ \sum _{j=0}^{n} u(x_j,t)P_{j}^{(\ell )}(x), &{} \text { second case } \end{array}\right. } \end{aligned}$$
(16)

where \(D_j^{(\ell )}\) and \(P_{j}^{(\ell )}(x)\) are defined in (9) and (15).

5 Numerical experiments

In this section we report the results of some numerical experiments on the nonlocal diffusion model (1) for different choices of the kernel function \(\varphi (y-x)\). Without loss of generality we assume \(a=1\) and integrate up to time \(T=10\) throughout all our simulations, with the exception of Examples 5.5 and 5.6, in which we set \(a=2\) and \(a=3\) respectively.

To show the reliability of the proposed algorithm, we consider at first some examples constructed so that the analytical solution u(x, t) is known. In such cases we report the maximum absolute errors attained by the scheme. Denoting by \(u_n(x,t)\) the numerical solution of the discretized model for a fixed number n of meshnodes, we set

$$\begin{aligned} e_n(u) = \sup _{t \in [0,10]} \; \max _{x \in [-a,a]} |u(x,t)- u_n(x,t) |. \end{aligned}$$

The tables also display the Estimated Order of Convergence (EOC) and the Mean Estimated Order of Convergence defined as follows:

$$\begin{aligned} \text {EOC}_{n} = \frac{\log \left( \frac{e_{n/2}(u)}{e_{n}(u)}\right) }{\log 2}, \quad \text {EOC}_{\text {mean}}=\frac{1}{M-2} \sum _{k=3}^{M} \text {EOC}_{2^k}, \end{aligned}$$

where M is a fixed integer. In our case we set \(M=8\).

All the computed examples are carried out in Matlab R2022a in double precision on an M1 MacBook Pro under the macOS 12.4 operating system.

For the sake of brevity, from now on we also introduce the notation

$$\begin{aligned} \varvec{x}=(x_0,x_1,\ldots ,x_{n-1},x_n) \in {\mathbb {R}}^{n+1}. \end{aligned}$$

In Examples 5.1 and 5.2 the solution u(x, t) is known and the functions \(\varphi (y-x)\) are both smooth. Therefore, the chosen method is based on the Generalized Bernstein formula given in Sect. 4.1. As Tables 1 and 2 show, the \(\text {EOC}_{\text {mean}}\) is coherent with the expected value 4, that coincides with the order of the divided difference schemes employed.

Table 1 Example 5.1 - Numerical results
Full size table
Table 2 Example 5.2 - Numerical results
Full size table

Example 5.3 considers a kernel of the type \(\sin (\omega (y-x))\). In this case the quadrature formula for the discretization of J(u, x, t) in (1) is the product formula described in Sect. 4.2. Table 3 shows the performances of the method for four different choices of the oscillatory parameter \(\omega \), while Table 4 makes a direct comparison between the results obtained by the method based on the quadrature (9) and on the product rule (15) respectively. Note that for high values of \(\omega \) the results indicate that the latter turns out to be the optimal choice to obtain good approximations of the solution u(x, t).

Table 3 Example 5.3 - Numerical results for different values of \(\omega \)
Full size table
Table 4 Example 5.3 - Performance comparison of the quadrature formulae
Full size table
Table 5 Example 5.4 - Numerical results for different values of \(\omega \)
Full size table
Table 6 Example 5.3 - Mean EOC for different values of \(\omega \)
Full size table
Table 7 Example 5.4 - Mean EOC for different values of \(\omega \)
Full size table
Table 8 Example 5.5-Numerical results
Full size table
Table 9 Example 5.6-Numerical results
Full size table

Example 5.4 has the same known solution u(x, t) of Example 5.3, but the kernel \(\varphi (y-x)\) is of the type \(\cos (\omega (y-x))\). This choice is made in order to consider the case of applications in which the kernel function is of oscillatory type, namely \(\varphi (y-x)=e^{i\omega (y-x)}\), as described in Sect. 4.2. The good performances of the method based on the product formula are displayed in Table 5 using the same four values \(\omega \) of the previous example. Note that also these examples share almost the same \(\text {EOC}_{\text {mean}}\), which again is approximately 4, as underlined in Tables 6 and 7. Furthermore, according to the theoretical estimates of the described quadrature formulae, convergence to the exact solution is achieved.

Examples 5.5 and 5.6 are variations of Examples 5.1 and 5.4 respectively. We consider them to underline that the increment of the value a does not substantially affect the error propagation. In the first case we set \(a=2\) and in the second one \(a=3\) and \(\omega =80\). Tables 8 and 9 display the obtained results.

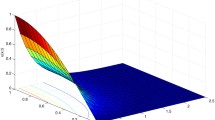
Finally, in Examples 5.7 and 5.8 the solution u(x, t) of the problem (1) is not known explicitly. Here the choices of \(\varphi (y-x)\) respectively are \(\sin (\omega (y-x))\) and \(e^{-(y-x)}\). Since in the previous examples we already tested the accuracy of our method, we just plot the approximated solution \(u_n(x,t)\) for \(n=256\). Hence, Figs. 2 and 3 display the approximated solutions, each of them obtained by the method based on the more suitable quadrature formula, according to the nature of the considered kernel \(\varphi (y-x)\). In both cases the plotted solutions \(u_{256}(x,t)\) satisfy the given initial and boundary conditions. Moreover, from Fig. 2 one can notice that the approximated solutions inherit the oscillating behavior of the kernel \(\sin (\omega (y-x))\): this can be easily observed when approaching the end of the time span [0, 10].

Overall from these results we infer that the proposed line method is a suitable and reliable discretization method for the problem (1).

Example 5.1

$$\begin{aligned} u(x,t)= & {} x^2t, \qquad \varphi (y-x)=\sin (y-x), \\ u(\varvec{x},0)= & {} (0,\ldots ,0), \quad u(-1,t)=u(1,t)=t. \end{aligned}$$
Fig. 2
figure 2

Example 5.5-Plot of the approximated solution u(x, t) for different values of \(\omega \)

Full size image

Example 5.2

$$\begin{aligned} u(x,t)= & {} x^2+t, \qquad \varphi (y-x)=e^{-(y-x)}, \\ u(\varvec{x},0)= & {} (x_0^2,\ldots ,x_n^2), \quad u(-1,t)=u(1,t)=1+t. \end{aligned}$$

Example 5.3

$$\begin{aligned} u(x,t)= & {} 2t-3x^2, \qquad \varphi (y-x)=\sin (\omega (y-x)), \\ u(\varvec{x},0)= & {} (-3x_0^2,\ldots ,-3x_n^2), \quad u(-1,t)=u(1,t)=2t-3. \end{aligned}$$
Fig. 3
figure 3

Example 5.6-Plot of the approximated solution u(x, t)

Full size image

Example 5.4

$$\begin{aligned} u(x,t)= & {} 2t-3x^2, \qquad \varphi (y-x)=\cos (\omega (y-x)), \\ u(\varvec{x},0)= & {} (-3x_0^2,\ldots ,-3x_n^2), \quad u(-1,t)=u(1,t)=2t-3. \end{aligned}$$

Example 5.5

$$\begin{aligned}&a=2, \quad u(x,t)=x^2t, \quad \varphi (y-x)=\sin (y-x), \\&u(\varvec{x},0)=(0,\ldots ,0), \quad u(-2,t)=u(2,t)=4t. \end{aligned}$$

Example 5.6

$$\begin{aligned}&a=3, \quad u(x,t)=2t-3x^2, \quad \varphi (y-x)=\cos (80(y-x)), \\&u(\varvec{x},0)=(-3x_0^2,\ldots ,-3x_n^2), \quad u(-3,t)=u(3,t)=2t-27. \end{aligned}$$

Example 5.7

$$\begin{aligned} \varphi (y-x)= & {} \sin (\omega (y-x)), \\ u(\varvec{x},0)= & {} (1,\ldots ,1), \quad u(-1,t)=u(1,t)=t^2+1. \end{aligned}$$

Example 5.8

$$\begin{aligned} \varphi (y-x)= & {} e^{-(y-x)}, \\ u(\varvec{x},0)= & {} \left( \frac{1}{5},\ldots ,\frac{1}{5}\right) , \quad u(-1,t)=u(1,t)=\log (t+1). \end{aligned}$$

6 Conclusions

In this paper we have presented a line method for the numerical solution of evolution equations of nonlocal type. It is fourth order accurate in both space and time. In contrast to other currently employed methods that, after possible previous reformulation of the original integro-differential equation, use order-two-accurate finite difference schemes, we propose a fourth order line method. Our numerical scheme relies on a good and efficient discretization of the integral term. This is achieved by using state-of-the-art quadratures based on Generalized Bernstein polynomials. The numerical examples support the analytical findings, if the kernel of the integral is smooth or, alternatively, presents weak singularities or high frequency oscillations. The case of strongly singular kernels, presenting additional difficulties, is currently being under investigation and will be examined in future research.