Fundamental functions for local interpolation of quadrilateral meshes with extraordinary vertices

Abstract

The aim of this work is to present a general and simple strategy for the construction of compactly supported fundamental spline (piecewise-polynomial) functions for local interpolation, that are defined over quadrangulations of the real plane with extraordinary vertices. The proposed strategy — which extends the univariate framework introduced in Antonelli et al. (Adv Comput Math 40:945–976, 2014) and Beccari et al. (J Comput Appl Math 240:5–19, 2013)—consists in considering a suitable combination of bivariate polynomial interpolants with blending functions that are the natural generalization of odd-degree tensor-product B-splines. These blending functions are constructed as basic limit functions of the bivariate, primal subdivision schemes developed simultaneously in Stam (Comput Aided Geom Des 18:397–427, 2001) and Zorin et al. (Comput Aided Geom Des 18:483–502, 2001). As an application example of our constructive strategy we present the compactly supported $C^2$ fundamental functions for local interpolation that arise by considering as blending functions the basic limit functions of the celebrated Catmull–Clark subdivision scheme proposed in Catmull and Clark (Comput Aided Des 46:103–124, 2016).

1 Introduction

Local interpolation methods aim at constructing a smooth interpolant $F: \, \Omega \rightarrow \mathbb {R}$ ($\Omega \subset \mathbb {R}^s$) that locally depends on the given set of vertices $\{ p_j \in \mathbb {R}, \, j \in J \}$ to be interpolated at the parameter values $\{ {{\varvec{x}}}_j \in \Omega , \, j \in J \}$. Locality is an extremely crucial property in applications since, in several situations, one may want to update the interpolant because new data has occurred, or to modify it only in a circumscribed region. The main challenge of local interpolation methods is to construct basis functions $\Psi _j$ that allow one to explicitly write F as

$$\begin{aligned} F({{\varvec{x}}})=\sum _{j \in J} {p}_j \, \Psi _j({{\varvec{x}}}), \qquad {{\varvec{x}}} \in \Omega . \end{aligned}$$

(1)

For F to satisfy the property $F({{\varvec{x}}}_j)={p}_j$ for all $j \in J$, we need that $\Psi _j$ are fundamental functions for interpolation (i.e., for $\Psi _j: \mathbb {R}^s \rightarrow \mathbb {R}$ that means $\Psi _j({{\varvec{x}}}_j)=1$ and $\Psi _j({{\varvec{x}}}_i)=0$ for all $i \ne j$). Moreover, for F to depend locally on the interpolation points, we need each $\Psi _j$ to be compactly supported and its support to be a compact set of the parametric domain $\Omega$. Finally, the smoothness of F will be the minimum smoothness of all the involved fundamental functions, and what one normally wants is that it is the smoothest possible for a selected support width.

In the univariate context ($s=1$) the most popular open problem of the last two decades has been the derivation of univariate subdivision schemes that allow one to construct fundamental functions for interpolation that compare favorably with those achievable via piecewise polynomial (or even piecewise exponential-polynomial) functions either in terms of support width, polynomial/exponential-polynomial reproduction or global smoothness (see, e.g., [6, 7, 9, 11]). Very recently in [10] it was shown that non-uniform univariate subdivision schemes have the potential to generate fundamental functions for interpolation that are smoother than those of uniform schemes with the same support size of the subdivision rule. Precisely, it was shown that $C^2$ basic limit functions can be generated by a non-uniform 4-point scheme, thus increasing the smoothness of the classical uniform 4-point scheme with the same support size [9] by one.

In the bivariate context ($s=2$), starting from the pioneering proposals in [17, 18], several uniform subdivision schemes have been proposed to construct compactly supported $C^2$ fundamental functions for interpolation that are defined on regular domains isomorphic to $\mathbb {Z}^s$. Alternative approaches other than subdivision schemes were also proposed (already from the end of the eighties) to build compactly supported $C^2$ fundamental solutions for cardinal interpolation in the context of shift invariant spaces [5, 8]. However, none of the above approaches has yet been adequately extended to obtain compactly supported $C^2$ basis functions which are fundamental for interpolation of arbitrary quadrilateral meshes (see Fig. 1).

Fig. 1

Example of a quadrangulation with one extraordinary vertex of valence 5

Definition 1

Let $\Omega$ be a simply connected subset of $\mathbb {R}^2$ with a polygonal boundary. Then we say that $\Omega$ is an arbitrary quadrangulation of the plane if it is partitioned into polygons where all faces are four sided, edges are shared by at most two faces and only intersect at vertices, and an arbitrary number of edges can intersect at the same vertex.

Definition 2

Let ${{\varvec{x}}}_j$ be an inner vertex of $\Omega$. If ${{\varvec{x}}}_j$ is the intersection point of four edges, then ${{\varvec{x}}}_j$ is termed regular, otherwise it is called irregular or extraordinary. The number of edges that are incident to ${{\varvec{x}}}_j$ is called the valence of ${{\varvec{x}}}_j$.

While generating globally $C^2$ basis functions for interpolation that are defined on a compact subset of $\Omega$ which includes only regular vertices turns out to be a trivial task, the construction of $C^2$ fundamental functions including also extraordinary vertices within their compact support is quite a complex issue. Motivated by the lack of general results and aware of the difficulties that arise from facing the general case, the goal of our paper is to propose an effective and simple strategy to build globally $C^2$ bivariate fundamental functions for local interpolation defined over arbitrary quadrangulations of the real plane. The first possible approach that we could consider to reach our goal is certainly to generalize the non-uniform univariate refinement rules proposed in [10] to quadrilateral meshes with extraordinary vertices. However, the current knowledge gaps on the design of extraordinary rules capable of achieving $C^2$ smoothness at extraordinary vertices [16] prevent this road from being considered viable. Another constructive strategy that turns out to be unsatisfactory to our purposes is also the one recently introduced in [14] for generating basis functions for interpolation that are locally supported over portions of quadrilateral meshes with extraordinary vertices. Indeed such a strategy yields basis functions that are not globally $C^2$ as we would like to get. Taking into account our past experience and our previously achieved results, the most feasible way is certainly to consider an appropriate extension of the univariate proposal presented in [1, 3]. Indeed in such papers we provided a very general method for constructing the entire class of univariate, piecewise-polynomial local interpolants that lends itself well to a bivariate generalization. In [2] the univariate method has been already generalized to interpolate the vertices of quadrilateral meshes that are either (i) regular or (ii) containing isolated extraordinary vertices. However, case (ii) was handled with an ad-hoc approach which consists in replacing the N mesh faces sharing an extraordinary vertex with N parametric surface elements connected with continuity of type $G^1$ (i.e., continuity of the tangent plane) or $G^2$ (i.e., continuity of curvature). Additionally, the approach in [2] requires information like first derivatives, and possibly second derivatives, along the edges of the region to be filled, that are often unavailable in practice. Therefore, starting from these past results, we aim to devise a more general strategy for constructing local interpolants to the vertices of a given quadrilateral mesh, which does not require any restriction on the number of its extraordinary vertices, and which can guarantee $C^2$ continuity at extraordinary vertices without any additional input data such as first and second derivatives. The first task towards the construction of globally $C^2$ surfaces of arbitrary topology is to build compactly supported globally $C^2$ basis functions for interpolation that are defined over arbitrary quadrangulations of the real plane. This will be the precise purpose of this paper where we focus on fundamental functions for interpolation that may contain in their compact support extraordinary vertices. The construction of the fundamental functions will rely on a suitable linear combination between bivariate polynomials interpolating subsets of the given data points, and compactly supported blending functions selected within the class of globally $C^1$ basic limit functions of spline-based bivariate subdivision schemes. In this combination, the polynomials will be designed to ensure that the interpolation constraints are satisfied, while the blending functions will blend together the polynomials in such a way that the smoothness of the resulting fundamental functions will be of one order higher than that of the blending functions.

More precisely, the paper is laid out as follows. Section 2 provides a brief review of the strategy introduced in [1, 3] to construct piecewise-polynomial univariate fundamental functions for local interpolation. Section 3 presents a generalization of the univariate strategy to build bivariate fundamental functions for local interpolation. Section 4 discusses the main properties (i.e., interpolation, compact support and global smoothness) of the bivariate fundamental functions produced by the new strategy we propose. Section 5 presents the globally $C^2$ fundamental functions generated by using the Catmull–Clark basic limit functions as a specific example of blending functions. Moreover, Sect. 5 illustrates examples of globally $C^2$ parametric surfaces built-upon such fundamental functions, that interpolate the vertices of a quadrilateral mesh with an extraordinary vertex. Finally, Sect. 6 identifies issues that deserve further investigation.

2 A brief review of the univariate strategy

In [1, 3] it was devised a general strategy for the construction of piecewise-polynomial univariate fundamental functions for local interpolation that may attain arbitrary smoothness, degree and support width. In the following we denote by $\{x_i\}$ a strictly increasing and finite sequence of nodes placed on the real line, and by $\Psi _j$ the fundamental function centered at the parameter value $x_j$, i.e. the fundamental function that satisfies $\Psi _{j}(x_i)=\delta _{i,j}$. The idea introduced in the above mentioned papers consists in defining $\Psi _j$ as a linear combination between univariate polynomials that interpolate subsets of the data points $(x_i, \delta _{i,j})$ and compactly supported blending functions. In this combination, the polynomials are designed to ensure that the interpolation constraints are satisfied, while the blending functions blend together the polynomials in such a way that $\Psi _j$ has the desired support width and smoothness. Hereinafter, the univariate polynomial interpolating a finite number of consecutive data $(x_k, \delta _{k,j})$ with $k \ge \ell$ is denoted by $\mathcal{P}_{\ell }$, whereas the blending function having compact support with first endpoint $x_{\ell }$ is denoted by $\Phi _{\ell }$. For the sake of simplicity (but also because it is the only background we need to introduce the bivariate strategy of Sect. 3), in this review we assume that the blending functions are polynomial B-spline basis functions of arbitrary degree, and that their knots coincide with the interpolation nodes $\{x_i\}$. Due to this choice, the support width of the blending functions is an integer. The combination of $\mathcal{P}_{\ell }$ and $\Phi _{\ell }$ that gives rise to $\Psi _j$ reads as

$$\begin{aligned} \Psi _{j}(x)= \sum _{\ell } \mathcal{P}_{\ell -\sigma }(x) \, \Phi _{\ell }(x), \qquad \sigma \in \mathbb {Z}. \end{aligned}$$

(2)

Here, the integer $\sigma$ can be arbitrarily selected keeping in mind that the nodes $x_i$ not interpolated by $\mathcal{P}_{\ell -\sigma }$ cannot lie in the support of $\Phi _{\ell }$. This yields the bounds $-1 \le \sigma \le m-w+1$ with m denoting the degree of each polynomial $\mathcal{P}_{\ell }$ and the integer w the support width of each blending function $\Phi _{\ell }$ involved in (2). Among these admissible choices of $\sigma$, the only value that guarantees the achievement of centrally symmetric functions, in case of symmetric sequences of nodes, is

$$\begin{aligned} \sigma =\left\lfloor \frac{m-w}{2} \right\rfloor . \end{aligned}$$

Examples of centrally symmetric fundamental functions for local interpolation are shown in Fig. 2. In general, independently of the admissible value assigned to $\sigma$, the fundamental function $\Psi _j$ defined in (2) has been shown to fulfill the following properties.

Fig. 2

Left: the $C^2$ fundamental function supported on $[-3,3]$ that is obtained by using our constructive approach with the quadratic B-splines as blending functions. Right: the $C^3$ fundamental function supported on $[-3,3]$ that is obtained by using our constructive approach with the cubic B-splines as blending functions. In both figures the interpolating polynomials blended by the B-splines (dashed graphs) are the dotted graphs

Proposition 1

(Interpolation)[3, Prop.1]. If the polynomials $\mathcal{P}_{\ell -\sigma }$ multiplying the non-vanishing blending functions $\Phi _{\ell }$ at the node $x_i$ are all interpolating the value $\delta _{i,j}$, then $\Psi _{j}$ satisfies the condition $\Psi _{j}(x_i)=\delta _{i,j}$.

Proposition 2

(Compact Support)[3, Prop.4]. If each $\mathcal{P}_{\ell -\sigma }$ is a univariate polynomial of degree m and each blending function $\Phi _{\ell }$ has support width w, then the support width of $\Psi _j$ is $m+w$.

Proposition 3

(Smoothness)[3, Prop.2]. Under the assumptions of Proposition 1 and 2, if every blending function $\Phi _{\ell }$ is $C^k$, then $\Psi _j$ is $C^{k+1}$.

The illustrative example in Fig. 2 left (respectively, right) shows the degree-5 fundamental function with compact support $[-3,3]$, that is obtained when selecting $\Phi _{\ell }$ as a degree-2 (respectively, degree-3) polynomial B-spline and $\mathcal{P}_{\ell }$ as a degree-3 (respectively, degree-2) polynomial interpolating a subset of four (respectively, three) consecutive points $(x_k, \delta _{k,j})$, $k \ge \ell$. Since the assumption of Proposition 1 is fulfilled, $\Psi _j$ is a fundamental function for interpolation. Moreover, according to Proposition 2, since $m=3$ and $w=3$ (respectively, $m=2$ and $w=4$), then the support width of $\Psi _j$ is 6. Finally, according to Proposition 3, since $\Phi _{\ell }$ is $C^1$ (respectively, $C^2$) then $\Psi _j$ is $C^{2}$ (respectively, $C^3$).

3 The bivariate strategy

The goal of the bivariate strategy is the construction of compactly supported, smooth fundamental functions for interpolation that are defined on an arbitrary quadrangulation of the plane denoted with $\Omega$ (see Definition 1). For the sake of simplicity, in this preliminary paper we assume that the compact support of each fundamental function may contain one extraordinary vertex at most. Moreover, to extend the idea introduced in Sect. 2, we assume that each fundamental function is obtained by combining bivariate polynomial interpolants with compactly supported bivariate blending functions. Since we deal with a domain whose boundary is a closed polygonal line, without loss of generality we may assume that $\Omega$ is defined in such a way that any arbitrary vertex ${{\varvec{x}}}_{\ell }$ used below to denote the center of a blending function, is always an inner vertex of $\Omega$ with a sufficient number of connected rings of faces around it, that allows for the following definitions.

Definition 3

The 0-ring neighbourhood of the vertex ${{\varvec{x}}}_{\ell } \in \Omega$ is the vertex itself.

Definition 4

For all $k \in \mathbb {N}$, the k-ring neighbourhood of ${{\varvec{x}}}_{\ell } \in \Omega$ is the union of its $(k-1)$-ring neighbourhood with all the quadrilateral faces of $\Omega$ that are incident to any vertex of the $(k-1)$-ring neighbourhood.

Definition 5

Let ${\varvec{x}}_{\ell } \in \Omega$. We denote by $\mathcal{R}_{\ell }^k$ ($k \in \mathbb {N}_0=\mathbb {N}\cup \{0\}$) the k-ring neighbourhood of ${\varvec{x}}_{\ell }$.

For the sake of clarity, in Table 1 we illustrate the 1-ring neighbourhood of a vertex of $\Omega$ of valence 3, 4, 5, 6.

Table 1 Graphical illustration of the 1-ring neighbourhood $\mathcal{R}_{\ell }^1$ of a vertex ${\varvec{x}}_{\ell } \in \Omega$ of valence 3, 4, 5, 6

Mimicking the univariate proposal, the bivariate fundamental function centered at ${\varvec{x}}_j$ is denoted by $\Psi _{j,n}$ and defined by the formula

$$\begin{aligned} \Psi _{j,n}({\varvec{x}})= \sum _{\ell } \mathcal{P}_{\ell , n}({\varvec{x}}) \ \Phi _{\ell ,n}({\varvec{x}}), \quad n \in \mathbb {N}. \end{aligned}$$

(3)

Here, $\Phi _{\ell ,n}$ denotes a bivariate blending function that is centered at the vertex ${\varvec{x}}_{\ell } \in \Omega$ and has compact support $\mathcal{R}_{\ell }^{n+1}$, namely the $(n+1)$-ring neighbourhood of ${\varvec{x}}_{\ell }$. For each ${\varvec{x}}_{\ell }$ we also introduce the notation

$$\begin{aligned} \mathcal{L}_{\ell }^n=\{ i \in \mathbb {N} : \ {{\varvec{x}}}_{i} \in \mathcal{R}_{\ell }^{n}\} \end{aligned}$$

to refer to the index set identifying all the vertices of $\Omega$ in $\mathcal{R}_{\ell }^{n}$. Moreover, for a suitable positive integer d, we denote with $\mathcal{P}_{\ell ,n}$ a bivariate polynomial of total degree d which satisfies the $\#\mathcal{L}_\ell ^n$ interpolation constraints

$$\begin{aligned} \mathcal{P}_{\ell ,n}({{\varvec{x}}_{k}})=\delta _{k,j} \quad \hbox {for \ all} \quad {k}\in \mathcal{L}_\ell ^n, \end{aligned}$$

(4)

and approximates in the least-squares sense the points $({{\varvec{x}}_{k}},0)$ with ${\varvec{x}}_{k} \in \Omega _\ell \setminus \mathcal{R}_{\ell }^{n}$, where $\Omega _\ell$ is a suitable subset of $\Omega$ (see section 3.2).

The challenging task is now to identify suitable blending functions and bivariate polynomial interpolants that, combined together, can provide well-performing $\Psi$ functions. As already highlighted in the introduction, the most desirable solution is the one that guarantees $\Psi$ functions having the highest possible smoothness for the selected support. In the following we introduce a family of blending functions (see section 3.1) and bivariate polynomial interpolants (see section 3.2) that, in the simplest case (i.e., in the case $n=1$), allow us to get a family of fundamental functions $\Psi _{j,1}$ that are compactly supported on $\mathcal{R}_{j}^{3}$ and globally $C^2$.

3.1 Blending functions to be used in the bivariate strategy

In order to construct a compactly supported bivariate function $\Phi _{\ell ,n}$ that is either centered at an extraordinary vertex or containing an extraordinary vertex within its support, and can play as a blending function in our approach, we consider the natural extension of the univariate odd-degree B-spline that is generated by the family of bivariate, primal subdivision schemes developed simultaneously by Stam [20] and Zorin and Schröder [21]. Indeed, the n-th member of this family is a subdivision scheme that gets back the degree-$(2n+1)$ tensor-product B-spline in the regions containing only regular vertices (also called regular regions), and yields smooth limit surfaces for any arbitrary quadrilateral mesh. Precisely, as shown in these papers, for all valences, the function $\Phi _{{\ell },n}$ is compactly supported on $\mathcal{R}_{\ell }^{n+1}$, and its smoothness is $C^{2n}(\mathbb {R}^2)$ if all the vertices within its support are valence-4 vertices, but only $C^1(\mathbb {R}^2)$ in case extraordinary vertices are within the support. Indeed, independently of the choice of n, the smoothness achieved at the extraordinary vertex is always $C^1$ only. Additionally, exactly as the univariate B-splines, these functions are strictly positive within their support and constitute a partition of unity.

A very famous subcase of the above family of primal subdivision schemes is given by the Catmull–Clark subdivision scheme [4]. This is exactly the first family member (corresponding to the choice $n=1$), which generates basic limit functions $\Phi _{{\ell },1}$ that are compactly supported on $\mathcal{R}_{{\ell }}^{2}$, coincide with the cubic $C^{2}(\mathbb {R}^2)$ tensor-product B-spline in the regular regions, and are only $C^1(\mathbb {R}^2)$ when extraordinary vertices are within the support. The analytic evaluation of the Catmull–Clark basic limit functions can be achieved by means of the procedure introduced in [19]. The illustration of the basic limit functions $\Phi _{\ell ,1}$ centered at an extraordinary vertex of valence 3, 5, 6 is displayed in the central column of Fig. 5, while the right column of Fig. 5 shows examples of basic limit functions $\Phi _{\ell ,1}$ centered at a valence-4 vertex ${\varvec{x}}_{\ell }$ that lies on the first ring around an extraordinary vertex of valence 3, 5, 6 respectively. All other blending functions centered at valence-4 vertices that lie on outer rings of the extraordinary vertex are not displayed since entirely defined on regular quadrilateral grids.

3.2 Polynomial interpolants to be used in the bivariate strategy

As we will prove in the next section, requiring that each polynomial $\mathcal{P}_{\ell ,n}$ involved in (3) satisfies the interpolation conditions (4) guarantees that the function $\Psi _{j,n}$ has the desired interpolation properties, i.e. that $\Psi _{j,n}({\varvec{x}}_k)=\delta _{k,j}$, for all ${\varvec{x}}_k\in \Omega$. To make sure that a polynomial $\mathcal{P}_{\ell ,n}$ provides enough degrees of freedom to satisfy the constraints (4), it is necessary to build it of a suitable degree d such that

$$\begin{aligned} \mathrm {dim}(\Pi _d)=\frac{(d+1)(d+2)}{2}\geqslant \#\mathcal {L}_\ell ^n, \end{aligned}$$

(5)

where $\Pi _d$ denotes the space of bivariate polynomials of degree less than or equal to d. In general, for a fixed degree d, the number of degrees of freedom which comes out from the above condition is higher than the number of interpolation constraints, and thus additional conditions should be introduced to identify each $\mathcal{P}_{\ell ,n}$. To this end, we have found convenient to require that the polynomial $\mathcal{P}_{\ell ,n}$ approximates in the least-squares sense other points $({{\varvec{x}}_{k}},0)$ with ${\varvec{x}}_{k} \in \Omega _\ell {\setminus } \mathcal{R}_{\ell }^n$, where $\Omega _\ell$ is a given subset of $\Omega$. Though the set $\Omega _\ell$ can be arbitrarily chosen, in practice it is advisable to select it so that the fundamental function $\Psi _{j,n}$ obtained from (3) will preserve symmetries in the data. There are of course many symmetry-preserving strategies for fixing $\Omega _\ell$, amongst which, we have chosen to set $\Omega _\ell = \mathcal{R}_{\ell }^{n+1}$, i.e. to approximate all the points $({{\varvec{x}}_{k}},0)$ with ${\varvec{x}}_k\in \mathcal{R}_{\ell }^{n+1}{\setminus } \mathcal{R}_{\ell }^{n}$. From the theoretical results in [12, Section 1.2] the existence of such a polynomial $\mathcal{P}_{\ell ,n}$ is guaranteed whenever d is sufficiently high, and the fact that we exploit the degrees of freedom to approximate all the points $({{\varvec{x}}_{k}},0)$ in the least-squares sense allows us to determine a specific polynomial. Note that, if $\ell \notin \mathcal{L}_j^n$, then the polynomial $\mathcal{P}_{\ell ,n}$ satisfying the conditions (4) has to interpolate points that are all of the form $({\varvec{x}}_k,0)$. In this case we take $\mathcal{P}_{\ell ,n}$ to be identically zero in order to guarantee that $\Psi _{j,n}$ is compactly supported on $\mathcal{R}_{j}^{2n+1}$ (see Proposition 4).

4 Properties of the bivariate fundamental functions for local interpolation

This section is devoted to prove the main properties of the fundamental functions $\Psi _{j,n}$ that are generated by the approach proposed in Sect. 3.

Proposition 4

Assume that, for all $\ell$, the blending functions $\Phi _{\ell ,n}$ are compactly supported on $\mathcal{R}_{\ell }^{n+1}$ and the bivariate polynomials $\mathcal{P}_{\ell , n}$ are constructed as in section 3.2. Then, the function $\Psi _{j,n}$ obtained from (3) is compactly supported on $\mathcal{R}_{j}^{2n+1}$.

Proof

To prove that $\Psi _{j,n}$ is equal to zero when evaluated at any $\bar{{\varvec{x}}}\in \Omega \setminus \mathcal{R}_{j}^{2n+1}$, we start recalling that the sum in (3) runs over all $\ell$ such that ${\varvec{x}}_\ell \in \Omega$ and ${\varvec{x}}_\ell$ is surrounded by a sufficient number of connected faces, i.e. rings, so as to allow the definition of the polynomials and blending functions. Since for any $\ell \notin \mathcal {L}_j^n$, the polynomial $\mathcal{P}_{\ell ,n}$ has been taken identically zero by construction, it turns out that, in (3), all the blending functions nonvanishing at $\bar{{\varvec{x}}}\in \Omega {\setminus } \mathcal{R}_{j}^{2n+1}$ are multiplied by zero polynomials and $\Psi _{j,n}(\bar{{\varvec{x}}})=0$. At any $\bar{{\varvec{x}}}$ on the boundary of $\mathcal{R}_{j}^{2n+1}$, the functions $\Phi _{\ell ,n}$, $\ell \in \mathcal {L}_j^n$, which multiply nonzero polynomials, are zero in view of their compact support and hence (3) is equal to zero too. Finally, at any parameter value $\bar{{\varvec{x}}}$ in the interior of $\mathcal{R}_{j}^{2n+1}$, in general, (3) will be nonzero since not all products $\mathcal{P}_{\ell ,n}(\bar{{\varvec{x}}}) \ \Phi _{\ell ,n}(\bar{{\varvec{x}}})$ will vanish. $\square$

Remark 1

Due to Proposition 4, equation (3) can be rewritten as

$$\begin{aligned} \Psi _{j,n}({\varvec{x}})= \sum _{\ell \in \mathcal{L}_j^n} \mathcal{P}_{\ell ,n}({\varvec{x}}) \ \Phi _{\ell ,n}({\varvec{x}}), \quad n \in \mathbb {N}. \end{aligned}$$

(6)

Proposition 5

$\Psi _{j,n}$ is a fundamental function for local interpolation, i.e., $\Psi _{j,n}({\varvec{x}}_i)=\delta _{i,j}$ for all ${\varvec{x}}_i \in \mathcal{R}_{j}^{2n+1}$.

Proof

On account of the fact that $\mathcal{P}_{\ell ,n}({\varvec{x}}_j)=1$ for each $\ell \in \mathcal {L}_j^n$ and of the partition of unity property of the blending functions $\{\Phi _{\ell ,n}\}$, relation (6), evaluated in ${\varvec{x}}_j$, yields

$$\begin{aligned} \Psi _{j,n}({\varvec{x}}_j)= \sum _{\ell \in \mathcal {L}_j^n} \Phi _{\ell ,n}({\varvec{x}}_j)=1. \end{aligned}$$

According to Proposition 4, we know that $\Psi _{j,n}({\varvec{x}}_i)=0$ for each ${\varvec{x}}_i$ on the boundary of $\mathcal{R}_{j}^{2n+1}$. Moreover, $\Psi _{j,n}({\varvec{x}}_i)=0$ also for each ${\varvec{x}}_i \ne {\varvec{x}}_j$ in the interior of $\mathcal{R}_{j}^{2n+1}$ due to the fact that $\mathcal{P}_{\ell ,n}({\varvec{x}}_i)=0$ for all $\ell \in \mathcal {L}_j^n$. $\square$

Proposition 6

For all j and n, the fundamental function $\Psi _{j,n}$ is globally $C^{2}(\mathbb {R}^2)$.

Proof

We recall from section 3.1 that the blending functions $\{\Phi _{\ell ,n}\}$ are $C^{2n}(\mathbb {R}^2)$ everywhere, except at the parameter value ${\varvec{x}}_k$ that is an extraordinary vertex of $\Omega$, where they are $C^{1}$ only. There follows that $\Psi _{j,n}$ is $C^{2n}$ everywhere by construction, except at the extraordinary vertex, if such a vertex is contained in its support.

Suppose hence that the extraordinary vertex, which we denote by ${\varvec{x}}_k$ (to stress that it is not necessarily the vertex where $\Psi _{j,n}$ is centered), is contained in the support of $\Psi _{j,n}$. In this case, we will prove that $\Psi _{j,n}$ is $C^2$ at ${\varvec{x}}_k$. To this end, we first observe that, by construction, $\Psi _{j,n}$ is $C^1$ at ${\varvec{x}}_k$ since all blending functions are globally $C^1$. To show that $\Psi _{j,n}$ is even $C^2$ at ${\varvec{x}}_k$, we recall that $\Psi _{j,n}$ is $C^{2n}$ (and thus at least $C^2$) everywhere else. Hence it suffices to show the continuity of the second partial derivatives of $\Psi _{j,n}({\varvec{x}})$ at ${\varvec{x}}_k$ with respect to two independent domain directions which we denote by $x_1$ and $x_2$.

Indeed, using the partition of unity property of the blending functions, we can write that, in any arbitrary patch around the extraordinary vertex, $\Psi _{j,n}({\varvec{x}})$ has the following expression:

$$\begin{aligned} \Psi _{j,n}({\varvec{x}})&= \mathcal{P}_{h,n}({\varvec{x}}) \ \Phi _{h,n}({\varvec{x}}) + \sum _{\ell \in \mathcal {L}_j^n, \ell \ne h} \mathcal{P}_{\ell ,n}({\varvec{x}}) \ \Phi _{\ell ,n}({\varvec{x}})\\&=\mathcal{P}_{h,n}({\varvec{x}}) \ \left( 1- \sum _{\ell \in \mathcal {L}_j^n, \ell \ne h} \Phi _{\ell ,n}({\varvec{x}}) \right) + \sum _{\ell \in \mathcal {L}_j^n, \ell \ne h} \mathcal{P}_{\ell ,n}({\varvec{x}}) \ \Phi _{\ell ,n}({\varvec{x}})\\&=\mathcal{P}_{h,n}({\varvec{x}}) + \sum _{\ell \in \mathcal {L}_j^n, \ell \ne h} \left( \mathcal{P}_{\ell ,n}({\varvec{x}})-\mathcal{P}_{h,n}({\varvec{x}}) \right) \ \Phi _{\ell ,n}({\varvec{x}}). \end{aligned}$$

Hence, in any arbitrary patch around the extraordinary vertex, we can write

$$\begin{aligned} \frac{\partial ^2}{\partial x_1^2} \Psi _{j,n}({\varvec{x}})&=\frac{\partial ^2}{\partial x_1^2} \mathcal{P}_{h,n}({\varvec{x}}) \nonumber \\&+\sum _{\ell \in \mathcal {L}_j^n, \ell \ne h} \frac{\partial ^2}{\partial x_1^2}\left( \mathcal{P}_{\ell , n}({\varvec{x}})-\mathcal{P}_{h,n}({\varvec{x}}) \right) \ \Phi _{\ell ,n}({\varvec{x}}) \nonumber \\&+2\sum _{\ell \in \mathcal {L}_j^n, \ell \ne h} \frac{\partial }{\partial x_1} \left( \mathcal{P}_{\ell ,n}({\varvec{x}})-\mathcal{P}_{h,n}({\varvec{x}}) \right) \ \frac{\partial }{\partial x_1} \Phi _{\ell ,n}({\varvec{x}}) \nonumber \\&+\sum _{\ell \in \mathcal {L}_j^n, \ell \ne h} \left( \mathcal{P}_{\ell ,n}({\varvec{x}})-\mathcal{P}_{h,n}({\varvec{x}}) \right) \ \frac{\partial ^2}{\partial x_1^2} \Phi _{\ell ,n}({\varvec{x}}). \end{aligned}$$

(7)

The first three addends in the right-hand side of (7) are products of continuous functions. Due to the fact that $\left( \mathcal{P}_{\ell ,n}({\varvec{x}})-\mathcal{P}_{h,n}({\varvec{x}}) \right) \rightarrow 0$ when ${\varvec{x}}$ tends to ${\varvec{x}}_k$, we can conclude that $\partial ^2/\partial x_1^2 \, \Psi _{j,n}({\varvec{x}})$ is a continuous function at ${\varvec{x}}_k$. The continuity of $\partial ^2/\partial x_2^2 \, \Psi _{j,n}({\varvec{x}})$ and $\partial ^2/\partial x_1 \partial x_2 \, \Psi _{j,n}({\varvec{x}})$ at ${\varvec{x}}_k$ can be proven in a similar way, so concluding the proof.

We additionally observe that the equality in (7) also shows that, in general, $\Psi _{j,n}({\varvec{x}})$ cannot be smoother than $C^2$ at ${\varvec{x}}_k$, due to the fact that the blending functions $\{\Phi _{\ell ,n}\}$ are $C^1$ only at the extraordinary vertex ${\varvec{x}}_k$. $\square$

Remark 2

As stated in Proposition 6 the fundamental function $\Psi _{j,n}$ is globally $C^2$. This is due to the fact it is $C^{2n+1}$ everywhere except at the extraordinary vertex where it is only $C^2$. Thus, the smoothness of the fundamental function is indeed of one order higher than that of the blending functions everywhere.

5 An illustrative example and the solution to a long-standing problem

In this section we illustrate the bivariate fundamental functions for local interpolation that are obtained by our general strategy when selecting as blending functions the basic limit functions of the Catmull–Clark subdivision scheme (namely those of the case $n=1$) and as bivariate polynomial interpolants the ones constructed as described below. Due to space limitations, our in-depth analysis and experimentation will focus on valences 3, 5, 6 only.

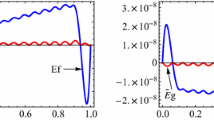
As to the polynomial interpolants, since when $n=1$ condition (5) must hold for $\#\mathcal {L}_\ell ^1=2N_\ell +1$ with $N_{\ell } \in \{3,4,5,6\}$ denoting the valence of ${\varvec{x}}_{\ell }$, we should require that $\dim (\Pi _d) \geqslant \max \{ 2N_\ell \} +1$. In our experiments we have worked with polynomials $\mathcal{P}_{\ell ,1}$ of total degree $d=4$, as it is a reasonably low degree that allows us to satisfy the condition (5) for all valences up to 6. Hence, for a vertex ${\varvec{x}}_\ell$ of valence $N_\ell \leqslant 6$, we have computed the 15 coefficients of the degree-4 polynomial $\mathcal{P}_{\ell ,1}$ by solving a weighted least-squares fitting problem with big weights assigned to the $2N_\ell +1$ interpolation points with parameter values in $\mathcal{R}_{\ell }^1$. Examples of degree-4 bivariate polynomials that interpolate the $2N_{\ell }+1$ points $({\varvec{x}}_k, \delta _{k,\ell })$, ${\varvec{x}}_k \in \mathcal{R}_{\ell }^1$ and approximate in the least-squares sense the $4N_{\ell }$ points $({\varvec{x}}_k, 0)$, ${\varvec{x}}_k \in \mathcal{R}_{\ell }^2 {\setminus } \mathcal{R}_{\ell }^1$ when the valence of ${\varvec{x}}_{\ell }$ is $N_{\ell } \in \{3, 5, 6\}$, are shown in Fig. 3. In order to handle higher valences one could work in an analogous way, but with polynomials of suitably high degree.

Fig. 3

Degree-4 bivariate polynomials that interpolate the $2N_{\ell }+1$ points $({\varvec{x}}_k, \delta _{k,\ell })$, ${\varvec{x}}_k \in \mathcal{R}_{\ell }^1$ and approximate in the least-squares sense the $4N_{\ell }$ points $({\varvec{x}}_k, 0)$, ${\varvec{x}}_k \in \mathcal{R}_{\ell }^2 {\setminus } \mathcal{R}_{\ell }^1$ when the valence of ${\varvec{x}}_{\ell }$ is $N_{\ell } \in \{3, 5, 6\}$

Fig. 4

Left: fundamental function for local interpolation that is defined on a regular subregion of $\Omega$ and is $C^3$ everywhere. Right: globally $C^2$ fundamental function that is centered at a valence-4 vertex and contains a valence-5 vertex in its support

In light of the fact that, in our construction, the bivariate polynomial interpolants are blended by the basic limit functions of the Catmull–Clark subdivision scheme, and the latter ones are $C^2$ everywhere when defined on regular regions, we can guarantee that the fundamental function that is centered at a valence-4 vertex and contains in its support only valence-4 vertices (see Fig. 4 left) is $C^3$ everywhere. Differently, when the fundamental function is centered at a valence-4 vertex but the vertices of its 2-ring neighbourhood are not all valence-4 vertices (see, e.g., Fig. 4 right), it is no longer $C^3$ everywhere, but only globally $C^2$, since the linear combination in (3) involves also blending functions (like the ones in the second and third column of Figure ) that instead of being $C^2$ everywhere are only globally $C^1$.

Fig. 5

First column: globally $C^2$ fundamental functions for local interpolation centered at an extraordinary vertex of valence 3, 5, 6. Second column: globally $C^1$ basic limit functions of the Catmull–Clark subdivision scheme centered at an extraordinary vertex of valence 3, 5, 6. Third column: examples of globally $C^1$ basic limit functions of the Catmull–Clark subdivision scheme that are centered at a valence-4 vertex but contain a valence 3, 5, 6 vertex in their support

Fig. 6

Globally $C^2$ interpolants (first column) passing through all the vertices $\{\mathbf{p}_j \in \mathbb {R}^3, \, j \in J\}$ (black dots) of the quadrilateral mesh (second column) with a valence 3 (first row) and a valence 6 (second row) extraordinary vertex. Third column: corresponding quadrangulations $\Omega$ containing a sufficient number of rings to completely define the parametric interpolants

Analogously to Fig. 4 right, in Fig. 5 (first column) we display other globally $C^2$ fundamental functions, namely the ones centered at extraordinary vertices of valence 3, 5, 6. Next to each fundamental function we also show some of the globally $C^1$ blending functions that contribute to their construction through formula (3).

Remark 3

It is important to emphasize that the globally $C^2$ fundamental functions here presented offer a solution to a long-standing problem, faced unsuccessfully by numerous researchers in the last decades. For example, the fundamental functions we have constructed compare favourably with the globally $C^1$ basic limit functions of the interpolatory subdivision scheme proposed in [15] as well as in all references therein. Moreover, they also compare favourably with the globally $C^1$ basis functions for interpolation recently introduced in [14] for polygonal domains of arbitrary topology.

Remark 4

If one would like to use smoother blending functions with the same support, one option could be to replace the basic limit functions of the Catmull–Clark subdivision scheme with those proposed in [13]. There, thanks to the introduction of a multisided patch covering the extraordinary region, $G^2$ smoothness with adjacent patches and $C^2$ smoothness within the patches is guaranteed.

The concluding examples in Fig. 6 show in the first column a globally $C^2$ parametric surface passing through all the vertices $\{\mathbf{p}_j \in \mathbb {R}^3, \, j \in J\}$ of a quadrilateral mesh (second column) with a valence 3 (first row) and valence 6 (second row) extraordinary vertex. The parametric interpolants have been obtained by applying component-wise the explicit representation in (1) where the fundamental functions $\Psi _{j,1}$ to be used as building blocks, are globally $C^2$ functions defined on the corresponding quadrangulation $\Omega$ in the third column.

6 Future work

As a continuation of this work we want to extend the construction of the globally $C^2$ fundamental functions (defined on arbitrary quadrangulations of a planar domain) so that a globally $C^2$ parametric surface passing through all the vertices of a given quadrilateral mesh of arbitrary topology (with no restriction on the number of extraordinary vertices) is obtained.