Abstract
In this work, three genetic regulatory networks are considered, that model the post–transcriptional regulation of the PTEN onco–suppressor gene, mediated by microRNAs and competitive endogenous RNAs, in glioblastoma multiforme, the most severe of brain tumours. We simulate solutions of the resulting stochastic differential systems and discuss the effects of this miRNA–fashioned regulation on PTEN expression.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the human body, cells contain the approximately twenty thousand genes encoded in the human genome. Genes get selectively expressed (or turned on) within each cell, thus determining its type, shape and behaviour. A gene regulatory network (GRN) is a network inferred from gene expression data [11], so it is a tool for describing gene–gene (as well as potential protein–protein) interactions and the way genes can turn each other on and off. In other words, a GRN provides information about the regulatory interactions between regulators and their potential targets, interactions that can be incredibly complicated, even in a network of very few genes, allowing a cell to respond to signals in various complex ways [11].
GRN modelling represents, therefore, an important postgenomic–era challenge, and it has indeed gained more and more interest, also in computational bio–mathematics. Several methods have been proposed for estimating gene networks from gene expression data, where both stochastic and deterministic approaches are pursued [4, 5, 22, 28].
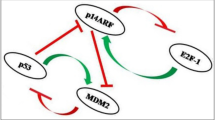
In this work, the focus is on the regulation of PTEN (Phosphatase and TENsin homolog) gene expression specifically in the brain, considering transcriptional and post–transcriptional interactions, and excluding translation in the PTEN protein, for which we refer to [8]. PTEN is found at locus 10q\(23.31\,\) on chromosome 10, and includes instructions to produce a protein that helps govern the cell life–death cycle by preventing cells from growing and multiplying too rapidly and uncontrollably. PTEN is thus an onco–suppressor, but it is also one of the most frequently mutated or silenced in human cancer [9]. Loss of chromosomal segment 10q is indeed proved to be linked to glioblastoma multiforme (GBM), a very aggressive brain tumour [21, 29]. Even in the absence of genetic loss or mutation, therefore in a situation where PTEN levels should be normal, PTEN is found to be low in about \(70\,\%\) of GBM cases, which prompted research on PTEN regulation in an attempt to justify this unexplained low expression.
In the GRNs we consider, the crucial factors involved are short non–coding RNAs (microRNAs or miRNAs) and competitive endogenous RNAs (ceRNAs) [25]. To understand their role in gene expression control, it is useful to synthesise it as a process consisting of a sequence of steps, involving transcription of DNA to mRNA, namely an RNA intermediary or messenger RNA, and translation of mRNA into the final functional product, the protein. After transcription, miRNAs negatively regulate expression of their target mRNAs, where one miRNA can regulate many mRNAs, while the same mRNA can be regulated by a number of miRNAs. As a consequence of this down–regulation, a miRNA can be an onco–suppressor or an onco–promoter. The activity of miRNAs can be influenced by the presence of ceRNAs: a miRNA controls expression of a gene by binding to its mRNA, and ceRNAs compete for miRNA binding sites. The result is a complex network, in which miRNAs and ceRNAs interact and affect the mRNA level of the gene considered (PTEN in our case), available to be translated into the final protein.
The importance of PTEN ceRNA–mediated regulation in tumour cells is studied in [17, 25, 26], but a clear quantitative understanding of its miRNA–mediated regulation is still lacking [12]. One attempt is represented by the mass–action mathematical deterministic model in [1], used to determine optimal conditions for ceRNAs activity in silico. A stochastic and discrete model can be found in [8], where translation into PTEN protein and transcriptional and translational delays are also considered. A complex network of a miRNA pool acting in the brain, including corresponding ceRNAs competing with PTEN for the same miRNAs, is introduced and analysed numerically in [7], where the continuous and deterministic setting, modelled by ordinary differential equations, was used to overcome computational and time complexity.
In the present article, we model the effects of three of the miRNAs included in the pool studied in [7], one at a time, so to make clearer their specific contribution within the network [20]. Given the reduced computational complexity of the reacting systems, the more realistic stochastic and continuous (rather than deterministic) modelling regime is employable here.
2 GRNs modelling and simulation regimes
When simulating a Gene Regulatory Newtwork (GRN), three modelling regimes can be considered: stochastic and discrete, stochastic and continuous, deterministic and continuous; additional complexity exists, related to simultaneously considering temporal and spatial effects, which is not dealt with in this article [19].
The discrete stochastic regime (also called slow) is characterised by the use of a Stochastic Simulation Algorithm (SSA), the first of which is due to Gillespie [13]. It is an essentially exact procedure for numerically simulating the evolution of a set of chemical reactions in a well–stirred and homogeneous chemical reaction system, taking into account inherent randomness.
If \(\, \mathrm{X}_1, \ldots , \mathrm{X}_{n_s}\,\) represent molecular species, interacting through \(\,R_1, \ldots , R_{n_r}\,\) reaction channels, then the system evolution is described by a discrete non–linear Markov process in which a vector \(\, \mathrm{\mathbf{X}}(t), \) holding numbers (integer values) of the molecular species at time t, evolves through time.
The state vector \(\, \mathrm{\mathbf{X}}(t)\, \) is thus a discrete jump Markov process, whose time evolution equation, the so–called Chemical Master Equation (CME) reminded in (1) below, describes the probability \(\, P(\mathrm{\mathbf{X}},\, t \, \vert \, {{\textbf {X}}}_0, t_0)\, \) that, given an initial condition \(\, \mathrm{\mathbf{X}}(t_0) = \mathrm{\mathbf{X}}_0, \) then \(\, \mathrm{\mathbf{X}}(t) = \mathrm{\mathbf{X}} \,. \)
Now, any set of \(\,n_r\,\) chemical reactions is uniquely characterised by stoichiometric vectors \(\varvec{\nu }_1, \ldots , \varvec{\nu }_{n_r}\, \) and by propensity functions \(\, \mathrm{a}_1( \mathrm{\mathbf{X}}(t)), \ldots , \mathrm{a}_{n_r}( \mathrm{\mathbf{X}}(t)).\) Vectors \(\,\varvec{\nu }_{j},\) each of dimension \(\, n_s,\) represent the update of the numbers of molecules in the system if \(\,R_1, \ldots , R_{n_r}\,\) respectively occur, while functions \(\, \mathrm{a}_{j} = \mathrm{a}_{j}( \mathrm{\mathbf{X}}(t))\,\) describe the relative probabilities of \(\,R_1, \ldots , R_{n_r}\) occurring, again respectively.
Hence, the CME takes the following form:
In general, (1) is a discrete parabolic partial differential equation too difficult to solve, either analytically or numerically: other techniques are therefore needed to simulate \(\, \mathrm{\mathbf{X}}(t)\,. \)
SSAs, which are rigorously based on the same microphysical premise that underlies the CME, can be employed when there are low molecular numbers and intrinsic, or internal, noise cannot be ignored; the latter is linked to the fact that it is unknown which reaction is firing, and at what time it is firing.
An SSA yields a more realistic representation of a system evolution, compared to the deterministic Reaction Rate Equation (RRE), i.e. system (2) of ordinary differential equations that ignores the presence of noise:
where \(\,{{\textbf { a}}}=(\mathrm{a}_1, \ldots , \mathrm{a}_{\mathrm{n_r}})^T\; \) is the propensity vector, while \(\, \mathrm{S} = \big (\, \nu _\mathrm{k\,j}\, \big ) \,\) is the stoichiometric matrix of dimensions \(\, \mathrm{n_s}\times \mathrm{n_r},\) whose columns are the stoichiometric vectors.
The RRE intervenes when the chemical reaction system is too large to be treated within the discrete stochastic setting. The SSA, in fact, remains a computationally demanding approach, though many authors have attempted to enhance its performance [6, 16]; this limits its applicability, in particular to the large reaction networks required for modelling realistic gene networks.
In such a situation, as said, the RRE can come into play, namely solution is sought within the third regime, deterministic and continuous, aimed at describing, in an averaged manner, the behaviour of a system in which the number of molecules is so large that we can speak of concentrations of reactants and products. This averaged behaviour can be modelled as an Initial Value Problem formed by (2) together with an initial condition \(\, \mathrm{\mathbf{X}}(t_0) = \mathrm{\mathbf{X}}_0, \) where usually \(\, t_0 = 0. \)
The third regime (also named fast) is, indeed, the standard one in chemical kinetics where the Law of Mass Action applies, i.e. the solution to the RRE satisfies this law, and is mainly used to model complex GRNs [7], when the first and second regimes fail computationally, or when the deterministic component dominates the noise terms. Note, though, that the RRE is not appropriate if the molecular population of some critical reactant species is so small that microscopic fluctuations can produce macroscopic effects, which is essentially true for genetic/enzymatic reactions in living cells [2, 10, 15].
In this article, we consider the second regime, where noise effects are still important, but continuity arguments hold up; this continuous stochastic regime is also referred to as intermediate regime, since it represents a good compromise between accuracy of SSAs and fastness of RRE solvers.
By applying the Central Limit Theorem and matching the first two moments of the CME, it is possible to write a stochastic ordinary differential equation (SODE) that describes the evolution of \(\, \mathrm{\mathbf{X}}(t)\, \) [14]. This equation is the so–called Chemical Langevin Equation (CLE) and takes the form:
where matrix \(\, \mathrm{B}= \Big ( \mathrm{S} \cdot \Sigma _a \cdot \mathrm{S}^T \Big )^{1/2}\;\) and the diagonal matrix \(\, \Sigma _a = \mathrm{diag}(\mathrm{\mathbf{a}})\; \) have dimensions \(\, n_s\times n_s\,\) and \(\, n_r\times n_r,\) respectively, while vector \(\, {\mathbf {W}} = {\mathbf {W}}(t) = \Big (\mathrm{W_1}(t), \ldots , \mathrm{W_{n_s}}(t)\Big )^T\,\) is formed by independent standard Wiener processes, each with zero drift and unit volatility.
Equation (3) is an It\(\hat{\mathrm{o}}\) SODE that models the continuous stochastic evolution equation and takes into account intrinsic noise [14].
General classes of methods can be used to solve (3) in non–stiff cases. The simplest is the Euler–Maruyama method, where the stochastic increments, at each time step, take the form:
These Wiener increments are distributed according to a normal random variable of zero mean and variance given by their length \(\, h\,. \)
The Euler–Maruyama method converges with strong order 1/2 to the It\(\hat{\mathrm{o}}\) solution of (3) [3, 18, 27].
Before leaving this section, we recall that both SSA and (3) admit solutions converging, in the limit of large numbers of reactants, to the solution of (2), thus satisfying the Law of Mass Action [14].
3 miRNAs
Three particular miRNAs, involved in the onset of brain cancer, are considered in Sects. 3.1, 3.2, and 3.3. For each of them, the interaction is modelled with the PTEN onco-suppressor gene, as well as other genes concurrent with PTEN, namely the ceRNAs. In particular, for miRNA\(_{214},\) the PTENP1 pseudo–gene acts as ceRNA; for miRNA\(_{19b},\) CNOT6L gene and PTENP1 pseudo–gene act as ceRNAs; finally, for miRNA\(_{17},\) VAPA and CNOT6L genes and PTENP1 pseudo–gene act as ceRNAs.
3.1 miRNA\(_{214}\)
We consider a set of \(\, \mathrm{n_{r}}\, \) chemical reactions, monomolecular or bimolecular with distinct reactants, where \(\, \mathrm{n_s}\, \) is the total number of \(\mathrm{X}\)–species that interact through such reactions. Set (4) represents a realistic example of a system of ten reactions involving seven \(\mathrm{X}\)–species.
By introducing differential variables \(\,\mathrm{X_k} = \mathrm{X_k(t)},\) each representing the \(\, \mathrm{k}\)-th \(\;\mathrm{X}\)-species observed and its biological state at time \(\,\mathrm{t},\) the reaction set can be translated into a system of \(\, \mathrm{n_{s}}\, \) differential equations in \(\, \mathrm{n_{s}}\, \) variables. Table 1 shows the correspondence between \(\;\mathrm{X}\)-species and differential variables, so that (4) becomes (5). We seek its solution \(\, \mathbf{X}(t) = ( \mathrm{X_1}(t), \ldots , \mathrm{X_{n_s}}(t))^T,\) namely the state vector whose evolution in time \(\, t\,\) is that of the differential system under consideration. To ease the notation, in the following we often set \(\, \mathbf{X}= \mathbf{X}(t). \)

For each \(\mathrm{j}\)-th reaction, a propensity function \(\, \mathrm{a_j} = \mathrm{a_j\left( \mathbf{{X}}(t)\right) } \,\) is defined, to express the link between the reactants involved and the probability \(\, \mathrm{c_j}\,\) (per time unit) that a randomly chosen combination of these reactants will indeed react. In the numerical simulations presented in Sect. 4, the \(\, c_j\,\) values are inferred according to what is known in the literature, for which we refer the reader to [7] and references therein, and in the GeneCard database [24].
The propensity functions corresponding to reactions (5) are shown in equalities (6), where dependence on time \(\, \mathrm{t}\,\) has been temporarily discarded, again to simplify the notation.
In addition to the propensity vector \(\,{{\textbf { a}}}=(\mathrm{a}_1, \ldots , \mathrm{a}_{\mathrm{n_r}})^T, \) the other information needed, to set up the It\({\hat{\mathrm{o}}}\) process related to a chemical reaction system, is its stoichiometry.
As seen in Sect. 2, in fact, propensity and stoichiometry values are the ingredients to build the SODE (3) associated with the set of reactions under observation: vector a and the \(\, n_s \times n_r\,\) matrix \(\, \mathrm{S} = \big (\, \nu _\mathrm{k\,j}\, \big ) \,\) determine, in fact, both deterministic and stochastic components in Eq. (3).
Now, for each \(\, \mathrm{j}\)-th reaction, the corresponding column of \(\, \mathrm{S}\,\) is:
Hence, in the case of system (5), the \(\,\mathrm{S}\)–matrix is as in Table 2.
Tables 3 and 4 contain, respectively, initial conditions and \(\, c_j\,\) coefficients employed, in the numerical simulation Sect. 4, to set and solve the SODE associated with reactions (5).
3.2 miRNA\(_{19b}\)
Set (8) represents a realistic example of a thirteen reaction system involving nine \(\mathrm{X}\)–species. This time, the chemical reactions are written directly in terms of differential variables. Table 5 shows the correspondence between \(\;\mathrm{X}\)-species and differential variables in (8).

Propensity and stoichiometry values for reactions (8) are given respectively in equalities (9) and (10); these latter only report non–zero values in the S–matrix associated with set (8).
Tables 6 and 7 contain, respectively, initial conditions and \(\, c_j\,\) coefficients employed, in Sect. 4, to set and solve the SODE associated with reactions (8).
3.3 miRNA\(_{17}\)
Set (11) represents a realistic example of a system of sixteen reactions involving eleven \(\mathrm{X}\)–species, where the correspondence between \(\mathrm{X}\)-species and differential variables is given in Table 8.

The propensity functions associated with reactions (11) are given in equalities (12), while the stoichiometric matrix has dimensions \(\, 11\times 16\,\) and non–zero values reported in (13).
Tables 9 and 10 contain, respectively, initial conditions and \(\, c_j\,\) coefficients employed, in Sect. 4, to set and solve the SODE associated with reactions (11).
Plots of species \(\, \mathrm{X}_2\,\) and \(\,\mathrm{X}_4,\) respectively PTEN and miRNA\(_{214},\) for reactions (5) over twenty minutes (top), one day (centre left), four days (centre right), one month (bottom left), two months (bottom right). PTEN always settles around a mean value that is two orders of magnitude greater than that of miRNA\(_{214}\,\)
Plots of species \(\, \mathrm{X}_2\,\) and \(\,\mathrm{X}_4,\) respectively PTEN and miRNA\(_{19b},\) for reactions (8) over twenty minutes (top), one day (centre left), four days (centre right), one month (bottom left), two months (bottom right). PTEN always settles around a mean value that is higher than that of miRNA\(_{19b},\) although of the same order of magnitude
Plots of species \(\, \mathrm{X}_2\,\) and \(\,\mathrm{X}_4,\) respectively PTEN and miRNA\(_{17},\) for reactions (11) over twenty minutes (top), one day (centre left), four days (centre right), one month (bottom left), two months (bottom right). miRNA\(_{17}\,\) rapidly grows and, within a very short time, induces a dramatic decay in the PTEN level
4 Numerical simulations
In this section, systems (5), (8) and (11) are dealt with within the intermediate modelling regime, stochastic and continuous. An It\({\hat{\mathrm{o}}}\) SODE equation of type (3) is then written for each of the three systems considered, and is solved numerically with the Euler–Maruyama method.
All experiments were carried out on a DELL XPS notebook computer, with 7th generation Intel Core i7 processor at 2.8 GHz, and 16 GB RAM at 2400 MHz, running under Ubuntu 20.04.4 LTS operating system. The problem solving environment of Mathematica, version 13, is employed to set up each model, integrate the resulting SODE, and plot its solution [23]. Timing results, averaged over ten runs for each experiment, show that the computational time taken by the definition of the It\({\hat{\mathrm{o}}}\) process is around seven seconds, most of which is spent to form the matrix \(\, B\,\) in (3), while its integration requires about six seconds.
In all experiments, the focus is on the interaction between PTEN and miRNA, that is \(\, \mathrm{X}_2\, \) and \(\, \mathrm{X}_4\,. \) This is done to establish whether down–regulation of \(\, \mathrm{X}_2\, \) or \(\, \mathrm{X}_4\, \) implies over–expression of the other. Furthermore, the evolution is plotted along five temporal intervals, to cover short–and long–term behaviours.
Figure 1 illustrates the solution for reactions (5). Simulations show that miRNA\(_{214}\) remains expressed at a very low costant level, so it does not affect the PTEN regulation. In fact, after a short initial phase during which there is a fairly dramatic increase of PTEN, its value settles around a constant mean value. This is exactly what we expect in a physiological, non–pathological, situation within a cell. In particular, it can be observed that the mean level of miRNA\(_{214}\,\) remains close to that of its initial condition of order \(\,10^0, \) while that of PTEN oscillates around a value at an order of magnitude \(10^2. \)
Figure 2 illustrates the solution for reactions (8). Simulations with miRNA\(_{19b}\) show that its expression grows, initially and rapidly, up to a value of about 150, and then it stabilises, reaching a situation similar to the miRNA\(_{214}\) case. In fact, even if in this case both PTEN and miRNA\(_{19b}\) oscillate around a mean value at the same order of magnitude \(10^2,\) miRNA\(_{19b}\) has, once again, no effect on PTEN expression.
Figure 3 illustrates the solution for reactions (11). Simulations with miRNA\(_{17}\) show how it can cause a situation that is no longer physiological inside a cell, but rather pathological. Here, in fact, miRNA\(_{17}\) grows dramatically to a mean value of order of magnitude \(10^3,\) large enough to induce the same dramatic down–regulation of PTEN. Due to this highly reduced function of PTEN as an onco–suppressor, the cell is greatly exposed to tumour occurence.
5 Conclusions
This article investigates the impact of three different miRNAs on the regulation of the PTEN gene, an onco–suppressor whose low expression is observed in the majority of cases of glioblastoma multiforme, one of the most aggressive brain tumours. We considered miRNA\(_{214}\), miRNA\(_{19b}\) and miRNA\(_{17}\), each targeting different genes other than PTEN, called ceRNAs. The three resulting GRNs are simulated in a stochastic and continuous setting, via systems of stochastic ordinary differential equations derived from jump Markov processes, modelling appropriate chemical reactions. Our simulations show that, unless miRNAs grow in such a way to exceed PTEN levels by at least one order of magnitude, PTEN preserves its physiological oscillatory behaviour, around a mean value of order \(\, 10^2.\) The above situation occurs with miRNA\(_{214}\) and miRNA\(_{19b}.\) In the case of miRNA\(_{17},\) simulations show that it rapidly becomes over–expressed, while PTEN is dramatically down–regulated, leaving the cell much more unprotected from tumour genesis. A more faithful adherence to reality could be obtained by considering the stochastic and discrete processes underlying the GRNs models. This choice is currently under investigation, leading to the use of a stochastic simulation algorithm and incorporating delays in the reactions that represent transcription of DNA to RNA, both for PTEN and ceRNAs.
Data Availibility
Data supporting reported results can be found in the cited GeneCards database.
References
Ala, U., Karreth, F.A., Bosia, C., Pagnani, A., Taulli, R., Leopold, V., Tay, Y., Provero, P., Zecchina, R., Pandolfi, P.P.: Integrated transcriptional and competitive endogenous RNA networks are cross-regulated in permissive molecular environments. PNAS 110(18), 7154–7159 (2013)
Arkin, A., Ross, J., McAdams, H.H.: Stochastic kinetic analysis of developmental pathway bifurcation in phage lambda-infected Escherichia coli cells. Genetics 149, 1633–1648 (1998)
Burrage, K., Tian, T.: A note on the stability properties of the Euler methods for solving stochastic differential equations. New Zealand J. Maths. 29, 115–127 (2000)
Burrage, K., Tian, T.: Effective simulation techniques for Biological Systems, in Fluctuations and Noise in Biological, Biophysical and Biomedical Systems II. Proc. SPIE 5467, 311–325 (2004)
Burrage, K., Tian, T., Burrage, P.M.: A multi-scaled approach for simulating chemical reaction systems. Progress Biophys. Molecular Biology 85, 217–234 (2004)
Cao, Y., Gillespie, D.T., Petzold, L.R.: The slow-scale stochastic simulation algorithm. J. Chem. Phys. 122, 014116–18 (2005)
Carancini, G., Carletti, M., Spaletta, G.: Modeling and Simulation of a miRNA Regulatory Network of the PTEN Gene. Mathematics 9(15), 1803–1818 (2021)
Carletti, M., Montani, M., Meschini, V., Bianchi, M., Radici, L.: Stochastic modelling of PTEN regulation in brain tumors: A model for glioblastoma multiforme. Math. Biosci. Eng. 12, 965–981 (2015)
Carracedo, A., Alimonti, A., Pandolfi, P.P.: PTEN level in tumor suppression: How much is too little? Cancer Res. 71, 629–633 (2011)
Elowitz, M.B., Leibler, S.: A synthetic oscillatory network of transcriptional regulators. Nature 403, 335–338 (2000)
Emmert-Streib, F., Dehmer, M., Haibe-Kains, B.: Gene regulatory networks and their applications: understanding biological and medical problems in terms of networks. Frontiers in Cell and Developmental Biology 2(38), 1–7 (2014)
Figliuzzi, M., Marinari, E., De Martino, A.: MicroRNAs as a selective channel of communication between competing RNAs: a steady-state theory. Biophys. J. 104(5), 1203–1213 (2013)
Gillespie, D.T.: A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 22, 403–434 (1976)
Gillespie, D.T.: A rigorous derivation of the chemical master equation. Physica A 188, 404–425 (1992)
Gonze, D., Halloy, J., Goldbeter, A.: Robustness of circadian rythms with respect to molecular noise. PNAS 99, 673–678 (2002)
Haseltine, E.L., Rawlings, J.B.: Approximate simulation of coupled fast and slow reactions for stochastic chemical kinetics. J. Chem. Phys. 117, 6959–6969 (2002)
Karreth, F.S., Tay, Y., Perna, D., Ala, U., Mynn Tan, S., Rust, A.G., De Nicola, G., Webster, K.S., Weiss, D., Mancera, P.A.P., Krauthammer, M., Halaban, R., Provero, P., Adams, D.J., Tuveson, D.A., Pandolfi, P.P.: In Vivo Identification of Tumor-Suppressive PTEN ceRNAs in an Oncogenic BRAF-Induced Mouse Model of Melanoma. Cell 147, 382–395 (2011)
Kloeden, P.E., Platen, E.: Numerical Solution of Stochastic Differential Equations, 2nd edn. Springer, Berlin (1995)
Nicolau Jr, D.V., Burrage, K.: Stochastic simulation of chemical reactions in spatially complex media. Comput. Math. Appl. 55(5), 1007–1018 (2008)
Poliseno, L., Pandolfi, P.P.: PTEN ceRNA networks in human cancer. Methods 77–78, 41–50 (2015)
Sano, T., Lin, H., Chen, X., Langford, L.A., Koul, D., Bondy, M.L., Hess, K.R., Myers, J.N., Hong, Y., Yung, W.K.A., Steck, P.A.: Differential Expression of MMAC-PTEN in Glioblastoma Multiforme: Relationship to Localization and Prognosis. Cancer Res. 59, 1820–1824 (1999)
Shmulevic, I., Aitchison, J.D.: Deterministic and Stochastic models of Genetic Regulatory Networks. Methods Enzymol 467, 335–356 (2009)
Sofroniou, M., Knapp, R.: Advanced Numerical Differential Equation solving in Mathematica. WRI Tutorial; Wolfram Research Inc., Champaign, IL, USA (2003)
Stelzer, G., Rosen, N., Plaschkes, I., Zimmerman, S., Twik, M., Fishilevich, S., Stein, T.I., Nudel, R., Lieder, I., Mazor, Y., et al.: The GeneCards Suite: From gene data mining to disease genome sequence analyses. Curr. Protoc. Bioinform. 54, 1.30.1-1.30.33 (2016)
Sumazin, P., Yang, X., Chiu, H.S., Chung, W.J., Iyer, A., Llobet-Navas, D., Rajbhandari, P., Bansal, M., Guarnieri, P., Silva, J., Califano, A.: An Extensive MicroRNA-Mediated Network of RNA-RNA Interactions Regulates Established Oncogenic Pathways in Glioblastoma. Cell 147, 370–381 (2011)
Tay, Y., Kats, L., Salmena, L., Weiss, D., Tan, S.M., Ala, U., Karreth, F., Poliseno, L., Provero, P., Di Cunto, F., Lieberman, J., Rigoutsos, I., Pandolfi, P.P.: Coding Independent Regulation of the Tumor Suppressor PTEN by Competing Endogenous mRNAs. Cell 147, 344–357 (2011)
Tian, T., Burrage, K.: Stochastic Models for Regulatory Networks of the Genetic Toggle Switch. PNAS 103(22), 8372–8377 (2006)
Vijesh, N., Chakrabarti, S., Sreekumar, J.: Modeling of gene regulatory networks: A review. J. Biomed. Sci. Eng. 6, 223–231 (2013)
Wang, S.I., Puc, J., Li, J., Bruce, J.N., Cairns, P., Sidransky, D., Parsons, R.: Somatic Mutations of PTEN in Glioblastoma Multiforme. Cancer Res. 57, 4183–4186 (1997)
Acknowledgements
The authors wish to dedicate this work to the late Professor Ilio Galligani, who taught them how attention to problem modelling, numerical solver and real–life application should always be a universitas rerum, at the center of a numerical analyst’s work. He also encouraged the authors to work together, which they ultimately did, anticipating that their collaboration would be fruitful and enjoyable, as it indeed is. The authors also wish to thank the Referees for their helpful comments and for the very kind attention and appreciation of this work, and Dr. Mark Sofroniou for many useful discussions.
Funding
Open Access funding provided by the University of Urbino Carlo Bo within the CRUI-CARE Agreement. This research received no external funding.
Author information
Authors and Affiliations
Contributions
The authors contributed equally to this work. The authors share the content of this work, which is unpublished and has not been submitted to other journals.
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare no conflic of interest.
Ethics approval
Not applicable.
Consent to participate
Not applicable.
Editorial Policies
for Springer journals and proceedings: https://www.springer.com/gp/editorialpolicies.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Carletti, M., Spaletta, G. Stochastic modelling and simulation of PTEN regulatory networks with miRNAs and ceRNAs. Ann Univ Ferrara 68, 645–659 (2022). https://doi.org/10.1007/s11565-022-00416-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11565-022-00416-7
Keywords
- Numerical modelling
- Stochastic ordinary differential equations
- Euler–Maruyama method
- Propensity function
- Stoichiometric matrix
- PTEN onco–suppressor gene