Abstract
While existing research has suggested that delegating foreign aid allocation decisions to a multilateral aid fund may incentivize recipient countries to invest in bureaucratic quality, our analysis links the fund’s decision rules to recipient-country investment by explicitly modeling the decision-making within multilateral aid funds. We find that majority rule induces stronger competition between recipients, resulting in higher investments in bureaucratic quality. Despite this advantage, unanimity can still be optimal since the increased investment under majority comes at the cost of low aid allocation to countries in the minority. The qualitative predictions of our model rationalize our novel empirical finding that, relative to organizations that use a consensus rule, organizations that use majority are more responsive to changes in recipient-country quality.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
When allocating foreign aid, donor countries face a problem of incentivizing recipient countries to invest in bureaucratic quality in an effort to increase the effectiveness of aid spending. To address this problem, a new wave of aid conditionality—political conditionality—has emerged with the intention of incentivizing needed investments and reforms (see Molenaers et al. 2015). However, political conditionality suffers from the same difficulty with credible implementation that has led many observers to claim that aid conditionality has failed (see Collier 1997, Alesina and Weder 2002, Dreher 2009 and Öhler et al. 2012). In particular, conditional aid faces a problem of non-contractibility—measures of good governance are partially subjective, and donor countries often face an ex post incentive to circumvent conditionality. The problem of non-contractibility results in a “Samaritan’s problem” that occurs when the recipient country, knowing it will receive assistance in any case, has no incentive to implement costly reforms (see Mosley et al. 1995 and Pedersen 1996 for a discussion of problems of time-inconsistency in aid spending).Footnote 1
Given the difficulty of implementing conditionality in bilateral aid, several papers consider the delegation of the allocation decision to a third party as a solution to the Samaritan’s problem (see Svensson 2000, Hagen 2006 and Annen and Knack 2018; see also Schneider and Slantchev 2013 for an argument that delegation can solve commitment problems in international cooperation). Delegation is a well-known solution to hold-up problems in general (see Aghion and Tirole 1997), and may facilitate commitment to aid conditionality in the case of the Samaritan’s problem. However, this solution depends on the existence of an independent party with verifiable preferences that diverge from the donor country’s in the precise direction that facilitates recipient-country investment. Therefore, delegation to international aid agencies may not always mitigate the Samaritan’s problem—as argued by Easterly (2003) and Hagen (2006), aid agencies often focus on ease of disbursement or recipient-country need rather than aid effectiveness.
In practice, donor countries most commonly retain decision rights on aid allocation, even after committing funds to a multilateral organization. A typical example is the European Development Fund, where country representatives from each of the 27 EU-member states jointly decide on the allocation of aid to recipient countries. As illustrated in the following quote, since the donor countries have divergent preferences over where to allocate aid, discussion and bargaining is required to reach a collective decision:
...the European Union (EU) has to decide on the allocation of aid to individual countries....as can be expected, this process is plagued with difficulties as each stakeholder argues in favour of its own criteria for allocation and country-specific interests. (Negre 2013, p.1)
Our paper studies a model of bargaining over aid allocation in multilateral organizations, and illustrates how this bargaining process can lead to a more efficient allocation of aid spending relative to bilateral aid allocation, and subsequently incentivizes recipient countries to invest in measures that increase the effectiveness of aid. Additionally, we analyze how the decision-making rule in the multilateral institution impacts the incentive of recipient countries to invest. We find that multilateral institutions that take decisions via majority rule provide recipient countries with a higher incentive to invest, which is consistent with our novel empirical finding that multilateral organizations that take decisions via majority are more responsive to changes in their recipient countries’ governance policies.
While the first part of our paper takes a positive approach and compares investment decisions under different institutions, we also consider a normative approach and detail which decision rule is optimal from the donor countries’ perspective. Here, we find that since the higher incentive to invest under a majority rule comes at a cost of limiting the total number of projects that are funded, it is not always optimal for multilateral organizations to adopt a majority rule. Instead, our analysis suggests that a majority rule should only be adopted when there are high positive spillovers of recipient countries’ investment on other areas, and when investment has an intermediate level of productivity.
Our model relies on two key assumptions. First, we assume donor countries have individual biases over which country receives aid—to make the Samaritan’s problem as stark as possible, each donor country only values the product of aid spending in one of the recipient countries. Footnote 2 There is a large empirical literature assessing country biases in both bilateral and multilateral aid spending (for a survey of this literature see Hoeffler and Outram 2011, and Fuchs et al. 2014), and this literature provides evidence that idiosyncratic political motivations influence the allocation of aid spending, particularly in bilateral aid. Since different donor countries exhibit different political biases, e.g., due to ties to former colonial countries, this is consistent with the notion that donor countries have individual biases. What is more, the scholarly literature that compares bilateral and multilateral aid typically argues that donor-country political interests are less prevalent for multilateral aid, and takes the relative absence of political motives as a reason why multilateral aid is more effective for promoting development (Headey 2008, Milner and Tingley 2013).Footnote 3 Our model provides a structured explanation for why multilateral aid is more effective: By bargaining over the allocation of aid spending, donor countries commit to a mechanism for allocating aid that mitigates individual donor-country biases.
Second, we assume that donor countries can commit to allocate aid spending via a bargaining process. In practice, donor countries most often commit funds to a multilateral organization prior to bargaining over the precise allocation of the aid spending to individual projects. For example, the European Development Fund (EDF) is funded on a voluntary basis according to a pre-set formula. The allocation of the EDF budget to projects in individual recipient countries, however, is determined after funds have already been committed to the general budget. Importantly, after the donor-countries’ aid budgets have been allocated to the EDF, the member countries have effectively committed to disburse this aid budget through the EDF—disagreement over where to allocate the joint aid budget does not result in an automatic reimbursement of the EDF’s budget and a reversion to bilateral aid.Footnote 4
Our model considers a setting of three donor and three recipient countries. The donor countries each have an aid budget, and commit to implement aid bilaterally or via a multilateral fund with a decision rule of either unanimity or majority.Footnote 5 The recipient countries then choose an observable, but non-contractible, level of investment that increases the expected effectiveness of aid spending, after which the donor countries determine the allocation of aid. In this setting, the donor countries would like to incentivize the recipient countries to invest ex ante to increase the productivity of aid spending. However, knowing that the donor countries will allocate all spending to their preferred recipient country ex post under bilateral aid, the recipient countries have no incentive to invest ex ante. Alternatively, if donor countries commit to allocate via a multilateral aid fund, then the donor countries bargain over allocation outcomes ex post à la Nash. In contrast to bilateral aid, Nash Bargaining results in an allocation outcome that reflects aggregate efficiency (that is, efficiency according to the donor countries’ preferences).
Therefore, under multilateral aid, a recipient country with a higher effectiveness will receive a higher level of aid, which in turn induces competition over ex ante investments by recipient countries and mitigates the Samaritan’s problem.Footnote 6 That is, it is precisely the process of preference aggregation in the multilateral fund that enables multilateral organizations to better implement aid conditionality—when donor countries with heterogenous preferences pool their resources, competition among recipient countries over aid intensifies since bargaining functions as a commitment to reward recipient countries for higher investments.
Additionally, by explicitly modeling the bargaining process of the multilateral fund, we are able to link the investment outcomes to the decision rule used to allocate funding. That is, our analysis demonstrates that the recipient countries’ incentive to invest in reform is also a function of the decision rule used within the fund. Specifically, we show that majority rule further increases the incentive for the recipient countries to invest, since higher investment increases the probability that a recipient’s project will be selected by the endogenous majority coalition. However, the higher incentive to invest comes at a cost of limiting the total number of projects that are funded, which implies that majority will only outperform unanimity when the productivity of donor-country investment is at an intermediate level.
Empirically, the predictions of our model are in line with the finding that aid allocated through multilateral agencies is more selective than bilateral aid (Eichenauer and Knack 2018), which suggests that multilateral allocation rewards recipient countries that invest in good governance. Our model also provides a clear prediction regarding the impact of decision rules on aid allocation: Majority results in a more selective budget allocation, and hence provides a greater incentive for recipient countries to invest in good governance. While there exists theoretical literature on optimal decision-rules in international organizations (see Harstad 2005, Maggi and Morelli 2006), empirical evidence regarding the relationship between decision rules and outcomes at the international level is lacking. Accordingly, we provide novel empirical evidence on the relationship between voting rules in multilateral organizations and the selectivity of aid allocation. We find that the qualitative prediction of our model is in line with the empirical evidence—multilateral organizations that take decisions via majority adjust aid allocation more in response to changes in their recipient countries’ governance policies, suggesting that recipient countries have a higher incentive to invest in good governance when multilateral funds allocate aid via majority.
Our paper’s main contribution is to the literature on aid conditionality (see Dreher 2009 and Molenaers et al. 2015 for an overview), showing that delegation to a multilateral fund functions as a commitment to implement conditionality due to the endogenous objective that arises when donor countries bargain over aid allocation. In particular, this result shows that the Samaritan’s problem can be mitigated through delegation even in the absence of an independent third party with appropriate preferences. Most closely related to our work is Annen and Knack (2018), who consider a model of delegation to an institution that exogenously maximizes the joint welfare of member nations, and focus on characterizing the decision of whether to join a fund as a function of the level of donor-country bias. Our model differs from theirs in the sense that we explicitly model decision-making within multilateral funds rather than assuming that the multilateral fund maximizes a certain objective, and are therefore able to characterize recipient-country investment as a function of the decision rules of the multilateral fund.Footnote 7
Additionally, our work contributes to the literature on optimal decision rules in international organizations (see Harstad 2005, Maggi and Morelli 2006, and Barbera and Jackson 2006).Footnote 8 In particular, our results regarding the optimal voting rule in multilateral funds are related to Harstad (2005), who shows how a majority rule can mitigate a holdup problem in a setting where investments by members of a club (or countries in a union) are expropriated ex post. A key difference in our findings, however, is that majority rule is not always optimal for donor countries, even though the costs of investment are fully borne by the recipient countries. Instead of simply choosing the decision rule that maximizes investments, unanimity may be optimal for multilateral aid organizations because it ensures that all recipient-country projects receive funding, whereas majority increases investment precisely by providing more funding to the most effective projects.
More broadly, our paper also relates to the literature on aid allocation and selectivity. A number of recent contributions investigates what determines the allocation of aid. Schneider and Tobin (2016) show that governments allocate more resources to multilateral organizations that are similar to the donor in terms of the countries they support.Footnote 9 Annen and Knack (2019) show that aid receipts increase with the quality of recipient-country governance.Footnote 10Dietrich (2013) shows that donors bypass national governments when institutional quality is low; Dietrich and Murdie (2017) report that shaming by International Non-Governmental Organizations has the same effect. According to Knack (2013), donors rely on recipient-country aid management systems to a larger degree when such systems are of higher quality, pointing to an allocation of aid that builds administrative capacity in recipient countries. Our analysis contributes to this literature by demonstrating how the design of decision-making institutions within multilateral funds can impact the investment choices of the recipient countries.
A number of recent papers also have investigated the conditions under which donors prefer bilateral over multilateral aid. According to the standard view, multilateral aid allows different donors to share the burden of aid-giving, at the cost of losing control over how exactly the aid is spent (Milner and Tingley 2013, Reinsberg et al. 2017). As holds true for multilateral cooperation at large, multilateral aid can realize efficiency gains, pool risks, materialize economies of scale, and encourage wide cost sharing (Abbott and Snidal 1998). However, it is important to note that bilateral aid also has access to benefits of scale in implementation since bilateral aid is often channeled through international institutions (see Eichenauer and Hug 2018 or Reinsberg et al. 2017 for analyses of donors’ decisions to participate in trust funds and the implementation of earmarked aid). Additionally, by avoiding the bargaining process inherent in multilateral aid, donors have more direct control and freedom to use bilateral aid as a tool to promote their own political interests. Our paper shows that, despite the ability to achieve economies of scale with bilateral aid, donor countries benefit from delegating aid to a bargaining process as a commitment to reward recipient countries for investment in administrative capacity and bureaucratic quality. Related, Dreher et al. (2020) show that powerful governments refer to multilateral organizations when they aim to hide contentious foreign policies from domestic audiences. They allocate aid bilaterally when extending favors to allies, while they channel funds via multilateral organizations to non-allied recipients, where more visible bilateral aid is more contentious.
Our paper proceeds as follows: Section 2 provides illustrating empirical evidence to motivate the formal analysis. Section 3 presents the theoretical framework. Section 4 contains the analysis of aid allocation (Section 4.1) and investment decisions (Section 4.2); Section 4.3 contains our normative analysis and characterizes the optimal decision rule. Section 5 concludes. We present formal proofs for all results in the Appendix.Footnote 11
2 Empirical analysis of decision rules and multilateral aid
Before we proceed with the model, we provide descriptive evidence regarding the relationship between voting rules in multilateral organizations and the sensitivity of aid allocation to changes in their recipient countries’ governance policies. To address this question, we draw on the Creditor Reporting System (CRS) of the OECD’s Development Assistance Committee (DAC), which provides recipient- and year-specific data on aid given by a broad range of international organizations. We consulted the statutory documents of these international organizations, as well as secondary sources, in order to code the organizations’ decision-making rules for allocating funds across members. Footnote 12
Out of the 46 international organizations included in the CRS, only five allocate funds via a strict unanimity rule. Footnote 13 This is too small a sample to provide sufficient empirical evidence on the difference between unanimity and majority. However, an additional 15 organizations take decisions via a consensus rule. While consensus rules have commonly been coded as unanimity in the literature on international organizations (Blake and Lockwood-Payton 2015), they differ from an explicit unanimity rule in the sense that country representatives are strongly encouraged to seek unanimity, but may fall back on a majority decision rule if unanimity cannot be attained (see Gould 2017 for a detailed discussion on the implementation of consensus rules).Footnote 14
Given the small number of organizations in our sample that use a traditional unanimity rule, we separate organizations that allocate funds according to a (weighted or unweighted) majority rule from those that explicitly encourage decisions via consensus in our empirical analysis. Therefore, our assumption is that the bargaining power of countries in the minority is higher under a consensus rule relative to a traditional majority rule—arguably, organizations with the strong norm of decision-making via consensus are closer to unanimity, in terms of our model, than organizations deciding based on majority rule alone.
Table A1 in the Online Appendix lists the 46 international organizations included in our data. For each organization, we list the main decision-making rule for allocating funds, in concert with information about whether we code decision-making to conform with the norm of consensus as well as sources on which we base our coding. As can be seen, 41 organizations decide with majority and five require unanimity. 20 organizations included in our data use either consensus or unanimity. In the empirical application, Consensus Rule is thus a binary indicator that is one for these 20 organizations, and zero for the others.
One way to test the impact of decision rules on aid allocation is to compare the weighted average governance quality of the aid portfolio across multilateral organizations. However, the multilateral organizations in our sample vary widely in their scope and regional focus, and a large degree of the variance in the allocation of aid spending may be unrelated to their ability to overcome the Samaritan’s problem. A test of the sensitivity of aid allocation to recipient country investment in good governance thus has to consider how the aid allocation of a given institution changes in response to changes in the recipient countries’ governance policies. Accordingly, we test the relationship between decision rules and aid allocation using the following regression equation:
where Aidijt is the amount of funds committed by international organization i to a specific member j in a year t in millions constant 2010 US$, Consensus Rule is a measure of consensual decision-making, Bureaucratic Quality an indicator of recipient country institutional quality, and X constitutes a set of control variables. One difficulty, in terms of translating the model to the empirical setting, is identifying the set of relevant recipient countries for each international organization. For example, most countries of the world are member of the International Bank for Reconstruction and Development (IBRD), but some have never received funding and are thus unlikely to adjust their policies in reaction to the IBRD’s decision rules. Our regressions therefore only include countries that have received funding from a specific organization in at least one of the years of our sample.Footnote 15
Our indicator of Bureaucratic Quality is from the International Country Risk Guide (PRS Group 2017), and measures whether bureaucracies are “somewhat autonomous from political pressure and ... have an established mechanism for recruitment and training,” on a zero to four scale. We control for the recipient country’s (log) GDP per capita (in constant 2010 US$), (log) population, and its share of exports relative to GDP, which are control variables included in most aid allocation regressions.Footnote 16
We estimate the aid allocation models with Tobit, which is well-suited for modeling the allocation of aid if we assume whether or not countries receive aid and, if they do, how much they receive are determined by the same process.Footnote 17 Aid allocation models are also often estimated as two step models, where a first set of regressions focuses on the decision whether or not to provide funding to a recipient in a year and the second stage explains the amount of funding received, given a country was selected to receive funding (e.g., Fleck and Kilby 2010). We provide such analyses for completeness. As is typical in the related literature, we focus on logged values of aid (adding a value of one to keep zero observations in the sample). For comparison, we also report results using an inverse hyperbolic sine transformation and a regression that does not transform aid (i.e., that focuses on absolute dollar values).Footnote 18
We estimate the model with a set of fixed effects.Footnote 19 Our preferred specification includes dummies for recipient countries (ηj) and years (τt), given that the decision-making rule is constant over time within donor organizations and thus collinear with donor fixed effects. We however also report a specification including dummies for donor organizations (ηi), where the coefficient of Bureaucratic Quality is captured by the fixed effects. The coefficient of the interaction is then exclusively identified by changes in Bureaucratic Quality within recipient-countries over time. We cluster standard errors at the international organization level.
Table 1 shows the results. Column 1 reports the basic Tobit regression, excluding fixed effects for donors, with log aid commitments as dependent variable.Footnote 20 Focusing on the coefficient of Qualityjt ∗ Consensusi, our results show that consensus rule results in a less selective budget allocation compared to majority rule.Footnote 21 This result holds when we use an inverse hyperbolic sine transformation (in column 2) or focus on the level of aid commitments (in column 3) rather than taking logs, include fixed effects for donors (in column 4) or exclude control variables (in column 5).
Results are very similar when we focus on the second stage of the aid allocation process, using the sample with positive aid commitments only. Both in terms of statistical significance and in quantitative terms, results from this OLS regression (shown in column 6) are very similar to those of column 1. To the contrary, results from a linear probability model of the binary selection stage shows no significant interaction (column 7).Footnote 22 It thus seems that the results from the Tobit analysis are driven by the second rather than the first stage. As we show in the robustness section of our formal model, this is consistent with a setting where donor countries have a partial bias so that recipient countries with high bureaucratic quality receive more, but not all, of the aid funds.
Quantitatively, the OLS results of column 6 imply that organizations which decide via consensus commit around 40 percent lower amounts of aid to countries that improve their bureaucratic score by one point compared to organizations that follow a strict majority rule. The corresponding decrease according to the Tobit estimates of column 1 (for countries that receive positive values in a year) is around 30 percent. In absolute numbers, the estimate of column 3 implies that organizations which decide consensually commit around US$ 50 million less to countries that improve their bureaucratic score by one point compared to organizations that follow a strict majority rule (with mean commitments of around US$ 30 million and a mean of US$ 106 million for positive commitments).
We conclude this section by testing whether the effect of Qualityjt ∗ Consensusi depends on the size of an international organizations’ resources in a year. To this end, we add an interaction of Qualityjt ∗ Consensusi with the yearly total of funds committed by an organization, to proxy their aid budget.Footnote 23 As one would expect, the effect turns stronger (i.e., more negative) when total commitment size increases.Footnote 24 This is in line with the interpretation that budgets have to be sufficiently large in order to work as incentive.
In summary, our conditional correlations provide some evidence that organizations with majority rule are more selective compared to those adopting decisions by consensus. This novel empirical finding can be rationalized in the context of our model: As we show below in Section 4.3, majority rule induces stronger competition between recipient countries since, relative to unanimity, the bargaining solution under majority is more responsive to changes in recipient country governance quality.
3 Framework
In this section we introduce our model. Specifically, there are three donor countries and three recipient countries, denoted as i = 1, 2, 3 and j = 1, 2, 3 respectively. Each donor country has an identical budget for foreign aid, x, to allocate across a set of recipient country aid projects.Footnote 25 We use the notation ai, j to indicate the amount of aid that donor country i allocates to recipient country j. Prior to making the aid allocation decision, the donor countries commit to distribute their aid budget via a specific institution; in particular, we compare bilateral aid allocation with a multilateral institution with a unanimity rule, and a multilateral institution with majority rule.
3.1 Preferences and actions
We model a situation in which donor countries are biased towards a particular recipient country. This bias could reflect preferences due to geographical proximity, trade relations or historical ties; as we discuss in the introduction, empirical research has shown that donors disproportionately allocate aid to countries that are former colonies and countries with which they have strong trade ties, suggesting a bias in preferences over allocations. To make the Samaritan’s problem as stark as possible, we make the assumption that each donor country i only values aid spending in one of the recipient countries, and denote the recipient country that donor country i values as recipient country j = i. This assumption also allows us to simply and clearly illustrate the main points of the model, and we discuss the robustness of our results to this assumption at the end of our analysis.
Additionally, each recipient country has a project quality, qj, that is either high quality, qj = h2 > 1, or low quality, qj = 1. One may for example think about governance structures that impact the effectiveness of aid.Footnote 26 Each recipient country can influence its own project quality by investing in δj ∈ [0,1] according to the cost function \(c(\delta _{j})={\delta _{j}^{2}}\). The quality of the project is in turn a stochastic function of the level of investment chosen by country j. Footnote 27
Specifically:
Conceptually, this is consistent with our example of investment in good governance: e.g., indirectly investing in good governance by decreasing corruption increases the probability that a recipient country’s project realizes as high quality. Investment, however, is observable but non-contractible, which implies only a limited scope for donor countries to condition allocations on investments.
Let aj denote the total amount of aid received by country j; i.e. \(a_{j} = {\sum }^{i} a_{i,j}\). Donor countries have utility functions over aj=i (we use the notation ai instead of aj=i henceforth) that are increasing and concave:
Note that we account for the possibility that donor countries directly value investment in good governance in recipient countries, independently from its impact on the quality of the project, by including the term gδi in the donor-country utility function. That is, given that good governance in recipient countries is frequently a policy goal of donor countries (as discussed in the introduction) we find it relevant to account for donor countries’ preferences for, say, decreased corruption or more democracy.
However, since donor countries distribute aid spending after observing recipient-country investment, the level of g does not impact the final allocation of aid spending (that is, the direct utility from δi is independent of the aid allocation, and therefore does not impact the Nash Bargaining solution). Therefore, our descriptive analysis of the impact of decision rules on aid allocation and recipient-country investment is independent of g. That is, the results of Sections 4.1 and 4.2 hold for any level of g, and therefore g will not feature in the positive analysis of the model. However, g plays an important role when it comes to determining the optimal decision rule; in our normative analysis in Section 4.3 we show that majority will be the preferred decision rule when donor countries place a high direct value on good governance in recipient countries.
Recipient countries have linear preferences over aid spending \(a_{j} = {\sum }^{i} a_{i,j}\):
Institutions for aid allocation: We consider three possible institutions for allocating aid: Bilateral, Multilateral-Unanimity and Multilateral-Majority. Under all institutions, donor countries make aid allocation decisions after recipient countries choose investment levels and {qj} is revealed. Under the multilateral institutions, we assume that donor countries bargain over aid allocation decisions, and that the donor countries have access to utility-transfers. We discuss this assumption in detail in the following subsection.
Bilateral
Under Bilateral aid allocation, donor countries simultaneously allocate their individual budgets, x, over the set of recipient-country projects. Country i’s choices are represented by the set {ai, j}, with \({\sum }^{j} a_{i,j} \leq x\).
Multilateral-unanimity
Under multilateral aid allocation, donor countries commit to allocating the joint aid budget, 3x, centrally. Under Multilateral-Unanimity, donor countries bargain over the allocation of the centralized aid budget à la Nash, given the condition that \({\sum }^{j} a_{j} \leq 3x\).
Multilateral-majority
If the donor countries use a majority rule then the budget allocation is determined according to the following procedure: One donor country is randomly chosen as formateur, F. Each donor country has an equal probability of being chosen. The formateur then selects a majority coalition, and bargaining over project funding and utility transfers occurs within the majority coalition.Footnote 28 Therefore, allocation under Majority is comparable to a two-country fund, consisting of the majority coalition, bargaining over the allocation of aid funding via Unanimity. However, since the majority coalition is chosen endogenously, Majority features the additional step of the formateur selecting the majority coalition that maximizes her expected utility. We assume that if the formateur is indifferent regarding which countries to include in the majority coalition, she chooses each country with equal probability. Also, utility transfers are restricted to the majority coalition, which implies that countries outside the majority coalition are not fully expropriated.
To summarize, the timing of Multilateral-Majority is as follows:
-
1.
Recipient countries choose δj and qj realizes.
-
2.
A donor country is randomly chosen as formateur, F.
-
3.
The formateur selects a majority coalition, \({\mathcal{M}}\).
-
4.
The majority coalition bargains over the allocation of project funding à la Nash.
We denote the subset of donor-country strategies that pertain to the choice of a majority coalition as \({\mathcal{M}}\).Equilibrium: The equilibrium we utilize is analogous to sub-game perfect Nash equilibrium, with the exception that, if the donor countries allocate aid via a multilateral aid fund, the allocation decision is determined via Nash Bargaining. We restrict the analysis to symmetric equilibria, where all target nations choose the same level of investment and, under Multilateral-Majority, all donor countries play a symmetric strategy, \({\mathcal{M}}(\{q_{j}\})\), conditional upon being selected as the formateur, which specifies the majority coalition chosen as a function of the realized project qualities. Lastly, we assume that the donor countries have access to utility transfers, and have a threat-point payoff of zero—in the sense that if donor countries do not agree on an allocation, then no aid is allocated and donor countries receive a payoff of ui(ai, qi, δi) = gδi.
Throughout the analysis, we consider the objective of the donor countries rather than, say, an objective of maximizing aggregate utility. We argue that this is a natural objective to consider when analyzing the political economy of multilateral aid funds. However, this does not imply that investments carried out by the recipient countries should be considered as non-productive for the population of these countries: While we assume that investment in good governance is costly for the regime of the recipient country, it is possible that these reforms provide utility benefits to the recipient countries’ population by increasing the effectiveness of the public sector.Discussion of key assumptions: Our analysis relies on two key assumptions: (1) that donor countries can commit their aid budgets to a multilateral organization, and (2) that the multilateral organization bargains over the allocation of aid spending and that the donor countries are able to transfer utility to each other through some dimension other than aid allocation. We discuss the robustness of our analysis at the end of the analysis section, and show how our results are robust to relaxing assumptions such as symmetric donor countries and partial bias. Also, assumption (1) is a basic premise of our analysis, and is consistent with the observation discussed above that donor countries cannot typically unilaterally withdraw aid funding that they commit to an international organization.
Our second key assumption, however, deserves a more detailed discussion. First, regarding the choice of an appropriate threat point, we follow the prescription of Binmore et al. (1986), who provide a non-cooperative foundation for the Nash Bargaining solution. Specifically, threat-point payoffs of zero are appropriate for modeling bargaining when (1) there is no risk of an exogenous breakdown of negotiations, or (2) agents receive payoffs of zero from bargaining in case of an exogenous breakdown. Note that in our model, a threat-point of zero does not imply that donor countries receive a utility of zero; rather, if bargaining breaks down a threat point of zero corresponds to donor countries receiving no payoff from aid spending (i.e., there is no utility surplus from the bargaining), but they may still receive positive utility from the direct value of recipient-country investment (gδi). The direct value of recipient-country investment received by the donor countries, however, does not impact the bargaining outcome, since the donor countries receive gδi whether they agree to a bargain or not.
In cases where there is both a risk of exogenous breakdown, and budget contributions are returned to agents following a breakdown, then the relevant threat-point is the utility countries receive from spending their budget contribution bilaterally. However, if the fund retains contributions even if negotiations were to break down, then a threat-point of zero is appropriate. Footnote 29
As we discuss in the introduction, the example of multilateral aid funds is consistent with a threat-point of zero: In most cases, disagreement over the allocation of aid funding does not result in an automatic liquidation of the multilateral fund and a reimbursement of the donor countries’ contributions. While some funds, in particular funds tied to regional banks, do have stipulations to return donations in the case of liquidation, the liquidation decisions are generally made via a weighted majority rule and are independent of allocation decisions.
Second, regarding the assumption that donor countries have access to utility transfers, we believe this to be an appropriate assumption when it comes to international organizations. The assumption of utility transfers effectively implies that donor countries can jointly bargain over aid allocation and some other dimension where the donor countries can effectively compensate other donor countries by making concessions in these other dimensions.
Therefore, utility transfers are typically considered to be an appropriate assumption in settings where agents interact across multiple different areas, or where agents are able to directly transfer money to each other. Arguably, donor countries do interact in other dimensions than just aid (the EDF discussed in the introduction is one such example); however, in the context of multilateral aid organizations the “other dimension” has a clear interpretation as the contributions to the central budget. That is, while we have assumed that donor countries simply give their aid budgets to the multilateral organization, a more realistic (but more complicated) model would also take into account bargaining over who contributes to the aid budget.
Note that if countries simultaneously bargain over how much each donor country contributes to the aid budget and how to allocate aid spending, then budget contributions will function as utility transfers, and the allocation of aid spending will be identical to the prediction of our model (which assumes utility transfers). Accordingly, our model can be considered a simplified version of a more general setting where country representatives bargain over both allocations and contributions to a fixed budget. This may be especially relevant for multilateral funds that need to raise money for their budget on a regular basis—in these cases, it is likely that bargaining over the budget allocation and budget contributions is linked.
However, in some cases, multilateral funds may bargain over budget contributions and aid allocation independently, and it is unclear that donor countries have access to another method of transferring utility. In the appendix of a previous version of this paper (Dreher et al. 2018), we analyze a model with the alternative assumption of no utility transfers and show that the Nash Bargaining solution is responsive to recipient-country investment even when utility is non-transferable. However, our comparison of Unanimity and Majority does rely on the assumption of some degree of utility transfers between donor countries since, without utility transfers, the formateur would be indifferent as to which other donor country joined the majority coalition.Footnote 30
4 Analysis
We solve the model by backward induction, and thus begin with the allocation decisions.
4.1 Allocation of aid
In the last step, donor countries decide how to allocate the aid budget to the set of projects {ai,1, ai,2, ai,3}. Importantly, the donor countries are committed to allocate bilaterally or multilaterally, and cannot at this point reverse their decision on the allocation mechanism.
4.1.1 Bilateral
If countries allocate their aid budgets bilaterally, each donor country i solves:
This maximization problem shows that, irrespective of the project quality, each donor country i will spend all of its budget in its preferred recipient country i, i.e., ai = x. This result already eludes to the Samaritan’s dilemma donor countries face when allocating their aid budget bilaterally: The preferred recipient country will receive the whole aid budget regardless of the level of reform effort they implement. Even though donor countries are free to allocate to a different country, their preferences make it impossible to commit to conditionality.
4.1.2 Multilateral-Unanimity
If donors have decided to allocate their aid budgets through a joint fund, at this stage they bargain over the allocation of the aggregate budget to the set of recipient country projects. The Nash Bargaining (NB henceforth) outcome maximizes the sum of utilities of the bargaining parties:Footnote 31
Note that the indirect utility benefit of recipient-country investment is not factored into the NB outcome, since gδi is independent of the allocation decision (i.e., the indirect utility benefit of investment is part of each donor country’s outside option).
Solving the maximization problem above gives the NB allocation outcome:
This equation shows that the division of funds under NB depends on the realized project qualities. Therefore, unlike with bilateral aid allocation, the expected share of the total aid budget that each target nation receives is sensitive to its investment in δj.
Since utility transfers are possible, donor countries share the created surplus equally. That is, Nash Bargaining allocates the aid budget to maximize the joint surplus, and specifies utility transfers such that all donor countries receive an equal share of the surplus. Formally, each receives:
4.1.3 Multilateral-majority
The aid allocation stage of Multilateral-Majority is identical to Multilateral-Unanimity, with the exception that bargaining over aid allocation only takes place within the majority coalition. Since donor countries only value aid spending in their respective recipient country, only recipient countries whose donor country is in the majority coalition will receive a positive level of aid funding.
Specifically, take a majority coalition of \({\mathcal{M}} = \{i,k\}\). NB among the majority coalition solves the following maximization problem:
which results in the following aid allocation for i = j in the majority coalition:
That is, if the donor country with i = j is in the majority coalition then aj is defined by the above expression, and if the donor country with i = j is not in the majority coalition then aj = 0.
Expression (8) characterizes aid allocation given a majority coalition. However, to fully characterize aid allocation as a function of {qj}, we must also detail the endogenous formation of the majority coalition. First note that donor country \(i\notin {\mathcal{M}}\) receives a utility of 0 since ai = 0. Therefore, F (the formateur) will select itself into the majority coalition (\(F \in {\mathcal{M}}\)).
Next, consider F’s choice of the additional country in the majority coalition. Take the majority coalition to be \({\mathcal{M}} = \{F,k\}\). Similar to Multilateral-Unanimity, NB results in an equal split of the utility surplus among the donor countries in the majority coalition. That is, F’s utility is equal to:
Given expression (9), it follows that to maximize the utility surplus of the majority coalition, the formatuer will select the donor country whose recipient country’s project has the highest quality.
It might seem counter-intuitive that the formateur selects the donor country whose recipient country’s project has the highest quality into the majority coalition, since recipient countries with high-quality projects will receive a higher amount of aid. However, since the donor countries have access to utility transfers, and donors in the majority coalition split the utility surplus equally, it is in the best interest of the formateur to maximize the joint surplus by selecting a donor country whose recipient country’s project has high quality.
The following lemma summarizes the endogenous choice of the majority coalition (\({\mathcal{M}}(\{q_{j}\})\)).
Lemma 1
Take donor countries {F, k1, k2} with corresponding project qualities \(\{q_{F},q_{k_{1}},q_{k_{2}}\}\).
The formatuer will select a majority coalition \({\mathcal{M}} = \{F,i\}\) with:
4.2 Investment decisions
Recipient countries move simultaneously when deciding their investment levels δj and take into account how their expected share of aid spending will change with the investment they make. Since recipient countries have linear utility, each recipient country chooses δj to maximize their expected aid minus the cost of investment:
That is, given the investment decisions of the other recipient countries, country j will select a level of investment that maximizes the return of investment—i.e., the expected aid spending—minus the cost of investment.
4.2.1 Bilateral aid
When aid is allocated bilaterally, recipient countries know that the donor who prefers to allocate aid to their project will do so irrespective of the quality of the projects {qj}. That is, recipient countries solve problem [10] given aj = x for all {qj}.
Lemma 2
When aid is allocated bilaterally, recipient countries do not invest in reforms; i.e., δj = 0 for all j.
This is a classic Samaritan’s problem in the context of aid conditionality—aid allocation does not change with investment—which illustrates that in the presence of donor country bias, donor countries face significant difficulties implementing aid conditionality when allocating aid bilaterally.
4.2.2 Multilateral-unanimity
In contrast to Bilateral aid allocation, under Multilateral allocation, aid spending is a function of the realized quality of the recipient countries’ projects. Therefore, recipient countries will internalize the effect that their reform efforts have on the final allocation of the fund’s budget and choose δj to maximize their expected utility, taking the allocation rule of the donor countries and the investment decisions of the other recipient countries as given.
To analyze recipient-country investment under Multilateral allocation, we introduce some additional notation to facilitate the analysis. Take Qj ∈ {0, 1, 2} to be equal to the number of recipient countries other than j that realize high quality projects:

Next, given that we have characterized the aid allocation that results for any given set of project qualities, we introduce a functional notation for the equilibrium level of aid spending given a set of project qualities. That is, take aj({q}) to be the NB allocation to j given project qualities \(\{q\} \equiv \{q_{j},q_{k_{1}},q_{k_{2}}\}\) under Unanimity, and {q} ≡ {qj, qk} under Majority given majority coalition of \({\mathcal{M}} = \{j,k\}\). The function aj({q}) is characterized by Expressions [6] and [8] in the previous subsection for Unanimity and Majority, respectively.
Following backward induction, we then characterize the equilibrium level of investment chosen by the recipient countries, who take aj({q}) as given. That is, given the results of the previous section we are able to specify an investment strategy under Unanimity that is a symmetric best response by characterizing the level of investment, δj, that solves:
and that satisfies δj = δu, which gives δu as the equilibrium level of investment under unanimity.
We leave the details of solving for δu to the Appendix. However, the main insight from the analysis is that, in contrast to bilateral aid, multilateral aid results in a positive level of recipient-country investment. The reason for this finding is that under multilateral aid, the expected amount of aid given to country j is increasing in the level of investment, δj.
We illustrate the intuition with the following example: assume that j knows with certainty that one of the other recipient country’s projects will be low quality and the other will be high quality (Qj = 1). In this case, when choosing their optimal level of investment, they will select δj to maximize the expected sum of aid spending on their project, aj(qj, h, l), minus the cost of investing, captured by the following expression:
Note that this shows that the first term in the above expression, E[aj(qj, h, l)|δj], is increasing in δj since a(h, h, l) > a(l, l, h). This implies that, given Qj = 1, j will select a positive level of investment, δj.
Moreover, the same is true for Qj = 0,2, which implies that the equilibrium level of investment, δu, will be positive, since a higher level of investment leads to a higher level of aid. Specifically, expanding on our simple example, given that the other two recipient countries select investment levels δu, recipient-country j will select δj to maximize the following expression:
This expression allows us to solve for the unique symmetric equilibrium level of investment under Unanimity using the first-order conditions, an exercise we leave for the Appendix but summarize in the following lemma:
Lemma 3
Under Multilateral-Unanimity, the unique equilibrium level of investment is characterized by:Footnote 32
Again, Lemma 3 illustrates one of the key insights of the analysis: When aid is allocated through a multilateral fund, the bargaining process induces competition between the recipient countries. Under Multilateral-Unanimity they thus have an incentive to invest in reforms in order to secure a larger share of the budget. Next, we illustrate how a majority rule in the multilateral fund impacts the recipient country’s incentive to invest in good governance.
4.2.3 Multilateral-majority
Under Majority, recipient countries have two reasons to invest in good governance: first, analogous to Unanimity, conditional upon i = j being selected to the majority coalition investment increases the expected allocation to aj; second, as illustrated by Lemma 1, higher investment increases the probability of i = j being selected to the majority coalition. Here we detail the impact of this second channel on recipient-country investment under majority rule.
As above, we illustrate the intuition with an example: again, assume that country j knows with certainty that one of the other recipient country’s projects will be low quality and the other will be high quality (Qj = 1). Additionally, assume that j knows with certainty that i = j will be chosen as the formateur. In this case, j’s expected level of aj as a function of δj is analogous to unanimity, since i = j is always in the majority coalition. That is:
Note that E[aj|δj] is still increasing in δj, since a(h, h) > a(l, h).
Next assume that i ≠ j with a high-quality project is selected as the formateur. In this case, j only receives positive aid funding with certainty if their project has high quality; that is, in this case:
Comparing the two cases, we see that the marginal rate of return on investment is higher when i ≠ j with a high-quality project is selected as the formateur—\(\partial E[a_{j}|\delta _{j}]/\partial \delta _{j} = a(h,h)-\frac {1}{2} a(l,h)\)—than when i = j is chosen as the formateur—∂E[aj|δj]/∂δj = a(h, h) − a(l, h).
This illustrates the additional incentive to invest provided by Majority relative to Unanimity. Below we list the expression for the expected utility of the recipient country as a function of the level of investment δj, which is similar to the expression for Unanimity, with the exception that in cases where i = j is not chosen as the formateur, there is an additional incentive to invest to increase the probability that i = j is chosen to the majority coalition:
As above, we leave the details of solving for the unique symmetric equilibrium to the Appendix, and summarize the result in the following lemma.
Lemma 4
Under Multilateral-Majority, the unique equilibrium level of investment is characterized by:
In the next subsection, we utilize the characterization results in Lemmas 3 and 4 to compare investment levels under Unanimity and Majority and detail the optimal decision rule.
4.3 Optimal decision rules
Given the characterization results above, we are able to compare the level of investment under Bilateral, Multilateral-Unanimity and Multilateral-Majority and introduce our first main result in the following proposition:
Proposition 1
The equilibrium level of investment under Majority, δm, is weakly greater than the level of investment under bilateral aid and the level of investment under Unanimity, δu.
Intuitively, recipient countries have a higher incentive to invest under Majority since majority rule incentivizes the recipient countries to invest via two channels: (1) to increase the expected allocation to aj, conditional upon i = j being selected to the majority coalition (analogous to Unanimity), and (2) to increase the probability of i = j being selected to the majority coalition. The addition of the second channel implies that recipient-country investment is always higher under Majority relative to Unanimity.
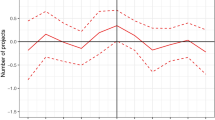
The comparison of Unanimity and Majority is also illustrated visually in Fig. 1, where we vary the value of the high-quality project, h, which represents the indirect value of investment to donor countries, for a fixed x. Reading the figures right-to-left, we see that under Unanimity, as h → 1 the incentive to invest approaches zero for the recipient countries, since aj approaches x for any qj. Under Majority, however, the incentive to invest stays strictly positive, since any country with qj = 1 is more likely to be left out of the majority coalition and receive aj = 0.
In Section 2, we established the novel empirical result that multilateral funds that allocate aid spending via majority rule are more sensitive to institutional quality in recipient countries. Intuitively, this empirical result suggests that recipient countries’ incentive to invest is higher under majority rule, consistent with Proposition 1. However, to show that our model can rationalize this empirical finding specifically, we also prove the following related result:
Proposition 2
At the equilibrium levels of investment δu and δm, expected aid spending is more responsive to recipient-country investment under Majority. That is:
Lastly, note that Propositions 1 and 2 only establish that Majority results in a higher level of investment—they do not show that it is optimal for multilateral funds to adopt a majority rule: While Majority results in a higher degree of partner-country investment, it does not necessarily result in a higher level of donor-country welfare. We explore donor-country welfare under the two different decision rules in the following section.
4.3.1 Comparing donor-country welfare
To determine the optimal decision rule, we compare donor-country utility under the different decision rules and show that under Majority, there exists a tradeoff between higher investment, characterized in Proposition 1, and a utility loss relative to Unanimity that stems from the fact that Majority limits funding to the two recipient countries in the majority coalition. Note that due to the higher investment levels under Majority, a crucial determinant of the optimal decision rule will be to what extent the donor countries place an independent value on reform in the recipient countries, captured by g in the utility function of the donor countries. As we discuss in the introduction, donor countries may value investment directly since an increase in good governance may have significant spillover effects to areas other than project quality.
Here, we characterize the optimal decision rule as a function of g, the direct value of investment in good governance to donor countries, and h, which represents the indirect value of investment to donor countries (indirect in the sense that the probability that h is realized is a function of investment). That is, as h increases, the expected value of recipient-country investment also increases since the donor countries receive a higher benefit from the project realizing high quality.
The impact of g on the optimal decision rule is straightforward: as the direct value of investment increases, majority rule becomes more beneficial to donor countries. The impact of h, however, is less straightforward. This is because as h increases, the incentive to invest increases under both Majority and Unanimity and, as illustrated in Fig. 1, the difference in investment under Majority and Unanimity is actually decreasing in h—by L’Hôpital’s Rule, both δm and δu approach \(\min \limits \{1,2x/(2+x)\}\) as \(h \to \infty \).
This suggests that if Majority outperforms Unanimity, then it will do so for intermediate values of h: When the productivity of investment (h) is very low then there is little benefit from incentivizing recipient countries to invest, and when the productivity of investment is very high then investment levels are high under both Majority and Unanimity. This implies that the relative benefit of instituting Majority for donor countries will be the highest for intermediate values of productivity of recipient-country investment, when the difference in the relative levels of investment between Majority and Unanimity and the benefit of investment are both high.
This intuition is formalized in the following proposition, which considers the utility difference between the two decision rules holding x fixed and varying h and g:
Proposition 3
There exists g∗, such that iff g > g∗, there exists an interval (1, ϕ] for some ϕ > 1 such that the expected utility of the donor countries is higher under Majority than Unanimity for h ∈ (1, ϕ].
This result is also illustrated in Fig. 2, which shows the expected utility under the two decision rules (upper graph) and the utility difference under the two voting rules (lower graph) as the productivity of investment (h) increases, for three different values of g. As we can see from the figure, the relative value of Majority is the highest for an intermediate value of h. Figure 2 also demonstrates that a range of h where Majority outperforms Unanimity need not exist. In fact, simulations show that if g = 0, then Unanimity is preferable to Majority for all x, h. This suggests that the higher investment achieved via Majority will only be beneficial to donor countries who place an independent value on recipient-country reform in good governance.
4.4 Robustness of the formal results
In this section we discuss the robustness of the formal results to relaxing some of the main assumptions of the model.
Asymmetric donor countries
First, consider the case where donor countries have aid budgets of different size, xi. Note that since there is full commitment, in the sense that aid budgets are given to the multilateral institution with “no strings attached,” this does not impact our formal results—the threat-point of Nash Bargaining remains zero and the results are unaffected. However, asymmetry in aid budgets may impact the decision to delegate to the multilateral institution. That is, while delegation results in higher investment, it also leads to an equal split of the utility surplus. Therefore, donor countries with relatively high aid budgets may be better off under bilateral aid and either opt out of the multilateral institution, or contribute only part of their aid budget to the multilateral institution.
Second, it may be the case that not all donor countries have equal weight in the bargaining process. For example, donor countries who contribute more to the budget may negotiate for a higher bargaining weight in the aid allocation process. Asymmetric bargaining weights may decrease the competition between recipient countries, since recipient countries whose donor country has a high/low bargaining weight may face an aid allocation that is less sensitive to investment. However, even with asymmetric weights, bargaining will still provide some incentive for recipient countries to invest, implying that delegation to a multilateral institution would still mitigate the Samaritan’s problem.
A similar intuition holds for asymmetric probabilities of being selected as the formateur under Majority. As is illustrated in the preceding section, this will decrease the incentive to invest for recipient countries with donor countries that have higher probabilities of being selected, but increase the incentive to invest for others, leaving the aggregate impact of this asymmetry unclear.
Partial bias
In our analysis, we make the assumption that donor countries only care about aid spending in a single recipient country. This makes the Samaritan’s problem as stark as possible, and highlights the ability of multilateral aid to overcome the Samaritan’s problem even in this extreme case. However, the qualitative results of our analysis hold even as this assumption is relaxed.
Assume donor countries have the following utility functions over aid allocation:
for some 𝜖 ∈ (0, 1). In this case donor countries place positive value on aid spending in all recipient countries, but favor country j = i by placing a higher weight on aid spending in this recipient country.
First, note that for 𝜖 small enough, under Bilateral aid it is still a best response for countries to give all aid to their favored recipient country regardless of project qualities, which shows that the Samaritan’s problem still exists with partial bias. Next, note that under Unanimity, the allocation of aid spending maximizes \((1+2\epsilon ){\sum }_{i} \sqrt {q_{i} a_{i}}\); i.e., it results in the exact same allocation as in the above analysis, which shows that all results for Unanimity also hold for partial bias.
Lastly, note that under Majority, the allocation of aid will maximize \((1+\epsilon ){\sum }_{i \in M} \sqrt {q_{i} a_{i}} + 2\epsilon \sqrt {q_{k} a_{k}}\), where k is not in the majority coalition. Therefore, the formateur will still select the highest-quality project into the majority coalition, and the recipient countries will have an additional incentive to invest under Majority relative to Unanimity, just as above. With a partial bias, however, the incentive to invest may be lower, since all recipient countries receive a positive level of aid from the majority coalition, although the recipient countries whose donor countries are in the majority coalition still receive more.
5 Conclusion
In this paper, we consider a formal model of the allocation of aid spending in an environment where donor countries face a bias over which recipient countries receive funding. Our analysis provides several important insights regarding the optimal design of multilateral aid organizations. As highlighted by Svensson (2000, 2003), multilateral aid organizations must focus on distributing aid in a manner that provides an incentive for developing nations to invest in reform. However, given competing national and special party interests, the question is how to enforce this objective. Here, we show that competition in the area of reform can arise endogenously when donor countries directly bargain over the allocation of aid funds, and that this competition is intensified under majority rule, as recipient countries invest in reform to increase the probability that their project will be selected by the endogenous majority coalition. These findings are consistent with our novel empirical finding that aid allocation by organizations deciding via majority is more responsive to changes in recipient-country governance quality.
From a policy perspective, our analysis suggests that a majority rule should only be adopted when there are high positive spillovers of recipient countries’ investment in reform on other areas, such as promoting good bureaucratic practices more widely, and when investment in reform has an intermediate level of productivity—if productivity is very low, then the utility loss of only funding a subset of projects is not worth the gain from additional investment in reform; and if productivity is very high, then both Unanimity and Majority result in high levels of investment in reform.
We emphasize that the predictions of our model only apply to multilateral aid funds that allocate aid spending via an unstructured bargaining process. In recent years, “earmarked” donations (aka multi-bi aid) have become increasingly common as donor countries seek to take advantage of the benefits of scale of international organizations, while ensuring that aid is distributed according to national priorities (Eichenauer and Hug 2018). However, as our paper shows, earmarking diminishes the incentive of recipient countries to invest in reforms, since it circumvents multilateral bargaining. Therefore, in this case, less structure can result in greater efficiency.
Notes
Gang and Epstein (2009) instead model the optimal allocation of aid when aid is contractable. They show that allocating aid in proportion to the quality of governance (rather than allocating all aid to the country with better governance) is optimal as long as recipient countries are sufficiently asymmetric.
Equivalently, donors might also be biased towards their own aid projects which are located in a subset of recipient countries, rather than valuing all aid to a recipient country equally. To correct for such bias in donor-country preferences and protect recipient countries, Auriol and Miquel-Florensa (2019) propose a tax scheme on unilateral projects.
For example, multilateral funds are typically less politicized, and are managed by technocrats and experts who have a longer-term perspective; however, the appointment of technocrats, rather than politicized agents, to multilateral funds may be a direct result of the mechanism we highlight here.
As we discuss in more detail in Section 3 below, our assumption is that if no agreement is reached over the allocation of aid spending, then there is no disbursement of aid and the aid budget is not reimbursed to the member nations. Some multilateral institutions do have provisions to reimburse donor countries if a decision is made to liquidate the multilateral fund. Importantly, however, disbursement does not occur automatically following disagreement over the allocation of aid spending; rather, the decision to liquidate the fund is taken independently of allocation decisions.
We focus on the contrast between bilateral aid and different decision rules within multilateral aid funds and do not consider delegation to an independent third party. The effectiveness of delegation to an independent party in overcoming the Samaritan’s problem depends crucially on the objective of that institution (see Svensson 2000)—here we consider the objective that endogenously emerges from direct bargaining between country representatives.
Svensson (2003) details how competition over aid spending incentivizes investment in state capacity. In our setting, donor countries cannot induce such competition under bilateral aid due to the non-contractibility of investments.
An earlier version of our paper also considered different levels of donor-country bias (Dreher et al. 2018)—to simplify the exposition, however, we focus on the results with equal donor-country biases.
For a broad overview of the political economy of international organizations see Dreher and Lang (2019).
In our robustness section, we show that even delegation to a multilateral fund whose members share similar, but not identical, preferences is sufficient to incentivize higher investment among recipient countries.
At the same time they show that policy-selective aid improves policies. Also see Smets and Knack (2016).
The Online Appendix is available on the Review of International Organizations’ web page.
Existing datasets do not cover a sufficient number of decision rules on how international organizations allocate funds. Blake and Lockwood-Payton (2015) include 26 banks in their data, but only 12 of those are included in the CRS. Hooghe et al. (2017) provide detailed data on decision-rules in 76 international organizations. Most of these organizations do not provide funding to their members however. Gould (2017) distinguishes unanimity from consensus, but again no detailed aid data are available for a sufficiently large number of organizations.
Climate Investment Funds, Green Climate Fund, Nordic Development Fund, OSCE, and United Nations Relief and Works Agency for Palestine Refugees.
A typical example is the statutory document of the Adaptation Fund (2018, p.6), which states that “Decisions of the Board shall be taken by consensus whenever possible.”
CRS data include a substantial amount of missings in earlier years. For example, data on commitments are reported by 70 percent of the DAC members in 1995, 90 percent in the year 2000, and 100 percent since 2003. See http://www.oecd.org/dac/stats/crsguide.htm, last accessed September 24, 2018. In the regressions we report below, we have replaced years with missing information on aid commitments with zero. We however also report results for a regression with positive values only. Our results are unchanged when we include only those IO-recipient-year observations as zeros that are reported in CRS. As we report in an earlier version of this paper (Dreher et al. 2018), our results are also unchanged when we use the absence of corruption or the level of democracy as indicators of institutional quality, when we focus on aid disbursements rather than commitments, and when we restrict the sample to years after 1999 or 2002 (with better data coverage).
See Alesina and Dollar (2000), Dreher et al. (2011), or Faye and Niehaus (2012). We take these variables from the World Bank (2018). Another set of variables typically included in bilateral aid allocation studies includes proxies for colonial history or political relations between the donor and recipient. As our focus is on multilateral donors we exclude such variables here (though geopolitics has been shown to matter in some international organizations as well, see Vreeland and Dreher 2014). Given that the choice of control variables always involves discretion, we also show results excluding them. Of course, our analysis provides conditional correlations with the intention to motivate the formal model rather than causal effects. A number of omitted variables at the level of international organizations might affect how voting rules interact with institutional quality in determining aid commitments. The most obvious one is an organization’s budget. While controlling for yearly totals of aid from an organization does not affect our results, this does not rule out potential effects of variables we cannot control for, such as the structure of organizations’ decision-making committee or preferences of its most powerful members.
Comparable work frequently used Tobit models (e.g., Alesina and Dollar 2000).
The inverse hyperbolic sine transformation allows to keep zero observations in the sample without adding an arbitrary constant. It is defined as \(\Tilde {x}=ln(x+\sqrt {x^{2} +1})\) and is frequently used in recent applied research (see Bellemare and Wichman 2020).
Note that the incidental parameter problem does not affect the coefficients of Tobit models (Greene 2004).
Due to missing data our regressions include a maximum of 45 donor organizations and 100 recipient countries, over the 1985-2016 period. The maximum number of observations is 63,986, of which 45,843 are zero; around 50 percent of the observations are allocated under consensus rule.
Aid commitments increase with population size and per capita GDP, while exports are not significant at conventional levels.
While results of a Logit model are similar, the interpretation of interacted variables is not straightforward in such non-linear models (Greene 2010).
In column 8 of Table 1, “Triple interaction” shows the coefficient of Consensual decision-making*Bureaucratic quality*IO Budget; while the level of IO Budget is absorbed by the year fixed effects, interactions of Consensual decision-making*IO Budget and Bureaucratic quality*IO Budget are included but not shown to reduce clutter.
This result is confirmed when we split the sample according to median aid commitments and estimate two separate regressions. The coefficient is significantly negative only in the sample with the larger budgets.
The assumption of identical budgets is without loss of generality for our model, which considers the allocation decision given that donor countries commit their aid budgets to the multilateral fund. However, asymmetric budgets may impact the decision to join the fund, and we discuss asymmetric budgets at the end of the analysis in a section that considers the robustness of our results.
Empirical studies disagree on whether and to what extent good governance improves the effectiveness of aid. Burnside and Dollar’s (2004) finding that aid effectiveness is higher in countries with higher levels of institutional quality has frequently been overturned (see, e.g., Doucouliagos and Paldam 2010).
An earlier version of this paper (Dreher et al. 2018) utilized a model with deterministic investments. The qualitative insights of the models with stochastic investments and deterministic investments are the same; however, there are no pure-strategy equilibria in the investment stage under Majority (we introduce the formal definitions for the different decision rules below). Therefore, we use a stochastic investment technology to make the analysis tractable and to more clearly illustrate the difference between Majority and Unanimity.
Our model of decision-making under majority closely follows the example of Harstad (2005), who models majority decisions in organizations such as the European Union. In general, the “formateur” model of decision-making is commonly used to model bargaining under majority (see Baron and Ferejohn 1989).
That is, we assume that donor countries have a fixed aid budget, and cannot costlessly produce a new aid budget to fund bilateral aid if negotiations in the multilateral fund break down.
Without utility transfers, Nash Bargaining results in the allocation of aid spending that maximizes the product of the payoff the donor countries receive from aid spending (\(\sqrt {q_{i} a_{i}}\))—since the max is independent of scaling, the level of recipient-country investment (qi) will not impact the allocation of aid spending, and Nash Bargaining will result in the same level of aid spending to the formateur’s preferred recipient country regardless of who they select to the majority coalition.
A complete description of the NB outcome would include utility transfers; however, since there is no need to refer to them directly, we simplify the notation by not explicitly introducing the utility transfers.
Note that if δu = 1 then the recipient’s project will be of high quality with probability one; therefore, recipient countries will never select δu to be greater than one, which is why a min-function characterizes the equilibrium level of investment. The same is true for the equilibrium level of investment under Majority, which we characterize below.
References
Abbott, K.W., & Snidal, D. (1998). Why states act through formal international organizations. Journal of Conflict Resolution, 42(1), 3–32.
Adaptation Fund. (2018). Rules of procedure of the adaptation fund board. https://www.adaptation-fund.org/wp-content/uploads/2018/04/Rules-of-procedure-of-the-Adaptation-Fund-Board.pdf, Accessed: September 2018.
Aghion, P., & Tirole, J. (1997). Formal and real authority in organizations. Journal of Political Economy, 105(1), 1–29.
Alesina, A., & Dollar, D. (2000). Who gives foreign aid to whom and why?. Journal of Economic Growth, 5(1), 33–63.
Alesina, A., & Weder, B. (2002). Do corrupt governments receive less foreign aid?. American Economic Review, 92(4), 1126–1137.
Annen, K., & Knack, S. (2018). On the delegation of aid implementation to multilateral agencies. Journal of Development Economics, 133, 295–305.
Annen, K., & Knack, S. (2019). Better policies from policy-selective aid? World Bank Policy Research working paper 8889.
Auriol, E., & Miquel-Florensa, J. (2019). Taxing aid to improve aid efficiency. Review of International Organizations, 14(3), 453–477.
Barbera, S., & Jackson, M.O. (2006). On the weights of nations: Assigning voting weights in a heterogeneous union. Journal of Political Economy, 114 (2), 317–339.
Baron, D., & Ferejohn, J. (1989). Bargaining in legislatures. American Political Science Review, 83(4), 1181–1206.
Bellemare, M.F., & Wichman, C.J. (2020). Elasticities and the inverse hyperbolic sine transformation. Oxford Bulletin of Economics and Statistics, 82, 50–61.
Binmore, K., Rubinstein, A., & Wolinsky, A. (1986). The nash bargaining solution in economic modelling. RAND Journal of Economics, 17(2), 176–188.
Blake, D., & Lockwood-Payton, A. (2015). Balancing design objectives: Analyzing new data on voting rules in intergovernmental organizations. Review of International Organizations, 10, 377–402.
Burnside, C., & Dollar, D. (2004). Aid, policies, and growth: Revisiting the evidence. World Bank Policy Research paper number O-2834.
Collier, P. (1997). The failure of conditionality. In Gwin, C., & Nelson, J. (Eds.) Perspectives on aid and development. Overseas Development Institute, Washington DC.
Dietrich, S. (2013). Bypass or engage: Explaining donor delivery tactics in foreign aid allocation. International Studies Quarterly, 57(4), 698–712.
Dietrich, S., & Murdie, A. (2017). Human rights shaming through INGOs and foreign aid delivery. Review of International Organizations, 12(1), 95–120.
Doucouliagos, H., & Paldam, M. (2010). Conditional aid effectiveness: A Meta-study. Journal of International Development, 22(4), 391–410.
Dreher, A. (2009). IMF conditionality: Theory and evidence. Public Choice, 141(1-2), 233–267.
Dreher, A., & Lang, V.F. (2019). The political economy of international organizations. In Congleton, R, Grofman, B, & Voigt, S (Eds.) The oxford handbook of public choice. Oxford University Press, Oxford, UK.
Dreher, A., Lang, V.F., Rosendorff, B.P., & Vreeland, J.R. (2020). Bilateral or multilateral? International financial flows and the dirty-work hypothesis. Centre for Economic Policy Research paper 13290.
Dreher, A., Nunnenkamp, P., & Thiele, R. (2011). Are ‘new’ donors different? Comparing the allocation of bilateral aid between NonDAC and DAC donor countries. World Development, 39(11), 1950–1968.
Dreher, A., Simon, J., & Valasek, J. (2018). The political economy of multilateral aid funds. Centre for Economic Policy Research, discussion paper 13297.
Easterly, W. (2003). Can foreign aid buy growth?. Journal of Economic Perspectives, 17(3), 23–48.
Eichenauer, V., & Hug, S. (2018). The politics of special purpose trust funds. Economics & Politics, 30(2), 211–255.
Eichenauer, V., & Knack, S. (2018). Poverty and policy selectivity of World Bank trust funds. Journal of International Development, 30(4), 707–7142.
Faye, M., & Niehaus, P. (2012). Political aid cycles. American Economic Review, 102(7), 3516–3530.
Fleck, R., & Kilby, C. (2010). Changing aid regimes? US foreign aid from the cold war to the war on terror. Journal of Development Economics, 9 (1), 185–197.
Fuchs, A., Dreher, A., & Nunnenkamp, P. (2014). Determinants of donor generosity: A survey of the aid budget literature. World Development, 56, 172–199.
Gang, I., & Epstein, G.S. (2009). Good governance and good aid allocation. Journal of Development Economics, 89(1), 12–18.
Gould, E. (2017). What consensus? Explaining the rise of consensus decision-making in international organizations. Mimeo.
Greene, W. (2004). Fixed effects and bias due to the incidental parameters problem in the tobit model. Econometrics Review, 23(2), 125–147.
Greene, W. (2010). Testing hypotheses about interaction terms in nonlinear models. Economics Letters, 107(2), 291–296.
Hagen, R. (2006). Samaritan agents? On the strategic delegation of aid policy. Journal of Development Economics, 79(1), 249–263.
Harstad, B. (2005). Majority rules and incentives. Quarterly Journal of Economics, 120(4), 1535–1568.
Headey, D. (2008). Geopolitics and the effect of foreign aid on economic growth: 1970-2001. Journal of International Development, 20(2), 161–180.
Hoeffler, A., & Outram, V. (2011). Need, merit, or self-interest—What determines the allocation of aid?. Review of Development Economics, 15(2), 237–250.
Hooghe, L., Marks, G., Lenz, T., Bezuijen, J., Ceka, B., & Derderyan, S. (2017). Measuring international authority: A postfunctionalist theory of governance. Oxfrod: Oxford University Press.
Knack, S. (2013). Building or bypassing recipient country systems: Are donors defying the Paris Declaration?. World Bank Policy Research working paper 6423.
Maggi, G., & Morelli, M. (2006). Self-enforcing voting in international organizations. American Economic Review, 96(4), 1137–1157.
Milner, H.V., & Tingley, D. (2013). The choice for multilateralism: Foreign aid and American foreign policy. Review of International Organizations, 8 (3), 313–341.
Molenaers, N., Dellepiane, S., & Faust, J. (2015). Political conditionality and foreign aid. World Development, 75, 2–12.
Mosley, P., Harrigan, J., & Toye, J. (1995). Aid and power (2nd ed), Volume 1 of The World Bank and Policy-Based Lending. London: Routledge.
Negre, M. (2013). Allocating the next European development fund for ACP countries. German Development Institute.
Öhler, H., Nunnenkamp, P., & Dreher, A. (2012). Does conditionality work? A test for an innovative US aid scheme. European Economic Review, 56 (1), 138–153.
Pedersen, K. (1996). Aid, investment and incentives. Scandinavian Journal of Economics, 98(3), 423–437.
PRS Group. (2017). International country risk guide (ICRG). https://epub.prsgroup.com/products/international-country-risk-guide-icrg, Accessed: September 2018.
Reinsberg, B., Michaelowa, K., & Knack, S. (2017). Which donors, which funds? Bilateral donors’ choice of multilateral funds at the World Bank. International Organization, 71(4), 767?802.
Schneider, C., & Tobin, J. (2016). Portfolio similarity and international development aid. International Studies Quarterly, 60(4), 647–664.
Schneider, C.J., & Slantchev, B.L. (2013). Abiding by the vote: Between-groups conflict in international collective action. International Organization, 67 (4), 759–796.
Smets, L., & Knack, S. (2016). World bank lending and the quality of economic policy. Journal of Development Studies, 52(1), 72–91.
Svensson, J. (2000). When is foreign aid policy credible? Aid dependence and conditionality. Journal of Development Economics, 61(1), 61–84.
Svensson, J. (2003). Why conditional aid does not work and what can be done about it?. Journal of Development Economics, 70(2), 381–402.
Vreeland, J., & Dreher, A. (2014). The political economy of the United Nations Security Council: Money and influence. Cambridge: Cambridge University Press.
World Bank. (2018). World Development Indicators. World Bank.
Acknowledgments
We thank the editor of the special issue “In memoriam: Stephen Knack”--Christopher Kilby--three reviewers, Vera Eichenauer, Steffen Huck, Lennart Kaplan, Anders Olofsgård, Maria Perrotta Berlin and Giancarlo Spagnolo for their valuable comments and suggestions.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The views expressed throughout the paper are the authors’ and do not necessarily correspond to the views of the German Federal Ministry of Labor and Social Affairs or the German Government.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dreher, A., Simon, J. & Valasek, J. Optimal decision rules in multilateral aid funds. Rev Int Organ 16, 689–719 (2021). https://doi.org/10.1007/s11558-020-09406-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11558-020-09406-w