Abstract
Hyperspectral images usually consist of hundreds of spectral bands, which can be used to precisely characterize different land cover types. However, the high dimensionality also has some disadvantages, such as the Hughes effect and a high storage demand. Band selection is an effective method to address these issues. However, most band selection algorithms are conducted with the high-dimensional band images, which will bring high computation complexity and may deteriorate the selection performance. In this paper, spatial feature extraction is used to reduce the dimensionality of band images and improve the band selection performance. The experiment results obtained on three real hyperspectral datasets confirmed that the spatial feature extraction-based approach exhibits more robust classification accuracy when compared with other methods. Besides, the proposed method can dramatically reduce the dimensionality of each band image, which makes it possible for band selection to be implemented in real time situations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Hyperspectral images usually consist of hundreds of spectral bands, and this abundant spectral information can be used to precisely characterize different land cover types [1]. However, the high dimensionality also gives rise to negative effects, such as the curse of dimensionality [2]. This means that when the dimensionality increases, the volume of the space increases so fast that the available data become sparse. This sparsity is problematic for any methods that require statistical significance. To obtain a statistically sound and reliable result, the amount of data needed to support the result often grows exponentially with the dimensionality. For hyperspectral images, band selection can be applied to address this issue. Because band selection can remove irrelevant bands and keep informative bands effectively. However, most band selection algorithms are conducted with the high-dimensional band images which will bring high computation complexity and may deteriorate the selection performance. In this paper, spatial feature extraction is applied to the high-dimensional band images to improve the band selection performance.
Feature extraction starts from an initial set of measured data and builds derived values that are intended to be informative and nonredundant, facilitating the subsequent learning and generalization steps. The new extracted features are linear or nonlinear combination of original features. One way of applying this method is to project the high-dimensional space into a lower dimensional space while retaining as much information as possible. Principal component analysis (PCA) is a statistical procedure that uses orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables [4]. Linear discriminant analysis (LDA) is a method used to find a linear combination of features that characterizes or separates two or more classes of objects or events [5]. Despite their great advances, PCA and LDA fail to address the high-order dependencies, and much of the information may be contained in the high-order relationships. Being linear techniques, PCA and LDA are incapable of handling the nonlinear relationships. Thus, the kernel trick is introduced to solve the problem. Using the kernel function, kernel principal component analysis (KPCA) [6] and kernel linear discriminant analysis (KLDA) [7] can exploit the nonlinear relationship between samples. Recently, Many manifold learning based methods were proposed for dimensionality reduction. Roweis et al. introduced an unsupervised learning algorithm that computes low-dimensional, neighborhood-preserving embeddings of high-dimensional inputs [8]. The complete isometric feature mapping (Isomap) can preserve the intrinsic geometry of the data [9]. And the relevant methods are also introduced for the classification of hyperspectral images [10, 11].
Differently, the band selection approach selects informative and discriminative bands from hyperspectral images without looking into the features [12, 13]. Because no new features are introduced, the physical meaning of the original features is retained. Depending on the availability of label information, the band selection can be categorized as supervised, semi-supervised or unsupervised. The former two methods require collecting the label information, which is expensive and time-consuming for remote sensing images. Therefore, in this study, we focus on the unsupervised method. Clustering is a widely used method of selecting representative and diverse bands, and the cluster centers are typically the selected bands. Sun et al. selected appropriate band subset using sparse subspace clustering [14]. Yuan et al. proposed a dual clustering method that includes the contextual information in the clustering process and introduced a new strategy that selects the cluster representatives jointly considering the mutual effects of each cluster [15]. Based on a hierarchical structure, Martinezuso et al. grouped bands to minimize the intra-cluster variance and maximize the inter-cluster variance [16]. Affinity propagation and the k-means are also used in band selection [17, 18]. Ranking-based methods are also widely applied, in which the importance of each band is first quantified according to a certain criterion, and then a given number of top-ranked bands in the sorted sequence is selected to form the subset [19]. Chang et al. proposed a constrained band selection for hyperspectral images, in which the correlation or dependence between different bands is minimized [20]. Further, Chang et al. proposed a band prioritization method based on the eigen decomposition of a matrix, from which a loading-factor matrix can be constructed for band prioritization by applying the corresponding eigenvalues and eigenvectors [21]. The combination of clustering and ranking techniques is also adopted in band selection. In this type of method, redundancies among bands and information contents are taken into consideration [22]. Another type of band selection method is maximum information retention, which tries to retain as much as possible information during the band selection. Du et al. proposed an unsupervised band selection algorithm based on band similarity measurement, in which a linear prediction is used to select the most dissimilar band one by one [23]. Based on the relationship between the volume of a subsimplex and the volume gradient of a simplex with respect to a hyperspectral image, Geng et al. proposed an efficient volume gradient-based band selection method that tries to remove the most redundant band successively [24]. Sparse representation-based methods are also widely used for the band selection [25].
A hyperspectral image usually contains hundreds of bands. In band selection, each band corresponds to a gray image, the dimensionality of one band is usually hundreds of thousands. Thus far, most band selection algorithms are still based on high-dimensional band images. Thus, the curse of dimensionality is still inevitable and even worse in band selection. To address this problem, some researchers have randomly selected a small portion of the pixels for band selection [21, 23]. However, it is very likely that the applied random selection sometimes discards important information, thus deteriorating the performance of band selection.
It should be noted that for each band image, all pixels constitute a meaningful scene, and all the band images have a similar spatial structure because they are collected from the same scene. In conventional band selection methods, bands are usually selected based on the original high-dimensional band images. However, this type of method presents three problems: (1) the dimensionality of the original band images is too high, (2) a large amount of irrelevant information may deteriorate the performance of band selection, and (3) some useful information cannot be exploited from the original images. In this study, instead of random sampling, spatial feature extraction is introduced to reduce the dimensionality of band images and improve the performance of band selection. To the best of our knowledge, this is the first work in which spatial feature extraction is explicitly used to improve the band selection. It should be noted that this method may not be suitable for other kinds of images, e.g., face images [26], because each face image is a sample and pixels at the same spatial position of different samples may come from the different parts of the face and cannot constitute any meaningful representation. The main contributions of our work are as follows:
-
1.
The spatial feature extraction is first used to improve the performance of band selection.
-
2.
Multiple different features are used to provide complementary information.
2 Band selection based on spatial feature extraction
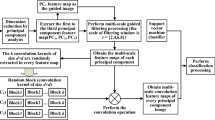
In conventional band selection, a high-dimensional band image is used as the sample, where a random sampling is carried out so as to reduce the dimensionality of the band image before band selection. However, random sampling may also discard a large amount of useful information. In this study, several different spatial feature extraction methods are used to extract complementary information from the band images. In the end, the extracted features are fused with PCA and then used for band selection. The basic steps of the proposed approach are illustrated in Fig. 1, where L is the number of band images of a hyperspectral image.
2.1 Four spatial feature extraction methods
2.1.1 Wavelet transformation
Wavelet transformation is one of the most popular time-frequency transformations and has been widely used in image denoising and image compression [27, 28]. Multiresolution analysis allows decomposing an image into a set of new images with increasingly coarser spatial resolutions (approximation images). In particular, it allows decomposing an image \(A_{2^j}\) at a resolution \(2^j\) into an approximation image \(A_{2^{j-1}}\) at a resolution \(2^{j-1}\) and into three wavelet coefficient images \(\text {DH}_{2^{j-1}}\), \(\text {DV}_{2^{j-1}}\), and \(\text {DD}_{2^{j-1}}\), which pick up, respectively, the horizontal, vertical, and diagonal details that are lost between the images \(A_{2^j}\) and \(A_{2^{j-1}}\). If the original image has M columns and N rows, the approximation image and the wavelet coefficient images obtained by applying this multiresolution decomposition have M / 2 columns and N / 2 rows.
2.1.2 Local binary patterns (LBP)
The LBP operator was originally designed for texture description [29]. The operator assigns a label to each pixel of an image by thresholding the \(3\times 3\)_neighborhood of each pixel with the center pixel value and by considering the result as a binary number. Then, the histogram of the labels can be used as a texture descriptor. Fig. 2 shows the basic LBP operator.
2.1.3 Gray histogram
A gray histogram is a graphical representation of the tonal distribution in a digital gray image. A normalized histogram can be regarded as an estimate of the probability distribution of the gray values.
2.1.4 Gray level co-occurrence matrices
A co-occurrence matrix is defined over an image to be the distribution of co-occurring pixel values at a given offset [30]. The offset, \((\Delta x,\Delta y)\), is a position operator that can be applied to any pixel in the image (ignoring edge effects): for instance, (1, 2) could indicate “one down, two right.” An image with p different pixel values will produce a \(p\times p\) co-occurrence matrix for the given offset. The (i, j) th value of the co-occurrence matrix gives the number of times in the image that the ith and jth pixel values occur in the relation given by the offset. For an image with p different pixel values, the \(p\times p\) co-occurrence matrix C is defined over an \(N\times M\) image I, parameterized by an offset \((\Delta x, \Delta y)\) as:
where x and y are the spatial positions in the image I.
The above four spatial feature extraction methods extract different but complementary information from the band image. More specifically, the approximation image in wavelet transformation retains most of the information in the original band image and depresses the noise effectively. LBP is a useful feature for extracting the texture information. A gray histogram can provide the magnitude information, and co-occurrence matrices combine the magnitude information and spatial information effectively. So, these four features are fused with PCA and used for band selection.
2.2 Three-band selection algorithms
In this study, instead of designing a new band selection algorithm, three published representative band selection algorithms are exploited to show the effect of spatial feature extraction. The three methods select bands based on different and widely used strategies.
2.2.1 Exemplar component analysis (ECA) [31]
ECA is a band-ranking method that uses an indicator termed exemplar score (ES) to measure the likelihood of a band to be an exemplar. This approach assumes that exemplars have the highest local density and are a relatively large distance away from points of higher density.
Assume that the hyperspectral image is \(X_{N \times L}=[x_1, x_2, \ldots , x_L]\), where \(x_i =[x_{1i}, x_{2i}, \ldots , x_{Ni}]^T\) is the ith band with N pixels. Let \(d_{ij}\) denote the Euclidean distance between bands \(x_i\) and \(x_j\),
Based on this distance, the local density of band \(x_i\) can be defined as
where \(\sigma\) is a parameter that controls the degradation rate. \(\delta _i\) is defined as the nearest distance to the bands of higher density from band i,
Then, the exemplar score of band \(x_i\) is defined as
Once the exemplar score of each band has been calculated, the bands are ranked according to their scores in descending order, and the top bands are selected.
2.2.2 Similarity-based band selection (SBBS) [23]
SBBS is a maximum information retention method that selects the most dissimilar bands sequentially. In contrast to the widely used metrics, such as distance and correlation, in which the measurement is taken for each pair of bands, SBBS computes the band similarity jointly instead of a pairwise manner.
Suppose \(B_1\) and \(B_2\) are two selected bands. Then, the third band B that is most dissimilar to \(B_1\) and \(B_2\) should be founded using the linear prediction equation:
where \(B^{'}\) is the linear prediction of band B; and \(a_0\), \(a_1\), and \(a_2\) are the parameters that can minimize the linear prediction error: \(e=||B-B^{'}||_2\). Let the parameter vector be \(a=(a_0\ a_1\ a_2)^{T}\), which can be determined by a least squares solution
where the size of Y is \(N\times 3\) , the first column is one, and the second and third columns are \(B_1\) and \(B_2\), respectively. The band B that yields the maximum error e is selected as \(B_3\). A similar procedure can be applied when the number of bands is larger than two.
The basic steps of SBBS can be described as follows:
-
(a)
Initialize the algorithm by choosing a pair of bands \(B_1\) and \(B_2\). Then, the resulting selected band subset is \(\Phi =\{B_1\ B_2\}\).
-
(b)
Find a third band \(B_3\) that is the most dissimilar from all the bands in the current \(\Phi\) based on the linear prediction error. Then, the selected band subset is updated as \(\Phi = \Phi \cup \{B_3\}\).
-
(c)
Continue step (b) until the desired number of bands is obtained.
2.2.3 k-means-based band selection [18]
Let \(X=\{x_i\} ,i=1,...L\) be the set of L N-dimensional band images to be clustered into a set of K clusters, \(C=\{c_k, k=1,...K\}\). The k-means algorithm finds a partition such that the squared error between the empirical mean of a cluster and the points in the cluster is minimized. Let \(\mu _k\) be the mean of cluster \(c_k\). The squared error between \(\mu _k\) and the points in the cluster \(c_k\) is defined as
The goal of the k-means is to minimize the sum of the squared error over all K clusters,
The minimization of this objective function is known to be an NP-hard problem. Thus, the k-means, which is a greedy algorithm, can only converge at a local minimum. After the clustering, the bands with the smallest Euclidean distance to the cluster centers are selected for classification.
3 Experiments
Three real hyperspectral datasets are used to show the effectiveness of the proposed method. In the wavelet transformation, the Daubechies wavelets are applied, and the level is set to 2. However, the dimensionality of the approximation image is still a bit high and thus is compressed with PCA; the reduced dimensionality is the same as the number of band images. In the gray level co-occurrence matrices, the image is scaled to 32 levels. The offset \((\Delta x,\Delta y)\) is set to (0,1). Given the four kinds of extracted features, the stacked feature is again compressed with the PCA; the final dimensionality is still the same as the number of band images. A support vector machine (SVM) with radial basis function (RBF) is used as the classifier, and the parameters are optimized by fivefold cross-validation. The overall accuracy is used to evaluate the performance of different band selection algorithms and all results are the averages of ten independent experiments.
In the experiments, four features are used in the band selection. The first feature is the vectorized band image, which is marked as “original image.” The second feature is the feature reduced by random sampling, which is marked as “random sampling”. L selected pixels are used in the band selection for this feature and L is the band number of hyperspectral images; The third feature is the proposed one, which is marked as “Spatial feature extraction”; The last feature is the co-occurrence matrices, which is marked as “ Co-occurrence”. Besides, a volume-gradient-based band selection method (VGBS) is also used for comparison [24].
3.1 Indian Pines scene
The Indian Pines scene was acquired by the NASA airborne visible/infrared imaging spectrometer (AVIRIS) sensor over the Indian Pines agricultural site in northwestern Indiana in June 1992, at 20-m spatial resolution and 10-nm spectral resolution over the range of 400–2500 nm. Most classes were crops located in fields with regular boundaries, resulting in a spatially structured dataset. Twenty water absorption bands (104–108, 150–163, and 220) were removed, resulting in a 200-band image. This dataset consists of \(145\times 145\) pixels.
As shown in Fig. 3, the random sampling method highly deteriorated the classification performance of ECA. For example, when ten bands were selected, the classification accuracy with the original image was 0.736. After the random sampling, the classification accuracy was only 0.637. However, using the proposed spatial feature extraction method, the classification accuracy was consistently improved with different band numbers. In SBBS, random sampling, VGBS and original image obtained very similar performance. The spatial feature extraction method increased the classification accuracy by 4–5% with different numbers of bands compared with the original image, as shown in Fig. 4. Though the co-occurrence method obtained better performance than original image method, its performance obviously lower than that of the spatial feature extraction method. The results of k-means is shown in Fig. 5, indicating that the spatial feature extraction method still obtains the best performance. The above findings show that the spatial feature extraction method improves the performance of different band selection algorithms using multiple kinds of complementary features.
3.2 Kennedy Space Center (KSC)
This dataset was acquired by the AVIRIS sensor over the KSC in March 1996, at 18-m spatial resolution and 10-nm spectral resolution over the range of 400–2500 nm. The data consist of a natural wetland/upland environment in which the classes have a poorly defined spatial structure. After the removal of noisy and water absorption bands, 176 bands were used in the analysis. This dataset consists of \(512\times 614\) pixels.
The result of the ECA algorithm, as shown in Fig. 6, indicates that the random sampling method obtained a much higher accuracy than the original image. Thus, random sampling can sometimes improve the band selection performance by reducing the dimensionality. However, random sampling was not found to be a robust method because it dramatically deteriorated the performance for the Indian Pines scene. Spatial feature extraction and co-occurrence had a slightly lower accuracy than random sampling; however, their accuracy was still much higher compared with the original image. The results of SBBS, as shown in Fig. 7, indicate that the VGBS and original image methods obtained almost the same performance. However, spatial feature extraction and co-occurrence achieved a much better performance than the other methods. Figure. 8 shows the results of the k-means. The VGBS has the worst performance. For KSC, the spatial feature extraction method consistently outperformed the other methods using different and complementary features.
3.3 Pavia scene
This scene was acquired by the reflective optics system imaging spectrometer (ROSIS) during a flight campaign over Pavia, northern Italy. The number of spectral bands was 102. Pavia Centre is an image composed of \(1096\times 1096\) pixels. However, some of the pixels contained no information and had to be discarded before the analysis; thus, only \(1096\times 715\) pixels were used in the analysis. The geometric resolution was 1.3 meters, and the image ground-truth differentiated 9 classes.
Figure 9 shows the results of ECA. As can be seen, the random sampling method achieved a much higher accuracy than the original image, with few selected bands. However, the difference in the performances of the two methods decreased with the increasing number of selected bands. Spatial feature extraction still obtained the best performance when the number of selected bands was greater than 10. In SBBS, as shown in Fig. 10, original image, random sampling and VGBS achieved very similar accuracies. Spatial feature extraction and co-occurrence had a better and similar performance. As shown in Fig. 11, in the k-means, the random sampling, original image and co-occurrence achieved almost the same performance with different number of selected bands. For these data, spatial feature extraction obtained a similar accuracy to that of the other methods when the number of bands exceeds 25; however, its accuracy was slightly lower than that of original image when fewer bands were selected. The reason is probably that the spatial feature extraction method discards too much information.
To give a more intuitive performance demonstration of spatial feature extraction, the performance ranks of original image, random sampling and spatial feature extraction are listed in Table 1. The above experimental results indicate that random sampling does influence the performance of different band selection algorithms. However, whereas it sometimes improves the performance, it sometimes deteriorate it, too. Therefore, random sampling is not a good choice for reducing the dimensionality of a hyperspectral image. Nevertheless, the proposed spatial feature extraction method achieved a better and robust performance using complementary information of different features.
3.4 Analysis of computational performance
Here, we use the Indian pines data to analyze the computational performance of different methods. In our experiments, we use a PC with an Intel i7 7700 CPU, and the running time is listed in Table 2. From this table, we can see that random sampling method consumes the least time. However, its classification performance is also the worst. Compared with random sampling, spatial feature extraction obtains higher classification accuracy with less consuming time. For band selection, the dimensionality of each band determines the computation complexity and storage requirement of band selection algorithms. For the Indian pines data, the original band dimensionality is \(145\times 145\), after the spatial feature extraction, the dimensionality of each band is reduced to 145. This makes it possible for band selection methods to run in real time situations. It needs to be noted that all codes in the experiments are implemented with Matlab. If the codes are implemented with C++, the running time can be reduced further.
4 Conclusion
Random sampling is commonly used to reduce the dimensionality of hyperspectral images, which have high dimensionality, before band selection. However, random sampling may not be a good choice for dimensionality reduction of hyperspectral images. This is because its performance is not sufficiently robust; whereas the method can effectively reduce the dimensionality, it also discards a large amount of useful information. To solve this problem, a multiple spatial feature extraction and fusion method is proposed. Using the complementary information of different features, the spatial feature extraction method may be a better choice for reducing the dimensionality of hyperspectral images before band selection. In the future work, more advanced features, such as deep learning-based features, can be considered to improve the performance further [32, 33]. Besides, the spectral and spatial information can be fused to obtain more powerful features [34, 35].
References
A. Plaza, J. A. Benediktsson, J. W. Boardman, et al., Recent advances in techniques for hyperspectral image processing, Remote Sens. Environ. 113 (2009)
Donoho, D. L.: High-dimensional data analysis: The curses and blessings of dimensionality. In: Lecture Math Challenges of Century, pp. 178–183 (2000)
Yang, H., Du, Q., Su, H., et al.: An efficient method for supervised hyperspectral band selection. IEEE Geosci. Remote Sens. Lett. 8(1), 138–142 (2011)
Turk, M., Pentland, A.: Eigenfaces for recognition. J Cogn. Neurosci. 3(1), 71–86 (1991)
Belhumeur, P.N., Hespanha, J.P., Kriegman, D.: Eigenfaces vs. fisherfaces: recognition using class specific linear projection. IEEE Trans. Pattern Anal. Mach. Intell. 19(7), 711–720 (1997)
Scholkopf, B., Smola, A.J., Muller, K.: Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 10(5), 1299–1319 (1998)
Roth, V., Steinhage, V.: Nonlinear discriminant analysis using kernel functions. Advances in Neural Information Processing Systems , 568–574 (2000)
Roweis, S.T., Saul, L.K.: Nonlinear dimensionality reduction by locally linear embedding. Science 290(5500), 2323 (2000)
Tenenbaum, J.B., De Silva, V., Langford, J.: A global geometric framework for nonlinear dimensionality reduction. Science 290(5500), 2319–2323 (2000)
Sun, W., Halevy, A., Benedetto, J.J., et al.: Nonlinear dimensionality reduction via the enh-ltsa method for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 7(2), 375–388 (2014)
Sun, W., Halevy, A., Benedetto, J.J., et al.: Ul-isomap based nonlinear dimensionality reduction for hyperspectral imagery classification. ISPRS J. Photogramm. Remote Sens. 89, 25–36 (2014)
Cao, X., Wu, B., Tao, D., et al.: Automatic band selection using spatial-structure information and classifier-based clustering. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 9(9), 4352–4360 (2016)
Cao, X., Han, J., Yang, S., et al.: Band selection and evaluation with spatial information. Int. J. Remote Sens. 37(19), 4501–4520 (2016)
Sun, W., Zhang, L., Du, B., et al.: Band selection using improved sparse subspace clustering for hyperspectral imagery classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 8(6), 2784–2797 (2015)
Yuan, Y., Lin, J., Wang, Q.: Dual-clustering-based hyperspectral band selection by contextual analysis. IEEE Trans. Geosci. Remote Sens. 54(3), 1431–1445 (2016)
Martinezuso, A., Pla, F., Sotoca, J.M., et al.: Clustering-based hyperspectral band selection using information measures. IEEE Trans. Geosci. Remote Sens. 45(12), 4158–4171 (2007)
Qian, Y., Yao, F., Jia, S.: Band selection for hyperspectral imagery using affinity propagation. IET Comput. Vis. 3(4), 213–222 (2008)
Ahmad, M., Haq, I.U., Mushtaq, Q., et al.: A new statistical approach for band clustering and band selection using k-means clustering. Int. J. Eng. Technol. 3(6), 606–614 (2011)
Jia, S., Tang, G., Zhu, J., et al.: A novel ranking-based clustering approach for hyperspectral band selection. IEEE Trans. Geosci. Remote Sens. 54(1), 88–102 (2016)
Chang, C., Wang, S.: Constrained band selection for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 44(6), 1575–1585 (2006)
Chang, C., Du, Q., Sun, T., et al.: A joint band prioritization and band-decorrelation approach to band selection for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 37(6), 2631–2641 (1999)
Datta, A., Ghosh, S., Ghosh, A.: Combination of clustering and ranking techniques for unsupervised band selection of hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 8(6), 2814–2823 (2015)
Du, Q., Yang, H.: Similarity-based unsupervised band selection for hyperspectral image analysis. IEEE Geosci. Remote Sens. Lett. 5(4), 564–568 (2008)
Geng, X., Sun, K., Ji, L., et al.: A fast volume-gradient-based band selection method for hyperspectral image. IEEE Trans. Geosci. Remote Sens. 52(11), 7111–7119 (2014)
Sun, W., Zhang, L., Zhang, L., et al.: A dissimilarity-weighted sparse self-representation method for band selection in hyperspectral imagery classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 9(9), 4374–4388 (2016)
Jiang, X., Lai, J.: Sparse and dense hybrid representation via dictionary decomposition for face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 37(5), 1067–1079 (2015)
Chang, S.G., Bin, Y., Vetterli, M.: Adaptive wavelet thresholding for image denoising and compression. IEEE Trans. Image Process. 9(9), 1532–1546 (2000)
Devore, R., Jawerth, B., Lucier, B.J.: Image compression through wavelet transform coding. IEEE Trans. Inf. Theory 38(2), 719–746 (1992)
Ojala, T., Pietikainen, M., Harwood, D.: A comparative study of texture measures with classification based on featured distributions. Pattern Recognit. 29(1), 51–59 (1996)
Haralick, R.M., Shanmugam, K.S., Dinstein, I.: Textural features for image classification. IEEE Trans. Syst. Man Cybern. 3(6), 610–621 (1973)
Sun, K., Geng, X., Ji, L.: Exemplar component analysis: A fast band selection method for hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 12(5), 998–1002 (2015)
Cheng, G., Li, Z., Yao, X., et al.: Remote sensing image scene classification using bag of convolutional features. IEEE Geosci. Remote Sens. Lett. 14(10), 1735–1739 (2017)
Cheng, G., Han, J., Lu, X.: Remote sensing image scene classification: Benchmark and state of the art. Proc. IEEE 105(10), 1865–1883 (2017)
Liu, W., Li, S., Lin, X., et al.: Spectralspatial co-clustering of hyperspectral image data based on bipartite graph. Multimed. Syst. 22(3), 355–366 (2016)
Yao, X., Han, J., Zhang, D., et al.: Revisiting co-saliency detection: A novel approach based on two-stage multi-view spectral rotation co-clustering. IEEE Trans. Image Process. 26(7), 3196–3209 (2017)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Cao, X., Ji, Y., Wang, L. et al. Fast hyperspectral band selection based on spatial feature extraction. J Real-Time Image Proc 15, 555–564 (2018). https://doi.org/10.1007/s11554-018-0777-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11554-018-0777-9