Abstract
Field trials to evaluate the performance of new varieties are an essential component of potato breeding. Besides the genetic differences, environmental factors can lead to variation in a trial. In variety trials, the observed differences amongst varieties should reflect genetic differences, without a large impact of the random or systematic variation in the field. One way to reduce within-field variation is to adjust the plot size and its shape in a trial. Two years of field trials in which individual plants in 90-plant plots of both diploid hybrid and tetraploid varieties were measured provided data to derive relationships between LSD% and plot size and shape. We provide a method to estimate the equations to calculate the expected variation when using different plot dimensions in a relatively homogeneous trial field for tuber yield, tuber volume, tuber count, tuber shape and the standard deviations of tuber volume and shape. Compared with the yield traits, the variation for tuber shape was relatively small. The effect of plot shape was minor. With these equations, breeders can determine what plot dimensions are needed to reach the desired precision for each trait.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Breeding of crop varieties with improved yield is an important route to keep up with the increasing demand for sustainably produced food in the world. Although potato is one of the most important staple food crops in the world (Zaheer and Akhtar 2016), breeding progress for potato grown for human consumption has been notoriously slow (Douches et al. 1996; Rijk et al. 2013). Due to complex genetics and a large number of relevant selection criteria, little genetic gain for yield traits was realised in many developed countries during the last century (Douches et al. 1996; Jansky et al. 2009). Recently, self-compatibility at the diploid level made hybrid breeding possible in potato (Lindhout et al. 2011, 2018; Jansky et al. 2016; De Vries et al. 2016; Eggers et al. 2021). Using diploid potato in hybrid breeding, QTLs can be detected efficiently and traits can be stacked in a short time resulting in an acceleration of the breeding process (Meijer et al. 2018; Korontzis et al. 2020; Su et al. 2020).
In the process of variety selection in potato, field trials are essential to evaluate the expression of genetic traits under diverse agronomic conditions. To assess such expression of different traits well, promising new genotypes need to be benchmarked against widely grown cultivars in different environments for their yield and stability across and interaction with diverse environments. A recent example for the hybrid potato breeding system was shown by Stockem et al. (2020) who compared a large number of cultivars and hybrid genotypes at different locations in NW Europe. Plot size is an important decision in plant breeding trials, as plots should be large enough to allow identification of superior genotypes, but small enough to not waste resources that could be used differently, such as for evaluating more genotypes. Plot size has been a topic of interest in potato as well as in other crops for a long time (Caligari et al. 1985; Vallejo and Mendoza 1992; Bisognin et al. 2006; Schmildt et al. 2016; Khan et al. 2017; Lavezo et al. 2017; Lohmor et al. 2017; Donato et al. 2018). Error variances and standard errors for phenotypic traits will be a function of the number of plants within a plot and the correlations between plants within a plot as a consequence of soil heterogeneity and inter plant competition. When there is no soil heterogeneity nor inter plant competition and correlations between neighbouring plants are zero, the error variance of a plot will be the error variance of a single plant divided by the number of plants in the plot: \({V}_{s}=\frac{{V}_{0}}{s}\), with \({V}_{s}\) the error variance for a plot of size s, for example a size of s plants, \({V}_{0}\) the maximum error variance for a plot, in this case a plot with a single plant, and s the plot size, here equal to the number of plants. However, typically, plants within a plot do influence each other and then the error variance for a plot does not follow simply from the error variance for single plants. Smith (1938) introduced a modification of the above rule for deriving the error variance for a plot of size s from the maximum error variance: \({V}_{s}=\frac{{V}_{0}}{{s}^{b}}\), where b is a heterogeneity factor that is equal to 1 for independent, or uncorrelated plants, and that becomes larger than 1 for correlated plants within a plot. Positive correlation between plants within plots will make the plot error to reduce less fast with increasing plant numbers than expected for independent plants. The heterogeneity factor, b, can be estimated from the slope of the regression of the logarithm of \({V}_{s}\) on the logarithm of \({V}_{0}\)
Not only size per se but also the shape of plots has been shown to affect the accuracy of field trials in several experiments (Zhang et al. 1994). In an anisotropic field, where soil physical properties differ along different directions, the plot shape that gives the most accurate results is rectangular with the highest number of plants in the direction of the largest heterogeneity of the soil whilst in a homogeneous field a square plot shape can be more advantageous (Zhang et al. 1994). Therefore, it can be advantageous to determine soil heterogeneity of a field before variety trials are performed, for example as described by Gomez and Gomez (1984). Indeed, effects of the shape of the plot on variation in yield data were found in Indian mustard and sunflower (Khan et al. 2017; Lohmor et al. 2017).
In potato, the plot shape is partly determined by the common practice to plant the seed tubers in ridges. The plot shape changes in different ways when adding extra plants within a row versus adding more rows, as inter-row spaces are larger, typically 75–90 cm, than intra-row spaces, ranging from 19 to 33 cm (Haverkort 2018).
In variety trials in the open field, it is important that differences between varieties can be attributed to genetic differences and are not obscured by field variation. Within a location, there can be multiple sources of variation, for example variation in nutrient distribution (Haefele and Wopereis 2005; Allaire et al. 2014), soil particle size (Santra et al. 2008) and in soil organisms (Lupatini et al. 2017), all leading to soil heterogeneity. This field variation can result in even more unexplained variation due to the interactions between the soil environment and the genotype (Portman and Ketata 1997). Also inter-plot interference is a major source of bias at plot level (Kempton 1997). Inter-plot interference occurs when neighbouring plots affect each other, for example by competing for resources (either above-ground or below-ground). In potato, inter-plot competition between cultivars was shown for plant height, tuber yield and dry matter content (Connolly et al. 1993; Bradshaw 1994). It can be minimised by using larger plots, placing similar varieties close to each other and using border plants around each plot (Bradshaw 1994, 2021; Kempton 1997), but these strategies either affect costs per plot or reduce randomness.
Variation in a field trial can also be present at individual plant level. In potato, growth of the plants is affected by the characteristics of the seed tubers. For example, a larger seed tuber results in a higher yield and in more stems per plant (Struik and Wiersema 2012). Moreover, plants are exposed to a specific and variable micro-environment (both above-ground and below-ground), whilst plant-plant interference can enlarge variation. For potato breeders, besides the gross yield, tuber traits like size or shape and variation in these traits are important traits of a new variety. For processing, tuber characteristics should be within well-defined and rather narrow ranges. For nitrate and dry matter content, it was shown that the major part of the variation amongst tubers of the same (uniform) field could be allocated to variation amongst tubers produced by the same plant and even by the same stem (Veerman et al. 1996).
In traditional tetraploid potato breeding, plot sizes in field trials are often limited by availability of starting material. These breeding trials always start from seed tubers that have been multiplied clonally, starting with a single tuber. This clonal multiplication is very slow, and generally tuber availability determines the plot size of variety trials, with multilocation performance trials taking place in year four of the selection cycle (Tiemens-Hulscher et al. 2013). With hybrid potato breeding, it becomes feasible to perform variety trials with an optimal plot size at an early stage of the selection or testing programme because starting material is not limiting in hybrid breeding. In contrast to traditionally bred potato, the starting material of hybrid potato is true seed. In hybrid breeding, it is possible to produce thousands of true seeds in the first year of selection. In the second year, these true seeds can be used to produce as many seed tubers as needed as described by Stockem et al. (2020). Hence, plot size can be optimised, without the limitation of starting material availability in variety trials to assess test hybrids.
The benefits and disadvantages of increasing plot size combined with the possibility of performing field trials that are not constrained by availability of planting material determine the need to assess the optimal plot size for testing hybrid varieties of potato, grown from seedling tubers. We therefore carried out two field trials testing hybrid potato genotypes, quantified in detail the sources of variation and analysed the effects of plot size and plot shape on accuracy of estimates of differences between genotypes.
Our paper addresses the following aims:
-
1)
To analyse the effect of plot size on the error variation of a trait that is measured at plot level. This will be done by analysing the least significant difference between cultivar means as a percentage of the trait mean (LSD%).
-
2)
To analyse the effect of plot shape on error variation amongst plots, and to define a plot shape that leads to the smallest error variation amongst plots for different plot sizes.
Material and Methods
Planting Material
Diploid test hybrids were produced in a hybrid potato breeding programme as described by Lindhout et al. (2011; 2018). True hybrid seeds were produced in the winter of 2015–2016 and in the winter of 2016–2017 for the field trials in 2017 and 2018, respectively. Seedling tubers were produced in the field season after the true seed production (2016 and 2017). Seedling tuber production was performed on heavy marine clay in Zeeland (The Netherlands), as described by Stockem et al. (2020). After harvest, the seedling tubers were stored at 4 °C until the end of February. The parents of the diploid hybrids were inbred lines that were self-pollinated for 4–7 generations. At this stage, the parent lines were not completely homozygous, so some variation will be present within the hybrids. Different hybrids were used in 2017 and 2018. The tetraploid cultivar Hermes was used as check in both years. Seed tubers from Hermes were produced and stored under optimal conditions for the cultivar, the seed tubers were classified in class E by the NAK (Nederlandse AlgemeneKeuringsdienst voor zaaizaad en pootgoed van landbouwgewassen, The Dutch General Inspection Service) classification system.
Design and Measurements
Two field trials were performed in Est, The Netherlands, on clay soil (33% clay) in two subsequent years (2017 and 2018). The field chosen was flat and relatively homogeneous, which was checked with a soil scan in 2018 (data not shown). The field was used for a 1:4 potato rotation for at least 20 years, with the ridges for potato cultivation always drawn in the same direction that was also used for this trial. In both years, seedling tubers of four different diploid hybrids and seed tubers of the tetraploid cultivar Hermes were planted in a randomised complete block design with three replicates. Each plot consisted of 90 plants that were grown on 6 ridges of 15 plants each. Ridges had a width of 75 cm and the planting distance within the ridge was 30 cm. On both sides, each plot was bordered by a row of the tetraploid cultivar Bergerac grown from seed tubers. In 2017, planting was done by hand, and in 2018, it was done by machine (Macon, Kraggenburg, the Netherlands). Weight of each seed(ling) tuber was determined before planting. The trials were planted in a farmer’s potato field and the crop management was according to farmer’s best practice. The tubers of each plant were harvested separately by hand. Fresh tuber yield was measured per plant. The number of tubers and dimensions were measured automatically using a 3D camera (RMA Techniek, ‘s Heer Arendskerke, the Netherlands).
Data Analysis
Volume and shape of each individual tuber were calculated using Eqs. 1 and 2, respectively. To determine the plot size that is needed to estimate the variation for tuber volume and shape present in a hybrid, the standard deviation of these traits was treated like a plant trait in the analysis. Plant characteristics of cv. Hermes and the diploid hybrids were compared by using an ANOVA and Fisher’s LSD test. Tuber count, tuber volume and the standard deviation of tuber volume and shape were analysed after logarithmic transformation.
Estimating Effect of Plot Size and Shape on Error Variation
Data for plots of varying size were created by subsampling ridges and plants within ridges from the complete plots of 90 plants, where the subsampled plots should be rectangular and consist of neighbouring ridges and consecutive plants within ridges. Therefore, plots contained from one to six ridges combined with one to 15 plants per ridge. Each combination of ridges and plants per ridge was sampled 100 times. Each data set was analysed by the same linear model that was used for the complete plot data, a randomised complete block design with three replicates and five genotypes; response = block + genotype. From this analysis, the least significant difference was retained for each data set, expressed as a percentage of the trial mean (LSD%). Subsequently, the LSD% was related to plot size following a method similar to the method of Smith (1938), using the statistical model described by Eq. 3, in which the logarithm of LSD% was regressed on the logarithm of plot size. Smith’s heterogeneity coefficient of 1 corresponds to a very homogeneous field with independent observations and a steep decrease in variance with an increase in plot size. A lower heterogeneity coefficient can be interpreted as lower independence of observations and slower decrease in variance with an increase in plot size. However, it should be noted that the estimated coefficient in this case will not be equal to Smith’s coefficient but half of it (dependent observations corresponding to 0.5).
The experimenter can visually inspect the curve to identify the plot size beyond which the variance does not decrease greatly. However, visual inspection is challenging because it depends on the plotting scale. One method to estimate optimal plot size is to include cost estimates in the formula. In the absence of cost estimates, an alternative method to standardise estimation of optimal plot size is to use the coefficient of variation instead of the variance in the linear regression model (Meier and Lessman 1971). Simple linear regression equations similar to Smith’s can be derived for other measures of variation. In this study, we recommend the use of the LSD as a more intuitive measure. This allows the experimenter to choose the plot size that will allow identification of genotypic differences that have a magnitude relevant for the breeding programme.
The estimated intercept and slope are inserted in Eq. 4 to predict LSD% for any plot size. Moreover, these predictions can be used to estimate the optimal plot size by the maximum curvature method provided by Meier and Lessman (1971) (Eq. 5). In this paper, the point of maximum curvature was used as a convenient point to compare traits with respect to the dependence of precision on plot size rather than considering it as optimal plot size.
where N is the plot size and LSD% the significant difference between two genotypes.
for i = {1 to 6} ridges and j = {1 to 15} plants on the ridge
where A is \({10}^{\mathrm{Intercept}}\) and B is − slope.
Plot Shape
The effect of plot shape on LSD% was studied to determine the relative contribution of ridges versus plants per ridge to LSD%. For this purpose, the simple regression model of Eq. (3) was altered into a multiple regression model with as predictors the number of ridges (\({N}_{\mathrm{R}}\)) and the number of plants per ridge (\({N}_{\mathrm{P}}\)) (Eq. 6). The use of this model is similar to the method of Zhang et al. (1994) and offers two slopes that can be used to assess the relative contributions of ridges and plants on the ridges to LSD%.
where NR is the number of ridges and NP the number of plants per ridge.
As a consequence of the use of this multiple regression model, LSD% can be predicted by:
Results
Plant Traits
To obtain an impression of the performance and characteristics of the tetraploid cv. Hermes and the diploid hybrids, we first analysed general plant performance. For that, we compared the yield, yield per seed(ling) tuber, number of stems per plant, number of tubers per plant and per stem, tuber volume, tuber shape and the standard deviations (SD) of tuber volume and shape as a measure of variation of the trait within the plant (Tables 1 and 2).
In both years, Hermes out-yielded the diploid hybrids (Table 2). Also, for yield per g seed(ling) tuber and for tuber volume Hermes out-performed the diploid hybrids. For stems per plant, tuber count, tubers per stem and tuber shape there were diploid hybrids with similar values as Hermes. Amongst the hybrids, significant differences were found for all traits in both years. In a breeding programme a lot of variation is present as well. Moreover, for different markets, the desired values for the tuber traits are different. To make this dataset representative for a breeding programme that breeds for different market types, this variation between the hybrids was needed.
Besides the tuber traits themselves, the within-plant-variation in tuber volume and shape, which are important determinants of number of marketable tubers for chips and fries, was analysed. As plants were harvested individually, we were able to measure the tuber characteristics per plant. This allowed us to calculate the standard deviation within one plant. Also, the standard deviation of tuber volume and shape differed amongst the hybrids and Hermes. Variation in the tubers should be as low as possible to enable industrial processing.
Plot Size
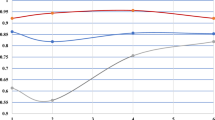
The optimal plot size was compared using the log–log regression method for tuber number, tuber weight, tuber volume and tuber shape, and for the standard deviation of tuber volume and tuber shape. For each trait, an equation was created to calculate the LSD% for different plot sizes. The decrease in LSD% for each trait when increasing the plot size is shown in Fig. 1. The dashed lines show the location of the point of maximum curvature for each trait. This point corresponds to the optimal plot size according to Meier and Lessman (1971), it is mainly useful to compare the LSD% between different traits.
Least significant difference between cultivar means as a percentage of the trait mean (LSD%) in its dependence on plot size in number of plants per plot. Traits include tuber weight, tuber count, tuber volume, SD of tuber volume, tuber shape and SD of tuber shape. The dashed line indicates the plot size corresponding to the point of maximum curvature and the dotted line the LSD% achieved at that plot size
The trait with the lowest LSD% was tuber shape, with also the point of maximum curvature at the smallest plot size (3.8 plants). This shows that there was less variation amongst plants for tuber shape compared with the other traits. The LSD% itself, as well as the decrease of LSD%, of the yield traits (tuber weight, count and volume) showed a similar trend, and the points of maximum curvature were very close to each other (11.8, 12.2 and 9.4 plants respectively). The LSD% for the standard deviation of tuber volume and shape was higher than that of the tuber traits themselves, and the point of maximum curvature was at a plot size of 10 plants for SD of tuber shape and 11.7 plants for SD of tuber volume.
Figure 1, together with the corresponding equations (Table 3), can be used to design a field trial with three replicates. For other numbers of replicates, the LSD% can be calculated by multiplying the LSD% determined with an equation of Table 3 with the square root of (3/nr), in which nr is the number of replicates. If a breeder is planning a variety trial to compare yield amongst varieties with a plot size of 4 plants Fig. 1 can be used to estimate the LSD%. The LSD% can also be calculated with the equation for tuber weight in Table 3: LSD% = 90.27/(4^0.48) = 46%. This means that the breeder can determine the difference in yield between two varieties when they differ at least 46%. When increasing the plot size to 10 plants, the LSD% decreases to 30%, so smaller differences amongst varieties can be assessed.
For tuber shape, the LSD% at a plot size of 4 plants is 12%, with a plot size of 10 plants it is 9%. This figure and the associated equations can be used by breeders as tools to design field trials that give the desired precision to compare the trait of interest amongst varieties.
Plot Shape
To determine whether plot shape is an important variable in decreasing variation, the number of rows per plot and number of plants per row were included in the model as separate factors. This was done for tuber weight, tuber count, tuber volume and tuber shape, and for the SD of tuber volume and shape.
This analysis revealed that the plot shape only had a limited effect on the LSD. Figure 2 shows the LSD% for different plot shapes for all traits, the corresponding equations are given in Table 3. In both directions (within and along the ridge), the LSD% mainly decreased with an increase in the number of plants, where it did not matter whether the increase of the number of plants came from more rows per plot or more plants per row. Only for tuber weight and count it was slightly better to increase the number of plants per row rather than number of rows per plot. For example, with a plot size of 10 plants two possibilities could be two rows per plot with five plants per row or five rows per plot with two plants per row. When using two rows per plot with five plants per row the LSD% for tuber weight would be 30%, for tuber shape it would be 9%. With five rows per plot with two plants per row, it would be 32% for tuber weight and 9% for tuber shape.
Discussion
In this study, we aimed to determine the plot size and shape that are needed to evaluate the performance of different diploid hybrids or tetraploid cultivars. This was done by creating a linear regression model between the logarithm of LSD% and plot size. The point of maximum curvature on the back transformed relationship between LSD% and plot size (Bisognin et al. 2006; Donato et al. 2018) was used as a convenient point to compare traits with respect to the dependence of precision on plot size. To assess optimal plot size, we provide equations to calculate LSD% for different plot sizes because plot size should be determined by the need of precision for a given trial or set of trials. The user can decide upon a wanted precision and use the plot of LSD% versus plot size to determine the required plot size.
Various statistical methods were used to determine the optimal plot dimensions on this dataset (unpublished results). A disadvantage of the used method, in which we used smaller subsamples in large plots, is that small plots were further apart than large plots. This could have led to an overestimation of LSD% in small plot sizes. Adjusting the results for spatial trends, for example using Spatial Analysis of Field Trials with Splines (SpATS) (Rodríguez-Álvarez et al. 2018), could have helped to decrease this over estimation. The authors intend to design a series of spatial models which will assist in quantifying the overestimation of the LSD%s.
To select the best hybrids, it is important that measured characteristics of the plants are reliable and based on genetics, not the result of random field variation. The results of this study should be applicable to variety trials with many different hybrids with different characteristics. To make sure that different characteristics were represented in this study, nine different genotypes, a tetraploid cultivar and eight diploid test hybrids, were used for the field trials. All measured plant and yield characteristics differed amongst the genotypes, with for example a low yield of hybrid 9 (469 g/plant) and a more than twice as high yield of Hermes in that year (1225 g/plant). These large differences are typical for varieties that are tested early in a breeding programme.
Optimal Plot Size Differs for Different Traits
In a variety trial, the optimal plot size and number of replications should be defined by the minimal difference that the breeder needs to detect for a certain trait. In this research, the number of replicates was not included as a variable. It is obvious that in addition to plot size, experimental design and the number of replicates will affect the plot error (Sripathi et al. 2017). Research by Caligari et al. (1985) and Bisognin et al. (2006) shows that increasing the number of replicates will be more effective for a higher precision of the trial than increasing plot size. Although the LSD% for different numbers of replicates can be estimated by multiplying the LSD% determined with an equation from Table 3 with the square root of (3/nr), in which nr is the number of replicates, it would be advisable to include different numbers of replicates in the analyses in future research.
To determine the plot size with three replications that is needed for a certain LSD% between cultivars, models were made for each trait that show the expected variation when using different plot sizes. The model for tuber count, tuber volume and tuber weight per plant showed that the error variation and the decrease in error variation with increasing plot size in these traits followed a similar slope. The variation in yield traits was high with an LSD% of still 21% at a plot size of 20 plants, although Talbot (1984) described high variation in potato yield trials compared with other crops. For tuber weight, the point of maximum curvature was a plot size of 12 plants, which is slightly higher than the optimal plot size found by Bisognin et al. (2006) using the same method of up to 10 plants, depending on the genotype.
The total variation found for tuber shape was lower than for the yield traits. In earlier research, it was shown that tuber shape is less affected by environmental conditions than tuber yield and number of tubers (Yildirim and Celal 1985; Stockem et al. 2020), which could explain the lower variation. The slope of decrease in variation, however, was similar to the slopes for the yield traits. One of the factors that leads to variation in potato plants is the quality of the seed tubers (Struik and Wiersema 2012). When testing hybrids, an alternative to using seed tubers as starting material is to use seedlings from true seed to prevent variation due to seed tuber quality, also from seedlings from true seeds relatively high yields up to 32 Mg/ha can be reached (Van Dijk et al. 2021).
Besides the tuber traits themselves, the LSD% of the standard deviation for tuber volume and tuber shape was analysed as a function of plot size (Fig. 2). The variation of these tuber traits is an important selection criterion for breeders and can be seen as a significant trait in itself. Tubers that are cultivated for processing, for example for chips, such as the cultivar Hermes, can only be used in a limited size and shape range to enable efficient mechanical processing. Variation in tuber traits within one plant can be the result of environmental conditions during the growing season (Struik et al. 1991). Moreover, stolon characteristics and timing of stolon and tuber formation can result in variation in tuber characteristics (Struik et al. 1991; Van Ittersum and Struik 1992; Kacheyo et al. 2021). The variation of the tuber traits was more difficult to estimate than the tuber traits themselves: the plot size and LSD% on the point of maximum curvature were higher for the models of SD of tuber volume and shape than for tuber volume and shape themselves.
Plot Shape had a Limited Effect
Several studies have dealt with the comparison of plot shapes (Gomez and Gomez 1984; Zhang et al. 1994). Christidis argued that rectangular shape is always better than square (Cristidis 1931). This is based on the idea that most fields are anisotropic (spatial correlation is dependent on the direction in the field) and that plots are chosen to be elongated in the direction of the field gradient. Zhang extended Smith’s method to anisotropic fields. He estimated two heterogeneity coefficients (slopes) in the same rationale with Smith: one coefficient for the decrease in variability when the number of columns is increased and number of rows is 1 and another coefficient when the number of rows is increased and number of columns is 1. He compared the sum of those 2 with a third coefficient estimated from plots with equal numbers of columns and rows to evaluate the adequacy of his method and showed that there was no interaction between number of rows and number of columns. Here, we applied Zhang’s method in a simpler way, by estimating the coefficients on all plot shapes and not only when the other dimension is 1.
Potato generally is grown in rows of 75- or 90-cm width, whilst space between plants within a row generally is between 19 and 33 cm (Haverkort 2018). Potentially this could result in a higher variation in a plot when adding more rows per plot compared with adding more plants per row. In our trials, plot size rather than plot shape determined the variance in the plot. For tuber volume, shape and the SD of these traits, the LSD of the different possible plot shapes were similar; for tuber weight and count, only a small effect of plot shape was found.
This confirmed that we conducted the trials in a homogeneous field as was intended. According to Zhang et al. (1994), the optimal shape in an isotropic field is a square. As we found no large effects of plot shape, we could not confirm this for the current trials. Therefore, the results from these trials probably are most useful for trials that will be performed in homogeneous fields as well. Further research in more heterogeneous fields would be useful to investigate whether shape has an effect and to provide tools to determine the most efficient plot shape for such fields as well.
Indeed, earlier research has shown that depending on the direction of the plot in the field, the coefficient of variation decreased (Khan et al. 2017; Lohmor et al. 2017). When including practical considerations in planning an optimal plot shape in a homogeneous field, probably a long-shaped plot is the most efficient. As potatoes are grown in rows, it is easier and faster to plant more tubers or plants in a few rows than making more rows.
Practical Implications
There is a trade-off between accuracy and costs when determining the ideal plot size to perform a field trial (Koch and Rigney 1951). Besides the costs for the land and the labour, costs of a field trial are for a large part determined by the production of starting material. On the other hand, the accuracy of a trial increased when the plot size increased. For example, in a breeding programme, it is important to perform variety trials in an efficient way. This means that the results need to be accurate enough to make selections, without making plots unnecessarily large resulting in higher costs. In this paper, we provide tools to determine the minimum needed plot size to determine tuber count, weight, volume and shape as well as the variation of tuber volume and shape in potato variety trials.
Conclusion
In conclusion, we present a method to derive equations, as well as the equations themselves, to calculate an LSD% for tuber weight per plant, tuber count per plant, tuber volume, tuber shape and the standard deviations of tuber volume and shape when using different plot sizes and shapes in a trial with three replicates. In fields that are similarly homogeneous as the one in our trials, the equations can be used in designing field trials to determine the optimal plot size for the required degree of precision for different traits. In more heterogeneous trials, the method can be used to define similar equations for plot size and shape.
References
Allaire SE, Cambouris AN, Lafond JA, Lange SF, Pelletier B, Dutilleul P (2014) Spatial variability of potato tuber yield and plant nitrogen uptake related to soil properties. Agron J 106(3):851–859. https://doi.org/10.2134/agronj13.0468
Bisognin DA, Storck L, da Costa LC, Bandinelli MG (2006) Plot size variation to quantify yield of potato clones. Hort Brasil 24:485–488
Bradshaw JE (1994) Assessment of five cultivars of potato (Solatium tuberosum L.) in a competition diallel. Ann Appl Biol 125:533–540. https://doi.org/10.1111/j.1744-7348.1994.tb04990.x
Bradshaw JE (2021) Potato breeding: Theory and practice. Chapter 3: Increasing potato yields: a conundrum. pp.125–187, Springer Nature Switserland AG
Caligari PDS, Brown J, Manhood CA (1985) The effect of varying the number of drills per plot and the amount of replication on the efficiency of potato yield trials. Euphytica 34:291–296. https://doi.org/10.1007/BF00022921
Connolly T, Currie ID, Bradshaw JE, McNicol JW (1993) Inter-plot competition in yield trials of potatoes (Solanum tuberosum L.) with single-drill plots. Ann Appl Biol 123:367–377. https://doi.org/10.1111/j.1744-7348.1993.tb04099.x
Cristidis B (1931) The importance of the shape of plots in field experimentation. J Agr Sci 21(1):14–37. https://doi.org/10.1017/S0021859600007942
De Vries M, ter Maat M, Lindhout P (2016) The potential of hybrid potato for East-Africa. Open Agriculture 1(1):151–156. https://doi.org/10.1515/opag-2016-0020
Donato SLR, Da Silva JA, Guimarães BVC, Oliveira De, e Silva S, (2018) Experimental planning for the evaluation of phenotipic descriptors in banana. Rev Bras Frutic 40:1–13. https://doi.org/10.1590/0100-29452018962
Douches DS, Maas D, Jastrzebski K, Chase RW (1996) Assessment of potato breeding progress in the USA over the last century. Crop Sci 26(6):1544–1552
Eggers EJ, van der Burgt A, van Heusden SAW, de Vries ME, Visser RGF, Bachem CWB, Lindhout P (2021) Neofunctionalisation of the Sligene leads to self-compatibility and facilitates precision breeding in potato. Nat Commun 12:4141. https://doi.org/10.1038/s41467-021-24267-6
Gomez KA, Gomez AA (1984) Statistical procedures for agricultural research. 2.ed. New York, John Wiley & sons
Haefele SM, Wopereis MCS (2005) Spatial variability of indigenous supplies for N, P and K and its impact on fertilizer strategies for irrigated rice in West Africa. Plant Soil 270:57–72. https://doi.org/10.1007/s11104-004-1131-5
Haverkort (2018) Potato handbook: Crop of the future, Potato world magazine, 2018, Enschede
Jansky SH, Jin LP, Xie KY, Spooner DM (2009) Potato production and breeding in China. Potato Res 52:57. https://doi.org/10.1007/s11540-008-9121-2
Jansky SH, Charkowski AO, Douches DS, Gusmini G, Richael C, Bethke PC, Spooner DM, Novy RG, De Jong H, De Jong WS, Bamberg JB, Thompson AL, Bizimungu B, Holm DG, Brown CR, Haynes KG, Sathuvalli VR, Veilleux RE, Miller JC Jr, Bradeen JM, Jiang J (2016) Reinventing potato as a diploid inbred line–based crop. Crop Sci 56:1412–1422. https://doi.org/10.2135/cropsci2015.12.0740
Kacheyo OC, van Dijk LCM, de Vries ME, Struik PC (2021) Augmented descriptions of growth and development stages of potato (Solanum tuberosum L.) grown from different types of planting material. Ann Appl Biol 178(3):1–18. https://doi.org/10.1111/aab.12661
Kempton RA (1997) Statistical methods for plant variety evaluation. Chapter 7: Interference between plots. Chapman & Hall, London, pp 101–115
Khan M, Hasija R, Tanwar N (2017) Optimum size and shape of plots based on data from a uniformity trial on Indian mustard in Haryana. Mausam 68:67–74
Koch EJ, Rigney JA (1951) A method of estimating optimum plot size from experimental data. Agron J 43(1):17–21. https://doi.org/10.2134/agronj1951.00021962004300010005x
Korontzis G, Malosetti M, Zheng C, Maliepaard C, Mulder HA, Lindhout P, Veerkamp RF, van Eeuwijk FA (2020) QTL detection in a pedigreed breeding population of diploid potato. Euphytica 216:145. https://doi.org/10.1007/s10681-020-02674-y
Lavezo A, Filho AC, de Bem CM, Burin C, Kleinpaul JA, Pezzini RV (2017) Plot size and number of replications to evaluate the grain yield in oat cultivars. Bragantia 76:512–520
Lindhout P, Meijer D, Schotte T, Hutten RCB, Visser RGF, van Eck HJ (2011) Towards F 1 hybrid seed potato breeding. Potato Res 54(4):301–312
Lindhout P, de Vries M, ter Maat M, Su Y, Viquez-Zamora M, van Heusden S (2018) Achieving sustainable cultivation of potatoes. Chapter 5: Hybrid potato breeding for improved varieties, pp. 99–117, Burleigh Dodds Science Publishing, Cambrige
Lohmor N, Khan M, Kapoor K, Bishnoi S (2017) Estimation of optimum plot size and shape from a uniformity trial for field experiment with sunflower (Helianthus annuus) crop in soil of Hisar. Int J Plant Soil Sci 15(5):1–5
Lupatini M, Korthals GW, de Hollander M, Janssens TKS, Kuramae EE (2017) Soil microbiome is more heterogeneous in organic than in conventional farming system. Front Microbiol 7:1–13. https://doi.org/10.3389/fmicb.2016.02064
Meier VD, Lessman KJ (1971) Estimation of optimum field plot shape and size for testing yield in Crambe abyssinica Hochst. Crop Sci 11(5):648–650. https://doi.org/10.2135/cropsci1971.0011183X001100050013x
Meijer D, Viquez-Zamora M, van Eck HJ, Hutten RCB, Su Y, Rothengatter R, Visser RGF, Lindhout WH, van Heusden AW (2018) QTL mapping in diploid potato by using selfed progenies of the cross S. tuberosum × S. chacoense. Euphytica 214(7):121
Portman P, Ketata H (1997) Statistical methods for plant variety evaluation. Chapter 2: Field plot technique. Chapman & Hall, London, pp 9–17
Rijk B, van Ittersum M, Withagen J (2013) Genetic progress in Dutch crop yields. Field Crop Res 149:262–268. https://doi.org/10.1016/j.fcr.2013.05.008
Rodríguez-Álvarez M X, Boer MP, van Eeuwijk FA, Eilers PHC (2018) Correcting for spatial heterogeneity in plant breeding experiments with P-splines. Spatial Statistics 23:52–71. https://doi.org/10.1016/j.spasta.2017.10.003
Santra P, Chopra U, Chakraborty D (2008) Spatial variability of soil properties and its application in predicting surface map of hydraulic parameters in an agricultural farm. Cur Sci 95(7):937–945
Schmildt E, Schmildt O, Cruz C, Cattaneo L, Ferreguetti G (2016) Optimum plot size and number of replications in papaya field experiment. Rev Bras Frutic. 38.https://doi.org/10.1590/0100-29452016373
Smith H (1938) An empirical law describing heterogeneity in the yields of agricultural crops. J Agr Sci 28(1):1–23. https://doi.org/10.1017/S0021859600050516
Sripathi R, Conaghan P, Grogan D, Casler MD (2017) Field design factors affecting the precision of ryegrass forage yield estimation. Agron J 109(3):858–869
Stockem J, de Vries M, van Nieuwenhuizen E, Lindhout P, Struik PC (2020) Contribution and stability of yield components 5 of diploid hybrid potatoes. Potato Res 63:345–366. https://doi.org/10.1007/s11540-019-09444-x
Struik PC, Vreugdenhil D, Haverkort AJ, Bus CB, Dankert R (1991) Possible mechanisms of size hierarchy among tubers on one stem of a potato (Solanum tuberosum L.) plant. Potato Res 34:187–203
Struik PC, Wiersema SG (2012) Seed potato technology. Chapter 4, Quality characteristics of seed tuber, pp. 65–91, Wageningen Academic Publishers, Wageningen
Su Y, Viquez-Zamora M, den Uil D, Sinnige J, Kruyt H, Vossen J, Lindhout P, van Heusden S (2020) Introgression of genes for gesistance against Phytophthora infestans in diploid potato. Am J Potato Res 97:33–42. https://doi.org/10.1007/s12230-019-09741-8
Talbot M (1984) Yield variability of crop varieties in the U.K. J Agric Sci (Camb) 102:315–321
Tiemens-Hulscher M, Delleman J, Eising J, Lammerts van Bueren ET (2013) Potato breeding. Drukkerij De Swart, Den Haag
Vallejo RL, Mendoza HA (1992) Plot technique studies on sweetpotato yield trials. J Am Soc Hortic Sci 117(3):508–511
van Ittersum MK, Struik PC (1992) Relation between stolon and tuber characteristics and the duration of tuber dormancy in potato. Neth J Arg Sci 40:159–172
van Dijk LCM, Lommen WJM, de Vries ME, Kacheyo OC, Struik PC (2021) Hilling of transplanted seedlings from novel hybrid true potato seeds does not enhance tuber yield but can affect tuber size distribution. Potato Res 64(3):353–374. https://doi.org/10.1007/s11540-020-09481-x
Veerman A, Struik PC, Timmermans PCJM (1996) Variation in tuber dry matter and nitrate content between and within plants and stems, In: Struik et al. (eds), Abstracts of Papers, Posters and Demonstrations of the 13th Triennial Conference EAPR, Veldhoven, The Netherlands, pp. 656–657
Yildirim MB, Celal F (1985) Genotype x environment interactions in potato. Am Potato J 62(7):371–375
Zaheer K, Akhtar MH (2016) Differences in shape direction depending on soil heterogeneity. Potato production, usage, and nutrition—a review. Crit Rev Food Sci Nutr 56(5):711–721. https://doi.org/10.1080/10408398.2012.724479
Zhang R, Warrick AW, Myer DE (1994) Heterogeneity, plot shape effect and optimum plot size. Geoderma 62:183–197. https://doi.org/10.1016/0016-7061(94)90035-3
Acknowledgements
We would like to thank Solynta for providing the experimental data.
Funding
George Korontzis and Stefan E. Wilson were supported by the NWO grant nr. 14520.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
PCS is the editor-in-chief of Potato Research. MED and JES are employees of Solynta.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stockem, J.E., Korontzis, G., Wilson, S.E. et al. Optimal Plot Dimensions for Performance Testing of Hybrid Potato in the Field. Potato Res. 65, 417–434 (2022). https://doi.org/10.1007/s11540-021-09526-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11540-021-09526-9