Linking Spontaneous Behavioral Changes to Disease Transmission Dynamics: Behavior Change Includes Periodic Oscillation

Abstract

Behavior change significantly influences the transmission of diseases during outbreaks. To incorporate spontaneous preventive measures, we propose a model that integrates behavior change with disease transmission. The model represents behavior change through an imitation process, wherein players exclusively adopt the behavior associated with higher payoff. We find that relying solely on spontaneous behavior change is insufficient for eradicating the disease. The dynamics of behavior change are contingent on the basic reproduction number $R_a$ corresponding to the scenario where all players adopt non-pharmaceutical interventions (NPIs). When $R_a<1$, partial adherence to NPIs remains consistently feasible. We can ensure that the disease stays at a low level or maintains minor fluctuations around a lower value by increasing sensitivity to perceived infection. In cases where oscillations occur, a further reduction in the maximum prevalence of infection over a cycle can be achieved by increasing the rate of behavior change. When $R_a>1$, almost all players consistently adopt NPIs if they are highly sensitive to perceived infection. Further consideration of saturated recovery leads to saddle-node homoclinic and Bogdanov–Takens bifurcations, emphasizing the adverse impact of limited medical resources on controlling the scale of infection. Finally, we parameterize our model with COVID-19 data and Tokyo subway ridership, enabling us to illustrate the disease spread co-evolving with behavior change dynamics. We further demonstrate that an increase in sensitivity to perceived infection can accelerate the peak time and reduce the peak size of infection prevalence in the initial wave.

Appendices

Dynamical Behaviors of System (3)

1.1 Comparing Trajectories from the Full Model (3) and its approximation (5)

To illustrate the rationale for analyzing the approximate system, we compared the solutions of the full System (3) and the approximate System (5) across a wide range of parameters. Through this comparison, we demonstrated that Model (5) can be considered a numerically validated approximation of Model (3). Figures 13 and 14 represent two specific examples under two different conditions outlined in Sect. 3.3. It is stated that the approximation arising from Assumption (4) in the main text is not restrictive and does not affect the dynamics behavior. As a consequence, for the sake of simplicity, only the approximated model is analyzed in both the main text.

Fig. 13

The time series of the approximate system Eq. (5) (represented by blue lines) and the full system Eq. (3) (denoted by black points) under various parameter settings. In the approximated system, E(t) corresponds to $E_n+E_a$ in the full system. The sector x(t) in the approximate system corresponds to $\left. (S_n+E_n)\big /(S_n+S_a+E_n+E_a)\right.$ in the full system. Parameters used in the simulations: $\mu =0$, $\eta =0.2$, $\beta =0.4$, $\delta =0.5$, $\gamma =0.1$, $\phi =50$, $k=0.2$ in (a–c) and $k=0.7$ in (d–f). This figure corresponds to Case (1) in Sect. 3.3 (Color figure online)

Fig. 14

The time series of the approximate system Eq. (5) (represented by blue lines) and the full system Eq. (3) (denoted by black points) under various parameter settings. In the approximated system, E(t) corresponds to $E_n+E_a$ in the full system. The sector x(t) in the approximate system corresponds to $\left. (S_n+E_n)\big /(S_n+S_a+E_n+E_a)\right.$ in the full system. Parameters used in the simulations: $\mu =0$, $\eta =0.5$, $\beta =0.3$, $\delta =0.5$, $\gamma =0.1$, $\phi =50$, $k=0.1$ in (a–c), $k=0.35$ in (d–f) and $k=0.6$ in (g–i). This figure corresponds to Case (2) in Sect. 3.3 (Color figure online)

1.2 The Proof Theorem 3

In what follows, we first introduce some necessary concepts and notations that facilitate our global stability analysis.

Assumption A. 1

The matrix $A>0 \ (<0)$ if A is symmetric positive (negative) definite.

Lemma A.1

(Cross 1978). Let A is an $n\times n$ real matrix. Then, all the eigenvalues of A have negative real parts if and only if there is a matrxia $H>0$, such that

$$\begin{aligned} HA+A^TH^T<0, \end{aligned}$$

where $A^T$ is the transpose of A.

Lemma A.2

(Cross 1978). The $n\times n$ matrix A is Volterra–Lyapunov stable if there is a positive diagonal $n\times n$ matrix M, such that

$$\begin{aligned} MA+A^TM^T<0, \end{aligned}$$

where $M^T$ is the transpose of M.

Lemma A.3

(Cross 1978; Rinaldi 1990). Let $D=\left[ \begin{array}{ll} d_{11} &{}\quad d_{12} \\ d_{21} &{}\quad d_{22} \\ \end{array} \right]$ be a $2\times 2$ matrix. Then D is Volterra–Lyapunov stable if and only if

$$\begin{aligned} d_{11}<0, \ d_{22}<0 \ \text {and} \ det(D)=d_{11}d_{22}-d_{12}d_{21}>0. \end{aligned}$$

Lemma A.4

(Redheffer 1985, 1986). Consider the nonsingular matrix $A=[a_{ij}]_{n\times n} (n\ge 2)$ and a positive diagonal $n\times n$ matrix $M=diag(m_1,...,m_n)$. Let $E=A^{-1}$ and $\widetilde{A}$ denote the $(n-1)\times (n-1)$ matrix obtained from A by deleting its last row and last column. Then, if

$$\begin{aligned} d_{nn}>0, \ \widetilde{M}\widetilde{E}+(\widetilde{M}\widetilde{E})^T>0 \ \text {and} \ \widetilde{M}\widetilde{A}+(\widetilde{M}\widetilde{A})^T>0, \end{aligned}$$

there is a $m_n>0$ such that $MA+A^TM^T>0$.

Theorem A.1

The matrix M is Volterra–Lyapunov stable when

$$\begin{aligned} k<1-X_{1}=I_{1}, \ R_a <4\frac{\mu +\gamma +\delta }{\delta }, \ \text {and} \ \delta >\frac{1}{2}. \end{aligned}$$

Proof

As for Matrix (17), we have

$$\begin{aligned} det(M)=-\delta m_{23}m_{31}-m_{33}\eta \beta (\mu +\gamma +\delta )(1-y_1-X_{1})<0 \end{aligned}$$

and

$$\begin{aligned} M^{-1}=\frac{1}{det(M)}\left[ \begin{array}{lll} \left[ \eta \beta (1-X_{1}-y_1)+(\mu +\delta )\right] m_{33} &{}\quad -\delta m_{33} &{}\quad -\delta m_{23}\\ \hat{m}_{21} &{}\quad (\mu +\gamma )m_{33} &{}\quad (\mu +\gamma )m_{23} \\ m_{31}\left[ \eta \beta (1-X_{1}-y_1)+(\mu +\delta )\right] &{}\quad -\delta m_{31} &{}\quad \hat{m}_{33}\\ \end{array} \right] , \end{aligned}$$

(A1)

with

$$\begin{aligned} \begin{array}{l} \hat{m}_{21}=m_{23}m_{31} +m_{33}\eta \beta \left[ (1-X_{1}-y_1)-(X_{1}-E_{1})\right] , \\ \hat{m}_{33}=\eta \beta (\mu +\gamma +\delta )(1-X_{1}-y_1). \end{array} \end{aligned}$$

And if $k<1-X_{1}$, $m_{33}>0$ is true. Let $\widetilde{M}$ and $\widetilde{M^{-1}}$ denote the $(n-1)\times (n-1)$ matrix obtained from M and $M^{-1}$ by deleting its last row and last column respectively. According to Lemma A.3, we get that the matrix $\widetilde{M}$ and $\widetilde{M^{-1}}$ are all Volterra–Lyapunov stable (Cross 1978) if $k<1-X_{1}$ since

$$\begin{aligned} \begin{array}{l} det(\widetilde{M})= (\mu +\gamma +\delta )\eta \beta (1-X_{1}-y_1)>0,\\ det(\widetilde{M^{-1}})= \frac{a_{33}}{(det(M))^2}\left[ (\mu +\gamma +\delta )\eta \beta (1-X_{1}-y_1)m_{33}+\delta m_{23} m_{31}, \right] >0 \end{array} \end{aligned}$$

and the diagonal elements of $\widetilde{M}$ or $\widetilde{M^{-1}}$ are all negative in this case. Let $\mathbb {M}=-M$, combining Lemma A.4, we get that if there is a constant diag matrix $W=diag(1,m,w_3)$ such that

$$\begin{aligned} (\widetilde{W}\widetilde{\mathbb {M}})+(\widetilde{W}\widetilde{\mathbb {M}})^T>0, \end{aligned}$$

(A2)

and

$$\begin{aligned} (\widetilde{W}\widetilde{\mathbb {M}^{-1}})+(\widetilde{W}\widetilde{\mathbb {M}^{-1}})^T>0, \end{aligned}$$

(A3)

for any $(y_1,y_2,y_3)\in \Omega _y$, the matrix M is Volterra–Lyapunov stable if $k<1-X_{1}$. Equation (A2) is equivalent to

$$\begin{aligned} \begin{array}{ll} &{} m^2\eta ^2\beta ^2(1-X_{1}-y_1)^2-2m^2\eta ^2\beta ^2(X_{1}-E_{1})(1-X_{1}-y_1) +m^2\eta ^2\beta ^2(X_{1}-E_{1})^2 \\ &{} \quad -2m(\mu +\gamma )(\mu +\delta ) -4m(\mu +\gamma )\eta \beta (1-X_{1}-y_1)-2m\delta \eta \beta (1-X_{1}-y_1)+\delta ^2<0 \end{array} \end{aligned}$$

(A4)

Since Eq. (A4) has to be true for any $0<1-X_{1}-y_1<1$,

$$\begin{aligned} m^2\eta ^2\beta ^2(X_{1}-E_{1})^2-2m(\mu +\gamma )(\mu +\delta )+\delta ^2\le 0 \end{aligned}$$

has to be satisfied. Then, we have

$$\begin{aligned} m=\frac{\delta ^2}{(\mu +\gamma )(\mu +\delta )}. \end{aligned}$$

(A5)

Substituting Eq. (A5) into Eq. (A4) gives

$$\begin{aligned} m\eta ^2\beta ^2-2m\eta ^2\beta ^2(X_{1}-E_{1})-4(\mu +\gamma )\eta \beta -2\delta \eta \beta <0, \end{aligned}$$

which is true if $R_a <4\frac{\mu +\gamma +\delta }{\delta }.$ Substituting Eq. (A5) into Eq. (A3) gives

$$\begin{aligned} \begin{array}{l} \frac{m_{23}m_{31}}{m_{33}}\left[ \frac{m_{23}m_{31}}{m_{33}}-4\delta +2(1-X_{1}-y_1)\right] \\ \quad \quad +(1-X_{1}-y_1)\left[ \eta ^2\beta ^2(1-X_{1}-y_1)m -4(\mu +\gamma +\delta )\eta \beta \right] <0. \end{array} \end{aligned}$$

Algebraic calculations show that if $R_a <4\frac{\mu +\gamma +\delta }{\delta }$,

$$\begin{aligned} \eta ^2\beta ^2(1-X_{1}-y_1)m -4(\mu +\gamma +\delta )\eta \beta <0 \end{aligned}$$

holds true. And if $\delta >\frac{1}{2}$,

$$\begin{aligned} \frac{m_{23}m_{31}}{m_{33}}-4\delta +2(1-X_{1}-y_1)<0 \end{aligned}$$

is true. Based on the above analysis, we can testify that the matrix M is Volterra–Lyapunov stable if

$$\begin{aligned} k<1-X_{1}=I_{1}, \ R_a <4\frac{\mu +\gamma +\delta }{\delta }, \ \text {and} \ \delta >\frac{1}{2}. \end{aligned}$$

That completes the proof. $\square$

1.3 The Local Stability of $\text {EE}^{*}$

The Jacobian matrix of System (6) evaluated at $E_{*}^{*}=(E_{*},I_{*},x_{*})$ is

$$\begin{aligned} J_{E_{*}^{*}}=\left( \begin{array}{lll} -a_{11} &{}\quad a_{12} &{}\quad a_{13} \\ \delta &{}\quad -(\mu +\gamma ) &{}\quad 0 \\ 0 &{}\quad -a_{32} &{}\quad a_{33} \\ \end{array} \right) , \end{aligned}$$

(A6)

where

$$\begin{aligned} \begin{array}{l} a_{11}=\frac{\delta (\mu +\delta )(1-I_{*})}{\delta -(\mu +\gamma +\delta )I_{*}}, \ \ a_{12}=(\mu +\delta )(\mu +\gamma ) \left( \frac{1}{\delta }-\frac{I_{*}}{\delta -(\mu +\gamma +\delta )I_{*}} \right) ,\\ a_{13}=(1-\eta )\beta \frac{\delta -(\mu +\gamma +\delta )I_{*}}{\delta }I_{*}, \ \ a_{33}=-(\mu +\gamma ) \frac{I_{*}}{1-I_{*}} \frac{x_{*}}{1-x_{*}},\\ a_{32}=(\mu +\gamma ) \frac{I_{*}}{(1-I_{*})^2(k-I_{*})} x_{*}\left( (1-I_{*})+(k-I_{*})\right) . \end{array} \end{aligned}$$

The corresponding characteristic equation is

$$\begin{aligned} |\lambda E-J_{E^{*}} |=\lambda ^3+b_1\lambda ^2+b_2\lambda +b_3=0, \end{aligned}$$

(A7)

where

$$\begin{aligned} \left\{ \begin{array}{l} b_1=a_{11}-a_{33}+\mu +\gamma>0, \\ b_2=\left( \mu +\gamma \right) (a_{11}-a_{33})- a_{11}a_{33}-\delta a_{12}>0, \\ b_3=\delta \left( a_{12}a_{33}+ a_{13}a_{32} \right) - \left( \mu +\gamma \right) a_{11}a_{33}>0. \end{array} \right. \end{aligned}$$

(A8)

According to the Hurwitz stability criterion, we know that the real parts of the eigenvalues of $J_{E_{*}^{*}}$ are negative if $b_1b_2-b_3>0$, indicating the local stability of the endemic equilibrium $E_{*}^{*}$.

Especially, when $k<I_M$, if $\phi \rightarrow +\infty$, $I_{*}\rightarrow k^{-}$ is true, then we have $a_{32}\rightarrow +\infty$, and $a_{11}$, $a_{12}$, $a_{13}$ and $a_{33}$ are values that fall within a finite range. Then $b_1b_2-b_3\rightarrow -\infty$ is true in this case, which indicates the unstable of the endemic equilibrium $E_{*}^{*}$. When $k>I_M$, if $\phi \rightarrow +\infty$, $I_{*}\rightarrow I_M^{-}$ is true, then we have $x_{*}\rightarrow 1^{-}$, which means that $a_{33}\rightarrow -\infty$, and $a_{11}$, $a_{12}$, $a_{13}$ and $a_{32}$ are values that fall within a finite range. Then $b_1b_2-b_3\rightarrow +\infty$ is true in this case, which indicates the local stability of the endemic equilibrium $E_{*}^{*}$.

And beyond that, $b_1b_2-b_3>0$ is equivalent to $Q_1(I_{*})>Q_2(I_{*})$, where

$$\begin{aligned} \begin{array}{l} \begin{array}{l} \frac{Q_1(I)}{(A_{11}+\mu +\gamma )}= \frac{\delta }{\delta -(\mu +\gamma +\delta )I}A_{33}\frac{A_{33}}{I} -(A_{11}+\mu +\gamma )\frac{\delta }{\delta -(\mu +\gamma +\delta )I}\frac{A_{33}}{I} \\ \quad \quad \quad \quad \quad \quad +(\mu +\gamma )(\mu +\delta )\frac{\delta (\mu +\gamma +\delta )}{(\delta -(\mu +\gamma +\delta )I)^2}, \end{array}\\ Q_2(I)=(1-\eta )\beta \delta A_{32}, \quad A_{11}=\delta (\mu +\delta )\frac{1-I}{\delta -(\mu +\gamma +\delta ) I}>0,\\ A_{33}=- X (1-\eta )\frac{(\mu +\gamma )}{\mu +\gamma +\delta } \frac{(\delta -(\mu +\gamma +\delta ) I)}{(I_{M}-I)}I,\\ A_{32}=(\mu +\gamma )X[\frac{1+ I}{(1- I)^2}+\frac{I}{(k-I)(1-I)}],\\ X=\frac{1}{1-\eta }\frac{1}{ R_0}\frac{1}{\delta -(\mu +\gamma +\delta )I} -\frac{\eta }{1-\eta }. \end{array} \end{aligned}$$

Algebraic calculations show that $Q_1'(I)>0$ and $Q_2'(I)>0$ in the interval $[\mathbb {I}_{m},\mathbb {I}_{M}]$ (see Eq. 11 for the specific form for this interval). If

$$\begin{aligned} R_a >\delta ^2\frac{1-\eta }{\eta } \frac{(\mu +\gamma +2\delta )(\mu +\gamma +\delta )}{3(\mu +\delta )(\mu +\gamma )\delta +(\mu +\gamma )^2(\mu +\gamma +\delta )}\doteq \widetilde{ R_a }, \end{aligned}$$

(A9)

and

$$\begin{aligned} k>I_{M}+I_{M} \frac{(1-\eta )\beta \delta (\mu +\gamma )(1+ I_{M})}{Q_1(I_{M})(1+ I_{M})^2-(1-\eta )\beta \delta (\mu +\gamma )(1+ I_{M})}\doteq k_0, \end{aligned}$$

(A10)

$Q_1(I_{m})>Q_2(I_{M})$ is true, where

$$\begin{aligned} Q_1(I_{m})=\left( R_a (1-I_{m})+\frac{\mu +\gamma }{\mu +\delta }\right) \frac{(\mu +\gamma )(\mu +\delta )^2}{\delta ^2}(\mu +\gamma +\delta )( R_a )^2, \end{aligned}$$

and

$$\begin{aligned} Q_2(I_{M})=(1-\eta )\beta \delta (\mu +\gamma )\left[ \frac{1+ I_{M}}{(1- I_{M})^2}+\frac{I_{M}}{(k-I_{M})(1-I_{M})}\right] . \end{aligned}$$

Combining the monotonicity of $Q_i(I)$ with $i=1,2$ and $I_{m}>0$ if $R_a >1$, we can conclude that if

$$\begin{aligned} R_a>max\{1,\widetilde{ R_a }\} \ \text {and} \ k>k_0, \end{aligned}$$

$Q_1(I)>Q_2(I)$ holds true when $\mathbb {I}_{m}<I<\mathbb {I}_{M}$, that is to say, $b_1b_2-b_3>0$ holds true in this case.

1.4 Uniform Persistence

Let X be a locally compact metric space with metric d and $\Gamma$ be a closed nonempty subset of X. $\Gamma _0\in \Gamma$ is an open set. Define $\partial \Gamma _0:=\Gamma \setminus \Gamma _0$. $\partial \Gamma _0$ need not be the boundary of $\Gamma _0$ as the notation suggests (Zhao 2003). $\Phi _t$ is a dynamical system defined on $\Gamma$. A set B in X is said to be invariant if $\Phi (B,t)=B$. Define $M_{\partial }:=\{ x\in \partial \Gamma _0:\Phi _t x\in \partial \Gamma _0,\forall t\ge 0 \}$. We have the following lemma.

Lemma A.5

(Zhao 2003; Sun and Hsieh 2010). Assume

• ($A_1$) $\Phi _t$ has a global attractor;

• ($A_2$) There exists an $M=\{M_1,...,M_k\}$ of pair-wise disjoint, compact, and isolated invariant set on $\partial \Gamma _0$ such that

  • (a) $\cup _{x\in M_{\partial }}w(x)\subset \cup _{j=1}^{k}M_j$;

  • (b) No subsets of M form a cycle on $\partial \Gamma _0$;

  • (c) Each $M_j$ is also isolated in $\Gamma$;

  • (d) $W^s(M_j)\cap \Gamma _0 = \emptyset$ for each $1\le j \le k$, where $W^s(M_j)$ is the stable manifold of $M_j$.

Then $\Phi _t$ is uniformly persistent with respect to $\Gamma _0$.

As for System (6), let

$$\begin{aligned} \Gamma =\Omega ,\quad \Gamma _0:=\{ (E,I,x)\in \Gamma : E,I>0\}, \quad \text {and} \quad \partial \Gamma _0:=\Gamma \setminus \Gamma _0. \end{aligned}$$

Obviously, $M_{\partial }=\{(0,0,x)\mid x\ge 0\}$. Since $\Omega$ is a positively invariant set of System (6), there always admits a global attractor, making ($A_1$) true. We can prove that $M=\{E_0^{0},E_0^{1}\}$, $w(x)={E_0^{1}}$ for all $x\in M_{\partial }{\setminus } E_0^{0}$. On $M_{\partial }$, System (6) reduces to $\dot{x}(t)= \phi x(1-x)k$ with $0\le x(0)\le 1$, in which $x(t)\rightarrow 1$ as $t\rightarrow \infty$ if $0<x(0)\le 1$. That means that hypothesis (a) and (b) hold. $E_0^{0}$ is always unstable and $E_0^{1}$ is unstable if $R_0>1$ according to Theorem 2. And beyond that, $W^s(M)\subset \partial \Gamma _0$. Hypothesis (c) and (d) are then satisfied. To sum up, we can reach the Theorem 5.

1.5 Hopf Bifurcations of System (6)

Figure 15 displays time series under various large $\phi$ values when periodic solutions are present. It indicates that as $\phi$ increases, not only does the maximum prevalence of infection decrease during a cycle, but both the period and cumulative cases over one cycle also decrease.

Fig. 15

Time series under different values of parameter $\phi$. The values of the remaining parameters are the same as in Fig. 5 (Color figure online)

Dynamical Behaviors of System (21)

1.1 Existence of Equilibria

Theorem B.1

The following statements on $\text {EE}^0$ of System (21) are true.

• (a) When $\frac{\mu }{\mu +\gamma }<R_a<1$, if $R_a<R_m$ or $R_a>R_M$, Model (21) has two $\text {EE}^0$s, represented by $E_{{*}_1}^0=(E_a,I_a,0)$ and $E_{{*}_2}^0=(E_b,I_b,0)$ with $I_a<I_b$. Further, $E_{{*}_1}^0$ is unstable saddle, $E_{{*}_2}^0$ is locally asymptotically stable node or focus if $\hat{H}(I_{b})<0$, but unstable node or focus if $\hat{H}(I_{b})>0$.

• (b) Model (21) has a unique $\text {EE}^0$ if one of the following conditions holds,

  • (b-1) $\frac{\mu }{\mu +\gamma }< R_a = R_m$ and $h>h_0$;

  • (b-2) $\frac{\mu }{\mu +\gamma }< R_a = R_M$ and $h>h_0$;

  • (b-3) $R_a >max\{1,R_M\}$ or $1<R_a<R_m$. In this case, this unique $\text {EE}^0$ is represented by ($E_b,I_b,0$), which is locally asymptotically stable node or focus if $\hat{H}(I_{b})<0$, but unstable node or focus if $\hat{H}(I_{b})>0$.

Here

$$\begin{aligned} \begin{array}{l} R_{m}=\frac{-W_1-\sqrt{(W_1)^2-4W_2W_0}}{2W_2} \ R_{M}=\frac{-W_1+\sqrt{(W_1)^2-4W_2W_0}}{2W_2},\\ I_{a}=\delta \frac{-H_0-\sqrt{\Delta }}{2h(\mu +\delta )}, \ \ I_{b}=\delta \frac{-H_0+\sqrt{\Delta }}{2h(\mu +\delta )}, \ \ I_{c}=\frac{-\delta H_0}{2h(\mu +\delta )}, \\ \Delta =(H_0)^2-4h\frac{\mu +\delta }{\delta }(\frac{1}{ R_a }-1), \ H_0=\frac{\mu +\delta +\gamma }{\delta }-h+\frac{\mu }{\mu +\gamma }\frac{1}{R_a}h,\\ h_0=\frac{\mu +\delta +\gamma }{\delta }\frac{(\mu +\gamma )R_a}{(\mu +\gamma )R_a-\mu }, \ \hat{H}(I)=\phi (1-I)(k-I)-(\mu +\frac{\gamma }{1+hI})\frac{I}{1-I},\\ W_2=(\frac{\mu +\delta +\gamma }{\delta }-h)^{2}+\frac{4 h (\mu +\delta )}{\delta }, \ W_1=-2 h\frac{ (\mu +\gamma ) (\mu +\delta )+\delta \gamma +\mu h \delta }{\delta (\mu +\gamma )}, \ W_0=\frac{h^{2} \mu ^{2}}{(\mu +\gamma )^{2}}. \end{array} \end{aligned}$$

Proof

As for System (21), the possible EE (E, I, x) with all players adopting an “altered” behavior satisfies

$$\begin{aligned} x=0, \ E=\frac{\mu }{\delta }I+\frac{\gamma }{\delta }\frac{I}{1+hI}, \ \hat{g}(I)=h\frac{\mu +\delta }{\delta }I^2 +H_0I +\frac{1}{ R_a }-1=0. \end{aligned}$$

(B1)

where

$$\begin{aligned} H_0=\frac{\mu +\delta +\gamma }{\delta }-h+\frac{\mu }{\mu +\gamma }\frac{1}{R_a}h. \end{aligned}$$

(B2)

The discriminant of Eq. (B1) is

$$\begin{aligned} \Delta =(H_0)^2-4h\frac{\mu +\delta }{\delta }(\frac{1}{ R_a }-1)=\frac{W_2(R_a)^2+W_1R_a+W_0}{(R_a)^2} \end{aligned}$$

and $\Delta >0$ holds true if $R_a<R_{m}$ or $R_a>R_{M}$, where

$$\begin{aligned} \begin{array}{l} W_2=(\frac{\mu +\delta +\gamma }{\delta }-h)^{2}+\frac{4 h (\mu +\delta )}{\delta }, \ W_1=-2 h\frac{ (\mu +\gamma ) (\mu +\delta )+\delta \gamma +\mu h \delta }{\delta (\mu +\gamma )}, \\ W_0=\frac{h^{2} \mu ^{2}}{(\mu +\gamma )^{2}}, \ (W_1)^2-4W_2W_0>0, \ W_2+W_1+W_0>0, \\ R_{m}=\frac{-W_1-\sqrt{(W_1)^2-4W_2W_0}}{2W_2} \ \text {and} \ R_{M}=\frac{-W_1+\sqrt{(W_1)^2-4W_2W_0}}{2W_2}. \end{array} \end{aligned}$$

According to the relationship between the roots and the coefficients of quadratic equations, the following can be obtained: If $R_m<R_a < R_M$, Eq. (B1) has no real roots. If $R_a=R_m$ or $R_a=R_M$, Eq. (B1) has a unique real and non-zero root, represented by $I_{c}=\delta \frac{-H_0}{2h(\mu +\delta )}$, which is positive if $H_0<0$. If $R_a<R_m$ or $R_a>R_M$, Eq. (B1) possesses two distinct real and non-zero roots, represented by

$$\begin{aligned} I_{a}=\delta \frac{-H_0-\sqrt{\Delta }}{2h(\mu +\delta )}<1 \quad \text {and} \quad I_{b}=\delta \frac{-H_0+\sqrt{\Delta }}{2h(\mu +\delta )}<1. \end{aligned}$$

And beyond that, $I_a<0<I_b$ holds true if $R_a>1$; $0<I_a<I_b$ is true if $R_a<1$ and $H_0<0$; $I_a<I_b<0$ is true if $R_a<1$ and $H_0>0$. $H_0<0$ holds true if

$$\begin{aligned} R_a>\frac{\mu }{\mu +\gamma } \ \text {and} \ h>h_0\doteq \frac{\mu +\delta +\gamma }{\delta }\frac{(\mu +\gamma )R_a}{(\mu +\gamma )R_a-\mu }. \end{aligned}$$

Furthermore,

$$\begin{aligned} 0\le E_{j}, I_{j}+E_{j}<1 \end{aligned}$$

holds true if $I_{j}>0$, where $E_{j}=\frac{\mu }{\delta }I_{j}+\frac{\gamma }{\delta }\frac{I_{j}}{1+hI_{j}}$ and $j\in \{a,b,c,d\}$. Then the existence of $\text {EE}^0$ can be obtained.

By checking the Jacobian matrix of System (21) at the possible EE (E, I, 0) with $E=\frac{\mu }{\delta }I+\frac{\gamma }{\delta }\frac{I}{1+hI}$, we get the corresponding characteristic equation

$$\begin{aligned} (\lambda ^2+\hat{a_1} \lambda +\hat{a_2})\left( \lambda -\hat{H}(I)\right) =0, \end{aligned}$$

(B3)

where

$$\begin{aligned} \hat{a_1}(I)= & {} \eta \beta I+(\mu +\delta )+\mu +\frac{\gamma }{(1+hI)^2}>0,\\ \hat{a_2} \left( I\right)= & {} \hat{f}'(I), \quad \hat{H}(I)=\phi (1-I)(k-I)-(\mu +\frac{\gamma }{1+hI})\frac{I}{1-I},\\ \hat{f}(I)= & {} \delta \eta \beta \frac{I}{(1+hI)}\hat{g}(I), \quad \hat{f}'(I)=\delta \eta \beta \left[ \frac{\hat{g}(I)}{(1+hI)^2}+\frac{I}{1+hI}\hat{g}'(I) \right] . \end{aligned}$$

When System (21) has two $\text {EE}^0$,

$$\begin{aligned} E_{{*}_1}^0=(E_a,I_a,0) \ \text {and} \ E_{{*}_2}^0=(E_b,I_b,0), \end{aligned}$$

with $I_{a}<I_{b}$. Combing with Eq. (B1), we have

$$\begin{aligned} \hat{g}(I_{a})=\hat{g}(I_{b})=0, \ \hat{g}'(I_{a})<0 \ \text {and} \ \hat{g}'(I_{b})>0, \end{aligned}$$

which means that $\lambda ^2+\hat{a_1}(I_{a}) \lambda +\hat{a_2}(I_{a})=0$ has a positive real root and a negative real root, and the real parts of the roots of $\lambda ^2+\hat{a_1}(I_{b}) \lambda +\hat{a_2}(I_{b})=0$ are all negative. That is to say, $E_{{*}_1}^0$ is a unstable saddle and $E_{{*}_2}^0$ is locally asymptotically stable node or focus if $\hat{H}(I_{b})< 0$ but unstable node or focus if $\hat{H}(I_{b})> 0$. Evidenced by the same token, if System (21) has the unique $\text {EE}^0$ ($E_b,I_b,0$), which is locally asymptotically stable node or focus if $\hat{H}(I_{b})<0$ but unstable node or focus if $\hat{H}(I_{b})>0$; That completes the proof. $\square$

It was evident that as for Model (21), the EE with all players adopting “normal” behaviors does not exist. But the EE where a fixed proportion of the players adopt “normal” behavior (denoted as $\text {EE}^{*}$) may exist, i.e., the equilibrium

$$\begin{aligned} E_{*}^{*}=(E_{*},I_{*},x_{*}) \end{aligned}$$

with $0<x_{*}<1$ and $I_{*}>0$ is feasible.

Theorem B.2

Model (21) may have 0-2 $\text {EE}^{*}$ if one of the following conditions holds,

• (a) $R_0> 1$;

• (b) $\frac{\mu }{\mu +\gamma }< R_0<1$ and $h>h_1\doteq \frac{\mu +\delta +\gamma }{\delta }\frac{(\mu +\gamma )R_0}{(\mu +\gamma )R_0-\mu }$.

Proof

As for System (21), the possible $\text {EE}^{*}$ (E, I, x) where a fixed proportion of the players adopt an “normal” behavior satisfies

$$\begin{aligned} \begin{array}{lr} E=\frac{\mu +\frac{\gamma }{1+hI}}{\delta }I, &{} (a) \\ x=\frac{1}{1-\eta }\frac{(\mu +\delta )(\mu +\frac{\gamma }{1+hI})}{\delta \beta } \frac{1}{1-\frac{\mu +\frac{\gamma }{1+hI}+\delta }{\delta }I} -\frac{\eta }{1-\eta },&{} (b) \\ (\mu +\frac{\gamma }{1+hI})I(1-\frac{\mu +\frac{\gamma }{1+hI}+\delta }{\delta }I)= \frac{\phi (1-I)^2(k-I)}{1-\eta }\\ \qquad \left( 1-\frac{\mu +\frac{\gamma }{1+hI}+\delta }{\delta }I -\frac{(\mu +\delta )(\mu +\frac{\gamma }{1+hI})}{\delta \beta }\right) .&{}(c) \end{array} \end{aligned}$$

(B4)

Due to requirement $0<x<1$, we know from Eq. (B4)b that

$$\begin{aligned} \begin{array}{lr} I<\frac{\delta }{\mu +\frac{\gamma }{1+hI}+\delta } \left( 1-\frac{(\mu +\delta )(\mu +\frac{\gamma }{1+hI})}{\delta \beta }\right) , &{} (a) \\ I>\frac{\delta }{\mu +\frac{\gamma }{1+hI}+\delta } \left( 1-\frac{(\mu +\delta )(\mu +\frac{\gamma }{1+hI})}{\eta \delta \beta }\right) ,&{} (b) \\ \end{array} \end{aligned}$$

(B5)

which is equivalent to

$$\begin{aligned} \begin{array}{lr} \frac{\mu +\delta }{\delta }hI^2+H_1 I+\frac{1}{ R_0}-1<0, &{} (a) \\ \frac{\mu +\delta }{\delta }hI^2+H_0 I+\frac{1}{ R_a }-1>0,&{} (b) \\ \end{array} \end{aligned}$$

(B6)

where $H_1=\frac{\mu +\delta +\gamma }{\delta }-h+\frac{\mu }{\mu +\gamma }\frac{1}{R_0}h$, $H_0=\frac{\mu +\delta +\gamma }{\delta }-h+\frac{\mu }{\mu +\gamma }\frac{1}{R_a}h$ and $H_1<H_0$. Let

$$\begin{aligned} \Delta _1=(H_1)^2-4h\frac{\mu +\delta }{\delta }\frac{1- R_0}{ R_0} =\frac{W_2(R_0)^2+W_1R_0+W_0}{(R_0)^2}, \end{aligned}$$

with

$$\begin{aligned} \begin{array}{l} W_2=(\frac{\mu +\delta +\gamma }{\delta }-h)^{2}+\frac{4 h (\mu +\delta )}{\delta }, \ W_1=-2 h\frac{ (\mu +\gamma ) (\mu +\delta )+\delta \gamma +\mu h \delta }{\delta (\mu +\gamma )}, \\ W_0=\frac{h^{2} \mu ^{2}}{(\mu +\gamma )^{2}}, \ (W_1)^2-4W_2W_0>0 \ \text {and} \ W_2+W_1+W_0>0. \end{array} \end{aligned}$$

we have that $\Delta _1>0$ if and only if $R_0<R_{m}$ or $R_0>R_{M}$, where

$$\begin{aligned} R_{m}=\frac{-W_1-\sqrt{(W_1)^2-4W_2W_0}}{2W_2} \ \text {and} \ R_{M}=\frac{-W_1+\sqrt{(W_1)^2-4W_2W_0}}{2W_2}. \end{aligned}$$

According to the relationship between the roots and the coefficients of quadratic equations, the following can be obtained: if $R_m< R_0< R_M$, Inequality (B6)a cannot be true for all $I>0$, which means that System (21) doesn’t have any $\text {EE}^{*}$ in this case; if $R_0<R_{m}$ or $R_0>R_{M}$, Inequality (B6)a is true for $I_1^1<I<I_2^1$, where

$$\begin{aligned} I_1^1=\delta \frac{-H_1-\sqrt{\Delta _1}}{2(\mu +\delta )h} \quad \text {and} \quad I_2^1=\delta \frac{-H_1+\sqrt{\Delta _1}}{2(\mu +\delta )h}. \end{aligned}$$

And beyond that, $I_1^1<0<I_2^1$ holds true if $R_0>1$; $0<I_1^1<I_2^1$ is true if $R_0<1$ and $H_1<0$. And $H_1<0$ holds true if

$$\begin{aligned} R_0>\frac{\mu }{\mu +\gamma } \ \text {and} \ h>h_1\doteq \frac{\mu +\delta +\gamma }{\delta }\frac{(\mu +\gamma )R_0}{(\mu +\gamma )R_0-\mu }. \end{aligned}$$

That is to say, except for the condition $R_0<R_{m}$ or $R_0>R_{M}$, $EE^{*}$ is feasible if $R_0>1$, or $\frac{\mu }{\mu +\gamma }<R_0<1$ and $h>h_1$.

Similarly, let

$$\begin{aligned} \Delta _2=(H_0)^2-4h\frac{\mu +\delta }{\delta }\frac{1- R_a}{ R_a} =\frac{W_2(R_a)^2+W_1R_a+W_0}{(R_a)^2}. \end{aligned}$$

$\Delta _2>0$ is true if $R_a<R_{m}$ or $R_a>R_{M}$. Note that $H_0$ is the same as Eq. (B2). We can also testify that if $R_{m}<R_a<R_{M}$, Inequality (B6)b holds true for all $I>0$; if $R_a<R_{m}$ or $R_a>R_{M}$, Inequality (B6)b is true if $I<I_1^2$ or $I>I_2^2$, where

$$\begin{aligned} I_1^2=\delta \frac{-H_0-\sqrt{\Delta _2}}{2(\mu +\delta )h}, \ I_2^2=\delta \frac{-H_0+\sqrt{\Delta _2}}{2(\mu +\delta )h} \ \text {and} \ I_2^1>I_2^2>I_1^2>I_1^1. \end{aligned}$$

And beyond that, $I_1^2<0<I_2^2$ holds true if $R_a>1$; $0<I_1^2<I_2^2$ is true if $R_a<1$ and $H_0<0$; and $I_1^2<I_2^2<0$ is true if $R_a<1$ and $H_0>0$. And $H_0<0$ holds true if

$$\begin{aligned} R_a>\frac{\mu }{\mu +\gamma } \ \text {and} \ h>h_0\doteq \frac{\mu +\delta +\gamma }{\delta }\frac{(\mu +\gamma )R_a}{(\mu +\gamma )R_a-\mu }. \end{aligned}$$

Inequality (B5)a means that

$$\begin{aligned} 1-(\mu +\frac{\gamma }{1+hI}+\delta )\frac{1}{\delta }I -(\mu +\delta )(\mu +\frac{\gamma }{1+hI})\frac{1}{\delta \beta }>0, \end{aligned}$$

then Inequality (B4)c holds true provided $I<k$. We can also testify that Eq. (B4)c is equivalent to $F_1(I)=F_2(I)$, where

$$\begin{aligned} F_1(I)= & {} \frac{\phi }{1-\eta }\frac{\delta \beta }{\mu +\delta }\frac{I}{(1-I)^2(k-I)} +\frac{\delta }{\delta -(\mu +\gamma _h+\delta )I},\\ F_2(I)= & {} \frac{\delta \beta }{(\mu +\delta )(\mu +\gamma _h)} \quad \text {and} \quad \gamma _h=\frac{\gamma }{1+hI}. \end{aligned}$$

Algebraic calculation shows that $F'_1(I)>0$, $F'_2(I)>0$ and the non-zero solution to $F_1(I)=F_2(I)$ is equivalent to

$$\begin{aligned} G_1(I)\doteq F_1(I)I^2=F_2(I)I^2\doteq G_2(I). \end{aligned}$$

Since functions $G_1(I)$ and $G_2(I)$ are both monotonically increasing concave functions on the interval [0, 1], there are at most two non-zero solutions to equation $F_1(I)=F_2(I)$, which means that System (21) has at most two $\text {EE}^{*}$. Besides, we have

$$\begin{aligned} F_1(0)=1, \ F_2(0)= R_0, \ F_1(I_i^1)>F_2(I_i^1) \ (i=1,2) \ \text {and} \ \lim \limits _{I\rightarrow k}F_1(I)=+\infty >F_2(k). \end{aligned}$$

Considering the zero point theorem and combining the monotonicity of $G_i(I)$, we can get the existence of $\text {EE}^{*}$ of System (21), which is shown in Table 2. That completes the proof. $\square$

Fig. 16

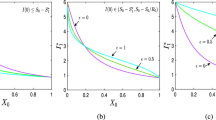
Local phase portraits of System (21) with different h ($h= 5.0033$ in a, $h=7.0050$ in b), other parameters are the same in Fig. 11. The blue (red) curves represent stable equilibria or stable period solutions (unstable equilibria). Curves in different colors indicate the trajectory of System (21) under different initial values and the arrow indicates the direction of the trajectory (Color figure online)

1.2 A Saddle-Node Homoclinic Bifurcation

A saddle-node homoclinic bifurcation, i.e., the birth of a limit cycle when the saddle-node disappears (Kuznetsov 2006), is illustrated in Fig. 11. It shows that, System (21) always has two unstable DFEs. When $0<h<4.0253$, System (21) has a locally asymptotically stable $\text {EE}^{*}$. As h increases beyond 4.0253, $\text {EE}^{*}$ becomes unstable through a Hopf bifurcation (say, H). Numerical simulation shows that the solutions of System (21) undergo oscillation when $4.0253<h<7.2935$. Further as h increases beyond 7.2935, the limit cycle disappears through a saddle-node homoclinic bifurcation and two $\text {EE}^0$s exist (say, SNH). Numerical simulation shows that the $\text {EE}^0$ with smaller I is always unstable and the $\text {EE}^0$ with larger I is locally asymptotically stable when $7.2935<h<10$. Besides, $\text {EE}^{*}$ disappears after colliding with the $\text {EE}^0$ with smaller I when h lies near 8.0105 (say, BP).

To further analyze how periodic orbits change, we plot the variation in period of cycles versus h in Fig. 11e, which shows that the periods eventually go to infinity at $h=7.2935$. Besides, we also draw phase diagrams with different parameters h, show in Fig. 16. When $h=7.2935$, System (21) exists a unstable saddle-node point, the location of this point is shown in the red dot marked with $E_{LP}$ in Fig. 16. Figure 16 shows that as h gets closer and closer to 7.2935, the minimum distance between all points on the stable periodic solution and $E_{LP}$ gets smaller and smaller and eventually approaches zero. These all indicate that a saddle-node homoclinic bifurcations does occur when $h=7.2935$.

1.3 A Hopf Bifurcation

Here, we analyze the case where $R_a>1$. In this scenario, a Hopf bifurcation can still occur, as shown in Fig. 17. It is noteworthy that when h is large, even though all players take “altered” behaviors, the prevalence of infection increases with the magnitude of h. This emphasizes the critical role of medical resources in controlling the scale of infection.

Fig. 17

Bifurcation diagram in different planes with h, where a displays the three-dimensional one-parameter bifurcation diagram of System (21) in space (h, I, x); b shows the parts of (a) with $I\ne 0$; c and d depict the projection of (b) onto the $h-I$ axes, and the $h-x$ axes, respectively; The black dot marked with “H” ($h=0.3053$) indicates that System (21) goes through Hopf bifurcation. The black dot marked with “BP” ($h=0.5953$) means that another equilibrium bifurcates from an equilibrium at this point. Here $\eta =0.5$, $\beta =0.3$, $\delta =0.5$, $\mu =0$, $\gamma =0.1$, $\phi =25$ and $k=0.4$ (Color figure online)

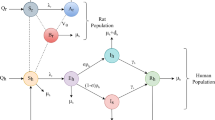
A Model Under the SEIRS Scheme

If we use an SEIRS scheme to describe disease and immunity states and consider the principles, the corresponding full equation is

$$\begin{aligned} \left\{ \begin{array}{rl} \dot{S}_n(t)&{}=\mu (S_n+E_n)-\beta S_nI-\mu S_n \\ &{}\quad +\frac{\omega }{\alpha }[S_a (S_n+E_n)\Delta P \mathcal {H}(\Delta P) + S_n (S_a+E_a)\Delta P \mathcal {H}(-\Delta P)],\\ \dot{S}_a(t)&{}=\mu (S_a+E_a+I)-\eta \beta S_aI-\mu S_a+m R \\ &{}\quad +\frac{\omega }{\alpha }[-S_a (S_n+E_n)\Delta P \mathcal {H}(\Delta P) -S_n (S_a+E_a)\Delta P \mathcal {H}(-\Delta P)],\\ \dot{E}_n(t)&{}=\beta S_nI-\delta E_n-\mu E_n \\ &{}\quad +\frac{\omega }{\alpha }[E_a (S_n+E_n)\Delta P \mathcal {H}(\Delta P) + E_n (S_a+E_a)\Delta P \mathcal {H}(-\Delta P)],\\ \dot{E}_a(t)&{}=\eta \beta S_aI-\delta E_a-\mu E_a \\ &{}\quad +\frac{\omega }{\alpha }[-E_a (S_n+E_n)\Delta P \mathcal {H}(\Delta P) -E_n (S_a+E_a)\Delta P \mathcal {H}(-\Delta P)],\\ \dot{I}(t)&{}=\delta (E_n+E_a)-(\mu + \gamma ) I-dI,\\ \dot{R}(t)&{}=\gamma I-(\mu +m) R, \end{array} \right. \end{aligned}$$

(C1)

where, m is the rate which recovered individuals return to the susceptible statue due to loss of immunity and d is the mortality rate caused by the disease. As for recovered individual, they face no risk of infection, so they don’t need to take any precautions. When they return to a susceptible status, they will take “altered” behaviors to mitigate the risk of reinfection. If condition (4) is still true, the approximated model would be System (22) of the main text. The corresponding positively invariant set is

$$\begin{aligned} \Omega{} & {} =\{(S,E,I,R,x)\in R^5 \mid 0\le S+E+I+R\le 1,\\{} & {} \quad 0\le S,E,I,R \le 1, \ 0\le x \le 1\}. \end{aligned}$$

The basic reproduction number without behavior change, represented by System (22) with $x\equiv 1$, is given by:

$$\begin{aligned} R_{0d}=\frac{\beta \delta }{(\mu +\delta )(\mu +\gamma +d)}. \end{aligned}$$

(C2)

The basic reproduction number where all individuals adopt “altered” behaviors, represented by System (22) with $x\equiv 0$, is given by:

$$\begin{aligned} R_{ad}=\eta R_{0d}. \end{aligned}$$

(C3)

It is evident that System (22) always has two DFEs: one where all players adopt “altered” behaviors $E_0^{0}=(1,0,0,0,0)$ (denoted as $\text {DFE}^0$), and another where all players adopt “normal” behaviors $E_0^{1}=(1,0,0,0,1)$ (denoted as $\text {DFE}^1$). Here, $\text {DFE}^0$ is always unstable. $\text {DFE}^1$ is locally asymptotically stable if $R_{0d}<1$ and unstable if $R_{0d}>1$. When $R_{ad}>1$, System (22) has an EE with all players adopting “altered” behaviors, denoted as $EE^0$, given by:

$$\begin{aligned} E_{*}^0=\left( S_1, E_1,I_1,R_1,0\right) , \end{aligned}$$

where

$$\begin{aligned} \begin{array}{l} S_1=\frac{1}{\eta R_{0d}}, \quad E_1=\frac{(\mu +m)\mu (\mu +\gamma +d)}{M}\left( 1-\frac{1}{\eta R_{0d}}\right) ,\\ I_1=\frac{(\mu +m)\mu \delta }{M}\left( 1-\frac{1}{\eta R_{0d}}\right) ,\quad R_1=\frac{\gamma \mu \delta }{M}\left( 1-\frac{1}{\eta R_{0d}}\right) ,\\ M=\mu (\mu +\gamma +d)(\mu +\delta +m)+m\delta (\mu +d). \end{array} \end{aligned}$$

(C4)

It’s worth noting that

$$\begin{aligned} I_1<\frac{\delta }{\mu +\gamma +\delta }\frac{R_a-1}{R_a}, \end{aligned}$$

meaning that for the EE where all players adopt “altered” behaviors, the corresponding infection prevalence in the SEIRS-based model is smaller than that in the SEIS-based model. The stability of this equilibrium can be examined.

Theorem C.1

Assume $R_{ad}>1$. $EE^{0}$ of System (22) is locally asymptotically stable if $k<\texttt {k}$ and unstable if $k>\texttt {k}$, where

$$\begin{aligned} \texttt {k}{} & {} =\frac{\eta R_{0d} (\eta R_{0d}-1) M \mu \delta (\mu +m) (\mu +d+\gamma )}{\phi [(\mu +m) \mu (\mu +d+\gamma ) \eta R_{0d}+\delta (\mu +m) (\mu +d)+\delta \mu \gamma ]^{2}} \nonumber \\{} & {} \quad +\frac{(\mu +m) \mu \delta }{M}\left( 1-\frac{1}{\eta R_{0d}}\right) . \end{aligned}$$

(C5)

Proof

The Jacobian matrix of System (22) evaluated at $EE^{0}$ gives characteristic equation

$$\begin{aligned} (\lambda ^4+\widetilde{a_3}\lambda ^3+\widetilde{a_2}\lambda ^2+\widetilde{a_1}\lambda +\widetilde{a_0})(\lambda -\widetilde{a_{55}})=0, \end{aligned}$$

where

$$\begin{aligned} \begin{array}{l} \widetilde{a_3}= \eta \beta I_1+P+m+3 \mu>0,\\ \widetilde{a_2}=(3 \mu +3 m+2 P) \mu +m (\gamma +d+\delta )+(2 \mu +m+P) \eta \beta I_1>0,\\ \widetilde{a_1}=\mu (\mu +m) (P+\mu )+((\mu +m+2 P) \mu +m P+\delta (\gamma +d)) \eta \beta I_1>0,\\ \widetilde{a_0}= \eta \beta M I_1>0,\quad P=\gamma +d+\mu +\delta ,\\ \widetilde{a_{55}}=-\frac{\mu (1-S_1-E_1)}{S_1+E_1}-\frac{m R_1}{S_1+E_1}+\phi (S_1+E_1) (k-I_1). \end{array} \end{aligned}$$

Since $\widetilde{a_3}\widetilde{a_2}-\widetilde{a_1}>0$ and $\widetilde{a_3}\widetilde{a_2}\widetilde{a_1}-\widetilde{a_0}(\widetilde{a_3})^2-(\widetilde{a_1})^2>0$, the real parts of the roots of $\lambda ^4+\widetilde{a_3}\lambda ^3+\widetilde{a_2}\lambda ^2+\widetilde{a_1}\lambda +\widetilde{a_0}=0$ are negative, implying that the local stability of $EE^0$ is determined only by the eigenvalue $\lambda _5=\widetilde{a_{55}}$. Algebraic calculation shows $\widetilde{a_{55}}<0$ is equivalent to $k<\texttt {k}$. That completes the proof. $\square$

An EE where a fixed proportion of the players adopt “normal” behavior, denoted as $EE^{*}$, is also feasible.

Theorem C.2

System (22) has a unique $EE^{*}$ if $R_{ad}<1<R_{0d}$, or $R_{ad}>1$ and $k>\texttt {k}$. When this equilibrium exists, it locally asymptotically stable if Conditions (C8) hold true.

Proof

The potential $EE^{*}$, represented by $E_{*}^{*}=(S_{*},E_{*},I_{*},x_{*})$ with $0<x_{*}<1$, satisfies

$$\begin{aligned} \left\{ \begin{array}{lr} S_{*}=1-\frac{M I_{*}}{\delta \mu (\mu +m)}, &{} (a)\\ E_{*}=\frac{(\mu +\gamma +d) I_{*}}{\delta }, &{}(b) \\ R_{*}=\frac{\gamma }{\mu +m} I_{*}, &{}(c)\\ x_{*}=F_1(I_{*}), &{} (d) \end{array} \right. \end{aligned}$$

(C6)

and $I_{*}$ is the root of $F_1(I)=F_2(I)$, where

$$\begin{aligned} \begin{array}{l} F_1(I)=\frac{1}{(1-\eta ) R_{0d} }\frac{\eta R_{0d} MI+(\mu +m) \mu \delta (-\eta R_{0d}+1)}{(\mu +m) \mu \delta -M I},\\ F_2(I)=1-\frac{\mu ^2 (\mu +m)^2 (\mu +d+\gamma ) I}{\phi (k-I) [\mu (\mu +m)-(\mu (\mu +d+\gamma )+m (\mu +d)) I]^2}. \end{array} \end{aligned}$$

Combing the inequality $0<x_{*}<1$ with Eq. (C6)d, we have $I_m<I_{*}<I_M$, where

$$\begin{aligned} I_m=\frac{\mu \delta (\mu +m) }{M}\left( 1-\frac{1}{\eta R_{0d}}\right) , \quad I_M=\frac{\mu \delta (\mu +m) }{M}\left( 1-\frac{1}{R_{0d}}\right) . \end{aligned}$$

$I_M>0$ provided $R_{0d}>1$, implying that System (22) may have $EE^{*}$ only if $R_{0d}>1$. Further considering the equation $F_1(I)=F_2(I)$, we have $0<F_2(I_{*})<1$ and

$$\begin{aligned} \mathbb {I}_{m}\doteq max\{0,I_{m}\}<I_{*}\le min\{k,I_{M}\}\doteq \mathbb {I}_M. \end{aligned}$$

(C7)

Then, we only need to consider the root of $F_1(I)=F_2(I)$ in the interval $(\mathbb {I}_{m},\mathbb {I}_{M})$.

It’s evident that on the interval $(\mathbb {I}_{m},\mathbb {I}_{M})$, the function $F_1(I)$ is increasing, while $F_2(I)$ is decreasing. When $R_{ad}<1<R_{0d}$, $\mathbb {I}_{m}=0$ and $F_1(0)<1=F_2(0)$ hold true. If $I_M<k$, we have $F_1(I_M)=1>F_2(I_M)$. If $I_M>k$, we have

$$\begin{aligned} F_1(k)>-\infty =\lim \limits _{I \rightarrow k^{-}} F_2(k). \end{aligned}$$

Thus System (22) has a unique $EE^{*}$ when $R_{ad}<1<R_{0d}$. Now, we focus on the case where $R_{0d}>1$. In this case, we have $\mathbb {I}_{m}=I_m$ and $F_1(\mathbb {I}_{M})>F_2(\mathbb {I}_{M}^{-})$ still holds true. Thus, when $R_{0d}>1$, System (22) has a unique $EE^{*}$ if $F_1(I_m)<F_2(I_m)$. The condition $F_1(I_m)<F_2(I_m)$ is further equivalent to $k>\texttt {k}$. See Eq. (C5) for the specific expression for $\texttt {k}$.

Fig. 18

Time series of system (22) under different values of parameter k or $\phi$. The values of the remaining parameters are $\mu =0.0001$, $\eta =0.25$, $\beta =0.36$, $m=0.024$, $\delta =0.5$, $\gamma =0.1$, $d=0.0001$, $k=0.1$, $\phi =80$ and $R_{ad}=0.8980<1<R_{0d}=3.5921$ (Color figure online)

Fig. 19

Time series of system (22) under different values of parameter k or $\phi$. The values of the remaining parameters are $\mu =0.0001$, $\eta =0.5$, $\beta =0.3$, $m=0.03$, $\delta =0.5$, $\gamma =0.1$, $d=0.0001$, $k=0.1$, $\phi =100$ and $1<R_{ad}=1.4967<R_{0d}=2.9934$ (Color figure online)

Fig. 20

a Change in positive COVID-19 cases by reported day from January 4, 2022 to 13, 2022 in Tokyo. b The total number of passengers (relative to the average number of users from January 20 to 24, 2020) passing through the ticket gates of the four Toei subway lines during three time periods in the morning. c Fitting results. The estimated parameter values are $\beta =0.2481$, $\eta =0.2085$, $m=0.015$, $k_x=0.2701$, $b_x=0.5703$, $\phi =9.6350$, $k_1=0.0126$, $k_2=0.0080$. The parameter m is the rate which recovered individuals return to the susceptible statue due to loss of immunity. Here, we also assume the incubation/latent period is five days and $\mu =0$. For simplicity, we further assume the infected person recovers after a week of infection and the disease-induced death rate d is 0.0001. The second wave began in week 19. For the parameter k, we use subscripts 1 and 2 to distinguish its values in the first and second waves, respectively. d–g The time series of System (22) with different $\phi$ and k. All other parameters are the same as in (c) (Color figure online)

The characteristic equation at this EE is

$$\begin{aligned} \lambda ^5+m_4\lambda ^4+m_3\lambda ^3+m_2\lambda ^2+ m_1\lambda +m_0=0, \end{aligned}$$

where

$$\begin{aligned} m_4&=m_5+\mu -m_{55}+\frac{\beta I_{*}}{R_{0d} S_{*}}>0,\\ m_3&=-(m_5+\mu ) m_{55}+m_6+\frac{\beta (m_5-m_{55})I_{*}}{R_{0d} S_{*}}>0,\\ m_2&=\beta (m_{51}-m_{53}) (1-\eta ) \delta I_{*} S_{*}-m_6 m_{55}+\widetilde{b_8}-\frac{I_{*} \beta m_5 m_{55}}{R_{0d} S}+\frac{I_{*} \beta m_7}{R_{0d} S}>0,\\ m_1&=(1-\eta ) I_{*}((d+m+2 \mu +\gamma ) m_{51}-m_{54} \gamma -m_{53} (m+2 \mu )) \delta S \beta \\&\quad -m_{55} m_8-\frac{I_{*}\beta m_{55} m_7}{R_{0d} S_{*}}+\frac{I_{*}M \beta }{R_{0d} S_{*}}>0,\\ m_0&=S_{*} \beta I_{*}(1-\eta ) ((m_{51}-m_{53}) \mu ^{2}-\frac{I_{*}m_{55} \beta M}{R_{0d} S_{*}}\\&\quad +((\gamma +d+m) m_{51}-m_{54} \gamma -m_{53} m) \mu +m_{51} m d) \delta>0,\\ m_{51}&=\frac{\mu x_{*}}{(S_{*}+E_{*})^{2}}+\frac{m x_{*} R}{(S_{*}+E_{*})^{2}}+\phi x_{*} (1-x_{*}) (k-I_{*})>0,\\ m_{53}&=-\phi x_{*} \left( 1-x_{*} \right) \left( S_{*} +E_{*} \right)<0,\\ m_{54}&=-\frac{m x_{*}}{S_{*}+E_{*}}<0,\quad m_{55}=-\phi x_{*}(S_{*}+E_{*})(k-I_{*})<0,\\ m_5&= 3 \mu +\delta +\gamma +d +m>0, \\ m_6&=5 \mu ^{2}+2 (d+m+\delta +\gamma ) \mu +m (\delta +\gamma +d+\mu )>0,\\ m_7&= (\delta +\gamma +d+\mu ) (m+2 \mu )+\mu (\mu +m)+\delta (d+\gamma )>0, \\ m_8&=\mu (\mu +m) (\delta +\gamma +d+2 \mu )>0. \end{aligned}$$

The real parts of the roots of this equation are all negative if the following conditions hold:

$$\begin{aligned} \begin{vmatrix} m_4&\quad m_2 \\ 1&\quad m_3 \\ \end{vmatrix}>0, \quad \begin{vmatrix} m_4&\quad m_2&\quad m_0 \\ 1&\quad m_3&\quad m_1\\ 0&\quad m_4&\quad m_2 \end{vmatrix}>0, \quad \begin{vmatrix} m_4&\quad m_2&\quad m_0&\quad 0 \\ 1&\quad m_3&\quad m_1&\quad 0\\ 0&\quad m_4&\quad m_2&\quad m_0\\ 0&\quad 1&\quad m_3&\quad m_1 \end{vmatrix} >0. \end{aligned}$$

(C8)

That completes the proof. $\square$

Numerical simulations additionally demonstrate that when this interior EE exists, if $R_{ad}<1<R_{0d}$, this EE is either globally asymptotically stable or unstable but with a stable periodic solution around it. Oscillations are also observed when k is small and $\phi$ is large, as illustrated in Fig. 18. Moreover, if $R_{ad}>1$, periodic solutions around this EE are also possible, occurring when k is at an intermediate value or when $\phi$ is large, as depicted in Fig. 19. Generally, the dynamic behaviors of System (22) and System (6) are similar.

Then, we utilize similar data to parameterize this SEIRS-based model (22), we can observe comparable results regarding the impact of behavioral changes on the timing and magnitude of the peak of the first wave, as shown in Fig. 20.