Abstract
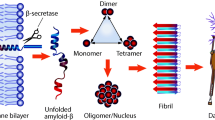
Epigallocatechin-3-gallate, as a representative amyloid inhibitors, has shown a promising ability against A\(\beta \) fibrillation by directly degradating the mature fibrils. Most previous studies have been focusing on its functional mechanisms, meanwhile its optimal dosage has been seldom considered. To solve this critical issue, we refer to the generalized Logistic model for amyloid fibrillation and inhibition and adopt the optimal control theory to balance the effectiveness and cost (or toxicity) of inhibitors. The optimal control trajectory of inhibitors is analytically solved, based on which the influence of model parameters, the difference between the optimal control strategy and several other traditional drug dosing strategies are systematically compared and validated through experiments. It is found that the strategy of multiple-times adding is more suitable for a long-term disease treatment, while single high-dose therapy is preferred for a short-term treatment. We hope our findings can shed light on the rational usage of amyloid inhibitors in clinic.







Similar content being viewed by others
References
Agusto FB, Marcus N, Okosun KO (2012) Application of optimal control to the epidemiology of malaria. Electron J Differ Equ 81:1–22
Alexander GC, Knopman DS, Emerson SS et al (2021) Revisiting fda approval of aducanumab. N Engl J Med 385:769–771. https://doi.org/10.1056/NEJMp2110468
Camacho E, Melara L, Villalobos M et al (2014) Optimal control in the treatment of retinitis pigmentosa. Bull Math Biol 76(2):292–313. https://doi.org/10.1007/s11538-013-9919-1
Cunningham JJ, Brown JS, Gatenby RA et al (2018) Optimal control to develop therapeutic strategies for metastatic castrate resistant prostate cancer. J Theor Biol 459:67–78. https://doi.org/10.1016/j.jtbi.2018.09.022
Cunningham J, Thuijsman F, Peeters R et al (2020) Optimal control to reach eco-evolutionary stability in metastatic castrate-resistant prostate cancer. PLoS ONE 15(e0243):386. https://doi.org/10.1371/journal.pone.0243386
Dear AJ, Michaels TC, Knowles TP et al (2021) Feedback control of protein aggregation. J Chem Phys 155(064):102. https://doi.org/10.1063/5.0055925
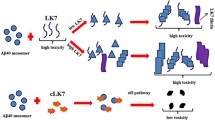
Ehrnhoefer DE, Bieschke J, Boeddrich A et al (2008) Egcg redirects amyloidogenic polypeptides into unstructured, off-pathway oligomers. Nat Struct Mol Biol 15:558. https://doi.org/10.1038/nsmb.1437
Geschwind DH (2003) Tau phosphorylation, tangles, and neurodegeneration: the chicken or the egg? Neuron 40:457–460. https://doi.org/10.1016/s0896-6273(03)00681-0
Goedert M, Spillantini MG (2006) A century of Alzheimer’s disease. Science 314:777–781. https://doi.org/10.1126/science.1132814
Hedaya MA (2012) Basic pharmacokinetics. CRC Press, Boca Raton
Jarrett AM, Faghihi D, Hormuth DA et al (2020) Optimal control theory for personalized therapeutic regimens in oncology: background, history, challenges, and opportunities. J Clin Med 9:1314. https://doi.org/10.3390/jcm9051314
Kamien MI, Schwartz NL (1992) Dynamic optimization: the calculus of variations and optimal control in economics and management. North-Holland, New York
Kelly MR Jr, Tien JH, Eisenberg MC et al (2016) The impact of spatial arrangements on epidemic disease dynamics and intervention strategies. J Biol Dyn 10(1):222–249. https://doi.org/10.1080/17513758.2016.1156172
Lemecha Obsu L, Feyissa Balcha S (2020) Optimal control strategies for the transmission risk of Covid-19. J Biol Dyn 14:590–607. https://doi.org/10.1080/17513758.2020.1788182
Lenhart S, Workman JT (2007) Optimal control applied to biological models. CRC Press, Boca Raton
Li G, Zhou Y, Yang WY et al (2021) Inhibitory effects of sulfated polysaccharides from the sea cucumber Cucumaria frondosa against A\(\beta \)40 aggregation and cytotoxicity. ACS Chem Neurosci 12:1854–1859. https://doi.org/10.1021/acschemneuro.1c00223
Lim YJ, Zhou Wh, Li G et al (2019) Black phosphorus nanomaterials regulate the aggregation of amyloid-\(\beta \). ChemNanoMat 5:606–611. https://doi.org/10.1002/cnma.201900007
Michaels TCT, Weber CA, Mahadevan L (2019) Optimal control strategies for inhibition of protein aggregation. Proc Natl Acad Sci 116:14593–14598. https://doi.org/10.1073/pnas.1904090116
Michel Petrovitch M (1901) Sur une manière d’étendre le théorème de la moyenne aux équations différentielles du premier ordre. Mathematische Annalen 54(3):417–436. https://doi.org/10.1007/BF01454261
Murray J (1990) Optimal control for a cancer chemotheraphy problem with general growth and loss functions. Math Biosci 98:273–287. https://doi.org/10.1016/0025-5564(90)90129-M
Pontryagin LS (1987) Mathematical theory of optimal processes. CRC Press, USA
Schättler H, Ledzewicz U (2015) Optimal control for mathematical models of cancer therapies. Springer, New York
Sharma P, Patel N, Prasad B et al (2021) Pharmacokinetics: theory and application in drug discovery and development. Drug Discov Dev Targets Mol Med 66:297–355
Sharomi O, Malik T (2017) Optimal control in epidemiology. Ann Oper Res 251:55–71. https://doi.org/10.1007/s10479-015-1834-4
Shen ZH, Chu YM, Khan MA et al (2021) Mathematical modeling and optimal control of the Covid-19 dynamics. Results Phys 31(105):028. https://doi.org/10.1016/j.rinp.2021.105028
Ueda K, Fukushima H, Masliah E et al (1993) Molecular cloning of cdna encoding an unrecognized component of amyloid in Alzheimer disease. Proc Natl Acad Sci 90:11282–11286. https://doi.org/10.1073/PNAS.90.23.11282
Weber TA, Kryazhimskiy A (2011) Optimal control theory with applications in economics. MIT Press, Cambridge
Yuan JM, Zhou HX (2017) Biophysics and biochemistry of protein aggregation: experimental and theoretical studies on folding, misfolding, and self-assembly of amyloidogenic peptides. World Scientific, Singapore
Acknowledgements
The authors acknowledged the financial supports from the National Natural Science Foundation of China (Grant Nos. 21877070, 22007044, 12205135), Guangdong Basic and Applied Basic Research Foundation (2023A1515010157), the Natural Science Foundation of Fujian Province of China (2020J05172, 2020J01864), and the Startup Funding of Minjiang University (mjy19033).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declared no conflict of interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Proof of Main Theorems
1.1 A.1 Some Related Lemmas on Optimal Control
The Bolza problem of optimal control reads
The Pontryagin’s Maximum Principle (PMP) provides a necessary condition, whose concrete form is stated as follows.
Lemma 1
(Pontryagin 1987) (PMP) Let \(u^*(t) \in \Theta \subset \mathbb {R}^{m}\) be a bounded, measurable and admissible control that optimizes Eq. (15), with \(\Theta \) be the control set, and \(X^*\) be its corresponding state trajectory. Define a Hamiltonian
where \(\lambda \in \mathbb {R}^d\). Then there exists an absolutely continuous process \(\lambda (t)\) such that
Here Eq. (16) reduces to the state equation under the optimal control, while the co-state \(\lambda ^*\) evolves backward according to Eq. (17) with a fixed terminal state \(\lambda ^*(T)\).
Lemma 2
(Lenhart and Workman 2007) Suppose that \(-f(X,u,t)\) and L(X, u, t) are both continuously difierentiable functions with respect to their three arguments and convex in X and u. Define a Hamiltonian
where \(\lambda \in \mathbb {R}^d\). Suppose \(u^*(t)\) is a control, with associated state \(X^*(t)\), and \(\lambda ^*(t)\), a piecewise difierentiable function, such that \(u^*(t), X^*(t)\), and \(\lambda ^*(t)\), together satisfy on \(0 \le t \le T \):
Then for all controls u, we have
Lemma 3
(Michel Petrovitch 1901) (Comparison Theorem) Let both functions f(x, y) and F(x, y) be continuous in the plane region G and satisfy the inequality
Let \(y=\phi (x)\) and \(y=\Phi (x)\) be solutions to the initial value problems
and
respectively on the interval \(a<x<b\), where \((x_{0},y_{0})\in G\). Then we have
By utilizing above lemmas, we can prove that the following boundary value problem has a solution.
Theorem 2
For \(t \in [0,T]\), the boundary value problem,
admits a solution.
Proof
By utilizing Lemma 3, we can deduce that
Let \( h_{1}(x, y)=k_{a}x(1-\frac{x}{M_{max}})-k_{d} x y \) and \( h_{2}(x, y)=\frac{k_{a}}{M_{max}}xy - \frac{k_{d}}{w^2}{x}^{2} \). Clearly, both \( h_{1} \) and \( h_{2} \) have continuous partial derivatives on \( \mathbb {R}^2 \). By employing the existence and uniqueness theorem for ordinary differential equations and the continuous dependence on initial values, the initial value problem
has a unique solution on the interval [0, T] , and the solution \( u=\phi (t, u_{0}) \) with respect to \( u_{0} \) is continuous.
Based on the comparison theorem, it is evident that \( u=\phi (T, k_{d}M_{max}^2T/w^2)>0 \) and \( u=\phi (T, 0)<0 \). Hence, there exists a \( u_{0} \in (0, k_{d}M_{max}^2T/w^2)\) such that \( u=\phi (T, u_{0})=0 \). Therefore, the boundary value problem has a solution. \(\square \)
Theorem 3
The analytical solution to the boundary value problem (22) is given by:
where
with \( C_{1} \) and \( C_{2} \) being constants determined by the conditions \( M(0)={m_{0}}\) and \(u(T)=0 \). Furthermore, \( A=\frac{k_{d}^{2}}{w^{2}}+\frac{k_{a}^{2}}{M_{max}^{2}} \) and \( B=-\frac{2k_{a}^{2}}{M_{max}}\).
Proof
Introduce function \( s(t)=\ln (M(t)) \). The boundary value problem in (22) can be transformed into:
Next, differentiate equation (27) with respect to t and substitute equations (28) and (27) into it. Now, we obtain
where \( A=\frac{k_{d}^{2}}{w^{2}}+\frac{k_{a}^{2}}{M_{max}^{2}} \) and \( B=-\frac{2k_{a}^{2}}{M_{max}}\). Integrating above formula once, we have:
where \( C_{1} \) is a constant.
By performing separation of variables and Euler’s substitution on both sides, we arrive at
where
and \( C_{1} \) and \( C_{2} \) are two constants. Considering equation (30), now we have
Its solution gives
\(\square \)
1.2 A.2 Proof of Theorem 1
The optimal control problem satisfying the constraint (6) is given by:
where \(M_{max} \ge M(t) \ge 0, \forall t \in [0,T]\).
According to Lemma 1, an optimal solution to (34) should satisfy the following equations,
We get \(u^*(t)=-k_{d}\lambda ^*M^*/2w^2\) by Eq. (37). Further, we can get
From Eq. (39), it can be asserted that \(u^* \ge 0\), otherwise it contradicts with \(u^*(T)=0\). By Lemma 3, we can further get \(u^*(t)<k_{d}M_{max}^2T/w^2\). To sum up, \(0 \le u^*<k_{d}M_{max}^2T/w^2\). We have demonstrated that if the optimal control problem has a solution, it must satisfy Eq. (39).
Theorem 4
The solution to problem (34) exists and satisfies the system of equations in (39).
Proof
From the above, we only need to show the existence of a solution for the problem (34).
Introduce the function \( s(t)=\ln (M(t)) \) and consider the equivalent problem obtained by the variable substitution, which will be referred as OC’ problem. The OC’ problem consists of three main components:
-
(i)
The control constraint set is the same as the problem (34).
-
(ii)
The control equation is:
$$\begin{aligned} \frac{d}{d t} s(t) =k_{a}(1-\frac{e^{s}}{M_{max}}) - k_{d} u, \qquad s(0)=\ln (m_{0}). \end{aligned}$$ -
(iii)
The objective functional is:
$$\begin{aligned} J[u(\cdot )] =\int _{0}^{T}e^{2s}+w^2 u(t)^2d t. \end{aligned}$$
The OC’ problem aims to minimize the above objective functional, and its equivalence to the problem (34) is evident.
Next, we verify the conditions of Lemma 2 for the existence of the OC’ problem. By Theorem 2, the boundary value problem for \(t \in [0, T]\) is given by:
and its solution exists.
By setting \( p=-\frac{2w^2}{k_{d}}u\), we have:
and
which implies
otherwise, it contradicts \( p(T)=0 \).
Now, we only need to check that \( -f(x, u)=-k_{a}(1-\frac{e^{x}}{M_{max}}) + k_{d} u \) and \( L(x, u)=e^{2x}+w^2 u(t)^2 \) are both convex functions. This can be done by directly computing the Hessian matrix. By using Lemma 2, the existence of solutions to the OC’ problem is verfied, which implies the solution to the problem (34) exists too. \(\square \)
1.3 A.3 A Feedback Control
Equation (7) can be transformed into a feedback control given by
First, we can derive from Eq. (7) that
As \({M^*(T)}^2=const\) by \(u^{*}(T)=0\), we have
and
It is found that, when \(M^*(t) \ll M_{max}\) is satisfied, the positive sign is initially chosen; and then at the intermediate time \(t_1\) which satisfies \(\frac{{M^*(T)}^2-{M^*(t_1)}^2}{w^2}+\left( \frac{k_{a}(M_{max}-M^*(t_1))}{M_{max}k_{d}}\right) ^2=0\), it changes to the minus sign until T. This choice will cause mass concentration of aggregates to decrease first and then increase. Otherwise, we just choose the minus sign for the entire control process. This choice results in a monotonous increase in the mass concentration of aggregates.
Appendix B: Derivation of the Analytical Solution
The optimal control problem under the linear approximation is given by
Additionally, based on the optimality condition, \(H(M^*(t),u^*(t),\lambda ^*(t),t) \ge H(M^*(t),u(t),\lambda ^*(t),t)\) with \(H(M,u,\lambda ,t)=\lambda (k_{a}M-k_{d} u M)-M^2-w^2u^2\),
we have
or equivalently,
It is straightforward to solve above algebraic equation, which leads to \(u^*(t)=-{k_{d} \lambda ^*(t) M^*(t)}/{2w^2}\) by noticing \(w^2>0\). Combining this with the terminal co-state \(\lambda ^*(T)=0\) deduces \(u^* (T)=0\).
In the next step, by taking the time derivative on both sides of the algebraic equation (49),
and substituting the ODEs of \(M^*\) and \(\lambda ^*\) in Eq. (47) into the above one, we arrive at
By multiplying \(-2k_{d}M^*/{w^2}\) on both sides of the first equation in (47) and substituting Eq. (50), a decoupled equation for the co-state variable \(u^*(t)\) is derived, i.e.
which is of the second order. Integration once gives
where C is an undetermined constant. The above equation can be rewritten as
whose solution gives the optimal trajectories of \(u^*\) and \(M^*\),
The constants \(C_1\) and \(C_2\) are determined by the boundary conditions \(M^*(0)={m_0}\) and \(u^* (T)=0\) as
which further gives
Appendix C: Analytical Solutions for Upper Bounded Cases
The optimal control problem with general upper bound constraints under the linear approximation is given by
Based on the optimality condition, \(H(M^*(t),u^*(t),\lambda ^*(t),t) \ge H(M^*(t),u(t),\lambda ^*(t),t)\) with \(H(M,u,\lambda ,t)=\lambda (k_{a}M-k_{d} u M)-M^2-w^2u^2\), we have
or equivalently,
Let \(Q = -{k_{d}M^{*}\lambda ^{*}}/{(2w^2)}\). Since \(dQ/dt = -k_{d}/(2w^2)d(M^{*}\lambda ^{*})/dt = - k_{d}(M^*)^2/w^2 < 0\), the axis of symmetry (also the position of maximal value) of \(A[u]:= -k_{d}M^*\lambda ^{*} u -w^2u^2\) decreases from \(-{k_{d}m_{0}\lambda ^{*}(0)}/{(2w^2)}\) to 0. Hence, at the initial time, if \(-{k_{d}m_{0}\lambda ^{*}(0)}/{(2w^2)}\not \in [0,u_{max}]\), we have \(u^{*} = u_{max}\), which persist to time \(t_{1}\) satisfying \(u^*(t_1)=-{k_{d} \lambda ^*(t_1) M^*(t_1)}/{2w^2}\). Within the interval \([t_{1}, T]\), the optimal control problem reduces to the unbounded case, and results in Appendix B apply.
Appendix D: Objective Functional with \(L_{1}\) Norm
The quadratic cost in the main text is adopted to illustrate our conclusions, alternative forms of the objective functional are allowed too, such as the \(L_{1}\) norm which reads
To keep the non-negativity of M(t) and u(t), additional constraints are introduced too, that is
According to the optimality condition, \(H(M^*(t),u^*(t),\lambda ^*(t),t) \ge H(M^*(t),u(t),\lambda ^*(t),t)\) with \(H(M,u,\lambda ,t)=\lambda (k_{a}M(1-M/M_{max})-k_{d} u M)-M-w u\), we have
The above description actually is a Bang–bang control.
So when do we have \((\lambda ^* M^* k_{d} +w)=0\)? It is found that this happens at only one time point. Based on PMP, we have
and
where \(N(t)=\lambda ^*(t) M^*(t)\). Since \(N(T)=0\), we assert that \(N(t)>-M_{max}/k_{a}\). It tells us an important fact that when \(w/k_{d}>M_{max}/k_{a}\), there must be \(u^*(t)=0, t\in [0,T]\). This states an extreme case when an inhibitor is too toxic and ineffective, we would better not to use it at all. Because of \((k_{a} N/M_{max}+1)M^*, N(t)\) increases monotonically to 0, which means \(-(\lambda ^* M^* k_{d} +w)=0\) holds at one time point at most. Solving Eq. (58), we get
If the switch happens at \(t_1\), it must satisfy the condition \(N(t_{1})=-w/k_{d}\). We have
Through calculations, \(t_{1}\) must satisfy
where \(n_{1}=k_{d}M_{max}/(k_{a}w)\) and \(n_{2}=1-k_{d}u_{max}/k_{a}\). To sum up, the Bang–bang control is given by
where \(t_{1}\) satisfies (60).
We have known that the optimal control trajectory is uniquely determined by the switching time \(t_{1}\). How the switching time is affected by parameters \(k_a, k_d, w\) and \(u_{max}\) is of great importance. As shown in Fig. 8a1, b1, the switching time remains zero (meaning no inhibitor) when the apparent fibril growth rate \(k_{a}\) is either too large or too small, or when the rate constant for fibril inhibition \(k_{d}\) is very small. In the presence of large fibril inhibition rate \(k_{d}\) or small toxicity of inhibitors w, the switching time is close to 1 (meaning using inhibitors at every time), as long as \(u_{max}\) remains small.
Influence of model parameters on the Bang–bang control. Subplots in the first row show how the switching time depends on \(k_a, k_d, w\) and \(u_{max}\). The corresponding optimal trajectories for the inhibitor concentration and fibril concentration with parameters at five marked positions are illustrated in second and third rows. Default parameters are set as \(m_0=2.7 \times 10^{-3}\) \(\mu \textbf{ M}\), \(k_{a}=5.5 \times 10^{-2} \min ^{-1}\), \(M_{max}=1\) \(\mu \textbf{ M}\), \(k_{d}=k_{a}\), \(w=1\) and \(u_{max}=10m_{0}\) for subplots (a–c). In subplots d, \(k_{d}=k_{a}/m_{0}\) is taken
Appendix E: Strategies for Drug Dosing
The strategies used for drug dosing in the maintext are summarized as follows:
Lump-sum adding All inhibitors will be added at the initial instant as shown in Fig. 7a, b. The corresponding ODEs for M(t) and u(t) are
Constant adding Inhibitors will be added at a constant rate during the whole procedure from \(t=0\) to \(t=T\),
Periodic adding
During the whole procedure, inhibitors are added intermittently. The adjacent adding of inhibitors and non-adding forms a cycle. Assume that there are \(N\) cycles \(\{0,1,2,\cdots ,N-1\}\). Each cycle includes a time interval \((T/N-t_1)\) during which inhibitors are added uniformly, and a time interval \(t_1\) when no inhibitor is added. Let
The following ODEs are obtained,
Multiple-times adding
In this strategy, inhibitors are equally divided into N pieces and each piece will be added sequentially into the solution after a constant time interval (see Fig. 7a, b for example). Acccordingly, the optimal control is given by
Appendix F: Experimental Setup
A\(\beta 40\) (purity \(>98\%\)) was purchased from ChinaPeptides. Other chemical reagents were bought from Aladdin. A\(\beta 40\) was pre-treated with ammonium hydroxide as previously described (Li et al. 2021). A\(\beta 40\) was then solubilized in 6 mM NaOH to \(100 \,\mu \textbf{ M}\) while ThT and EGCG were directly solubilized in PBS. For ThT kinetics, the final concentrations of A\(\beta 40\) and ThT were \(5 \,\mu \textbf{ M}\) and \(20 \,\mu \textbf{ M}\), respectively. Corning 3603 96-well plates were used and ThT kinetics was monitored at a Tecan Infinite M200 PRO microplate reader with continuously shaking. Fluorescence intensities at ex = 440 nm and em = 480 nm were recorded every 6 min.
For the “Lump-sum” group, \(10 \,\mu \textbf{M}\) EGCG was mixed with A\(\beta 40\) and ThT at \(t=0\) min.
For the “Twice adding” group, \(5~ \,\mu \textbf{ M}\) EGCG was mixed with A\(\beta 40\) and ThT at \(t=0\) min. Then stock solutions of EGCG (\(0.5\,\,m\textbf{M}\)) was added to the mixture at \(t=30\) min or \(t=60\) min to increase the concentration of EGCG to \(10~\,\mu \textbf{ M}\) while minimize the changes of A\(\beta 40\) concentration.
For the “Four times adding” group, \(2.5\,\mu \textbf{ M}\) EGCG was mixed with A\(\beta 40\) and ThT at \(t=0\) min. Then stock solutions of EGCG (\(0.5\,\,m\textbf{M}\)) was added to the mixture at \(t=30, 60, 90\) min or \(t=60, 120, 180\) min to increase the concentration of EGCG to 5, 7.5 and \(10~\mu \textbf{ M}\), respectively.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wang, M., Li, G., Peng, L. et al. Towards Optimal Control of Amyloid Fibrillation. Bull Math Biol 85, 99 (2023). https://doi.org/10.1007/s11538-023-01205-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11538-023-01205-9