Epidemic Spreading on Complex Networks as Front Propagation into an Unstable State

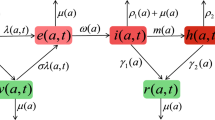
Abstract

We study epidemic arrival times in meta-population disease models through the lens of front propagation into unstable states. We demonstrate that several features of invasion fronts in the PDE context are also relevant to the network case. We show that the susceptible-infected-recovered model on a network is linearly determined in the sense that the arrival times in the nonlinear system are approximated by the arrival times of the instability in the system linearized near the disease-free state. Arrival time predictions are extended to general compartmental models with a susceptible-exposed-infected-recovered model as the primary example. We then study a recent model of social epidemics where higher-order interactions lead to faster invasion speeds. For these pushed fronts, we compute corrections to the estimated arrival time in this case. Finally, we show how inhomogeneities in local infection rates lead to faster average arrival times.

Appendix A Singular Perturbation Analysis of the Local Model 4.2

We consider (4.2) with the goal of motivating the approximate solution presented in (4.6). Our approach mimics the analysis of a model of an autocatalator chemical reaction model presented in Gucwa and Szmolyan (2009). We begin with the system (4.3) where we wish to track the solution to the initial value problem with initial conditions $S(0)=1-\kappa$, $I(0)=\kappa$ in the limit as $\epsilon =\frac{1}{\rho }\rightarrow 0$. As mentioned in Sect. 4 this system has two slow manifolds defined as curves of equilibrium when $\epsilon$ is set equal to zero; see (4.4). The slow manifold on the I axis is normally hyperbolic and it follows that the reduced flow on the slow manifold is, to leading order in $\epsilon$ given by $I'=-\beta I$ and so we obtain that after some critical time $\Omega$ the solution of I(t) can be described as in (4.6). The second slow manifold is given by the S axis, but this manifold lacks normal hyperbolicity so we are unable to track the solution of the initial value problem using linearization.

To overcome this lack of normal hyperbolicity we use geometric desingularization techniques or “blow-up” techniques to resolve the flow when I is small. Following Gucwa and Szmolyan (2009) we will change coordinates to

$$\begin{aligned} S=\bar{S}, \ I=r \bar{I}, \ \epsilon =r\bar{\epsilon }, \ \bar{I}^2+\bar{\epsilon }^2=1, \end{aligned}$$

effectively transforming the S axis to a cylinder with polar coordinates for the I and $\epsilon$ variables. It is often easier to study the flow in coordinate charts and we employ two distinct charts. The first is known as the rescaling chart with coordinates

$$\begin{aligned} S=S_1, \ I=r_1 I_1, \ \epsilon =r_1, \end{aligned}$$

while the second chart has coordinates

$$\begin{aligned} S=S_2, \ I=r_2, \ \epsilon =r_2\epsilon _2. \end{aligned}$$

The two charts can be related via

$$\begin{aligned} S_2=S_1, \ r_2=r_1I_1, \ \epsilon _2=\frac{1}{I_1}. \end{aligned}$$

Our goal is to track an initial condition with $S(0)=1-\kappa$, $I(0)=\kappa$ with $\kappa$ small as it evolves past the non-hyperbolic S axis to the section $\Sigma _{out}=\{ (S,I) \ | \ I=\eta \}$ for some $\eta >0$ at which the solution can be effectively described by a fast transition to the I axis followed by a slow relaxation along the I axis until the solution converges to the origin. In contrast to Gucwa and Szmolyan (2009), our estimates here are approximate and not rigorous. We believe that the estimates presented here could be made rigorous, but we do not pursue such an analysis here.

Analysis in first chart The first chart is known as the rescaling chart where $r_1$ is simply a proxy for $\epsilon$. Converting (4.3) to the coordinates of the first chart we find,

$$\begin{aligned} \frac{\textrm{d}S_1}{\textrm{d}\tau }= & {} -\alpha r_1^2 S_1 I_1-S_1r_1^2I_1^2 \nonumber \\ \frac{\textrm{d}I_1}{\textrm{d}\tau }= & {} \alpha r_1S_1I_1 -\beta r_1 I_1+S_1r_1 I_1^2 \nonumber \\ \frac{\textrm{d}r_1}{\textrm{d}\tau }= & {} 0 \end{aligned}$$

(A.1)

Rescaling the independent variable to divide the vector field by $r_1$, we find the desingularized system

$$\begin{aligned} \frac{\textrm{d}S_1}{\textrm{d}t}= & {} -\alpha r_1 S_1 I_1-S_1r_1I_1^2 \nonumber \\ \frac{\textrm{d}I_1}{\textrm{d}t}= & {} \alpha S_1I_1 -\beta I_1+S_1 I_1^2 \nonumber \\ \frac{\textrm{d}r_1}{\textrm{d}t}= & {} 0. \end{aligned}$$

(A.2)

Let $\eta >0$ and define the section $\Sigma _1=\{ (S_1,I_1,r_1) \ | \ I_1=\eta \}$. Suppose that we start with initial conditions $I(0)=\kappa$ and $S(0)=1-\kappa$ which correspond to initial conditions $S_1(0)=1-\kappa$ and $I_1(0)=\frac{\kappa }{\epsilon }$. We therefore require $\kappa$ to scale smaller than $\epsilon$ so that $I_1(0)$ is near zero. To obtain a leading order description of the dynamics, we set $r_1=0$ in (A.2) and approximate $S_1(t)=1$. Then $I_1$ obeys (to leading order in $\epsilon$)

$$\begin{aligned} \frac{\textrm{d}I_1}{\textrm{d}t} = (\alpha -\beta )I_1 + I_1^2, \quad I_1(t)=\frac{C(\alpha -\beta )e^{(\alpha -\beta )t}}{1-Ce^{(\alpha -\beta )t}}, \ C=\frac{\kappa }{\kappa +\epsilon (\alpha -\beta )}. \end{aligned}$$

Define $\Omega _1$ such that $I_1(\Omega _1)=\eta$. Using the leading-order description for $I_1(t)$, we estimate

$$\begin{aligned} \Omega _1\approx \frac{1}{\alpha -\beta } \log \left( \frac{\eta (\kappa +\epsilon (\alpha -\beta ))}{(\alpha -\beta +\eta )\kappa }\right) \end{aligned}$$

We now convert our solution to the coordinates of the second chart and proceed with tracking the solution.

Analysis in second chart Converting (4.3) to the coordinates of the second chart we find,

$$\begin{aligned} \frac{\textrm{d}S_2}{\textrm{d}\tau }= & {} -\alpha r_2^2\epsilon _2 S_2-r_2^2S_2 \nonumber \\ \frac{\textrm{d}r_2}{\textrm{d}\tau }= & {} \alpha r_2^2\epsilon _2 S_2 -\beta r_2^2 \epsilon _2+S_2r_2^2 \nonumber \\ \frac{\textrm{d}\epsilon _2}{\textrm{d}\tau }= & {} -\alpha r_2\epsilon _2^2 S_2 +\beta r_2 \epsilon _2^2-S_2r_2\epsilon _2 \end{aligned}$$

(A.3)

Rescaling the dependent variable to divide the vector field by the nonzero factor $\alpha r_2\epsilon _2S_2-\beta r_2\epsilon _2+S_2r_2$ we obtain the desingularized system

$$\begin{aligned} \frac{\textrm{d}S_2}{\textrm{d}s}= & {} -r_2\left( \frac{1}{1-\frac{\beta \epsilon _2}{\alpha \epsilon _2S_2 +S_2}}\right) \nonumber \\ \frac{\textrm{d}r_2}{\textrm{d}s}= & {} r_2 \nonumber \\ \frac{\textrm{d}\epsilon _2}{\textrm{d}s}= & {} -\epsilon _2. \end{aligned}$$

(A.4)

Define $\Sigma _2=\{ (S_2,r_2,\epsilon _2) \ | \ r_2=\eta \}$ with $\eta$ defined as before and recall the initial conditions in the section $\Sigma _1$ which correspond to $S_2(0)=1-\kappa +\mathcal {O}(\epsilon )$, $r_2(0)=\eta \epsilon$, $\epsilon _2(0)=\frac{1}{\eta }$. The transition time between sections can then be evaluated explicitly, it terms of the transformed time-scale s, as $s=-\log \epsilon$. To determine estimates for the transition time $\tau _2$ in the $\tau$ time-scale we note that the timescales are related by the integral

$$\begin{aligned} \tau _2=\int _0^{-\log (\epsilon )} \frac{1}{\alpha r_2\epsilon _2 S_2(\sigma )-\beta r_2\epsilon _2 +S_2(\sigma )r_2(\sigma )} d\sigma \end{aligned}$$

We will obtain an approximation to $t_2$ by setting $S_2(\sigma )=1$ in the integral. We are then able to integrate (recalling that $r_2\epsilon _2=\epsilon$) and find

$$\begin{aligned} \tau _2\approx & {} \frac{1}{\epsilon (\alpha -\beta )}\left( -\log (\epsilon )+\log \left( \frac{\epsilon (\alpha -\beta )+\epsilon \eta }{\epsilon (\alpha -\beta )+\eta }\right) \right) , \\\approx & {} \frac{1}{\epsilon (\alpha -\beta )}\left( -\log (\epsilon )+\log \left( \frac{\epsilon }{\eta }\frac{(\alpha -\beta )+\eta }{1+\frac{\epsilon }{\eta }(\alpha -\beta )}\right) \right) \\\approx & {} \frac{1}{\epsilon (\alpha -\beta )}\left( -\log (\eta )+\log \left( \frac{\alpha -\beta +\eta }{1+\frac{\epsilon }{\eta }(\alpha -\beta )}\right) \right) \end{aligned}$$

Rescaling the independent variable from $\tau$ to t we obtain an estimate on the total transit time of the initial condition $I(0)=\kappa \epsilon$ to $I(t)=\eta$ as

$$\begin{aligned} \Omega\approx & {} \frac{1}{\alpha -\beta }\left( \log \left( \eta \frac{ (\kappa +\epsilon (\alpha -\beta ))}{(\alpha -\beta +\eta )\kappa }\right) -\log (\eta )+ \log \left( \frac{\alpha -\beta +\eta }{1+\frac{\epsilon }{\eta }(\alpha -\beta )}\right) \right) \\\approx & {} \frac{1}{\alpha -\beta }\left( \log \left( \frac{ (\kappa +\epsilon (\alpha -\beta ))}{\kappa }\right) +\log \left( \frac{1}{1+\frac{\epsilon }{\eta }(\alpha -\beta )}\right) \right) . \end{aligned}$$

Using $\frac{\kappa }{\epsilon }$ small and $\epsilon \ll 1$ we find the approximation in (4.5).