Coupling the Within-Host Process and Between-Host Transmission of COVID-19 Suggests Vaccination and School Closures are Critical

Abstract

Most models of COVID-19 are implemented at a single micro or macro scale, ignoring the interplay between immune response, viral dynamics, individual infectiousness and epidemiological contact networks. Here we develop a data-driven model linking the within-host viral dynamics to the between-host transmission dynamics on a multilayer contact network to investigate the potential factors driving transmission dynamics and to inform how school closures and antiviral treatment can influence the epidemic. Using multi-source data, we initially determine the viral dynamics and estimate the relationship between viral load and infectiousness. Then, we embed the viral dynamics model into a four-layer contact network and formulate an agent-based model to simulate between-host transmission. The results illustrate that the heterogeneity of immune response between children and adults and between vaccinated and unvaccinated infections can produce different transmission patterns. We find that school closures play a significant effect on mitigating the pandemic as more adults get vaccinated and the virus mutates. If enough infected individuals are diagnosed by testing before symptom onset and then treated quickly, the transmission can be effectively curbed. Our multiscale model reveals the critical role played by younger individuals and antiviral treatment with testing in controlling the epidemic.

1 Introduction

COVID-19 was first reported in December 2019 (Wu et al. 2020) and as of November 18, 2022, has resulted in 633,263,617 confirmed cases and 6,594,491 deaths (WHO 2022), which forced most affected countries to adopt unprecedented interventions (Min et al. 2020; Hellewell et al. 2020). At the early stage of the pandemic, children made up a small fraction of the total reported cases globally, with a lower risk of severe disease (Sun et al. 2020; Shim et al. 2020). This was a different phenomenon compared to pandemic influenza and has resulted in priority given to adult vaccination (Moore et al. 2021). At the time of writing, over 73% of adults have been fully vaccinated in western Europe (COVID-19 Vaccine Tracker 2022). However, the persistent mutation of the virus weakens the protection rate of the vaccine; consequently, the Delta variant has caused many regions in Europe to experience a fourth epidemic wave (Bernal et al. 2021; World Health Organization 2022). Vaccine effectiveness against infection for the Delta variant is reduced (Bernal et al. 2021), while a booster program has been developed for the Omicron variant. Compared to the beginning of the epidemic, the distribution of incidence for adults and children was inverted in the subsequent outbreak of COVID-19 (World Health Organization 2022). However, it is not clear what drives different transmission patterns.

The low proportion of infected children in the first epidemic wave has been analyzed from different perspectives. It was originally thought that children were not getting infected as frequently (Sun et al. 2021; Davies et al. 2020). However, some contact-tracing studies reported similar attack rates across all age groups (Bi et al. 2020; Lavezzo et al. 2020). It has been suggested that school closures changed the risk of exposure to SARS-CoV-2 infection by reducing the contact rates that children have. As schools reopened in Europe in September 2020 (Gaythorpe et al. 2021), however, there were still no school-based outbreaks (Danis et al. 2020; Heavey et al. 2020). Meanwhile, it was discovered that children generally have milder clinical symptoms and are not a driver of family transmission, which is indicative of reduced infectiousness (Swann et al. 2020; Ludvigsson 2020). Jones et al. found that the viral loads of infected younger subjects were lower than that of the older subjects and concluded that the lower viral load results in younger patients with milder clinical symptoms and lower infectiousness (Jones et al. 2021); other studies showed that there was no significant difference in viral loads between young and old patients (He et al. 2020). Recently, immunologists suggested that the stronger innate immunity and less adaptive immune response in children may be responsible for the phenomenon (Mallapaty 2021; Cohen et al. 2021).

As more people get vaccinated and the virus continues to mutate (Mlcochova et al. 2021; Tartof et al. 2021), their mixing effect on the transmission of disease remains unclear. A quantitative understanding of the relationships between multiscale factors such as immune response, viral loads, infectiousness, vaccination and contacts is critical for implementing both pharmaceutical and nonpharmaceutical interventions. First, quantifying the relationship between viral load and infectiousness would allow for precise prediction of infectiousness of infected individuals based on their viral loads. This could in turn give us a chance to measure the effect of the antiviral drug PAXLOVID (Pfizer 2021) on the infectiousness of infected individuals and then on the between-host transmission of COVID-19. Second, evaluating the association between immune response and viral dynamics could lead to quantification of the contribution of different age groups to the overall transmission in a community and help shape public-health policy. This could provide better insights into school-based interventions. Third, as the virus mutation may lead to higher viral loads (Mlcochova et al. 2021) and the vaccine may decrease viral loads in breakthrough infections (Levine-Tiefenbrun et al. 2021), a multi-scale quantification will inform how factors such as virus mutation and booster doses will affect infectiousness and transmission.

Mathematical models have been applied to quantitatively understand the spread of SARS-CoV-2 in the population and to evaluate the effect of interventions (Chen et al. 2021; Thurner et al. 2020; Karaivanov 2020; Sofonea et al. 2021; Matrajt et al. 2021; Kucharski et al. 2020; Xue et al. 2020), but most of these studies are developed at a single scale, and the relationship between different scales is rarely quantified. Multiscale models have been used in some diseases, such as HIV (Shen et al. 2015; Park and Bolker 2017; Doekes et al. 2017), but only a couple of models have thus far integrated multiple scales of COVID-19 infection. Ford and Ciupe built a multi-scale immuno-epidemiological model that connects the virus profile of infected individuals with transmission and testing at the population level in order to quantify rapid COVID-19 testing, finding that employing low-sensitivity tests at high frequency is an effective tool (Forde and Ciupe 2021a). The same authors also used a multiscale COVID-19 model in a vaccinated population to predict the role of testing in an outbreak with variants of increased transmissibility, finding that testing was most effective when vaccination levels were low (Forde and Ciupe 2021b).

We develop a data-driven multi-scale mathematical model by linking the within-host viral dynamics to the between-host transmission dynamics on a contact network. Specifically, by combining viral loads and epidemiological data, we model the viral dynamics and infer the relationship between viral load and infectiousness of an infected individual. Then we embed the viral dynamics model into a 4-layer contact network and formulate an agent-based stochastic model to mimic the infections in a community. Based on the simulations of the stochastic multi-scale model, we describe the key epidemiological conditions and investigate their effects on the transmission of disease. We use the model to evaluate the impact of interventions from different macro and micro scales—including school closures and antiviral treatment—on the spread of the epidemic.

2 Multi-Scale Infectious Disease Model

To investigate the relationship between immune response, viral load and infectiousness, we coupled the within-host viral dynamics to the between-host transmission dynamics and modelled the spread of disease on a multilayer contact network using a “bottom-up” approach.

2.1 Within-Host Viral Dynamic Model

If individual i is infected at time $t_i$ with initial viral load $V_0$, then the within-host viral dynamics are described by

$$\begin{aligned} \frac{dV(\tau )}{d\tau }=rV(\tau )-e(\tau )V(\tau ), \end{aligned}$$

(1)

with infection age $\tau =t-t_i,$ $t\ge t_{i}$. Here, r is the net replication rate of virus and $e(\tau )$ represents the clearance rate of virus influenced by immune response. We describe this using a Hill function (To et al. 2020), written as

$$\begin{aligned} e(\tau )=\frac{a}{1+\exp [-(\tau -b)/c]}, \end{aligned}$$

where a is the maximal clearance rate of virus, b is the time-delayed response of the immune system and c controls the steepness of immune curve during infection. For $\tau <b$, $e(\tau )$ is increasing with c; for $\tau >b$, $e(\tau )$ is decreasing with c. It follows that when c increases, a faster immune response can be mounted at the early stage of infection, and the overall immune effect $e(\tau )$ is more flat.

2.2 Transforming the Viral Load into Infectiousness

Transmission depends on the infectiousness of the infected host, which varies with infection age, due to changes in disease biology (notably viral shedding) and contact with other infected individuals (Grassly and Fraser 2008; Ferretti et al. 2020). Hence the infectiousness at time t can be defined as

$$\begin{aligned} \beta (t)=C(t)\cdot \beta _b(t-t_i), \end{aligned}$$

(2)

where C(t) is the contact rate and $\beta _{b}(t-t_i)$ is the biological infectiousness. In particular, the biological infectiousness is an increasing function of the viral load (Quinn et al. 2000). Here, we assume the biological infectiousness of an infected individual is proportional to the within-host viral load (Fraser et al. 2007). That is,

$$\begin{aligned} \beta _{b}(\tau )=\beta _0V(\tau ). \end{aligned}$$

(3)

The biological infectiousness measures the probability that an infected individual infects a susceptible, with infection age changing. Note that this quantity is for a specific population; an infectious individual in a more protected population would have lower infectiousness, even if there were no difference in viral load.

2.3 Between-Host Transmission Model

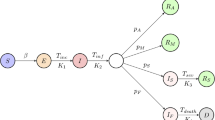
Transmission occurs at the population level through contact between susceptible and infected individuals. Given a population with the real-time contact matrix $\mathcal {C}(t)=\{C_{ij}(t)\}$ among N individuals, transmission occurs in discrete events in this population. After infection, the viral load in the host follows model (1) with an initial condition, while the infectiousness is given by (2). We divide the (continuous) disease-progression status into the classic SIR framework with three compartments: a susceptible individual (S) enters the infective (I) compartment after successful infection, and the infected individual enters the recovered (R) compartment after the within-host viral load drops below a threshold $V_e$. This segment of our model is guided by the between-host model of Kucharski et al. (2020), which also considered multiple layers of transmission (household, work, school, other). Our modelling differs from theirs by the inclusion of within-host dynamics and using different probability calculations for the transitions between states.

2.3.1 Transition from S to I

For any infected individual j with infection time $t_j$, the force of infection the susceptible individual i faces at time t is

$$\begin{aligned} h_{i}(t)=\sum \limits _{j=1}^nC_{ij}(t)\beta _b(t-t_j), \end{aligned}$$

(4)

where $C_{ij}(t)$ represents contact between individual i and individual j at time t. Then, the probability that susceptible individual i is not infected until time t is

$$\begin{aligned} H_{i}(t)=\exp \left[ -\int _{t_0}^{t}h_{i}(\iota )d\iota \right] . \end{aligned}$$

Consequently, the probability of susceptible individual i being infected during the period $(t,t+\delta t]$ is

$$\begin{aligned} P_{i}(t,\delta t)=\frac{H_{i}(t)-H_{i}(t+\delta t)}{H_{i}(t)}=1-\exp \left[ \int _{t}^{t+\delta t}h_{i}(l)dl\right] . \end{aligned}$$

(5)

To implement the transmission event in the simulations, we sample a random number u from the uniform distribution U(0, 1). The individual i can be infected successfully during this period if $u\in [0,P_{i}]$.

2.3.2 Transition from I to R

The infected individual j becomes a recovered individual at time t if the within-host viral loads drop to a sufficiently low level $V_{e}$:

$$\begin{aligned} V_j(t-t_j)\le V_{e}, \end{aligned}$$

where $t-t_j$ is the infection age of individual j. For simplicity, we assume lifelong immunity, so the recovered compartment (R) is the final state of the infected individuals.

2.4 The Structure of the Contact Network

Consider a population of N individuals. To mimic the contacts between them, we formulate a time-varying multilayer contact network $\mathcal {C}(t)=\{\mathcal {C}_h(t), \mathcal {C}_s(t),\mathcal {C}_w(t), \mathcal {C}_p(t)\}$, describing household, school, workplace and community layers. Both the household layer and community layer contain all individuals, while the school layer and the workplace layer divide these individuals into two complementary parts. In the household layer, there are $n_h$ disconnected families with different household sizes. In the community layer, there is only one single component. In the school and workplace layers, there are $n_s$ and $n_w$ disconnected schools and workplaces. $N_s$ individuals, including teachers and students, are assigned to the school layer, while the remaining $N_w=N-N_s$ adults are assigned to the workplace layer. Note that if there exists high-resolution data, students/workers can be assigned to different schools/workplaces based on school-size/workplace-size distribution (Liu et al. 2018). However, most countries or regions lack complete data for these settings, so researchers generally assume that contact numbers are not directly dependent on the school or workplace size, since it is unlikely that each student or worker is in close contact with all other individuals (Kerr et al. 2021). We hence set $n_{s}=1, n_{w}=1$.

The contact number depends on which layer an individual is in and has a large variance (Mossong et al. 2008). In household layer, we assume that each individual is in contact with all family members. We let $D_s(n)$, $D_w(n)$ and $D_p(n)$ denote the probability mass function of the number of contacts in the school, workplace and community layers, respectively. For each individual i ($i=1,2,...,N$), we sample a triple $(n^s_i (t),n^w_i (t),n^p_i (t))$ from the probability mass functions $D_s(n)$, $D_w(n)$ and $D_p(n)$ to represent the contact number of individual i in each layer at time t. At this time step, individual i has $(n^s_i (t),n^w_i (t),n^p_i (t))$ connected neighbours randomly selected from a corresponding cluster in each layer. Note that $n^s_i (t)\times n^w_i (t)=0$ because individual i cannot be in both school and workplace layers simultaneously.

At time t, we characterize the contact network $\mathcal {C}_{k}(t)$ $(k\in \{h,s,w,p\})$ by a layer-specific adjacency matrix $C^{k}(t)$ with elements $C_{ij}^{k}(t)=c_k$ if there is a link connecting individual i and individual j in layer k; otherwise, $C_{ij}^{k}(t)=0$, where $c_k$ represents layer-specific connection strength and is related to the duration that individuals stay in layer k. Consequently, the connection between individuals i and j in the multilayer contact network $\mathcal {C}(t)$ can be characterized as

$$\begin{aligned} C_{ij}(t)=\sum \limits _{k\in \{h,s,w,p\}} C_{ij}^{k}(t). \end{aligned}$$

(6)

This contact matrix is used in the epidemic transmission model (4) and can be estimated using demographic data and contact data.

3 Computational Analysis and Parameter Estimation

3.1 Dynamics of SARS-CoV-2 and Biological Infectiousness

To estimate the parameters of system (1), we use the growth kinetics of viral RNA concentrations from in vitro experiments (Mlcochova et al. 2021) and the time series of detected viral loads in confirmed cases (Wölfel et al. 2020; Kim et al. 2021). We first use the in vitro data to estimate the net replication rate r. For in vitro experiments, we can omit the immune response (i.e., we set $e(\tau )=0$). System (1) implies $V(\tau )=V_0e^{r\tau }$, which yields

$$\begin{aligned} \ln (V(\tau ))=r\tau +\ln (V_0). \end{aligned}$$

(7)

Based on formula (7), we use linear regression on the in vitro data (Fig. 1A) and obtain $r=3.45$/day.

Jones et al. found that the expected degradation rate of viral load is almost constant after the peak time and that the peak viral load occurs prior to the onset of symptoms (Jones et al. 2021). The serum antibody responses during infection by SARS-CoV-2 (To et al. 2020) also imply that the immune response is very sharp after activation. Consequently, we assume that the immune response has already reached the maximum at the onset time $\tau _{on}$ (i.e., $e(\tau _{on})\approx a$). Therefore, after the onset of symptoms, the temporal profiles of the within-host viral load can be approximated by $V(\tau -\tau _{on})=V(\tau _{on})e^{(r-a)(\tau -\tau _{on})}$, which yields

$$\begin{aligned} \ln (V(\tau -\tau _{on}))=(r-a)(\tau -\tau _{on})+\ln (V(\tau _{on})). \end{aligned}$$

(8)

Based on formula (8), we obtain $a=4.17$/day using linear regression on the in vivo data (Fig. 1B).

Fig. 1

Within-host viral dynamics and biological infectiousness. A Virus growth kinetics in vitro. The growth rate is net replication rate of SARS-CoV-2. B Viral RNA concentrations in confirmed cases. Data below the limit of quantification (virus concentration of 100 copies/ml) are defaulted to 10. C Estimated viral load kinetics in the infected individual. The blue circles are the median of in vivo data, and the curve is the result of fitting model (1) to viral loads. D Estimated infectiousness of the infected individual over their entire infection age (Color figure online)

The incubation period of COVID-19 is 5–6 days, and peak viral load occurs one day prior to the onset of symptoms (Jones et al. 2021), (He et al. 2020). Hence, we assume the onset time of symptoms is $\tau _{on}=5.5$ and the peak time of viral load is $\tau _{p}=4.5$. From model (1), at peak time $\tau _{p}$, we obtain $rV(\tau _{p})-e(\tau _{p})V(\tau _{p})=0$, which implies

$$\begin{aligned} c=\frac{b-\tau _{p}}{\ln (a/r-1)}. \end{aligned}$$

(9)

We initialize the model using different values and then estimate the remaining unknown parameters by fitting model (1) to the median of in vivo data. Comparing different fitting results (Fig. 1C), we select $V_0=10^{3.5}$ copies/ml as our initial value and obtain the estimates $b=3.62$ and $c=0.56$.

The infectiousness (2) determines the basic reproduction number $R_0$ of new infections caused by one infectious individual i in a population (Heffernan et al. 2005). The relationship is

$$\begin{aligned} R_0=\int _{t_i}^\infty \beta (t)dt= \lim _{n\rightarrow \infty }\sum _{k=1}^n\int _{t_{i+k-1}}^{t_{i+k}}C(t)\beta _b(t-t_i)dt, \end{aligned}$$

(10)

where $t_i$ is the time when individual i was infected and $[t_{i+k-1},t_{i+k}]$ refers to the kth day after infection. Using the first mean-value theorem for definite integrals on $[t_{i+k-1},t_{i+k}]$, we have $\int _{t_{i+k-1}}^{t_{i+k}}C(t)\beta _b(t-t_i)dt=\beta _b(t_k^\sigma -t_i)\int _{t_{i+k-1}}^{t_{i+k}}C(t)dt$ with $t_k^\sigma \in [t_{i+k-1},t_{i+k}]$. Viral dynamics (Fig. 1C) show that the within-host viral load is already relative low in the limited days after infection. Combining with (3), we obtain

$$\begin{aligned} \beta _0=\frac{R_0}{\sum _{k=1}^nV(t_k^\sigma -t_i)\int _{t_{i+k-1}}^{t_{i+k}}C(t)dt}, \end{aligned}$$

(11)

where $\int _{t_{i+k-1}}^{t_{i+k}}C(t)dt$ represents the contact number of individual i during the kth day after infection. Based on the data (Locatelli et al. 2021), we set $R_0=2.2$ and the number of contacts that one person has per day in our research population is set to $C(t)=12.84$. We take $t_k^\sigma =(t_{i+k-1}+t_{i+k})/2$ and set $n=25$, after which the viral load is very low (Fig. 1C). Consequently, we obtain $\beta _0=1.97\times 10^{-10}$, which can affect the biological infectiousness of one typical infectious individual in the population. See Fig. 1D.

3.2 Contact Network

Based on demographic and contact data of some western European countries, we formulate a detailed network to mimic the contacts in a typical western European community. First, to construct the synthetic population, we consider $n_h=3000$ disconnected families. The size of each family is sampled from the household-size distribution $D_h(n)$, which is derived from the POLYMOD data. (Mossong et al. 2008) Figure 2A plots the household-size distribution $D_h(n)$ with household type. Based on this distribution, we divide all individuals into youth (age $\le 18$) with size $N_y=3057$ and adults (age $>18$) with size $N_a=6889$. We make the assumption that all individuals in the youth group are students and are mapped onto the school layer. The number of teachers in the school layer on the basis of the teacher-to-student ratio of UK is $0.028N_y$ (OECD 2019). Consequently, there are $N_s=3143$ individuals in the school layer and $N_w=6803$ individuals in the workplace layer. Here, we assume there is only a single component ($n_s=1$ or $n_w=1$) in the school and workplace layer, separately, because of the small size of the synthetic population and the lack of data.

Fig. 2

(Color Figure Online) Construction of the multi-level contact network. A The distribution of household size with household type. The degree distribution of contacts at B school/workplace and C community for individuals younger or older than 18

To construct the connection between individuals, we calculated the daily contacts of individuals using the BBC Pandemic dataset (Kucharski et al. 2020). Figure 2B and C plot the probability mass functions $D_s(n)$, $D_w(n)$ and $D_p(n)$ for youth and adults in different layers. The number of individual contacts is highly heterogeneous, ranging from 0 to hundreds. Here, we assume that an individual will contact all family members and fixed classmates (or colleagues) during each day. However, one’s community contacts are different at each step. Specifically, at time t, for individual i, the triple $(n^s_i (t),n^w_i (t),n^p_i (t))=(n^s_i,0,n^p_i (t))$ if this individual comes from the youth group. The elements $n^s_i$ and $n^c_i (t)$ are sampled from the contact distribution for youth in Fig. 2B and C, respectively. Similarly, at time t, the triple $(n^s_i (t),n^w_i (t),n^p_i (t))=(0,n^w_i,n^p_i (t))$ if this individual is an adult, and the nonzero elements are sampled from the distribution for adults. The neighbours of individual i are determined by random sampling from the corresponding layer. Note that if an individual i is a teacher, the $n^w_i$ connections are sampled from the school layer.

Table 1 Estimated parameters of multi-scale model by data fitting

We determined the layer-specific connection strength $c_{k}$ by combining the relative duration spent in different layers and having a weighted mean close to the $R_{0}=2.2$ value for a well-mixed population (Kerr et al. 2021). Based on survey data (OECD 2014), we set the time an individual spends in the household (minus 8h for sleeping time), school/workplace and community settings as 5, 8 and 3 hours per day, respectively. Note that individuals sleeping at night is similar to the quarantine-at-home policy (CDC 2022b), so we assume that infected individuals will not transmit virus during this time, since they will not be interacting with other individuals. Although some people are couples and sleep in the same bed, we assume that they already have ample opportunities to infect each other throughout the day or evening. Next, we set the layer-specific connection strength as $c_{h}=5k_0, c_{s/w}=8k_0$ and $c_{p}=3k_0$. To keep consistency with the basic reproduction number (10) of an infected individual in a well-mixed population, we calculated the average number of contacts of a typical individual in different layers: $C_{h}=3.26$, $C_{s/w}=5.93$ and $C_{p}=3.65$. Note that $C_{h}+C_{s/w}+C_{p}=12.84$. Hence we can define

$$\begin{aligned} R_0= \lim _{n\rightarrow \infty }\sum _{k=1}^n\int _{t_{i+k-1}}^{t_{i+k}}(c_{h}C_{h}+c_{s/w}C_{s/w}+c_p C_{p})\beta _b(t-t_i)dt, \end{aligned}$$

(12)

which implies that $c_{h}=0.86, c_{s/w}=1.3755$ and $c_{p}=0.516$. Consequently, the contact matrix (6) is determined by these estimates.

4 Application and Results

Using our multi-scale framework of how viral loads and infectiousness vary with time since infection and subsequently how the disease spreads in the contact network, we will analyze the impact of individual immune response, virus mutation and vaccination on the transmission patterns and further investigate some strategies from different scales and subpopulations, which cannot be evaluated using a single scale or homogenous model.

4.1 Individual Immune Response Impacts on Viral Load and Transmission

To mimic the stronger innate immunity and weaker adaptive immunity in children, we increased the value of the parameter c, which controls the steepness of an individual’s immune response to the virus. Figure 3A plots the immune response curve $e(\tau )$ and viral load within an infected individual for different values of c. When c increases, a faster immune response can be mounted at the early infected stage, and the overall immune effect $e(\tau )$ is more flat, which is consistent with the stronger innate immunity (Mallapaty 2021) and observed lower T-cell concentration in infected children compared to adults (Cohen et al. 2021). Hence, in the following investigations, we assume $c=0.56$ for adults and increase c to represent the parameter value of viral dynamics within children.

Fig. 3

(Color Figure Online) The effect of an individual’s immune response on within-host viral load and between-host disease transmission. A Variations of immune effective curve and viral load with respect to c in infected individuals. A higher value of c corresponds to a faster immune response at the early infected stage, and the overall immune effect $e(\tau )$ is more flat. B Dynamics of new infected children and adults when the immune responses are identical ($c=0.56$). Curves represent the mean new infections, and shaded areas represent the interquartile ranges (IQR, Q1–Q3), from 200 simulations. C The time series of new infected children and adults for the viral dynamics parameter $c=0.56$ in adults and $c=1$ in children. D The cumulative incidence of children and adults in an outbreak, calculated by the sum of new infections in young/adult subpopulation during 6 months, dividing the number of all young individuals/adults in the whole synthetic population, separately. Larger c values for viral dynamics of children can produce the observed lower incidence. Coloured bars represent the mean cumulative incidence, and vertical lines represent the interquartile ranges (IQR, Q1–Q3)

Our simulations show that younger individuals have a lower viral load, especially in the early stages after infection (Fig. 3A), while the viral loads of infected individuals in different ages would be very close after the onset of symptoms (5.5 days after infection). In observational cohort studies, some researchers found the viral load was lower in younger individuals (To et al. 2020), while others found no significant difference between children and old people (He et al. 2020). Our simulation implies a possibility for these differing observations: namely, that the viral load of most infected individuals was tested after the onset of illness, which introduces a bias to the sample. We also found that there is a bigger difference between different age groups around the peak of viral load in the simulations. This is consistent with the experimental data of a previous study (Jones et al. 2021).

To study the effect of different immune responses in children, we simulate the between-host disease transmission. In each simulation, we initialize two infected children and two infected adults and then follow the between-host transmission model (5). Figure 3B and C plot the simulated daily new infections of both children and adults. In Fig. 3B, there is no difference in immune response between infected children and adults. In Fig. 3C, we take parameter $c=1$ in children to generate stronger innate immunity and weaker adaptive immunity in children compared to adults. The number of infected children in this context is smaller than the results in Fig. 3B, which is more in line with the characteristics of the observed data in the first year of COVID-19.

To further investigate the effects of the immune response in children on the spread of COVID-19, we calculate the cumulative incidence in the young and adult subpopulations for one outbreak using repeated simulations. Cumulative incidence is defined as the sum of new infections in the young/adult subpopulation during 6 months, dividing the number of all young individuals/adults separately. From Fig. 3D, we found that the cumulative incidence in children would be slightly lower than adults if there is no difference in immune response between infected child and infected adult. With the increase of c in children, the difference in cumulative incidence between children and adults becomes larger. For $c=1$ in children, the cumulative incidence of children is about 60% of adults, which is essentially the same as in the European Union (World Health Organization 2022). In conclusion, by modelling and simulating the differences in the immune systems of the two age groups, we found that even if there is no difference in susceptibility between children and adults, we can still reproduce the phenomenon that children have lower incidence in the population. Our results give an explanation for the observations in immune response, viral load and disease transmission.

4.2 Virus Mutation and Vaccination Can Reshape the Transmission of COVID-19

To mimic the mutation of SARS-CoV-2, we increase the replication rate (r) of the virus (Mlcochova et al. 2021). Here we consider three different values of parameter r (Fig. 4A). As a baseline, $r=3.45$ represents the original strain, which caused the first wave of COVID-19, corresponding to the basic reproduction number $R_0=2.2$ [51]. We take $r=3.6$ to represent the Delta strain, which can generate the basic reproduction number $R_0=5$ (Liu and Rocklöv 2021). We take a larger value $r=3.68$ to represent Omicron, which produces the basic reproduction number $R_0=8$. In short, the simulation predicts that the increased replication rate of the virus alone can increase its biological infectiousness. Without further interventions, the new strain with a higher replication rate would cause more people to be infected.

Fig. 4

(Color Figure Online) The effect of virus mutation and vaccination on biological infectiousness and disease transmission. A Biological infectiousness of individuals infected with different strains of the virus. The virus with higher replication rate induces higher biological infectiousness. B The influence of vaccination on within-host viral loads. Here the baseline represents the Delta strain. Smaller b means that the vaccination triggers a more timely immune response in the infected individuals, although larger b values produce higher, if later, peaks in the viral load. C The adults-only vaccination scheme changes the epidemic pattern in the population, making the incidence of children higher than that of adults. Colored bars represent mean cumulative incidence, and vertical lines represent the interquartile ranges (IQR, Q1–Q3) from 200 simulations. D The cumulative incidence in the population (i.e., the total fraction of the new infections over 6 months) with the variations of virus replication rate and vaccine effectiveness

To simulate faster viral clearance (Singanayagam et al. 2021) and lower viral loads (Levine-Tiefenbrun et al. 2021) in breakthrough infections, we varied b, which represents the time-delay of immune response of an infected individual in model (1). Here we consider three values of parameter b, with $b=3.62$ representing the immune response in unvaccinated individuals and smaller b representing the faster immune response, which is consistent with the results obtained in Levine-Tiefenbrun et al. (2021). Therefore, in the following, we describe the difference in immune responses between breakthrough infections and unvaccinated infections by changing the parameter value b. Figure 4B plots the immune effect curve $e(\tau )$ and the within-host dynamics of Delta ($r=3.6$) with the variations of b. The simulations show that the viral load for breakthrough infections becomes lower than that of unvaccinated individuals as the immune response advances, which is consistent with previous research (Levine-Tiefenbrun et al. 2021). This result also implies that the infectiousness of vaccinated individuals is lower.

To investigate the mixed effect of virus mutation and vaccination, we used our multi-scale model and simulated the transmission of the Delta strain in the synthetic population with vaccination. In Western Europe, about 86% of adults have been fully vaccinated as of June 2022, and the vaccine effectiveness against infection after five months of waning is 47% (Tartof et al. 2021). We classify individuals effectively protected by the vaccine as recovered. We introduced four infected individuals in the population initially and consider different values of b under the virus replication rate $r=3.6$. Figure 4C plots the simulated cumulative incidence of the young subpopulation and adults with different immune response lag b. If there is no difference in immune response between infected vaccinators and unvaccinated individuals ($b=3.62$), the cumulative incidence of adults is still higher than that of children. However, if the immune response in vaccinated infected individuals is faster than unvaccinated individuals (Fig. 4C), the transmission pattern would be inverted. In particular, if $b=3.08$, the cumulative incidence of adults is about 60% that of children, which is consistent with the transmission situation of the Delta strain in the European Union (World Health Organization 2022). Comparing Fig. 4C and D, we found the mixture of virus mutation and age-specific vaccination reverses the epidemic pattern of COVID-19 in the population.

The Omicron variant has spread widely and aroused the vigilance of various countries, although its transmission characteristics are still unclear. Since virus mutation and the effectiveness of the vaccine declines over time (Tartof et al. 2021; Bernal et al. 2021), booster shots have been put on the agenda. Here we considered different viral replication rates and vaccine effectiveness. The baselines for virus replication and vaccine effectiveness are 3.6 and 0.47, respectively. Figure 4D plots the simulated cumulative incidence in the synthetic population, which is the total fraction of new infections over the course of the epidemic (6 months). On the one hand, we found the current vaccine scheme can prevent the outbreak of disease caused by original variant ($r=3.45$). Vaccination with booster shots to maintain the effectiveness at a high level is critical to suppress more transmittable variants. On the other hand, the cumulative incidence seems to be very sensitive to virus mutations. From the upper left corner to the lower right corner of Fig. 4D, the cumulative incidence increases significantly, even though vaccination effectiveness grows substantially.

4.3 The Effects of Macro Interventions Targeted at the School Layer

The mixed effect of virus mutation and vaccination reshaped the transmission patterns of COVID-19 (Fig. 4C). The incidence of COVID-19 in younger individuals, especially primary- and middle-school students, has becomes very significant as the epidemic has worn on (World Health Organization 2022). Hence, we investigate the effect of some macro interventions targeted at the school layer. As a comparison, we first consider the effects of school closure before age-related vaccination and virus mutation (setting the replication rate of virus to be relatively low at $r=3.45$). We simulated school closures by removing the contacts occurring in the school layer. Figure 5A plots the time series of new infections and the cumulative incidence in the population when schools are both closed and open. We find that school closure has little effect on suppressing viral transmission and only results in a 14% reduction in the cumulative incidence. After considering virus mutation ($r=3.6$) and vaccination, we repeated the same simulations in the synthetic population and visualized the results in Fig. 5B. The result demonstrates that the closure of schools now has a very significant effect on the prevention and control of the epidemic, which can reduce the cumulative incidence by 90%.

Fig. 5

(Color Figure Online) The effects of interventions targeted at the school layer. A New infections and cumulative attack rate before vaccination and virus mutation. Curves represent mean new infections, and shaded areas show the density distribution of new infections obtained in the 200 realizations. B New infections and cumulative incidence with adult vaccination and virus mutation. C Variations of the cumulative incidence with different proportions of children in the school layer. Colored bars represent the mean cumulative incidence, and vertical lines represent the 0th–100th percentiles from all 200 simulations. D Variations of the cumulative incidence in different vaccination age groups

We further investigated some moderating measures such as online/offline combined classes and vaccinating younger students. For the first strategy, we simulated the infections when different proportions of children are in school. Figure 5C shows that reducing the number of students in school is effective in preventing and controlling the epidemic. When the proportion of offline students is only 25% of the total, the cumulative incidence is less than half of the previous rate. To some extent, this is consistent with the result of Best et al. (2021) that it is efficient to mitigate disease transmission by reducing class size such as online/offline combined classes. To test the effect of vaccination in the school layer, we consider three age-dependent vaccination strategies. As a baseline, the vaccination only covers adults (age $>18$), as in previous simulations. Other vaccination schemes assume that all children in the corresponding age group are vaccinated and that the effectiveness of the vaccine is consistent with that of adults. Figure 5D plots the cumulative incidence with different vaccination strategies being implemented. The results show that expanding vaccination coverage is of great significance to epidemic prevention if the effectiveness of vaccines can be maintained. If all students older than 10 are vaccinated, the infections can be reduced by more than 70%. Furthermore, we found that expanding vaccination coverage to younger ages (14–18 years old) would be more effective than implementing vaccine boosters if vaccine effectiveness is less than 60%.

4.4 The Influence of Antiviral Treatment Targeted at the Individual Level

Effective therapeutics may lead to reduced viral loads within an infected individual. Our modelling approach is well suited to quantify the impact of antiviral treatment on the infectiousness of a person and the subsequent transmission potential. Pfizer announced a novel oral antiviral candidate PAXLOVID (Protease Inhibition) on November 5th, 2021. The scheduled interim analysis showed an 89% reduction in risk of COVID-19-related hospitalization or death within three days of symptom onset (Pfizer 2021). Hence, we will further investigate the effect of usage of antiviral drugs on viral dynamics and disease transmission by extending the above multi-scale mathematical model to couple Pharmacokinetics into the viral dynamical model. See model (15) in the Appendix.

Fig. 6

(Color Figure Online) The effects of antiviral treatment on the transmission of disease. A Time-varying drug concentration in an infected individual with treatment. B The corresponding time-varying pharmacodynamics effect within a treated individual. C Viral loads within a treated adult without uptake of vaccination under three different treatment-initiation times. D Cumulative incidence under different initiation times and proportions of treatment

Figure 6A and B describe the time-varying drug concentration and time-varying effectiveness of drug in an infected individual with antiviral treatment using models (13) and (14) in the Appendix. We chose three different treatment-initiation times, based on days after infection onset. We find that plasma approaches periodic oscillation more quickly than the pharmacodynamics effect $\eta (t)$, which has an approximately two-day delay. The impact of treatment on the within-host viral dynamics is displayed in Fig. 6C. We plot the viral loads of a treated adult without vaccine uptake. The results show that treatment accelerates viral clearance and hence mitigates new infections as the basic reproduction number declines. Early treatment can control viral loads at a low level and decrease the basic reproduction number below the outbreak threshold 1.

Consequently, we further simulate the infections in the population to investigate the effects of antiviral treatment on transmission and control of disease. Specifically, we calculated the cumulative incidence by changing the initiation time and proportion of treatment in the infected population, as shown in Fig. 6D. These results demonstrate that when treatment begins from the 7th day post-infection (i.e., after symptom onset), an outbreak always occurs, even though all infections are treated. If treatment begins from the 5th day after infection onset, around the peak time of virus, a 75% treatment rate can completely control the transmission of disease. If treatment occurs by the third day, only half of the infections need to be treated to prevent the outbreak. This means that if enough infected individuals can be diagnosed by RT-PCR or antigen testing before or around symptom onset and are treated in a timely fashion, then disease transmission can effectively be curbed. This is similar to the strategies adopted for some universities (Lopman et al. 2021; Brook et al. 2021)

5 Discussion

Many mathematical models have been developed to understand the transmission dynamics of COVID-19 and to explain the different transmission patterns between COVID-19 and influenza, but most of them are implemented at a single micro or macro scale, ignoring the interplay between immune response, viral dynamics, individual infectiousness and contact networks. We developed a data-driven multi-scale model that coupled the viral dynamics to the transmission dynamics on a contact network in order to analyze the key epidemiological conditions and produced transmission patterns both before and after age-related vaccination and viral mutation. We used this coupled framework to investigate the role that school closures and antiviral treatment play during the epidemic.

Our research provides a method to fuse multi-source data in order to more fully reflect the actual situation by simultaneously including the two most important factors in epidemic dynamics: viral dynamics of infected individuals and the contact network of the population. Our approach extends existing multi-scale models (Ke et al. 2021; Wang et al. 2020) by including the heterogeneity of contacts and also extends agent-based network models (Atti et al. 2008; Thurner et al. 2020; Karaivanov 2020) by describing the heterogeneity of patient infectiousness.

Using this model, we first investigated the key epidemiological factors and gave a possible answer to what drives different transmission patterns of COVID-19, which are not clearly quantified by previous studies. Specifically, we considered the heterogeneity of immune responses between children and adults and between vaccinated and unvaccinated individuals, which influences the viral dynamics and hence the infectiousness. We found that the heterogeneity of immune response between adults and children produced the observed phenomenon that children have lower incidence (Ferguson et al. 2006). The differing immune responses between vaccinated and unvaccinated infections could reshape the transmission dynamics. Further, we used our multi-scale framework to investigate some strategies at different scales to reduce the potential SARS-CoV-2 transmission. We found that, in contrast to the role that schools play during influenza (Fumanelli et al. 2016), school closures had little effect at the beginning of the outbreak of COVID-19, but their influence became critical as more adults got vaccinated. This may suggest that the transmission pattern of COVID-19 is evolving into the pattern of influenza. If antiviral treatment begins after symptom onset, an outbreak may occur. If 75% (resp. 50%) of infected individuals can be diagnosed by RT-PCR or antigen testing around (resp. before) symptom onset, and be treated in a timely fashion, then the transmission of the disease can be effectively curbed.

Our model has some limitations, which should be acknowledged. First, our population only included 10,000 individuals due to computational limits. Second, in the contact network, the school and workplace layers were not given a detailed substructure. The contacts occurring in different layers have different impacts, which depend on several factors such as type of contact, distance during contact, etc. However, we only weighted them by the relative fraction of a day an individual stays at different places, since we do not have detailed data. We omitted transmission events that may occur for couples sleeping in the same bed, which may underestimate the effects of household infection. Third, to simulate school closures, we only removed contacts occurring in the school layer, but did not consider the effects of this measure on contacts occurring in other layers because of the lack of relevant data. Fourth, Ke et al. (2021) found that there is a saturation effect on the infectious of viruses when the viral load is very high (e.g., $10^{9}$ copies/mL). However, we assume the relationship between the viral load and infectiousness is linear, since our estimation for peak value of the viral load is less than $10^{9}$.

It follows that some interventions targeted to children after higher vaccination rates in adults have taken effect can have significant effects on mitigating the subsequent spread of disease. On the micro scale, if enough infected individuals are diagnosed by testing before symptoms and then treated in a timely fashion, the transmission can effectively be curbed. On the macro scale, school closures can play a crucial role as vaccination uptake rates increase. Our results demonstrate that a multiscale approach to COVID-19 allows for perspectives that cannot easily be gleaned from a single scale or homogenous mixing model.

Appendix: Coupling Pharmacokinetics into Viral Dynamics

If individual i is treated by antiviral drug with intake interval T, the pharmacokinetics are given by

$$\begin{aligned} \left. \begin{array}{llll} \begin{array}{rl} \displaystyle \frac{dD_{a}}{d\tau }&{}=-K_{a}D_{a},\\ \displaystyle \frac{dD}{d\tau }&{}=FK_{a}D_{a}-K_{e}D,\\ \end{array} &{}\bigg \} \tau \ne mT,\\ \begin{array}{rl} D_{a}(mT^+)&{}=D_{0}+D_{a}(mT),\\ D(mT^+)&{}=D(mT),\\ \end{array} &{}\bigg \} \tau =mT,\\ D_{a}(t_0)=D_{0}, D(t_0)=0, \end{array} \right. \end{aligned}$$

(13)

where $D_{a}(\tau )$ and $D(\tau )$ represent drug dosage in the absorption and central compartments at time $\tau ,$ $K_{a}$ is the absorption rate constant, $K_{e}$ is the elimination rate constant and F is the bioavailability.

For $\tau \in (nT,(n+1)T],$ the drug dosages $D_{a}(\tau )$ and $D(\tau )$ are given by

$$\begin{aligned} D_{a}(\tau )&=\frac{1-e^{-K_a nT}}{1-e^{-K_a T}}D_{0}e^{-K_a (\tau -nT)},\\ D(\tau )&=\frac{D_0 FK_a }{K_a-K_e}\left[ \frac{1-e^{-K_e nT}}{1-e^{-K_e T}}e^{-K_e (\tau -nT)}-\frac{1-e^{-K_a nT}}{1-e^{-K_a T}}e^{-K_a (\tau -nT)}\right] . \end{aligned}$$

The corresponding plasma concentration of drug is

$$\begin{aligned} C(\tau )=\frac{D_0 FK_a }{V_d(K_a-K_e)}\left[ \frac{1-e^{-K_e nT}}{1-e^{-K_e T}}e^{-K_e (\tau -nT)}-\frac{1-e^{-K_a nT}}{1-e^{-K_a T}}e^{-K_a (\tau -nT)}\right] , \end{aligned}$$

where $V_{d}$ is the apparent volume of distribution of the central compartment.

Based on the description of dose–response relationships, the pharmacodynamic effect is

$$\begin{aligned} \eta (\tau )=\frac{1}{1+(\frac{\text {IC}_{50}}{C(\tau )})^{{\theta }}}, \end{aligned}$$

(14)

where $\text {IC}_{50}$ is the drug concentration that causes $50\%$ of the maximum inhibitory effect and $\theta$ is a slope parameter mathematically analogous to the Hill coefficient.

With anti-viral treatment, the viral dynamics are described by

$$\begin{aligned} \frac{dV(\tau )}{d\tau }=(1-\eta (\tau ))rV(\tau )-e(\tau )V(\tau ). \end{aligned}$$

(15)

We determine the parameters of the model using some results derived from the population pharmacokinetics of lopinavir/ritonavir in HIV and COVID-19 patients. See Table 2.

Table 2 Parameters of pharmacokinetics and pharmacodynamics