Skip to main content
SpringerLink
Log in

Inhibitor-Induced Wavetrains and Spiral Waves in an Extended FitzHugh–Nagumo Model of Nerve Cell Dynamics

  • Original Article
  • Published:
Bulletin of Mathematical Biology Aims and scope Submit manuscript

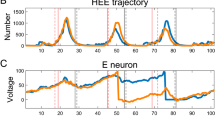
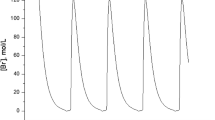
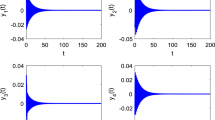
Abstract

It is well known that the FitzHugh–Nagumo model is one of the simplified forms of the four-variable Hodgkin–Huxley model that can reflect most of the significant phenomena of nerve cell action potential. However, this model cannot capture the irregular action potentials of sufficiently large periods in a one-parameter family of solutions. Motivated by this, we propose a modified FitzHugh–Nagumo reaction-diffusion system by changing its recovery kinetics. First, we investigate the parameter regime to know the existence of the wavetrains. Second, we conceive the occurrence of Eckhaus bifurcations of solutions that divide the solution region into two parts. The essential spectra at different grid points explore the occurrence of bifurcations of the waves. We find that the wavetrains of sufficiently large periods cross the stability boundary. This characteristic phenomenon is absent in the standard FitzHugh–Nagumo model. Finally, we observe a reasonable agreement between the direct PDE simulations and the solutions in the traveling wave ODEs. Furthermore, the model exhibits spiral wave for monotone and non-monotone cases that agrees with the waves observed in cellular activity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  • Bär M, Brusch L (2004) Breakup of spiral waves caused by radial dynamics: eckhaus and finite wavenumber instabilities. New J Phys 6:5

    Article  Google Scholar 

  • Bauer S, Röder G, Bär M: Alternans and the influence of ionic channel modifications: cardiac three–dimensional simulations and one-dimensional numerical bifurcation analysis. Chaos: An Interdiscip J Nonlinear Sci 17, 015104 (2007)

  • Bierman SM, Fairbairn JP, Petty SJ, Elston DA, Tidhar D, Lambin X (2006) Changes over time in the spatiotemporal dynamics of cyclic populations of field voles (microtus agrestis l.). Am Nat 167(4):583–590

    Article  Google Scholar 

  • Bordiougov G, Engel H (2006) From trigger to phase waves and back again. Phys D 215:25–37

    Article  MathSciNet  MATH  Google Scholar 

  • Bordyugov G, Engel H (2006) Creating bound states in excitable media by means of nonlocal coupling. Phys Rev E 74:016205

    Article  MathSciNet  Google Scholar 

  • Bordyugov G, Fischer N, Engel H, Manz N, Steinbock O (2010) Anomalous dispersion in the belousov-zhabotinsky reaction: experiments and modeling. Phys D: Nonlinear Phenom 239(11):766–775

    Article  MATH  Google Scholar 

  • Davidenko JM, Pertsov AV, Salomonsz R, Baxter W, Jalife J (1992) Stationary and drifting spiral waves of excitation in isolated cardiac muscle. Nature 355(6358):349–351

    Article  Google Scholar 

  • DeVille REL, Eijnden EV (2007) Wavetrain response of an excitable medium to local stochastic forcing. Nonlinearity 20(1):51

    Article  MathSciNet  MATH  Google Scholar 

  • Doedel EJ, Kernevez J (1986) Auto: software for continuation and bifurcation problems in ordinary differential equations. Applied Mathematics Report, California Institute of Technology, Pasadena, USA

    Google Scholar 

  • Echebarria B, Röder G, Engel H, Davidsen J, Bär M (2011) Supernormal conduction in cardiac tissue promotes concordant alternans and action potential bunching. Phys Rev E 83:040902

    Article  Google Scholar 

  • Epstein IR, Showalter K (1996) Nonlinear chemical dynamics: oscillations, patterns, and chaos. J Phys Chem 100(31):13132–13147

    Article  Google Scholar 

  • Ermentrout GB, Kleinfeld D (2001) Traveling electrical waves in cortex: insights from phase dynamics and speculation on a computational role. Neuron 29(1):33–44

    Article  Google Scholar 

  • Ermentrout GB, Kleinfeld D (2001) Traveling electrical waves in cortex: insights from phase dynamics and speculation on a computational role. Neuron 29(1):33–44

    Article  Google Scholar 

  • FitzHugh R (1961) Impulse and physiological states in theoretical models of nerve membrane. Biophys. J. 1:445–465

    Article  Google Scholar 

  • Gani MO, Ogawa T: (2014). Alternans and spiral breakup in an excitable reaction-diffusion system: a simulation study. Int Sch Res Not 2014(459675)

  • Gani MO, Ogawa T (2015) Instability of periodic traveling wave solutions in a modified FitzHugh-Nagumo model for excitable media. Appl Math Comput 256:968–984

    MathSciNet  MATH  Google Scholar 

  • Gani MO, Ogawa T (2016) Stability of periodic traveling waves in the aliev-panfilov reaction-diffusion system. Commun in Nonlinear Sci Numer Simul 33:30–42

    Article  MathSciNet  MATH  Google Scholar 

  • Gorelova NA, Bureš J (1983) Spiral waves of spreading depression in the isolated chicken retina. J neurobiol 14(5):353–363

    Article  Google Scholar 

  • Gray CM (1989) Singer W : Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. Proceed National Acad Sci 86(5):1698–1702

    Article  Google Scholar 

  • Hecke MV (2003) Coherent and incoherent structures in systems described by the 1d cgle: experiments and identification. Phys D: Nonlinear Phenom 174(1):134–151

    Article  MathSciNet  MATH  Google Scholar 

  • Huang X et al (2004) Spiral waves in disinhibited mammalian neocortex. J Neurosci 24(44):9897–9902

    Article  Google Scholar 

  • Izhikevich EM : (2007). Dynamical systems in neuroscience. MIT press

  • Jalife J (2003) Rotors and spiral waves in atrial fibrillation. J Cardiovasc Electrophysiol 14(7):776–780

    Article  Google Scholar 

  • Kopell N, Howard LN (1973) Plane-wave solutions to reaction-diffusion equations. Stud Appl Math 52:291–328

    Article  MathSciNet  MATH  Google Scholar 

  • Lechleiter J et al (1991) Spiral calcium wave propagation and annihilation in xenopus laevis oocytes. Science 252(5002):123–126

    Article  Google Scholar 

  • Ma J, Jia Y, Yi M, Tang J, Xia YF (2009) Suppression of spiral wave and turbulence by using amplitude restriction of variable in a local square area. Chaos, Solitons & Fractals 41(3):1331–1339

    Article  Google Scholar 

  • Maginu K (1980) Existence and stability of periodic travelling wave solutions to nagumo’s nerve equation. J Math Biol 10(2):133–153

    Article  MathSciNet  MATH  Google Scholar 

  • Meron E (1992) Pattern formation in excitable media. Phys Rep (Rev sect Phys Lett) 218:1–66

    MathSciNet  Google Scholar 

  • Morton KW, Mayers DF : (2005). Numerical solution of partial differential equations: an introduction. Cambridge university press

  • Nagumo JS, Arimoto S, Yoshizawa S (1962) An active pulse transmission line simulating nerve axon. Proc IRE 50:2061–2071

    Article  Google Scholar 

  • Oreanu CR, Georgescu A, Eanu NG : (2000) The FitzHugh-Nagumo Model: Bifurcation and Dynamics. Kluwer Academic Publishers

  • Rademacher JD, Sandstede B, Scheel A (2007) Computing absolute and essential spectra using continuation. Phys D: Nonlinear Phenom 229(2):166–183

    Article  MathSciNet  MATH  Google Scholar 

  • Ranta E, Kaitala V (1997) Travelling waves in vole population dynamics. Geochim Cosmochim Acta 61:3503–3512

    Google Scholar 

  • Saarloos WV (2003) Front propagation into unstable states. Phys report 386(2):29–222

    Article  MATH  Google Scholar 

  • Sakaguchi H, Maruyama T (2008) Elimination of pulses and spirals by external forces in luo-rudy model. J Phy Soc Japan 77:1–5

    Article  Google Scholar 

  • Sherratt JA (2012) Numerical continuation methods for studying periodic travelling wave (wavetrain) solutions of partial differential equations. Appl Math & Comput 218:4684–4694

    MathSciNet  MATH  Google Scholar 

  • Sherratt JA (2013) Numerical continuation of boundaries in parameter space between stable and unstable periodic travelling wave (wavetrain) solutions of partial differential equations. Adv Comput Math 39:175–192

    Article  MathSciNet  MATH  Google Scholar 

  • Sherratt JA, Lord GJ (2007) Nonlinear dynamics and pattern bifurcations in a model for vegetation stripes in semi-arid environments. Theor popul biol 71(1):1–11

    Article  MATH  Google Scholar 

  • Sherratt JA, Smith MJ (2008) Periodic travelling waves in cyclic populations: field studies and reaction-diffusion models. J Royal Soc Interface 5(22):483–505

    Article  Google Scholar 

  • Steinberg V, Fineberg J, Moses E, Rehberg I (1989) Pattern selection and transition to turbulence in propagating waves. Phys D: Nonlinear Phenom 37:359–383

    Article  Google Scholar 

  • Vanag VK, Epstein IR (2008) Design and control of patterns in reaction-diffusion systems. Chaos :An Interdiscip J Nonlinear Sci 18(2):026107

    Article  Google Scholar 

  • Verkhratsky A, Orkand RK, Kettenmann H (1998) Glial calcium: homeostasis and signaling function. Physiol Rev 78(1):99–141

    Article  Google Scholar 

  • Wu JY, Guan L, Bai L, Yang Q (2001) Spatiotemporal properties of an evoked population activity in rat sensory cortical slices. J Neurophysiol 86(5):2461–2474

    Article  Google Scholar 

  • Yu G, Ma J, Jia Y, Tang J (2010) Dynamics of spiral wave in the coupled hodgkin-huxley neurons. Int J Modern Phys B 24(23):4555–4562

    Article  MATH  Google Scholar 

Download references

Acknowledgements

It is acknowledged the support provided by the GCOE program entitled “Formation and Development of Mathematical Sciences Based on Modeling and Analysis”, of the Meiji University, Japan, where this work was carried out.

Author information

Authors and Affiliations

  1. Mathematical and Computational Biology (MCB) Research Group, Department of Mathematics, Jahangirnagar University, Dhaka, 1342, Bangladesh

    M. Osman Gani & M. Humayun Kabir

  2. Center for Mathematical Modeling and Applications (CMMA), Meiji University, Tokyo, 164-8525, Japan

    M. Osman Gani & M. Humayun Kabir

  3. Graduate School of Advanced Mathematical Sciences, Meiji University, 4-21-1, Nakano-ku, Tokyo, 164-8525, Japan

    Toshiyuki Ogawa

  4. Meiji Institute for Advanced Study of Mathematical Sciences, Meiji University, 4-21-1 Nakano, Nakano-ku, Tokyo, 164-8525, Japan

    Toshiyuki Ogawa

Authors
  1. M. Osman Gani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Humayun Kabir
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Toshiyuki Ogawa
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Osman Gani.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Modeling, Analysis, and Simulation of Biological Systems (in memory of Masayasu Mimura).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gani, M.O., Kabir, M.H. & Ogawa, T. Inhibitor-Induced Wavetrains and Spiral Waves in an Extended FitzHugh–Nagumo Model of Nerve Cell Dynamics. Bull Math Biol 84, 145 (2022). https://doi.org/10.1007/s11538-022-01100-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11538-022-01100-9

Keywords

Mathematics Subject Classification

Search

Navigation