Long-Term Forecast of HIV/AIDS Epidemic in China with Fear Effect and 90-90-90 Strategies

Abstract

We formulate a compartmental model considering behavioral changes of susceptible individuals due to fear to assess the transmission dynamics of HIV/AIDS in mainland China. Stability and uniform persistence are analyzed. Markov chain Monte Carlo simulations and Latin hypercube sampling are used to estimate the basic reproduction number and its sensitivity to parameter variations. The estimated mean reproduction number is 1.2138 (95% CI 1.0834–1.3442). The basic reproduction numbers of aware susceptible individuals and high-risk susceptible individuals are $5.6776 \times {10^{-10}}$ (95% CI $4.7883\times {10^{{-10}}}$–$6.7039 \times {10^{{-10}}}$) and 1.2138 (95% CI 1.0834–1.3442), respectively. Global sensitivity analysis shows that preventive measures are more effective than post-infection measures in eliminating the epidemic. We incorporate 90-90-90 strategies to predict the new HIV/AIDS cases in China in the next few decades, and the results show that it takes at least 26 years to achieve the goal of zero new HIV/AIDS cases.

1 Introduction

In June 1981, the Centers for Disease Control and Prevention (CDC) reported five cases on Morbidity and Mortality Weekly. This is the first official record of AIDS in the world. In 1982, this disease was named ‘acquired immune deficiency syndrome,’ that is, AIDS. At the same time, the AIDS epidemic has spread rapidly worldwide with increasing numbers of cases and deaths annually. According to the report released in 2020 by The Joint United Nations Programme on HIV/AIDS (UNAIDS) (Joint 2020), there were about 1,700,000 new HIV infections, 38,000,000 individuals carrying HIV, and 690,000 deaths in 2019. Moreover, the progress in mitigating the spread of AIDS is not as ideal as expected. Reducing the incidence of HIV infection and ending AIDS-related deaths are slowing down. Especially in terms of antiretroviral therapy, 12,600,000 out of the 38,000,000 HIV-infected individuals are unable to receive fundamental treatment (Joint 2020).

In 1985, a foreigner who traveled to China died of an illness and was later confirmed as AIDS. This is the first time that AIDS has been found in China. From April 2005 to June 2016, the first to fourth editions of the National Free AIDS Antiviral Treatment Manual were issued by China (Chinese 2020). According to the joint assessment by China CDC, UNAIDS, and WHO, about 850,000 those carrying HIV and 262,000 died of AIDS-related diseases in China by the end of September 2018 (National 2018). Currently, sex transmission is the main way of spreading AIDS in China. There are about 80,000 new infections annually, and the incidence rate is about nine per million, which is low in China compared with those in other countries (National 2018).

In 2014, UNAIDS proposed the 90-90-90 targets for prevention and control of HIV/AIDS, that is, by 2020, 90% infected people knew their infection status, 90% of those diagnosed as HIV/AIDS received antiviral treatment, and the virus was under control in 90% of the patients treated (People’s Daily Online 2014). On July 20, 2020, UNAIDS released the 2020 global AIDS prevention and control progress report (Joint 2020). The report pointed out that only 14 countries have achieved the 90-90-90 targets. The report also warns that if no further actions are taken, the achievements already obtained in the prevention and control of the HIV/AIDS epidemic will be ruined by COVID-19, and the time to achieve the targets will be further delayed. Further, UNAIDS suggests that in the next ten years, we need to take daily action to end the AIDS epidemic by 2030.

Infectious diseases have a large impact on society, as they may cause morbidity, mortality, unemployment, inequality, and other side effects. Behavioral change is one of the most effective ways in reducing the spread of AIDS worldwide due to the lack of an effective vaccine or other biomedical interventions (Ghosh et al 2018; Sharma and Misra 2014; Samanta and Chattopadhyay 2014). Self-motivated behavioral changes due to psychological fear may have a significant impact on the transmission of infectious diseases. The number of effective contacts between a patient and susceptible individuals per unit time is called adequate contact rate (Anderson and May 1982), which reflects the patient’s activity, environmental conditions, and the virulence of the virus. The concept of adequate contact can be extended to effective awareness of infection. If a susceptible individual with awareness is afraid of being infected, then the number of adequate contact between this individual and infected individuals will be reduced (Ghosh et al 2018; Papst 2015; Wang et al 2016b).

Similarly, the reduction of disease transmission through externally imposed measures should be considered. AIDS has become one of the notifiable infectious diseases in China, but not everyone knows the cause of the disease and the way it spreads, etc. According to China CDC (Li et al 2019), the number of college students among new diagnosed cases has increased by 30–50% annually in the past few years. Only 49.7% of sexually active college students use condoms in China (Song and Ji 2010). Sex education failure or lack of sex education may lead to the emergence of some high-risk groups, such as men who have sex with men (MSM), FRs (foreigner residents), FSWs (female sex workers), and IDUs (injection drug users) (Wu and Zhao 2020, 2021). Typically, this high-risk group are independent of the group that have become alert due to sex education. A survey by UNAIDS found that effective sex education programs delayed the onset of sexual activity, reduced the number of sex partners among sexually active youth, and lowered the incidence of sexually transmitted diseases (Starkman and Rajani 2002). Other factors, such as media coverage and reporting, vaccination, population migration, stigmatization, discrimination, etc., also have great impacts on disease transmission (Huo et al 2020; Jing et al 2020; Huo et al 2018; Cui et al 2008; Xiang et al 2019; Wang et al 2019; Bhunu et al 2009; Levy et al 2021; Mukandavire and Garira 2007; Hove-Musekwa et al 2011).

The main objective of our work is to understand the transmission dynamics of AIDS in China and predict future epidemics accurately. Mathematical models are valuable tools in understanding and describing the transmission dynamics of infectious diseases (Ghosh et al 2018). Our model is fitted to the data on the number of new HIV/AIDS cases in mainland China. Many important epidemiological parameters and the basic reproduction number are estimated. Further, the model combines 90-90-90 strategies to predict the new HIV/AIDS cases in the next few decades in China. In addition, some dynamic behaviors of the model, such as local stability and uniform persistence, are analyzed rigorously.

2 The Mathematical Model

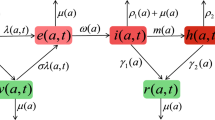
To formulate the mathematical model of HIV/AIDS transmission, we assume that the entire population (N) is divided into six mutually exclusive compartments, namely pre-susceptible individuals ($S_{u}$), aware susceptible individuals ($S_{a}$), high-risk susceptible individuals ($S_{h}$), infected but not yet diagnosed (I), diagnosed HIV-positive individuals who have not yet progressed to AIDS ($D_{I}$), and those with clinical AIDS ($D_{A}$). We consider that there is a sex education period before a newborn becomes susceptible, during which the education agency, parents, and health authorities need to work together to develop HIV prevention and care policies (Li et al 2019). The individual before becoming susceptible is called a pre-susceptible individual and enters the pre-susceptible class at a rate $\Lambda$. Further, the existence of high-risk groups indicates the possibility of sex education failure or lack of sex education. We use $\frac{1}{\alpha }$ to represent the average education period. After this period, some newborns grow into aware susceptible at the rate $\rho$, and the rest of them become high-risk susceptible individuals.

Ghosh et al. in (Ghosh et al 2018) assumed that the number of unaware susceptible individuals (${{S_u}}$) infected by all infected individuals (${I_h}$ and ${I_a}$) per unit time is ${\beta \frac{{\left( {{I_h} + {I_a}} \right) }}{N}{S_u}}$, where ${\beta }$ represents the adequate contact rate. On the other hand, the number of aware susceptible individuals (${{S_a}}$) infected by all infected individuals per unit time is ${\frac{{\beta \left( {{I_h} + {I_a}} \right) {S_a}}}{{1 + \kappa \left( {{S_a} + {I_h} + {I_a}} \right) }}}$, where $\kappa$ represents the fear of infection. If $\kappa$ is large, the above assumption is reasonable. However, if $\kappa$ is small, the probability of infection of an aware susceptible individual is likely to be greater than that of an unaware susceptible individual.

Following (Ghosh et al 2018; Wang et al 2016b), we classify susceptible groups according to their levels of awareness. We take the awareness of high-risk groups (${{S_h}}$) as the baseline, then individuals (${{S_a}}$) who are aware of infectious diseases have a lower probability of being infected (Joint 2007). The proportions of high-risk susceptible individuals and aware susceptible individuals in the total population N are $\frac{{{S_h}}}{N}$ and $\frac{{{S_a}}}{N}$, respectively. Some individuals who are diagnosed to be HIV-positive deliberately infect others (Suprme 2018). Hence, we assume that the number of high-risk susceptible individuals infected by all infected individuals (I, ${{D_I}}$, and ${{D_A}}$) per unit time is ${\beta _1}{c_1}\frac{{{S_h}}}{N}\left( {I + {\theta _1}{D_I} + {\theta _2}{D_A}} \right)$, where ${\beta _1}$ represents the probability of infection per contact (sexual activity or needle sharing) between the infected individual and susceptible individual, ${c_1}$ represents the number of contacts between an infected individual and high-risk susceptible individuals per unit time, and ${{\theta _1}}$ and ${{\theta _2}}$ represent the modification factors in adequate contact rate ${\beta _1}{c_1}$ of ${{D_I}}$ and ${{D_A}}$, respectively. On the other hand, the number of aware susceptible individuals (${{S_a}}$) infected by all infected individuals per unit time is ${\beta _1}\frac{{{c_1}}}{{1 + \kappa \left( {{S_a} + {D_I} + {D_{A}}} \right) }}\frac{{{S_a}}}{N}\left( {I + {\theta _1}{D_I} + {\theta _2}{D_A}} \right)$, where $\kappa$ represents the fear of infection. The number of contacts between the aware susceptible individuals and all the infected individuals per unit time is affected by the following four factors, namely the level of fear, the number of aware susceptible individuals, diagnosed as HIV-positive individuals who have not yet progressed to AIDS, and those with clinical AIDS. When the fear coefficient $\kappa$ is 0, the adequate contact rates of two susceptible groups are the same, and when $\kappa >0$, the adequate contact rate of ${S_h}$ is greater than that of ${S_a}$.

As mentioned above, some students do not realize that they are at a high risk of infection due to sex education failure or lack of sex education. In this regard, health authorities have taken a series of measures, such as conducting open courses on AIDS prevention in universities (Center 2020). We assume that high-risk groups will refuse high-risk behaviors after knowing about the situation of people infected with HIV/AIDS at the rate ${\beta _2}\frac{{{S_h}}}{N}{f_1}\left( {{D_I} + \mu {D_A}} \right)$, where ${\beta _2}$ represents the proportion of high-risk susceptible individuals who become aware susceptible under each sex education, ${f_1}\left( {{D_I} + \mu {D_A}} \right)$ represents the number of sex education per unit time, ${f_1}$ is the conversion coefficient from the number of diagnosed infected individuals to the intensity of sex education, and $\mu$ is the modification factor in conversion coefficient of ${D_A}$. Sex education will be intensified with the increase in the number of individuals diagnosed infected with HIV.

Further, we assume that all HIV carriers (I) will be identified by self-testing or clinical symptoms (Williams and Anderson 1994), $\delta$ denotes the diagnosis rate, and $\eta$ is the proportion of diagnosed individuals who have not yet progressed to AIDS. Among all the HIV-positive individuals, the deterioration of the condition of diagnosed HIV-positive individuals who have not yet progressed to AIDS ($D_{I}$) can only be delayed and will progress to the stage of AIDS ($D_{A}$) at the rate $\omega$. We assume that all individuals die at a constant rate d, and the mortality rates of $D_{I}$ and $D_{A}$ classes are ${d_I}$ and ${d_A}$, respectively.

Based on the above analysis, let ${\lambda _1} = f\frac{{{S_h}}}{N}\left( {{D_I} + \mu {D_A}} \right)$, ${\lambda _2} = \beta \frac{{{S_h}}}{N}\left( {I + {\theta _1}{D_I} + {\theta _2}{D_A}} \right)$, ${\lambda _3} = \frac{\beta }{{1 + \kappa \left( {{S_a} + {D_I} + {D_A}} \right) }}\frac{{{S_a}}}{N}\left( {I + {\theta _1}{D_I} + {\theta _2}{D_A}} \right)$, where $\beta = {\beta _1}{c_1}$, $f = {\beta _2}{f_1}$, then the population flow among those compartments is shown in the following diagram (Fig. 1), and the parameters are described in Table 1.

Fig. 1

(Colour figure online) Schematic diagram of the model

Table 1 Parameter description of model (1)

The dynamics of HIV/AIDS can be depicted by the following system of ordinary differential equations:

$$\begin{aligned}&\frac{dS_{u}}{dt}=\Lambda - \left( {\alpha + d} \right) {S_u},\nonumber \\&\frac{{d{S_a}}}{{dt}} = \rho \alpha {S_u} + \frac{{f\left( {{D_I} + \mu {D_A}} \right) {S_h}}}{N} - \frac{{\beta \left( {I + {\theta _1}{D_I} + {\theta _2}{D_A}} \right) {S_a}}}{{N\left[ {1 + \kappa \left( {{S_a} + {D_I} + {D_A}} \right) } \right] }} - d{S_a},\nonumber \\&\frac{{d{S_h}}}{{dt}} = \left( {1 - \rho } \right) \alpha {S_u} - \frac{{f\left( {{D_I} + \mu {D_A}} \right) {S_h}}}{N} - \frac{{\beta \left( {I + {\theta _1}{D_I} + {\theta _2}{D_A}} \right) {S_h}}}{N} - d{S_h},\nonumber \\&\frac{{dI}}{{dt}} = \frac{{\beta \left( {I + {\theta _1}{D_I} + {\theta _2}{D_A}} \right) {S_a}}}{{N\left[ {1 + \kappa \left( {{S_a} + {D_I} + {D_A}} \right) } \right] }} + \frac{{\beta \left( {I + {\theta _1}{D_I} + {\theta _2}{D_A}} \right) {S_h}}}{N} - \left( {\delta + d} \right) I,\nonumber \\&\frac{dD_{I}}{dt}=\eta \delta I - \left( {\omega + d + {d_I}} \right) {D_I},\nonumber \\&\frac{dD_{A}}{dt}=\left( {1 - \eta } \right) \delta I + \omega {D_I} - \left( {d + {d_A}} \right) {D_A}. \end{aligned}$$

(1)

It is worth noting that the feasible region for system (1) is given in the following Theorem 1, which is stated without proof (Freedman and So 1985).

Theorem 1

The set

$$\begin{aligned} \Omega = \left\{ {\left( {{S_u},{S_a},{S_h},I,{D_I},{D_A}} \right) \in R_ + ^6:0 \le {S_u},{S_a},{S_h},I,{D_I},{D_A} \le \frac{\Lambda }{d}} \right\} , \end{aligned}$$

where ${R _ + ^6}$ is the nonnegative cone in ${R ^6}$, and satisfies

(i):

$\Omega$ is positively invariant,

(ii):

for all $\left( {{S_u}\left( 0 \right) ,{S_a}\left( 0 \right) ,{S_h}\left( 0 \right) ,I\left( 0 \right) ,{D_I}\left( 0 \right) ,{D_A}\left( 0 \right) } \right) \in R_ + ^6$,

$$\begin{aligned} \left( {{S_u}\left( t \right) ,{S_a}\left( t \right) ,{S_h}\left( t \right) ,I\left( t \right) ,{D_I}\left( t \right) ,{D_A}\left( t \right) } \right) \rightarrow \Omega \quad \text {as} \quad t \rightarrow \infty . \end{aligned}$$

3 Analysis of the Model

Since it is difficult to obtain the exact solutions of the nonlinear system (1), we study the long-term behavior of the system by using the stability theory of differential equations. In the following, we derive equilibrium points and analyze the stability.

3.1 Equilibrium Analysis

The system (1) has at least two nonnegative equilibria as follows:

(i):

The disease-free equilibrium

$$\begin{aligned} {E_0} = \left( {{S_{u0}},{S_{a0}},{S_{h0}},{I_0},{D_{I0}},{D_{A0}}} \right) = \left( {\frac{\Lambda }{{\alpha + d}},\frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}},\frac{{\left( {1 - \rho } \right) \alpha }}{d}\frac{\Lambda }{{\alpha + d}},0,0,0} \right) , \end{aligned}$$

which is always feasible.

(ii):

The endemic equilibrium ${E_*} = \left( {{S_{u*}},{S_{a*}},{S_{h*}},{I_*},{D_{I*}},{D_{A*}}} \right)$. Feasibility of the equilibrium ${E_*}$ is shown below.

From the first and last two equilibrium equations of system (1), we have ${S_{u*}} = \frac{\Lambda }{{\alpha + d}} = {a_1},$ and

$$\begin{aligned} {D_{I * }} = {a_2}{I_ * },{D_{A * }} = {a_3}{I_ * }, \end{aligned}$$

(2)

where

$$\begin{aligned} {a_2} = \frac{{\eta \delta }}{{d + {d_I} + \omega }}, {a_3} = \frac{{\left( {1 - \eta } \right) \delta }}{{d + {d_A}}} + \frac{{\eta \delta \omega }}{{\left( {d + {d_I} + \omega } \right) \left( {d + {d_A}} \right) }}. \end{aligned}$$

From the second, third and fourth equilibrium equations of system (1), we have

$$\begin{aligned} {I_ * } = {a_4}\left[ {{a_1}\alpha - d\left( {{S_{a * }} + {S_{h * }}} \right) } \right] , \text {where} \ {a_4} = \frac{1}{{d + \delta }}. \end{aligned}$$

(3)

When ${I_*}$ is positive, we obtain $S_{a * } + {S_{h * }} < \frac{{\alpha \Lambda }}{{d\left( {d + \alpha } \right) }}$, and the above region is defined as follows

$$\begin{aligned} {\Omega _1} = \left\{ {\left( {{S_{a * }},{S_{h * }}} \right) :0< {S_{a * }} + {S_{h * }} < \frac{{\alpha \Lambda }}{{d\left( {d + \alpha } \right) }}} \right\} . \end{aligned}$$

Using Eqs. (2) and (3) in the second and third equilibrium equations of system (1), we obtain the following two equations in $S_{a * }$ and $S_{h * }$

$$\begin{aligned}&\rho \alpha {a_1} + \frac{{fG\left( {{a_2} + \mu {a_3}} \right) {S_{h * }}}}{N} - \frac{{\beta G\varsigma {S_{a * }}}}{{N\left[ {1 + \kappa {S_{a * }} + \kappa G\left( {{a_2} + {a_3}} \right) } \right] }} - d{S_{a * }} = 0, \end{aligned}$$

(4)

$$\begin{aligned}&\left( {1 - \rho } \right) \alpha {a_1} - \frac{{fG\left( {{a_2} + \mu {a_3}} \right) {S_{h * }}}}{N} - \frac{{\beta G\varsigma {S_{h * }}}}{N} - d{S_{h * }} = 0, \end{aligned}$$

(5)

where $N = {a_1} + {S_{a * }} + {S_{h * }} + {a_4}\left[ {{a_1}\alpha - d\left( {{S_{a * }} + {S_{h * }}} \right) } \right] \left( {1 + {a_2} + {a_3}} \right)$, $G = {a_4}\left[ {{a_1}\alpha - d\left( {{S_{a * }} + {S_{h * }}} \right) } \right]$, $\varsigma = 1 + {\theta _1}{a_2} + {\theta _2}{a_3}$. The isoclines (4) and (5) intersect in the interior of the first quadrant, denoted by ${\left( {{S_{a*}},{S_{h*}}} \right) }$. The existence of the point ${\left( {{S_{a*}},{S_{h*}}} \right) }$ is shown in Fig. 2.

Fig. 2

(Colour figure online) Schematic diagram of the existence of endemic equilibrium ${\left( {{S_{a*}},{S_{h*}}} \right) }$, which is the intersection of isoclines (4) and (5), where $\Lambda = 100, d = \frac{1}{{75}}, {d_A} = \frac{1}{{30}}, {d_I} = \frac{1}{5}, {\beta } = {{0.8}}, \eta = 0.5, \alpha = \frac{1}{{20}}, \kappa = 10, \omega = \frac{1}{9}, \rho = 0.2, \mu = 5, {\theta _1} = 0.5, {\theta _2} = 0.1, f = 0.5, \delta = 0.5$

3.2 Basic Reproduction Number

We apply the next generation matrix approach (Van den Driessche and Watmough 2002) to determine ${R_0}$ for the system (1). In order to compute ${R_0}$, it is important to identify new infections. Progression from ${{S_a}}$ and ${{S_h}}$ to I is considered as new infections, while progression from I to ${D_I}$, I to ${D_A}$, and ${D_I}$ to ${D_A}$ is considered as the transfer of individuals among various compartments.

Let $x = {\left( {I,{D_I},{D_A},{S_u},{S_a},{S_h}} \right) ^T}$, then system (1) can be rewritten as

$$\begin{aligned} \frac{{dx}}{{dt}} = \mathcal {F}\left( x \right) + \mathcal {V}^ +\left( x \right) - \mathcal {V}^ -\left( x \right) , \end{aligned}$$

where

$$\begin{aligned} \mathcal {F}\left( x \right) = \left( {\begin{array}{*{20}{c}} {\frac{{\beta \left( {I + {\theta _1}{D_I} + {\theta _2}{D_A}} \right) {S_a}}}{{N\left[ {1 + \kappa \left( {{S_a} + {D_I} + {D_A}} \right) } \right] }} + \frac{{\beta \left( {I + {\theta _1}{D_I} + {\theta _2}{D_A}} \right) {S_h}}}{N}}\\ 0\\ 0\\ 0\\ 0\\ 0 \end{array}} \right) , \end{aligned}$$

and

$$\begin{aligned}&\mathcal {V}^ +\left( x \right) = \left( {\begin{array}{*{20}{c}} 0\\ {\eta \delta I}\\ {\left( {1 - \eta } \right) \delta I + \omega {D_I}}\\ \Lambda \\ {\rho \alpha {S_u} + \frac{{f\left( {{D_I} + \mu {D_A}} \right) {S_h}}}{N}}\\ {\left( {1 - \rho } \right) \alpha {S_u}} \end{array}} \right) ,\\&\mathcal {V}^ -\left( x \right) = \left( {\begin{array}{*{20}{c}} {\left( {\delta + d} \right) I}\\ {\left( {\omega + d + {d_I}} \right) {D_I}}\\ {\left( {d + {d_A}} \right) {D_A}}\\ {\left( {\alpha + d} \right) {S_u}}\\ {\frac{{\beta \left( {I + {\theta _1}{D_I} + {\theta _2}{D_A}} \right) {S_a}}}{{N\left[ {1 + \kappa \left( {{D_I} + {D_A}} \right) } \right] }} + d{S_a}}\\ {\frac{{f\left( {{D_I} + \mu {D_A}} \right) {S_h}}}{N} + \frac{{\beta \left( {I + {\theta _1}{D_I} + {\theta _2}{D_A}} \right) {S_h}}}{N} + d{S_h}} \end{array}} \right) , \end{aligned}$$

where $\mathcal {F}\left( x \right)$ is the rate of appearance of new infections, $\mathcal {V}^ +\left( x \right)$ represents the rate of transfer of individuals into the compartment by all other means, and $\mathcal {V}^ -\left( x \right)$ refers to the rate of transfer of individuals out of the compartment.

Let $\mathcal {V}\left( x \right) =\mathcal {V}^ +\left( x \right) + \mathcal {V}^ -\left( x \right) .$ The derivatives $D\mathcal {F}\left( {{E_0}} \right)$ and $D\mathcal {V}\left( {{E_0}} \right)$ are partitioned as

$$\begin{aligned} D\mathcal {F}\left( {{E_0}} \right) = \left( {\begin{array}{*{20}{c}} {{{ {F} }_{3 \times 3}}}&{}0\\ 0&{}0 \end{array}} \right) , D\mathcal {V}\left( {{E_0}} \right) = \left( {\begin{array}{*{20}{c}} {{V_{3 \times 3}}}&{}0\\ {{J_1}}&{}{{J_2}} \end{array}} \right) , \end{aligned}$$

where $F={F_{{S_a}}} + {F_{{S_h}}}$, and

$$\begin{aligned} {F_{{S_a}}} = \left( {\begin{array}{*{20}{c}} {\frac{{\beta {S_{a0}}}}{{\left( {1 + \kappa {S_{a0}}} \right) \left( {{S_{a0}} + {S_{u0}} + {S_{h0}}} \right) }}}&{}{\frac{{{\beta }{\theta _1}{S_{a0}}}}{{\left( {1 + \kappa {S_{a0}}} \right) \left( {{S_{a0}} + {S_{u0}} + {S_{h0}}} \right) }}}&{}{\frac{{{\beta }{\theta _2}{S_{a0}}}}{{\left( {1 + \kappa {S_{a0}}} \right) \left( {{S_{a0}} + {S_{u0}} + {S_{h0}}} \right) }}}\\ 0&{}0&{}0\\ 0&{}0&{}0 \end{array}} \right) , \\ {F_{{S_h}}} = \left( {\begin{array}{*{20}{c}} {\frac{{\beta {S_{h0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}}&{}{\frac{{\beta {\theta _1}{S_{h0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}}&{}{\frac{{\beta {\theta _2}{S_{h0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}}\\ 0&{}0&{}0\\ 0&{}0&{}0 \end{array}} \right) , \\ V = \left( {\begin{array}{*{20}{c}} {d + \delta }&{}0&{}0\\ { - \eta \delta }&{}{\omega + d + {d_I}}&{}0\\ { - \left( {1 - \eta } \right) \delta }&{}{ - \omega }&{}{d + {d_A}} \end{array}} \right) . \end{aligned}$$

Following (Diekmann et al 1990), we call $F{V^{ - 1}}$ the next generation matrix of system (1), and the expression for the basic reproduction number is

$$\begin{aligned} {R_0} = {R_{{s_a}}} + {R_{{s_h}}}, \end{aligned}$$

(6)

where

$$\begin{aligned} {R_{{s_a}}} = \frac{{\beta {S_{a0}}}}{{\left( {1 + \kappa {S_{a0}}} \right) \left( {{S_{a0}} + {S_{u0}} + {S_{h0}}} \right) }} \times R, \quad {R_{{s_h}}} = \frac{{\beta {S_{h0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}} \times R, \end{aligned}$$

and

$$\begin{aligned} R = \frac{1}{{d + \delta }} + \frac{{{\theta _1}\eta \delta }}{{\left( {d + \delta } \right) \left( {\omega + d + {d_I}} \right) }} + {\theta _2}\frac{{\left( {1 - \eta } \right) \delta \left( {d + {d_I} + \omega } \right) + \eta \delta \omega }}{{\left( {d + {d_A}} \right) \left( {d + \delta } \right) \left( {d + {d_I} + \omega } \right) }}. \end{aligned}$$

As is shown in (6), ${R_0}$ is the sum of two quantities, namely the number of secondary infected individuals in aware susceptible population and the number of secondary infected individuals in high-risk susceptible population during an epidemic. Note that each term of the aforementioned expression for ${R_{{s_a}}}$ and ${R_{{s_h}}}$ has clear epidemiological interpretation (Xiao et al 2013). An HIV-infected individual, with the controlled contact rate $\frac{\beta }{{1 + \kappa {S_{a0}}}}\frac{{{S_{a0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}$, and mean duration ${\frac{1}{{d + \delta }}}$, gives a contribution of $\frac{\beta }{{1 + \kappa {S_{a0}}}}\frac{{{S_{a0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}\frac{1}{{d + \delta }}$. A proportion $\frac{{\eta \delta }}{{d + \eta }}$ goes from I to the diagnosed class ${{D_I}}$, with the controlled contact rate $\frac{\beta }{{1 + \kappa {S_{a0}}}}\frac{{{S_{a0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}{\theta _1}$ and mean duration ${\frac{1}{{\omega + d + {d_I}}}}$, giving a contribution of $\frac{\beta }{{1 + \kappa {S_{a0}}}}\frac{{{S_{a0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}{\theta _1}\frac{{\eta \delta }}{{\left( {d + \delta } \right) \left( {\omega + d + {d_I}} \right) }}$. A proportion ${\frac{{\left( {1 - \eta } \right) \delta }}{{d + \delta }}}$ directly goes from I to the (diagnosed) AIDS class ${{D_A}}$, with the controlled contact rate $\frac{\beta }{{1 + \kappa {S_{a0}}}}\frac{{{S_{a0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}{\theta _2}$ and mean duration ${\frac{1}{{d + {d_A}}}}$, giving a contribution of $\frac{\beta }{{1 + \kappa {S_{a0}}}}\frac{{{S_{a0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}{\theta _2}\frac{{\left( {1 - \eta } \right) \delta }}{{\left( {d + \delta } \right) \left( {d + {d_{A}}} \right) }}$. A proportion $\frac{{\eta \delta \omega }}{{\left( {d + \delta } \right) \left( {\omega + d + {d_I}} \right) }}$ indirectly goes from I to the (diagnosed) AIDS class ${{D_A}}$ via class ${{D_I}}$, with the controlled contact rate $\frac{\beta }{{1 + \kappa {S_{a0}}}}\frac{{{S_{a0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}{\theta _2}$ and mean duration ${\frac{1}{{d + {d_A}}}}$, giving a contribution of $\frac{\beta }{{1 + \kappa {S_{a0}}}}\frac{{{S_{a0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}} \times {\theta _2}\frac{{\eta \delta \omega }}{{\left( {d + \delta } \right) \left( {d + {d_A}} \right) \left( {\omega + d + {d_I}} \right) }}$. The sum of the contribution by these individuals is ${R_{{s_a}}}$. The biological meaning of ${R_{{s_h}}}$ can be similarly explained.

3.3 Local Stability of the Disease-Free Equilibrium

Following (Van den Driessche and Watmough 2002), regarding the local stability of the disease-free equilibrium ${E_0}$ of the system (1), we propose the following theorem.

Theorem 2

For system (1), the disease-free equilibrium ${E_0}$ is locally asymptotically stable if ${R_0} < 1$.

Proof

The Jacobian matrix of system (1) evaluated at the disease-free equilibrium ${E_0}$ can be written as

$$\begin{aligned} {J_{{E_0}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{{\beta _0}{S_{a0}}}}{{\left( {1 + \kappa {S_{a0}}} \right) \left( {{S_{a0}} + {S_{u0}} + {S_{h0}}} \right) }} + \frac{{{\beta _0}{S_{h0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}} - \left( {d + \delta } \right) }&{}{\frac{{{\beta _0}{\theta _1}{S_{h0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}} + \frac{{{\beta _0}{\theta _1}{S_{a0}}}}{{\left( {1 + \kappa {S_{a0}}} \right) \left( {{S_{a0}} + {S_{u0}} + {S_{h0}}} \right) }}}\\ {\eta \delta }&{}{ - \left( {d + {d_I} + \omega } \right) }\\ {\left( {1 - \eta } \right) \delta }&{}\omega \end{array}} \right. \\ \left. {\begin{array}{*{20}{c}} {\frac{{{\beta _0}{\theta _2}{S_{h0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}} + \frac{{{\beta _0}{\theta _2}{S_{a0}}}}{{\left( {1 + \kappa {S_{a0}}} \right) \left( {{S_{a0}} + {S_{u0}} + {S_{h0}}} \right) }}}\\ 0\\ { - \left( {d + {d_A}} \right) } \end{array}} \right] . \end{aligned}$$

Three eigenvalues of the matrix ${J_{{E_0}}}$ are ${ - d}$, ${ - d}$, and ${ - \left( {d + \alpha } \right) }$, while other three are given by the roots of the following equation

$$\begin{aligned} {\lambda ^3} + {b_1}{\lambda ^2} + {b_2}{\lambda ^1} + {b_3} = 0, \end{aligned}$$

(7)

where

$$\begin{aligned} {b_1} =&\left( {d + {d_I} + \omega } \right) + \left( {d + {d_A}} \right) - \left( {\frac{{{\beta _0}{S_{a0}}}}{{\left( {1 + \kappa {S_{a0}}} \right) \left( {{S_{a0}} + {S_{u0}} + {S_{h0}}} \right) }} + \frac{{{\beta _0}{S_{h0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}} \right) \\&+\left( {d + \delta } \right) ,\\ {b_2} =&\left[ {\left( {d + \delta } \right) - \left( {\frac{{{\beta }{S_{a0}}}}{{\left( {1 + \kappa {S_{a0}}} \right) \left( {{S_{a0}} + {S_{u0}} + {S_{h0}}} \right) }} + \frac{{{\beta }{S_{h0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}} \right) } \right] \left( {d + {d_I} + \omega } \right) \\&+ \left[ {\left( {d + \delta } \right) + \left( {d + {d_I} + \omega } \right) - \left( {\frac{{\beta {S_{a0}}}}{{\left( {1 + \kappa {S_{a0}}} \right) \left( {{S_{a0}} + {S_{u0}} + {S_{h0}}} \right) }} + \frac{{\beta {S_{h0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}} \right) } \right] \left( {d + {d_A}} \right) \\&- \eta \delta \left( {\frac{{\beta {\theta _1}{S_{a0}}}}{{\left( {1 + \kappa {S_{a0}}} \right) \left( {{S_{a0}} + {S_{u0}} + {S_{h0}}} \right) }} + \frac{{\beta {\theta _1}{S_{h0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}} \right) \\&- \left( {1 - \eta } \right) \delta \left( {\frac{{\beta {\theta _2}{S_{a0}}}}{{\left( {1 + \kappa {S_{a0}}} \right) \left( {{S_{a0}} + {S_{u0}} + {S_{h0}}} \right) }} + \frac{{\beta {\theta _2}{S_{h0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}} \right) ,\\ {b_3} =&\left[ {\left( {d + \delta } \right) - \left( {\frac{{\beta {S_{a0}}}}{{\left( {1 + \kappa {S_{a0}}} \right) \left( {{S_{a0}} + {S_{u0}} + {S_{h0}}} \right) }} + \frac{{\beta {S_{h0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}} \right) } \right] \left( {d + {d_I} + \omega } \right) \left( {d + {d_A}} \right) \\&- \left( {d + {d_A}} \right) \eta \delta \left( {\frac{{\beta {\theta _1}{S_{a0}}}}{{\left( {1 + \kappa {S_{a0}}} \right) \left( {{S_{a0}} + {S_{u0}} + {S_{h0}}} \right) }} + \frac{{\beta {\theta _1}{S_{h0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}} \right) \\&- \eta \delta \omega \left( {\frac{{\beta {\theta _2}{S_{a0}}}}{{\left( {1 + \kappa {S_{a0}}} \right) \left( {{S_{a0}} + {S_{u0}} + {S_{h0}}} \right) }} + \frac{{\beta {\theta _2}{S_{h0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}} \right) \\&- \left( {1 - \eta } \right) \delta \left( {d + {d_I} + \omega } \right) \left( {\frac{{\beta {\theta _2}{S_{a0}}}}{{\left( {1 + \kappa {S_{a0}}} \right) \left( {{S_{a0}} + {S_{u0}} + {S_{h0}}} \right) }} + \frac{{\beta {\theta _2}{S_{h0}}}}{{{S_{a0}} + {S_{u0}} + {S_{h0}}}}} \right) \\ =&\left( {d + \delta } \right) \left( {d + {d_A}} \right) \left( {d + {d_I} + \omega } \right) \left( {1 - {R_0}} \right) . \end{aligned}$$

According to Routh–Hurtwitz criterion (Murray 1998), we have

$$\begin{aligned} {H_1} = {b_1}> 0, {H_2} = \left| {\begin{array}{*{20}{c}} {{b_1}}&{}1\\ {{b_3}}&{}{{b_2}} \end{array}} \right| = {b_1}{b_2} - {b_3}>0. \end{aligned}$$

It is clear that both roots of the Eq. (7) are either negative or have negative real parts if ${R_0} < 1$. Thus, the disease-free equilibrium ${E_0}$ is locally asymptotically stable if ${R_0} < 1$. $\square$

We choose the following set of hypothetical parameter values in the system (1)

$$\begin{aligned}&\Lambda = 50, d = \frac{1}{{50}}, {d_A} = \frac{1}{{30}}, {d_I} = \frac{1}{35}, {\beta } = 0.0003, \eta = 0.8, \alpha = \frac{1}{{20}}, \kappa = 50, \nonumber \\&\rho = 0.01, \mu = 10, {\theta _1} = 0.5, {\theta _2} = 0.2, f = 0.1, \omega = \frac{1}{2}, \omega = \frac{1}{2}, \delta = 0.6. \end{aligned}$$

(8)

The existence of the point ${E_0}$ is shown in Fig. 3. With the above parameters, we note that ${R_0} = 0.0012 <1$. Therefore, the roots of Eq. (7) are either negative or have negative real parts. Hence, the disease-free equilibrium ${E_0}$ is locally asymptotically stable with these parameter values.

Fig. 3

(Colour figure online) Local stability of the disease-free equilibrium ${E_0} = \left( 714.2857,17.8571,1767.9,{{0}},{{0}},{{0}} \right)$ inside the region of attraction $\Omega$ in ${S_a}- {S_h}$ spaces

3.4 Uniform Persistence of the Disease

In order to prove that system (1) is uniformly persistent, according to the uniform persistence theorem (Wang and Zhao 2004; Zhao 2017), we define $f:X \rightarrow X$ be a continuous map associated with system (1), and

$$\begin{aligned}&X := \left\{ {\left( {{S_u},{S_a},{S_h},I,{D_I},{D_A}} \right) :{S_u} \ge 0,{S_a} \ge 0,{S_h} \ge 0,I \ge 0,{D_I} \ge 0,{D_A} \ge 0} \right\} ,\\&{X_0} := \left\{ {\left( {{S_u},{S_a},{S_h},I,{D_I},{D_A}} \right) \in X: I> 0,{D_I}> 0,{D_A} > 0} \right\} ,\\&\partial {X_0} = X\backslash {X_0}. \end{aligned}$$

Suppose that there exists a maximal compact invariant set ${A_\partial }$ of f in $\partial {X_0}$, that is, ${A_\partial }$ is compact, invariant, possibly empty, and contains every compact invariant subset of $\partial {X_0}$ (Wang and Zhao 2004).

Lemma 1

(See Theorem 1.3.1. in (Zhao 2017)) Assume that

• (1) $f\left( {{X_0}} \right) \subset {X_0}$ and f has a global attractor A;

• (2) The maximal compact invariant set ${A_\partial } = A \cap {M_\partial }$ of f in $\partial {X_0}$ is possibly empty, and admits a Morse decomposition $\left\{ {{M_1}, \ldots ,{M_k}} \right\}$ with the following properties:

  • (a) ${M_i}$ is isolated in X;

  • (b) ${W^S}\left( {{E_0}} \right) \cap {X_0} = \emptyset$ for each $1 \le i \le k$.

Then there exists $\delta > 0$ such that for any compact internally chain transitive set L with $L \notin {M_i}$ for all $1 \le i \le k$, we have ${\inf _{x \in L}}{} \mathbf{d}\left( {x,\partial {X_0}} \right) > \delta$.

Theorem 3

When ${R_0} > 1$, system (1) is uniformly persistent.

Proof

Obviously, both X and ${X_0}$ are positively invariant, and $\partial {X_0}$ is relatively closed in X. Theorem 1 implies that the system is point dissipative. Thus, the solution of the system admits a global attractor A.

Define

$$\begin{aligned}&{M_\partial } = \left\{ {\left( {{S_u}\left( 0 \right) } \right. } \right. ,{S_a}\left( 0 \right) ,{S_h}\quad \left( 0 \right) ,I\left( 0 \right) ,{D_I}\left( 0 \right) ,\left. {{D_A}\left( 0 \right) } \right) \in \partial {X_0}:\\&\left( {{S_u}\left( t \right) ,{S_a}\left( t \right) ,{S_h}\left( t \right) ,I\left( t \right) ,{D_I}\left( t \right) ,{D_A}\left( t \right) } \right) \left. { \in \partial {X_0},\forall t \ge 0} \right\} . \end{aligned}$$

Next, we prove that

$$\begin{aligned} {M_\partial } = \left\{ {\left( {{S_u},{S_a},{S_h},0,0,0} \right) \in X:{S_u} \ge 0,{S_a} \ge 0,{S_h} \ge 0} \right\} . \end{aligned}$$

(9)

Note that $\left\{ {\left( {{S_u},{S_a},{S_h},0,0,0} \right) \in X:{S_u} \ge 0,{S_a} \ge 0,{S_h} \ge 0} \right\} \subseteq {M_\partial }$. Hence, we only need to prove that ${M_\partial } \subseteq \left\{ {\left( {{S_u},{S_a},{S_h},0,0,0} \right) \in X:{S_u} \ge 0,{S_a} \ge 0,{S_h} \ge 0} \right\}$. For any ${\varphi _0} = \left( {{S_u}\left( 0 \right) ,{S_a}\left( 0 \right) ,{S_h}\left( 0 \right) ,I\left( 0 \right) ,{D_I}\left( 0 \right) ,{D_A}\left( 0 \right) } \right) \in {M_\partial }$, we assume that one of ${I\left( 0 \right) }$, ${{D_I}\left( 0 \right) }$, ${{D_A}\left( 0 \right) }$ is nonzero, such as ${{D_A}\left( 0 \right) }$, then we have

$$\begin{aligned} I\left( t \right) =&{e^{ - \left( {\delta + d} \right) t}}\left[ {I\left( 0 \right) + \int _0^t {\left( {\frac{{\beta \left[ {I\left( {{s_1}} \right) + {\theta _1}{D_I}\left( {{s_1}} \right) + {\theta _2}{D_A}\left( {{s_1}} \right) } \right] {S_a}\left( {{s_1}} \right) }}{{N\left( {{s_1}} \right) \left[ {1 + \kappa \left[ {{S_a}\left( {{s_1}} \right) + {D_I}\left( {{s_1}} \right) + {D_A}\left( {{s_1}} \right) } \right] } \right] }}} \right. } } \right. \\&+ \left. {\left. {\frac{{{\beta }\left[ {I\left( {{s_1}} \right) + {\theta _1}{D_I}\left( {{s_1}} \right) + {\theta _2}{D_A}\left( {{s_1}} \right) } \right] {S_h}\left( {{s_1}} \right) }}{{N\left( {{s_1}} \right) }}} \right) {e^{\left( {\delta + d} \right) {s_1}}}d{s_1}} \right]> 0,\;\;\;{} \forall t \ge 0,\\ {D_I}\left( t \right) =&{e^{ - \left( {\omega + d + {d_I}} \right) t}}\left[ {{D_I}\left( 0 \right) + \int _0^t {\eta \delta I\left( {{s_1}} \right) {e^{\left( {\omega + d + {d_I}} \right) {s_1}}}d{s_1}} } \right]> 0,\;\;\;{} \forall t \ge 0,\\ {D_A}\left( t \right) =&{e^{ - \left( {d + {d_A}} \right) t}}\left[ {{D_A}\left( 0 \right) + \int _0^t {\left( {\left( {1 - \eta } \right) \delta I\left( {{s_1}} \right) + \omega {D_I}\left( {{s_1}} \right) } \right) {e^{\left( {d + {d_A}} \right) {s_1}}}d{s_1}} } \right] > 0,\;\;\;{} \forall t \ge 0. \end{aligned}$$

For any

$$\begin{aligned} {\varphi _0}&= \left( {{S_u}\left( 0 \right) ,{S_a}\left( 0 \right) ,{S_h}\left( 0 \right) ,I\left( 0 \right) ,{D_I}\left( 0 \right) ,{D_A}\left( 0 \right) } \right) \\&\notin \left\{ {\left( {{S_u},{S_a},{S_h},0,0,0} \right) \in X:{S_u} \ge 0,{S_a} \ge 0,{S_h} \ge 0} \right\} , \end{aligned}$$

we have $\left( {{S_u}\left( t \right) ,{S_a}\left( t \right) ,{S_h}\left( t \right) ,I\left( t \right) ,{D_I}\left( t \right) ,{D_A}\left( t \right) } \right) \notin \partial {X_0}$, $t > 0$ is sufficiently small. This means that ${\varphi _0} = \left( {{S_u}\left( 0 \right) ,{S_a}\left( 0 \right) ,{S_h}\left( 0 \right) ,I\left( 0 \right) ,{D_I}\left( 0 \right) ,{D_A}\left( 0 \right) } \right) \notin {M_\partial }$, which contradicts with the assumption that ${\varphi _0} \in {M_\partial }$. Hence, ${M_\partial } \subseteq \left\{ {\left( {{S_u},{S_a},{S_h},0,0,0} \right) \in X:{S_u} \ge 0} \right.$, $\left. {{S_a} \ge 0,{S_h} \ge 0} \right\}$. This proves (9).

Let ${\varphi _0}$ be an initial value, then there is a unique equilibrium ${E_0}\left( {{S_{u0}},{S_{a0}},{S_{h0}},0,0,0} \right)$ in ${M_\partial }$, and ${ \cup _{{\varphi _0} \in {M_\partial }}} = {E_0}$. Therefore, ${E_0}$ is a compact and isolated invariant set for ${\varphi _0}$ in set ${M_\partial }$, and ${A_\partial } = \left\{ {\left( {{S_{u0}},{S_{a0}},{S_{h0}},0,0,0} \right) } \right\}$ is the maximal compact invariant set of f in $\partial {X_0}$.

In the following, we prove that ${E_0}$ is isolated in set X and ${W^S}\left( {{E_0}} \right) \cap {X_0} = \emptyset$, where ${W^S}\left( {{E_0}} \right)$ denotes the stable manifold of ${{E_0}}$. The above proposition is equivalent to claiming that there exists a positive constant $\delta$ such that for any solution ${\Phi _t}\left( {{\varphi _0}} \right)$, ${\varphi _0} \in {X_0}$,

$$\begin{aligned} \mathop {\lim }\limits _{t \rightarrow \infty } \sup \mathbf{d}\left( {{\Phi _t}\left( {{\varphi _0}} \right) ,{E_0}} \right) \ge \delta , \end{aligned}$$

where $\mathbf{d}$ is a distant function in ${X_0}$. Suppose that the claim is not true, then $\mathop {\lim }\limits _{t \rightarrow \infty } \sup \mathbf{{d}}$ $\left( {{\Phi _t}\left( {{\varphi _0}} \right) ,{E_0}} \right) < \delta$ for any $\delta$; namely, there exists a positive constant T, such that $\frac{\Lambda }{{\alpha + d}} - \xi \le {S_u}\left( t \right) \le \frac{\Lambda }{{\alpha + d}} + \xi$, $\frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} - \xi \le {S_a}\left( t \right) \le \frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + \xi$, $\frac{{\left( {1 - \rho } \right) \alpha }}{d}\frac{\Lambda }{{\alpha + d}} - \xi \le {S_h}\left( t \right) \le \frac{{\left( {1 - \rho } \right) \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + \xi$, $0 \le I\left( t \right) \le \xi$, $0 \le {D_I}\left( t \right) \le \xi$, $0 \le {D_A}\left( t \right) \le \xi$, for $\forall t > T$, where $\xi$ is a small constant to be determined. When $t > T$, we have

$$\begin{aligned} \frac{{dI}}{{dt}}&\ge \frac{{\beta \left( {\frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} - \xi } \right) \left( {I + {\theta _1}{D_I} + {\theta _2}{D_A}} \right) }}{{\left( {\frac{\Lambda }{{\alpha + d}} + \frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + \frac{{\left( {1 - \rho } \right) \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + 6\xi } \right) \left[ {1 + \kappa \left( {\frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + 3\xi } \right) } \right] }} - \left( {\delta + d} \right) I\\&+ \frac{{\beta \left( {\frac{{\left( {1 - \rho } \right) \alpha }}{d}\frac{\Lambda }{{\alpha + d}} - \xi } \right) \left( {I + {\theta _1}{D_I} + {\theta _2}{D_A}} \right) }}{{\frac{\Lambda }{{\alpha + d}} + \frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + \frac{{\left( {1 - \rho } \right) \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + 6\xi }},\\ \frac{{d{D_I}}}{{dt}}&= \eta \delta I - \left( {\omega + d + {d_I}} \right) {D_I},\\ \frac{{d{D_A}}}{{dt}}&= \left( {1 - \eta } \right) \delta I + \omega {D_I} - \left( {d + {d_A}} \right) {D_A}. \end{aligned}$$

Consider an auxiliary system

$$\begin{aligned} u' = M\left( \xi \right) u, \end{aligned}$$

(10)

where vector $u = {\left( {{u_1},{u_2},{u_3}} \right) ^T}$ and

$$\begin{aligned} M\left( \xi \right) =&\left( {\begin{array}{*{20}{c}} {\frac{{{\beta }\left( {\frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} - \xi } \right) }}{{\left( {\frac{\Lambda }{{\alpha + d}} + \frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + \frac{{\left( {1 - \rho } \right) \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + 6\xi } \right) \left[ {1 + \kappa \left( {\frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + 3\xi } \right) } \right] }} + \frac{{{\beta }\left( {\frac{{\left( {1 - \rho } \right) \alpha }}{d}\frac{\Lambda }{{\alpha + d}} - \xi } \right) }}{{\frac{\Lambda }{{\alpha + d}} + \frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + \frac{{\left( {1 - \rho } \right) \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + 6\xi }} - \left( {\delta + d} \right) }\\ {\eta \delta }\\ {\left( {1 - \eta } \right) \delta } \end{array}} \right. \\&\begin{array}{*{20}{c}} {{\theta _1}\left[ {\frac{{\beta \left( {\frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} - \xi } \right) }}{{\left( {\frac{\Lambda }{{\alpha + d}} + \frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + \frac{{\left( {1 - \rho } \right) \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + 6\xi } \right) \left[ {1 + \kappa \left( {\frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + 3\xi } \right) } \right] }} + \frac{{\beta \left( {\frac{{\left( {1 - \rho } \right) \alpha }}{d}\frac{\Lambda }{{\alpha + d}} - \xi } \right) }}{{\frac{\Lambda }{{\alpha + d}} + \frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + \frac{{\left( {1 - \rho } \right) \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + 6\xi }}} \right] }\\ { - \left( {\omega + d + {d_I}} \right) }\\ \omega \end{array}\\&\left. {\begin{array}{*{20}{c}} {{\theta _2}\left[ {\frac{{\beta \left( {\frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} - \xi } \right) }}{{\left( {\frac{\Lambda }{{\alpha + d}} + \frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + \frac{{\left( {1 - \rho } \right) \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + 6\xi } \right) \left[ {1 + \kappa \left( {\frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + 3\xi } \right) } \right] }} + \frac{{\beta \left( {\frac{{\left( {1 - \rho } \right) \alpha }}{d}\frac{\Lambda }{{\alpha + d}} - \xi } \right) }}{{\frac{\Lambda }{{\alpha + d}} + \frac{{\rho \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + \frac{{\left( {1 - \rho } \right) \alpha }}{d}\frac{\Lambda }{{\alpha + d}} + 6\xi }}} \right] }\\ 0\\ { - \left( {d + {d_A}} \right) } \end{array}} \right) . \end{aligned}$$

Recall that the stability modulus of a $3 \times 3$ matrix M is defined as

$$\begin{aligned} s\left( M \right) := \max \left\{ {{\mathop {\mathrm{Re}}\nolimits } \lambda :\lambda \text { is an eigenvalue of } M} \right\} . \end{aligned}$$

If ${R_0} > 1$, then $s\left( {M\left( 0 \right) } \right) > 0$ (Wang and Zhao 2004; Wang et al 2016a). Since $s\left( {M\left( \xi \right) } \right)$ is continuous for small $\xi$, there exists $\xi$ small enough such that $s\left( {M\left( \xi \right) } \right) > 0$. Thus, there is a positive eigenvalue of ${M\left( \xi \right) }$ with a positive eigenvector. Let $u\left( t \right) = {\left( {{u_1}\left( t \right) ,{u_2}\left( t \right) ,{u_3}\left( t \right) } \right) }$ be a solution of Eq. (10), which is strictly increasing ${u_i}\left( t \right) \rightarrow \infty$ as $t \rightarrow \infty$, $i = 1,2,3$. Since the system (10) is a quasi-monotonic system, applying the comparison principle (Lakshmikantham et al 1989) yields

$$\begin{aligned} \mathop {\lim }\limits _{t \rightarrow \infty } I\left( t \right) = \infty , \mathop {\lim }\limits _{t \rightarrow \infty } {D_I}\left( t \right) = \infty , \mathop {\lim }\limits _{t \rightarrow \infty } {D_A}\left( t \right) = \infty , \end{aligned}$$

which contradicts with $0 \le I\left( t \right) \le \xi$, $0 \le {D_I}\left( t \right) \le \xi$, and $0 \le {D_A}\left( t \right) \le \xi$. Hence, ${E_0}$ is an isolated invariant set in X and ${W^S}\left( {{E_0}} \right) \cap {X_0} = \emptyset$. By Lemma 1, f is uniformly persistent with respect to $\left( {{X_0},\partial {X_0}} \right)$. Therefore, the system is uniformly persistent if ${R_0} > 1$. $\square$

4 Estimation of AIDS Epidemic in China

HIV/AIDS has been one of the most challenging health issues in China. It is necessary to assess the situation accurately and evaluate the effectiveness of various prevention and control measures. For simplicity, new HIV-positive cases are assumed to be new diagnosed HIV-positive individuals who have not yet progressed to AIDS, and new AIDS cases are assumed to be new individuals with clinical symptoms of AIDS.

We obtain data on the number of new HIV-positive and new AIDS cases in mainland China from China CDC (Chinese 2021a). In 2012, China CDC revised the statistical rules for new infection cases. In February 2020, UNAIDS claimed that it is not clear how many infected people in China are affected by COVID-19 (Joint 2020). Thus, we focus on the annual number of reported new cases from 2013 to 2018 to assess the HIV/AIDS epidemic in China (see Fig. 4). The data indicate that HIV transmission does not show obvious seasonality.

Fig. 4

(Colour figure online) Number of new diagnosed HIV-positive individuals and AIDS patients in mainland China from 2013 to 2018

The initial values of state variables and fixed parameters are provided below:

(i):

As of December 31, 2012, 240,174 diagnosed HIV-positive individuals and 145,643 AIDS patients had survived (Chinese 2020). Hence, we assume that ${{{D}}_I}\left( 0 \right) = {{24.0174}} \times {10^4}$, ${{{D}}_A}\left( 0 \right) = {{14.5643}} \times {10^4}$.

(ii):

Based on the data given by the China Statistics Abstract (National Bureau of Statistics of China 2021), it can be estimated that the average number of births per year $\Lambda$ and natural mortality d from 2013 to 2019 are $1600 \times {10^4}$ and $\frac{1}{76.34}$, respectively.

(iii):

By calculation, the proportion of new AIDS cases (excluding previous $D_I$ transferred into $D_A$ this year) in new cases from 2013 to 2017 is 0.7046, 0.7154, 0.7075, 0.7046, and 0.7103, respectively. Hence, we assume that $\eta$ is the average, that is, $\eta =0.7085$.

We estimate the unknown parameters ${\widehat{\theta }} = \left( {{\beta },\alpha ,\kappa ,\rho ,\mu ,{\theta _1},f,\delta } \right)$ by Markov chain Monte Carlo (MCMC) simulation using the annual number of new HIV/AIDS cases from 2013 to 2018 (see Table 2). Figure 5 A and C shows the fitting results of the annual number of new HIV/AIDS cases. In addition, Fig. 5B and D shows the Pearson coefficients between the fitting results and reported new cases, which indicates that the fitting result is acceptable.

Fig. 5

(Colour figure online) A, C Fitting the annual number of new diagnosed HIV-positive cases and AIDS cases (excluding previous $D_I$ transformed into $D_A$ this year) in China. The red and blue dots mark the new cases, and the solid black line represents the model solution. Shaded regions indicate 95% confidence interval; B, D Pearson coefficients between the fitting results and reported new cases. The larger the absolute value of the coefficient, the better the fitting result, and the maximum value is one

Table 2 Estimated parameters and their mean values given in 95% CI

Based on the estimation of unknown parameters, the mean value of the basic reproduction number is estimated as 1.2138, with a 95% confidence interval (1.0834–1.3442) (see Fig. 6A). The basic reproduction numbers of ${S_a}$ and ${S_h}$ are $5.6776 \times {10^{{{-10}}}}$ ($4.7883\times {10^{{{-10}}}}$–$6.7039 \times {10^{{{-10}}}}$) and 1.2138 (1.0834–1.3442), respectively (see Fig. 6B and C). The above analysis shows that if all susceptible individuals receive sex education on prevention and become alert, then the epidemic will eventually die out naturally. However, if all susceptible individuals perform high-risk behaviors, then the epidemic will persist and become endemic.

Fig. 6

(Colour figure online) Basic reproduction numbers A $R_{S_a}$ and $R_{S_h}$; B $R_{S_a}$; C ${R_{S_h}}$ calculated by the last 10000 samples of the MCMC fitting results

5 Sensitivity Analysis

We perform global sensitivity analysis following the techniques presented in (Blower and Dowlatabadi 1994; Marino et al 2008) to identify the most influential parameters that have a significant impact on an important output variable. Since the parameters with large partial rank correlation coefficient (PRCC) values and corresponding small p values ($p < 0.01$) are generally considered to be the most influential parameters on the output variable, we consider that the absolute values of PRCC$> 0.4$ represent a strong correlation between input parameters and output variables, while values between 0.2 and 0.4 represent moderate correlation, and values between 0 and 0.2 represent no correlation (Xiao et al 2013). The parameters of the model are set as input variables, and ${R_{{s_a}}}$ and ${R_{{s_h}}}$ are the output variables. Keeping $d = \frac{1}{{{{76.34}}}}$, ${d_I} = 0.172$, ${d_A} = 0.318$, $\Lambda = 1600 \times {10^4}$, ${\theta _2} = 0$, $\eta = 0.7085$, $\omega = 0.116$ fixed while taking the last 10000 sampling values of the remaining parameters from the MCMC fitting results.

Fig. 7

(Colour figure online) Partial rank correlation coefficients illustrating the dependence of A ${R_{{S_a}}}$; B ${R_{{S_h}}}$ on model parameters, where $\beta$ represents the adequate contact rate, $\alpha$ represents the rate of transition from being pre-susceptible to being aware susceptible or being high-risk susceptible, $\kappa$ represents the fear of infection, $\rho$ represents the rate of individuals who receive sex education and become alert, ${{\theta _1}}$ represents the modification factor in adequate contact rate of diagnosed HIV-positive patients, $\delta$ denotes the diagnosis rate, and parameters with significant PRCCs are indicated as $*$ ($p < 0.01$ and $\left| {PRCC} \right| > 0.2$)

Table 3 PRCCs of model parameter on ${R_{{S_a}}}$ and ${R_{{S_h}}}$ with corresponding values of p

Figure 7 and Table 3 show the dependence of ${R_{{s_a}}}$ and ${R_{{s_h}}}$ on model parameters. The sensitivity analysis suggests that the parameters significantly related to ${R_{{s_a}}}$ are ${\beta }$ and $\kappa$, and the parameters that are strongly correlated to ${R_{{s_h}}}$ are ${\beta }$, $\alpha$, and $\rho$. Specifically, the adequate contact rate ${\beta }$ has the strongest positive correlation with ${R_{{s_a}}}$ and ${R_{{s_h}}}$. The transition rate $\alpha$ has a great positive impact on ${R_{{s_h}}}$. Typically, a long education period helps to reduce the number of high-risk susceptible individuals, thereby reducing the value of ${R_{{s_h}}}$. Among the parameters that are negatively correlated with ${R_{{s_a}}}$ and ${R_{{s_h}}}$, the PRCC values of fear coefficient $\kappa$ and the rate of individuals who receive sex education and become alert $\rho$ are the largest. We define $\alpha$, $\kappa$, $\rho$ as preventive measures and $\delta$ as post-infection measure. We can conclude that the PRCC values of these preventive measures are much greater than those of post-infection measures, that is, preventive measures are more effective than post-infection measures in eliminating the AIDS epidemic. Hence, the health authorities should not only strengthen the diagnosis of HIV carriers but also pay attention to the sex education of pre-susceptible and susceptible individuals.

6 HIV Epidemic Estimated in the Future Considering 90-90-90 Strategies

As early as 2003, China launched a free antiviral treatment project. At the early stage of the implementation of free antiviral treatment, the mortality of disease-related was greatly reduced. However, the reduction of mortality and the extension of individual survival time are also affected by gender, route of infection, medication compliance, and other factors. Hence, as of 2018, the number of new HIV/AIDS cases has been increasing annually.

On November 23, 2018, the National Health Commission of the People’s Republic of China held a news conference to show the progress of AIDS prevention and control in China (National 2018). For the first 90%, about 30% infected people have not been found. The second target of treatment coverage is going smoothly, while the medical resources in some regions are relatively insufficient. The third target has been basically achieved in a short time with the current treatment approach. This target has not been completely achieved so far due to some problems such as drug resistance.

Fig. 8

(Colour figure online) Prediction for the annual number of new HIV/AIDS cases from 2019 to 2030 in China. A Number of new diagnosed HIV-positive individuals who have not yet progressed to AIDS; B number of new AIDS cases. The red solid line and blue solid line indicate that the prediction starts from the current year

Figure 5 shows that the number of new HIV/AIDS cases in China has been increasing annually from 2013 to 2018. Figure 8 predicts that the number of new HIV/AIDS cases will increase annually from 2019 to 2030. Therefore, AIDS cannot be eradicated in China by 2030 if the current surveillance, testing, and intervention strategies remain. In addition, the 90-90-90 targets in 2020 have not been completed (Joint 2020). In May 2019, China promised to achieve the three zero goals, namely zero new HIV/AIDS infection, zero discrimination, and zero AIDS-related deaths, and emphasized that three zeroes are the key goal of epidemic prevention and control for China. It is necessary to predict the spread of the epidemic so that relevant policies can be revised at any time. Therefore, we re-predict the epidemic in the next few years. The objective of this forecast is to estimate when the goal of zero new HIV/AIDS cases can be completed.

Fig. 9

(Colour figure online) Quantifying the 90-90-90 targets mathematically. A 90% infected people know their infection status; B 90% of those diagnosed with HIV/AIDS receive antiviral treatment, and the virus is under control in 90% of the patients treated

We quantify the 90-90-90 targets mathematically and add the quantization results as a strategy to the model. The quantization process is shown in Fig. 9. As shown in Fig. 9A, when 90% of HIV carriers are diagnosed, that is, after the testing period, 90% of HIV carriers (I) become HIV-positive individuals (${D_I}$) or AIDS patients (${D_A}$). We assume that 90% of HIV carriers are diagnosed in unit time. Therefore, the rate from I to $D_I$ can be expressed as $\eta \times 0.9 \times I \times \frac{1}{{{\text {unit time}}}}$, and the rate from I to $D_A$ can be expressed as $\left( {1{{-}}\eta } \right) \times 0.9 \times I \times \frac{1}{{{\text {unit time}}}}$.

The quantification process of the second and third 90% targets is shown in Fig. 9B. It is assumed that 90% of the diagnosed individuals receive antiviral treatment, and the virus in 90% of treated individuals is under control regardless of drug resistance (Wu and Zhao 2021), that is, they will no longer infect susceptible individuals. The above analysis can be expressed as $0.9\times 0.9\times \left( {{D_I}+{D_A}}\right) \times \frac{1}{{{\text {unit time}}}}$. It is assumed that the virus in 10% of the diagnosed individuals may keep reproducing due to many factors such as drug resistance when receiving antiviral treatment, and their survival times are the same as those diagnosed individuals who gave up treatment. Note that we do not consider the mortality rate due to HIV (${d_I}$) in this case. The above process can be expressed by $0.9 \times 0.1 \times {D_I} \times \omega$, $0.1 \times {D_I} \times \omega$, $0.9 \times 0.1 \times {D_A} \times {d_A}$, and $0.1 \times {D_A} \times {d_A}$, respectively.

Based on the above assumptions, we consider whether China can achieve the goal of zero new HIV/AIDS cases in 2030 when China realizes the 90-90-90 targets by the end of 2022. We analyze the following three cases:

• 1. 90% infected individuals know their infection status;

• 2. 90% of those diagnosed with HIV/AIDS receive antiviral treatment, and the virus is under control in $90\%$ of the patients treated;

• 3. 90% HIV-infected individuals know their infection status, 90% of those diagnosed with HIV/AIDS receive antiviral treatment, and the virus is under control in 90% of the patients treated.

For the above cases, we carry out numerical simulations. Figure 10A and B is based on the assumption that the first 90% target will be completed by the end of 2022. In this case, the number of new HIV/AIDS cases in 2030 will be greater than one. Therefore, even if the diagnosis rate realizes 90% by the end of 2022, it will be impossible to achieve the goal of zero new HIV/AIDS cases in 2030. Figure 10C and D shows that even if the second and third 90% targets are completed by the end of 2022, it will be impossible to achieve the goal of zero new HIV/AIDS cases by 2030. In the numerical simulations in Figure 10E and F, we assume that the 90-90-90 targets have been completed by the end of 2022, then the goal of zero new HIV/AIDS cases will not be achieved by 2030. It is necessary to study when China can achieve the goal of zero new HIV/AIDS cases. Figure 11A and B shows that if the targets of 90-90-90 are achieved by the end of 2022, zero new AIDS cases will be achieved by 2048. We assume that the year of achieving the 90-90-90 targets will be postponed by a year, then the year for achieving the goal of zero new HIV/AIDS cases will have to be postponed for one year. Under the above two assumptions, it takes 26 years to achieve the same goal, and the peak of the new HIV/AIDS cases is higher in the latter. The medical expenses of these patients are high.

Fig. 10

(Colour figure online) Numerical simulation of A, B Case 1; C, D Case 2; E, F Case 3 using data from 2013 to 2018, predicts the number of new HIV/AIDS cases each year from 2019 to 2030. The red solid line or blue solid line indicates that the 90% targets have been reached since the current year

Fig. 11

(Colour figure online) Numerical simulation of Case 3 using data from 2013 to 2018 predicts the number of new HIV/AIDS cases each year from A, B 2019 to 2048; C, D 2019 to 2049. The red solid line or blue solid line indicates that the 90% targets have been reached since the current year

The worldwide COVID-19 pandemic occurred in late 2019. In 2020, UNAIDS reported that we cannot take the fund for a specific disease to treat another disease. If we want to avoid massive deaths, we must provide adequate funding for the prevention and treatment of HIV/AIDS and COVID-19 (Joint 2020). However, it is impossible to exclude the possibility that China’s medical resources, such as drugs, equipments, and health workers will be deployed to fight against COVID-19. Therefore, it is necessary to assume that the time to achieve the 90-90-90 targets will be greatly delayed. Under this assumption, we study how long it takes for China to achieve the goal of zero new HIV/AIDS cases. When the time for completing the 90-90-90 targets is extended to 2029 and 2030, Fig. 12 shows an interesting phenomenon. The simulation results of the above two assumptions show that it takes 26 years to achieve the goal of zero new HIV/AIDS cases, which is the same as the above analysis.

Fig. 12

(Colour figure online) Numerical simulation of Case 3 using data from 2013 to 2018 predicts the number of new HIV/AIDS cases each year from A, B 2019 to 2055; C, D 2019 to 2056. The red solid line or blue solid line indicates that the 90% targets have been reached since the current year

From the above analysis, whether the time to achieve the 90-90-90 targets is the end of 2022 or the end of 2030, it will take 26 years to achieve the goal of zero new HIV/AIDS cases. However, the peak of new HIV/AIDS cases is significantly higher when the latter is considered, and a higher peak indicates more medical funds have to be invested. Hence, China can only achieve the targets of 90-90-90 as soon as possible to avoid more infections, deaths, and medical costs.

7 Discussion

Many years ago, an HIV patient who was recognized as the ‘Berlin patient’ was cured (Brown 2015). In 2017, an adult who was infected with HIV was known as the ‘London patient.’ Within 30 months after stopping antiretroviral treatment, the virus in the patient was undetectable (Gupta et al 2019, 2020). These are two cases of cured HIV that have been recorded so far. Notably, it is unclear which treatments or factors determine the HIV elimination in these two individuals.

It has been more than 40 years since AIDS was first reported. Many methods have been developed to prevent HIV infection, such as pre-exposure prophylaxis, which is highly effective at reducing HIV acquisition through sex (The Lancet 2021). In addition, the reproduction of the virus can be controlled by antiretroviral therapy, even some infected individuals lose their infectivity after treatment. However, there are still some limitations. The most difficult and urgent problem is to achieve universal health coverage so that the needs of marginalized populations without judgment or prejudice (The Lancet 2021). Moreover, ending AIDS cannot be achieved without targeted programs that are tailored to key populations such as high-risk susceptible individuals (The Lancet 2021).

We proposed a mathematical model to estimate the AIDS epidemic in mainland China on the basis of surveillance data, including estimation of the reproduction number, prediction of the AIDS epidemic, and evaluation of the effectiveness of various strategies. We estimated that the mean reproduction number is 1.2138 (95% CI 1.0834–1.3442), where the basic reproduction numbers of aware susceptible individuals and high-risk susceptible individuals are $5.6776 \times {10^{{{-10}}}}$ (95% CI $4.7883\times {10^{{{-10}}}}$–$6.7039 \times {10^{{{-10 }}}}$) and 1.2138 (95% CI 1.0834–1.3442), respectively. The discrepancy in the two estimates may be partly attributable to the fear effect. The estimation of ${R_{{S_h}}}$ is less than those obtained through a metapopulation model (Xiao et al 2013), which is 1.708 (95% CI 1.440–1.977). It shows that HIV/AIDS prevention and control in China has obtained great success in recent years, but the basic reproduction number is still greater than one. Therefore, it is necessary to strengthen HIV/AIDS prevention and treatment. PRCC values of some important parameters for the basic reproduction numbers ${R_{{S_a}}}$ and ${R_{{S_h}}}$ suggest that reducing the effective contact (the number of contacts and the probability of infection per contact) between susceptible individuals and infected individuals remain a priority for the health authorities. In addition, we found that prevention interventions (such as sex education) are far more effective in eliminating the epidemic than post-infection interventions (the diagnostic rate of infected individuals). These findings not only support AIDS prevention education but also affirm the role of psychological fear will effectively decrease the transmission potential of the epidemic.

The results of our work indicate that sex education and improving the alertness of susceptible people are essential to prevent the spread of AIDS. These measures may enhance the fear of infection. Efforts should be made on radical behavioral changes at both individual and group levels, in particular among those who perform high-risk behaviors, to eradicate AIDS. Moreover, we should promote the use of condoms and other protective measures before exposure to reduce the effective contact rate. Furthermore, encouraging self-testing and providing services for those who are willing to be tested after exposure can promote early detection and early diagnosis. The time of achieving the targets of 90-90-90 may be delayed because of COVID-19. Every additional year of delay means that more susceptible people are infected. Therefore, we must ensure that people affected by COVID-19 can receive fundamental AIDS prevention and treatment, and we should enhance the surveillance to ensure that intervention strategies are being implemented properly.

Our study still has several limitations. First, due to the change in statistical rules and the impact of COVID-19, we can only get data from 2013 to 2018. In addition, we cannot separate cases caused by mother-to-child transmission from the total number of cases, which account for less than 1% of the total cases. Second, the first 90% strategy should consider that the sum of the number of individuals diagnosed with HIV and individuals diagnosed with clinical symptoms of AIDS (excluding those transformed from HIV-positive individuals) accounts for 90% of all infected individuals, which is more realistic, but it is difficult to obtain the data. Third, we cannot know whether infected people who maliciously spread HIV are receiving treatment on time. Hence, we assume that the infected individuals who receive treatment on time will not maliciously spread the virus when considering the second and third 90% strategies, then the number of new cases based on this assumption is less than the actual number.