A Mosquito Population Suppression Model by Releasing Wolbachia-Infected Males

Abstract

Due to the role of cytoplasmic incompatibility (CI), releasing Wolbachia-infected male mosquitoes into the wild becomes a very promising strategy to suppress the wild mosquito population. When developing a mosquito suppression strategy, our main concerns are how often, and in what amount, should Wolbachia-infected mosquitoes be released under different CI intensity conditions, so that the suppression is most effective and cost efficient. In this paper, we propose a mosquito population suppression model that incorporates suppression and self-recovery under different CI intensity conditions. We adopt the new modeling idea that only sexually active Wolbachia-infected male mosquitoes are considered in the model and assume the releases of Wolbachia-infected male mosquitoes are impulsive and periodic with period T. We particularly study the case where the release period is greater than the sexual lifespan of the Wolbachia-infected male mosquitoes. We define the CI intensity threshold, mosquito release thresholds, and the release period threshold to characterize the model dynamics. The global and local asymptotic stability of the origin and the existence and stability of T-periodic solutions are investigated. Our findings provide useful guidance in designing practical release strategies to control wild mosquitoes.

Appendix

To prove Theorems 3.1, 3.2 and 3.3, we need the following five lemmas which play an important role in their proofs.

Lemma 5.1

For any given initial value $u>0$,

• (i) If $h(u)>u$, then sequence $\{h_{n}(u)\}^{+\infty }_{0}$ and $\{{\bar{h}}_{n}(u)\}^{+\infty }_{0}$ are strictly increasing.

• (ii) If $h(u)=u$, then $h_{n}(u)=u$ for $n=0,1,2,\cdots .$ Furthermore, w(t; 0, u) is a T-periodic solution of system (2).

• (iii) If $h(u)<u$, then sequence $\{h_{n}(u)\}^{+\infty }_{0}$ and $\{{\bar{h}}_{n}(u)\}^{+\infty }_{0}$ are strictly decreasing.

• (iv) We must have $\lim _{n\rightarrow \infty }h_{n}(u)=l,$ where l satisfies $h(l)=l.$

Proof

The proofs of (i), (ii) and (iii) come from Lemma 3.1 of Yu and Li (2020). We focus on the proof of part (iv).

If $h(u)=u$, then the conclusion follows immediately.

Suppose $h(u)>u$. Then, from part (i), sequence $\{h_{n}(u)\}^{+\infty }_{0}$ is strictly increasing. Furthermore, we must have $0<u<M$ and $0<h_{n}(u)<M,~n=0,1,2\cdots .$ Hence, $\{h_{n}(u)\}^{+\infty }_{0}$ is a monotonically increasing sequence with an upper bound. Then, there exists $l\ge 0$ such that $\lim _{n\rightarrow \infty }h_{n}(u)=l.$ Since $h_{n+1}(u)=h(h_{n}(u))$, taking the limit of both sides, we have $h(l)=l.$

The proof for the case of $h(u)<u$ can be done in a similar matter to the case $h(u)>u$. We thus omit it. $\square$

Lemma 5.2

Assume that $T>T^{*}.$ Then, the following statements hold.

• (a) If $\frac{4s^*_{h}}{3}<s_{h}\le 1$ and $c>c_{1}^{*},$ then Eq. (2) has a unique T-periodic solution.

• (b) If $s_{h}\le \frac{4s^*_{h}}{3}$ and $c>\widehat{c^*},$ then Eq. (2) has a unique T-periodic solution,

where $s^*_{h}$, $c_{1}^{*}$, and $\widehat{c^*}$ are given in (9), (10), and (14).

Proof

We only focus on the proof of part (a). Part (b) can be proved in a similar way.

From (28), $\lim \limits _{u\rightarrow 0}\frac{h(u)}{u}>1$ for $T>T^{*}$. Hence, there is sufficiently small $\delta >0$ such that

$$\begin{aligned} \begin{aligned} h(u)>u, \text {for}~u\in (0,\delta ). \end{aligned} \end{aligned}$$

(31)

Since $c>c_{1}^{*}$, then solution $w(t)=w(t;0,M)$ is strictly decreasing for $t\in (0,{\bar{T}}]$. Hence, ${\bar{h}}(M)<M$, which implies that $h(M)<M$. Therefore, there must be $u_{0}\in (\delta ,M)$ such that $h(u_{0})=u_{0}$ and

$$\begin{aligned} \begin{aligned} h(u)>u, \ \ \text {for}\ u\in (0,u_{0}). \end{aligned} \end{aligned}$$

(32)

Thus, $w(t;0,u_{0})$ is a T-periodic solution of Eq. (2).

Now we prove the uniqueness of the T-periodic solution of Eq. (2) by contradiction.

Assume that Eq. (2) has another T-periodic solution $u_{1}\in (u_{0},M)$ such that $h(u_{1})=u_{1}$ and

$$\begin{aligned} \begin{aligned} h(u)<u,\ \ \text {for}\ u\in (u_{1},M). \end{aligned} \end{aligned}$$

(33)

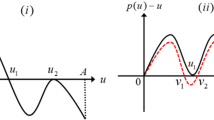
It follows from (32) that there exists $u_{2}\in [u_{0},u_{1}]$ such that one of the following cases is satisfied. (See also Fig 4).

$$\begin{aligned}&h'(u_{0})\le 1, \ h'(u_{2})\ge 1, \ h'(u_{1})\le 1. \end{aligned}$$

(34a)

$$\begin{aligned}&u_{0}=u_{2}, \ h'(u_{0})=1, \ h'(u_{1})\le 1. \end{aligned}$$

(34b)

$$\begin{aligned}&h'(u_{0})\le 1, \ u_{1}=u_{2}, \ h'(u_{1})=1. \end{aligned}$$

(34c)

$$\begin{aligned}&h'(u_{0})=h'(u_{2})=1, \ h'(u_{1})\le 1. \end{aligned}$$

(34d)

$$\begin{aligned}&h'(u_{0})=1,\ h'(u_{2})\le 1, \ h'(u_{1})=1. \end{aligned}$$

(34e)

$$\begin{aligned}&h'(u_{0})\le 1, \ h'(u_{2})=h'(u_{1})=1. \end{aligned}$$

(34f)

Fig. 4

Figures (a)–(f) are for Cases (34a), (34b), (34c), (34d), (34e) and (34f), respectively

Since we assume $c>c_{1}^{*},$ we prove (34) for $c\in (c_{1}^{*},c_{2}^{*})$, $c=c_{2}^{*}$, and $c>c_{2}^{*}$, respectively, as in the following steps.

i) For the case $c\in (c_{1}^{*},c_{2}^{*})$, we know $B>0.$ Set

$$\begin{aligned} F(u)=u^{\alpha }\left( (u-A)^{2}+B\right) ^{\frac{\beta }{2}}e^{\frac{\gamma }{\sqrt{B}} \tan ^{-1}\left( \frac{u-A}{\sqrt{B}}\right) }. \end{aligned}$$

Simple calculation yields

$$\begin{aligned} F'(u)=\left( \frac{\alpha }{u}+\frac{\beta (u-A)+\gamma }{((u-A)^{2}+B)}\right) F(u). \end{aligned}$$

From (22), we have

$$\begin{aligned} F({\bar{h}}(u))=F(u)e^{-\xi {\bar{T}}}. \end{aligned}$$

(35)

Taking the derivative with respect to u in (35) yields

$$\begin{aligned} F'({\bar{h}}(u)){\bar{h}}'(u)=F'(u)e^{-\xi {\bar{T}}}, \end{aligned}$$

which implies that

$$\begin{aligned} \left( \frac{\alpha }{{\bar{h}}(u)}+\frac{\beta ({\bar{h}}(u)-A)+\gamma }{(({\bar{h}}(u)-A)^{2}+B)} \right) {\bar{h}}'(u)=\left( \frac{\alpha }{u}+\frac{\beta (u-A)+\gamma }{((u-A)^{2}+B)}\right) , \end{aligned}$$

or, equivalently,

$$\begin{aligned} {\bar{h}}'(u)=\frac{{\bar{h}}(u)(({\bar{h}}(u)-A)^{2}+B)(u+2c)}{u((u-A)^{2}+B)({\bar{h}}(u)+2c)}. \end{aligned}$$

Taking the derivative with respect to u in (25), we obtain

$$\begin{aligned} \frac{h'(u)}{h(u)(M-h(u))}=\frac{{\bar{h}}'(u)}{{\bar{h}}(u)(M-{\bar{h}}(u))}. \end{aligned}$$

(36)

By simple algebra, we have

$$\begin{aligned} h'(u)=\frac{h(u)\left[ \left( \left( mM-A(m-1)\right) h(u)-MA\right) ^{2}+B(M+(m-1)h(u))^{2}\right] (u+2c)}{uM\left[ (u-A)^{2}+B\right] \left[ 2Mc+(mM-2c(1-m))h(u)\right] },\nonumber \\ \end{aligned}$$

(37)

where $m=e^{-M\xi (T-{\bar{T}})}.$ We further obtain

$$\begin{aligned} h'(u_{0})= & {} \dfrac{\left[ \left( (mM-A(m-1))u_{0}-MA\right) ^{2}+B(M+(m-1) u_{0})^{2}\right] (u_{0}+2c)}{M\left[ (u_{0}-A)^{2}+B\right] \left[ 2Mc+(mM-2c(1-m)) u_{0}\right] },\nonumber \\ h'(u_{1})= & {} \dfrac{\left[ \left( (mM-A(m-1))u_{1}-MA\right) ^{2}+B(M+(m-1) u_{1})^{2}\right] (u_{1}+2c)}{M\left[ (u_{1}-A)^{2}+B\right] \left[ 2Mc+(mM-2c(1-m)) u_{1}\right] },\nonumber \\ h'(u_{2})= & {} \dfrac{\left[ \left( (mM-A(m-1))u_{2}-MA\right) ^{2}+B(M+(m-1) u_{2})^{2}\right] (u_{2}+2c)}{M\left[ (u_{2}-A)^{2}+B\right] \left[ 2Mc+(mM-2c(1-m)) u_{2}\right] }.\nonumber \\ \end{aligned}$$

(38)

Case (34a) can be equivalently written as

$$\begin{aligned} \begin{aligned}&l_{1}u^{2}_{0}+l_{2}u_{0}+l_{3}\le 0,\\&l_{1}u^{2}_{1}+l_{2}u_{1}+l_{3}\le 0,\\&l_{1}u^{2}_{2}+l_{2}u_{2}+l_{3}\ge 0, \end{aligned} \end{aligned}$$

case (34b) can be equivalently written as

$$\begin{aligned} \begin{aligned}&l_{1}u^{2}_{0}+l_{2}u_{0}+l_{3}=0,\\&l_{1}u^{2}_{1}+l_{2}u_{1}+l_{3}\le 0, \end{aligned} \end{aligned}$$

case (34c) can be equivalently written as

$$\begin{aligned} \begin{aligned}&l_{1}u^{2}_{0}+l_{2}u_{0}+l_{3}\le 0,\\&l_{1}u^{2}_{1}+l_{2}u_{1}+l_{3}=0, \end{aligned} \end{aligned}$$

case (34d) can be equivalently written as

$$\begin{aligned} \begin{aligned}&l_{1}u^{2}_{0}+l_{2}u_{0}+l_{3}=0,\\&l_{1}u^{2}_{1}+l_{2}u_{1}+l_{3}\le 0,\\&l_{1}u^{2}_{2}+l_{2}u_{2}+l_{3}=0, \end{aligned} \end{aligned}$$

case (34e) can be equivalently written as

$$\begin{aligned} \begin{aligned}&l_{1}u^{2}_{0}+l_{2}u_{0}+l_{3}=0,\\&l_{1}u^{2}_{1}+l_{2}u_{1}+l_{3}=0,\\&l_{1}u^{2}_{2}+l_{2}u_{2}+l_{3}\le 0, \end{aligned} \end{aligned}$$

and case (34f) can be equivalently written as

$$\begin{aligned} \begin{aligned}&l_{1}u^{2}_{0}+l_{2}u_{0}+l_{3}\le 0,\\&l_{1}u^{2}_{1}+l_{2}u_{1}+l_{3}=0,\\&l_{1}u^{2}_{2}+l_{2}u_{2}+l_{3}=0, \end{aligned} \end{aligned}$$

where

$$\begin{aligned}&l_{1}=(A^{2}+B)(1-m)+(2mMA+2cM-mM^{2}), \end{aligned}$$

(39)

$$\begin{aligned}&l_{2}=[2c(A^{2}+B)-4cMA](1-m)-[2cM^{2}(m+1)+2M(A^{2}+B)], \end{aligned}$$

(40)

$$\begin{aligned}&l_{3}=[-2cM(A^{2}+B)+4M^{2}Ac+M^{2}(A^{2}+B)]. \end{aligned}$$

(41)

Set

$$\begin{aligned} P(u)=l_{1}u^{2}+l_{2}u+l_{3}. \end{aligned}$$

(42)

Then,

$$\begin{aligned} P(M)=-(A^{2}+B)mM^{2}-2cmM(A^{2}+B)+(mM^{3}+2cmM^{2})(-M+2A).\nonumber \\ \end{aligned}$$

(43)

Since $\frac{4s^*_{h}}{3}<s_{h}\le 1$ and $c\in (c_{1}^{*},c_{2}^{*}),$ $-M+2A<0,$ $A^{2}+B>0.$ Hence, we have $P(M)<0.$

Now for $c\in (c_{1}^{*},c_{2}^{*})$, we consider $c\in (c^{*},c_{2}^{*})$, $c=c^{*},$ and $c\in (c_{1}^{*},c^{*})$, respectively.

ia) If $c\in (c^{*},c_{2}^{*}),$ then

$$\begin{aligned} P(0)=l_{3}=\frac{(a-2\mu )[-8\xi ^{2}c^{2}-4a\xi s_{h}c +as_{h}(a-2\mu )]c}{4\xi ^3}<0. \end{aligned}$$

Hence, P(u) is a convex quadratic polynomial with $l_{1}<0,$ $l_{2}>0$ and $l_{3}<0.$ On the other hand,

$$\begin{aligned} 0>2cl_{1}-l_{2}=4cMA+4c^{2}M+2cM^{2}+2M(A^{2}+B)=\frac{2M(\xi c^{2}+as_{h}c)}{\xi }>0, \end{aligned}$$

which leads to a contradiction. Thus, cases (34a)-(34f) cannot happen.

ib) If $c=c^{*},$ then $l_{3}=0,$ which implies that $P(0)=0.$ Combined with $P(M)<0$, we immediately know that cases (34a)-(34f) are impossible.

ic) Now, we consider the case $c\in (c_{1}^{*},c^{*}).$ In this case, $P(0)>0$  and  $P(M)<0.$ Then, clearly cases (34a), (34c), (34d), (34e) and (34f) are impossible. We then focus on case (34b).

For sufficiently small $\varepsilon >0,$ we have $m(1+\varepsilon )<1$ and

$$\begin{aligned} c<\frac{-as_{h}+(a-2\mu )(1-x)+\sqrt{[as_{h}-(a-2\mu )(1-x)]^{2}+2as_{h}(a-2\mu )x}}{4\xi },\nonumber \\ \end{aligned}$$

(44)

where $x=\frac{1-m-m\varepsilon }{(1-m)(1+\varepsilon )}$. Furthermore, fix $\varepsilon >0,$ such that $h(u)-(1+\varepsilon )u$ has three roots ${\tilde{u}}_{1},$ ${\tilde{u}}_{2}$ and ${\tilde{u}}_{3}$ that satisfy

$$\begin{aligned} 0<{\tilde{u}}_{1}<u_{0}<{\tilde{u}}_{2}<{\tilde{u}}_{3}<u_{1} \end{aligned}$$

and

$$\begin{aligned} h'({\tilde{u}}_{1})\le 1+\varepsilon ,~h'({\tilde{u}}_{2})\ge 1+\varepsilon ,~h'({\tilde{u}}_{3})\le 1 +\varepsilon . \end{aligned}$$

From (37), we have

$$\begin{aligned}&\dfrac{h'({\tilde{u}}_{i})}{(1+\varepsilon )({\tilde{u}}_{i}+2c)}\nonumber \\&\quad =\dfrac{\left[ \left( \left( mM-A(m-1)\right) (1+\varepsilon ){\tilde{u}}_{i}-MA\right) ^{2} +B(M+(m-1)(1+\varepsilon ){\tilde{u}}_{i})^{2}\right] }{M\left[ ({\tilde{u}}_{i}-A)^{2} +B\right] \left[ 2Mc+(mM-2c(1-m))(1+\varepsilon ){\tilde{u}}_{i}\right] },\nonumber \\ \end{aligned}$$

(45)

for $i=1,2,3.$ Similarly, we can obtain that

$$\begin{aligned} \begin{aligned} l_{1\varepsilon }{\tilde{u}}^{2}_{1}+l_{2\varepsilon }{\tilde{u}}_{1}+l_{3\varepsilon }\le 0,\\ l_{1\varepsilon }{\tilde{u}}^{2}_{2}+l_{2\varepsilon }{\tilde{u}}_{2}+l_{3\varepsilon }\le 0,\\ l_{1\varepsilon }{\tilde{u}}^{2}_{3}+l_{2\varepsilon }{\tilde{u}}_{3}+l_{3\varepsilon }\ge 0, \end{aligned} \end{aligned}$$

(46)

where

$$\begin{aligned} \begin{aligned} l_{1\varepsilon }=&(A^{2}+B)(1-m)^{2}(1+\varepsilon )^{2}\\&+(1+\varepsilon )[2mMA(1-m)(1+\varepsilon )+2cM-mM^{2}(1-m)(1-m-m\varepsilon )],\\ l_{2\varepsilon }=&[2c(A^{2}+B)(1-m)(1+\varepsilon ) -4cMA(1-m-m\varepsilon )](1-m)(1+\varepsilon )\\&-[2cM^{2}(1-m-m\varepsilon )(m+m\varepsilon +1)+2M(A^{2}+B)(1-m)], \end{aligned} \end{aligned}$$

and

$$\begin{aligned} l_{3\varepsilon }= & {} [-2cM(A^{2}+B)(1-m)(1+\varepsilon )+4M^{2}Ac(1-m-m\varepsilon )\\&+M^{2}(A^{2}+B)(1-m-m\varepsilon )]. \end{aligned}$$

Set

$$\begin{aligned} P_{\varepsilon }(u)=l_{1\varepsilon }u^{2}+l_{2\varepsilon }u+l_{3\varepsilon }. \end{aligned}$$

(47)

From (44), we have

$$\begin{aligned} P_{\varepsilon }(0)=l_{3\varepsilon }>0. \end{aligned}$$

(48)

and from (46), we see

$$\begin{aligned} P_{\varepsilon }({\tilde{u}}_{1})\le 0,~P_{\varepsilon }({\tilde{u}}_{2})\le 0,~P_{\varepsilon }({\tilde{u}}_{3})\ge 0. \end{aligned}$$

(49)

It thus follows that the quadratic polynomial $P_{\varepsilon }(u)$ has a root in each of the three intervals $(0,{\tilde{u}}_{1}],$ $({\tilde{u}}_{1},{\tilde{u}}_{2}]$ and $({\tilde{u}}_{2},{\tilde{u}}_{3}]$. It is impossible.

ii) For the case $c=c_{2}^{*},$ differentiating (24) with respect to u gives

$$\begin{aligned} \left( \frac{\alpha }{{\bar{h}}(u)}+\frac{\beta }{({\bar{h}}(u)-A)}+\frac{\gamma }{({\bar{h}}(u)-A)^{2}} \right) {\bar{h}}'(u)=\left( \frac{\alpha }{u}+\frac{\beta }{(u-A)}+\frac{\gamma }{(u-A)^{2}} \right) ,\nonumber \\ \end{aligned}$$

(50)

or, equivalently,

$$\begin{aligned} {\bar{h}}'(u)=\frac{{\bar{h}}(u)(({\bar{h}}(u)-A)^{2})(u+2c)}{u((u-A)^{2})({\bar{h}}(u)+2c)}. \end{aligned}$$

It follows from (36) and a series of computations that

$$\begin{aligned} h'(u)=\frac{h(u)\left[ \left( \left( mM-A(m-1)\right) h(u)-MA\right) ^{2}\right] (u+2c)}{uM\left[ (u-A)^{2}\right] \left[ 2Mc+(mM-2c(1-m))h(u)\right] }. \end{aligned}$$

(51)

Set

$$\begin{aligned} {\widetilde{P}}(u)={\widetilde{l}}_{1}u^{2}+{\widetilde{l}}_{2}u+{\widetilde{l}}_{3}, \end{aligned}$$

(52)

where

$$\begin{aligned} \begin{aligned}&{\widetilde{l}}_{1}=A^{2}(1-m)+(2mMA+2cM-mM^{2}),\\&{\widetilde{l}}_{2}=[2cA^{2}-4cMA](1-m)-[2cM^{2}(m+1)+2MA^{2}],\\&{\widetilde{l}}_{3}=-2cMA^{2}+4M^{2}Ac+M^{2}A^{2}<0~\hbox {when}~c=c_{2}^{*}. \end{aligned} \end{aligned}$$

(53)

We can get the contradiction by a similar argument as the proof of ia) .

iii) For the case $c>c_{2}^{*},$ it is easy to see that $B<0$. Set

$$\begin{aligned} {\widetilde{F}}(u)=u^{\theta }(u-E^{-}_{1}(c))^{\kappa }(u-E^{-}_{2}(c))^{\sigma } \text {for}~u\in (0,M). \end{aligned}$$

(54)

Then,

$$\begin{aligned} {\widetilde{F}}'(u)=[\frac{\theta }{u}+\frac{\kappa }{u-E^{-}_{1}(c)} +\frac{\sigma }{u-E^{-}_{2}(c)}]{\widetilde{F}}(u) ~\text {for}~u\in (0,M). \end{aligned}$$

(55)

From (23), we see

$$\begin{aligned} {\widetilde{F}}({\bar{h}}(u))={\widetilde{F}}(u)e^{-\xi {\bar{T}}}. \end{aligned}$$

(56)

Taking the derivative with respect to u in (56) yields

$$\begin{aligned} {\widetilde{F}}'({\bar{h}}(u)){\bar{h}}'(u)={\widetilde{F}}'(u)e^{-\xi {\bar{T}}}, \end{aligned}$$

which implies that

$$\begin{aligned}{}[\frac{\theta }{{\bar{h}}(u)}+\frac{\kappa }{{\bar{h}}(u)-E^{-}_{1}(c)} +\frac{\sigma }{{\bar{h}}(u)-E^{-}_{2}(c)}]{\bar{h}}'(u)=[\frac{\theta }{u} +\frac{\kappa }{u-E^{-}_{1}(c)}+\frac{\sigma }{u-E^{-}_{2}(c)}], \end{aligned}$$

or, equivalently,

$$\begin{aligned} \left[ \frac{{\bar{h}}(u)+2c}{{\bar{h}}(u)({\bar{h}}(u)-E^{-}_{1}(c))({\bar{h}}(u)-E^{-}_{2}(c))} \right] {\bar{h}}'(u)=\left[ \frac{u+2c}{u(u-E^{-}_{1}(c))(u-E^{-}_{2}(c))}\right] \end{aligned}$$

Similarly, (36) and a direct calculation gives

$$\begin{aligned} \begin{aligned}&\dfrac{h'(u)}{h(u)(u+2c)[-ME^{-}_{1}(c)+(mM+(1-m)E^{-}_{1}(c))h(u)]}\\&=\dfrac{[-ME^{-}_{2}(c)+(mM+(1-m)E^{-}_{2}(c))h(u)]}{uM(u-E^{-}_{1}(c))(u-E^{-}_{2} (c))[2cM+(mM-2c(1-m))h(u)]}, \end{aligned} \end{aligned}$$

(57)

Hence, set

$$\begin{aligned} Q(u)=q_{1}u^{2}+q_{2}u+q_{3}, \end{aligned}$$

(58)

where

$$\begin{aligned} q_{1}=-M^{2}m+mM(E_{1}(c)+E_{2}(c))+(1-m)E^{-}_{1}(c)E^{-}_{2}(c)+2cM,\quad \end{aligned}$$

(59)

$$\begin{aligned} \begin{array}{ll} q_{2}=&{}-2cM^{2}(m+1)-2cM(1-m)(E^{-}_{1}(c)+E^{-}_{2}(c))\\ &{}+[2c(1-m)-2M]E^{-}_{1}(c)E^{-}_{2}(c), \end{array}\quad \end{aligned}$$

(60)

$$\begin{aligned} q_{3}=M^{2}E^{-}_{1}(c)E^{-}_{2}(c)+2cM^{2}(E^{-}_{1}(c)+E^{-}_{2}(c))-2cME^{-}_{1}(c)E^{-}_{2}(c),\quad \end{aligned}$$

(61)

Furthermore, since $c>c_{2}^{*},$ it immediately implies

$$\begin{aligned} \begin{aligned} q_{3}=l_{3}=\frac{(a-2\mu )[-8\xi ^{2}c^{3}-4a\xi s_{h}c^{2}+as_{h}c(a-2\mu )]}{4\xi ^{3}}<0. \end{aligned} \end{aligned}$$

(62)

Hence, we claim that cases (34a), (34b), (34c), (34d), (34e) and (34f) are impossible by a similar argument as the proof of ia) . $\square$

Lemma 5.3

Assume $T=T^{*}.$ Then, the following statements hold.

• (a) Assume that $\frac{4s^*_{h}}{3}<s_{h}\le 1$. Then,

  • (1) If $c_{1}^{*}<c<c^{*},$ Eq. (2) has a unique T-periodic solution.

  • (2) If $c\ge c^{*}$, $h(u)<u$ for all $u>0$.

• (b) Assume that $s_{h}\le \frac{4s^*_{h}}{3}$ and $c>\widehat{c^*},$ then $h(u)<u$ for all $u>0.$

Proof

(a) (1) Since $c_{1}^{*}<c<c^{*},$ then $B>0.$ Hence, from (22) and (25), we see

$$\begin{aligned} \frac{h(u)}{u}=\frac{M-h(u)}{M-{\bar{h}}(u)}\cdot \frac{\left( (u-A)^{2}+B\right) ^{\frac{\beta }{2\alpha }}e^{\frac{\gamma }{\alpha \sqrt{B}}\tan ^{-1}\left( \frac{u-A}{\sqrt{B}}\right) }}{\left( ({\bar{h}}(u)-A)^{2}+B\right) ^{\frac{\beta }{2\alpha }}e^{\frac{\gamma }{\alpha \sqrt{B}} \tan ^{-1}\left( \frac{{\bar{h}}(u)-A}{\sqrt{B}}\right) }}. \end{aligned}$$

(63)

Set

$$\begin{aligned} \begin{aligned} G(u)=(M-u)^{\alpha }\left( (u-A)^{2}+B\right) ^{\frac{\beta }{2}}e^{\frac{\gamma }{\sqrt{B}} \tan ^{-1}\left( \frac{u-A}{\sqrt{B}}\right) }>0, \end{aligned} \end{aligned}$$

(64)

for $u\in (0,M)$. Then,

$$\begin{aligned} \frac{h(u)}{u}=\frac{M-h(u)}{M-u}\cdot \left( \frac{G(u)}{G({\bar{h}}(u))}\right) ^{\frac{1}{\alpha }}. \end{aligned}$$

(65)

Thus, we have $h(u)=u$ if and only if $G(u)=G({\bar{h}}(u))$.

Since $h(M)<M,$ the main idea of this proof is to determine $h(u)>u$ for $u\in (0,M)$.

Taking the derivative of G(u), we obtain

$$\begin{aligned} \begin{aligned} G'(u)&=\left[ \frac{(\beta M-1)u+M-2\beta AM-2c}{(M-u)[(u-A)^{2}+B]}\right] G(u)\\&=\frac{(\beta M-1)}{(M-u)[(u-A)^{2}+B]}(u-u^{*})G(u)\\&=\frac{-J_{2}(c)}{(M-u)[(u-A)^{2}+B]}(u-u^{*})G(u). \end{aligned} \end{aligned}$$

(66)

Here $u^{*}$ is defined by

$$\begin{aligned} \begin{aligned} u^{*}=\frac{J_{1}(c)}{J_{2}(c)}=\frac{M-2\beta AM-2c}{1-\beta M}, \end{aligned} \end{aligned}$$

(67)

where

$$\begin{aligned} J_{1}(c)=M-2\beta AM-2c=\frac{-8\xi ^{2}c^{2}-4a\xi s_{h}c+as_{h}(a-2\mu )}{2\xi (2\xi c+2\mu -a(1-s_{h}))} \end{aligned}$$

and

$$\begin{aligned} J_{2}(c)=1-\beta M =\frac{2\xi c+as_{h}}{2\xi c+2\mu -a(1-s_{h})}. \end{aligned}$$

Clearly, $J_{1}(c)>0$ and $J_{2}(c)>0$ for $\frac{4s^*_{h}}{3}<s_{h}\le 1$, and $c_{1}^{*}<c<c^{*}.$ Thus, $u^{*}>0$ for $c_{1}^{*}<c<c^{*}$.

If $c_{1}^{*}<c<c^{*},$ then G(u) is strictly increasing for $u\in (0,u^{*})$, and strictly decreasing for $u\in (u^{*},M),$ which immediately implies that $G(u)>G({\bar{h}}(u))$ for $u\in (0,u^{*})$.

Simple calculation yields

$$\begin{aligned} \frac{h(u)}{u}=\frac{M-h(u)}{M-u}\cdot \left( \frac{G(u)}{G({\bar{h}}(u))}\right) ^{\frac{1}{\alpha }}>\frac{M-h(u)}{M-u}~\hbox {for}~ u\in (0,u^{*}), \end{aligned}$$

(68)

which implies that $h(u)>u$ for $u\in (0,u^{*})$. Therefore, there must be $u_{0}\in (0,M)$ such that

$$\begin{aligned} h(u_{0})=u_{0}~\text {and}~h(u)>u, ~\text {for}~u\in (0,u_{0}). \end{aligned}$$

(69)

We now prove the uniqueness of the T-periodic solution of Eq. (2) by contradiction. Assume that Eq. (2) has another T-periodic solution $u_{1}\in (u_{0},M)$ such that

$$\begin{aligned} h(u_{1})=u_{1}~\text {and}~h(u)<u, ~\text {for}~u\in (u_{1},M). \end{aligned}$$

(70)

Based on the properties of function G(u), we have

$$\begin{aligned} u^{*}<u_{0}<u_{1}~\text {and}~u^{*}>{\bar{h}}(u_{0})>{\bar{h}}(u_{1}), \end{aligned}$$

(71)

and from the properties of function ${\bar{h}}(u)$, we have

$$\begin{aligned} u_{0}<u_{1}~\text {and}~{\bar{h}}(u_{0})<{\bar{h}}(u_{1}), \end{aligned}$$

(72)

which leads to a contradiction.

• (a) (2). The proof of case (2) of part (a) is similar to the proof of part (b) that follows. Thus, we omit its proof and focus on part (b) shown below.

• (b) . For $s_{h}\in (s^*_{h},\frac{4s^*_{h}}{3})$, if $c\in (\widehat{c^*},c_{1}^{*})~\hbox {or}~(c_{2}^{*},+\infty ),$ then $B<0$. From (23) and (25), we obtain

  $$\begin{aligned} \frac{h(u)}{u}=\frac{M-h(u)}{M-{\bar{h}}(u)}\cdot \left( \frac{u-E^{-}_{1}(c)}{{\bar{h}}(u)-E^{-}_{1}(c)}\right) ^{\frac{\kappa }{\alpha }}\cdot \left( \frac{u-E^{-}_{2}(c)}{{\bar{h}}(u)-E^{-}_{2}(c)}\right) ^{\frac{\sigma }{\alpha }}. \end{aligned}$$

  (73)

If $c=c_{1}^{*}~\hbox {or}~c=c_{2}^{*},$ then $B=0$. Then, from (24) and (25), we have

$$\begin{aligned} \frac{h(u)}{u}=\frac{M-h(u)}{M-{\bar{h}}(u)}\cdot \left( \frac{u-A}{{\bar{h}}(u)-A} \right) ^{\frac{\beta }{\alpha }}\cdot \frac{e^{-\frac{\gamma }{\alpha (u-A)}}}{e^{-\frac{\gamma }{\alpha ({\bar{h}}(u)-A)}}}. \end{aligned}$$

(74)

If $c\in (c_{1}^{*},c_{2}^{*}),$ then $B>0$. Set

$$\begin{aligned} G_{1}(u)=(M-u)^{\alpha }\left( u-E^{-}_{1}(c)\right) ^{\kappa }\left( u-E^{-}_{2}(c)\right) ^{\sigma }>0, \end{aligned}$$

(75)

for $u\in (0,M)$ and $c\in (\widehat{c^*},c_{1}^{*})\cup (c_{2}^{*},+\infty )$, and

$$\begin{aligned} G_{2}(u)=(M-u)^{\alpha }\left( u-A\right) ^{\beta }e^{-\frac{\gamma }{(u-A)}}>0, \end{aligned}$$

(76)

for $u\in (0,M)$ and $c=c_{1}^{*}$, or $c=c_{2}^{*}$.

Taking the derivative of $G_{1}(u)$, we obtain,

$$\begin{aligned}&\frac{(M-u)(u-E^{-}_{1}(c))(u-E^{-}_{2}(c))G'_{1}(u)}{G_{1}(u)}\\&=[(M-u)(u-E^{-}_{1}(c))(u-E^{-}_{2}(c))]\left( \frac{-\alpha }{M-u}+\frac{\kappa }{u-E^{-}_{1}(c)}+\frac{\sigma }{u-E^{-}_{2}(c)}\right) \\&= \left[ \kappa (M-E^{-}_{1}(c))+\sigma (M-E^{-}_{2}(c))\right] u-[\frac{-2cM(E^{-}_{1}(c)+E^{-}_{2}(c))}{E^{-}_{1}(c)E^{-}_{2}(c)}-M+2c]\\&=\left[ \frac{-2\xi c-as_{h}}{2\xi c+2\mu -a(1-s_{h})}\right] u+\frac{-8\xi ^{2}c^{2}-4a\xi s_{h}c+as_{h}(a-2\mu )}{2\xi (2\xi c+2\mu -a(1-s_{h}))}\\&=-J_{2}(c)(u-u^{*}), \\ ~\text {for}~u\in&(0,M)~\text {and}~c\in ({\widehat{c}}^*,c_{1}^{*})~\hbox {or}~(c_{2}^{*},+\infty ). \end{aligned}$$

Taking the derivative of $G_{2}(u)$, we obtain,

$$\begin{aligned} \begin{aligned} G'_{2}(u)&=\left( \frac{-\alpha }{M-u}+\frac{\beta }{u-A}+\frac{\gamma }{(u-A)^{2}}\right) G_{2}(u)\\&=\frac{(\beta M-1)}{(M-u)(u-A)^{2}}(u-u^{*})G_{2}(u)\\&=\frac{-J_{2}(c)}{(M-u)(u-A)^{2}}(u-u^{*})G_{2}(u), \end{aligned} \end{aligned}$$

for $u\in (0,M)$ and $c=c_{1}^{*}$, or $c=c_{2}^{*}.$

Also, from (66)

$$\begin{aligned} \begin{aligned} G'(u)&=\frac{-J_{2}(c)}{(M-u)[(u-A)^{2}+B]}(u-u^{*})G(u), \end{aligned} \end{aligned}$$

for $u\in (0,M)$, and $c\in (c_{1}^{*}, c_{2}^{*})$.

Moreover, since $c^{*}<\widehat{c^*}<c_{1}^{*}$ for $s_{h}\in (s^*_{h},\frac{4s^*_{h}}{3})$, we have $u^{*}<0$, and $G_{1}(u),$ $G_{2}(u)$ and G(u) are all strictly decreasing for $u\in (0,M)$ and $c>\widehat{c^*}.$ Based on these analyses, it is easy to see that $G(u)<G({\bar{h}}(u))$ for $u\in (0,M)$ and $c>\widehat{c^*}.$

Direct calculation yields

$$\begin{aligned} \begin{aligned} \frac{h(u)}{u}=\frac{M-h(u)}{M-u}\cdot \left( \frac{G(u)}{G({\bar{h}}(u))}\right) ^{\frac{1}{\alpha }} <\frac{M-h(u)}{M-u}, \end{aligned} \end{aligned}$$

(77)

for $u\in (0,M)$, which implies that $h(u)<u$ for $u\in (0,M)$ and $c\in (c_{1}^{*},c^{*})$.

For the case $s_{h}={4s^*_{h}}/{3},$ we have $c^{*}=\widehat{c^*}=c_{1}^{*}.$ Hence, the proof can be done in a similar fashion as the proof for case $s_{h}\in (s^*_{h},\frac{4s^*_{h}}{3})$, for $c\in (c_{2}^{*},+\infty )$ and $c\in (c_{1}^{*},c_{2}^{*})$ .

If $s_{h}<s^*_{h}$, we have $B<0$, and can prove our result by a similar argument as the proof for the case $s_{h}\in (s^*_{h},\frac{4s^*_{h}}{3})$, for $c\in (\widehat{c^*},c_{1}^{*})$ or $(c_{2}^{*},+\infty )$ . We omit the details here. The proof of Lemma 5.3 is complete. $\square$

Lemma 5.4

Assume $T<T^{*}$. Then, $h(u)<u$ for all $u>0$, if one of the following conditions is satisfied.

• (a) $\frac{4s^*_{h}}{3}<s_{h}\le 1$ and $c\ge c^{*}$;

• (b) $s_{h}\le \frac{4s^*_{h}}{3}$ and $c>\widehat{c^*}.$

Proof

We only prove (a). The proof for (b) is similar and will be omitted.

It follows from (28) that $\lim \limits _{u\rightarrow 0}\frac{h(u)}{u}<1$ for $T<T^{*}$. Hence, there is sufficiently small $\delta >0$ such that

$$\begin{aligned} \begin{aligned} h(u)<u, \text {for}~u\in (0,\delta ). \end{aligned} \end{aligned}$$

(78)

Since $c\ge c^{*}$, solution $w(t)=w(t;0,M)$ is strictly decreasing for $t\in (0,{\bar{T}}]$. Hence ${\bar{h}}(M)<M$ which implies $h(M)<M$. Assume that there exists ${\tilde{u}}\in (\delta ,M)$ such that $h({\tilde{u}})\ge {\tilde{u}}.$ Then, there must be $u^{'}\in (0,{\tilde{u}}]$ such that

$$\begin{aligned} \begin{aligned} h(u^{'})=u^{'}, h'(u^{'})\ge 1. \end{aligned} \end{aligned}$$

(79)

Thus, from (42), (52) and (58), we see

$$\begin{aligned} \begin{aligned} l_{1}u^{'2}+l_{2}u^{'}+l_{3}\ge 0, ~\text {for}~ c\in [c^{*},c_{2}^{*}),\\ {\widetilde{l}}_{1}u^{'2}+{\widetilde{l}}_{2}u^{'}+{\widetilde{l}}_{3}\ge 0, ~\text {for}~ c=c_{2}^{*},\\ q_{1}u^{'2}+q_{2}u^{'}+q_{3}\ge 0 ~\text {for}~ c>c_{2}^{*}. \end{aligned} \end{aligned}$$

(80)

For $c\in [c^{*},c_{2}^{*})$, further calculation gives

$$\begin{aligned} \begin{array}{l}[(A^{2}+B)+2cM]u^{'2}+[2c(A^{2}+B)-4cMA-2cM^{2}-2M(A^{2}+B)]u^{'}+l_{3}\\ \ge [m(A^{2}+B)-2mMA+mM^{2}]u^{'2}+m[2c(A^{2}+B)-4cMA+2cM^{2}]u^{'}>0. \end{array} \end{aligned}$$

Set

$$\begin{aligned} {\tilde{G}}_{1}(u)= & {} [(A^{2}+B)+2cM]u^{2}+[2c(A^{2}+B)-4cMA-2cM^{2}\\&-2M(A^{2}+B)]u+l_{3}. \end{aligned}$$

Hence, ${\tilde{G}}_{1}(u^{'})>0.$

The quadratic polynomial ${\tilde{G}}_{1}(u)$ is concave up. Since ${\tilde{G}}_{1}(0)=l_{3}\le 0$ for $c\ge c^{*},$ ${\tilde{G}}_{1}(M)=0$ and ${\tilde{G}}_{1}(u)<0$ for $u\in (0,M).$ Thus, it contradicts the assumption of ${\tilde{G}}_{1}(u^{'})>0.$

For the case $c=c_{2}^{*}$, we can use a proof similar to the above. Thus, we omit it.

If $c>c_{2}^{*}$, we obtain

$$\begin{aligned}&(E^{-}_{1}(c)E^{-}_{2}(c)+2cM)u^{'2}+[2cE^{-}_{1}(c)E^{-}_{2}(c)-2cM(E^{-}_{1}(c) +E^{-}_{2}(c))]u^{'}+q_{3}\nonumber \\&\quad \ge [M^{2}m-mM(E^{-}_{1}(c)+E^{-}_{2}(c)) +mE^{-}_{1}(c)E^{-}_{2}(c)]u^{'2}\nonumber \\&\qquad +[2cM^{2}(m+1)-2cmM(E^{-}_{1}(c)+E^{-}_{2}(c))\nonumber \\&\qquad +2cmE^{-}_{1}(c)E^{-}_{2}(c) +2ME^{-}_{1}(c)E^{-}_{2}(c)]u^{'}\nonumber \\&\quad >0. \end{aligned}$$

(81)

Set

$$\begin{aligned} {\tilde{G}}_{2}(u)= & {} (E^{-}_{1}(c)E^{-}_{2}(c)+2cM)u^{2}+[2cE^{-}_{1}(c)E^{-}_{2}(c)\nonumber \\&-2cM(E^{-}_{1}(c)+E^{-}_{2}(c))]u+q_{3}. \end{aligned}$$

Hence, ${\tilde{G}}_{2}(u^{'})>0$.

Clearly, quadratic polynomial ${\tilde{G}}_{2}(u)$ is concave up. Since ${\tilde{G}}_{2}(0)=q_{3}=l_{3}<0$ for $c>c_{2}^{*},$ ${\tilde{G}}_{2}(M)=0$ and ${\tilde{G}}_{2}(u)<0$ for $u\in (0,M).$ Thus, it contradicts the assumption of ${\tilde{G}}_{2}(u^{'})>0.$ $\square$

Proof of Theorem 3.1

(a) Assume that $E_{0}$ is locally asymptotically stable. Since $h_{n}(u_{0})=w(nT;0,u_{0}),$ $n=0,1,2\cdots$, there exists $\delta (\varepsilon )>0$ small enough such that if $|u_{0}|<\delta (\varepsilon ),$ then $\lim _{n\rightarrow \infty }h_{n}(u_{0})=0.$

Now, we prove $T<T^{*}$ by contradiction. Suppose $T\ge T^{*}.$ From (28), we see, if $T>T^{*}$, then there is $\delta _{1}>0$ small enough such that $h(u_{0})>u_{0},$ for $u_{0}\in (0,\delta _{1}).$ If $T=T^{*}$, then from the proof of Lemma 5.3, we see that there is $\delta _{2}>0$ small enough such that $h(u_{0})>u_{0},$ for $u_{0}\in (0,\delta _{2})$, which implies that $h_{n}(u)$ is strictly increasing and $\lim \limits _{n\rightarrow \infty }h_{n}(u_{0})\ne 0$ for $u\in (0,{\hat{\delta }}),$ where ${\hat{\delta }}=\min \{\delta _{1},\delta _{2}\},$ a contradiction. Hence $T<T^{*}.$

If $T<T^{*}$, then it follows from (28) that $h^{'}(0)=e^{M\xi (T-T^{*})}<1$ and furthermore, there is sufficiently small $\delta >0$ such that

$$\begin{aligned} \begin{aligned} h(u_{0})<u_{0}, \text {for}~u_{0}\in (0,\delta ). \end{aligned} \end{aligned}$$

(82)

Hence, the spectral radius of h(0) is less than 1, which implies that the origin $E_{0}$ of Eq. (2) is locally stable.

We next prove that every solution of (2) goes to zero. That is, for above $\delta ,$ if $0<u_{0}<\delta ,$ then

$$\begin{aligned} \lim _{t\rightarrow \infty }w(t;0,u_{0})=0~\text {or}~\lim _{n\rightarrow \infty }h_{n}(u_{0})=0. \end{aligned}$$

It follows from (82) and Lemma 5.1 that $\{h_{n}(u_{0})\}^{\infty }_{0}$ is strictly decreasing, and thus there exists $l\ge 0$ such that $\lim _{n\rightarrow \infty }h_{n}(u_{0})=l.$ If $l\ne 0,$ then we must have

$$\begin{aligned} \begin{aligned} h(l)=l, \text {for}~l\in (0,\delta ). \end{aligned} \end{aligned}$$

(83)

This is contradictory to (82).

(b) We assume that Eq. (2) has a unique globally asymptotically stable T-periodic solution. Then, $T\ge T^{*}$ can be justified from the above conclusion. We now show that if $T\ge T^{*}$, then Eq. (2) has a unique globally asymptotically stable T-periodic solution.

Based on Lemma 5.2 and 5.3, we denote the unique T-periodic solution of Eq. (2) by

$$\begin{aligned} {\bar{w}}(t):=w(t;0,{\bar{u}}),~\text {for} ~{\bar{u}}\in (0,M). \end{aligned}$$

We then show that ${\bar{w}}(t)$ is stable.

For any $\varepsilon >0$, choosing $\delta =\varepsilon$, we claim that $|u-{\bar{u}}|<\delta$ implies

$$\begin{aligned} |w(t)-{\bar{w}}(t)|<\varepsilon ,~\text {for}~t\ge 0. \end{aligned}$$

(84)

We show (84) by contradiction.

Suppose that (84) is not true. Then, there exists ${\bar{t}}>0$ such that

$$\begin{aligned} |w(t)-{\bar{w}}(t)|<\varepsilon , \end{aligned}$$

for $t\in [0,{\bar{t}})$, and $|w({\bar{t}})-{\bar{w}}({\bar{t}})|=\varepsilon$. Without loss of generality, we assume that

$$\begin{aligned} w({\bar{t}})-{\bar{w}}({\bar{t}})=\varepsilon . \end{aligned}$$

Then, there must be a nonnegative integer k such that either ${\bar{t}}=kT$, or ${\bar{t}}=kT+{\bar{T}}$, or ${\bar{t}}\in (kT,kT+{\bar{T}})\cup (kT+{\bar{T}},(k+1)T)$.

If ${\bar{t}}=kT,$ then we must have $k\ge 1$ and

$$\begin{aligned} w(t)-{\bar{w}}(t)<\varepsilon ,~\text {for}~t\in [0,kT),~~ w(kT)-{\bar{w}}(kT)=\varepsilon , \end{aligned}$$

which implies that

$$\begin{aligned} w((k-1)T)<{\bar{w}}((k-1)T)+\varepsilon ={\bar{w}}(kT)+\varepsilon =w(kT). \end{aligned}$$

Hence, the series $\{w(kT)\}$ is strictly increasing, which implies that Eq. (2) has another T-periodic solution. This contradicts the uniqueness of the T-periodic solution of Eq. (2).

If ${\bar{t}}=kT+{\bar{T}},$ then we see

$$\begin{aligned} w(t)-{\bar{w}}(t)<\varepsilon , \ \text {for}~t\in [0,kT+{\bar{T}}),\ \text {and}\ w(kT+{\bar{T}})-{\bar{w}}(kT+{\bar{T}})=\varepsilon . \end{aligned}$$

Using (25), we obtain

$$\begin{aligned} \begin{aligned} w(kT)=&\dfrac{Mw((k-1)T+{\bar{T}})}{mM-(1-m)w((k-1)T+{\bar{T}})}\\ <&\dfrac{M({\bar{w}}((k-1)T+{\bar{T}})+\varepsilon )}{mM-(1-m)({\bar{w}}((k-1)T+{\bar{T}})+\varepsilon )}\\ =&\dfrac{M({\bar{w}}(kT+{\bar{T}})+\varepsilon )}{mM-(1-m)({\bar{w}}(kT+{\bar{T}})+\varepsilon )}\\ =&\dfrac{Mw(kT+{\bar{T}})}{mM-(1-m)w(kT+{\bar{T}})}\\ =&w((k+1)T). \end{aligned} \end{aligned}$$

(85)

Hence, a contradiction again.

If ${\bar{t}}\in (kT,kT+{\bar{T}})\cup (kT+{\bar{T}},(k+1)T)$, then $w'({\bar{t}})\ge {\bar{w}}'({\bar{t}})$. We just need to prove that ${\bar{t}}\in (kT+{\bar{T}},(k+1)T)$ is not true, since the proof of the case ${\bar{t}}\in (kT,kT+{\bar{T}})$ is similar.

Integrating Eq. (5) over $({\bar{t}},(k+1)T)$, yields,

$$\begin{aligned} \begin{array}{ll} \dfrac{w((k+1)T)}{M-w((k+1)T)}&{}=\left( \frac{w({\bar{t}})}{M-w({\bar{t}})}\right) e^{M\xi ((k+1)T-{\bar{t}})}\\ &{}=\left( \dfrac{{\bar{w}}({\bar{t}})+\varepsilon }{M-({\bar{w}}({\bar{t}})+\varepsilon )}\right) e^{M\xi ((k+1)T-{\bar{t}})}\\ &{}=\left( \dfrac{{\bar{w}}({\bar{t}}-T)+\varepsilon }{M-({\bar{w}}({\bar{t}}-T)+\varepsilon )}\right) e^{M\xi ((k+1)T-{\bar{t}})}. \end{array} \end{aligned}$$

Similarly, integrating Eq. (5) over $({\bar{t}}-T,kT)$, we obtain

$$\begin{aligned} \left( \frac{w({\bar{t}}-T)}{M-w({\bar{t}}-T)}\right) e^{M\xi ((k+1)T-{\bar{t}})}\\ =\frac{w(kT)}{M-w(kT)}. \end{aligned}$$

Since $w({\bar{t}}-T)<{\bar{w}}({\bar{t}}-T)+\varepsilon ,$ then

$$\begin{aligned} \left( \dfrac{w({\bar{t}}-T)}{M-w({\bar{t}}-T)}\right) <\left( \dfrac{{\bar{w}}({\bar{t}}-T)+\varepsilon }{M-({\bar{w}}({\bar{t}}-T)+\varepsilon )}\right) , \end{aligned}$$

which implies that

$$\begin{aligned} \frac{w((k+1)T)}{M-w((k+1)T)}>\frac{w(kT)}{M-w(kT)}. \end{aligned}$$

Thus, we have $w(kT)<w((k+1)T)$, a contradiction, and hence, ${\bar{w}}(t)$ is stable.

Finally, in order to prove that the periodic solution is globally asymptotically stable, we only need to prove its global attractivity, that is,

$$\begin{aligned} \lim _{t\rightarrow \infty }w(t)-{\bar{w}}(t)=\lim _{t\rightarrow \infty }w(t;0,u)-w(t;0,{\bar{u}})=0, \end{aligned}$$

(86)

for any $u>0$.

It follows from (iv) of Lemma 5.1 that

$$\begin{aligned} \lim _{t\rightarrow \infty }h_{n}(u)=l, \hbox {where~}l~\hbox {satisfies~}h(l)=l. \end{aligned}$$

(87)

Applying the uniqueness of the T-periodic solution, we know $l=0,~\hbox {or}~{\bar{u}}.$ If $l=0,$ from (a), we see $T<T^{*}.$ It contradicts the assumption of $T\ge T^{*}.$ Thus, the proof is finished.