A Comparison Study of Predator–Prey Model in Deterministic and Stochastic Environments with the Impacts of Fear and Habitat Complexity

Abstract

In theoretical ecology, recent field experiments on terrestrial vertebrates observe that the predator–prey interaction can not only be curtailed by direct consumption but also governed by some indirect effects such as the fear of predator which may reduce the reproduction rate of prey individuals. Based on this fact, we have developed and explored the predator–prey interaction with the influence of both cost and benefit of fear effect (felt by prey). A Holling type III functional response with the effect of habitat complexity has been taken to consume the prey biomass. Positivity and boundedness of the studied system prove that the model is well-behaved. The uniform persistence of the studied system is derived analytically under some parametric restrictions. The feasibility conditions and stability criteria of each equilibrium points have been discussed. Next, we have exhibited the existence of Hopf-bifurcation around the interior equilibrium point. Our mathematical analyses show that habitat complexity and fear effect both have a great impact on the persistence of the predator biomass. Furthermore, we have investigated the effect of breeding delay parameter such that the system loses its stability behaviour and enters into a limit cycle oscillations through Hopf-bifurcation. Numerical simulations are illustrated to verify our analytical outcomes. Numerically, we have perturbed the death rates of prey and predator species with Gaussian white noise terms due to the effects of environmental fluctuations.

Appendices

Appendix A

Here, we will deduce the conditions for existence of equilibrium points and perform their stability analysis corresponding to system (3) ($\theta =0$).

System (3) has three feasible equilibrium points:

(i) $\widetilde{E_0}(0, 0)$ (unstable), (ii) $\widetilde{E_1}(k, 0)$ (LAS if $m > 1-\frac{d_{2}}{\beta k^2 (\gamma -d_{2}h)}$) and (iii) ${\widetilde{E}}({\widetilde{x}}, {\widetilde{y}})$ where ${\widetilde{x}}=\sqrt{\frac{d_{2}}{\beta (1-m)(\gamma -d_{2}h)}}$ and ${\widetilde{y}}=\frac{\gamma r {\widetilde{x}}\left( 1-\frac{{\widetilde{x}}}{k}\right) }{d_{2}}$. Now, ${\widetilde{E}}({\widetilde{x}}, {\widetilde{y}})$ exists if $1-\frac{{\widetilde{x}}}{k} > 0 \displaystyle \Rightarrow 0< m < 1-\frac{d_{2}}{\beta k^2 (\gamma -d_{2}h)}$ provided $d_{2} < \frac{\gamma }{h}$. Otherwise, ${\widetilde{E}}({\widetilde{x}}, {\widetilde{y}})$ goes towards predator-free equilibrium point $\widetilde{E_1}(k, 0)$. In ecological point of view, interior equilibrium point exists if the strength of habitat complexity is less than its threshold value ${\widetilde{m}}=1-\frac{d_{2}}{\beta k^2 (\gamma -d_{2}h)}$.

${\widetilde{E}}({\widetilde{x}}, {\widetilde{y}})$ has two eigenvalues with negative real parts if

$$\begin{aligned} r\left( 1-\frac{2{\widetilde{x}}}{k}\right)&< \frac{2\beta (1-m){\widetilde{x}} {\widetilde{y}}}{\left( 1+\beta (1-m)h{\widetilde{x}}^2\right) ^2}\\ \Rightarrow \left( 1-\frac{2{\widetilde{x}}}{k}\right)&<\frac{2\gamma \beta (1-m){\widetilde{x}}^2\left( 1-\frac{{\widetilde{x}}}{k}\right) }{d_{2}\left( 1+\beta (1-m)h{\widetilde{x}}^2\right) ^2} \left[ \text {putting the value of } {\widetilde{y}}\right] \\ \Rightarrow \left( 1-\frac{2{\widetilde{x}}}{k}\right)&<\frac{2\left( 1-\frac{{\widetilde{x}}}{k}\right) (\gamma -d_{2}h)}{\gamma }\\&\quad \left[ \text {using the fact } \beta (1-m){\widetilde{x}}^2=\frac{d_2}{\gamma -d_{2}h}\right] \\ \Rightarrow {\widetilde{x}}&> \frac{k(2d_{2}h-\gamma )}{2d_{2}h}\\ \Rightarrow \sqrt{\frac{d_{2}}{\beta (1-m)(\gamma -d_{2}h)}}&> \frac{k(2d_{2}h-\gamma )}{2d_{2}h}\\ \Rightarrow m&> 1-\frac{4d_{2}^3h^2}{\beta k^2(\gamma -d_{2}h)(2d_{2}h-\gamma )^2 } \text {, provided } \frac{\gamma }{2h} \\&< d_{2} < \frac{\gamma }{h}. \end{aligned}$$

Theorem 8.1

${\widetilde{E}}({\widetilde{x}}, {\widetilde{y}})$ of system (3) exists and is LAS if the strength of habitat complexity satisfies the following:

$$\begin{aligned} 1-\frac{4d_{2}^3h^2}{\beta k^2(\gamma -d_{2}h)(2d_{2}h-\gamma )^2 }< m< 1-\frac{d_{2}}{\beta k^2(\gamma -d_{2}h)}\quad \text {with}\quad \frac{\gamma }{2h}< d_{2} < \frac{\gamma }{h}. \end{aligned}$$

Now, we rewrite system (3) in the form:

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}= & {} xg(x)- yp(x),\quad x(0)> 0 \nonumber \\ \frac{\mathrm{d}y}{\mathrm{d}t}= & {} \left( \gamma p(x)-d_{2}\right) y, \quad y(0) > 0 \end{aligned}$$

(38)

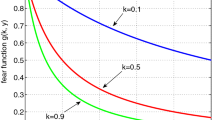
where $g(x)=r\left( 1-\frac{x}{k}\right)$, $p(x)=\frac{\beta (1-m) x^2}{1+\beta (1-m) h x^2}$.

Following Theorem 4.2 of Kuang and Freedman (1988), we arrive at Lemma 8.2:

Lemma 8.2

Suppose in system (38):

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}x}\left\{ \frac{g(x)+xg'(x)-xg(x)\frac{p'(x)}{p(x)}}{-d_{2}+\gamma p(x)}\right\} \le 0 \end{aligned}$$

in $0 \le x < {\widetilde{x}}$ and ${\widetilde{x}} < x \le k$. Then system (38) has unique limit cycle which is globally asymptotically stable in the set $\left\{ (x, y)\big |x>0, y> 0\right\} \setminus \left\{ {\widetilde{E}}\right\}$, where $g'(x)=\frac{\mathrm{d}}{\mathrm{d}x} g(x)$ and $p'(x)=\frac{\mathrm{d}}{\mathrm{d}x}p(x)$.

Theorem 8.3

For system (3), if $0< m < 1-\frac{4d_{2}^3h^2}{\beta k^2(\gamma -d_{2}h)(2d_{2}h-\gamma )^2 }$, then ${\widetilde{E}}({\widetilde{x}}, {\widetilde{y}})$ is unstable in int ${\mathbb {R}}_{+}^2$ and there exists a unique stable limit cycle which is globally asymptotically stable.

Proof

Proof is similar of Theorem 4.2.1 in Wang et al. (2021). $\square$

Remark 1

${\widetilde{E}}({\widetilde{x}}, {\widetilde{y}})$ of system (3) is globally asymptotically stable if

$$\begin{aligned} 1-\frac{4d_{2}^3h^2}{\beta k^2(\gamma -d_{2}h)(2d_{2}h-\gamma )^2 }< m< 1-\frac{d_{2}}{\beta k^2(\gamma -d_{2}h)} \quad \text {with}\quad \frac{\gamma }{2h}< d_2 < \frac{\gamma }{h}. \end{aligned}$$

Remark 2

When the prey and predator population coexist at ${\widetilde{E}}({\widetilde{x}}, {\widetilde{y}})$, the biomass of both the prey and predator population depend on the parameter m (strength of habitat complexity). We have: $\frac{\mathrm{d}{\widetilde{x}}}{\mathrm{d}m}=\sqrt{\frac{d_{2}}{\beta \left\{ \gamma -d_{2}h\right\} }}\left( \frac{1}{2(1-m)^\frac{3}{2}}\right) >0 \text { since } m \in (0, 1)$, i.e. increasing the value of m can increase the biomass of prey population.

Similarly, we have: $\frac{\mathrm{d}{\widetilde{y}}}{\mathrm{d}m}=\frac{\gamma r}{d_2}\left( 1-\frac{2{\widetilde{x}}}{k}\right) \frac{\mathrm{d}{\widetilde{x}}}{\mathrm{d}m}<0 \text { if } m > 1-\frac{4d_{2}}{\beta k^2\left\{ \gamma -d_{2}h\right\} }$, i.e. ${\widetilde{y}}$ is a decreasing function of m when $m \in \left( 1-\frac{4d_{2}}{\beta k^2\left\{ \gamma -d_{2}h\right\} }, 1-\frac{d_{2}}{\beta k^2\left\{ \gamma -d_{2}h\right\} }\right)$.

Appendix B

Using the transformation $x=X+{\widehat{x}}$ and $y=Y+{\widehat{y}}$, system (20) can be rewritten as follows:

$$\begin{aligned} \frac{\mathrm{d}X}{\mathrm{d}t}&=\frac{b(X(t-\tau )+{\widehat{x}})}{1+\theta (Y(t-\tau )+{\widehat{y}})}-d_{1}(X+{\widehat{x}})-a(X+{\widehat{x}})^2\nonumber \\&\quad -\frac{\beta (1-m) (X+{\widehat{x}})^2 (Y+{\widehat{y}})}{\left( 1+\beta (1-m) h (X+{\widehat{x}})^2\right) (1+\theta )} \nonumber \\&=F(t, X(t), Y(t), X(t-\tau ), Y(t-\tau ))\nonumber \\ \frac{\mathrm{d}Y}{\mathrm{d}t}&= \frac{\gamma \beta (1-m) (X+{\widehat{x}})^2 (Y+{\widehat{y}})}{\left( 1+\beta (1-m) h (X+{\widehat{x}})^2\right) (1+\theta )}-d_{2}(Y+{\widehat{y}})\nonumber \\&=G(t, X(t), Y(t), X(t-\tau ), Y(t-\tau )). \end{aligned}$$

(39)

At the interior equilibrium point $({\widehat{x}}, {\widehat{y}})$,

$$\begin{aligned} \frac{\partial F}{\partial X}\bigg |_{({\widehat{x}}, {\widehat{y}})}&=\frac{be^{-\lambda \tau }}{1+\theta {\widehat{y}}}-d_1-2a{\widehat{x}}^2-\frac{2\beta (1-m){\widehat{x}} {\widehat{y}}}{\left( 1+\beta (1-m)h{\widehat{x}}^2\right) (1+\theta )}\\&\quad +\frac{2\beta ^2(1-m)^2h{\widehat{x}}^3{\widehat{y}}}{\left( 1+\beta (1-m)h{\widehat{x}}^2\right) ^2(1+\theta )}, \\ \frac{\partial F}{\partial Y}\bigg |_{({\widehat{x}}, {\widehat{y}})}&=-\frac{b\theta {\widehat{x}}e^{-\lambda \tau }}{\left( 1+\theta {\widehat{y}}\right) ^2}-\frac{\beta (1-m){\widehat{x}}^2}{\left( 1+\beta (1-m)h{\widehat{x}}^2\right) (1+\theta )}, \\ \frac{\partial G}{\partial X}\bigg |_{({\widehat{x}}, {\widehat{y}})}&=\frac{2\gamma \beta (1-m){\widehat{x}}{\widehat{y}}}{\left( 1+\beta (1-m)h{\widehat{x}}^2\right) ^2(1+\theta )}, \\ \frac{\partial G}{\partial Y}\bigg |_{({\widehat{x}}, {\widehat{y}})}&=0. \end{aligned}$$

So, the linearization of system (20) at $({\widehat{x}}, {\widehat{y}})$ has the form:

$$\begin{aligned} \frac{\mathrm{d}Z}{\mathrm{d}t}=A_{1}^{'}Z(t-\tau )+A_{2}^{'}Z(t) \end{aligned}$$

where $Z=[X, Y]^T$, $A_{1}^{'}=\begin{bmatrix} c_{2} &{} c_{3}\\ 0&{} 0 \end{bmatrix}$ and $A_{2}^{'}=\begin{bmatrix} q_{11}+ c_{1} &{} c_{4} \\ q_{21} &{} q_{22} \end{bmatrix}$, $c_{1}=-\frac{b}{1+\theta {\widehat{y}}}$, $c_{2}=\frac{b}{1+\theta {\widehat{y}}}$, $c_{3}=-\frac{b\theta {\widehat{x}}}{\left( 1+\theta {\widehat{y}}\right) ^2}$, $c_{4}=q_{12}+\frac{b\theta {\widehat{x}}}{\left( 1+\theta {\widehat{y}}\right) ^2}$, $q_{11}={\widehat{x}}\left\{ -a-\frac{\beta (1-m){\widehat{y}}\left[ 1-\beta (1-m)h {\widehat{x}}^2\right] }{\left( 1+\beta (1-m)h{\widehat{x}}^2\right) ^2(1+\theta )}\right\}$, $q_{12}=-\frac{b\theta {\widehat{x}}}{(1+\theta {\widehat{y}})^2}-\frac{\beta (1-m){\widehat{x}}^2}{\left( 1+\beta (1-m)h{\widehat{x}}^2\right) (1+\theta )}$, $q_{21}=\frac{2\gamma \beta (1-m){\widehat{x}}{\widehat{y}}}{\left( 1+\beta (1-m)h{\widehat{x}}^2\right) ^2(1+\theta )}$ and $q_{22}=0$.