Assessing Age-Specific Vaccination Strategies and Post-vaccination Reopening Policies for COVID-19 Control Using SEIR Modeling Approach

Abstract

As the availability of COVID-19 vaccines, it is badly needed to develop vaccination guidelines to prioritize the vaccination delivery in order to effectively stop COVID-19 epidemic and minimize the loss. We evaluated the effect of age-specific vaccination strategies on the number of infections and deaths using an SEIR model, considering the age structure and social contact patterns for different age groups for each of different countries. In general, the vaccination priority should be given to those younger people who are active in social contacts to minimize the number of infections, while the vaccination priority should be given to the elderly to minimize the number of deaths. But this principle may not always apply when the interaction of age structure and age-specific social contact patterns is complicated. Partially reopening schools, workplaces or households, the vaccination priority may need to be adjusted accordingly. Prematurely reopening social contacts could initiate a new outbreak or even a new pandemic out of control if the vaccination rate and the detection rate are not high enough. Our result suggests that it requires at least nine months of vaccination (with a high vaccination rate > 0.1%) for Italy and India before fully reopening social contacts in order to avoid a new pandemic.

1 Introduction

In 2020, novel coronavirus (SARS-CoV-2) pneumonia broke out in the world. As of December 28, 2020, a total of 80.724 million confirmed cases and 1.764 million deaths have been reported worldwide, according to the latest data from Johns Hopkins University website (Johns Hopkins University 2020). In the past 24 h, 443,000 cases have been confirmed and 7000 deaths have increased worldwide. At the same time, the cases infected by the new variants of the SARS-CoV-2 have been confirmed in many countries, including the UK, South Africa, France, Japan, Thailand, Canada, Portugal and so on. Great efforts in the world have been made for controlling COVID-19 pandemic in the past year, but unfortunately, the COVID-19 epidemic is still deteriorating in many countries. The global epidemic situation is still very severe.

In such a severe situation, the development and use of vaccines have been a great hope to control COVID-19 epidemic. There are over 100 COVID-19 vaccines under development in the past year. It is gratifying that a great progress has been made in vaccine development, some vaccines have been approved to use and some others are undergoing phase 3 clinical trials (Corum et al. 2020). Many countries are preparing to implement and deliver vaccination sequentially based on some priority guidelines. In the early stage of COVID-19 epidemic, the main research focus is to assess the basic reproductive number, infection scale and the impact of population mobility on COVID-19 transmission (Tang et al. 2020a, b, c, d; Nishiura et al. 2020; Zhao et al. 2020). With the wide spread of the epidemic, the research focus was quickly shifted to develop and evaluate the effectiveness of control measures (Kucharski et al. 2020; Karatayeva et al. 2020; Flaxman et al. 2020; Tang et al. 2020a, b, c, d; Wang et al. 2021). The development of COVID-19 vaccines is accelerated, but the capacity of vaccine production is limited and it may take time to make vaccine available to all the people who are willing to receive it. Thus, it is badly needed to develop vaccination strategies in order to maximize the benefit of vaccination in controlling COVID-19 epidemic.

Recently in several modeling studies (Abbas et al. 2020; Shen et al. 2020; Bubar et al. 2020; Tang et al. 2020a, b, c, d; Matrajt et al. 2020), researchers have tried to investigate the optimal control of vaccination in mitigating the epidemics. Shen et al. (2020) investigated the effect of vaccination on COVID-19 epidemic and suggested that only a highly effective vaccine will enable to restore to normal life for the USA (Shen et al. 2020). Tang et al. investigated the reopening strategies for different countries assuming the availability of vaccines (2020a, b, c, d), and they suggested that country level-based reopening strategies should be considered, according to the quarantine rate, testing ability and the condition of vaccines. Considering the limitation of initial supply of SARS-CoV-2 vaccines, five vaccine prioritization strategies are examined for the USA using an age-stratified SEIR model (Bubar et al. 2020). In fact, the age has been shown to be an important factor for susceptibility and death rate (Goldstein et al. 2020; Davies et al. 2020; Zhang et al. 2020; Keeling et al. 2020); thus, the age structure plays an important role in vaccination strategies. We noticed that different countries have different age structures and different contact networks among different age groups (Population Pyramid 2019). Based on this observation, we extended the age-structured SEIR model to identify the optimal age-specific vaccination distributions for different countries with different age structures and different contact networks. In addition, we further explored the post-vaccination reopening policies based on the model with the optimal vaccination distributions.

2 Methods

2.1 Model

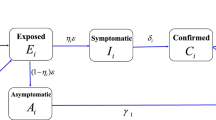
We propose the following age-structured SEIR model (Fig. 1):

$$\left\{ {\begin{array}{*{20}l} {S_{i}^{^{\prime}} = - p_{i}^{I} S_{i} \sum\nolimits_{j = 1}^{n} {c_{ij} I_{j} } {/}N - p_{i}^{A} S_{i} \sum\nolimits_{j = 1}^{n} {c_{ij} A_{j} } {/}N - \nu_{i} S_{i} } \hfill \\ {E_{i}^{\prime } = p_{i}^{I} S_{i} \sum\nolimits_{j = 1}^{n} {c_{ij} I_{j} } {/}N + p_{i}^{A} S_{i} \sum\nolimits_{j = 1}^{n} {c_{ij} A_{j} } {/}N - \sigma E_{i} } \hfill \\ {A_{i}^{\prime } = \sigma (1 - \rho_{i} )E_{i} - \gamma_{A} A_{i} } \hfill \\ {I_{i}^{\prime } = \sigma \rho_{i} E_{i} - \delta I_{i} } \hfill \\ {H_{i}^{\prime } = \delta I_{i} - d_{H} IFR_{i} H_{i} - \gamma_{H} H_{i} } \hfill \\ {R_{i}^{\prime } = \gamma_{A} A_{i} + \gamma_{H} H_{i} } \hfill \\ {V_{i}^{\prime } = \nu_{i} S_{i} } \hfill \\ \end{array} } \right.\quad i = 1,2, \ldots ,16$$

(1)

Fig. 1

The flowchart of the model.

In order to consider the effect of different age-specific vaccination strategies to control the epidemic in different countries (e.g., China, India and Italy), we divided the whole population into 16 age groups (0-4, 5-9, 10-14,...,75+), according to the contact data (Population Pyramid 2019). We also divided the population as the susceptible (S), the exposed (E), the asymptomatic infected (A), the symptomatic infected (I), the hospitalized (H), the recovered (R) and the vaccinated (V). We assumed that people with different ages had different susceptibility ($p_{i}^{I}$), and the proportion of asymptomatic infections ($\rho_{i}$) also depended on ages (Prem et al. 2020). We also assume that the asymptomatic infected individuals are less infectious compared to the symptomatic infected individuals ($p_{i}^{A} = \theta p_{i}^{I} ,\,\,i = 1,2, \ldots ,n$). $\sigma$ is the transition rate from the exposed to the infected, $\gamma_{\rm A}$ and $\gamma_{\rm H}$ are recovery rates, $d_{H} {\text{IFR}}_{i}$ is the death rate of age group $i$, ${\text{IFR}}_{i}$ is the age-specific infection fatality rate for age group $i$ (Levin et al. 2020), $\nu_{i}$ is effective vaccination rate of age group $i$, and $c_{ij}$ is the contact rate of age group $j$ by age group $i$ (Population Pyramid 2019).

In order to accurately describe the variation of control strategies in this model, we assume that the contact rate $c_{ij} (t)$ is decreasing(or increasing) as the increasing (or decreasing) intensity of the control strategy with respect to time t. In this study, we focus on three countries, China, India and Italy (Fig. 2). The function of $c_{ij} (t)$ for China and India is given by

$$c_{ij} (t) = \left\{ {\begin{array}{*{20}l} {c_{ij}^{0} } \hfill & {\quad t \le t_{{\text{c}}} } \hfill \\ {(c_{ij}^{0} - c_{ij}^{f} )e^{{ - r_{c} (t - t_{c} )}} + c_{ij}^{f} } \hfill & {\quad t > t_{{\text{c}}} } \hfill \\ \end{array} } \right.$$

(2)

Fig. 2

Observed daily new cases (circle), observed daily deaths (circle) and model fitting results (solid curve) for China (a, d), Italy (b, e) and India (c, f)

where $c_{ij}^{0}$ denotes the baseline contact rate at the initial time and $c_{ij}^{f} = q_{{\text{c}}} c_{ij}^{0}$ denotes the minimum contact rate under the contact control measures before $t_{c}$, where $0 \le q_{{\text{c}}} \le 1$ quantifies the intensity of contact control measures with ${q}_{\mathrm{c}}=0$ indicating the strongest contact control measures to make the final contact rate as 0, and ${q}_{\mathrm{c}}=1$ indicating “no any effect” of the contact control measures at all. Parameter $r_{{\text{c}}}$ denotes the exponential decreasing rate of the contact rate after the contact control measures are implemented.

In Italy, the emergency control was established after the first case reported, but shops, theaters and cinemas gradually returned to open in June. In October and November, a number of decrees were issued on strengthening control measures (https://www.acaps.org/covid-19-government-measures-dataset). Thus, the trajectory of the control measures in Italy was initially strong, then relaxed and strong again. Accordingly, we model the function of $c_{ij} (t)$ for Italy as follows,

$$c_{ij} (t) = \left\{ {\begin{array}{*{20}l} {(c_{ij}^{0} - c_{ij}^{{f_{1} }} )e^{{ - r_{{c_{1} }} (t)}} + c_{ij}^{{f_{1} }} } \hfill & {\quad t \le t_{{c_{1} }} } \hfill \\ {(c_{ij}^{{f_{1} }} - c_{ij}^{{f_{2} }} )e^{{ - r_{{c_{2} }} (t - t_{{c_{1} }} )}} + c_{ij}^{{f_{2} }} } \hfill & {\quad t_{{c_{1} }} < t \le t_{{c_{2} }} } \hfill \\ {(c_{ij}^{{f_{2} }} - c_{ij}^{{f_{3} }} )e^{{ - r_{{c_{3} }} (t - t_{{c_{2} }} )}} + c_{ij}^{{f_{3} }} } \hfill & {\quad t > t_{{c_{2} }} } \hfill \\ \end{array} } \right.$$

(3)

where $c_{ij}^{{f_{1} }}$ ($c_{ij}^{{f_{1} }} = q_{{c_{1} }} c_{ij}^{0}$), $c_{ij}^{{f_{2} }}$ ($c_{ij}^{{f_{2} }} = q_{{c_{2} }} c_{ij}^{{f_{1} }}$) and $c_{ij}^{{f_{3} }}$($c_{ij}^{{f_{3} }} = q_{{c_{3} }} c_{ij}^{{f_{2} }}$) are the minimum or the maximum contact rate under control strategies or due to relaxation of control.$r_{{c_{1} }}$, $r_{{c_{2} }}$ and $r_{{c_{3} }}$ denote how an exponential increase or decrease in the contact rate is affected by strengthening control or relaxation of control, $t_{{c_{1} }}$ and $t_{{c_{2} }}$ are the switching time of control strength.

We also set the transition rate $\delta (t)$ as an increasing function with respect to time t, with the following form:

$$\delta (t) = \left\{ {\begin{array}{*{20}l} {\delta_{0} } \hfill & {\quad t \le t_{{\text{c}}} } \hfill \\ {(\delta_{0} - \delta_{{\text{f}}} )e^{{ - r_{\delta } (t - t_{{\text{c}}} )}} + \delta_{{\text{f}}} } \hfill & {\quad t > t_{{\text{c}}} } \hfill \\ \end{array} } \right.$$

(4)

where ${\delta }_{0}$ is the initial rate of confirmation (detection), ${\delta }_{\mathrm{f}}$ is the fastest confirmation rate ($\delta_{f} = q_{\delta } \delta_{0} ,q_{\delta } > 1$), and $r_{\delta }$ is the exponentially increasing rate. The critical time $t_{{\text{c}}}$ for China is January 23th, 2020 when Wuhan city and all parts of the country continued to take stringent control measures. The onset time of the epidemic in Italy was later than January 23, 2020, so we set $t_{c}$ for Italy to be 0. Besides, according to the curve of the daily confirmed cases, we set the confirmation rate $\delta (t)$ for India to be piecewise constant, which is an extreme case of formula (4). The expression is as follows:

$$\delta (t) = \left\{ \begin{gathered} \delta_{0} ,\begin{array}{*{20}c} {} & {t \le t_{{c_{1} }} } \\ \end{array} \hfill \\ \delta_{{\text{f}}} ,\begin{array}{*{20}c} {} & {t > t_{{c_{1} }} } \\ \end{array} \hfill \\ \end{gathered} \right.$$

(5)

Considering the development of medical technology over time, we set the death rate of H for Italy and India to be as follows:

$$d_{H} = \left\{ {\begin{array}{*{20}l} {d_{H1} ,} \hfill & {\quad t \le t_{c1} } \hfill \\ {d_{H2} ,} \hfill & {\quad t > t_{c1} } \hfill \\ \end{array} } \right.$$

(6)

where $d_{H1}$ and $d_{H2}$ are two constant death rate in the two time stages.

In order to compare the impact of different vaccination strategies on the epidemic, we considered two vaccination strategies: one is the uniform vaccination strategy, and the other is the age-specific vaccination strategy. In the case of the uniform vaccination strategy, we assume $\nu_{1} = \nu_{2} = \cdots = \nu_{16} = \nu$. For the age-specific vaccination strategy, we assume that $\nu_{i} = \kappa p_{i} ,\,\,\,i = 1, \ldots ,16$, where $\kappa$ is a scaling factor and $p_{i}$ is the vaccination probability of the ith age group. In order to maintain the consistency of the number of vaccinations everyday, we assume $\mathrm{v}\sum_{i=1}^{16}{S}_{i}(t)=\upkappa \sum_{i=1}^{16}{p}_{i}{S}_{i}(t)$. Considering that Beta distribution is defined in a finite interval and its density function is very flexible (it can be either unimodal or U-shaped), so, to reduce the number of parameters, we assume that the vaccination age distribution follows a Beta distribution, $Beta(\alpha ,\beta )$ with parameters $\alpha$ and $\beta$. Specifically, the vaccination age distribution is a discrete beta distribution, i.e., the vaccination probability of the ith age group is $p_{i} = F(i/16|\alpha ,\beta ) - F((i - 1)/16|\alpha ,\beta )$, where $F(x|\alpha ,\beta )$ is the Beta cumulative distribution function. Moreover, the uniform distribution is a special case of Beta distribution, i.e., $\alpha { = }\beta { = }1$. In this case, the vaccination probability of each age group is equal.

The basic reproduction number (R₀) can be calculated according to Driessche and Watmough (2002), which is the principal eigenvalue of the following matrix $\Lambda$ (see more details in the Appendix):

$$\begin{aligned}\Lambda &= \frac{1}{{N\gamma_{\rm A} }}\left( {\begin{array}{*{20}c} {(1 - \rho_{1} )p_{1}^{A} S_{10} c_{11} } & {(1 - \rho_{1} )p_{1}^{A} S_{10} c_{12} } & \ldots & {(1 - \rho_{1} )p_{1}^{A} S_{10} c_{1n} } \\ {(1 - \rho_{2} )p_{2}^{A} S_{20} c_{21} } & {(1 - \rho_{2} )p_{2}^{A} S_{20} c_{22} } & \ldots & {(1 - \rho_{2} )p_{2}^{A} S_{20} c_{2n} } \\ \ldots & \ldots & \ldots & \ldots \\ {(1 - \rho_{n} )p_{n}^{A} S_{n0} c_{n1} } & {(1 - \rho_{n} )p_{n}^{A} S_{n0} c_{n2} } & \ldots & {(1 - \rho_{n} )p_{n}^{A} S_{n0} c_{nn} } \\ \end{array} } \right) \\ & \quad + \frac{1}{{N(\delta + \alpha_{I} )}}\left( {\begin{array}{*{20}c} {\rho_{1} p_{1}^{I} S_{10} c_{11} } & {\rho_{1} p_{1}^{I} S_{10} c_{12} } & \ldots & {\rho_{1} p_{1}^{I} S_{10} c_{1n} } \\ {\rho_{2} p_{2}^{I} S_{20} c_{21} } & {\rho_{2} p_{2}^{I} S_{20} c_{22} } & \ldots & {\rho_{2} p_{2}^{I} S_{20} c_{2n} } \\ \ldots & \ldots & \ldots & \ldots \\ {\rho_{n} p_{n}^{I} S_{n0} c_{n1} } & {\rho_{2} p_{n}^{I} S_{n0} c_{n2} } & \ldots & {\rho_{2} p_{n}^{I} S_{n0} c_{nn} } \\ \end{array} } \right)\end{aligned}$$

$$R_{0} = g(\Lambda )$$

(7)

where g(.) denotes the spectral radius of a matrix.

2.2 Data and parameter calibration

Three countries (China, Italy and India) with different population age distributions (Fig. 3) are chosen to be analyzed in this study. The data for the population age distribution are obtained from https://www.populationpyramid.net/japan/2019/ (Population Pyramid 2019). The data of daily reported COVID-19 cases and the cumulative number of deaths (Fig. 2) were obtained from https://github.com/CSSEGISandData. We parameterize the contact matrices at the initial time for each country using the age-dependent contact rates estimated by Prem et al. (2017). The contact matrix of different locations (households $c_{ij}^{h}$, workplaces $c_{ij}^{w}$, schools $c_{ij}^{s}$ and other locations $c_{ij}^{o}$) is given in the study of Prem et al. The summation of the contacts across different sites was used to be the baseline contact matrix ($c_{ij}^{0} = c_{ij}^{s} + c_{ij}^{w} + c_{ij}^{h} + c_{ij}^{o}$), which is shown in Suppl. Fig. S1. The susceptibility of different age groups $p_{i}^{I}$ can be derived from the estimation in Keeling et al. (2020). According to Prem et al. (2020), we also assume that the younger individuals are more likely to be asymptomatic, so the proportion of asymptomatic infections ($\rho_{i}$) is assumed to be 0.4 when $i \le 4$, and 0.8 when $i > 4$. Moreover, we assume that the infectiousness of asymptomatic is less than that of the symptomatic individuals, and $\theta$ is assumed to be 0.25 (Prem et al. 2020). The parameter values related to COVID-19 and its transmission such as the probability of infected individual’s transmission per contact, the latent period, the death rate and so on are derived from related references (shown in Table 1). Other parameters related to control measures such as the variation of contact rate and detection rate, and some initial conditions such as initial values of the exposed individuals and infected individuals are estimated by fitting the model to the daily reported cases and the daily number of deaths (Suppl. Fig. S3; Table 1) by the Markov Chain Monte Carlo(MCMC) method. Here, we assume all confirmed cases are reported. We assume that the measurement error of the data $\varepsilon_{1}$ and $\varepsilon_{2}$ follows a normal distribution with mean 0 and variance $\sigma_{1}^{2}$ and $\sigma_{2}^{2}$. Then the observed data model is assumed to be

$$Y(t) = N_{I} (t) + \varepsilon_{1} ,D(t) = N_{\rm d} (t) + \varepsilon_{2}$$

Fig. 3

The population age distribution for the three countries (China, Italy and India).

Table 1 Parameter definitions and estimation for the age structured SEIR model.

where $Y(t)$ is the observed daily confirmed cases and $D(t)$ is the observed daily number of deaths. $N_{I} (t)$ is the predicted daily confirmed cases which can be calculated by $N_{I} (t) = \sum\nolimits_{i = 1}^{16} {\int_{t - 1}^{t} {\delta I_{i} (t){\text{d}}t} }$, $N_{{\text{d}}} (t)$ is the predicted daily number of deaths which can be calculated by $N_{{\text{d}}} (t) = \sum\nolimits_{i = 1}^{16} {\int_{t - 1}^{t} {d_{{\text{H}}} {\text{IFR}}_{i} H_{i} (t){\text{d}}t} }$. The objective function is

$$L( \cdot ) = \sum\limits_{t = 1}^{T} {(Y(t) - N_{{\text{I}}} (t))^{2} } + \sum\limits_{t = 1}^{T} {(D(t) - N_{{\text{d}}} (t))^{2} }$$

(8)

where $T$ is the length of the data used for model fitting. The MCMC method was used to do parameter estimation, and implemented with MATLAB toolbox of Laine (2008). The algorithm was run for 10,000 iterations and we discarded with the first 5000 iterations as a burn-in period. The mean and 95% confidence intervals (95%CI) of each estimated parameter are listed in Table 1. Here, since there are few exposed and infected persons at the beginning of the epidemic, we assume that the number of exposed persons and the number of infected persons (asymptomatic and symptomatic) in different age groups are equal. Moreover, sensitivity analysis of these parameters is performed by evaluating partial rank correlation coefficients (PRCCs) (Saltelli et al. 2000; Marino et al. 2008) for various input parameters against output variables (cumulative number of confirmed cases) (shown in Suppl. Fig. S2).

2.3 Evaluation of the Optimal Age-Specific Vaccination Distribution

The basic reproduction number (R₀), the cumulative number of infections (I_c) and the cumulative number of deaths (D_c) are the key indicators of the severity of infectious diseases and public health concerns, and thus are used as the endpoints or outcomes to evaluate the effectiveness of different vaccination strategies in this study. Since the Beta distribution of the age-specific vaccination can be uniquely determined by the two parameters $\alpha$ and $\beta$, we will evaluate each of the three endpoints as a function of the two parameters $\alpha$ and β. We assume that the vaccine will be delivered continuously for 180 days in a fixed rate. The optimal $\alpha$ and $\beta$, i.e., the optimal age-specific vaccination distribution, can be determined by minimizing each of the three endpoints from the vaccination initiating time (T) to T + 180 days for each country. Considering that the epidemic in China has been well controlled by now and the sporadic outbreaks in different cities are mainly due to overseas imports, we assume that all people in China are susceptible and one infected individual is imported from overseas to potentially initiate a new epidemic. The detection rate and the contact rate are fixed to be ${\delta }_{\mathrm{f}}$ and $c_{ij}^{0}$ in our model evaluations.

2.4 The Model Considering Reduction of Susceptibility, Severity and Mortality After Vaccination

In model (1), we assumed that the vaccinated people cannot be infected again. However, in fact, vaccine does not completely block the transmission of the virus, but reduces the venerability of the people from having severe symptoms and also reduces the chance of being infected and dying from SRAS-CoV-2 infection. So, considering the fact that the SRAS-CoV-2 vaccine reduces the susceptibility, severity and mortality of people vaccinated, we extend model (1) to be the following model:

$$\left\{ {\begin{array}{*{20}l} {S_{i}^{\prime } = - p_{i}^{I} S_{i} \sum\nolimits_{j = 1}^{n} {c_{ij} (I_{j} + I_{mj} )} /N - p_{i}^{A} S_{i} \sum\nolimits_{j = 1}^{n} {c_{ij} (A_{j} } + A_{mj} )/N - \nu_{i} S_{i} } \hfill \\ {E_{i}^{\prime } = p_{i}^{I} S_{i} \sum\nolimits_{j = 1}^{n} {c_{ij} (I_{j} + I_{mj} )} /N + p_{i}^{A} S_{i} \sum\nolimits_{j = 1}^{n} {c_{ij} (A_{j} } + A_{mj} )/N - \sigma E_{i} } \hfill \\ {A_{i}^{\prime } = \sigma (1 - \rho_{i} )E_{i} - \gamma_{A} A_{i} } \hfill \\ {I_{i}^{\prime } = \sigma \rho_{i} E_{i} - \delta I_{i} } \hfill \\ {H_{i}^{\prime } = \delta I_{i} - d_{H} IFR_{i} H_{i} - \gamma_{H} H_{i} } \hfill \\ {R_{i}^{\prime } = \gamma_{A} A_{i} + \gamma_{H} H_{i} } \hfill \\ {S_{mi}^{\prime } = \nu_{i} S_{i} - \eta_{1} p_{i}^{I} S_{mi} \sum\nolimits_{j = 1}^{n} {c_{ij} (I_{j} + I_{mj} )} /N - \eta_{1} p_{i}^{A} S_{mi} \sum\nolimits_{j = 1}^{n} {c_{ij} (A_{j} } + A_{mj} )/N} \hfill \\ {E_{mi}^{\prime } = \eta_{1} p_{i}^{I} S_{mi} \sum\nolimits_{j = 1}^{n} {c_{ij} (I_{j} + I_{mj} )} /N + \eta_{1} p_{i}^{A} S_{mi} \sum\nolimits_{j = 1}^{n} {c_{ij} (A_{j} } + A_{mj} )/N - \sigma E_{mi} } \hfill \\ {A_{mi}^{\prime } = \sigma (1 - \eta_{2} \rho_{i} )E_{mi} - \gamma_{A} A_{mi} } \hfill \\ {I_{mi}^{\prime } = \sigma \eta_{2} \rho_{i} E_{mi} - \delta I_{mi} } \hfill \\ {H_{mi}^{\prime } = \delta I_{mi} - \eta_{3} d_{H} IFR_{i} H_{mi} - \gamma_{H} H_{mi} } \hfill \\ {R_{mi}^{\prime } = \gamma_{A} A_{mi} + \gamma_{H} H_{mi} } \hfill \\ \end{array} } \right.\quad i = 1,2, \ldots ,16$$

(9)

Here,$S, E, A, I,H,R$ represent the unvaccinated population, and ${S}_{mi}, {E}_{mi}, {A}_{mi}, {I}_{mi}, {H}_{mi}, {R}_{mi}$ represent the vaccinated population. $\eta_{1} ,\eta_{2}$ and $\eta_{3}$ represent vaccine effectiveness which are the proportion of the reduction of susceptibility, severity and mortality, respectively. Other parameters are assumed to be the same as those in model (1).

3 Results

3.1 Model Fitting and Parameter Estimation Results

Figure 2 shows the data of daily confirmed new cases (circle), the data of daily deaths (circle) and the results of model fitting (solid curve) for the three countries, China, India and Italy. Ninety-five percent confidence intervals of the simulation results are also shown in Fig. 2(blue shadow). We can see that the fitted models capture the trends of the observed data very well. In particular, a small wave and a big peak of the epidemic in Italy were captured on March 21 and November 13, respectively (Fig. 2b), and a single wave of the epidemic in China and India was captured on February 12 and September 16 by the model (Fig. 2a, c). The estimated model parameters as well as the derived parameters from literature are shown in Table 1.

3.2 The Optimal Age-Specific Vaccination Distribution

We evaluated the effect of different age-specific vaccination distributions on the control of COVID-19 epidemic, so that we could determine the optimal age-specific vaccination distribution by minimizing the aforementioned three endpoints for different countries (China, India and Italy), respectively. For each case, we set the vaccination rate $v$ as 0.05%, 0.1% and 0.15%, respectively. Figure 4 shows the optimal age-specific vaccination distributions and the contour plot of the three endpoints as a function of the two Beta distribution parameters $\alpha$ and $\beta$ for India. From this figure, we can see that the optimal distribution obtained by minimizing the basic reproduction number and the cumulative number of infections are similar when $v = 0.1\%$(Fig. 4$a_{4}$, $b_{4}$). This suggests that for India, the priority of vaccination should be given to teenagers and young people, i.e., those around 10–34 years old, in order to minimize the basic reproduction number and the cumulative number of infections. From the contour plots (Fig. 4; Suppl. Fig. S3 and Fig. S4) for each of the three endpoints as a function of $\alpha$ and $\beta$, we can see that effects of age-specific vaccination distributions on the basic reproduction number and the cumulative number of infections are similar (see also Table 2; Suppl. Table S1). This is presumably because R₀ is directly related to the spread of infections in the SEIR model. Thus, the optimal age vaccination distributions for these two endpoints are also similar (Table 2; Suppl. Table S1). However, the effect of age-specific vaccination distributions on the cumulative number of deaths can be significantly different from that for other two endpoints (Fig. 4). In order to minimize the cumulative deaths, the optimal age vaccination distribution (Fig. 4c4) suggests that the high priority should be given to elders in India. Notice that the effect of age vaccination distribution on the cumulative deaths is complicated and there are possible multiple solutions for the optimal age distribution. For example, when the vaccination rate is 0.15%, the contour plot for the cumulative deaths (Fig. 4$c_{3}$) shows two troughs with two optimal age-specific vaccination distributions(blue areas), and both solutions could keep the number of deaths under 16,380. One solution (Beta(7,20)) is similar to that for the basic reproduction number and the cumulative infections, and the other is when $\beta$ is very small and $\alpha$ is very large, i.e., (Beta(20,1)). In general, the vaccination priority should be given to the elderly in order to control the cumulative deaths, since the death rate is much higher for the elderly (Levin et al. 2020). However, giving priority to young people can also reduce the number of deaths to less than 16,380, while also keeping the total infection number slow in India. We also noticed that it is not effective to control COVID-19 epidemic to give vaccination priority to children for all the cases that we have considered. We also observed that the effect of age-specific vaccination distribution on the three endpoints is larger when the vaccination rate is higher (Fig. 4; Suppl. Fig. S3 and Fig. S4). For the case in India, the optimal age-specific vaccination strategy can reduce the cumulative infections by 140,324 (9.6%) cases or reduce the total deaths by 908 (4.8%) compared to that of the uniform vaccination strategy.

Fig. 4

The contour plot of the three endpoints: the basic reproduction number (R₀, 1st row), the cumulative number of infections (I_c, 2nd row) and the cumulative number of deaths (D_c, 3rd row) for India. The optimal age-specific vaccination distributions for these three endpoints are shown in a4, b4 and c4, respectively, when $v = 0.1\%$.$O_{R}$,$O_{I}$ and $O_{D}$ are the optimal points obtained by minimizing the three endpoints (R₀, I_c, D_c), respectively.

Table 2 The final outcomes (mean and 95% CI) with the optimal age-specific distributions vs. the uniform distribution ($v = 0.1\%$) for the three countries (China, Italy and India).

The effect of age vaccination distributions on the three endpoints in Italy is similar to that in India (Suppl. Fig. S3), which resulted in similar optimal age-specific vaccination distributions. Thus, the vaccination priority should be given to young and middle aged people in order to control the total number of infections while the priority should be given to the elderly in order to control the total deaths. However, for the case of China, the effect of age vaccination distributions on the basic reproduction number and cumulative infections is similar to that in India and Italy (Suppl. Fig. S4), which resulted in similar conclusions to control the total number of infections; but the effect of age vaccination distributions on the cumulative deaths is different from other two countries. The optimal distribution obtained by minimizing the cumulative number of deaths is also similar to that of other two endpoints (see Suppl. Fig. S4c₄). Interesting, we also observed that the optimal age-specific vaccination distribution has only a small effect on the total number of infections and deaths in Italy when $v = 0.1\%$ (Table 2). However, the optimal age-specific vaccination strategy has a big effect on the total number of infections and deaths for the case of China. Use of the optimal age-specific vaccination strategy could reduce the total number of infections from 153,938 to 80,292 (47.8% reduction) or it can reduce the total deaths from 4917 to 3154 (35.9% reduction) compared to that of uniform distribution in China (Table 2).

Considering the fact that vaccine reduces the venerability of the people from having severe symptoms and also reduces the chance of being infected and dying from SRAS-CoV-2 infection, we also investigated the optimal age-specific vaccination distribution by minimizing the number of infections and deaths for model (9). We assumed that the reduction of susceptibility after vaccination is 1/5($\eta_{1} = 1/5$) and the reductions of severity and mortality are 1/10($\eta_{2} = \eta_{3} = 1/10$). As shown in Table 3, the optimal age-specific vaccination distributions for model (9) are consistent with those for model (1). Comparing the results of model (9) and model (1), we can find that the number of infections and deaths under their optimal age-specific vaccination distributions of model (9) are increased. Specifically, the number of infections and deaths of China increased significantly (22.8% and 20.5%), but the number of infections and deaths of Italy (India) only increased 0.2% and 0.2%(3.8% and 2.3%). Besides, similar results when $\eta_{1} = \eta_{2} = \eta_{3} = 1/10$ are also shown in Suppl. Table S2.

Table 3 The final outcomes (mean and 95% CI) with the optimal age-specific distributions versus the uniform distribution ($v = 0.1\%$) for the three countries (China, Italy and India), when $\eta_{1} = 1/5,\eta_{2} = \eta_{3} = 1/10$ (model 9).

3.3 Optimal Reopening Strategies to Restore Social Contacts with Vaccination

After COVID-19 vaccines are administered among the population, it is expected to reopen or even gradually restore social contacts as normal as that before the COVID-19 epidemic. Here, we further explore the effect of gradual reopening polices from contact control measures under the optimal age-specific vaccination strategy obtained by minimizing the cumulative number of infections. We simulated the total number of infections during a time period of 6 months under different degrees of contact control release and for different daily vaccination rates $\nu$ = 0–0.15% with the initiation time of vaccination as $T + 1$. We considered the following scenarios of contact control release at different sites:

• (a) Reopen the schools: $c_{ij} (t) = qc_{ij}^{s} (0) + (c_{ij}^{w} (t) + c_{ij}^{h} (t) + c_{ij}^{o} (t)),$$t > T$

• (b) Reopen the workplace: $c_{ij} (t) = qc_{ij}^{w} (0) + (c_{ij}^{s} (t) + c_{ij}^{h} (t) + c_{ij}^{o} (t))$, $t > T$

• (c) Reopen households:$c_{ij} (t) = qc_{ij}^{h} (0) + (c_{ij}^{w} (t) + c_{ij}^{s} (t) + c_{ij}^{o} (t))$, $t > T$

• (d) Reopen other locations: $c_{ij} (t) = qc_{ij}^{o} (0) + (c_{ij}^{w} (t) + c_{ij}^{h} (t) + c_{ij}^{s} (t))$, $t > T$

• (e) Reopen all above: $c_{ij} (t) = qc_{ij}^{0} = q(c_{ij}^{s} (0) + c_{ij}^{w} (0) + c_{ij}^{h} (0) + c_{ij}^{o} (0))$, $t > T$

where $q_{\rm c} < q \le 1$. Notice that the contact control is completely released (restored to normal life) when $q = 1$.

Figure 5 shows the simulation results for the cumulative number of infections (in log10 scale) for India during the time period of 180 days [T + 1, T 180] with different vaccination rates $\nu$ (ranging 0–1.5%) and different degrees of reopening $q$(ranging ${q}_{\mathrm{c}}$ to 1) under different releasing times, T + 1, T + 30 and T + 60. From Fig. 5, we can see that the releasing rate $q$ has a significant effect on the number of infections. For the case of releasing all contact controls completely, the number of infections may exceed 100 million in 6 months in India if $q > 0.7$ without vaccination, i.e., $\nu = 0$ (Fig. 5$e_{1}$). Moreover, even with vaccination initiated, it may result in a high number of infections if the contact control measure is released too early, i.e., early release for one month may lead to almost fivefold difference in the number of infected people in India (see Fig. 5$e_{2}$, $e_{3}$). For the cases of partial contact control release at different sites, releasing “other contacts” brings the highest number of infected people, followed by releasing schools and households. The risk of releasing contacts in workplace is minimal.

Fig. 5

Simulation results for the number of infections (in log10 scale) for India during the time period [T + 1, T + 180] for five different scenarios of contact control release (a–e) for different values of $q$ and $\nu$ under different releasing times, T + 1 (1st row), T + 30 (2nd row) and T + 60 (3rd row). The optimal age-specific vaccination strategy with the initiation time of vaccination as $T + 1$ was assumed for all the simulation scenarios.

For the case of Italy (Suppl. Fig. S5), the effect of different releasing strategies and releasing times is similar to that in India. In addition, reopening schools would have a small effect on the number of infections compared to that reopening other sites (Suppl. Fig. S5). For the case of China, we investigated the number of infections after reopening different sites if one infected case would be imported (shown in Suppl. Fig. S6). When the detection rate is high, δ = 0.55, partially reopening some sites will not cause a pandemic, but dozens of people could be infected (Suppl. Fig. S6) if the reopening rate is high and vaccination rate is low, say, $q > 0.9$ and $v \le 0.05\%$. However, if the detection rate is low, δ  =  0.2, it might cause millions of people to be infected within 6 months if all the sites would be reopened.

Considering that partially reopening different sites or locations for social contacts may lead to changes of the optimal age-specific vaccination distribution, we evaluated the effect of partially reopening different sites on the optimal age vaccination distributions. In Fig. 6, we show the optimal age-specific distributions for the endpoint of the basic reproduction number under different partially reopening policies, i.e., only releasing contacts in schools, workplaces, households or other locations compared to that with full reopening. We assumed the vaccination rate ν  = 0.1%. From Fig. 6, we can see that the vaccination priority should be given toward younger people (10–30 years old) in China if the social contacts are just open for schools or households, while the vaccination priority might need to be given to elder people (30–45 years old) in China if the workplace is open first (Fig. 6a). For the case of Italy, the vaccination priority might need to shift toward younger population if the household is opened, but reopening schools and workplaces in Italy do not have much effect on the optimal age distribution (Fig. 6b). For the case of India, the vaccination priority might need to shift toward adult population if the workplace is opened, but reopening schools and households in India has little effect on the optimal age distribution (Fig. 6c). The differences in the effect of partially reopening different sites on the optimal age distributions for different countries are presumably due to the differences in age structures of their population (Fig. 3) and social contact patterns (Suppl. Fig. S1).

Fig. 6

Heat map of the optimal age-specific distribution under different reopening strategies. The vertical coordinates represent different reopening strategies: only release contacts in schools, only release contacts in workplaces, only release contacts in households, only release contacts in other locations and reopen all.

If the post-vaccination reopening is too fast and the detection rate is not high enough, it is possible to cause a new outbreak of COVID-19. Based on our model, we examined the basic reproduction number (R₀) as a function of the reopening rate ($q$) and detection rate (δ) under the optimal age-specific vaccination distribution. The contour plots of R₀ for the three countries (India, Italy and China) are shown in Fig. 7. Suppl. Figure S7 and Fig. S8, respectively. From Fig. 7 for the case of India, the estimated value of detection rate is ${\delta }_{\mathrm{f}}\hspace{0.17em}$= 0.4 and reopening rate is q = 0.48 and the basic reproduction number R₀< 1; thus, the epidemic is under control. However, if the detection rate is kept as the same and the vaccination lasts for 3 months with the vaccination rate ν = 0.1%, the reopening rate q is increased to > 0.7, it would result in R₀> 1, which would cause a new pandemic (Fig. 7a). However, if the vaccination lasts longer with a higher vaccination rate, the epidemic is still under check. For example, if the vaccination could last for 9 months (6 months) with a vaccination rate ν  = 0.1% (ν = 0.15%), the full reopening (q = 1) could not cause a new outbreak (Fig. 7d) in India (R₀< 1) if the detection rate is kept as the same. For the case of Italy, a similar trend is observed, it looks safe to fully open the social contacts if the vaccination could last for 9 months or longer with a high vaccination rate ν > 0.1% (Suppl. Fig. S7). For the case of China, it only requires 3 months with a vaccination rate around 0.1% to be safe for fully reopening social contacts if the high detection rate is kept (Suppl. Fig. S8).

Fig. 7

Contour plot of the basic reproduction number as a function of the contact control release rate (q) and the detection rate (δ) with different daily vaccination rates v = 0.1% (the solid line) and v = 0.15% (the dash line) under the optimal age-specific vaccination strategy in India. The vaccination periods are set to be 3 months (a), 6 months (b), 9 months (c) and 12 months (d). The red dot is the current value of these two parameters. (Color figure online)

4 Conclusions and Discussions

The COVID-19 is still widely spreading around the world and many people die of it every day. Vaccines offer a great hope for ending the COVID-19 pandemic, but an effective vaccination strategy is badly needed in order to quickly stop the epidemic and restore the normal life of people. Due to the limited manufacturing capacity, COVID-19 vaccines may not be immediately available to all the people who are willing to receive. It is necessary to develop priority guidelines for different groups of people to receive vaccines sequentially. Intuitively the high risk populations such as first responders, elderly and people with high-risk health conditions should receive the vaccines first (Dooling et al. 2020). The question is, how to prioritize the rest of the population for vaccination after the high risk population. In this study, we used the SEIR modeling approach to investigate the optimal age-specific vaccination strategies. The proposed age-structured SEIR model parameters are derived from literature or calibrated based on the observed data of COVID-19 epidemic. In particular, we also utilized the information of the age structure of the population (Fig. 3) and contact network (Suppl. Fig. S1) data in order to optimize the age-specific vaccination strategy for different countries. Compared with the previous literature (Bubar et al. 2020; Matrajt et al. 2020; Jentsch et al. 2021; Hunziker 2021), we used a continuous function, Beta distribution, to approximate the age-specific vaccination distribution, so that we could conveniently optimize the age distribution by minimizing the three endpoints with respect to the Beta distribution parameters ($\alpha$ and $\beta$).

Our results show that the optimal age-specific vaccination distribution of model (1) and model (9) is consistent and the vaccination priority are different for different outcomes. To minimize the total number of deaths, the vaccination priority should be given to the elderly, while the vaccination priority should be given to socially active younger people if the goal is to minimize the total number of infections. This general principle can be different for different countries since the age structure of the population and social contact patterns are different for different countries (Fig. 3; Suppl. Fig. S1). For example, the vaccination priority given to the middle-age people could minimize both total number of infections and total number of deaths in China, presumably due to the complicated interactions between the age structure of the population and the social contact patterns. This also indicates that sometimes vaccinating those younger people to interrupt transmission might prevent more deaths than vaccinating older people (Jentsch et al. 2021). The results based on the basic reproduction number and the number of infections are similar, presumably because the basic reproduction number is directly related to the spread of infections. Since in most of countries, the vaccine is supplied only for individuals younger than 65 and older than 18, we further consider the situation when individuals in the 4–13th age groups are uniformly vaccinated (19 < age < 65) (shown in Table 2). The results indicate that the current vaccination strategy is not the best in terms of transmission control or death control, but may be better than the uniform vaccination strategy in terms of control transmission for China.

It is worth noting that in our model, we assumed that the asymptomatic infections cannot be detected and the symptomatic infections could be detected and confirmed with a confirmation rate $\delta (t)$. Under this circumstance, the real reporting ratio of the total infections could be calculated by dividing the cumulative number of reported cases by the cumulative number of infections (symptomatic infections and asymptomatic infections), as shown in Suppl. Fig. S9. It follows from Suppl. Fig. S9 that the reporting ratios of China and Italy gradually increased and finally reached about 75%, while the reporting ratio of India reaches only 63%. Considering that China has taken very strict prevention and control measures and has made great efforts in testing, it is reasonable to assume that all symptomatic infected people will be found. However, this assumption may overestimate the reporting ratios of Italy and India. In addition, considering that the ratio of the symptomatic infections ($\rho$) may affect the reporting ratio of the total infections, we also implemented the sensitivity analysis of the parameter $\rho$, by reducing the value of $\rho$ by half and then doing parameter estimation and evaluating the optimal age-specific vaccination distributions of India and Italy. The reporting ratios of Italy and India at this time are shown in Suppl. Fig. S10 (39% and 31%). The optimal age-specific vaccination distributions for Italy and India are the same as those shown in Suppl. Table S1. So, our results show that the reporting ratio could not affect the optimal age-specific vaccination distribution.

With availability of effective vaccines, we expect to quickly restore normal life with regular social contacts. However, prematurely reopening social contacts during the vaccination stage may cause large number of infections or deaths, even initiate a new pandemic. A good strategy is to gradually or partially reopen some necessary sites or locations with a phased plan. We also examined the post-vaccination reopening strategies using the established age-structured SEIR model under the optimal age-specific vaccination distributions. Our simulation results show that it is safer to partially reopen the schools and workplaces, instead of households and other locations for the case in India (see Fig. 5). In addition, the optimal age-specific vaccination strategy needs to be adjusted accordingly if this is the case. If the schools are reopened, the vaccination priority should be shifted more toward children and teenagers; if the workplaces are reopened, the vaccination priority should be shifted more toward middle-aged people in India (see Fig. 6). It seems that, if all the sites are fully reopened for social contacts too early, it may cause a large number of infections (Fig. 5) or even initiate a new pandemic, possibly out of control (R₀> 1) in India if the vaccination rate and detection rate are not high enough (Fig. 7). For the cases of Italy and China, similar general principles can be applied, but the detailed reopening strategies need to be tailored due to the differences in age structures of the population and social contact patterns.

In conclusion, our results show that the age structures of the population and social contact patterns have a significant impact on the effect of age-specific vaccination strategies. In the case of limited vaccine resources, it needs to consider different age-specific priority guidelines for general population in order to control the COVID-19 pandemic more effectively. Moreover, different countries need to develop specific vaccination strategies according to the age structures of their population and social contact patterns. Our established age-structured SEIR models can also be used to evaluate post-vaccination reopening policies in order to safely restore to normal life. Although our models and methods are developed based on the data and situation of COVID-19 epidemic, the proposed age-structured modeling principles are generally applicable for future outbreaks of any infectious diseases.

We also recognize some limitations in our modeling practice. To obtain the optimal age vaccination distributions, we minimized the three endpoints, the basic reproduction number, the cumulative number of infections and the cumulative number of deaths, with respect to the two Beta distribution parameters (α, β), which may fall on the boundary of the search space (Fig. 4; Table 2). Actually this indicates that the age distribution is optimized toward the maximum or minimum of the age. Another endpoint, “years of life lost (YLL),” was also used to evaluate the effectiveness of vaccination strategies (Bubar et al. 2020; Hunziker 2021), which may result in shifting the vaccination priority to younger people. The proposed age-specific SEIR model contains many parameters, which are not identifiable based on the observed epidemic data only (daily cases and/or deaths). It is necessary to use the literature to determine the values for some of these parameters. Some sensitivity results show that that the uncertainty of these parameter values would not change the conclusions and principles of the modeling results (See the Supplementary Materials), although it may have some effects on the quantitative results. The proposed optimal age-specific vaccination strategies can be implemented in the vaccination scheduling system, that requires additional programming effort, compared to the simple uniform distribution or first-come-first-served strategies. But it is worth the effort if it can save thousands of lives or reduce the large number of infections. Moreover, due to the limitation of data and in order to simplify the model and reduce the number of estimated parameters, we do not consider the risk of breakthrough infection, re-infection or changes in the transmission or death rate of mutated variants of SARS-CoV-2, as well as their immune escape features. Besides, the impact of the side effects of vaccines during the early vaccine promoting stage on the vaccine uptake strategic decision making process is not considered. These can be investigated in the future.