1 Introduction

The COVID-19 pandemic, a massive global health crisis, has been bringing a great threat to global health. As of July 15, 2022, the new coronavirus (SARS-CoV-2) has spread to over 200 countries with 557,917,904 confirmed cases and 6,358,899 deaths (WHO 2022). The genetic variants of SARS-CoV-2, including Alpha variants, Delta variants, Omicron variants, etc., have been altering the course of COVID-19 pandemic (Walensky et al. 2021; Christensen et al. 2022; Abdool and de Oliveira 2021). Because of the persistent increasing of transmissibility, newly emerged variants quickly spread to most part of the world and replace the dominate strain (Shah et al. 2021; Krause et al. 2021). Furthermore, evidences were well documented to support that the continuous variation of SARS-CoV-2 can significantly increase the risk of vaccines breakthrough infections (Christensen et al. 2022).

During the last two years, many regions and countries experienced multiple epidemic waves or new outbreaks even with various non-pharmaceutical interventions (NPIs) such as lockdown, keeping social distancing (WHO 2022) and widespread availability of effective and safe vaccines (Krause et al. 2021). It is suspected that the series of epidemic waves were due to the lifting of lockdown in order to revive the economy. That is, the existing strategy is to interactively enhance and release the NPIs, which can easily result in the resurgence of COVID-19 epidemics. Therefore, the enhanced and persistent of the present NPIs are expected to avoid subsequent waves (Hsiang et al. 2020; Kucharski et al. 2020; Worby et al. 2020), as which have been demonstrated to be effective in mitigating the COVID-19 pandemic (Karatayeva et al. 2020; Kucharski et al. 2020; Tang et al. 2020a; Du et al. 2020).

As we mentioned above, this public health crisis has required the comprehensive NPIs and placed significant psychological burdens on individuals, which have definitely driven large-scale behaviour changes (Myers et al. 2020; Van Bavel et al. 2020; Betsch 2020; Yin et al. 2021). Driven by the lifting or enhancing of NPIs or the shifting of self-awareness of infection risks, human behaviour changes were proved to have significantly influenced the transmission dynamics of infectious diseases. As pointed out by Fergeson (2007), the prevalence or perceived risk-driven behaviour change plays an important role in the spread of infectious diseases. In particular, the study by Manfredi and d’Onofrio (2009) showed that human behaviour change might be a critical explaining factor for oscillations in infectious disease endemics. A number of models were formulated to investigate the interaction between behaviour changes and resurgence of infections (Funk et al 2010; Verelst et al. 2016; Manfredi and d’Onofrio 2013; Poletti et al. 2009, 2012). Game theory was widely used to formulate the dynamics of human behavioural changes, by assuming that individuals would make the best decisions based on a trade-off between two different strategies, adopting normal or altered behaviours (Poletti et al. 2009, 2012; Jentsch et al. 2021).

Recently, there are several studies that examined the impact of behavioural changes on COVID-19 epidemics, by assuming a constant proportion of the population choosing to change their behaviours (Buonomo and Della Marca 2020; Acuña-Zegarra et al. 2020), or including the reduced contact rate and/or the increased quarantine rate (Zhou et al. 2020). In the study (Moyles et al. 2021), by dividing the population into three statuses with different level of social distancing, the authors presented many interesting results on how the shifting of social distancing, driven by the measured active and total cases as well as the perceived cost of isolating, affects the transmission dynamics of COVID-19 in Ontario, Canada. In this study, we propose a new multi-scale model to quantify the co-evolution of behaviour changes and COVID-19 epidemics to reveal the insight and underlying mechanisms of multiple epidemic waves. Using the concept of game theory for cost-benefit consideration of alternative decisions, we further identify the key factors of behaviour change to mitigate the epidemics, and finally provide the quantitative guidance for relieving NPIs with continuous vaccination.

2 Method

2.1 Model Formulation

Fig. 1
figure 1

Schematic diagram for coupling the COVID-19 transmission dynamics and behavioural change dynamics

Full size image

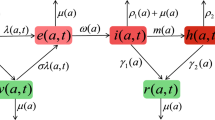
We propose a co-evolution model linking the behavioural change dynamics to the disease transmission dynamics (Fig. 1), which extends the model presented by Poletti et al. (2009, 2012) and Jentsch et al. (2021). The SEIR model is modified to an SEIAHR model to describe the transmission dynamics of COVID-19 considering that infective individuals may suffer symptoms or no symptoms. In details, the total population N is divided into susceptible individuals (S), exposed individuals (E), infectives with symptoms (I), asymptomatic infectives (A), confirmed and isolated individuals (H) and symptomatic recovered individuals (\(R_I\)) and asymptomatic recovered individuals (\(R_A\)). As the confirmed population have limited social activities, we assume that they immediately become isolated once confirmed, hence cannot transmit SARS-CoV-2 further during their infectious period. Because the asymptomatically infected individuals show no symptoms, a large ratio of them weren’t tested and confirmed (Weitz et al. 2020a; Subramanian et al. 2021). Therefore, we assume that the asymptomatically infected individuals do not move to the confirmed and isolated class (H) and will recover directly (Weitz et al. 2020a; Subramanian et al. 2021).

Though only susceptible individuals are exposed to the risk of COVID-19 infection, asymptomatically infected and recovered individuals who did not suffer symptoms have no awareness of their infection, thus would behave similarly as susceptible individuals. Thus, in this study, we assume that the self-protection behaviours can be adopted by not only susceptible individuals, but also asymptomatic infectives and recovered individuals who did not experience symptoms. In contrast, we assume that all symptomatic infected individuals would take the same actions (i.e., no behavioural changes in this class). Thus, in our model, individuals suffering no symptoms (\(S,E,A,R_A\)) are supposed to be able to reduce their susceptibility or infectivity by changing behaviours in response to COVID-19 outbreaks. Thus, reduction of contact rates or transmission probability (i.e., transmission rate) can be achieved by adopting self-protective behaviours, such as limiting travels, keeping social distancing, wearing masks, washing hands, etc.

Basically, an individual’s behaviour change is assumed to be driven by the evaluation and comparison of payoffs between the two behaviours. With the cost-benefit consideration, individuals are supposed to change their behaviours when they realize that the other behaviour is more beneficial with low cost. The integrated co-evolution model is the result of coupling two dynamic processes: the disease transmission process and the behavioural change process, as illustrated in Fig. 1. The two processes were modelled in two different time scales since the contacts related to the transmission of virus are physical person-to-person interactions, which is less frequently than the contacts related to the spread of information, which could be accessed by telephone, media and online, etc. Thus, we introduce two time-units: t as the time unit of disease transmission and \(\tau \) as the time unit of behavioural changes, and assume that \(t=\varepsilon \tau \), where \(\varepsilon \) is a scaling parameter. In this study, given the transmission dynamics of COVID-19, we take the time unit t as day.

Disease Transmission Dynamics With the above assumptions, the susceptible, exposed, asymptomatic infected and asymptomatic recovered individuals are divided into two subclasses: individuals adopting the normal behaviour (\(S_n,E_n,A_n,R_{A_n}\)) and individuals adopting the altered behaviour (\(S_a,E_a,A_a,R_{A_a}\)). Then the model of disease transmission process is given as follows:

$$\begin{aligned} \left\{ \begin{array}{lcl} {S'_{n}}(t)&{}=&{}- \lambda S_{n}, \\ {S'_{a}}(t)&{}=&{}- q\lambda S_{a}, \\ {E'_{n}}(t)&{}=&{}\lambda S_{n} - \sigma E_{n}, \\ {E'_{a}}(t) &{}=&{}q\lambda S_{a} - \sigma E_{a}, \\ {I'(t)}&{}=&{}\varrho \sigma E_{n} + \varrho \sigma E_{a} - \left( {\delta _{I}(t) + \gamma _{I}} \right) I, \\ {A'_{n}(t)}&{}=&{}\left( {1 - \varrho } \right) \sigma E_{n} - \gamma _{A}A_{n}, \\ {A'_{a}(t)}&{}=&{}\left( {1 - \varrho } \right) \sigma E_{a} - \gamma _{A}A_{a}, \\ {H'(t)}&{}=&{}\delta _{I}(t)I - \left( {\alpha (t) + \gamma _{H}} \right) H, \\ {R'_{I}(t)}&{}=&{}\gamma _{I}I + \gamma _{H}H, \\ {R'_{A_{n}}(t)}&{}=&{}\gamma _{A}A_{n}, \\ {R'_{A_{a}}(t)}&{}=&{}\gamma _{A}A_{a}, \\ \end{array} \right. \end{aligned}$$
(1)

where \(\lambda =(\beta _I I+\beta _A A_n+q\beta _A A_a)/N\) is the force of infection, which is composed of three parts: the infection by symptomatic infected individuals (\(\beta _I I/N\)), the infection by asymptomatic infected individuals adopting the normal behaviour (\(\beta _A A_n/N\)), and the infection by asymptomatic infected individuals adopting the altered behaviour (\(q\beta _A A_a/N\)). \((\beta _I,\beta _A)\) are the transmission rates of symptomatic infected and asymptomatic infected individuals, respectively. As behaviour changed, the infectivity of asymptomatic infected individuals and the susceptibility of susceptible individuals could be reduced. That is, the transmission rate related to the humans with altered behaviours is lower than those with normal behaviours, where the parameter \(q(0\le q\le 1)\) is the corresponding multiplier factor of the reduction of transmission rate due to alternative behaviours. \(1/\sigma \) is the incubation period and \(\varrho \) is the probability with symptoms after being infected. \(\delta _I(t)\) is the time-varying diagnosis rate of symptomatic infected individuals and \(\alpha (t)\) is the time-dependent disease-induced death rate. \((\gamma _I,\gamma _A,\gamma _H)\) are the recovery rates of symptomatic infected, asymptomatic infected and confirmed individuals, respectively.

Behavioural Change Dynamics Models by integrating disease transmission dynamics and behavioural change dynamics have been proposed to study the spread of infectious diseases, including COVID-19 (Funk et al 2010; Verelst et al. 2016; Manfredi and d’Onofrio 2013; Poletti et al. 2009, 2012; Jentsch et al. 2021). The modeling framework and concept of game theory were used to explain the behavioural change dynamics during an outbreak of infectious diseases and their effects on the disease epidemics. Here we review and use these modeling frameworks and concepts to develop our multi-scale models for COVID-19 epidemics.

Perceived Infection The perceived risk of infection contributes to the evolution of human behavioural changes in response to the scare of being infected, which is a comprehensive index describing the perceived information of the epidemic risk. Usually, human behavioural changes appear to be compelled largely due to the lifting and enhancing of NPIs. Therefore, the perceived infection (or information index) is assumed to be stimulated by the self-awareness of the epidemic state and indirectly stimulated by the NPIs implemented by the government. It is reasonable to assume that the intensity of self-awareness is proportional to the number of daily reported cases, with a response rate \(\eta _1\). The response function of the perceived infection to the shifting of NPIs can be various forms following the patterns of the implementation of NPIs. For simplicity, we assume that it’s also proportional to the daily reported cases with a response rate \(\eta _2\). And, the perceived infection (or information index) is assumed to be faded through an exponentially memory fading mechanism. Thus, we have the following equation:

$$\begin{aligned} M'(t)=\eta \delta _I(t)I-\nu M, \end{aligned}$$
(2)

where M(t) is an information variable governing the signal available to individuals as a function of daily reported cases, and \(\eta =\eta _1+\eta _2\) denotes the response rate of self-awareness and NPIs on the number of newly confirmed cases. \(\nu \) is the decay rate of the perceived infection (or information index).

Payoffs The expected payoffs to adopt two different behaviours: normal behaviour and altered behaviour, which can be recognized as the negative of the costs, are assumed to be linearly dependent on the perceived infection. In addition to the cost for the risk of infection (which is assumed to be higher for normal behaviour), individuals adopting altered behaviour pay an extra constant cost. Thus, the payoffs with the normal behaviour and the altered behaviour are respectively:

$$\begin{aligned} P_n (t)=-m_n M(t),~~ P_a(t)=-k-m_a M(t) \end{aligned}$$
(3)

with \(m_n>m_a\), where \(m_n\) and \(m_a\) are parameters related to the risk of infection by adopting two different strategies and k is the extra cost of changing behaviours.

Imitation Process The dynamics of behavioural changes can be described by the imitation dynamics, which is a learning process. Expected payoffs of two different behavioural strategies are compared with each other and individuals may change strategy when they become aware that their payoff can be increased if adopting another behaviour. Denote \(\Delta P=P_n-P_a\), then the imitation dynamics in a two-strategy game can be described by

$$\begin{aligned} x'=\vartheta x(1-x)\phi \Delta P=\omega x(1-x)\Delta P, \end{aligned}$$
(4)

where x and \(1-x\) are the fractions of population performing the two strategies. \(\varrho \) is the rate at which individuals communicate with each other and \(\phi \) is the probability of changing decision. Then the sign of \(x'\) is determined by \(\Delta P\), illustrating the changing direction of behaviours (from normal to altered or from altered to normal). The imitation process has no concern with the transition among epidemiological classes, but only drives behaviour changing. Hence encounters between individuals in the imitation process would only result in migration between (\(S_n\) and \(S_a\)), (\(E_n\) and \(E_a\)), (\(A_n\) and \(A_a\)), and (\(R_{A_n}\) and \(R_{A_a}\)). In particular, when susceptible individuals with the normal behaviour (\(S_n\)) compare their payoff with those adopting the altered behaviour (\(S_a,E_a,A_a,R_{A_a}\)), and find that \(\Delta P<0\), then \(S_n\) will migrate to \(S_a\), and vice versa. The migration between (\(E_n\) and \(E_a\)), (\(A_n\) and \(A_a\)), and (\(R_{A_n}\) and \(R_{A_a}\)) are similar. Thus, we can model the imitation dynamics in the population with two alternative behaviours as follows:

$$\begin{aligned} \left\{ \begin{array}{rcl} {S'_{n}}(\tau )&{}=&{}\frac{\omega S_{a}\left( {S_{n} + E_{n} + A_{n} + R_{n}} \right) \mathrm {\Delta }P\mathcal {H}\left( {\mathrm {\Delta }P} \right) }{N} + \frac{\omega S_{n}\left( {S'_{a} + E_{a} + A_{a} + R_{a}} \right) \mathrm {\Delta }P\mathcal {H}\left( {- \mathrm {\Delta }P} \right) }{N}, \\ {S'_{a}}(\tau )&{}=&{}- \frac{\omega S_{a}\left( {S_{n} + E_{n} + A_{n} + R_{n}} \right) \mathrm {\Delta }P\mathcal {H}\left( {\mathrm {\Delta }P} \right) }{N} - \frac{\omega S_{n}\left( {S_{a} + E_{a} + A_{a} + R_{a}} \right) \mathrm {\Delta }P\mathcal {H}\left( {- \mathrm {\Delta }P} \right) }{N}, \\ {E'_{n}}(\tau )&{}=&{}\frac{\omega E_{a}\left( {S_{n} + E_{n} + A_{n} + R_{n}} \right) \mathrm {\Delta }P\mathcal {H}\left( {\mathrm {\Delta }P} \right) }{N} + \frac{\omega E_{n}\left( {S_{a} + E_{a} + A_{a} + R_{a}} \right) \mathrm {\Delta }P\mathcal {H}\left( {- \mathrm {\Delta }P} \right) }{N}, \\ {E'_{a}}(\tau )&{}=&{}- \frac{\omega E_{a}\left( {S_{n} + E_{n} + A_{n} + R_{n}} \right) \mathrm {\Delta }P\mathcal {H}\left( {\mathrm {\Delta }P} \right) }{N} - \frac{\omega E_{n}\left( {S_{a} + E_{a} + A_{a} + R_{a}} \right) \mathrm {\Delta }P\mathcal {H}\left( {- \mathrm {\Delta }P} \right) }{N}, \\ {A'_{n}(\tau )}&{}=&{}\frac{\omega A_{a}\left( {S_{n} + E_{n} + A_{n} + R_{n}} \right) \mathrm {\Delta }P\mathcal {H}(\mathrm {\Delta }P)}{N} + \frac{\omega A_{n}\left( {S_{a} + E_{a} + A_{a} + R_{a}} \right) \mathrm {\Delta }P\mathcal {H}( - \mathrm {\Delta }P)}{N}, \\ {A'_{a}(\tau )}&{}=&{}- \frac{\omega A_{a}\left( {S_{n} + E_{n} + A_{n} + R_{n}} \right) \mathrm {\Delta }P\mathcal {H}\left( {\mathrm {\Delta }P} \right) }{N} - \frac{\omega A_{n}\left( {S_{a} + E_{a} + A_{a} + R_{a}} \right) \mathrm {\Delta }P\mathcal {H}\left( {- \mathrm {\Delta }P} \right) }{N}, \\ {R'_{n}(\tau )}&{}=&{}\frac{\omega R_{a}\left( {S_{n} + E_{n} + A_{n} + R_{n}} \right) \mathrm {\Delta }P\mathcal {H}\left( {\mathrm {\Delta }P} \right) }{N} + \frac{\omega R_{n}\left( {S_{a} + E_{a} + A_{a} + R_{a}} \right) \mathrm {\Delta }P\mathcal {H}\left( {- \mathrm {\Delta }P} \right) }{N}, \\ {R'_{a}(\tau )}&{}=&{}- \frac{\omega R_{a}\left( {S_{n} + E_{n} + A_{n} + R_{n}} \right) \mathrm {\Delta }P\mathcal {H}\left( {\mathrm {\Delta }P} \right) }{N} - \frac{\omega R_{n}\left( {S_{a} + E_{a} + A_{a} + R_{a}} \right) \mathrm {\Delta }P\mathcal {H}\left( {- \mathrm {\Delta }P} \right) }{N}. \\ \end{array} \right. \end{aligned}$$
(5)

Co-evolution Model by Coupling Two Dynamic Processes Coupling the transmission model (1) and the imitation model (5), then we have

$$\begin{aligned} \begin{array}{lcll} {S'_{n}}(t)&{}=&{}- \lambda S_{n} + \frac{1}{\alpha }&{}\\ &{}&{} \left[\frac{\omega S_{a}\left( {S_{n} + E_{n} + A_{n} + R_{n}} \right) \mathrm {\Delta }P\mathcal {H}(\mathrm {\Delta }P)}{N} + \frac{\omega S_{n}\left( {S_{a} + E_{a} + A_{a} + R_{a}} \right) \mathrm {\Delta }P\mathcal {H}( - \mathrm {\Delta }P)}{N} \right],\quad (6a)\\ {S'_{a}}(t)&{}=&{}- q\lambda S_{a} - \frac{1}{\alpha }&{}\\ &{}&{}\left[\frac{\omega S_{a}\left( {S_{n} + E_{n} + A_{n} + R_{n}} \right) \mathrm {\Delta }P\mathcal {H}\left( {\mathrm {\Delta }P} \right) }{N} + \frac{\omega S_{n}\left( {S_{a} + E_{a} + A_{a} + R_{a}} \right) \mathrm {\Delta }P\mathcal {H}( - \mathrm {\Delta }P)}{N} \right], \quad (6b)\\ {E'_{n}}(t)&{}=&{}\lambda S_{n} - \sigma E_{n} + \frac{1}{\alpha }&{}\\ &{}&{}\left[\frac{\omega E_{a}\left( {S_{n} + E_{n} + A_{n} + R_{n}} \right) \mathrm {\Delta }P\mathcal {H}(\mathrm {\Delta }P)}{N} + \frac{\omega E_{n}\left( {S_{a} + E_{a} + A_{a} + R_{a}} \right) \mathrm {\Delta }P\mathcal {H}( - \mathrm {\Delta }P)}{N} \right], \quad (6c)\\ {E'_{a}}(t)&{}=&{}q\lambda S_{a} - \sigma E_{a} - \frac{1}{\alpha }&{}\\ &{}&{}\left[\frac{\omega E_{a}\left( {S_{n} + E_{n} + A_{n} + R_{n}} \right) \mathrm {\Delta }P\mathcal {H}\left( {\mathrm {\Delta }P} \right) }{N} + \frac{\omega E_{n}\left( {S_{a} + E_{a} + A_{a} + R_{a}} \right) \mathrm {\Delta }P\mathcal {H}\left( {- \mathrm {\Delta }P} \right) }{N} \right],\quad (6d)\\ {I'(t)}&{}=&{}\varrho \sigma E_{n} + \varrho \sigma E_{a} - \left( {\delta _{I}(t) + \gamma _{I}} \right) I,\quad (6e)\\ {A'_{n}(t)}&{}=&{}\left( {1 - \varrho } \right) \sigma E_{n} - \gamma _{A}A_{n} +\frac{1}{\alpha }\quad \\ &{}&{}\left[\frac{\omega A_{a}\left( {S_{n} + E_{n} + A_{n} + R_{n}} \right) \mathrm {\Delta }P\mathcal {H}(\mathrm {\Delta }P)}{N} + \frac{\omega A_{n}\left( {S_{a} + E_{a} + A_{a} + R_{a}} \right) \mathrm {\Delta }P\mathcal {H}( - \mathrm {\Delta }P)}{N} \right],\quad (6f)\\ {A'_{a}(t)}&{}=&{}\left( {1 - \varrho } \right) \sigma E_{a} - \gamma _{A}A_{a} -\frac{1}{\alpha }\\ &{}&{}\left[\frac{\omega A_{a}\left( {S_{n} + E_{n} + A_{n} + R_{n}} \right) \mathrm {\Delta }P\mathcal {H}(\mathrm {\Delta }P)}{N} + \frac{\omega A_{n}\left( {S_{a} + E_{a} + A_{a} + R_{a}} \right) \mathrm {\Delta }P\mathcal {H}( - \mathrm {\Delta }P)}{N} \right], \quad (6g)\\ {H'(t)}&{}=&{}\delta _{I}(t)I - \left( {\alpha (t) + \gamma _{H}} \right) H,\quad (6h)\\ {R'_{I}(t)}&{}=&{}\gamma _{I}I + \gamma _{H}H,\quad (6i)\\ {R'_{n}(t)}&{}=&{}\gamma _{A}A_{n} + \frac{1}{\alpha }\\ &{}&{}\left[\frac{\omega R_{a}\left( {S_{n} + E_{n} + A_{n} + R_{n}} \right) \mathrm {\Delta }P\mathcal {H}\left( {\mathrm {\Delta }P} \right) }{N} + \frac{\omega R_{n}\left( {S_{a} + E_{a} + A_{a} + R_{a}} \right) \mathrm {\Delta }P\mathcal {H}\left( {- \mathrm {\Delta }P} \right) }{N} \right],\quad (6j)\\ {R'_{a}(t)}&{}=&{}\gamma _{A}A_{a} -\frac{1}{\alpha }\\ &{}&{} \left[{\frac{\omega R_{a}\left( {S_{n} + E_{n} + A_{n} + R_{n}} \right) \mathrm {\Delta }P\mathcal {H}\left( {\mathrm {\Delta }P} \right) }{N} + \frac{\omega R_{n}\left( {S_{a} + E_{a} + A_{a} + R_{a}} \right) \mathrm {\Delta }P\mathcal {H}\left( {- \mathrm {\Delta }P} \right) }{N}} \right],\quad (6k)\\ {M'(t)}&{}=&{}\eta \delta _{I}(t)I - \nu M.\quad (6l)\\ \end{array} \end{aligned}$$
(6)

where \(\mathcal {H}(\cdot )\) is the Heaviside function. \(\mathcal {H}(\Delta P)=1\) when \(\Delta P\ge 0\) and \(\mathcal {H}(\Delta P)=0\) when \(\Delta P<0\). Define \(B=(S_n+E_n+A_n+R_n)/(S+E+A+R_A)\), where \(S=S_n+S_a,E=E_n+E_a,A=A_n+A_a,R_A=R_n+R_a\). B(t) (\(1-B(t)\)) denotes the ratio of humans with normal behaviours (altered behaviours) in the corresponding population with potential shifting of behaviours at time t. Then by taking derivative of both sides of (\(S_n+E_n+A_n+R_n )=B(S+E+A+R_A)\) with respect to time t, we have that (\(S_n+E_n+A_n+R_n)'=B'(S+E+A+R_A )+B(S+E+A+R_A)'\), where \((S_n+E_n+A_n+R_n)'\) can be obtained by adding equations (6a), (6c), (6f) and (6j) of model (6) and \((S+E+A+R_A)'\) can also be obtained by adding Eqs. (6a)–(6d), (6f), (6g), (6j), (6k) in model (6). Assuming that \(S_n/S=E_n/E=A_n/A=R_n/R_A =B\), the above equation can be significantly reduced and the equation of \(B'\) can be derived. Further, by adding the equations of \(E_n\) and \(E_a\), we can obtain the equation of E, similarly, we have the equations for the rest compartments. Through the above process, model (6) can be reduced to the following co-evolution model of the transmission dynamics and the behavioural change dynamics:

$$\begin{aligned} \left\{ \begin{array}{lcl} S'&{}=&{}- \lambda \left[{B + q\left( {1 - B} \right) } \right]S, \\ E'&{}=&{}\lambda \left[{B + q\left( {1 - B} \right) } \right]S - \sigma E, \\ I'&{}=&{}\varrho \sigma E - \left( {\delta _{I}(t) + \gamma _{I}} \right) I, \\ A'&{}=&{}\left( {1 - \varrho } \right) \sigma E - \gamma _{A}A, \\ H'&{}=&{}\delta _{I}(t)I - \left( {\alpha (t) + \gamma _{H}} \right) H, \\ R'_{I}&{}=&{}\gamma _{I}I + \gamma _{H}H, \\ R'_{A}&{}=&{}\gamma _{A}A, \\ M'&{}=&{}\eta \delta _{I}(t)I - \nu M, \\ B'&{}=&{}\frac{\rho B\left( {1 - B} \right) \left( {1 - mM} \right) \left( {S + E + A + R_{A}} \right) }{N}, \\ \end{array} \right. \end{aligned}$$
(7)

where \(\rho =k\omega /\varepsilon , m=(m_n-m_a)/k\) and \(\lambda =(\beta _I I+[B+q(1-B)]\beta _A A)/N\). \(1-mM\) represents the balance between payoffs associated with two behaviours, and 1/m defines a threshold determining which behaviour is more beneficial, and \(\rho \) can be recognized as the speed of spontaneous behavioural changes with respect to transmission dynamics. The definitions and values of parameters are given in Table 1. There are four key factors related to the behavioural change dynamics: m, the sensitivity of individuals to perceived infection (a higher value of m indicating the higher sensitivity); \(\eta \), the speed of raising the risk awareness; \(\nu \), the persistence to maintain the risk awareness; \(\rho \), the spread rate of the behaviour changes among individuals. In our model framework, there are two aspects of behaviour changes affecting the transmission dynamics of COVID-19: one is the ratio of the population with altered behaviour (\(1-B(t)\)), and the other aspect is the reduction factor q in the transmission. Note further that the NPIs can also drive the behavioural changes. Therefore, due to the difference and the shifting of NPIs, the efficacy of the altered behaviours in the reduction of transmission rate can be different in different regions and can also shift over time in the fixed region. We will therefore deeply analyze how the two aspects determine the development trend of COVID-19 epidemics, and identify the key role in generating the different patterns of multiple epidemic waves.

Basic Reproduction Number When all individuals are adopting the normal behaviour, i.e., \(B=1\), the basic reproduction number can be obtained as

$$\begin{aligned} R_{0}^{n} = \frac{\varrho \beta _{I}}{\delta _{I} + \gamma _{I}} + \frac{(1 - \varrho )\beta _{A}}{\gamma _{A}}. \end{aligned}$$
(8)

When all individuals are adopting the altered behaviours, i.e., \(B=0\), the basic reproduction number can be derived as

$$\begin{aligned} R_{0}^{a} = \frac{q\varrho \beta _{I}}{\delta _{I} + \gamma _{I}} + \frac{q^{2}(1 - \varrho )\beta _{A}}{\gamma _{A}}.~ \end{aligned}$$
(9)

Considering the co-evolution of behavioural changes and the disease transmission dynamics (\(B\ne 0\) and \(B\ne 1\)), the proportion of individuals adopting altered behaviours and the number of susceptible individuals are time-varying, under which we could obtain the time-varying reproduction number R(t), referring to as the effective reproduction number,

$$\begin{aligned} R(t) = \frac{\varrho \beta _{I}}{\delta _{I} + \gamma _{I}}\left[{B + q\left( {1 - B} \right) } \right]+ \frac{\left( {1 - \varrho } \right) \beta _{A}}{\gamma _{A}}\left[{B + q\left( {1 - B} \right) } \right]^{2}.~ \end{aligned}$$
(10)

This is a combination of the above two basic reproduction numbers.

Model Extension by Involving Vaccination Considering a continuous vaccination regime, we can extend model (7) to the following system

$$\begin{aligned} \left\{ \begin{array}{lcl} S'&{}=&{}- \lambda \left[{B + q\left( {1 - B} \right) } \right]S - p\mu (t)S, \\ E'&{}=&{}\lambda \left[{B + q\left( {1 - B} \right) } \right]S - \sigma E, \\ I'&{}=&{}\varrho \sigma E - \left( {\delta _{I}(t) + \gamma _{I}} \right) I, \\ A'&{}=&{}\left( {1 - \varrho } \right) \sigma E - \gamma _{A}A, \\ H'&{}=&{}\delta _{I}(t)I - \left( {\alpha (t) + \gamma _{H}} \right) H, \\ R'_{I}&{}=&{}\gamma _{I}I + \gamma _{H}H, \\ R'_{A}&{}=&{}\gamma _{A}A, \\ V'&{}=&{}p\mu (t)S, \\ M'&{}=&{}\eta \delta _{I}(t)I - \nu M, \\ B'&{}=&{}\frac{\rho B\left( {1 - B} \right) \left( {1 - mM} \right) \left( {S + E + A + R_{A}} \right) }{N}, \\ \end{array} \right. \end{aligned}$$
(11)

where \(\mu (t)\) is the time-dependent vaccination rate, as it should be small initially since the availability of the number of vaccine doses was limited at the beginning in December 2020, and then exponentially increase as the production of COVID-19 vaccines was accelerated, and finally it could be plateaued to a constant level depending on the daily vaccination capacity. Thus, we model \(\mu (t)\) as a logistic increasing function of time t with the following form:

$$\begin{aligned} \mu (t) = \frac{\mu _{0}\mu _{b}}{\mu _{0} + \left( \mu _{b} - \mu _{0} \right) e^{- r_{\mu }t}}, \end{aligned}$$
(12)

where \(\mu _0\) (\(\mu _b\)) is the initial (maximum) vaccination rate, \(r_{\mu }\) is the exponential increasing rate of the vaccination. The vaccination efficacy is denoted by p with \(p=95\%\) in the USA (CDC 2021a, b) and the effectively vaccinated population is assumed to be immune to COVID-19 and moved to the class V (the effectively vaccinated compartment). Consequently, the time-dependent vaccination coverage can be defined as:

$$\begin{aligned} VC(t) = \frac{\int _{t_{0}}^{t}{\mu (t)S(t)dt}}{N(t)}, \end{aligned}$$
(13)

where \(t_0\) is the starting time of vaccination, which was set as December 20th, 2020 for USA.

Table 1 Parameter definition and estimation
Full size table

2.2 Data

The COVID-19 epidemic data were obtained from the Johns Hopkins University Center for Systems Science and Engineering (JHU CCSE) and the data are available on the Github and the Humanitarian Data Exchange (Github 2021; HDE 2021). We used the data of daily COVID-19 confirmed cases and accumulative death cases in Hongkong, Japan, USA, and the world (including 273 countries or regions), as shown in Fig. 2. We assumed that the local community transmission began when there were continuously reported cases for 5 days. Consequently, the data collected in Hongkong, Japan, USA, and the whole world started on February 4th, 11th, 29th, and January 23rd, 2020 respectively. As we can see from the epidemic data, Hongkong, Japan and USA have experienced multiple epidemic waves during 2020, and the last wave was much more serious with a much higher peak in Japan and USA than that of the first two waves. We obtained the data of daily vaccinated population in USA (who received two doses) from the US Centers for Disease Control and Prevention (CDC 2021c). The data were released and analyzed anonymously.

2.3 Model Fitting and Parameter Estimation Methods

We fixed some parameters in model (7) including the incubation period (\(1/\sigma \)), recovery rate of asymptomatic infections (\(\gamma _A\)) and symptomatic infections (\(\gamma _I\)), based on the existing literatures as listed in Table 1. The initial total population was fixed as the whole population in the corresponding regions or countries, and the initial confirmed and isolated, and recovered populations were obtained from the database (Table 1). Considering the continuous improvement of testing capacity, the diagnosis rate is set to be an increasing function of time t with the following form (Tang et al. 2020d, 2022):

$$\begin{aligned} \delta _{I}(t) = \left( {\delta _{I0} - \delta _{Im}} \right) e^{- rt} + \delta _{Im},~ \end{aligned}$$
(14)

where \(\delta _{I0}\) is the initial diagnosis rate while \(\delta _{Im}\) is the maximum diagnosis rate, and r is the corresponding exponential increasing rate. As reported in several studies (Fan et al. 2020; Rajgor et al. 2020), the COVID-19 fatality rate is varying overtime. Hence, the disease-induced death rate \(\alpha \) is set to be a piecewise function of time t with three phases:

$$\begin{aligned} \alpha (t) = \left\{ \begin{matrix} {\alpha _{1},0< t< T_{d1},~~~~} \\ {\alpha _{2},T_{d1}< t< T_{d2},~~} \\ {\alpha _{3},T_{d2} < t.~~~~~~~~~~~} \\ \end{matrix} \right. \end{aligned}$$
(15)

Here, we assume that \(T_{d1}=150,100,80,80\) (day) and \(T_{d2}=250,220,200,200\) (day) in Hongkong, Japan, USA, and global area, respectively. Correspondingly, till December 20th, 2020, we name the time period \(0<t<T_{d1}\) as Phase 1, \(T_{d1}<t<T_{d2}\) Phase 2, and \(T_{d2}<t\) Phase 3.

It follows from the epidemic data that Hongkong experienced three apparent epidemic waves till December, 2020 (see Fig. 2). And, the three epidemic waves of Hongkong have a very similar pattern in terms of the peak value and outbreak period. This means that the feedback between the reported cases and the ratio of humans with altered behaviours is similar during the three epidemic waves. Consequently, we assume that all the behaviour changes dynamics-related parameters (\(m,\nu ,\rho ,\eta \)) and the reduction of the transmission by the altered behaviours (q) are constants when we fit model (7) to the epidemic data in Hongkong. Similarly, the global epidemic of COVID-19 only experienced one epidemic wave (still in the increasing phase) till December 20th, 2020, we set these parameters as constants for the global epidemic. In contrast, we find it difficult to fit the data of Japan and USA well by fixing q as a constant. The potential reason is that the daily reported cases in USA (or in the third wave of Japan) experienced a continued increasing trend before decreasing to a low level (see Fig. 2). That is, the shifting of daily reported cases may not drive the population resume to normal behaviours but maintain altered behaviours, hence no fluctuation of B(t). Therefore, the reduction of the transmission rate by altered behaviours should be the key driver to the significant increasing of daily reported cases under this situation. Because of a long-term of maintaining altered behaviours, the epidemic fatigue can result in the weak adherence to NPIs. Consequently, the reduction of the transmission rate by the altered behaviours q is set to be a piecewise function of time t in USA and Japan.

Fig. 2
figure 2

COVID-19 epidemic data, including the daily reported cases and accumulative death cases for Hongkong, Japan, USA and the world from the Johns Hopkins University Center for Systems Science and Engineering (JHU CCSE) and the data are available on the Github and the Humanitarian Data Exchange (Github 2021; HDE 2021)

Full size image

We then generate 500 bootstrap samples of the time series data of daily reported cases and accumulative death cases based on Poisson distributions (Chowell and Luo 2021). That is, for each data point we assume that the number of daily reported cases and the number of daily death cases follow a Poisson distribution with the mean being assumed as the observed counts. Based on this assumption, we then sample 500 times of numbers of daily reported cases and death cases in the preset distributions, consequently, obtain 500 samples of the time series data. We firstly fit model (7) to each time series of the 500 bootstrap samples of daily reported cases and accumulative death cases using the least squared (LS) method. We then fit model (11) to each of the 500 bootstrap samples of daily reported cases and the daily vaccinated population in USA by fixing the parameters in model (7), except the behaviour change related and vaccination related parameters. Note that, the 500 fittings can produce 500 parameter sets, consequently, generate 500 solutions of daily or accumulative reported cases. We then calculate the 2.5% and 97.5% percentiles of the 500 solutions to generate the 95% confidence interval (CI) for quantile of the fitting results.

In more details, we use the least square method with a priori distribution for each parameter to fit the model to the data using the software of MATLAB, where the ODE system is solved by the “ODE45” function while the “fmincon” function is used to search the optimal solutions of the objective function. It should be mentioned that the unknown initial conditions, including the initial values for exposed, asymptomatically/symptomatically infected individuals, perceive prevalence, and the ratio with normal behaviour, are also taken as unknown parameters when carrying out the fitting process. Therefore, a priori distribution is also provided for each initial value for the unknown variables.

3 Main Results

3.1 Model Fitting

The best fitting results are shown in Fig. 3, and the estimated parameter values and their standard deviations are listed in Table 1. In particular, the empirical distributions of the estimated key parameters for behavioural changes, \((q,\rho ,\eta ,\nu ,m)\), for Hongkong and the world from the bootstrap method (500 bootstrap samples), are shown in Fig. 4. We also obtained the estimate of the effective reproduction numbers and their confidence intervals for the three regions/countries (Hongkong, Japan, USA) and the world based on the bootstrap method (Fig. 3). It follows from the estimation results that the initial ratio of humans with altered behaviours highly depends on the initial time of the epidemics. The COVID-19 epidemic of Hongkong starts relatively quick and early compared with those in USA, Japan and the globe. This results in a quick increasing of the awareness of infection risks, hence almost all the population in Hongkong altered their behaviour already at the initial time. On the other hand, the estimated diagnosis rate can reach its maximum value in a short period. This is in line with the fact that the testing ability can be highly improved quickly all over the world (Sung et al. 2020). One interesting issue arising from this observation is whether we can just set the diagnosis rate as a constant instead of a function of time t, and how will this assumption affect the estimation of other parameters and the fitting results, which requires more works. The multi-scale model is proposed to capture the transmission dynamics of COVID-19 epidemics as well as the evolution of behavioural changes, and the model was calibrated based on COVID-19 epidemic data from multiple sources, and then used to evaluate the impact of enhancing/relieving NPIs upon vaccination. More details are available in Sect. 2.3.

Fig. 3
figure 3

Model fitting results for model (7): The blue curves are the estimated curves with the shadow areas as the corresponding 95% confidence band. The red cycles are the observed data of the daily reported cases and the accumulative death cases

Full size image
Fig. 4
figure 4

Empirical distributions of the estimated behavioural dynamic parameters by fitting model (7) to the observed epidemic data from Hongkong and the world based on 500 bootstrap samples

Full size image
Fig. 5
figure 5

Estimated behavioural dynamics: \(1-B(t)\) and M(t). The solid curves are the estimated dynamic curves with the shadow areas as the corresponding 95% confidence intervals based on the bootstrap method. The black dash curves are the estimated daily reported cases from model (7)

Full size image

3.2 Evolution of Behavioural Changes and Multiple Epidemic Waves

Based on the model fitting results, we obtained the estimate of evolution of perceived infection (M(t)) and the dynamics of proportion of the humans with behavioural changes (\(1-B(t)\)) for three regions/countries and the world, as shown in Fig. 5. It is worth noting that the estimated perceived infection and its corresponding behavioural change oscillate, in particular, for Japan and Hongkong, which might be the main factor to induce multiple epidemic waves in these two regions/countries. Taking Hongkong as an example, as the epidemic initially increased quickly, the individuals consciously or compulsively chose to change their behaviours to reduce the risk of being infected and the proportion of the population with behavioural changes quickly increased close to 100% around the time of the first epidemic peak. A change in behaviour caused the epidemic to decline swiftly and the daily reported cases reduced to almost zero. This in turn drove individuals to return back to normal behaviours, and consequently the susceptible population size rebounded back to a higher level, which induced another epidemic wave. This feedback loop, epidemic increasing \(\rightarrow \) behaviour changing \(\rightarrow \) epidemic declining \(\rightarrow \) behaviour changing back \(\rightarrow \) epidemic resurging, could repeat multiple times to drive multiple COVID-19 epidemic waves as observed in Hongkong or Japan (Figs. 3 and 5). From Fig. 3, we can see that by integrating behavioural change dynamics and the disease transmission dynamics, our proposed model can capture the observed multiple waves of COVID-19 epidemics very well.

To further analyze the mechanism on how our model can generate oscillations, we plotted the population of symptomatic infections (I(t)) and the ratio of humans with normal behaviours (B(t)) in Fig. 6 by fixing all the parameters as constants. In Fig. 6A, we observed the oscillations of symptomatically infected individuals and the fluctuations of the ratio of humans with normal behaviours. In comparison, by fixing the parameter values as the same as those in Fig. 6A, we plotted the daily reported cases without the shifting of human behaviours, that is, let \(B(t)=0\) and \(B(t)=1\) in Fig. 6C, D, respectively. We find that the oscillations vanished in Fig. 6C, D. This means that behaviour change in the modelling framework with game theory can indeed drive the epidemic oscillations. Moreover, the oscillation is sensitive to parameter q, and Fig. 6B shows that an increase in the value of parameter q leads to the oscillation vanished.

On the other hand, we observe the third epidemic wave in Japan that lasted longer and peaked higher than the first two waves, although most people chose to change their behaviours during the third wave. Similar phenomenon was observed in USA and the global COVID-19 epidemics (Fig. 5). As we can see from Fig. 5, B(t) of USA quickly decreases to and maintains around zero. It’s not surprised to observe the result since human beings prefer to adopting altered behaviours according to the game theory when the perceived risk exceeds the threshold. As the number of daily reported cases is of an increasing trend, the perceived risk will continuously increase as well, consequently, maintain above the threshold in USA, hence B(t) maintained around zero. Then, the interesting question is why the behavioural change did not significantly induce the epidemic to decline in the later waves. To address this question, we further examine the evolution of key parameters related to behavioural changes. The estimates of behaviour-related dynamic parameters, the reduced transmission rate due to alternative behaviours (q), the response rate of perceived infection prevalence (\(\eta \)), and the spreading rate of behaviour changes (\(\rho \)) for Japan and USA are shown in Fig. 7. We can see that the parameter q(t), the reduced transmission rate due to alternative behaviours, exhibited an increasing trend during the multiple waves for USA and Japan. This suggests that the effect of behavioural changes in terms of reduction in transmission rate significantly decreased in later waves either due to waning of adherence to the NPIs or pandemic fatigue (i.e., fatigue of risk awareness of self-protection). Therefore, not only the proportion of the population, but also the effectiveness of alternative behaviours to reduce the risk of being infected is critical to prevent the epidemic from continuously surging.

Fig. 6
figure 6

Solutions of model (7) by fixing all the parameters as constants with \(\delta _I=0.7,\alpha =0.008\). Particularly, \(q=0.33\) in A, \(q = 0.85\) in B, \(B(0)=1\) in C, and \(B(0)=0\) in D. The other parameters and initial conditions are fixed as those of Hongkong listed in Table 1

Full size image
Fig. 7
figure 7

Evolution of the estimated values of the three key parameters related to behavioural changes in Japan and USA

Full size image

3.3 Effect of Behavioural Changes on Controlling Multiple COVID-19 Epidemic Waves

We further evaluate whether the subsequent epidemic waves could be avoided if the effectiveness of behavioural changes was enhanced after the first wave. If the adherence of NPIs and awareness of self-protection were enhanced so that the reduced transmission rate due to the alternative behaviours (q) during the second and third waves was the same as that during the first wave, the simulated daily new cases in USA and Japan are shown in Fig. 8A, B, from which we can see that the magnitude of second and third waves could be significantly reduced or completely avoided. This suggests that even though almost all the population have altered their behaviours (i.e. B(t) maintains at around zero), it’s important to promote and maintain the high awareness of self-protection and well adherence to the NPIs in order to avoid subsequent epidemic waves. This is in line with the results in the existing studies (Giordano et al. 2020; Buckner et al. 2021) that the transmission rate is usually the most sensitive parameter in affecting the outcomes of COVID-19 outbreaks. Similarly, by controlling other behavioural change parameters, (\(\eta ,\rho ,m,\nu \)), it could also mitigate COVID-19 epidemics, which is demonstrated for the case of Hongkong in Fig. 8C–F. That is, when the reduction of the transmission rate by the altered behaviours is fixed, the peak magnitude of subsequent waves could be reduced by accelerating the risk awareness, spreading of behavioural changes and increasing the sensitivity of individuals to perceived infection (i.e., increasing the values of (\(\eta ,\rho ,m\)) as well as prolonging the period of higher risk awareness (reducing the value of \(\nu \)).

Fig. 8
figure 8

Simulated daily reported cases based on model (7) with different assumptions of behavioural dynamic parameters. A, B Daily reported cases in USA and Japan under different scenarios by decreasing the values of q in Phases 2 and 3. C–F Daily reported cases in Hongkong by varying the four parameters related to behavioural change dynamics. The subscript ‘e’ indicates the estimated value from the observed data. The values of all other parameters were set as those listed in Table 1

Full size image

3.4 Relaxation of NPIs Under Vaccination

The COVID-19 vaccines started to be available from December 2020. With vaccination, people’s perceived risk of infection might be changed and this may affect the behavioural changes. To investigate the evolution of behavioural changes under vaccination and the trade-off effect between relaxation of NPIs and vaccination on COVID-19 epidemics, we extend model (7) to include the effect of vaccination, i.e. model (11). We re-estimate the parameters related to behavioural changes, (\(q,\rho ,\eta ,m,\nu \)) and other vaccination-related parameters by fitting model (11) to the observed epidemic data (daily new cases) and daily vaccinated population data between December 21st, 2020 to February 14th, 2021 (Phase 4) in the USA where the COVID-19 vaccination was implemented during this period. We fixed other model parameters as those in model (7) before vaccination started. The model fitting results are shown in Fig. 9. The updated estimates of behavioural change-related parameters \(q_4,\rho _4,\eta _4,m_4,\) and \(\nu _4\) in Phase 4 (i.e., the phase with vaccination) and the estimated values of vaccination rates \(\mu _0,r_{\mu },\) and \(\mu _b\), are listed in Table 2. From Tables 1 and 2, we can see that the reduced transmission rate due to alternative behaviours q is less than that in the previous two phases (i.e., \(q_4<q_2<q_3\)), which indicates the enhanced implementation of NPIs and/or the greater adherence to NPIs during Phase 4. We can also see from Fig. 9C that the vaccination coverage (received two doses of vaccines) only reached around 5% by February 14th, 2020, which was still far from enough.

The number of daily reported cases in USA has been declining since December 20th, 2020. To identify which factor mainly contribute to the declining trend, we did simulations for the epidemic from December 20th to June 30th, 2021 using the established model (11) by considering two scenarios of the reduced transmission rate due to alternative behaviours q: one as the estimated values for Phase 4 and another as returning to the higher level of Phase 3, under the condition with and without vaccination (the vaccination rate \(\mu _0\) was set as the estimated values for Phase 4). The simulated results for the four cases are shown in Fig. 10A, from which we can see that the epidemic curves with and without vaccination are very close to each other during the period between December 20th, 2020 to February 14th, 2021. This means that in this phase vaccination plays a very limited role in mitigating the epidemic as the vaccination coverage is small (about 5%). Note that the ratio of humans with altered behaviours has reached and maintained around 1 during this period. Based on these facts, incorporating that the daily reported cases can decrease greatly as q decreases, the key factor for the significant decline of observed daily cases during this period is more likely due to the reduction of the transmission rate by adopting the altered behaviours, instead of vaccination effect. While, as the vaccination persistently continues, it starts to play its role in mitigating the epidemic, which could be seen by a big divergence between the two epidemic curves with and without vaccination in later times.

It is expected that the widespread availability of COVID-19 vaccines would lead to less adherence of NPIs of the altered behaviours, corresponding to a bigger value of q, due to the perceived immunity from the vaccine among the population. We performed simulations to predict the COVID-19 epidemic trend from February 14th to June 30th, 2021 (Phase 5) using the established model (11) by assuming q to increase from \(q_4,q_3\) and 10% to 20% higher than \(q_3\). The two cases with and without vaccination (the vaccination rate \(\mu _0\) was set as the estimated value for Phase 4) were simulated and the results are shown in Fig. 10C, E, respectively. The predicted results show that a higher value of q due to relaxation of NPIs could induce another big epidemic wave in USA during Phase 5 without vaccination (Fig. 10E); but fortunately, continued vaccination could flatten the new wave significantly (Fig. 10C). To further evaluate the effect of accelerated vaccination during Phase 5, we simulate the scenario that the maximum vaccination rate would be tripled during Phase 5 under the worst condition of reduced transmission rate due to alternative behaviours, \(q=1.2q_3\). The results are shown in Fig. 10B, D and F, indicating that the accelerated vaccination could effectively flatten or even avoid the subsequent epidemic waves due to relaxation of NPIs.

Table 2 Definitions and estimated values of additional parameters in the vaccination model (11) for USA
Full size table

4 Discussion and Conclusion

Fig. 9
figure 9

A, B Model fitting results for the vaccination model (model (11)) to the data between December 20th, 2020 to February 14th, 2021 in USA. C The estimated time-varying vaccination coverage in USA. The red cycles are the observed data, the blue curves are the estimated curves with the shadows as the corresponding 95% confidence interval from the bootstrap method

Full size image
Fig. 10
figure 10

Simulation and prediction results from the vaccination model (model (11)) for USA. A Two scenarios of the reduced transmission rate due to alternative behaviours (q): one as the estimated values for Phase 4 \((q_4=q_{4_e})\) and another as returning to the higher level of Phase 3 \((q_4=q_{3_e})\), under the condition with vaccination (the vaccination rate \(\mu _0\) was set as the estimated values for Phase 4, \(\mu _0=\mu _{0e}\)) and without vaccination (\(\mu _0=0\)). C and E q increased from February 14th, 2021, where the vaccination rate was set as the estimated value from the data in C and no vaccination was used in E. q increased to 20% higher than that in Phase 3 from February 14th, 2021 and the different vaccination rates were used in B, D and F. The vaccination coverage can reach around 40% till the end of June 2021 under the estimated vaccination rate from the current data, while the coverage could increase to over 60% by tripling the maximum vaccination rate \(\mu _b\). The subscript ‘e’ indicating the estimated value from the data

Full size image

Multiple waves were clearly observed from many local and nationwide COVID-19 epidemic data since early 2020 (Fig. 2). It is critical to understand the underlying mechanism and identify the main drivers for multiple epidemic waves in order to prevent future COVID-19 waves and outbreaks (Kaxiras and Neofotistos 2020; Weitz et al. 2020b; Tkachenko et al. 2021). In this study, using the modelling idea by game theory (Poletti et al. 2009, 2012; Jentsch et al. 2021), we extended the SEIAHR transmission dynamic model of COVID-19, and proposed a multi-scale model by linking the behavioural change dynamics to the disease transmission dynamics (Poletti et al. 2009, 2012; Jentsch et al. 2021). We explicitly modeled the perceived infection (M(t)) and the proportion of individuals who have altered their behaviours (\(1-B(t)\)), with key behavioural change parameters such as the sensitivity to the infection risk, the speed of raising the risk awareness, the persistence to maintain the risk awareness, and the spreading rate of behavioural changes among individuals. The effect of vaccination was also considered in the model. The game theory based on the feedback loop between behavioural changes and COVID-19 transmission dynamics could be used to explain the observed multiple epidemic waves. Based on the developed model with the estimated behavioural dynamic parameters and vaccination-related parameters, we investigated the interplays among vaccine uptake, behavioural change and relaxation of NPIs as well as their effects on future COVID-19 epidemics.

The main modeling results reveal that the behavioural change dynamics, driven by the perceived COVID-19 epidemic and its effect on adherence of NPIs, play an essential role in inducing multiple epidemic waves. By comparing the epidemics in Hongkong and USA, we found that two aspects of behaviour changes (concluded in Sect. 2.1) can lead to different patterns of the epidemics. In details, Hongkong experienced three epidemic waves, with the number of daily reported cases fluctuating (increase and decrease) apparently. This drives the fluctuations of the choice of human behaviours, resulting in the oscillations of the ratio of humans with altered behaviours (see Fig. 5). In return, the shifting of the ratio can affect the transmission of COVID-19 pandemic. This generates a feedback loop between the behaviour change dynamics and transmission dynamics, and this feedback loop is the key to drive the multiple epidemic waves in Hongkong. Note that, we also showed that the behavioural dynamic-related parameters, the sensitivity to the infection risk (m), persistence of maintaining the risk awareness (\(\nu \)), and speed of raising risk awareness (\(\eta \)) play more important roles in mitigating the COVID-19 epidemics and avoiding the subsequent waves (Fig. 8). In contrast, for USA, the continued high level in daily reported cases results in a high level of perceived infection in the population, which lead to a higher payoff of the altered behaviours for a long time period. Thus, based on our model framework with game theory, almost all population altered their behaviours and maintained the altered behaviours (see Fig. 5), i.e. no fluctuation of the ratio of humans with altered behaviour. In such situation, the persistent promotion of NPIs in a long time period could result in the effect of behavioural changes on mitigating the epidemic weakened, corresponding to the increases of q as shown in Fig. 7. This is presumably because of pandemic fatigue and lower adherence to the NPIs. As a result, much higher subsequent epidemic waves occurred, as shown in Fig. 3.

Given the availability of COVID-19 vaccines at the end of 2020, it is expected to gradually lift the NPIs to restore to normal life. However, our modeling results show that it should be cautious to avoid relaxing NPIs prematurely. During the early stage of vaccination, relaxation of NPIs may induce another big epidemic wave. With continuous vaccination when a significant proportion of the population are vaccinated, the vaccine effect could counteract the relaxing of NPIs to avoid a new epidemic wave as expected. Thus, accelerated vaccination could allow to lift NPIs and restore normal life earlier. But the interplay between vaccine uptake and relaxation of NPIs should be carefully evaluated and the caution should be taken before relaxing NPIs. In summary, we fitted the proposed model to the COVID-19 epidemic data with multiple waves in different regions/countries, from which the extended SEIR model, coupled with the model of behavioural change dynamics, could fit the data well and flexibly capture the asymmetric dynamics with multiple waves by considering pandemic fatigue (waning of adherence to the NPIs). This supports that our model framework based on the game theory can well capture the behaviour change characters in these countries/regions, and identify the key role of behaviour changes in driving the multiple epidemic waves with different patterns. As the impact of NPIs is involved in the behavioural change dynamics of our model, the main results can also provide the important guidance to balance the vaccine uptake and relaxation of NPIs, aiming at controlling the new epidemic waves.

We finally state the limitations in the current study. We ignored the mutations of SARS-CoV-2 in our model, the high transmission ability can definitely increase and accelerate the spread of COVID-19. On the other hand, the high transmissibility, incorporating the reports of vaccines breakthrough cases of new variants, may also raise risk awareness and consequently induce a new round of behavioural changes. Complicated behavioural dynamics, driven by multiple factors including efficacy and coverage of COVID-19 vaccines, transmission properties of the mutated strains, may need to be considered in the future work. When fitting the daily reported cases in Japan and USA, we set a piecewise function of q. Note that, a different degree of the reduction of transmission rate (corresponding to different values of q) would change the cost of altered behaviours, hence the extra cost k should be a function of q instead of a constant. When fitting the vaccination data, we assumed that only the susceptible population is vaccinated, which can lead to the over estimation of the vaccination rate. In reality, the exposed and asymptomatically infected individuals may also be vaccinated, taking these factors can improve the vaccination function. When modelling the response function of perceived infection to the shifting of NPIs, we assumed that it’s proportional to the daily reported cases. Human behavioural changes appear to be compelled largely due to different levels of NPIs at different phases. This means that the response term can be a piecewise continuous function. One interesting issue is how this non-smooth function affects the transmission dynamics of the COVID-19, which is left for our future works. It is not trivial to estimate the behavioural dynamic parameters based on the observed epidemic data only, especially the identifiability of nonlinear differential equation models is a fundamental and challenging problem (Miao et al. 2021). Collection and use of behavioural data during the epidemic period could fill the gap to further refine the proposed model in the future.