Impact of the WHO Integrated Stewardship Policy on the Control of Methicillin-Resistant Staphyloccus aureus and Third-Generation Cephalosporin-Resistant Escherichia coli: Using a Mathematical Modeling Approach

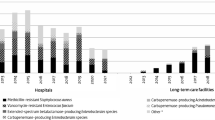
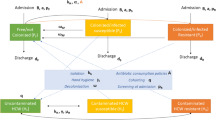
Abstract

Methicillin-resistant Staphylococcus aureus (MRSA) and third-generation cephalosporin-resistant Escherichia coli (3GCREc) are community and hospital-associated pathogens causing serious infections among populations by infiltrating into hospitals and surrounding environment. These main multi-drug resistant or antimicrobial resistance (AMR) bacterial pathogens are threats to human health if not properly tackled and controlled. Tackling antimicrobial resistance (AMR) is one of the issues for the World Health Organization (WHO) to design a comprehensive set of interventions which also helps to achieve the end results of the developing indicators proposed by the same organization. A deterministic mathematical model is developed and studied to investigate the impact of the WHO policy on integrated antimicrobial stewardship activities to use effective protection measures to control the spread of AMR diseases such as MRSA and 3GCREc in hospital settings by incorporating the contribution of the healthcare workers in a hospital and the environment in the transmission dynamics of the diseases. The model also takes into account the parameters describing various intervention measures and is used to quantify their contribution in containing the diseases. The impact of combinations of various possible control measures on the overall dynamics of the disease under study is investigated. The model analysis suggests that the contribution of the interventions: screening and isolating the newly admitted patients, improving the hygiene in hospital settings, decolonizing the pathogen carriers, and increasing the frequency of disinfecting the hospital environment are effective tools to contain the disease from invading the population. The study revealed that without any intervention, the diseases will continue to be a major cause of morbidity and mortality in the affected communities. In addition, the study indicates that a coordinated implementation of the integrated control measures suggested by WHO is more effective in curtailing the spread of the diseases than piecemeal strategies. Numerical experiments are provided to support the theoretical analysis.

Appendices

Appendix A: Biologically Feasible Region

Theorem A.1

Model (10) is a dynamical system on the biologically feasible region

$$\begin{aligned} \Omega= & {} \Big \{(P,P_{CCA},P_{ICA}, P_{CHA},P_{IHA}, H_{UW}, H_{CW}, E) \in \mathbb {R}_{+}^8: 0\le N_P\le \frac{\Lambda _1}{\gamma _P},\;\nonumber \\&~&0 \le N_H(t) \le \frac{\Lambda _2}{\mu },\; \text{ and }\;~0 \le E\le M\Big \} \end{aligned}$$

(A1)

where $M=\frac{1}{\nu }\left( (\xi _1+\xi _2)\frac{\Lambda _1}{\gamma _P}+\xi _3\frac{\Lambda _2}{\mu }\right)$.

Proof

We want to show that for non-negative initial data (4), system (10) possesses a unique non-negative solution in the region $\Omega$ for all time $t\ge 0$. The proof will follow two steps.

Following the approach in Busenberg and Cooke (1993), Terefe (2020) and Kassa et al. (2021), it can be shown that any solution of (10) corresponding to non-negative initial conditions is non-negative.

In a second step, we show that any solution of model system (10) satisfies some a priori estimates. By adding the first five equations of (10), we obtain

$$\begin{aligned} N'_P(t)= & {} \Lambda _1-(\gamma _P P+\gamma _{CCA}P_{CCA}+\delta _{ICA}P_{ICA}+\gamma _{CHA}P_{CHA}+\delta _{IHA}P_{IHA}), \nonumber \\\le & {} \Lambda _1-\mu _m( P+P_{CCA}+P_{ICA}+P_{CHA}+P_{IHA})=\Lambda -\mu _m N_P(t), \end{aligned}$$

(A2)

where

$$\begin{aligned} \mu _m=\min \{\gamma _P , \gamma _{CCA}, \delta _{ICA}, \gamma _{CHA}, \delta _{IHA}\}. \end{aligned}$$

By applying Gronwall inequality on (A2), we obtain

$$\begin{aligned} N_P(t)\le \frac{\Lambda _1}{\mu _m}+\left( N_{P0}-\frac{\Lambda _1}{\mu _m}\right) \exp (-\mu _m t). \end{aligned}$$

(A3)

Hence, for $0 \le N_{P0} \le \frac{\Lambda _1}{\mu _m}$, we get

$$\begin{aligned} 0\le N_P(t)\le \frac{\Lambda _1}{\mu _m} \end{aligned}$$

for all $t\ge 0$.

If $N_P(t)> \frac{\Lambda _1}{\mu _m}$, then from (A3), we get

$$\begin{aligned} \frac{\Lambda _1}{\mu _m}+\left( N_{P0}-\frac{\Lambda _1}{\mu _m}\right) \exp (-\mu _m t)\le N_P(t). \end{aligned}$$

Thus

$$\begin{aligned} N_P(t)\rightarrow \frac{\Lambda _1}{\mu _m}\;~~~\text{ as }\;~~t \rightarrow \infty . \end{aligned}$$

Likewise, by adding the last two equations of (10) related to the healthcare workers, we obtain

$$\begin{aligned} N'_H(t)= \Lambda _2-\mu N_H, \end{aligned}$$

which leads into

$$\begin{aligned} 0 \le N_H(t)=\frac{\Lambda _2}{\mu }+\left( N_{H0}-\frac{\Lambda _2}{\mu }\right) \exp (-\mu t)\le \frac{\Lambda _2}{\mu }. \end{aligned}$$

Then, for $0\le N_{H0}\le \frac{\Lambda _2}{\mu }$,

$$\begin{aligned} N_H(t)\rightarrow \frac{\Lambda _2}{\mu }\;~~~\text{ as }\;~~t \rightarrow \infty . \end{aligned}$$

Finally, from the last equation of (10) which is related to the contaminated environment, we obtain

$$\begin{aligned} E' \le M-\nu E, \;~~\text{ where }\;~~M=(\xi _1+\xi _2)\frac{\Lambda _1}{\gamma _P}+\xi _3 \frac{\Lambda _2}{\mu }. \end{aligned}$$

(A4)

By applying Gronwall inequality, we have

$$\begin{aligned} E(t)\le \frac{M}{\nu }+(E_0-\frac{M}{\nu })\exp (-\nu t). \end{aligned}$$

(A5)

Hence, from (A5), when $0\le E_0\le \frac{M}{\nu }$, we infer that

$$\begin{aligned} 0\le E(t)\le \frac{M}{\nu }\; ~~ \text{ for } \text{ all }\;~t\ge 0. \end{aligned}$$

Combining the above results and using Theorem 2.1.5 in Stuart and Humphries (1998), we conclude that (10) defines a dynamical system on $\Omega$. $\square$

Appendix B: Computation of the Reproduction Number

By using the theory of next generation operator in Diekmann and Heesterbeek (2000); van den Driesche and Watmough (2002) and the notation in the references, the matrix F (for the new infection terms) with $X=(P_{CCA},P_{ICA},P_{CHA},P_{IHA},H_{CW},E)$, is given by

$$\begin{aligned} F = \left[ \begin{array}{cccccc} \beta _{CA}(1-\eta _P)\sigma _1 &{} \beta _{CA}(1-\eta _P) &{} 0 &{} 0 &{} \beta _{CA}\epsilon _1(1-\eta _H)\frac{\mu \Lambda _1}{\Lambda _2\gamma _P} &{} \frac{\beta _e\Lambda _1}{K\gamma _P} \\ 0 &{} 0 &{} \beta _{HA}\sigma _2(1-\eta _P)&{} \beta _{HA}(1-\eta _P) &{} \beta _{HA}\epsilon _2(1-\eta _H)\frac{\mu \Lambda _1}{\Lambda _2\gamma _P} &{} \frac{\beta _e\Lambda _1}{K\gamma _P} \\ \beta _{CA}(1-\eta _P)\sigma _1\frac{\gamma _P\Lambda _2}{\Lambda _1\mu } &{} \beta _{CA}(1-\eta _P)\frac{\gamma _P\Lambda _2}{\Lambda _1\mu } &{} \beta _{HA}\sigma _2(1-\eta _P)\frac{\gamma _P\Lambda _2}{\Lambda _1\mu } &{} \beta _{HA}(1-\eta _P)\frac{\gamma _P\Lambda _2}{\Lambda _1\mu } &{} \beta _{HA}(1-\eta _P) &{} \frac{\beta _e\Lambda _2}{K\mu } \\ 0 &{} 0&{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array} \right] . \end{aligned}$$

(B6)

The matrix for transition terms linearized at the disease-free equilibrium is given by

$$\begin{aligned} V = \left[ \begin{array}{cccccc} k_1 &{} -\phi _{ICA} &{} 0 &{} 0 &{} 0 &{} 0 \\ -\tau _{CCA} &{} k_2 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} k_4 &{} -\phi _{IHA} &{} 0 &{} 0 \\ 0 &{} 0 &{} -\tau _{CHA} &{} k_5 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} k_3 &{} 0 \\ 0 &{} -\xi _1 &{} 0 &{} -\xi _2 &{} -\xi _3 &{} \nu \end{array} \right] . \end{aligned}$$

(B7)

The inverse of matrix V can be obtained to be

$$\begin{aligned} \begin{aligned} V^{-1} = \left[ \begin{array}{cccccc} \frac{(1-\Phi _{CIHA})}{k_1\Phi _{M}}&{} \frac{\phi _{ICA}(1-\Phi _{CIHA})}{k_1k_2\Phi _{M}} &{} 0 &{} 0 &{} 0 &{} 0 \\ \frac{\tau _{CCA}(1-\Phi _{CIHA})}{k_1k_2\Phi _{M}} &{} \frac{(1-\Phi _{CIHA})}{k_2\Phi _{M}}&{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} \frac{(1-\Phi _{CICA})}{k_4\Phi _{M}} &{} \frac{\phi _{IHA}(1-\Phi _{CICA})}{k_4k_5\Phi _{M}} &{} 0 &{} 0\\ 0 &{} 0 &{} \frac{\tau _{CHA}(1-\Phi _{CICA})}{k_4k_5\Phi _{M}} &{} \frac{(1-\Phi _{CICA})}{k_5\Phi _{M}} &{} 0&{}0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \frac{1}{k_3} &{} 0 \\ \frac{\xi _1\tau _{CCA}(1-\Phi _{CIHA})}{\nu k_1k_2\Phi _{M}} &{}\frac{\xi _1(1-\Phi _{CIHA})}{\nu k_2\Phi _{M}}&{} \frac{\xi _2\tau _{CHA}(1-\Phi _{CICA})}{\nu k_4k_5\Phi _{M}} &{} \frac{\xi _2(1-\Phi _{CICA})}{\nu k_5\Phi _{M}} &{} \frac{\xi _3}{\nu k_3} &{} \frac{1}{\nu } \end{array} \right] \end{aligned} \end{aligned}$$

where $\Phi _{CIHA} = \frac{\tau _{CHA}\phi _{IHA}}{k_4k_5}$, $\Phi _{CICA} = \frac{\tau _{CCA}\phi _{ICA}}{k_1k_2}$, $\Phi _M = (1-\Phi _{CIHA}-\Phi _{CICA}+\Phi _{CIHA}\times \Phi _{CICA})$.

Then the reproduction number $\mathcal {R}_0$ of the model is given as the spectral radius of the matrix $FV^{-1}$.

Appendix C: Global Stability of the Disease-Free Equilibrium

Theorem C.1

The disease-free equilibrium $E_0$ of model (10) given at (12) is globally asymptotically stable if $\mathcal {R}_0 <1$ .

Proof

To prove the global asymptotic stability of $E_0$ for $\mathcal {R}_0<1$, we apply the method investigated in Kamgang and Sallet (2008). Let $X=(X_1,X_2)$ with

$$\begin{aligned} X_1=(P,H_{UW})\in \mathbb {R}^2\;~~\text{ and }\;~~ X_2=(P_{CCA}, P_{ICA},P_{CHA},P_{IHA},H_{CW}, E)\in \mathbb {R}^{6} \end{aligned}$$

denote the number of uninfected and infected individuals in system (10), respectively. Then the system in (10) can be written as

$$\begin{aligned} \dot{X}_1= & {} A_1(X)(X_1-X_1^*)+A_{12}(X)X_2, \end{aligned}$$

(C8)

$$\begin{aligned} \dot{X}_2= & {} A_2(X)X_2, \end{aligned}$$

(C9)

where $X_1^*=\left( \frac{\Lambda _1}{\gamma _P},\frac{\Lambda _2}{\mu }\right)$,

$A_1(X)=\left( \begin{array}{cc} -\gamma _P&{} 0 \\ 0 &{} -\mu \\ \end{array} \right)$,

$$\begin{aligned} \begin{aligned} A_{12}(X)&= \left( \begin{array}{cccccc} -\frac{\beta _{CA}\sigma _1P}{N_P}+\alpha _{CCA} &{} -\frac{\beta _{CA}P}{N_P} &{}-\frac{\beta _{HA}\sigma _2P}{N_P}+\alpha _{CHA} &{} -\frac{\beta _{HA}P}{N_P}&{}-\left( \frac{\beta _{CA}\epsilon _1P}{N_H}+\frac{\beta _{HA}\epsilon _2P}{N_H}\right) &{}-\frac{\beta _eP}{K+E} \\ -\frac{\beta _{CA}\sigma _1 H_{UW}}{N_P}&{} -\frac{\beta _{CA} H_{UW}}{N_P} &{}-\frac{\beta _{HA}\sigma _2H_{UW}}{N_P}&{} -\frac{\beta _{HA} H_{UW}}{N_P} &{}-\frac{\beta _H H_{UW}}{N_H} &{}-\frac{\beta _eH_{UW}}{K+E}\\ \end{array} \right) \end{aligned} \end{aligned}$$

(C10)

and

$$\begin{aligned} \begin{aligned} A_2(X)=\left( \begin{array}{cccccc} \frac{\beta _{CA}\sigma _1P}{N_P}-k_1&{} \frac{\beta _{CA}P}{N_P}+\phi _{ICA}&{}0&{}0&{} \frac{\beta _{CA}\epsilon _1P}{N_H} &{}\frac{\beta _eP}{K+E} \\ \tau _{CCA}&{}-k_2&{}0&{}0&{}0&{}0\\ 0&{}0&{} \frac{\beta _{HA}\sigma _2P}{N_P}-k_3&{} \frac{\beta _{HA}P}{N_P}+\phi _{IHA}&{} \frac{\beta _{HA}\epsilon _2P}{N_H} &{}\frac{\beta _eP}{K+E} \\ 0&{}0&{} \tau _{CHA}&{}-k_4&{}0&{}0\\ \frac{\beta _{CA}\sigma _1H_{UW}}{N_P}&{} \frac{\beta _{CA}H_{UW}}{N_P}&{}\frac{\beta _{HA}\sigma _2H_{UW}}{N_P}&{} \frac{\beta _{HA}H_{UW}}{N_P}&{} \frac{\beta _H H_{UW}}{N_H}-k_5 &{}\frac{\beta _eH_{UW}}{K+E} \\ 0&{} \xi _1&{}0&{}\xi _2&{} \xi _3 &{} -\nu \\ \end{array} \right) \end{aligned} \end{aligned}$$

(C11)

The five sufficient conditions of Kamgang–Sallet theorem are checked as follows:

• 1. System (10) is a dynamical system on $\Omega$. This is proved in Theorem A.1.

• 2. The equilibrium $X_1^*$ is GAS for the subsystem $\dot{X}_1=A_1(X_1,0)(X_1-X_1^*)$. More precisely, we obtain

  $$\begin{aligned} \dot{X}_1= & {} \left( \begin{array}{c} \Lambda _1-\gamma _p P\\ \Lambda _2-\mu H_{UW}\\ \end{array} \right) , \text{ then }\; X_1 = \left( \begin{array}{c} \frac{\Lambda _1}{\gamma _P}+\left( P_0-\frac{\Lambda _1}{\gamma _P}\right) e^{(-\gamma _p t)}\\ \frac{\Lambda _2}{\mu }+\left( H_{UW0}-\frac{\Lambda _2}{\mu }\right) e^{(-\mu t)}\\ \end{array} \right) \rightarrow \left( \begin{array}{c} \frac{\Lambda _1}{\gamma _P}\\ \frac{\Lambda _2}{\mu }\\ \end{array} \right) \\= & {} X^*_1\;~\text{ as }\;~t\rightarrow \infty . \end{aligned}$$

  Hence, $X^*_1$ is globally asymptotically stable.

• 3. The matrix $A_2(X)$ is Metzler (i.e., all the off-diagonal elements are non-negative) and irreducible for any given $X\in \Omega$.

• 4. There exists an upper-bound matrix $\bar{A}_2$ for the set

  $$\begin{aligned} \mathcal {M}=\left\{ A_2(X):X\in \Omega \right\} . \end{aligned}$$

  Indeed, the upper bound of $\mathcal {M}$ is given by $\bar{A}_2=\left( \begin{array}{cccccc} \beta _{CA} \sigma _1 -k_1&{} \beta _{CA} +\phi _{ICA}&{}0&{}0&{} \frac{\beta _{CA}\epsilon _1 \Lambda _1}{\gamma _P}&{}\frac{\beta _e \Lambda _1}{\gamma _P K}\\ \tau _{CCA}&{}-k_2 &{} 0&{}0&{}0&{}0 \\ 0&{}0&{} \beta _{HA} \sigma _2 -k_3&{} \beta _{HA} +\phi _{ICA}&{} \frac{\beta _{HA}\epsilon _2 \Lambda _1}{\gamma _P}&{}\frac{\beta _e \Lambda _1}{\gamma _P K}\\ 0&{}0&{} \tau _{CHA}&{}-k_4&{} 0&{}0 \\ \frac{\beta _{CA}\sigma _1 \Lambda _2}{\mu }&{} \frac{\beta _{CA}\Lambda _2}{\mu }&{} \frac{\beta _{HA}\sigma _2 \Lambda _2}{\mu }&{} \frac{\beta _{HA}\Lambda _2}{\mu }&{}\frac{\beta _H \Lambda _2}{\mu }-k_5&{}\frac{\beta _e \Lambda _2}{\mu K} \\ 0&{}\xi _1&{}0&{}\xi _2&{}\xi _3&{}-\nu \\ \end{array} \right) .$

• 5. For $\mathcal {R}_0<1$ in (14)

  $$\begin{aligned} \alpha (\bar{A}_2)=\max \left\{ Re(\lambda ):\lambda \;~eigenvalue \;~of \bar{A}_2\right\} \le 0. \end{aligned}$$

Hence, by the Kamgang–Sallet global stability theorem in Kamgang and Sallet (2008), the disease-free equilibrium is globally asymptotically stable for $\mathcal {R}_0<1$. $\square$