Dynamics of Stoichiometric Autotroph–Mixotroph–Bacteria Interactions in the Epilimnion

Abstract

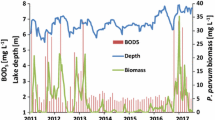
Autotrophs, mixotrophs and bacteria exhibit complex interrelationships containing multiple ecological mechanisms. A mathematical model based on ecological stoichiometry is proposed to describe the interactions among them. Some dynamic analysis and numerical simulations of this model are presented. The roles of autotrophs and mixotrophs in controlling bacterioplankton are explored to examine the experiments and hypotheses of Medina–Sánchez, Villar–Argaiz and Carrillo for La Caldera Lake. Our results show that the dual control (bottom-up control and top-down control) of bacteria by mixotrophs is a key reason for the ratio of bacterial and phytoplankton biomass in La Caldera Lake to deviate from the general tendency. The numerical bifurcation diagrams suggest that the competition between phytoplankton and bacteria for nutrients can also be an important factor for the decrease of the bacterial biomass in an oligotrophic lake.

Appendix

Proof of Theorem 1

Let $\Phi =AQ_{a}+MQ_{m}+qB+N$. It follows from (1) that

$$\begin{aligned} \frac{d\Phi }{dt}=&\frac{D}{L}(N_{b}-(AQ_{a}+MQ_{m}+qB+N))\\&-\left( d_{a}+\frac{v_a}{L}\right) AQ_{a}-\left( d_{m}+\frac{v_m}{L}\right) AQ_{m}-d_{b}qB\\ \le&\frac{D}{L}(N_{b}-\Phi ), \end{aligned}$$

and then $\limsup \limits _{t\rightarrow \infty }\Phi (t)\le N_{b}$. Note that $Q_{\min ,a}\le Q_a(t)\le Q_{\max ,a},Q_{\min ,m}\le Q_m(t)\le Q_{\max ,m}$ for all $t\ge 0$. Then

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }A(t)\le \frac{N_{b}}{Q_{\min ,a}},~~\limsup \limits _{t\rightarrow \infty }M(t)\le \frac{N_{b}}{Q_{\min ,m}}. \end{aligned}$$

From the last equation of (1), we have

$$\begin{aligned} \frac{dC}{dt}\le & {} \mu _c(A,Q_a,M,Q_m)-\frac{D}{L}C\le r_{a}A+r_{m}M-\frac{D}{L}C\\\le & {} \left( \frac{r_{a}}{Q_{\min ,a}}+\frac{r_{m}}{Q_{\min ,m}}\right) N_{b}-\frac{D}{L}C \end{aligned}$$

for sufficiently large t and

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }C(t)\le \frac{LN_{b}}{D}\left( \frac{r_{a}}{Q_{\min ,a}}+ \frac{r_{m}}{Q_{\min ,m}}\right) . \end{aligned}$$

This means that the set $\Delta$ is a globally attracting region and system (1) is dissipative. $\square$

Proof of Theorem 2

By using local bifurcation theory in (Crandall and Rabinowitz 1971), we first show that $E_3$ bifurcates from $E_2$ at $d_b=d_{b1}$. Define a mapping $F:{\mathbb {R}}^+\times {\mathbb {R}}^5\rightarrow {\mathbb {R}}^5$ by

$$\begin{aligned} F(d_b,A,Q_a,N,B,C) =\begin{pmatrix} \mu _a(A,Q_a)A-d_aA-\frac{v_a+D}{L}A\\ \rho _a(Q_a)g_a(N)-\mu _a(A,Q_a)Q_a\\ \frac{D}{L}(N_b-N)-\rho _a(Q_a)g_a(N)A-qr_bg_b(N,C)B\\ r_bg_b(N,C)B-d_bB-\frac{D}{L}B\\ \mu _c(A,Q_a)-\frac{1}{\gamma }r_bg_b(N,C)B-\frac{D}{L}C \end{pmatrix}. \end{aligned}$$

It is easy to see that $F(d_{b},A_2,Q_{a_2},N_2,0,C_2)=0$. Let

$$\begin{aligned} P:=F_{(A,Q_a,N,B,C)}(d_{b1},A_2,Q_{a2},N_2,0,C_2). \end{aligned}$$

For any $(\xi _1,\xi _2,\xi _3,\xi _4,\xi _5)\in {\mathbb {R}}^5$, we have

$$\begin{aligned} P[\xi _1,\xi _2,\xi _3,\xi _4,\xi _5]= \begin{pmatrix} p_1(\xi _1,\xi _2)\\ p_2(\xi _1,\xi _2,\xi _3)\\ p_3(\xi _1,\xi _2,\xi _3,\xi _4)\\ 0\\ p_4(\xi _1,\xi _2,\xi _4,\xi _5) \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}p_1(\xi _1,\xi _2)=&\frac{\partial \mu _{a}}{\partial A}(A_2,Q_{a2})A_2\xi _1+\frac{\partial \mu _{a}}{\partial Q_a}(A_2,Q_{a2})A_2\xi _2,\\p_2(\xi _1,\xi _2,\xi _3)=&-\!\frac{\partial \mu _{a}}{\partial A}(A_2,Q_{a2}) Q_{a2}\xi _1\!\!+\!\!\left( \frac{\partial \rho _{a}}{\partial Q_{a}}(Q_{a2})g_a(N_2)\!\!-\!r_a\bar{I}_a(A_2,0)\right) \xi _2\\ {}&+\!\rho _a(Q_{a2})\frac{\partial g_a}{\partial N}(N_2)\xi _3,\\p_3(\xi _1,\xi _2,\xi _3,\xi _4)=&-\rho _{a}(Q_{a2})g_{a}(N_2)\xi _1-\frac{\partial \rho _{a}}{\partial Q_{a}}(Q_{a2})g_{a}(N_{2})A_2\xi _2\\ {}&-\left( \frac{D}{L}+\rho _{a}(Q_{a2})\frac{\partial g_a}{\partial N}(N_2)A_2\right) \xi _3 -qr_bg_b(N_2,C_2)\xi _4,\\p_4(\xi _1,\xi _2,\xi _4,\xi _5)=&\frac{\partial \mu _{c}}{\partial A}(A_2,Q_{a2})\xi _1{+}\frac{\partial \mu _{c}}{\partial Q_{a}}(A_2,Q_{a2})\xi _2{-}\frac{1}{\gamma }r_{b}g_{b}(N_2,C_2)\xi _4{-}\frac{D}{L}\xi _5.\end{aligned} \end{aligned}$$

If $(\xi _1,\xi _2,\xi _3,\xi _4,\xi _5) \in \ker P$, then

$$\begin{aligned} \begin{aligned}&p_1(\xi _1,\xi _2,\xi _4)=0,~ p_2(\xi _1,\xi _2,\xi _3,\xi _4)=0,~ p_3(\xi _1,\xi _2,\xi _3,\xi _4)=0,\\&p_4(\xi _1,\xi _2,\xi _4,\xi _5)=0. \end{aligned} \end{aligned}$$

(A.1)

Let $\xi _4=1$, then it is clear that (A.1) has a unique solution $(\hat{\xi }_{1},\hat{\xi }_{2},\hat{\xi }_{3},1,\hat{\xi }_{5})$. Then $\dim \ker P=1$ and $\ker P={{\,\mathrm{span}\,}}\{\hat{\xi }_{1},\hat{\xi }_{2},\hat{\xi }_{3},1,\hat{\xi }_{5}\}$. It is also noted that ${{\,\mathrm{codim}\,}}{{\,\mathrm{range}\,}}P=1$ as

$$\begin{aligned} {{\,\mathrm{range}\,}}P=&\left\{ (\sigma _1,\sigma _2,\sigma _3,\sigma _4,\sigma _5)\in {\mathbb {R}}^5:\sigma _4=0\right\} , \end{aligned}$$

and

$$\begin{aligned}&P_{d_b(A,Q_a,N,B,C)}(d_{b1},A_2,Q_{a_2},N_2,0,C_2)(\hat{\xi }_{1}, \hat{\xi }_{2},\hat{\xi }_{3},1,\hat{\xi }_{5})\\&\quad =(0,0,0,-1,0)\notin {{\,\mathrm{range}\,}}P. \end{aligned}$$

From Theorem 1.7 in (Crandall and Rabinowitz 1971), there exists a $\delta _1>0$ such that all positive coexistence steady states of (3) near $(d_{b1},A_2,Q_{a_2},N_2,0,C_2)$ lie on a smooth curve

$$\begin{aligned} \Gamma _{ba}=\{(d_b(s),A_{3}(s),Q_{a3}(s),N_{3}(s),B_{3}(s),C_{3}(s)):0<s<\delta _1\} \end{aligned}$$

with the form

$$\begin{aligned} {\left\{ \begin{array}{ll} A_{3}(s)=A_{2}+s\hat{\xi }_1+o(s), Q_{a3}(s)=Q_{a2}+s\hat{\xi }_2+o(s), N_{3}(s)=N_2+s\hat{\xi }_3+o(s),\\ B_{3}(s)=s+o(s), C_{3}(s)=C_2+s\hat{\xi }_5+o(s). \end{array}\right. } \end{aligned}$$

Then part (ii) holds.

We next establish global bifurcation of positive coexistence steady states of (3). Let $\Upsilon$ be the set of all positive coexistence steady states of (3). It can be seen that the conditions of Theorem 3.3 and Remark 3.4 in (Shi and Wang 2009) hold. This shows that there exists a connected component $\Upsilon ^+$ of $\Upsilon$ such that it includes $\Gamma _{ba}$, and its closure contains the bifurcation point $(d_{b1},A_2,Q_{a2},N_2,0,C_2)$. Moreover, $\Upsilon ^+$ has one of the following three cases:

• (1) it is not compact in ${\mathbb {R}}^6$;

• (2) it includes another bifurcation point $(\bar{d}_{b},A_2,Q_{a2},N_2,0,C_2)$ with $\bar{d}_{b}\ne d_{b1}$;

• (3) it includes a point $(d_b,A_2+\hat{A},Q_{a2}+\hat{Q}_a,N_2+\hat{N},\hat{B},C_2+\hat{C})$ with $0\ne (\hat{A},\hat{Q}_a,\hat{N},\hat{B},\hat{C})\in Z$, where Z is a closed complement of $\ker P={{\,\mathrm{span}\,}}(\hat{\xi }_{1},\hat{\xi }_{2},\hat{\xi }_{3},1,\hat{\xi }_{5})$ in ${\mathbb {R}}^5$.

If the case (3) occurs, then $\hat{B}=0$, which is a contradiction to $\hat{B}>0$ since it is a positive steady state. Assume that the case (2) holds and $\bar{d}_{b}$ is another bifurcation value from $\Gamma _a$. Hence, there exists a positive coexistence steady state sequence $\{(d_{b}^n,A^n,Q_a^n,N^n,B^n,C^n)\}$ satisfying

$$\begin{aligned} \{(d_{b}^n,A^n,Q_a^n,N^n,B^n,C^n)\}\rightarrow (\bar{d}_{b},A_2,Q_{a2},N_2,0, C_2) \end{aligned}$$

as $n\rightarrow \infty$. From the fourth equation in (3), we have

$$\begin{aligned} r_bg_b(N^n,C^n)-d_b^n-\frac{D}{L}=0. \end{aligned}$$

Hence

$$\begin{aligned} r_bg_b(N_2,C_2)-\bar{d}_b-\frac{D}{L}=0 \end{aligned}$$

when $n\rightarrow \infty$, which means that $\bar{d}_b=d_{b1}$.

The above analysis shows that the case (1) must happen. Then $\Upsilon ^+$ is not compact in ${\mathbb {R}}^6$. It follows from Theorem 1 that

$$\begin{aligned}Q_{\min ,a}\le Q_{a3}\le Q_{\max ,a},~A_3Q_{a3}+qB_3+N_3\le N_b,~C_3\le \frac{r_aLN_b}{DQ_{\min ,a}} \end{aligned}$$

for all $d_b\in (0,d_{b1})$. This indicates that the projection of $\Upsilon ^+$ onto $d_b$-axis contains $(0,d_{b1})$. This proves part (i). $\square$

Proof of Theorem 3

• (i) It is obvious that $E_4$ always exists. The Jacobian matrix at $E_4$ is

  $$\begin{aligned} J(E_4)= \begin{pmatrix} a_{11} &{}\quad 0 &{}\quad 0&{}\quad 0&{}\quad 0\\ a_{21} &{}\quad a_{22} &{}\quad a_{23}&{}\quad a_{24} &{}\quad 0\\ a_{31} &{}\quad 0&{}\quad a_{33} &{}\quad 0 &{}\quad 0\\ 0 &{} \quad 0 &{}\quad 0&{}\quad a_{44} &{}\quad 0\\ a_{51} &{}\quad a_{52} &{}\quad 0 &{}\quad a_{54}&{}\quad a_{55} \end{pmatrix}, \end{aligned}$$

  where

  $$\begin{aligned} a_{11}&=\mu _{m}(0,Q_{m4},0)-d_{m}-\frac{v_{m}+D}{L}, a_{21}=-\frac{\partial \mu _{m}}{\partial M}(0,Q_{m4},0)Q_{m4},\\ a_{22}&=\frac{\partial \rho _m}{\partial Q_m}(Q_{m4})g_m(N_b)-r_m\bar{I}_m(0,0), a_{23}=\rho _{m}(Q_{m4})\frac{\partial g_m}{\partial N}(N_b),\\ a_{24}&=\frac{aq}{\delta }-\frac{\partial \mu _{m}}{\partial B}(0,Q_{m4},0)Q_{m4}, a_{31}=-\rho _{m}(Q_{m4})g_{m}(N_{b}),~ a_{33}=-\frac{D}{L},\\ a_{44}&=-d_{b}-\frac{D}{L}, a_{51}=\frac{\partial \mu _{c}}{\partial M}(0,Q_{m4}), a_{52}=\frac{\partial \mu _{c}}{\partial Q_{m}}(0,Q_{m4}),\\ a_{54}&=-\frac{r_{b}}{\gamma }g_{b}(N_b,0), a_{55}=-\frac{D}{L}. \end{aligned}$$

  It can be observed that $J(E_4)$ has five eigenvalues $a_{ii}$, $i=1,\cdots ,5$. Note that $a_{ii}<0$ for $i=2,3,4,5.$ Therefore, if $d_m>d_m^*$ holds, then $a_{11}<0$. This means that all the five eigenvalues of $J(E_4)$ have negative real parts. This shows that $E_4$ is locally asymptotically stable.

• (ii) The existence of $E_5$ is from Theorem 2 in (Wang et al. 2007). The Jacobian matrix at $E_5$ is

  $$\begin{aligned} J(E_{5})= \begin{pmatrix} a_{11} &{}\quad a_{12} &{}\quad 0&{}\quad a_{14}&{}\quad 0\\ a_{21} &{}\quad a_{22} &{}\quad a_{23}&{} \quad a_{24} &{}\quad 0\\ a_{31} &{}\quad a_{32}&{}\quad a_{33} &{}\quad a_{34} &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad a_{44} &{}\quad 0\\ a_{51} &{}\quad a_{52} &{}\quad 0 &{}\quad a_{54}&{}\quad a_{55} \end{pmatrix}, \end{aligned}$$

  where

  $$\begin{aligned} \begin{aligned} a_{11}&=\frac{\partial \mu _{m}}{\partial M}(M_{5},Q_{m5},0)M_5,\\a_{12}&=\frac{\partial \mu _{m}}{\partial Q_{m}}(M_5,Q_{m5},0)M_5,\\a_{14}&=\frac{\partial \mu _{m}}{\partial B}(M_5,Q_{m5},0)M_5,\\ a_{21}&=-\frac{\partial \mu _{m}}{\partial M}(M_5,Q_{m5},0)Q_{m5}, a_{22}=\frac{\partial \rho _m}{\partial Q_m}(Q_{m5})g_m(N_5)-r_m\bar{I}_m(0,M_5),\\ a_{23}&=\rho _{m}(Q_{m5})\frac{\partial g_m}{\partial N}(N_5), a_{24}=\frac{aq}{\delta }-\frac{\partial \mu _{m}}{\partial B}(M_{5},Q_{m5},0)Q_{m5},\\ a_{31}&=-\rho _{m}(Q_{m5})g_{m}(N_{5}), a_{32}=-\frac{\partial \rho _m}{\partial Q_m}(Q_{m5})g_m(N_5)M_5,\\ a_{33}&=-\frac{D}{L}-\rho _{m}(Q_{m5})\frac{\partial g_{m}}{\partial N}(N_5)M_5, a_{34}=-qr_bg_b(N_5,C_5),\\ a_{44}&=r_{b}g_{b}(N_5,C_5)-d_{b}-\frac{D}{L}-\frac{a}{\delta }M_5, a_{51}=\frac{\partial \mu _{c}}{\partial M}(M_5,Q_{m5}),\\ a_{52}&=\frac{\partial \mu _{c}}{\partial Q_{m}}(M_5,Q_{m5}), a_{54}=-\frac{r_{b}}{\gamma }g_{b}(N_5,C_5), a_{55}=-\frac{D}{L}. \end{aligned} \end{aligned}$$

  $J(E_5)$ has eigenvalues $a_{44}$, $a_{55}$, and the remaining three eigenvalues satisfy

  $$\begin{aligned} \lambda ^3+A_1\lambda ^2+A_2\lambda +A_3=0, \end{aligned}$$

  where

  $$\begin{aligned} A_1&=-(a_{11}+a_{22}+a_{33}),\\ A_2&=a_{11}a_{22}+(a_{11}+a_{22})a_{33}-(a_{23}a_{32}+a_{12}a_{21}),\\ A_3&=-a_{11}a_{22}a_{33} -a_{12}a_{23}a_{31}+a_{11}a_{23}a_{32}+a_{12}a_{21}a_{33}. \end{aligned}$$

  A direct calculation gives $A_i>0$, $i=1,2,3$ and $A_1A_2-A_3>0$. According to the Routh–Hurwitz criterion, the three eigenvalues have negative real parts. It is clear that $a_{55}<0$. If $d_b>d_{b2}$ holds, then $a_{44}<0$. This shows that all the five eigenvalues of $J(E_5)$ have negative real parts if $d_b>d_{b2}$ holds. Hence, $E_5$ is locally asymptotically stable.

(iii)-(iv) Define a mapping $G:{\mathbb {R}}^+\times {\mathbb {R}}^5\rightarrow {\mathbb {R}}^5$ by

$$\begin{aligned} G(d_b,M,Q_m,N,B,C)=\begin{pmatrix} \mu _m(M,Q_m,B)M-d_mM-\frac{v_m+D}{L}M\\ \rho _m(Q_m)g_m(N)+qf(B)-\mu _m(M,Q_m,B)Q_m\\ \frac{D}{L}(N_b-N)-\rho _m(Q_m)g_m(N)M-qr_bg_b(N,C)B\\ r_bg_b(N,C)B-d_bB-\frac{D}{L}B-f(B)M\\ \mu _c(M,Q_m)-\frac{1}{\gamma }r_bg_b(N,C)B-\frac{D}{L}C\\ \end{pmatrix}. \end{aligned}$$

It follows that $G(d_b,M_5,Q_{m5},N_5,0,C_5)=0$. Let

$$\begin{aligned}H:=G_{(M,Q_m,N,B,C)}(d_{b2},M_5,Q_{m5},N_5,0,C_5).\end{aligned}$$

For any $(\zeta _1,\zeta _2,\zeta _3,\zeta _4,\zeta _5)\in {\mathbb {R}}^5$, we have

$$\begin{aligned} H[\zeta _1,\zeta _2,\zeta _3,\zeta _4,\zeta _5]= \begin{pmatrix} h_1(\zeta _1,\zeta _2,\zeta _4)\\ h_2(\zeta _1,\zeta _2,\zeta _3,\zeta _4)\\ h_3(\zeta _1,\zeta _2,\zeta _3,\zeta _4)\\ 0\\ h_4(\zeta _1,\zeta _2,\zeta _4,\zeta _5) \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} h_1(\zeta _1,\zeta _2,\zeta _4)=&\frac{\partial \mu _{m}}{\partial M}(M_{5},Q_{m5},0)M_5\zeta _1+\frac{\partial \mu _{m}}{\partial Q_{m}}(M_5,Q_{m5},0)M_5\zeta _2\\ {}&+\frac{\partial \mu _{m}}{\partial B}(M_5,Q_{m5},0)M_5\zeta _4,\\h_2(\zeta _1,\zeta _2,\zeta _3,\zeta _4)=&-\frac{\partial \mu _{m}}{\partial M}(M_5,Q_{m5},0)Q_{m5}\zeta _1\\ {}&+\left( \frac{\partial \rho _m}{\partial Q_m}(Q_{m5})g_m(N_5)-r_m\bar{I}_m(0,M_5)\right) \zeta _2\\ {}&+\rho _{m}(Q_{m5})\frac{\partial g_m}{\partial N}(N_5)\zeta _3+\left( {\frac{aq}{\delta }}-\frac{\partial \mu _{m}}{\partial B}(M_{5},Q_{m5},0)Q_{m5}\right) \zeta _4,\\h_3(\zeta _1,\zeta _2,\zeta _3,\zeta _4)=&-\rho _{m}(Q_{m5})g_{m}(N_{5})\zeta _1-\frac{\partial \rho _m}{\partial Q_m}(Q_{m5})g_m(N_5)M_5\zeta _2\\ {}&-\left( \frac{D}{L}+\rho _{m}(Q_{m5})\frac{\partial g_{m}}{\partial N}(N_5)M_5\right) \zeta _3-qr_bg_b(N_5,C_5)\zeta _4,\\h_4(\zeta _1,\zeta _2,\zeta _4,\zeta _5)\!=&\frac{\partial \mu _{c}}{\partial {M}}(M_5,Q_{m5})\zeta _1 \!+\!\frac{\partial \mu _{c}}{\partial Q_{m}}(M_5,Q_{m5})\zeta _2\!-\!\frac{r_{b}}{\gamma }\!g_{b}(N_5,C_5)\zeta _4 \!-\!\frac{D}{L}\zeta _5. \end{aligned} \end{aligned}$$

If $(\zeta _1,\zeta _2,\zeta _3,\zeta _4,\zeta _5) \in \ker H$, then

$$\begin{aligned} \begin{aligned}&h_1(\zeta _1,\zeta _2,\zeta _4)=0,~ h_2(\zeta _1,\zeta _2,\zeta _3,\zeta _4)=0,\\&\quad h_3(\zeta _1,\zeta _2,\zeta _3,\zeta _4)=0, h_4(\zeta _1,\zeta _2,\zeta _4,\zeta _5)=0. \end{aligned} \end{aligned}$$

(A.2)

Let $\zeta _4=1$, then (A.2) has a unique solution $(\hat{\zeta }_{1},\hat{\zeta }_{2},\hat{\zeta }_{3},1,\hat{\zeta }_{5})$. This implies that $\dim \ker H=1$ and $\ker H={{\,\mathrm{span}\,}}\{\hat{\zeta }_{1},\hat{\zeta }_{2},\hat{\zeta }_{3},1,\hat{\zeta }_{5}\}$. It is also easy to show that ${{\,\mathrm{codim}\,}}{{\,\mathrm{range}\,}}H=1$ as

$$\begin{aligned} {{\,\mathrm{range}\,}}H=&\left\{ (\omega _1,\omega _2,\omega _3,\omega _4,\omega _5)\in {\mathbb {R}}^5:\omega _4=0\right\} , \end{aligned}$$

and

$$\begin{aligned}&G_{d_b(M,Q_m,N,B,C)}(d_{b5},M_5,Q_{m5},N_5,0,C_5)(\hat{\zeta }_{1}, \hat{\zeta }_{2},\hat{\zeta }_{3},1,\hat{\zeta }_{5})\\&\quad =(0,0,0,-1,0)\notin {{\,\mathrm{range}\,}}H. \end{aligned}$$

By using Theorem 1.7 in (Crandall and Rabinowitz 1971), there exists a $\delta _2>0$ such that all positive steady states of (8) near $(d_{b5},M_5,Q_{m5},N_5,0,C_5)$ lie on a smooth curve

$$\begin{aligned}\Gamma _{bm}=\{(d_b(s),M_{6}(s),Q_{m6}(s),N_{6}(s),B_{6}(s),C_{6}(s)):0<s<\delta _2\}\end{aligned}$$

with the form

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} M_{6}(s)=M_{5}{+}s\hat{\zeta }_1{+}o(s),\\ Q_{m6}(s)=Q_{m5}{+}s\hat{\zeta }_2{+}o(s),\\ N_{6}(s)=N_5{+}s\hat{\zeta }_3{+}o(s),&{}\\ B_{6}(s)=s+o(s),~ C_{6}(s)=C_5+s\hat{\zeta }_5+o(s).&{} \end{array}\right. } \end{aligned} \end{aligned}$$

This completes the proof of part (iv). Note that the proof of part (iii) is similar to those in Theorem 2. Then we omit it here. $\square$