1 Introduction

1.1 Epidemiology of COVID-19 Outbreak

The COVID-19 pandemic is the first truly global pandemic of the twenty-first century. In recorded history, the world has witnessed at least nine influenza-type outbreaks, such as the 1918 influenza pandemic (H1N1 virus), the 1957–1958 pandemic/Asian flu (a new influenza A (H2N2) virus), and the 1968 pandemic (H3N2 virus). (Jefferson & Heneghan, 2020; Kilbourne, 2006) The coronavirus is the tenth pandemic and ultimately may take its place among the deadliest ones, as it spreads more easily than the common flu and causes serious illness in many people. The COVID-19 pandemic has directly affected 181 million infections, almost 5 million deaths (as of July 13–2021).

1.2 Waves in Incidence as a Challenge for Public Health

Much discussion worldwide has centered around the possibility that the infection might rise and ebb with time, each time presenting the public health system with unique challenges. The maiden introduction of ‘wave’ in the context of influenza-type infections dates to the 1889–92 outbreak that manifested rises and falls in time. The term ‘wave’ prefixed by first/second/third, etc., is used to quantify the number of times an outbreak resurfaces after a substantial amount of time has passed. Geographic diversity, population dynamics, healthcare systems, administrative structures, and general public awareness have all played a role in modulating the occurrence of waves of COVID-19 at various places around the globe. Moreover, COVID-19’s impact has been affected by another factor, which makes modeling the spread of the disease more challenging than the past outbreaks, politicization of competing risk measures. The unpredictable behavior of the vulnerable groups toward preventive measures such as use of face masks, face shields, or social distancing adds a layer of uncertainty that is almost impossible to quantify with mathematical or statistical methods.

1.3 Challenges in Existing Data and Models of COVID-19

The modeling community has explored aspects of the pandemic using epidemiological modeling, statistical analysis, big-data techniques, and spatial methods incorporating what is known about the etiology of COVID-19, and about patterns of infection and their modulation by preventive measures, vaccines, medications, and other interventions. Even though the vaccination process has already started in several countries like the UK, USA, India, it may take several months for vaccines to be more broadly available. Here, we explore several cutting-edge issues (vaccine hopes, testing progress, models, and data projection) related to COVID-19 and its control/prevention. Intervention measures have been imposed and followed worldwide to curb the spread of SARS-CoV-2.

1.4 Synergistic Activities in Enhancing COVID-19 Information

Synergistic activities bring together different interdisciplinary approaches, drawing together ideas and leaders from disciplines such as biostatistics, epidemiology, mathematics, physics, and public health to identify and address important questions in reference to available COVID data. We discuss the gap between modeling and policy, and the probe that causes such a gap. Different models adhere to different methods, assumptions, and data which attract different policy discussions. One of the main goals of this commentary is therefore to shed a light on important modeling attempts by answering crucial questions in an effort to explore the connection between the policy decisions and their impact on the disease’s impact. In other words, with this commentary, it is not our intention to examine the mathematical properties of the rapidly growing world of modeling in detail or compare model performances. Instead, we are hoping to draw a picture of COVID-19 and COVID-19 related preventive strategies in a way that is widely accessible to most, if not, all parts of the populations vulnerable to COVID-19. Although technical in nature, we have taken initiative to make this commentary a suitable read not only for applied mathematicians but also for individuals with basic understanding of mathematics and science. Therefore, we consider the following research questions of paramount importance in our discussion:

  1. 1.1.

    How does the distribution of use of non-pharmaceutical interventions change temporally and spatially, and how the distribution can be used to study its impact on the dynamics of COVID-19 and vaccine implementation strategies?

  2. 2.2.

    How do you evaluate the predictive capability of epidemic models using non-pharmaceutical and epidemiological data in the presence of nonlinear population behavior?

  3. 3.3.

    How are current model projections being used in policy decisions and implementations?

COVID-19 pandemic has shown limitations in existing models and the modeling process itself. Here, we address and stress the need for adaptation of much broader perspective in the modeling process that is expected to increase not only community understanding and the ability to respond to system in crises but also will have higher acceptability of model-evaluated policies by the population itself, which is in dire need of urgent lifesaving and economically efficient policies. Hence, we propose a novel Multiresolution Modeling Framework which connects multiple dimensions such as epidemiological, ecological and social mechanisms, empirical information, optimization criteria and stakeholders.

The organization of our commentary is as follows: In Sect. 2, we describe the brief review of the three questions. In Sect. 3, we provide some examples of data critical for epidemic models mentioned in Sect. 4. In Sect. 4, we discuss potential models. Figure 1 collects models and empirical information needed for them. Section 5 describes the key components of our novel Multiresolution Modeling Framework that also connects and incorporates models and data from Sect. 3and Sect. 4. We end with a discussion in Sect. 6.

Fig. 1
figure 1

Critical models and methods considered here in this article

Full size image

2 The Three Identified Challenges from the Literature and Using the Delphi Method

We explore these three questions using a selected literature review which is further substantiated using the Delphi Method (Gordon, 1994; Linstone et al. 1975), which is a process that involves informal surveys of a panel of experts, though of small sample size. We consulted renowned experts (the size of eight experts, an acceptable minimum in Delphi Method, were considered) from biostatistics, computational biology, epidemiology, physics, and public health (including three of our webinar panelists Dr. Giridhar R Babu, Professor and Head Life-course epidemiology, Public Health Foundation of India; Dr. Bhramar Mukherjee, Professor of Epidemiology and Global Public Health, University of Michigan School of Public Health; Dr. Gautam Menon, Professor Biology and physics professor, Ashoka University, India). The experts had experience with modeling of infectious diseases and their views on the three questions mentioned in the Introduction section were collected. The summary of responses of these experts is outlined below and supplemented with the literature.

There are also other forms of collection methods for gathering data, used for parameterizing/validating models. Besides Delphi method, other common consensus group methods include nominal group technique (NGT), analytical hierarchy process (AHP), and expert elicitation methods (EEM), which are used to synthesize expert opinions when evidence is lacking. On the other hands, traditional examples of surveillance data include seroprevalence surveys, COVID diagnostic test’s reliability surveys to identify test sensitivity and specificity, and other follow-up population-level surveys. These data along with properly estimated models could then eventually provide useful implications that may be useful for designing intervention strategies.

The study of the effectiveness of social distancing and PPE measures in bringing down infection relies on two important factors: (a) knowing the percentage of population complying with intervention guidelines and (b) having population movement data, both intra-state and inter-state. A recent article (Peeples, 2020) suggests that by the end of February 2021, approximately 511 thousand deaths may be seen in the USA. This could be reduced by 130 thousand with a 95% population compliance with the usage of masks and by 95 thousand with an 80% usage of masks in public places.

As one of the most populous countries in the world, India stands as a worthwhile case study to investigate the way COVID impacted the country, and the way government policies impacted the speared of the disease. In India, even though some data show that 60–70% of people use masks, the source of information on this percentage is not clear. Good data on the granular level of the absorption of masks remain missing. Further, the movement of individuals needs to be monitored and incorporated into existing models to efficiently map the surge in infections with rising/restricted public movement. There have been applications launched by various countries’ administration for tracking population movement, but their success rate has been backed by the degree of ease with which the technology was accepted by the masses and evoked mixed responses. For instance, population movement data obtained by one such study from the Indian state of Karnataka proved to be of immense help while tackling the surge in infections within the state (World Health Organization, 2020b). However, the success rate of the application was not uniform throughout the Indian subcontinent, failing miserably in a few states. A few protocols which can cater to these issues will involve local/state-driven data and the sequential upgrade of models quantifying mask usage and social distancing. Another important measure involves using ‘mobile app data’ to monitor inter-state mobility of a concerned population. The methodology of data collection can help in upgrading the estimates for the future. Countries with heterogenous populations, like India, should lay emphasis on state/region-wise model development plans and data collection strategies. These local models, as opposed to global models, can help immensely in the distribution of vaccines.

The interactions between the scientific community and policy makers have been informal and confined to the personal interest of policy makers in learning about model predictions. For example, in India, the lack of interactions between modelers and policy makers is a major concern. India needs to formalize a means to ensure the direct exchange of information between researchers and policy makers. There are excellent examples where such relationships have shown miraculous outcomes. For example, in the USA, simulations derived from the models which employed evolutionary computing and machine learning-based parameter estimation techniques produced highly accurate forecasts in addition to the ones that are used by the surge planning committee to curb rising numbers (Bennet & Geraghty, 2020). In the Indian state of Karnataka, policy makers are looking into models for the prediction of cases in the future and to locate the time and region of surges (World Health Organization, 2020a).

Another worthy example in this context is the discussion of lockdown strategies between researchers (including students) in epidemiology at the University of Michigan and the governor of the State of Michigan, the USA, as well as how projection models are used by the Government of Michigan. The governor of Michigan worked with epidemiologists to inform their decisions about statewide stay at home orders and lockdowns. Although these recommendations did not always manifest as policy, the communication process was transparent and may have helped establish a norm of communication between government and scientists in Michigan, the USA (Hutchinson, 2021). Collaborative efforts (between researchers at the Universities, Public Health Departments, and Policy Makers) bring out inputs that can aid states with data-driven models. Adhering to proper risk-communication and understanding the implications of the models need to be done by policy makers. Models have their own limitations: Thus, forecasting may only be accurate over the short term.

This void can be filled to a certain extent by scientists, channeling their voice through social media platforms, putting out their findings and suggestions for general public awareness, time to time. Understanding the optimal deployment of healthcare resources, vaccine distributions, and risk stratifications should be the target for upcoming models. Vaccine distribution needs to be evidence based. Models may not provide precise point estimates but can precisely provide fact-based evidence to decision makers to choose a direction which may converge to a similar conclusion. In case they diverge, the information can be extracted through the differences in estimates. In the next sections, we discuss, in brief, three major areas diagnostic testing efficacy, vaccination implementation strategies, and estimating parameters of models.

3 Examples of Data Sources for Parameterizing Dynamical Models

Epidemiological data and non-pharmaceutical measures have been recorded in a limited capacity, as shown in Tables 1, 2, 3. Here, we describe some of this data, how it can be applied to models, as well as some short comings in data.

Table 1 Examples of different types of diagnostic tests and characteristics
Full size table
Table 2 Diagram comparing sensitivity and specificity with false positive and false negative
Full size table
Table 3 Non-pharmaceutical data collected from three telephone surveys in Hong Kong. Confidence intervals and sample size can be found in Table 3A (Cowling et al., 2020)
Full size table

In Table 1, we summarize the types of COVID-19 diagnostic tests along with their sensitivity and specificity. The two metrics to measure accuracy of a test can be defined as: (i) Sensitivity measures the ability of a test to correctly identify those with the disease (true positive rate) out of those who have the disease, and (ii) specificity measures the ability of a test to correctly identify people without the disease. In Table 4, brief descriptions of a few vaccines for the COVID-19 are collected. The values in the two Tables can be used in mathematical models to study the impact of different testing and vaccine policies. In Sect. 4, we provide details about types of models and on methods of linking models to data.

Table 4 Examples of different vaccines and characteristics
Full size table

In Table 1, 93% sensitivity for the IgG Antibody Testing- ELISA indicates that out of all the tests that came back positive, 93% of them were correctly diagnosed as positive and 7% of the positive tests were false positives and contributed to a Type I error. On the other hands, for the same test, a 97% specificity indicates that of the tests that came back negative 3% were false negatives and contributed to a Type II error. Sensitivity and specificity and their relationship to Type I and Type II error are further described in Table 2.

4 Predictive Models for Implications from Implementing Diagnostic Tests Strategies and Vaccines Implementation

In this section, we explore three modeling approaches: diagnostic test models, vaccination models, and multiple virus strain models. These models highlight the need for relationships between scientists and policy makers. Active scientific communication is necessary to respond to changes in public behavior, changes in policy and healthcare, and virus mutations.

We can also develop a simple epidemic model for understanding the role of a particular non-pharmaceutical intervention on the dynamics of the disease outbreak. In such models, the population can be divided into two subgroups: a subpopulation who uses non-pharmaceutical interventions (such as a mask-wearing group) and others who do not use interventions. People move back and forth between the two subgroups groups at certain constant per capita rate. Individuals in subgroups will be characterized based on their epidemiological status: susceptible \(\left( {S\;{\text{and}}\;S_{m} } \right),\) infectious \(\left( {I\;{\text{and}}\;I_{m} } \right)\) and recovered (R) individuals.

In such model, there will be two forces of infection λ, one for each subgroup. For example, the force of infection for the individuals who use intervention will incorporate the probability of transmission per contact, the reduced number of contacts because of symptomatic infection (θ), and the effectiveness of the mask in reducing either susceptibility (\(\phi_{S}\)) or infectivity (\(\phi_{I}\)). The force of infection will be written by

$$\lambda_{m} = \beta \left[ {\left( {1 - \phi_{S} } \right)\frac{\theta }{{N - \left( {1 - \theta } \right)\left( {I + I_{m} } \right)}} + \left( {1 - \phi_{S} } \right)\left( {1 - \phi_{I} } \right)\frac{{\theta I_{m} }}{{N - \left( {1 - \theta } \right)\left( {I + I_{m} } \right)}}} \right]$$

The estimates of \(\phi_{S}\) and \(\phi_{I}\) can be estimated using Table 3. Note, \(\phi_{S}\) and \(\phi_{I}\) can be a function of time (for example, three time points are shown in Table 3) and location.

4.1 Diagnostic Test Model

The high testing rates may seem an important focus, but other characteristics related to tests themselves are likely more germane. False positive tests are more probable than positive tests when the overall population has a low prevalence of the disease, even with highly accurate tests (Petherick, 2020). Although much attention has been focused on the number of tests being conducted (Gray et al., 2020; Horton, 2020a), not enough attention has been given to the issues of imperfect testing (Horton, 2020b). The public is learning about the differences between the tests for detecting active cases and the tests for the presence of antibodies. These different tests emphasize different test characteristics. Since active viral tests measure who is currently infected, maximizing sensitivity will help minimize the risk of spreading infection. On the other hands, antibody detection should maximize specificity to reduce false negative values.

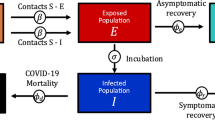
Minimizing false negatives emphasizes a strategy that involves detecting those who have successfully overcome the virus and are likely to have some level of immunity (or at least reduced susceptibility to more serious illness if they are infected again) and thus are relatively safe to relax their personal social distancing measures. Therefore, this strategy would require a high test’s specificity that aims to minimize how often a test tells someone they have had the disease, when they have not. There are two factors that make a “good” test: sensitivity and specificity. Using these tests appropriately will help develop effective strategies to reduce the spread of infection. A good test is only effective in a carefully designed strategy. To explore the effect of imperfect testing on the disease dynamics when strategies are employed to relax the current social distancing measures, Gray et al. (2020) proposed a modified SIR model by adding three new classes to the model. We considered here a modified and extended version of their model, and its brief structure is shown in the flow chart given in Fig. 2.

Fig. 2
figure 2

Structure of modified SIR model incorporating diagnostic tests

Full size image

The modified extended testing model system in Fig. 2 could be given by the following system (where parameters can be identified in Table 5),

$$\begin{aligned} \frac{{{\text{d}}S}}{{{\text{d}}t}} = & - \frac{\beta SI}{{N - \left( {Q_{s} + Q_{I} + Q_{R} } \right)}} + \alpha R + \phi \left( {1 - \tau_{B} } \right)Q_{S} - \rho \left( {1 - \tau_{A} } \right)S \\ \frac{{{\text{d}}Q_{s} }}{{{\text{d}}t}} = & \rho \left( {1 - \tau_{A} } \right)S - \phi \left( {1 - \tau_{B} } \right)Q_{s} \\ \frac{{{\text{d}}I}}{{{\text{d}}t}} = & \frac{\beta SI}{{N - \left( {Q_{s} + Q_{I} + Q_{R} } \right)}} - \rho \sigma_{A} I - \gamma I \\ \frac{{{\text{d}}Q_{I} }}{{{\text{d}}t}} = & \rho \sigma_{A} I - \gamma Q_{I} \\ \frac{{{\text{d}}R}}{{{\text{d}}t}} = & \gamma \left( {I + Q_{I} } \right) - \rho \left( {1 - \tau_{A} } \right)R + \phi \sigma_{B} Q_{R} - \alpha Ra \\ \frac{{{\text{d}}Q_{R} }}{{{\text{d}}t}} = & \rho \left( {1 - \tau_{A} } \right)R - \phi \sigma_{B} Q_{R} \\ \end{aligned}$$
(1)

The reproduction number corresponding to the above model can be calculated by next-generation method. We rewrite the infected compartment équations of the system as

$$x^{^{\prime}} = f\left( {x,y} \right) - v\left( {x,y} \right)$$

where

$$x = \left( {I,Q_{I} } \right)^{T} ,\;\;y = \left( {S,Q_{S} ,R,Q_{R} } \right)^{T} ,\;\;f\left( {x,y} \right) = \left( {\begin{array}{*{20}c} {\frac{\beta SI}{{N - \left( {Q_{S} + Q_{I} + Q_{R} } \right)}}} \\ 0 \\ \end{array} } \right)\;\;{\text{and}}\;\;v\left( {x,y} \right) = \left( {\begin{array}{*{20}c} {\rho \sigma_{A} I + \gamma I} \\ {\rho \sigma_{A} I + \gamma Q_{I} } \\ \end{array} } \right)$$

by calculating the Jacobian of \(f\) and \(v\), we obtain

$$F = \left( {\begin{array}{*{20}c} {\frac{{S\left( {S + R} \right)\beta }}{{\left( {S + I + R} \right)^{2} }}} & 0 \\ 0 & 0 \\ \end{array} } \right)\;\;{\text{and}}\;\;V = \left( {\begin{array}{*{20}c} {\gamma + \rho \sigma_{A} } & 0 \\ { - \rho \sigma_{A} } & \gamma \\ \end{array} } \right)$$

we can consider the disease-free equilibrium (DFE) \(E_{0} = \left( {S\left( 0 \right),0,0,0,0,0,} \right)\) where \(S\left( 0 \right)\) is the initial size of the susceptible population. Therefore, by calculating the Jacobian at \(E_{0}\), we obtain

$$F_{{E_{0} }} = {\mathcal{F}} = \left( {\begin{array}{*{20}c} \beta & 0 \\ 0 & 0 \\ \end{array} } \right),\;\;{\text{and}}\;\;V_{{E_{0} }} = {\mathcal{V}} = \left( {\begin{array}{*{20}c} {\gamma + \rho \sigma_{A} } & 0 \\ { - \rho \sigma_{A} } & \gamma \\ \end{array} } \right)$$

Further,

$${\mathcal{V}}^{ - 1} = \left( {\begin{array}{*{20}c} {\frac{1}{{\gamma + \rho \sigma_{A} }}} & 0 \\ {\frac{{\rho \sigma_{A} }}{{\gamma^{2} + \gamma \rho \sigma_{A} }}} & {\frac{1}{\gamma }} \\ \end{array} } \right)$$

We obtain the next generation matrix \(\left( {{\mathcal{F}\mathcal{V}}^{ - 1} } \right)\) as

$${\mathcal{F}\mathcal{V}}^{ - 1} = \left( {\begin{array}{*{20}c} {\frac{\beta }{{\gamma + \rho \sigma_{A} }}} & 0 \\ 0 & 0 \\ \end{array} } \right)$$

Therefore, the basic reproduction number is the largest eigen values as \(R_{0} = \frac{\beta }{{\gamma + \rho \sigma_{A} }}\).

The table for the parameters can be found in the appendix in Table 6, and the force of infection can be described as \(\lambda = \frac{\beta I}{{N - \left( {Q_{S} + Q_{I} + Q_{R} } \right)}}\). Here, we see that the force of infection depends on the ratio of the transmission coefficient (\(\beta\)) with the number of infected (\(I\)) and the difference between the total population (\(N\)) and the total number of quarantined individuals (\(Q_{S} + Q_{I} + Q_{R}\)). Additionally, the reproduction number can be written as the transmission coefficient divided by the sum of the per capita recovery rate (\(\gamma\)) and the product of the natural mortality rate (\(\rho\)) and test sensitivity (\(\sigma_{A}\)): \(R_{0} = \frac{\beta }{{\gamma + \rho \sigma_{A} }}\).

Test performance and test capacity play key roles in determining the dynamics of COVID-19. The sensitivity and specificity parameters of the model system (1) could be estimated once we have counted the number of false positive, true negative, total infected, and uninfected individuals (Dehning, Zierenberg, et al., 2020). For example, sensitivity (\(\sigma_{A}\)) and specificity (\(\tau_{A}\)) can be estimated using values in Table 1. To interpret the diagnostic value of a positive or negative test result, we can also compute, prevalence, positive predictive value (PPV), negative predictive value (NPV), just by following the Bayes rule (Dehning, Zierenberg et al., 2020). The sensitivity of the model system (1) could be discussed with varying levels of prevalence, infection test sensitivities, antibody test sensitivities, and specificities. In particular, the impact of variations (low and high sensitivity) in sensitivity can also be discussed. More importantly, this model can be used to study the long-term burden of the disease when one or multiple types of novel diagnostic tests are used for testing and contact tracing intervention. Thus, this model can be used to study long-term burden of the disease when one or multiple types of novel diagnostic tests are used for testing and contact tracing interventions.

4.2 Vaccine Model

The knowledge of key concepts in vaccine epidemiology (such as basic reproductive numbers, force of infection, vaccine efficacy and effectiveness, vaccine failure, herd immunity, herd effect, epidemiological shift, disease modeling) and their applications are significant both at program levels (policy makers, immunization program managers) and in the practice by epidemiologists, pediatricians, family physicians, public health experts, and other experts/individuals involved in immunization service delivery (Gray et al., 2020). As we are in the process of production of a few authorized vaccinations, vaccination efficacy is an important aspect to be investigated. Makhoul et al. (2020) discussed how the vaccination impact can be accessed at various efficacies using an age-structured model in reference to the disease transmission and progression. The impact of vaccination can be assessed by quantifying its effectiveness, that is, computing the number of vaccinations needed to avert one infection or one adverse disease outcome (ratio of number of vaccinations relative to that of averted outcomes). The results revealed that if there is a vaccine with efficacy against acquisition (VES) ≥ 70%, infection can be eliminated. A vaccine with VES < 70% still would have a major impact and infections can be reduced if the number of infectious or the infection duration can be reduced through additional measures, such as social distancing, and supplemented with herd immunity.

The flowchart in Fig. 3 is an extended model of the model suggested by Makhoul et al. (2020), which incorporated levels of vaccination. In the vaccine model, it can be assumed that exposed (E) and mild infectious individuals (M) have reduced infectivity \(\alpha_{1}\) and \(\alpha_{2}\), respectively. Also, the parameter \(r\) defined as the behavior compensation post-vaccination can be interpreted as the increase in contact rates among those vaccinated, which may undermine vaccine impact. Since VEI represents the effectiveness of the vaccine, the force of infection of vaccine model can be written as:

$$\lambda = \beta \left[ {\frac{{\left( {\alpha_{1} E + I_{S} + \alpha_{2} I_{M} } \right) + \left( {1 - VE_{I} } \right) * \left( {\alpha_{1} E^{V} + I_{S}^{V} + \alpha_{2} I_{M}^{V} } \right)}}{N}} \right]$$
Fig. 3
figure 3

Flowchart of vaccine implementation model described in Sect. 4.2. The subscripts M, S, and DS represent mild, severe, and severe disease, respectively. The parameters \(\delta^{ - 1} ,\eta^{ - 1} ,f, \omega\) and \(\gamma\) represent the duration of latent infection, the duration of infection, the proportion of infections that become either mild or severe, the duration of vaccine protection, and the per capita vaccination rate, respectively. After vaccination, changes in behavior are represented by the parameter \(r\)

Full size image

The parameters and variables of the vaccine model are explained in the appendix in Table 7. Keeping in mind the current scenario where the vaccines are supposed to be administrated in two doses, the model can be helpful in examining the strategy of vaccinating a large population by full two dose of vaccine versus vaccinating only with a single dose. Different parameters affecting the course of infection can be analyzed to recognize whether a one-dose or two-dose strategy is more effective. The information which could be looked into is the initiation of vaccination with respect to the start of the epidemic, primary response level (defined as the percentage of the full vaccine efficacy that will be reached after the first dose), vaccination coverage, the kinetics of the vaccine efficacies post-vaccination as functions of time, and transmissibility of the virus, measured through the basic reproduction number, R0. Two simple models and R0 values are described below for reference. The first model (\(M_{1}\)) gives a glimpse of a mathematical model without vaccination along with the basic reproduction number, whereas the second model (\(M_{2}\)) explicitly takes into the number of vaccinated individuals.

MODEL (\({\varvec{M}}_{1}\))

$$\begin{aligned} \frac{{{\text{d}}S}}{{{\text{d}}t}} = & - \lambda S - \mu S \\ \frac{{{\text{d}}E}}{{{\text{d}}t}} = & \lambda S - \left( {\delta + \mu } \right)E \\ \frac{{{\text{d}}I}}{{{\text{d}}t}} = & f\delta E - \left( {\eta + \mu } \right)I \\ \frac{{{\text{d}}R}}{{{\text{d}}t}} = & \eta I - \mu R \\ \end{aligned}$$

where \(\lambda = \beta \sigma \frac{1}{N}\) is the force of infection when \(\beta\) is the infectious contact rate, and \(\sigma\) is the susceptibility profile to the infection. The reproduction number obtained by the next-generation method is \(\sqrt {\frac{\beta \sigma f\delta }{{\left( {\delta + \mu } \right)\left( {\eta + \mu } \right)}}}\).

MODEL ( \({\varvec{M}}_{2}\) )

$$\begin{aligned} \frac{{{\text{d}}S}}{{{\text{d}}t}} = & \lambda S - \mu S - \gamma S + \omega V \\ \frac{{{\text{d}}V}}{{{\text{d}}t}} = & \gamma S - \left( {1 - VE_{S} } \right)\left( {1 + r} \right)\lambda V - \left( {\delta + \mu } \right)V - \omega V \\ \frac{{{\text{d}}E}}{{{\text{d}}t}} = & \left( {1 - VE_{S} } \right)\left( {1 + r} \right)\lambda V - \left( {\delta + \mu } \right)E \\ \frac{{{\text{d}}I}}{{{\text{d}}t}} = & \left( {\left( {1 - VE_{p2} } \right) + \frac{{VE_{p2} }}{f}} \right)f\delta E - \left( {\frac{\eta }{{\left( {1 - VE_{p1} } \right)}} + \mu } \right)I \\ \frac{{{\text{d}}R}}{{{\text{d}}t}} = & \frac{\eta }{{1 - VE_{p1} }}I - \mu R \\ \end{aligned}$$

The basic reproduction number obtained by the next-generation method is

$$\sqrt {\frac{{\beta \sigma f\delta \left( {1 - VE_{S} } \right)\left( {1 + r} \right)\left( {1 - VE_{p2} + \frac{{VE_{p2} }}{f}} \right)\left( {\lambda + \mu + r} \right)}}{{\omega \left( {\frac{\eta }{{1 - VE_{p2} }} + \mu } \right)\left( {\delta + \mu } \right)}}}$$

4.3 Multiple Strain Model

Variant strains of the coronavirus have already emerged (Koyama et al., 2020; Rouchka et al., 2020). Although experts expect the current vaccines to be effective against these strains (Koyama et al., 2020), future mutations may render current immunization efforts moot or may only grant partial immunity. This potential problem highlights the necessity for close working relationships between scientists and policy makers, so that virus mutations can be addressed with science as quickly as possible. Models that account for multiple strains of a virus already exist for pandemics (Castillo-Chavez et al., 1989; Chung & Lui, 2016; Khyar & Allali, 2020; Kucharski et al., 2016; Nuno et al., 2005) and can be modified to fit the parameters of our current pandemic. Overall, the effect of variant pathogens depends on differences in parameters such as infection rates, recovery rates, and cross-immunity. Cross-immunity describes the phenomenon where the host is granted some amount of immunity to a different viral strain given the two strains are antigenically similar enough. If the antigens produced by multiple strains are identical, then we would expect full immunity, or complete cross-immunity, through the infections of one strain. As strains become more antigenically dissimilar, we would expect some amount of cross-immunity, or partial cross-immunity, until the dissimilarities became significant enough to warrant no amount of cross-immunity. Overall, cross-immunity is difficult to quantify. Evidence for cross-immunity can be found through challenge studies, longitudinal cohort studies, and with phylogenetic evidence (Adams et al., 2006; Huang et al., 2020). Cross-immunity can be detected using in vitro studies (Adams et al., 2006; Khoury et al., 2020) by determining whether antibodies are able to prevent the virus from binding to human protein, but these results are difficult to verify in vivo. In addition, cross-immunity could be measured using seroprevalence surveys that indicate how much of a population has antibodies toward COVID-19, but these surveys may have similar short comings to those discussed in Sect. 4.1.

Figure 4 describes a modified flow chart from Castillo-Chavez et al. (1989), Chung and Lui (2016), Khyar and Allai (2020), Kucharski et al. (2016), and Nuno et al. (2005) where there are two strains of a virus and infection from one strain can grant partial or complete cross-immunity to another strain of the same virus. Here, we also assume that an individual cannot be infected with both variants of the virus simultaneously. This model was originally created for influenza and has been modified for COVID-19 with additional compartments for disease severity as described in Sect. 4.2. After being infected with one strain of the virus, there is a potential for either partial or complete cross-immunity for another strain of the virus. The parameters and variables of the multiple strain model are explained in appendix Table 8.

Fig. 4
figure 4

Flowchart of multiple strain model described in Sect. 4.3. The subscripts 1, 2, 1C, or 2C help define each compartment or parameter as either from variant 1, from variant 2, from variant 1 with cross-immunity from 2, or from variant 2 with cross-immunity from 1, respectively. The remaining compartments and parameters can be found in Fig. 3 and the appendix

Full size image

Partial cross-immunity could still decrease rates of infection for portions of the population that have already been infected. Currently, the variant strains of COVID-19 are believed to grant complete cross-immunity, but as the virus continues to mutate there is a chance that different strains will only grant partial cross-immunity. However, as discussed in Sect. 4.2, partial immunity may be enough to cull the pandemic with additional efforts such as social distancing and other non-pharmaceutical preventatives. Based on results from influenza models, it has been shown that certain similarities and differences among transmission rates, cross-immunity factors, and contact rates can lead to cyclic outbreaks (Castillo-Chavez et al., 1989; Chung & Lui, 2016; Nuno et al., 2005) indicating that COVID-19 could be around episodically for many years to come.

The model in Fig. 4 has been modified to account for two strains of the virus, but as mutations increase, so can the number of strains. Therefore, planning for multiple, or n, strains of the coronavirus is beneficial. However, the model becomes exponentially more complicated with each additional strain. As an individual gains partial cross-immunity, they may have a reduced susceptibility \(\tau\) or a reduction in infectiousness \(\sigma\). Thus, infection rates become dependent on individual infection histories and the number of possible histories grows exponentially with each additional strain. Therefore, finding a way to simplify the model described in Fig. 4 such that each virus strain only has three possible compartments, S, I, and R, will be beneficial. Similar to the models in (Kucharski et al., 2016), a model with n strains is easily managed by using set notation such that \(N = \left\{ {1, \ldots ,n} \right\}\) represents the set of all strains and \(X\) is a subset of \(N\). Then, \(S_{0}\) represents the susceptible proportion of the population that has not been infected by any strain, \(S_{1}\) represents the susceptible proportion of the population that has been infected by strain 1, and \(S_{X}\) represents the susceptible proportion of the population that has been infected by the set of \(X\)-strains. Here, cross-immunity is represented with reduced transmission as well as reduced susceptibility. To account for the infection history, we let \(i \in N\) and \(j \in X\) and \(i \notin j\), so that \(E_{i,j}\) represents the proportion of the population exposed to strain i with an infection history j. Similarly, we denote \(I_{M,i,j} ,I_{S,i,j}\) and \(D_{S,i,j}\) to be the compartments contributing to strain i with an injection history j. \(\tau \left( {j,i} \right)\) represents a reduction in susceptibility for strain \(i\) given an infection history of \(j\), \(\sigma \left( {j,i} \right)\) represents a reduction in infectiousness due to an infection history of j, and \(\eta \left( {j,i} \right)\) represents the recovery rate for strain i given an infection history j (Kucharski et al., 2016). Due to the large number of equations and variables, there is benefit in creating a linear combination \(\hat{I}_{i}\) of compartments \(E,I_{M} ,I_{S} ,\) and \(D_{S}\) where coefficients are the parameters \(\tau \left( {j,i} \right)\) and \(\sigma \left( {j,i} \right)\) so that we now have a multiple strain \(S\hat{I}R\) model where \(\hat{I}_{i}\) represents the sum of all compartments contributing to strain i. In addition, \(\lambda_{i}\) represents the transmission factor of strain \(i\). Then, the force of infection is \(\lambda_{i} = {\upbeta }\hat{I}_{i}\). If the average time that one is infected with strain \(i\) across all possible infection histories is \(\theta_{i}\) then we find that the reproductive number for the ith strain is \(R_{i} = \frac{\beta }{{\theta_{i} }}\) (Nuno et al., 2005).

Due to the complexity of an n strain epidemiology model, the information here has been simplified, and more details about models for n variants of influenza can be found in (Kucharski et al., 2016) and then modified for COVID-19. Future models could be further extended by including aspects from the vaccination model under different assumptions of immunity and cross-immunity.

4.4 Linking Models to Data

In the testing, vaccination, and multiple strain models, the most critical parameter that influences dynamics is the transmission coefficient (β), which depends on the average contact rate. Average contact rate, and thus the transmission coefficient, varies based on the implementation of non-pharmaceutical interventions (like social distancing, lockdown, and facemasks) and mobility patterns of the population. Due to changes in contact rates over time, it is often challenging to estimate it with precision directly from data. Instead, transmission coefficient (β) is indirectly estimated by fitting mathematical model to reported incidence data by different estimation methods.

Linking between data and models is an essential aspect for a modeler so that accurate predictions can be done which may be even utilized by the government/policy makers. Vaccination distribution is essentially an important aspect which must be dealt with meticulously in this pandemic. As modelers, it is our moral responsibility to suggest models which can provide the government with the crucial information which may be helpful to them while designing strategies for vaccination distribution. Lahariya (2016) has addressed this question for HINI influenza and can really provide us with a detailed knowledge on vaccination distribution which can be even replicated for the current pandemic. The structure of developing and analyzing the model can be briefly summarized in terms of the flowchart shown in Fig. 5.

Fig. 5
figure 5

Flowchart for the development and analysis of models

Full size image

The results of these models can indicate the importance of the timing of the vaccination, and they particularly emphasize how important it is to start administering vaccines before the peak of the outbreak in different regions. Further, it is also important to consider the stages of the outbreak at different locations and deploy vaccines with a preference to regions with more severe outbreaks to maximize the benefit. Another aspect of developing and analyzing a mathematical model is the robustness of the results with respect to statistical and dynamical modeling assumptions, as well as complementary data sources. Why is there such a wide variation in model predictions, even among predictions made using transmission models based on either the SIR or SEIR framework? It is simply because of too little information at the beginning of the outbreak and the lack of data (except for the confirmed case data) that could be used for model calibration? In reference to COVID-19, it is extremely important that the model developed should be able to cater to sudden changes in parameters, like the spreading rate due to implementation of non-pharmaceutical interventions and concurrent changes in behavior. Studies (Abraham et al., 2020; Dehning, et al., 2020a) formulate an epidemiological model combining Bayesian inference to enable a robust assessment of the spread of infectious diseases in a timely manner. A Bayesian approach is able to detect and quantify the effect of non-pharmaceutical interventions and can forecast the future number of cases. The Bayesian approach captures uncertainty in measurement errors that are inherent in all data sets whether it is gathered from surveillance system or through common consensus group methods. We provide here the summary of steps to understand Bayesian parameter inference method, although we do not show any example of its use. The Bayesian framework allows for the posterior inference of parameters, which updates prior beliefs based on a data-driven likelihood. The posterior inference is governed using Bayes theorem, \(P\left( {W{|}D,M} \right) = \frac{{P\left( {D{|}W,M} \right)P\left( {W|M} \right)}}{P\left( D \right)}\), where \(P\left( {W{|}D,M} \right)\) is the posterior distribution of a vector of model parameters (W) given the model \(\left( M \right)\) and observed data \(\left( D \right)\), P(D|W, M) is the likelihood, and \(P\left( D \right)\) is the evidence. The likelihood indicates the probability of observing the reported case data given the assumed model. Often Gaussian likelihood is taken as it reasonably minimizes discrepancies between the predicted and observed reported cases. Parameter prior distributions encode some prior subject matter knowledge into parameter estimation. In the case of COVID-19 model parameters, priors incorporate literature-based expected values of parameters such as recovery rate (μ), transmission/spreading rate (λ), and change points based on policy interventions.

The analysis in (Abraham et al., 2020; Dehning et al., 2020b; Dehning et al., 2020a) highlights the importance of precise timing and the magnitude of interventions for future case numbers. It stresses the importance of including the reporting delay D between the date of infection and the date of the confirmed case in the model. The reporting delay D, together with the time required to implement interventions, means that changes in our behavior today can only be detected in confirmed cases in two weeks’ time. This delay, combined with a spreading rate close to zero, indicates that careful planning of future measures is essential. A simple time discrete version of SIR model is proposed with stationary spreading rate which is:

$$\frac{{{\text{d}}S}}{{{\text{d}}t}} = - \lambda \frac{SI}{N},\;\;\frac{{{\text{d}}I}}{{{\text{d}}t}} = \lambda \frac{SI}{N} - \mu I,\;\;\frac{{{\text{d}}R}}{{{\text{d}}t}} = \mu I$$

During the onset phase of an epidemic, only a very small fraction of the population is infected (I) or recovered (R), and thus S ≈ N >> I such that S/N ≈ 1. Therefore, the differential equation for the infected reduces to a simple linear equation, exhibiting an exponential growth.

$$\frac{{{\text{d}}I}}{{{\text{d}}t}} = \left( {\lambda - \mu } \right)I,\;\;{\text{with}}\;\;I\left( t \right) = I\left( 0 \right)e^{{\left( {\lambda - \mu } \right)t}}$$

Because the dataset is discrete in time (Δt = 1 day), the above differential equations is solved with a discrete time step (dI/dt ≈ ΔI/Δt), such that

$$S\left( t \right) - S\left( {t - 1} \right) = - \lambda \Delta t\frac{{S\left( {t - 1} \right)I\left( {t - 1} \right)}}{N} = - I_{t}^{{{\text{new}}}}$$
$$R\left( t \right) - R\left( {t - 1} \right) = \mu \Delta tI\left( {t - 1} \right) = R_{t}^{{{\text{new}}}}$$
$$I\left( t \right) - I\left( {t - 1} \right) = \left( {\lambda \frac{{S\left( {t - 1} \right)}}{N} - \mu } \right)\Delta tI\left( {t - 1} \right) = \left( {I_{t}^{{{\text{new}}}} - R_{t}^{{{\text{new}}}} } \right)$$

\(I\left( t \right)\) models the number of all (currently) active infected people, whereas \(I_{t}^{{{\text{new}}}}\) is the number of new infections that will eventually be reported according to standard World Health Organization (WHO) convention. They explicitly included a reporting delay D between new infections \(I_{t}^{{{\text{new}}}}\) and newly reported cases \({\text{C}}\left( {\text{t}} \right)\) as \(C_{t - D}^{{{\text{new}}}}\). The estimation starts at time \(t = 0\) where the initial infected class is \(I_{0}\). In the model, reported data \(C\left( t \right)\) for \(t > D\) can be incorporated. The model can be then extended to consider weekly report modulation and change points in spreading rate. Further, the spreading rate λi, i = 1, …, n may change at certain time points ti from λi–1 to λi, linearly over a time window of Δti days. Thereby, considering mitigation measures, the parameters ti, Δti, and \(\lambda_{i}\) are added to the parameter set of the simple model above, and the differential equations are augmented by the time-varying λi. In addition, a weekly modulation to account for lower case reports around the weekend is also included; these cases subsequently accumulate during the week. To model the systematic variation of case reports during the week, the newly reported cases are modified with a reporting fraction.

$$C\left( t \right) = C_{t - D}^{{{\text{new}}}} \left( {1 - f\left( t \right)} \right),\;\;{\text{with}}\;\;f\left( t \right) = \left( {1 - f_{w} } \right)\left( {1 - \left| {\sin \left( {\frac{\pi }{7}t - \frac{1}{2}\phi_{w} } \right)} \right|} \right)$$

\(f_{w} \;{\text{and}}\;\phi_{w}\) can be constrained from the data. Therefore, a forecast can be done with Bayesian inference and MCMC (Markov-Chain Monte-Carlo) sequentially as mentioned below:

  • Estimate the set of model parameters \(\theta = \lambda_{i} ,t_{i} ,\mu ,D,\sigma ,I_{0} ,f_{w} ,\phi_{w}\) using Markov-Chain Monte-Carlo (MCMC).

  • Initialize the Markov Chains via variational inference. The posterior distribution is approximated by Gaussian distributions ignoring correlations between parameters through automatic differentiation variational inference (ADVI) and from this distribution, four starting points for four chains are sampled.

  • Each chain performs 1000 burn-in (tuning) steps, which are not recorded. This serves as equilibration in order to sample from an equilibrium distribution in the next step.

  • Each chain performs 4000 steps, which are used to approximate the posterior distribution. To ensure that the chains are equilibrated and sampled from the whole posterior distribution (ergodicity), we verified that the R-hat statistic (for comparing prior to posterior distribution) is below 1.05.

  • The rank normalized R-hat diagnostic tests for lack of convergence by comparing the variances within chains and between chains. When the within and between chain variances are equal, for which R-hat is equal to 1, convergence is achieved. This indicates that the resulting forecast has the maximum accuracy and precision.

Another point of interest can also be incorporation of human mobility data, which can easily be incorporated in the above Bayesian estimation method. The human mobility patterns have significantly been changed due to COVID-19 pandemic. Therefore, capturing of impacts of different changes in mobility patterns on SARS-CoV-2 via epidemiological models may provide more applicable and equitable policy decisions. Recently, Chang et al. (2021) introduced meta-population model SEIR integrating dynamics mobility networks to simulate the spread of COVID-19 in ten metropolitan areas of US. The study of Chang et al. (2021) predicted that “a small minority of ‘superspreader’ points of interest account for a large majority of the infections, and that restricting the maximum occupancy at each point of interest is more effective than uniformly reducing mobility.”

5 Multiresolution Modeling Approach

5.1 Epidemic Nowcasting

During an outbreak, policymakers focus on obtaining accurate, real-time estimates of disease characteristics and spread, which are often challenged by reporting delays and underreporting. Epidemic nowcast is an approach that attempts to estimate accurate disease burden in real time using modeling techniques and current multiple reported empirical information. Traditionally, modeling methods ignore aspects of changing reporting methodology and use same fixed parameter estimates over time to evaluate policies and draw conclusions. However, three aspects are critical to understanding of progression of an epidemic: (i) how reporting methodology changes over time, (ii) what new biological information on pathogen is known (which may help in obtaining changes in estimates of model parameters), and (iii) what features of the disease and surveillance system contribute to reporting delays. The goal of the nowcast models is to estimate the number of occurred-but-not-yet-reported events at any given time based on an incomplete set of reports from surveillance, the literature and modeling assumptions. Such models have been used for HIV, influenza and other diseases in the past (Wu et al., 2021).

5.2 Multi-objective Optimization Problem

COVID-19 control has shown that stringent measures, such as lockdown orders, while help in limiting spread of infection, also bring huge economic losses. A crucial aim of policymakers has been to identify correct balance between severity of control measures and the cost–benefit analysis of interventions. Then, a further motivating objective is to maximize the "net social gain" which includes cost–benefit consideration. The problem is not just limited to cost minimization. It is about net gains for society over time, e.g., if we lock the community today, with expectation of gains in the future, it also reduces loss of human resources (e.g., deaths), etc. Typically, studies evaluating policies try to build optimization problem with a single criterion and solve it as a single-objective optimization problem. However, public health department often is faced with decisions that have multiple objectives some of which may have contradicting goals. This can be achieved by using the epidemiological model-based multi-objective planning criteria to find a set of Pareto-optimal policies. A representative set of Pareto-optimal policies (i.e., a set of mathematically equivalent optimal decisions) are the policies that cannot be improved for one objective without deteriorating the value of at least one another criterion (Eftekhari et al., 2020; Pirotta et al., 2015). The Pareto-optimal policies set is a part of the frontier of the feasible policies set, and a decision within this set is the best according to the preferences of the decision maker. The type of framework not only help in providing prediction goals under each policy but also provides a real-time decision support tool for policymakers. The principle of Pareto-optimality has been used in multi-objective optimization with applications in many fields. For example, it is often used to identify frontier in cost-effectiveness analysis of interventions, representing the optimal trade-off between costs and benefits, while evaluating interventions. In practical scenarios, decision makers generally have to choose group of different interventions into several ordered levels with increasing strictness at different time points and then choose among them. In case of multi-objective optimization problem, objectives can have conflicting goals with each other. Modeler therefore faces a problem of making the trade-off and intervenes at the right time and in the right amount to minimize the overall cost to the stakeholders. The eventual goal of a decision analysis is to determine the best decision among a number of available choices according to the preferences of the decision makers and modeler.

For example, a standard optimal control problem typically has two components: (i) a SIR-type epidemic model, which consists of some number of controls and (ii) an objective function, which contains state variables of epidemic model and control functions. The aim is to use optimal control theory to find the optimal values of controls such that the associated state variables trajectories are solution of system of the epidemic model in a finite time interval and minimize the objective function (Yousefpour et al., 2020). Because of fixed values of the model parameters and weights of controls in the objective function, a large range of alternatives remains unexplored, and the decision maker get limited options on policy evaluation. On the other hands, the above single objective may consist of multiple objectives representing the social, medical and economical perspectives that may have the conflicting nature of the underlying decision problem. Hence, in such case, a multi-objective optimization problem might be better to construct and optimization problem is repeated with different parameter settings to approximate Pareto-optimal policies set (or Pareto-optimal solutions set) (Denysiuk et al., 2018).

5.3 Participatory Modeling

The purpose of this commentary is to take viewpoints and concerns from modelers, policy makers, the public, and the pathogen itself in order to guide and analyze how COVID-19 models, as well as models for future pandemics, can be developed to address the needs of all the participants in policy creation and response to better cull the spread of infectious diseases. This process is known as participator modeling. As defined by Voinov et al. (2018), participatory modeling is “a purposeful learning process for action that engages the implicit and explicit knowledge of stakeholders to create formalized and shared representations of reality.” The goal of this article is not complete the entire participatory modeling process (Voinov & Gaddis, 2008) and results in a final aggregated model, but to explore how this process can improve current COVID-19 models and incorporate the needs of multiple groups invested in the development, execution, and response to decisions surrounding the pandemic. Traditionally, a mathematical modeler follows following steps in a modeling study: (i) identify problems surrounding the pandemic, (ii) gather information through surveys and by using the Delphi method, and (iii) address models that have been created without a participatory modeling mindset. These models focus on one stakeholder’s frame of reference and ultimately ignore the concerns or responses of other participants. Individually, these models may address specific research questions, but for a complete view and understanding of the intricate interactions throughout a pandemic, these models should overlay one another. These models could play a role in the soft systems methodology (SSM) used for participatory modeling. This method considers multiple steps and progresses from problem selection and modeling with pictures to the development of models and eventually to the initiation of change to help improve a situation (Voinov & Gaddis, 2008).

Remark:

In this commentary, we have attempted to design a novel Multiresolution Modeling Framework in which we stress on not only on changing knowledge of epidemiological characteristics of the disease (collected in Sect. 2), advancing empirical information (discussed in Sect. 3), consideration of appropriate ensemble of mathematical models (discussed in Sect. 4) and statistical inference methodology (mentioned in Sect. 4.4) but also relevant output computation procedures (such as Nowcasting), multi-objective optimization criteria (computation of Pareto frontier) for different stakeholders (i.e., use of participatory modeling). In the context of the focused questions in the present article, we also stress the requirement of (i) proper understanding of mechanisms and quantification of distribution of spatial–temporal use of different non-pharmaceutical interventions, typically only measured in limited ways via public health surveillance system. Several studies (such as Chen et al., 2021) are available in which authors have explored the impacts of different factors (non-pharmaceutical interventions, human behavior, rainfall, temperature, humidity, geographical location, population density, economical structures, etc.) on the spatiotemporal distribution of COVID-19 burden. However, data are limited for some of these factors. The application of effective modeling methods and precise prediction of a disease using important data, highlighted in this article, for modeling will provide timely information for the faster implementation and appropriate distribution of non-pharmaceutical interventions. Focused modeling analysis of COVID-19 outbreak may provide valuable information about the disease burden for policy design and pandemic preparedness.

6 Discussion

6.1 Interdisciplinary Approaches

It is important to build a reasonable comprehensive model for COVID-19 type epidemic which incorporates significant interventional and epidemiological factors such as testing, vaccination, mask use, and circulating pathogen strains. Additionally, social-behavior aspects are critical in epidemic models (Mubayi et al., 2020) which many models in the literature lack. One of the main strengths of models is to understand role of selected mechanisms on dynamics and less forecasting, which even sophisticated ensemble of climate models have difficulty in predicting for more than a week. Particularly policies and cultural aspects can have drastic implications on interactions in populations unlike data for climate variables. Communication between disciplines and policy makers has been unprecedented due to this pandemic.

When it comes to mitigating crisis as described herein, successful strategies end up being the ones that implement interdisciplinary approaches (Kaxiras & Neofotistos, 2020). While face coverings and social distancing seem to be the epitome of protective measures, without incorporating population movement and restrictions one might expect to see waves with higher peak intensities. As a result, countries with heterogenous populations may see higher success in crisis mitigation if they treat their regions and subregions as separate and hence homogeneous entities, determining different estimates and policies, as they would do for a country alone (Gupta et al., 2020). This concept can also be applied to the policies for vaccine distribution across heterogenous populations. Relevant research and findings need to reach the masses whether via social networking platforms, journals, media both audio and visual, print media, conferences and symposiums-one of this kind with interdisciplinary approach. Additionally, the spread of misinformation has been drowning out credible sources of information during current pandemic (Mian and Khan 2020). In case of COVID-19, the global rise in the spread and popularity of misinformation via unverified sources of information and social networking platforms has really been a challenge for credible organization of information (e.g., WHO and CDC). For example, recently, we have seen multiple theories regarding the origin of COVID-19 virus and some of them were just originated as misinformation from social media and some of websites. Such misleading news amass millions of engagements per day. The huge impact of such misinformation on the populous may lead to devastation. To avoid such devastation and to protect credible sources of information, we require strong communication from government and authorities and therefore the role of more centralized authorities (such as WHO, CDC) along with public–private partnerships. More precisely, in the face of pandemic, the different public health agencies first need to update their technologies and then to educate, manage and address the people’s issues more appropriately. Lessons from the Bombay fever of 1918 clearly indicate that the present crisis may not vanish within a few weeks or months. Hence, expecting instantaneous revival of prevailing circumstances or abrupt eradication of the infection will lead to nothing but dismay and fatigued efforts. We do not have a terminus in this context. Instead, we can look forward to versatile short-term and long-term goals to efficiently deal with the current third wave, and counter upcoming waves in the near future. Overall, the article’s motive here is not only to summarize the answers to some of our questions, but it is also a cautious effort to make people aware about some significant contributions with respect to statistical and dynamical modeling which could be helpful in this critical situation of COVID-19 in relation to social distancing, face covers, testing accuracy, vaccination efficacy and its distribution.

6.2 Future Models

A large number of modeling approaches that employ a variety of models that focus on producing a broad range of outcomes have been made. The predictions have far-reaching consequences regarding governmental policies to curb the pandemic. However, the epidemiological models are primarily useful to estimate the effects of different interventions in reducing the disease burden rather than precise quantitative predictions. Therefore, along with our focus on improving the data sets related to infections, mortality, and premature predictions, we also try to develop precise epidemiological mathematical models to estimate the effect of different parameters that deal with different aspects of life (economic, social, epidemiological, etc.). Further, apart from looking into this crisis practically, we desperately need a humanitarian touch as well to raise and rectify mental health issues and our Multiresolution Modeling Framework is capable of capturing these features. It is fundamental that we keep an open line of communication with scientists. The good news across the world is that the people are trying to be safe by wearing face coverings, social distancing, and practicing good hygiene. Community healthcare workers and officials are regularly announcing suitable measures that could be used by the public to reduce the spread of the coronavirus. The year 2020 has been a string quartet between governments, the public, scientists, and the private sector where the conductor has been the coronavirus. This string quartet is not always in harmony, but it may continue until we have a vaccine. In the meantime, we all must manage our personal risks taking all the health precautions. This is how we will need to live our lives alongside the virus. Finally, as models get more complicated in the future, it is also important for researchers to understand the limitations that they come with that can affect decisions in healthcare as the novel coronavirus is constantly changing. While the models are appropriate given the scientific knowledge at the occasion of their creation; however, our understanding of COVID-19 continues to necessitate the inclusion of more refined and/or sophisticated mathematical assumptions (Seshaiyer et al., 2020).