Abstract
The number of publications on mathematical modeling of cancer is growing at an exponential rate, according to PubMed records, provided by the US National Library of Medicine and the National Institutes of Health. Seminal papers have initiated and promoted mathematical modeling of cancer and have helped define the field of mathematical oncology (Norton and Simon in J Natl Cancer Inst 58:1735–1741, 1977; Norton in Can Res 48:7067–7071, 1988; Hahnfeldt et al. in Can Res 59:4770–4775, 1999; Anderson et al. in Comput Math Methods Med 2:129–154, 2000. https://doi.org/10.1080/10273660008833042; Michor et al. in Nature 435:1267–1270, 2005. https://doi.org/10.1038/nature03669; Anderson et al. in Cell 127:905–915, 2006. https://doi.org/10.1016/j.cell.2006.09.042; Benzekry et al. in PLoS Comput Biol 10:e1003800, 2014. https://doi.org/10.1371/journal.pcbi.1003800). Following the introduction of undergraduate and graduate programs in mathematical biology, we have begun to see curricula developing with specific and exclusive focus on mathematical oncology. In 2018, 218 articles on mathematical modeling of cancer were published in various journals, including not only traditional modeling journals like the Bulletin of Mathematical Biology and the Journal of Theoretical Biology, but also publications in renowned science, biology, and cancer journals with tremendous impact in the cancer field (Cell, Cancer Research, Clinical Cancer Research, Cancer Discovery, Scientific Reports, PNAS, PLoS Biology, Nature Communications, eLife, etc). This shows the breadth of cancer models that are being developed for multiple purposes. While some models are phenomenological in nature following a bottom-up approach, other models are more top-down data-driven. Here, we discuss the emerging trend in mathematical oncology publications to predict novel, optimal, sometimes even patient-specific treatments, and propose a convention when to use a model to predict novel treatments and, probably more importantly, when not to.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 The Past and Present of Mathematical Oncology
Mathematical modeling in cancer has a long history as reviewed in multiple publications (Araujo and McElwain 2004; Lowengrub et al. 2010; Altrock et al. 2015; Friedman 2004). According to PubMed records provided by the US National Library of Medicine and the National Institutes of Health, the number of publications on mathematical modeling of cancer is growing at an exponential rate (Fig. 1). Early conceptual mathematical models highlighted the universal dynamics of cancer growth (Agur et al. 2002; Brú et al. 2003; Guiot et al. 2003) and the emergent properties of proliferation and invasion mechanisms (Anderson et al. 2006; Hillen 2006). As cancer is an umbrella term for more than 100 different diseases with different intrinsic dynamics and unique environmental and ecological niches, mathematical models have begun to focus on the properties of specific cancers such as leukemia (Michor et al. 2005) and glioma (Eikenberry et al. 2010) or cancers of the breast (Enderling et al. 2006), prostate (Swanson et al. 2001), or bladder (Bunimovich-Mendrazitsky et al. 2008) among many others. To this success, model parameters need to be carefully assigned, often from the experimental and the clinical literature of the specific cancer. Numerous mathematical oncology publications stand out by virtue of their truly integrative nature and deliberate and interdisciplinary model calibration and validation effort (Kozusko et al. 2001; Anderson et al. 2009; Leder et al. 2013; Marusyk et al. 2014; Prokopiou et al. 2015; Poleszczuk and Enderling 2018; Kaznatcheev et al. 2019). One of the mainstays of mathematical oncology is modeling of the various oncological treatments including surgery (Hanin et al. 2015; Enderling et al. 2005), radiation therapy (McAneney and O’Rourke 2007; Kempf et al. 2010; Alfonso et al. 2014; Gao et al. 2013), chemotherapy (Powathil et al. 2007; Castorina et al. 2009; Hinow et al. 2009; Vainstein et al. 2011; Powathil et al. 2012), anti-angiogenic therapy (Poleszczuk et al. 2015; Sachs et al. 2001; Poleszczuk et al. 2011; Hutchinson et al. 2011), virotherapy (Dingli et al. 2006; Friedman et al. 2006; Mahasa et al. 2017; Santiago et al. 2017), and immunotherapy (Kogan et al. 2012; Elishmereni et al. 2011; Nani and Freedman 2000; Kuznetsov and Knott 2001; Castiglione and Piccoli 2007; Kirschner and Tsygvintsev 2009) as well as their numerous possible combinations (Hawkins-Daarud et al. 2015; Bunimovich-Mendrazitsky et al. 2011; Alfonso et al. 2019).
Several agencies have provided funding mechanisms for mathematical oncology, including the National Science Foundation (NSF) and the National Cancer Institute (NCI) in the USA, the Engineering and Physical Sciences Research Council (EPSRC) and Cancer Research UK, the German Cancer Research Center (DKFZ), and multinational frameworks within the European Union. Several mathematical modeling research groups and even mathematical oncology departments have become established in cancer centers and medical schools around the world. As a result, we begin to witness the translation and evaluation of mathematical model-derived treatment protocols in prospective clinical trials (NCT03557372, NCT03768856, NCT03656133) (Leder et al. 2013; Prokopiou et al. 2015; Alfonso et al. 2018). Mathematical exploration of the evolutionary dynamics underlying the development of prostate cancer resistance to hormone therapy (Cunningham et al. 2011; Gatenby et al. 2009; Gatenby and Brown 2018) led to a clinical trial of adaptive hormone therapy with treatment holidays to prevent competitive release of resistant cancer cells (NCT02415621). Early results indicate that most patients maintained stable oscillations of tumor burdens, thereby significantly increasing time to progression from 13 to at least 27 months. Interestingly, on average, patients received less than half of the treatment dose than conventional continuous therapy (Zhang et al. 2017). With these mathematical oncology success stories, cancer biologists and oncologists begin to embrace mathematical modeling as a valuable methodology. With this, the mathematical oncology community has the opportunity and responsibility to clearly identify the purpose of developed models and critically evaluate and discuss if model predictions are an academic exercise or have true translational merit.
As many mathematical models have become increasingly complex through the iterative inclusion of the growing biological knowledge, the field of mathematical modeling has slipped into parameterization from multiple sources often mixing cancer types, experimental conditions, and even spatio-temporal scales. It has become routine to provide references for parameter values from other theoretical studies; in selected instances, the parameter value reference trail may follow back many publications to an initially “assumed” value without any biological or clinical data supporting the assumption. Incorrectly calibrated and unvalidated mathematical models risk simulating cancer growth and treatment response dynamics that are, albeit being interesting, biologically and clinically unrealistic. Yet, it has become an increasing trend to use inadequately parameterized mathematical cancer models to predict untested treatment protocols, to propose optimize therapy combinations and, in some cases, to develop personalized optimal therapy approaches.
Bottom-up phenomenological mathematical models often formalize biological mechanisms. Model analysis and numerical simulations demonstrate evolving population level dynamics based on these mechanisms. This allows the study of complex biological and mathematical systems, and how perturbations to individual mechanisms or rate constants qualitatively change tumor growth or treatment response. Vis-à-vis the bottom-up approach is the top-down approach, where population level dynamics are used to infer the mechanisms that most likely underlie the observed data. With sparse data, this often limits complexity of mathematical oncology models. Another crucial distinction to make is mathematical oncology vs. oncological mathematics. While the former uses mathematical modeling as a purposely built tool to help answer specific oncological questions, the latter uses cancer biology to motivate development of interesting mathematics. Both approaches provide valuable scientific contributions and are not necessarily mutually exclusive. However, as many cancer modelers lack access to high-resolution cancer biology or oncology data including independent training and validation data sets, many models are merely academic and not positioned to speculate on optimal therapy.
1.2 The Future of Mathematical Oncology Predictions for Novel Cancer Therapies
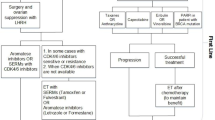
Before a mathematical model can make reliable, testable and translational predictions about novel therapeutic doses, treatment protocols or combination therapies, we propose that six successive steps have to be followed (Fig. 2):
-
1.
Identify a putative biomarker
To simulate cancer and cancer therapy, a biomarker of tumor burden needs to be identified. This may be the number of cancer cells in a petri dish or in the patient’s blood for liquid tumors, tumor volume derived from medical images or caliper measurements from mouse experiments for solid cancers, or surrogate markers such as prostate-specific antigen (PSA) in liquid biopsies. In contrast to statistical models that correlate random variables (such as pre-treatment tumor size with treatment outcome), mathematical modeling simulates the dynamics of the tumor and their underlying mechanisms. Therefore, the data of putative biomarkers for mechanistic modeling should be temporally resolved.
-
2.
Develop mechanistic model
The change of the putative biomarker over time is described using dynamic models such as mechanistic differential equations or cellular automata or agent-based models (here, we focus on differential equations but the application to discrete models is intuitive). If only temporal data are available, ordinary differential equations (ODE) are often sufficient. Partial differential equations (PDE) should only be used if spatio-temporally resolved data are available, or temporal dynamics alone are insufficient to explain the observed biomarker dynamics. The number of model variables and parameters should be determined with utmost care and limited based on the available data. Information criteria offer invaluable analyses to balance model complexity with degrees of freedom (Akaike 1974; Ludden et al. 1994).
If longitudinal data are limited (as often in clinical studies), non-mechanistic or statistical models may be considered that simulate the dynamics of the biomarker without resolution of the underlying mechanisms. Such models, however, will have limited ability to predict novel treatment protocols beyond considerations for treatment holidays.
-
3.
Calibrate model with existing data
The mathematical model is only suitable to simulate and predict novel treatment protocols if it can fit and predict the data of known therapies. If possible, model parameters should not be taken from the empirical wisdom or the literature but derived from the data within realistic bounds. A variety of machine learning and established statistical methods are already available to identify model parameters for simple models. To further aid in parameter estimation for larger models and across multiple data sets, however, major advances are still required to reliably calibrate mathematical models. Model analysis should be performed to test parameter identifiability (Eisenberg and Jain 2017). Non-identifiable parameters or parameters with low sensitivity may be represented as (non-)linear combination of other model parameters or assigned nominal values from the appropriate literature.
For individual patient data and models built with the intent to predict patient-specific treatment protocols, it is important to identify which parameters drive individual response dynamics, and which parameters can be held uniform across a patient population. As above, the number of patient-specific parameters should be kept to a minimum to be able to learn these parameter values from patient data to simulate and predict personalized treatment protocols.
-
4.
Validate model with untrained data
Once calibrated with data, the mathematical model must be validated against independent data. The learned model parameters should be held constant, and the model’s ability to fit untrained data should be evaluated via methods such as R2 analyses. If independent training and testing data sets are not available, data should be randomly stratified into model calibration and validation cohorts. For smaller data sets, leave-one-out studies may be required to learn and test model parameters. This step provides an internal control and prevents overfitting to training data.
-
5.
Evaluate predictive performance for known treatment
A model’s ability to fit data does not imply that it is predictive. Many models may fit data equally well but make different predictions forward in time (Murphy et al. 2016). Before a mathematical model should be used to predict novel treatments, the model must be able to predict responses to treatment protocols for which data are available. As above, an independent prediction evaluation cohort is the gold standard, but random stratification of a single data set into model training, validation, and prediction performance evaluation may be required and acceptable. How to evaluate model prediction performance depends on the purpose of the model. If the model aims to predict binary events (response, resistance, survival), statistical tools such as the concordance index or area under the receiver operating characteristic curve may be applicable (Steyerberg et al. 2010). To further understand and assess clinical utility, the positive predictive value (PPV) and negative predictive value (NPV) for model prediction should be calculated (Janes et al. 2015). If and only if the predictive performance for known treatment responses and outcomes is sufficiently high (a conventional notion of acceptable cutoffs for predictive performance is yet to be established in the field of mathematical oncology), models may be used to simulate and predict untested treatments.
-
6.
Simulate and predict untested treatments
To use calibrated and validated model parameters to simulate alternative treatments, it is important to limit the exploration space to treatments that can be derived from the calibrated and validated model. Treatments that the model was not trained to predict should not be simulated. Furthermore, if, for example, the training data contain only single-dose levels and the biological dose response curves are unknown, predictions into untested doses should be met with caution and limited confidence.
While it is straightforward to simulate arbitrary treatment protocols, clinical feasibility (for example, radiation therapies can rarely be delivered more than twice a day or on the weekend due to logistical constraints) and biologically important bounds (such as drug agent half-life or toxicity) must be honored. Additionally, when comparing predicted responses to innovative treatments with the data, one can only draw conclusions about the evaluated regimes. To claim ‘optimal therapy,’ rigorous optimal control approaches and an exhaustive analysis should be provided.
2 Conclusions
Mathematical oncology has contributed significant scientific insights into the dynamics of tumor growth and treatment response and is uniquely positioned to help map the multidimensional treatment response space (Enderling et al. 2018). The art of the mathematical oncology profession must deploy a standard to only predict novel treatments if the model is properly trained and validated to do so. We call for the convention to up-front identify model purpose and model predictions as either ‘academic’ or ‘translational’ in nature. Shortcuts to translational treatment predictions (Fig. 2) may hurt the field of mathematical oncology that is in the advent of earning the trust of oncologists and, ultimately, may hurt patients that would be prospectively treated with ill-informed, model-suggested treatment protocols.
References
Agur Z, Daniel Y, Ginosar Y (2002) The universal properties of stem cells as pinpointed by a simple discrete model. J Math Biol 44:79–86
Akaike H (1974) A new look at the statistical model identification. IEEE Trans Autom Control 19:716–723. https://doi.org/10.1109/tac.1974.1100705
Alfonso J, Jagiella N, Núñez L, Herrero MA, Drasdo D (2014) Estimating dose painting effects in radiotherapy: a mathematical model. PLoS ONE 9:e89380. https://doi.org/10.1371/journal.pone.0089380
Alfonso J, Parsai S, Joshi N, Godley A, Shah C, Koyfman SA, Caudell JJ, Fuller CD, Enderling H, Scott JG (2018) Temporally feathered intensity-modulated radiation therapy: A planning technique to reduce normal tissue toxicity. Med Phys 45:3466–3474. https://doi.org/10.1002/mp.12988
Alfonso J, Poleszczuk J, Walker R, Kim S, Pilon-Thomas S, Conejo-Garcia JJ, Soliman H, Czerniecki B, Harrison LB, Enderling H (2019) Immunologic consequences of sequencing cancer radiotherapy and surgery. JCO Clin Cancer Inform. https://doi.org/10.1200/cci.18.00075
Altrock PM, Liu LL, Michor F (2015) The mathematics of cancer: integrating quantitative models. Nat Rev Cancer 15:730–745. https://doi.org/10.1038/nrc4029
Anderson AR, Chaplain M, Newman E, Steele R, Thompson A (2000) Mathematical modelling of tumour invasion and metastasis. Comput Math Methods Med 2:129–154. https://doi.org/10.1080/10273660008833042
Anderson AR, Weaver AM, Cummings PT, Quaranta V (2006) Tumor morphology and phenotypic evolution driven by selective pressure from the microenvironment. Cell 127:905–915. https://doi.org/10.1016/j.cell.2006.09.042
Anderson AR, Hassanein M, Branch KM, Lu J, Lobdell NA, Maier J, Basanta D, Weidow B, Narasanna A, Arteaga CL, Reynolds AB, Quaranta V, Estrada L, Weaver AM (2009) Microenvironmental independence associated with tumor progression. Cancer Res 69:8797–8806. https://doi.org/10.1158/0008-5472.can-09-0437
Araujo R, McElwain D (2004) A history of the study of solid tumour growth: the contribution of mathematical modelling. Bull Math Biol 66:1039–1091. https://doi.org/10.1016/j.bulm.2003.11.002
Benzekry S, Lamont C, Beheshti A, Tracz A, Ebos JM, Hlatky L, Hahnfeldt P (2014) Classical mathematical models for description and prediction of experimental tumor growth. PLoS Comput Biol 10:e1003800. https://doi.org/10.1371/journal.pcbi.1003800
Brú A, Albertos S, Subiza J, García-Asenjo J, Brú I (2003) The universal dynamics of tumor growth. Biophys J 85:2948–2961. https://doi.org/10.1016/s0006-3495(03)74715-8
Bunimovich-Mendrazitsky S, Byrne H, Stone L (2008) Mathematical model of pulsed immunotherapy for superficial bladder cancer. Bull Math Biol 70:2055–2076. https://doi.org/10.1007/s11538-008-9344-z
Bunimovich-Mendrazitsky S, Gluckman J, Chaskalovic J (2011) A mathematical model of combined bacillus Calmette-Guerin (BCG) and interleukin (IL)-2 immunotherapy of superficial bladder cancer. J Theor Biol 277:27–40. https://doi.org/10.1016/j.jtbi.2011.02.008
Castiglione F, Piccoli B (2007) Cancer immunotherapy, mathematical modeling and optimal control. J Theor Biol 247:723–732. https://doi.org/10.1016/j.jtbi.2007.04.003
Castorina P, Carcò D, Guiot C, Deisboeck TS (2009) Tumor growth instability and its implications for chemotherapy. Cancer Res 69:8507–8515. https://doi.org/10.1158/0008-5472.can-09-0653
Cunningham JJ, Gatenby RA, Brown JS (2011) Evolutionary dynamics in cancer therapy. Mol Pharm 8:2094–2100. https://doi.org/10.1021/mp2002279
Dingli D, Cascino MD, Josić K, Russell SJ, Bajzer Ž (2006) Mathematical modeling of cancer radiovirotherapy. Math Biosci 199:55–78. https://doi.org/10.1016/j.mbs.2005.11.001
Eikenberry SE, Nagy JD, Kuang Y (2010) The evolutionary impact of androgen levels on prostate cancer in a multi-scale mathematical model. Biol Direct 5:24. https://doi.org/10.1186/1745-6150-5-24
Eisenberg MC, Jain HV (2017) A confidence building exercise in data and identifiability: Modeling cancer chemotherapy as a case study. J Theor Biol 431:63–78. https://doi.org/10.1016/j.jtbi.2017.07.018
Elishmereni M, Kheifetz Y, Søndergaard H, Overgaard R, Agur Z (2011) An integrated disease/pharmacokinetic/pharmacodynamic model suggests improved interleukin-21 regimens validated prospectively for mouse solid cancers. PLoS Comput Biol 7:e1002206. https://doi.org/10.1371/journal.pcbi.1002206
Enderling H, Anderson AR, Chaplain MA, Munro AJ, Vaidya JS (2005) Mathematical modelling of radiotherapy strategies for early breast cancer. J Theor Biol 241:158–171. https://doi.org/10.1016/j.jtbi.2005.11.015
Enderling H, Chaplain MA, Anderson AR, Vaidya JS (2006) A mathematical model of breast cancer development, local treatment and recurrence. J Theor Biol 246:245–259. https://doi.org/10.1016/j.jtbi.2006.12.010
Enderling H, Kim S, Pilon-Thomas S (2018) The accelerating quest for optimal radiation and immunotherapy combinations for local and systemic tumor control. Ther Radiol Oncol 2:33. https://doi.org/10.21037/tro.2018.08.04
Friedman A (2004) A hierarchy of cancer models and their mathematical challenges. Discrete Contin Dyn Syst Ser B 4:147–160
Friedman A, Tian J, Fulci G, Chiocca AE, Wang J (2006) Glioma virotherapy: effects of innate immune suppression and increased viral replication capacity. Can Res 66:2314–2319. https://doi.org/10.1158/0008-5472.can-05-2661
Gao X, McDonald TJ, Hlatky L, Enderling H (2013) Acute and fractionated irradiation differentially modulate glioma stem cell division kinetics. Cancer Res 73:1481–1490. https://doi.org/10.1158/0008-5472.can-12-3429
Gatenby RA, Brown J (2018) The evolution and ecology of resistance in cancer therapy. Cold Spring Harb Perspect Med 1:2. https://doi.org/10.1101/cshperspect.a033415
Gatenby RA, Brown J, Vincent T (2009) Lessons from applied ecology: cancer control using an evolutionary double bind. Can Res 69:7499–7502. https://doi.org/10.1158/0008-5472.can-09-1354
Guiot C, Degiorgis PG, Delsanto PP, Gabriele P, Deisboeck TS (2003) Does tumor growth follow a “universal law”? J Theor Biol 225:147–151
Hahnfeldt P, Panigrahy D, Folkman J, Hlatky L (1999) Tumor development under angiogenic signaling: a dynamical theory of tumor growth, treatment response, and postvascular dormancy. Can Res 59:4770–4775
Hanin L, Seidel K, Stoevesandt D (2015) A “universal” model of metastatic cancer, its parametric forms and their identification: what can be learned from site-specific volumes of metastases Leonid Hanin, Karen Seidel & Dietrich Stoevesandt. J Math Biol 72:1633–1662. https://doi.org/10.1007/s00285-015-0928-6
Hawkins-Daarud AJ, Rockne RC, Corwin D, Anderson AR, Kinahan P, Swanson KR (2015) In silico analysis suggests differential response to bevacizumab and radiation combination therapy in newly diagnosed glioblastoma. J R Soc Interface 12:20150388. https://doi.org/10.1098/rsif.2015.0388
Hillen T (2006) M5 mesoscopic and macroscopic models for mesenchymal motion. J Math Biol 53:585–616. https://doi.org/10.1007/s00285-006-0017-y
Hinow P, Gerlee P, McCawley LJ, Quaranta V, Ciobanu M, Wang S, Graham JM, Ayati BP, Claridge J, Swanson KR, Loveless M, Anderson AR (2009) A spatial model of tumor-host interaction: application of chemotherapy. Math Biosci Eng 6:521–546
Hutchinson L, Mueller H-J, Gaffney E, Maini P, Wagg J, Phipps A, Boetsch C, Byrne H, Ribba B (2011) Modeling longitudinal preclinical tumor size data to identify transient dynamics in tumor response to antiangiogenic drugs. CPT: Pharmacom Syst Pharmacol 5:636–645. https://doi.org/10.1002/psp4.12142
Janes H, Pepe MS, Bossuyt PM, Barlow WE (2015) Measuring the performance of markers for guiding treatment decisions. Ann Intern Med 154:253–259. https://doi.org/10.7326/0003-4819-154-4-201102150-00006
Kaznatcheev A, Peacock J, Basanta D, Marusyk A, Scott JG (2019) Fibroblasts and alectinib switch the evolutionary games played by non-small cell lung cancer. Nat Ecol Evol 3:450–456. https://doi.org/10.1038/s41559-018-0768-z
Kempf H, Bleicher M, Meyer-Hermann M (2010) Spatio-temporal cell dynamics in tumour spheroid irradiation. Eur Phys J D 60:177–193. https://doi.org/10.1140/epjd/e2010-00178-4
Kirschner D, Tsygvintsev A (2009) On the global dynamics of a model for tumor immunotherapy. Math Biosci Eng 6:573–583
Kogan Y, Halevi-Tobias K, Elishmereni M, Vuk-Pavlović S, Agur Z (2012) Reconsidering the paradigm of cancer immunotherapy by computationally aided real-time personalization. Can Res 72:2218–2227. https://doi.org/10.1158/0008-5472.can-11-4166
Kozusko F, Chen P-H, Grant SG, Day BW, Panetta J (2001) A mathematical model of in vitro cancer cell growth and treatment with the antimitotic agent curacin A. Math Biosci 170:1–16. https://doi.org/10.1016/s0025-5564(00)00065-1
Kuznetsov V, Knott G (2001) Modeling tumor regrowth and immunotherapy. Math Comput Model 33:1275–1287. https://doi.org/10.1016/s0895-7177(00)00314-9
Leder K, Pitter K, Laplant Q, Hambardzumyan D, Ross BD, Chan TA, Holland EC, Michor F (2013) Mathematical modeling of PDGF-driven glioblastoma reveals optimized radiation dosing schedules. Cell 156:603–616. https://doi.org/10.1016/j.cell.2013.12.029
Lowengrub J, Frieboes H, Jin F, Chuang Y-LL, Li X, Macklin P, Wise S, Cristini V (2010) Nonlinear modelling of cancer: bridging the gap between cells and tumours. Nonlinearity 23:R1–R9
Ludden T, Beal S, Sheiner L (1994) Comparison of the Akaike Information Criterion, the Schwarz criterion and the F test as guides to model selection. J Pharmacokinet Biopharm 22:431–445
Mahasa K, Eladdadi A, de Pillis LG, Ouifki R (2017) Oncolytic potency and reduced virus tumor-specificity in oncolytic virotherapy. A mathematical modelling approach. PloS one. 12:e0184347-26. https://doi.org/10.1371/journal.pone.0184347
Marusyk A, Tabassum DP, Altrock PM, Almendro V, Michor F, Polyak K (2014) Non-cell-autonomous driving of tumour growth supports sub-clonal heterogeneity. Nature 514:54. https://doi.org/10.1038/nature13556
McAneney H, O’Rourke SFC (2007) Investigation of various growth mechanisms of solid tumour growth within the linear-quadratic model for radiotherapy. Phys Med Biol 52:1039–1054. https://doi.org/10.1088/0031-9155/52/4/012
Michor F, Hughes TP, Iwasa Y, Branford S, Shah NP, Sawyers CL, Nowak MA (2005) Dynamics of chronic myeloid leukaemia. Nature 435:1267–1270. https://doi.org/10.1038/nature03669
Murphy H, Jaafari H, Dobrovolny HM (2016) Differences in predictions of ODE models of tumor growth: a cautionary example. BMC Cancer 16:163. https://doi.org/10.1186/s12885-016-2164-x
Nani F, Freedman H (2000) A mathematical model of cancer treatment by immunotherapy. Math Biosci 163:159–199
Norton L (1988) A Gompertzian model of human breast cancer growth. Can Res 48:7067–7071
Norton L, Simon R (1977) Growth curve of an experimental solid tumor following radiotherapy. J Natl Cancer Inst 58:1735–1741
Poleszczuk J, Enderling H (2018) The optimal radiation dose to induce robust systemic anti-tumor immunity. Int J Mol Sci 19:3377. https://doi.org/10.3390/ijms19113377
Poleszczuk J, Bodnar M, Foryś U et al (2011) New approach to modeling of antiangiogenic treatment on the basis of Hahnfeldt et al. model. Math Biosci Eng 8:591–603. https://doi.org/10.3934/mbe.2011.8.591
Poleszczuk J, Hahnfeldt P, Enderling H (2015) Therapeutic implications from sensitivity analysis of tumor angiogenesis models. PLoS ONE 10:e0120007. https://doi.org/10.1371/journal.pone.0120007
Powathil GG, Kohandel M, Sivaloganathan S, Oza A, Milosevic M (2007) Mathematical modeling of brain tumors: effects of radiotherapy and chemotherapy. Phys Med Biol 52:3291–3306. https://doi.org/10.1088/0031-9155/52/11/023
Powathil GG, Gordon KE, Hill LA, Chaplain MA (2012) Modelling the effects of cell-cycle heterogeneity on the response of a solid tumour to chemotherapy: biological insights from a hybrid multiscale cellular automaton model. J Theor Biol 308:1–19. https://doi.org/10.1016/j.jtbi.2012.05.015
Prokopiou S, Moros EG, Poleszczuk J, Caudell J, Torres-Roca JF, Latifi K, Lee JK, Myerson RJ, Harrison LB, Enderling H (2015) A proliferation saturation index to predict radiation response and personalize radiotherapy fractionation. Radiat Oncol (London, England) 10:159. https://doi.org/10.1186/s13014-015-0465-x
Sachs R, Hlatky L, Hahnfeldt P (2001) Simple ODE models of tumor growth and anti-angiogenic or radiation treatment. Math Comput Model 33:1297–1305. https://doi.org/10.1016/s0895-7177(00)00316-2
Santiago DN, Heidbuechel JP, Kandell WM, Walker R, Djeu J, Engeland CE, Abate-Daga D, Enderling H (2017) Fighting cancer with mathematics and viruses. Viruses 9:239. https://doi.org/10.3390/v9090239
Steyerberg EW, Vickers AJ, Cook NR, Gerds T, Gonen M, Obuchowski N, Pencina MJ, Kattan MW (2010) Assessing the performance of prediction models. Epidemiology 21:128–138. https://doi.org/10.1097/ede.0b013e3181c30fb2
Swanson KR, True LD, Lin DW, Buhler KR, Vessella R, Murray JD (2001) A quantitative model for the dynamics of serum prostatespecific antigen as a marker for cancerous growth: an explanation for a medical anomaly. Am J Pathol 158(6):2195–2199
Vainstein V, Kirnasovsky OU, Kogan Y, Agur Z (2011) Strategies for cancer stem cell elimination: insights from mathematical modeling. J Theor Biol 298:32–41. https://doi.org/10.1016/j.jtbi.2011.12.016
Zhang J, Cunningham JJ, Brown JS, Gatenby RA (2017) Integrating evolutionary dynamics into treatment of metastatic castrate-resistant prostate cancer. Nature communications. 8:1–9. https://doi.org/10.1038/s41467-017-01968-5
Acknowledgements
This opinion article is not meant to be a thorough review. Therefore, we selected references to illustrate our opinion and apologize to the un-cited authors who significantly contributed to and continue to contribute to the field of mathematical oncology.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Brady, R., Enderling, H. Mathematical Models of Cancer: When to Predict Novel Therapies, and When Not to. Bull Math Biol 81, 3722–3731 (2019). https://doi.org/10.1007/s11538-019-00640-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11538-019-00640-x