Mathematical Analysis of the Transmission Dynamics of HIV Syphilis Co-infection in the Presence of Treatment for Syphilis

Abstract

The re-emergence of syphilis has become a global public health issue, and more persons are getting infected, especially in developing countries. This has also led to an increase in the incidence of human immunodeficiency virus (HIV) infections as some studies have shown in the recent decade. This paper investigates the synergistic interaction between HIV and syphilis using a mathematical model that assesses the impact of syphilis treatment on the dynamics of syphilis and HIV co-infection in a human population where HIV treatment is not readily available or accessible to HIV-infected individuals. In the absence of HIV, the syphilis-only model undergoes the phenomenon of backward bifurcation when the associated reproduction number (${\mathcal {R}}_{T}$) is less than unity, due to susceptibility to syphilis reinfection after recovery from a previous infection. The complete syphilis–HIV co-infection model also undergoes the phenomenon of backward bifurcation when the associated effective reproduction number (${\mathcal {R}}_{C}$) is less than unity for the same reason as the syphilis-only model. When susceptibility to syphilis reinfection after treatment is insignificant, the disease-free equilibrium of the syphilis-only model is shown to be globally asymptotically stable whenever the associated reproduction number (${\mathcal {R}}_{T}$) is less than unity. Sensitivity and uncertainty analysis show that the top three parameters that drive the syphilis infection (with respect to the associated response function, ${\mathcal {R}}_{T}$) are the contact rate ($\beta _S$), modification parameter that accounts for the increased infectiousness of syphilis-infected individuals in the secondary stage of the infection ($\theta _1$) and treatment rate for syphilis-only infected individuals in the primary stage of the infection ($r_1$). The co-infection model was numerically simulated to investigate the impact of various treatment strategies for primary and secondary syphilis, in both singly and dually infected individuals, on the dynamics of the co-infection of syphilis and HIV. It is observed that if concerted effort is exerted in the treatment of primary and secondary syphilis (in both singly and dually infected individuals), especially with high treatment rates for primary syphilis, this will result in a reduction in the incidence of HIV (and its co-infection with syphilis) in the population.

Appendices

Appendix A: Derivation of Model Equations

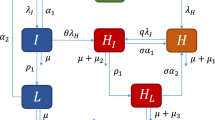
The susceptible population S(t) is generated by the recruitment of individuals (assumed susceptible) into the population at a rate $\Lambda$. The population of individuals in the S(t) compartment is reduced due to HIV and syphilis infections at the rates $\lambda _H$, $\lambda _S$, $\lambda _{SH}$ and $\lambda _{HS}$. The population is further reduced by natural death (at a rate $\mu$; natural death occurs in all epidemiological compartments at this rate). So that

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}=\Lambda - \lambda _S S - \lambda _H S - \lambda _{SH} S - \lambda _{HS} S - \mu S. \end{aligned}$$

The population of individuals exposed to syphilis is increased by those who acquire syphilis infection at the rates $\lambda _S$ and $\lambda _{SH}$ and those reinfected with syphilis after treatment, at the rates $\alpha _1\lambda _S$ and $\alpha _2\lambda _{SH}$, where $\alpha _1$ and $\alpha _2$ are modification parameters which account for the susceptibility of singly infected individuals with syphilis who recovered from syphilis. This population is reduced by progression to primary syphilis, at the rate $\gamma _1$, those who get infected with HIV at the rates $\lambda _H$ and $\lambda _{HS}$ and then by natural death. Hence

$$\begin{aligned} \frac{\mathrm{d} E_S}{\mathrm{d}} = \lambda _S S + \lambda _{SH} S + \alpha _1 \lambda _S R_S + \alpha _2 \lambda _{SH} R_S - (\gamma _1 + \mu ) E_S - \lambda _H E_S - \lambda _{HS} E_S. \end{aligned}$$

The population of infected individuals with primary syphilis is increased by those who progressed from the exposed stage and reduced by those who get infected with HIV at the rates $\phi _1\lambda _H$ and $\phi _2\lambda _{HS}$ (where $\phi _1$ and $\phi _2$ are modification parameters which account for their increased susceptibility to HIV infection). This population is further reduced by those who recover at the rate $r_1$, those who progress to the secondary stage of syphilis, at the rate $\gamma _2$, and by natural death. So that we have

$$\begin{aligned} \frac{\mathrm{d} I_P}{\mathrm{d}t}=\gamma _1 E_S -(\gamma _2 +r_1 +\mu )I_P -\phi _1 \lambda _H I_P - \phi _2 \lambda _{HS} I_P. \end{aligned}$$

The population of infected individuals with secondary syphilis is increased by those who progressed from the primary stage and reduced by those who get infected with HIV at the rates $\phi _3\lambda _H$ and $\phi _4\lambda _{HS}$ (where $\phi _3$ and $\phi _4$ are modification parameters which account for their increased susceptibility to HIV infection). This population is further reduced by those who recover at the rate $r_2$, those who progress to the early latent stage of syphilis, at the rate $\gamma _3$, and by natural death. Hence

$$\begin{aligned} \frac{\mathrm{d} I_S}{\mathrm{d}t} = \gamma _2 I_P -(\gamma _3 + r_2 + \mu )I_S - \phi _3\lambda _H I_S -\phi _4\lambda _{HS} I_S. \end{aligned}$$

The population of infected individuals with early latent syphilis is increased by those who progressed from the secondary stage and reduced by those who get infected with HIV at the rates $\phi _5\lambda _H$ and $\phi _6\lambda _{HS}$ (where $\phi _5$ and $\phi _6$ are modification parameters which account for their increased susceptibility to HIV infection). This population is further reduced by those who recover at the rate $r_3$, those who progress to the late latent stage of syphilis, at the rate $\gamma _4$, and finally by natural death. Hence

$$\begin{aligned} \frac{\mathrm{d} L_{S1}}{\mathrm{d}t} = \gamma _3 I_S -(\gamma _4 + r_3 + \mu )L_{S1} - \phi _5\lambda _H L_{S1} -\phi _6\lambda _{HS} L_{S1}. \end{aligned}$$

The population of infected individuals with late latent syphilis is increased by those who progressed from the early latent stage and reduced by those who get infected with HIV at the rates $\phi _7\lambda _H$ and $\phi _8\lambda _{HS}$ (where $\phi _7$ and $\phi _8$ are modification parameters which account for their increased susceptibility to HIV infection). This population is further reduced by those who recover at the rate $r_4$, those who progress to the tertiary stage of syphilis, at the rate $\gamma _5$, and by natural death. Hence

$$\begin{aligned} \frac{\mathrm{d}L_{S2}}{\mathrm{d}t} = \gamma _4 L_{S1} -(\gamma _5 + r_4 + \mu )L_{S2} - \phi _7\lambda _H L_{S2} -\phi _8\lambda _{HS} L_{S2}. \end{aligned}$$

The population of infected individuals with tertiary syphilis is increased by those who progress from the late latent stage and diminished by those who get infected with HIV at the rates $\phi _9\lambda _H$ and $\phi _{10}\lambda _{HS}$ (where $\phi _9$ and $\phi _{10}$ are modification parameters which account for their increased susceptibility to HIV infection). This population is further reduced by those who recover, at the rate $r_5$, and natural mortality. We therefore have that

$$\begin{aligned} \frac{\mathrm{d} I_T}{\mathrm{d}t} = \gamma _5 L_{S2} -( r_5 + \mu )I_T - \phi _9\lambda _H I_T -\phi _{10}\lambda _{HS} I_T. \end{aligned}$$

The population of those recovered from syphilis is increased by all singly infected individuals who recover from syphilis at the rates $r_1$, $r_2$, $r_3$, $r_4$ and $r_5$ and reduced by the those who get reinfected with syphilis, those who get infected with HIV, at the rates $\lambda _H$ and $\lambda _{HS}$, and also by natural death. We then have that

$$\begin{aligned} \frac{\mathrm{d} R_S}{\mathrm{d}t}= & {} r_1 I_P + r_2 I_S + r_3 L_{S1} + r_4 L_{S2} + r_5 I_T -\mu R_S- \alpha _1 \lambda _S R_S -\lambda _H R_S \\&\quad -\, \alpha _2\lambda _{SH} R_S - \lambda _{HS} R_S. \end{aligned}$$

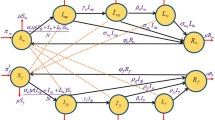
The population of individuals infected with HIV only is increased by HIV infection of susceptible individuals and individuals who recovered from a previous syphilis infection at the rates $\lambda _H$ and $\lambda _{HS}$. The population is further increased by HIV-infected individuals treated for syphilis at the primary, secondary, early latent, late latent and tertiary stages, at the rates $r_{S1}$, $r_{S2}$, $r_{S3}$, $r_{S4}$ and $r_{S5}$, respectively. The population is however diminished by those who get infected with syphilis at the rates $\psi _1\lambda _S$ and $\psi _2\lambda _{SH}$ (where $\psi _1$ and $\psi _2$ are modification parameters which account for the increased susceptibility of HIV-infected individuals to syphilis infection), as well as through natural mortality and an additional disease-induced death, at the rate $d_{H1}$. Hence

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d} H}{\mathrm{d}t}&=\lambda _H S + \lambda _{HS} S +\lambda _H R_S +\lambda _{HS} R_S - \psi _1 \lambda _S H - \psi _2\lambda _{SH} H - (\mu + d_{H1}) H\\&\quad +r_{S1} H_P+r_{S2} H_S+r_{S3} H_{S1}+r_{S4} H_{S2}+r_{S5} H_T. \end{aligned} \end{aligned}$$

The population of HIV-infected individuals who are exposed to syphilis is increased by individuals with HIV who get infected with syphilis and those exposed to syphilis who get infected with HIV at the rates $\lambda _H$ and $\lambda _{HS}$ but diminished by the progression of these individuals to the primary stage of syphilis infection, at the rate $\gamma _{S1}$, by natural mortality and disease-induced mortality, at the rates $\mu$ and $d_{H2}$, respectively. So we have

$$\begin{aligned} \frac{\mathrm{d} E_H}{\mathrm{d}t}=\psi _1 \lambda _S H + \psi _2\lambda _{SH} H+\lambda _H E_S +\lambda _{HS} E_S - (\gamma _{S1} + d_{H2} + \mu ) E_H. \end{aligned}$$

The population of HIV-infected individuals in the primary stage of syphilis is increased by those with primary syphilis who get infected with HIV at the rates $\phi _1\lambda _H$ and $\phi _2\lambda _{HS}$, and by individuals who progressed from the exposed stage of syphilis infection, at the rate $\gamma _{S1}$. This population is decreased by those who progress to secondary stage of syphilis, at the rate $\gamma _{S2}$, by those who are treated for syphilis, at the rate $r_{S1}$ and by disease-induced mortality, at the rate $d_{H3}$, as well as natural mortality. Hence

$$\begin{aligned} \frac{\mathrm{d} H_P}{\mathrm{d}t}=\gamma _{S1} E_H + \phi _1\lambda _H I_P + \phi _2\lambda _{HS} I_P - (\gamma _{S2} + r_{S1} + d_{H3} + \mu ) H_P. \end{aligned}$$

The population of HIV-infected individuals in the secondary stage of syphilis is increased by those with secondary syphilis who get infected with HIV, at the rates $\phi _3\lambda _H$ and $\phi _4\lambda _{HS}$, and by individuals who progressed from the primary stage of syphilis infection, at the rate $\gamma _{S2}$. This population is decreased by those who progress to early latent stage of syphilis, at the rate $\gamma _{S3}$, by those who are treated for syphilis, at the rate $r_{S2}$, and by disease-induced mortality, at the rate $d_{H4}$, as well as natural mortality. Hence

$$\begin{aligned} \frac{\mathrm{d} H_S}{\mathrm{d}t}=\gamma _{S2} H_P + \phi _3\lambda _H I_S + \phi _4\lambda _{HS} I_S - (\gamma _{S3} + r_{S2} + d_{H4} + \mu ) H_S. \end{aligned}$$

The population of HIV-infected individuals in the early latent stage of syphilis is increased by those with early latent syphilis who get infected with HIV, at the rates $\phi _5\lambda _H$ and $\phi _6\lambda _{HS}$, and by individuals who progressed from the secondary stage of syphilis infection at the rate $\gamma _{S3}$. This population is decreased by those who progress to late latent stage of syphilis, at the rate $\gamma _{S4}$, by those who are treated for syphilis, at the rate $r_{S3}$, and by disease-induced mortality, at the rate $d_{H5}$, as well as natural mortality. Hence

$$\begin{aligned} \frac{\mathrm{d} H_{S1}}{\mathrm{d}t}=\gamma _{S3} H_S + \phi _5\lambda _H L_{S1} + \phi _6\lambda _{HS} L_{S1} - (\gamma _{S4} + r_{S3} + d_{H5} + \mu )H_{S1}. \end{aligned}$$

The population of HIV-infected individuals in the late latent stage of syphilis is increased by those with late latent syphilis who get infected with HIV, at the rates $\phi _7\lambda _H$ and $\phi _8\lambda _{HS}$, and by individuals who progressed from the early latent stage of syphilis infection, at the rate $\gamma _{S4}$. This population is decreased by those who progress to the tertiary stage of syphilis, at the rate $\gamma _{S5}$, by those who are treated for syphilis, at the rate $r_{S4}$, and by disease-induced mortality, at the rate $d_{H6}$, as well as natural mortality. Hence

$$\begin{aligned} \frac{\mathrm{d} H_{S2}}{\mathrm{d}t}=\gamma _{S4} H_{S1} + \phi _7\lambda _H L_{S2} + \phi _8\lambda _{HS} L_{S2} - (\gamma _{S5} + r_{S4} + d_{H6} + \mu ) H_{S2}. \end{aligned}$$

The population of HIV-infected individuals in the tertiary stage of syphilis is increased by those with tertiary syphilis who get infected with HIV, at the rates $\phi _9\lambda _H$ and $\phi _{10}\lambda _{HS}$, and by individuals who progressed from the late latent stage of syphilis infection, at the rate $\gamma _{S5}$. This population is decreased by those who are treated for syphilis, at the rate $r_{S5}$, and by disease-induced mortality, at the rate $d_{H7}$, as well as natural mortality. Hence

$$\begin{aligned} \frac{\mathrm{d} H_T}{\mathrm{d}t}=\gamma _{S5} H_{S2} + \phi _9\lambda _H I_T + \phi _{10}\lambda _{HS} I_T - (r_{S5} + d_{H7} + \mu ) H_T. \end{aligned}$$

Appendix B: Positivity and Boundedness of Solutions

The basic qualitative properties of model (5) are given below. We claim the following.

Theorem 7.1

System (5) preserves positivity of solutions. That is, solutions with positive initial conditions remain positive for all time t.

Proof

Let

$$\begin{aligned} \begin{aligned} t_1&=\mathrm{sup}\{t>0:S(t)>0, E_S (t)>0, I_P (t)>0, I_S (t)>0, L_{S1} (t)>0,\\&\quad L_{S2} (t)>0, I_T (t)>0,\\&\quad R_S (t)>0, H (t)>0, E_H (t)>0, H_P (t)>0, H_S (t)>0, H_{S1} (t)>0, \\&\quad H_{S2} (t)>0, H_T (t)>0\}>0. \end{aligned} \end{aligned}$$

From the first equation of model (5), it follows that

$$\begin{aligned} \frac{\mathrm{d}S}{\mathrm{d}t}=\Lambda -(\lambda _S + \lambda _H +\lambda _{SH} + \lambda _{HS} + \mu ) S, \end{aligned}$$

when solved leads to

$$\begin{aligned} \begin{aligned} S(t_1)&=S(0)\exp \left[ -\mu t_1-\int _0^{t_1} (\lambda _S (\tau )+\lambda _H (\tau )+\lambda _{SH} (\tau )+\lambda _{HS} (\tau )) \mathrm {d}(\tau )\right] \\&\quad +\left\{ \exp \left[ -\mu t_1-\int _0^{t_1} (\lambda _S (\tau )+\lambda _H (\tau )+\lambda _{SH} (\tau )+\lambda _{HS} (\tau )) \mathrm {d}(\tau )\right] \right\} \\&\quad \int _0^{t_1}\Lambda \left[ \exp \left( \mu y+\int _0^y (\lambda _S (\tau )+\lambda _H (\tau )+\lambda _{SH} (\tau )+\lambda _{HS} (\tau ))\right) \right] \mathrm {d}y>0. \end{aligned} \end{aligned}$$

Using the same approach, we can equally show that all other state variable of model (5) will remain positive for all time $t>0$. $\square$

We now prove the positive invariance of the region, ${\mathcal {D}}$.

Lemma 7.1

Consider the biologically feasible region

$$\begin{aligned} {\mathcal {D}}= & {} \left\{ (S, E_S, I_P, I_S, L_{S1}, L_{S2}, I_T, R_S, H, E_H, H_P, H_S, H_{S1}, H_{S2}, H_T)\in {\mathbb {R}}^{15}_+:N\right. \\\le & {} \left. \frac{\Lambda }{\mu }\right\} . \end{aligned}$$

The closed set ${\mathcal {D}}$ is positively invariant and a global attractor of all positive solution of model (5).

Proof

Adding the equations of model (5) gives

$$\begin{aligned} {\dot{N}}= & {} \Lambda -\mu N-d_{H1}H-d_{H2}E_H-d_{H3}H_P-d_{H4}H_S-d_{H5}H_{S1}-d_{H6}H_{S2}\\&-d_{H7}H_T. \end{aligned}$$

Since the right-hand side of the above equality is bounded by $\Lambda -\mu N$, a standard comparison theorem (Lakshmikantham et al. 1989) can be used to show that

$$\begin{aligned} N(t) \le N(0)e^{-\mu t} + \frac{\Lambda }{\mu }(1-e^{-\mu t}). \end{aligned}$$

In particular, $N(t)\le \frac{\Lambda }{\mu }$ if $N(0)\le \frac{\Lambda }{\mu }$ for all $t>0$. Thus, ${\mathcal {D}}$ is a positively invariant set under the flow described by the model. The solutions with initial condition in ${\mathcal {D}}$ remain in ${\mathcal {D}}$ with respect to the model. Hence, the system is mathematically and epidemiologically well posed in ${\mathcal {D}}$ (Hethcote 2000). $\square$

Appendix C: Proof of Theorem 3.4

Proof

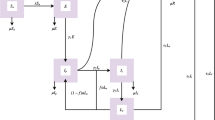
For system (13), let $S=x_1$, $E_S=x_2$, $I_P=x_3$, $I_S=x_4$, $L_{S1}=x_5$, $L_{S2}=x_6$, $I_T=x_7$ and $R_S=x_8$. So, the system of equations can be written as

$$\begin{aligned} \begin{aligned} \dot{x_1}\equiv f_1&=\Lambda -\beta _S\frac{(x_3+\theta _1 x_4)x_1}{x_1+x_2+x_3+x_4+x_5+x_6+x_7+x_8}-\mu x_1\\ \dot{x_2} \equiv f_2&=\beta _S\frac{(x_3+\theta _1 x_4)x_1}{x_1+x_2+x_3+x_4+x_5+x_6+x_7+x_8}-g_1 x_2 \\&\quad +\beta _S\frac{\alpha _1(X_3+\theta _1 X_4)X_8}{x_1+x_2+x_3+x_4+x_5+x_6+x_7+x_8}\\ \dot{x_3} \equiv f_3&=\gamma _1 x_2-g_2 x_3\\ \dot{x_4} \equiv f_4&=\gamma _2 x_3-g_3 x_4\\ \dot{x_5} \equiv f_5&=\gamma _3 x_4-g_4 x_5\\ \dot{x_6} \equiv f_6&=\gamma _4 x_5-g_5 x_6\\ \dot{x_7} \equiv f_7&=\gamma _5 x_6-g_6 x_7\\ \dot{x_8} \equiv f_8&=r_1 x_3+r_2 x_4+r_3 x_5+r_4 x_6+r_5 x_7-\mu x_8\\&\quad -\beta _S\frac{\alpha _1(x_3+\theta _1 x_4)x_8}{x_1+x_2+x_3+x_4+x_5+x_6+x_7+x_8}\\ \end{aligned} \end{aligned}$$

Consider the case with $\beta _S = \beta _S^{*}$ a bifurcation parameter. Solving for $\beta _S = \beta _S^{*}$ from ${\mathcal {R}}_T = 1$ gives

$$\begin{aligned} \beta _S=\beta _S^*=\frac{g_1 g_2 g_3}{\gamma _1(g_3+\gamma _2\theta _1)}. \end{aligned}$$

The Jacobian of the transformed system evaluated at the DFE with $\beta _S = \beta _S^{*}$ is given by

$$\begin{aligned} J(\xi _{S0}) = \begin{pmatrix} -\mu &{}\quad 0&{}\quad -\beta _S^*&{}\quad -\theta _1\beta _S^*&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad -g_1&{}\quad \beta _S^*&{}\quad \theta _1\beta _S^*&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad \gamma _1&{}\quad -g_2&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad \gamma _2&{}\quad -g_3&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad \gamma _3&{}\quad -g_4&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \gamma _4&{}\quad -g_5&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \gamma _5&{}\quad -g_6&{}\quad 0\\ 0&{}\quad 0&{}\quad r_1&{}\quad r_2&{}\quad r_3&{}\quad r_4&{}\quad r_5&{}\quad -\mu \\ \end{pmatrix} \end{aligned}$$

We obtain the right eigenvectors associated with the zero eigenvalue which is given as ${\mathbf {w}} = (\omega _1, \omega _2,...,\omega _{8})^T$, where

$$\begin{aligned} \omega _1= & {} -\frac{(\beta _S^*\omega _3+\theta _1\omega _4)}{\mu }, \quad \omega _2=\omega _2>0,\\ \omega _3= & {} \frac{\gamma _1\omega _2}{g_2}, \quad \omega _4=\frac{\gamma _1\gamma _2\omega _2}{g_2 g_3},\\ \omega _5= & {} \frac{\gamma _1\gamma _2\gamma _3\omega _2}{g_2 g_3 g_4}, \quad \omega _6=\frac{\gamma _1\gamma _2\gamma _3\gamma _4\omega _2}{g_2 g_3 g_4 g_5},\\ \omega _7= & {} \frac{\gamma _1\gamma _2\gamma _3\gamma _4\gamma _5\omega _2}{g_2 g_3 g_4 g_5 g_6}, \quad \omega _8=\frac{r_1\omega _3+r_2\omega _4 +r_3\omega _5+r_4\omega _6+r_5\omega _7}{\mu }. \end{aligned}$$

The components of the left eigenvector of $J(\xi _{S0}) |_{\beta _S = \beta _S^*}$, ${\mathbf {v}} = (\nu _1, \nu _2,...,\nu _{8})$, satisfying $\mathbf {v.w}=1$, are

$$\begin{aligned} \begin{aligned} \nu _1&=0,\quad \nu _2=\nu _2>0,\quad \nu _3=\left( \frac{\gamma _1\theta _1\beta _S^*}{g_2 g_3}+\frac{\beta _S^*}{g_2}\right) \nu _2\\ \nu _4&=\frac{\theta _1\beta _S^*\nu _2}{g_3}, \quad \nu _5=\nu _6=\nu _7=\nu _8=0\\ \end{aligned} \end{aligned}$$

It follows from Theorem 4.1 in Castillo-Chavez and Song (2004), if we compute the associated nonzero partial derivatives of F(x) (evaluated at the DFE $\xi _{S0}$), that the associated bifurcation coefficients a and b, defined by

$$\begin{aligned} a = \displaystyle \sum _{k,i,j=1}^{n} \nu _k \omega _i \omega _j \frac{\partial ^2 f_k}{\partial x_i \partial x_j} (0,0) \quad \text {and} \quad b = \displaystyle \sum _{k,i=1}^{n} \nu _k \omega _i \frac{\partial ^2 f_k}{\partial x_i \partial \beta _S^{*}} (0,0), \end{aligned}$$

are computed to be

$$\begin{aligned} a= & {} 2\nu _2\alpha _1\beta _S^*\frac{\mu }{\Lambda }(\omega _3\omega _8+\theta _1\omega _4\omega _8)\nonumber \\&-\,2\nu _2\beta _S^*\frac{\mu }{\Lambda }(\omega _2\omega _3+\omega _3\omega _5+\omega _3\omega _6+\omega _3\omega _7+\omega _3^2+\omega _3\omega _8+\omega _3\omega _4)\nonumber \\&-\,2\nu _2\theta _1\beta _S^*\frac{\mu }{\Lambda }(\omega _2\omega _4+\omega _4\omega _5+\omega _3\omega _4+\omega _4\omega _8+\omega _4^2+\omega _4\omega _6+\omega _4\omega _7)\qquad \end{aligned}$$

(23)

and

$$\begin{aligned} b&=\nu _2\omega _3+\theta _1\nu _2\omega _4>0, \end{aligned}$$

with $\nu _2$, $\omega _2$, $\omega _3$, $\omega _4$, $\omega _5$, $\omega _6$, $\omega _7$ and $\omega _8$ positive.

Since the bifurcation coefficient $b>0$, it follows from Theorem 4.1 in Castillo-Chavez and Song (2004) that system (13) will undergo a backward bifurcation if the backward bifurcation coefficient $a>0$. This is possible if

$$\begin{aligned} \alpha _1>\frac{(\omega _2+\omega _3+\omega _4+\omega _5+\omega _6+\omega _7+\omega _8)(\omega _3+\theta _1\omega _4)}{(\omega _8)(\omega _3+\theta _1\omega _4)}. \end{aligned}$$

(24)

Clearly, if $\alpha _1=0$, then $a<0$ and model (13) will not exhibit the backward bifurcation phenomenon at ${\mathcal {R}}_T=1$. $\square$

Appendix D: Proof of Theorem 3.5

Proof

Consider the following linear Lyapunov function

$$\begin{aligned} {\mathcal {V}}_2=\gamma _1(g_3+\gamma _2\theta _1)E_S+g_1(g_3+\gamma _2\theta _1)I_P + g_1 g_2 g_3 I_S, \end{aligned}$$

with Lyapunov derivative

$$\begin{aligned} \begin{aligned} \dot{{\mathcal {V}}_2}&=(I_P + \theta _1 I_S)\left( \frac{\beta _S S}{N}\left[ \gamma _1(g_3 +\gamma _2 \theta _1)\right] -g_1 g_2 g_3\right) \\ \dot{{\mathcal {V}}_2}&=g_1 g_2 g_3(I_P + \theta _1 I_S)\left( \frac{S}{N}{\mathcal {R}}_{T} -1\right) . \end{aligned} \end{aligned}$$

(25)

It follows from (29), noting that $S(t)\le N(t)$ and $N(t)\le \frac{\Lambda }{\mu }$ in ${\mathcal {D}}_2$ for all $t>0$, that

$$\begin{aligned} \dot{{\mathcal {V}}_2}\le g_1 g_2 g_3(I_P + \theta _1 I_S)({\mathcal {R}}_{T}-1). \end{aligned}$$

Hence, $\dot{{\mathcal {V}}_2}\le 0$ if ${\mathcal {R}}_{T} \le 1$ with $\dot{{\mathcal {V}}_2}= 0$ if and only if $E_S=I_P=I_S=L_{S1}=L_{S2}=I_T=R_S=0$. Therefore, ${\mathcal {V}}_2$ is a Lyapunov function in ${\mathcal {D}}_2$, and it follows from LaSalles invariance principle Salle and Lefschetz (1976) that every solution to the equations in (13) with initial conditions in ${\mathcal {D}}_2$ converges to $\xi _{S0}$ as $t\rightarrow \infty$. That is,

$$\begin{aligned} (E_S (t), I_P (t), I_S (t), L_{S1} (t), L_{S2} (t), I_T (t), R_S (t))\rightarrow (0, 0, 0, 0, 0, 0, 0, 0) \hbox { as } t\rightarrow \infty . \end{aligned}$$

Substituting $E_S=I_P=I_S=L_{S1}=L_{S2}=I_T=R_S=0$ into the first equation in model (13) with $\alpha _1=0$, gives $S(t)\rightarrow \frac{\Lambda }{\mu }$ as $t\rightarrow \infty$. Thus, $(S, E_S, I_P, I_S, L_{S1}, L_{S2}, I_T, R_S)\rightarrow (\frac{\Lambda }{\mu }, 0, 0, 0, 0, 0, 0, 0)$ as $t\rightarrow \infty$ for ${\mathcal {R}}_{T}\le 1$, so the DFE, $\xi _{S0}$, of model (13) with $\alpha _1=0$, is globally asymptotically stable in ${\mathcal {D}}_2$ if ${\mathcal {R}}_{T}\le 1$. $\square$

Appendix E: Proof of Theorem 3.6

Proof

Consider model (13) (with (22) and $\alpha _1=0$) and ${\mathcal {R}}_{T}>1$, so that the associated unique endemic equilibrium exists. Also, consider the nonlinear Lyapunov function of the Goh–Volterra type

$$\begin{aligned} \begin{aligned} {\mathcal {F}}_2&=S-S^{**}-S^{**}\ln \left( \frac{S}{S^{**}}\right) + E_S-E_S^{**}-E_S^{**}\ln \left( \frac{E_S}{E_S^{**}}\right) \\&\quad +\frac{\beta _S S^{**}}{(\mu +r_1+\gamma _2)}\left( 1+\frac{\gamma _2\theta _1}{(\mu +r_2+\gamma _3)}\right) I_P-I_P^{**}\\&\quad -I_P^{**}\ln \left( \frac{I_P}{I_P^{**}}\right) +\left( \frac{\beta _S \theta _1 S^{**}}{(\mu +r_2+\gamma _3)}\right) I_S-I_S^{**}-I_S^{**}\ln \left( \frac{I_S}{I_S^{**}}\right) , \end{aligned} \end{aligned}$$

with Lyapunov derivative,

$$\begin{aligned} \begin{aligned} \dot{{\mathcal {F}}_2}&={\dot{S}}-\frac{S^{**}}{S} {\dot{S}}+{\dot{E}}_S-\frac{E_S^{**}}{E_S} {\dot{E}}_S\\&\quad +\frac{\beta _S S^{**}}{(\mu +r_1+\gamma _2)}\left( 1+\frac{\gamma _2\theta _1}{(\mu +r_2+\gamma _3)}\right) {\dot{I}}_P\\&\quad -\frac{I_P^{**}}{I_P} {\dot{I}}_P+\frac{\beta _S \theta _1 S^{**}}{(\mu +r_2+\gamma _3)}\left( {\dot{I}}_S-\frac{I_S^{**}}{I_S} {\dot{I}}_S\right) . \end{aligned} \end{aligned}$$

(26)

It can be shown from model (13) with $\alpha _1=0$ that, at steady state,

$$\begin{aligned} \begin{aligned} \Lambda&={\bar{\beta }}_S(I_P^{**}+\theta _1 I_S^{**}) S^{**} +\mu S^{**},\\ \gamma _1+\mu&={\bar{\beta }}_S\frac{(I_P^{**}+\theta _1 I_S^{**}) S^{**}}{E_S^{**}} S^{**},\\ \gamma _2+r_1+\mu&=\frac{\gamma _1 E_S^{**}}{I_P^{**}},\\ \gamma _3+r_2+\mu&=\frac{\gamma _2 I_P^{**}}{I_S^{**}}.\\ \end{aligned} \end{aligned}$$

(27)

Substituting the time derivatives of $E_S$, $I_P$ and $I_S$, in (13) (with $\alpha _1=0$) as well as the relations in (27), into (26), we have that (after several algebraic calculations)

$$\begin{aligned} \begin{aligned} \dot{{\mathcal {F}}_2}&=\mu S^{**}\left( 2-\frac{S^{**}}{S}-\frac{S}{S^{**}}\right) +{\bar{\beta }}_S S^{**} I_P^{**}\left( 3-\frac{S^{**}}{S}-\frac{I_P^{**} E_S}{I_P E_S^{**}}-\frac{E_S^{**} I_P S}{S^{**}I_P^{**} E_S}\right) \\&\quad +{\bar{\beta }}_S \theta _1S^{**} I_P^{**}\left( 4-\frac{S^{**}}{S}-\frac{E_S^{**} I_S S}{S^{**}I_S^{**}E_S}-\frac{I_P^{**} E_S}{I_P E_S^{**}}-\frac{I_S^{**} I_P}{I_P^{**} I_S}\right) . \end{aligned} \end{aligned}$$

Finally, since the arithmetic mean is greater than the geometric mean, the following inequalities hold.

$$\begin{aligned} \begin{aligned}&\left( 2-\frac{S^{**}}{S}-\frac{S}{S^{**}}\right) \le 0, \quad \left( 3-\frac{S^{**}}{S}-\frac{I_P^{**} E_S}{I_P E_S^{**}}-\frac{E_S^{**} I_P S}{S^{**}I_P^{**} E_S}\right) \le 0\\&\quad and \left( 4-\frac{S^{**}}{S}-\frac{E_S^{**} I_S S}{S^{**}I_S^{**}E_S}-\frac{I_P^{**} E_S}{I_P E_S^{**}}-\frac{I_S^{**} I_P}{I_P^{**} I_S}\right) \le 0.\\ \end{aligned} \end{aligned}$$

Thus we have that $\dot{{\mathcal {F}}_2}\le 0$ for ${\mathcal {R}}_{T}>1$. Since the relevant variables in the equations for $L_{S1}$, $L_{S2}$, $I_T$ and $R_S$ are at endemic steady state, it follows that these can be substituted into the equations for $L_{S1}$, $L_{S2}$, $I_T$ and $R_S$ so that

$(L_{S1}(t), L_{S2}(t), I_T(t), R_S(t))\rightarrow (L_{S1}^{**}, L_{S2}^{**}, I_T^{**}, R_S^{**})$ as $t\rightarrow \infty$

Hence, ${\mathcal {F}}_2$ is a Lyapunov function in ${\mathcal {D}}_{3}|{\mathcal {D}}_{4}$ $\square$

Appendix F: Proof of Theorem 4.1

Proof

For system (5), let $S=x_1$, $E_S=x_2$, $I_P=x_3$, $I_S=x_4$, $L_{S1}=x_5$, $L_{S2}=x_6$, $I_T=x_7$, $R_S=x_8$, $H=x_9$, $E_H=x_{10}$, $H_P=x_{11}$, $H_S=x_{12}$, $H_{S1}=x_{13}$, $H_{S2}=x_{14}$ and $H_T=x_{15}$. So, the system of equations can be written as

$$\begin{aligned} \dot{x_1}\equiv f_1= & {} \Lambda -\beta _S\frac{(x_3+\theta _1 x_4)x_1}{N}-\beta _H\frac{x_9 x_1}{N}-\beta _S\frac{(\theta _2 x_{11}+\theta _3 x_{12})x_1}{N}\\&-\,\beta _H\frac{(x_{10}+\eta _1 x_{11}+\eta _2 x_{12}+\eta _3 x_{13}+\eta _4 x_{14}+\eta _5 x_{15})x_1}{N}-\mu x_1,\\ \dot{x_2} \equiv f_2= & {} \beta _S\frac{(x_3+\theta _1 x_4)x_1}{N}-g_1 x_2+\beta _S\frac{(\theta _2 x_{11}+\theta _3 x_{12})x_1}{N} \\&+\,\beta _S\frac{\alpha _1(x_3+\theta _1 x_4)x_8}{N}+\beta _S\frac{\alpha _2(\theta _2 x_{11}+\theta _3 x_{12})x_8}{N}-\beta _H\frac{x_9 x_2}{N}\\&-\,\beta _H\frac{(x_{10}+\eta _1 x_{11}+\eta _2 x_{12}+\eta _3 x_{13}+\eta _4 x_{14}+\eta _5 x_{15})x_2}{N},\\ \dot{x_3} \equiv f_3= & {} \gamma _1 x_2-g_2 x_3-\phi _1\beta _H\frac{x_9 x_3}{N}\\&-\,\phi _2\beta _H\frac{(x_{10}+\eta _1 x_{11}+\eta _2 x_{12}+\eta _3 x_{13}+\eta _4 x_{14}+\eta _5 x_{15})x_3}{N},\\ \dot{x_4} \equiv f_4= & {} \gamma _2 x_3-g_3 x_4-\phi _3\beta _H\frac{x_9 x_4}{N}\\&-\,\phi _4\beta _H\frac{(x_{10}+\eta _1 x_{11}+\eta _2 x_{12}+\eta _3 x_{13}+\eta _4 x_{14}+\eta _5 x_{15})x_4}{N},\\ \dot{x_5} \equiv f_5= & {} \gamma _3 x_4-g_4 x_5-\phi _5\beta _H\frac{x_9 x_5}{N}\\&-\,\phi _6\beta _H\frac{(x_{10}+\eta _1 x_{11}+\eta _2 x_{12}+\eta _3 x_{13}+\eta _4 x_{14}+\eta _5 x_{15})x_5}{N},\\ \dot{x_6} \equiv f_6= & {} \gamma _4 x_5-g_5 x_6-\phi _7\beta _H\frac{x_9 x_6}{N}\\&-\,\phi _8\beta _H\frac{(x_{10}+\eta _1 x_{11}+\eta _2 x_{12}+\eta _3 x_{13}+\eta _4 x_{14}+\eta _5 x_{15})x_6}{N},\\ \dot{x_7} \equiv f_7= & {} \gamma _5 x_6-g_6 x_7-\phi _9\beta _H\frac{x_9 x_7}{N}\\&-\,\phi _{10}\beta _H\frac{(x_{10}+\eta _1 x_{11}+\eta _2 x_{12}+\eta _3 x_{13}+\eta _4 x_{14}+\eta _5 x_{15})x_7}{N},\\ \dot{x_8} \equiv f_8= & {} r_1 x_3+r_2 x_4+r_3 x_5+r_4 x_6+r_5 x_7-\mu x_8-\beta _S\frac{\alpha _1(x_3+\theta _1 x_4)x_8}{N}\\&-\,\beta _H\frac{x_9 x_8}{N}-\beta _S\frac{\alpha _2(\theta _2 x_{11}+\theta _3 x_{12})x_8}{N}\\&-\,\beta _H\frac{(x_{10}+\eta _1 x_{11}+\eta _2 x_{12}+\eta _3 x_{13}+\eta _4 x_{14}+\eta _5 x_{15})x_8}{N}, \end{aligned}$$

$$\begin{aligned} \dot{x_9} \equiv f_9= & {} \beta _H\frac{x_9 x_1}{N}+\beta _H\frac{(x_{10}+\eta _1 x_{11}+\eta _2 x_{12}+\eta _3 x_{13}+\eta _4 x_{14}+\eta _5 x_{15})x_1}{N}\\&-\,g_7 x_9 +\beta _H\frac{x_9 x_8}{N}\\&+\,\beta _H\frac{(x_{10}+\eta _1 x_{11}+\eta _2 x_{12}+\eta _3 x_{13}+\eta _4 x_{14}+\eta _5 x_{15})x_8}{N}\\&-\,\psi _1\beta _S\frac{(x_3+\theta _1 x_4)x_9}{N}\\&-\,\psi _2\beta _S\frac{(\theta _2 x_{11}+\theta _3 x_{12})x_9}{N}+r_{S1} x_{11}+r_{S2} x_{12}+r_{S3} x_{13}\\&+\,r_{S4} x_{14}+r_{S5} x_{15},\\ \dot{x_{10}} \equiv f_{10}= & {} \psi _1\beta _S\frac{(x_3+\theta _1 x_4)x_9}{N}+\psi _2\beta _S\frac{(\theta _2 x_{11}+\theta _3 x_{12})x_9}{N}-g_8 x_{10}+\beta _H\frac{x_9 x_2}{N}\\&+\,\beta _H\frac{(x_{10}+\eta _1 x_{11}+\eta _2 x_{12}+\eta _3 x_{13}+\eta _4 x_{14}+\eta _5 x_{15})x_2}{N} ,\\ \dot{x_{11}} \equiv f_{11}= & {} \gamma _{S1} x_{10}+\phi _1\beta _H\frac{x_9 x_3}{N}\\&+\,\phi _2\beta _H\frac{(x_{10}+\eta _1 x_{11}+\eta _2 x_{12}+\eta _3 x_{13}+\eta _4 x_{14}+\eta _5 x_{15})x_3}{N}-g_9 x_{11},\\ \dot{x_{12}} \equiv f_{12}= & {} \gamma _{S2} x_{11}+\phi _3\beta _H\frac{x_9 x_4}{N}\\&+\,\phi _4\beta _H\frac{(x_{10}+\eta _1 x_{11}+\eta _2 x_{12}+\eta _3 x_{13}+\eta _4 x_{14}+\eta _5 x_{15})x_4}{N}-g_{10} x_{12},\\ \dot{x_{13}} \equiv f_{13}= & {} \gamma _{S3} x_{12}+\phi _5\beta _H\frac{x_9 x_5}{N}\\&+\,\phi _6\beta _H\frac{(x_{10}+\eta _1 x_{11}+\eta _2 x_{12}+\eta _3 x_{13}+\eta _4 x_{14}+\eta _5 x_{15})x_5}{N}-g_{11} x_{13},\\ \dot{x_{14}} \equiv f_{14}= & {} \gamma _{S4} x_{13}+\phi _7\beta _H\frac{x_9 x_6}{N}\\&+\,\phi _8\beta _H\frac{(x_{10}+\eta _1 x_{11}+\eta _2 x_{12}+\eta _3 x_{13}+\eta _4 x_{14}+\eta _5 x_{15})x_6}{N}-g_{12} x_{14},\\ \dot{x_{15}} \equiv f_{15}= & {} \gamma _{S5} x_{14}+\phi _9\beta _H\frac{x_9 x_7}{N}\\&+\,\phi _{10}\beta _H\frac{(x_{10}+\eta _1 x_{11}+\eta _2 x_{12}+\eta _3 x_{13}+\eta _4 x_{14}+\eta _5 x_{15})x_7}{N}-g_{13} x_{15}, \end{aligned}$$

where

$$\begin{aligned} N= & {} x_1+x_2+x_3+x_4+x_5+x_6+x_7+x_8+x_9+x_{10}\\&+\,x_{11}+x_{12}+x_{13}+x_{14}+x_{15}. \end{aligned}$$

The Jacobian of the transformed system evaluated at the DFE with is given by

$$\begin{aligned} J(\xi _0) = \begin{pmatrix} J1_{(8\times 8)} &{}J2_{(8\times 7)} \\ J3_{(7\times 8)}&{}J4_{(7\times 7)}\\ \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} J1= & {} \begin{pmatrix} -\mu &{}\quad 0&{}\quad -\beta _S^*&{}\quad -\theta _1\beta _S^*&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad -g_1&{}\quad \beta _S^*&{}\quad \theta _1\beta _S^*&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad \gamma _1&{}\quad -g_2&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad \gamma _2&{}\quad -g_3&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad \gamma _3&{}\quad -g_4&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \gamma _4&{}\quad -g_5&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \gamma _5&{}\quad -g_6&{}\quad 0\\ 0&{}\quad 0&{}\quad r_1&{}\quad r_2&{}\quad r_3&{}\quad r_4&{}\quad r_5&{}\quad -\mu \\ \end{pmatrix},\\ J2= & {} \begin{pmatrix} -\beta _H&{}\quad -\beta _H&{}\quad -(\theta _2\beta _S^*+\eta _1\beta _H)&{}\quad -(\theta _3\beta _S^*+\eta _2\beta _H)&{}\quad -\eta _3\beta _H&{}\quad -\eta _4\beta _H&{}\quad -\eta _5\beta _H\\ 0&{}\quad 0&{}\quad \theta _2\beta _S^*&{}\quad \theta _3\beta _S^*&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ \end{pmatrix},\\ J3= & {} \begin{pmatrix} 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ \end{pmatrix},\\ J4= & {} \begin{pmatrix} \beta _H-g_7&{}\quad \beta _H&{}\quad \eta _1\beta _H+r_{S1}&{}\quad \eta _2\beta _H+r_{S2}&{}\quad \eta _3\beta _H+r_{S3}&{}\quad \eta _4\beta _H+r_{S4}&{}\quad \eta _5\beta _H+r_{S5}\\ 0&{}\quad -g_8&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad \gamma _{S1}&{}\quad -g_9&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad \gamma _{S2}&{}\quad -g_{10}&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad \gamma _{S3}&{}\quad -g_{11}&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \gamma _{S4}&{}\quad -g_{12}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \gamma _{S5}&{}\quad -g_{13}\\ \end{pmatrix}. \end{aligned}$$

Without loss of generality, consider the case when ${\mathcal {R}}_{T}>{\mathcal {R}}_{H}$ and ${\mathcal {R}}_{C}=1$, so that ${\mathcal {R}}_{T}=1$. Furthermore, let $\beta _S=\beta _S^*$ be a bifurcation parameter. Solving for $\beta _S$ from ${\mathcal {R}}_{T}=1$ gives

$$\begin{aligned} \beta _S=\beta _S^*=\frac{g_1 g_2 g_3}{\gamma _1(g_3+\gamma _2\theta _1)} \end{aligned}$$

We obtain the right eigenvectors associated with the zero eigenvalue which is given as ${\mathbf {w}} = (\omega _1, \omega _2,...,\omega _{15})^T$, where

$$\begin{aligned} \begin{aligned} \omega _1&=-\frac{(\beta _S^*\omega _3+\theta _1\omega _4)}{\mu }, \quad \omega _2=\omega _2>0,\\ \omega _3&=\frac{\gamma _1\omega _2}{g_2}, \quad \omega _4=\frac{\gamma _1\gamma _2\omega _2}{g_2 g_3},\\ \omega _5&=\frac{\gamma _1\gamma _2\gamma _3\omega _2}{g_2 g_3 g_4}, \quad \omega _6=\frac{\gamma _1\gamma _2\gamma _3\gamma _4\omega _2}{g_2 g_3 g_4 g_5},\\ \omega _7&=\frac{\gamma _1\gamma _2\gamma _3\gamma _4\gamma _5\omega _2}{g_2 g_3 g_4 g_5 g_6}, \quad \omega _8=\frac{r_1\omega _3+r_2\omega _4 +r_3\omega _5+r_4\omega _6+r_5\omega _7}{\mu },\\ \omega _9&=\omega _{10}=\omega _{11}=\omega _{12}=\omega _{13}=\omega _{14}=\omega _{15}=0.\\ \end{aligned} \end{aligned}$$

The components of the left eigenvector of $J(\xi _0) |_{\beta _S = \beta _S^*}$, ${\mathbf {v}} = (\nu _1, \nu _2,...,\nu _{15})$, satisfying $\mathbf {v.w}=1$, are

$$\begin{aligned} \nu _1= & {} 0,\quad \nu _2=\nu _2>0,\quad \nu _3=\frac{\gamma _2\nu _4+\beta _S^*\nu _2}{g_2},\\ \nu _4= & {} \frac{\theta _1\beta _S^*\nu _2}{g_3}, \quad \nu _5=\nu _6=\nu _7=\nu _8=\nu _9=0,\\ \nu _{10}= & {} \frac{\gamma _{S1}\nu _{11}}{g_8}, \quad \nu _{11}=\frac{\gamma _{S2}\nu _{12}+\theta _2\beta _S^*\nu _2}{g_9},\\ \nu _{12}= & {} \frac{\theta _2\beta _S^*\nu _2}{g_{10}}, \quad \nu _{13}=\nu _{14}=\nu _{15}=0. \end{aligned}$$

It follows from Theorem 4.1 in Castillo-Chavez and Song (2004), if we compute the associated nonzero partial derivatives of F(x) (evaluated at the DFE $\xi _{S0}$), that the associated bifurcation coefficients a and b, defined by

$$\begin{aligned} a = \displaystyle \sum _{k,i,j=1}^{n} \nu _k \omega _i \omega _j \frac{\partial ^2 f_k}{\partial x_i \partial x_j} (0,0) \quad \text {and} \quad b = \displaystyle \sum _{k,i=1}^{n} \nu _k \omega _i \frac{\partial ^2 f_k}{\partial x_i \partial \beta _S^{*}} (0,0), \end{aligned}$$

are computed to be

$$\begin{aligned} a= & {} 2\nu _2\alpha _1\beta _S^*\frac{\mu }{\Lambda }(\omega _3\omega _8+\theta _1\omega _4\omega _8)\nonumber \\&-\,2\nu _2\beta _S^*\frac{\mu }{\Lambda }\left( \omega _2\omega _3+\omega _3\omega _5+\omega _3\omega _6+\omega _3\omega _7+\omega _3^2+\omega _3\omega _8+\omega _3\omega _4\right) \nonumber \\&-\,2\nu _2\theta _1\beta _S^*\frac{\mu }{\Lambda }\left( \omega _2\omega _4+\omega _4\omega _5+\omega _3\omega _4+\omega _4\omega _8+\omega _4^2+\omega _4\omega _6+\omega _4\omega _7\right) \qquad \end{aligned}$$

(28)

and

$$\begin{aligned} b&=\nu _2\omega _3+\theta _1\nu _2\omega _4>0, \end{aligned}$$

with $\nu _2$, $\omega _2$, $\omega _3$, $\omega _4$, $\omega _5$, $\omega _6$, $\omega _7$ and $\omega _8$ positive.

Since the bifurcation coefficient $b>0$, it follows from Theorem 4.1 in Castillo-Chavez and Song (2004) that system (5) will undergo a backward bifurcation if the backward bifurcation coefficient $a>0$. This is possible if

$$\begin{aligned} \alpha _1>\frac{(\omega _2+\omega _3+\omega _4+\omega _5+\omega _6+\omega _7+\omega _8)(\omega _3+\theta _1\omega _4)}{(\omega _8)(\omega _3+\theta _1\omega _4)}. \end{aligned}$$

(29)

Clearly, if $\alpha _1=0$, then $a<0$ and model (5) will not exhibit the backward bifurcation phenomenon at ${\mathcal {R}}_C=1$. $\square$

Appendix G: Discussion on Some Numerical Simulations

Figure 8 shows that, with increasing treatment rate for primary and secondary syphilis for both singly and dually infected individuals, there is a decrease in the cumulative incidence of HIV amongst individuals exposed to syphilis when the HIV infection is caused by dually infected individuals. This conclusion is also reached when we observe the impact of increasing treatment rates for primary and secondary syphilis (in both singly and dually infected individuals) on the cumulative incidence of HIV amongst individuals in the primary stage of syphilis infection (Fig. 9), secondary stage of syphilis infection (Fig. 10), early latent stage of syphilis infection (Fig. 11), late latent stage of syphilis infection (Fig. 12) and tertiary stage of syphilis infection (Fig. 13). However, when our interest is on investigating the impact of treatment of primary (and secondary) syphilis, for both singly and dually infected individuals, on the cumulative incidence of HIV amongst the aforementioned subpopulations, when the HIV infections are caused by HIV-only infected individuals, we observe that the relatively low treatment rates for primary and secondary syphilis ($r_1=r_2=r_{s1}=r_{s2}=5$) were losing its effectiveness on HIV control in the target subpopulations in the long run (see Figs. 8a, 9a, 10a, 11a, 12a, 13a). However, with higher treatment rates for primary and secondary syphilis (in both singly and dually infected individuals), i.e. $r_1=r_2=r_{S1}=r_{S2}=10$, $r_1=r_2=r_{S1}=r_{S2}=12$ and $r_1=r_2=r_{S1}=r_{S2}=15$, we observe a reduction in the cumulative incidence of HIV amongst the subpopulations, just as we observed when the HIV infections were caused by dually infected individuals (as we can see in Figs.  8b, 9b, 10b, 11b, 12b, 13b).

Fig. 8

Plots of cumulative incidence of HIV amongst individuals exposed to syphilis, due to infections caused by singly and dually infected individuals. a Here, we apply three different strategies, namely: $r_1=r_2=r_{S1}=r_{S2}=0$ ($\mathcal {R_T}=5.6756$), $r_1=r_2=r_{S1}=r_{S2}=5$ ($\mathcal {R_T}=1.4446$) and $r_1=r_2=r_{S1}=r_{S2}=10$ ($\mathcal {R_T}=0.7864$) and $\mathcal {R_H} = 2.2043$. All other parameter values are as given in Table 3. b $r_1=r_2=r_{S1}=r_{S2}=10$ ($\mathcal {R_T}=0.7864$), $r_1=r_2=r_{S1}=r_{S2}=12$ ($\mathcal {R_T}=0.6621$) and $r_1=r_2=r_{S1}=r_{S2}=15$ ($\mathcal {R_T}=0.5341$) and $\mathcal {R_H} = 2.2043$. All other parameter values are as given in Table 3

Fig. 9

Plots of cumulative incidence of HIV amongst infected individuals in the primary stage of syphilis, due to infections caused by singly and dually infected individuals. a Here, we apply three different strategies, namely: $r_1=r_2=r_{S1}=r_{S2}=0$ ($\mathcal {R_T}=5.6756$), $r_1=r_2=r_{S1}=r_{S2}=5$ ($\mathcal {R_T}=1.4446$) and $r_1=r_2=r_{S1}=r_{S2}=10$ ($\mathcal {R_T}=0.7864$) and $\mathcal {R_H} = 2.2043$. All other parameter values are as given in Table 3. b $r_1=r_2=r_{S1}=r_{S2}=10$ ($\mathcal {R_T}=0.7864$), $r_1=r_2=r_{S1}=r_{S2}=12$ ($\mathcal {R_T}=0.6621$) and $r_1=r_2=r_{S1}=r_{S2}=15$ ($\mathcal {R_T}=0.5341$) and $\mathcal {R_H} = 2.2043$. All other parameter values are as given in Table 3

Fig. 10

Plots of cumulative incidence of HIV amongst infected individuals in the secondary stage of syphilis infection, due to infections caused by singly and dually infected individuals. a Here, we apply three different strategies, namely: $r_1=r_2=r_{S1}=r_{S2}=0$ ($\mathcal {R_T}=5.6756$), $r_1=r_2=r_{S1}=r_{S2}=5$ ($\mathcal {R_T}=1.4446$) and $r_1=r_2=r_{S1}=r_{S2}=10$ ($\mathcal {R_T}=0.7864$) and $\mathcal {R_H} = 2.2043$. All other parameter values are as given in Table 3. b $r_1=r_2=r_{S1}=r_{S2}=10$ ($\mathcal {R_T}=0.7864$), $r_1=r_2=r_{S1}=r_{S2}=12$ ($\mathcal {R_T}=0.6621$) and $r_1=r_2=r_{S1}=r_{S2}=15$ ($\mathcal {R_T}=0.5341$) and $\mathcal {R_H} = 2.2043$. All other parameter values are as given in Table 3

Fig. 11

Plots of cumulative incidence of HIV amongst infected in the early latent stage of syphilis infection, due to infections caused by singly and dually infected individuals. a Here, we apply three different strategies, namely: $r_1=r_2=r_{S1}=r_{S2}=0$ ($\mathcal {R_T}=5.6756$), $r_1=r_2=r_{S1}=r_{S2}=5$ ($\mathcal {R_T}=1.4446$) and $r_1=r_2=r_{S1}=r_{S2}=10$ ($\mathcal {R_T}=0.7864$) and $\mathcal {R_H} = 2.2043$. All other parameter values are as given in Table 3. b Here, we apply three different strategies, namely: $r_1=r_2=r_{S1}=r_{S2}=10$ ($\mathcal {R_T}=0.7864$), $r_1=r_2=r_{S1}=r_{S2}=12$ ($\mathcal {R_T}=0.6621$) and $r_1=r_2=r_{S1}=r_{S2}=15$ ($\mathcal {R_T}=0.5341$) and $\mathcal {R_H} = 2.2043$. All other parameter values are as given in Table 3

Fig. 12

Plots of cumulative incidence of HIV amongst infected in the late latent stage of syphilis infection, due to infections caused by singly and dually infected individuals. a Here, we apply three different strategies, namely: $r_1=r_2=r_{S1}=r_{S2}=0$ ($\mathcal {R_T}=5.6756$), $r_1=r_2=r_{S1}=r_{S2}=5$ ($\mathcal {R_T}=1.4446$) and $r_1=r_2=r_{S1}=r_{S2}=10$ ($\mathcal {R_T}=0.7864$) and $\mathcal {R_H} = 2.2043$. b Here, we apply three different strategies, namely: $r_1=r_2=r_{S1}=r_{S2}=10$ ($\mathcal {R_T}=0.7864$), $r_1=r_2=r_{S1}=r_{S2}=12$ ($\mathcal {R_T}=0.6621$) and $r_1=r_2=r_{S1}=r_{S2}=15$ ($\mathcal {R_T}=0.5341$) and $\mathcal {R_H} = 2.2043$. All other parameter values are as given in Table 3

Fig. 13

Plots of cumulative incidence of HIV amongst infected in the tertiary stage of syphilis infection, due to infections caused by singly and dually infected individuals. a Here, we apply three different strategies, namely: $r_1=r_2=r_{S1}=r_{S2}=0$ ($\mathcal {R_T}=5.6756$), $r_1=r_2=r_{S1}=r_{S2}=5$ ($\mathcal {R_T}=1.4446$) and $r_1=r_2=r_{S1}=r_{S2}=10$ ($\mathcal {R_T}=0.7864$) and $\mathcal {R_H} = 2.2043$. All other parameter values are as given in Table 3. b Here, we apply three different strategies, namely: $r_1=r_2=r_{S1}=r_{S2}=10$ ($\mathcal {R_T}=0.7864$), $r_1=r_2=r_{S1}=r_{S2}=12$ ($\mathcal {R_T}=0.6621$) and $r_1=r_2=r_{S1}=r_{S2}=15$ ($\mathcal {R_T}=0.5341$) and $\mathcal {R_H} = 2.2043$. All other parameter values are as given in Table 3

Figure 14 reveals that increasing the treatment rates for singly infected individuals with primary and secondary syphilis infection, $r_1$ (Fig. 14a) and $r_2$ (Fig. 14a), respectively, results in a positive population-level impact on the burden of syphilis, as we observe a reduction in the prevalence of primary syphilis ($I_P$), secondary syphilis ($I_S$), early latent syphilis ($L_{S1}$), but a marginal effect on the prevalence of late latent syphilis ($L_{S2}$), in the long run.

Figure 15a shows that when the treatment rate of singly infected individuals with primary syphilis, ($r_1$), is varied, it has a positive population-level impact on the number of infected individuals with HIV and tertiary syphilis ($H_T$) but a marginal effect on the number of infected individuals with tertiary syphilis ($I_T$), in the long run, while Fig. 15b shows a decrease in the prevalence of HIV and syphilis co-infection as we increase the syphilis treatment rate of dually infected individuals with HIV and primary syphilis ($r_{S1}$), as expected.

Fig. 14

Plots of the number of infected individuals with primary syphilis, ($I_P$), secondary syphilis, ($I_S$), early latent syphilis, ($L_{S1}$), and late latent syphilis, ($L_{S2}$). a Here, we vary the treatment rate of singly infected individuals with primary syphilis, ($r_1$), from 2 to 10, where $\beta _S = 10$ and $\beta _H = 0.6$, with ${\mathcal {R}}_H = 1.6532$. All other parameter values are as given in Table 3. b Here, we vary the treatment rate of singly infected individuals with secondary syphilis, ($r_2$), from 2 to 10, where $\beta _S = 10$ and $\beta _H = 0.6$, with ${\mathcal {R}}_H = 1.6532$. All other parameter values are as given in Table 3

Fig. 15

Plots of the number of a infected persons with tertiary syphilis, ($I_T$), and HIV with tertiary syphilis, ($H_T$), where $\beta _S = 10$, $\beta _H = 0.6$ and ${\mathcal {R}}_H = 1.6532$ with variations in $r_1$. b HIV-infected individuals with primary syphilis ($H_P$), secondary syphilis ($H_S$), early latent syphilis ($H_{S1}$) and late latent syphilis ($H_{S2}$), where $\beta _S = 6$ and $\beta _H = 1$, with ${\mathcal {R}}_H = 2.7554$. All other parameter values are as given in Table 3. a Treatment rate of singly infected individuals with primary syphilis ($r_1$) is varied from 2 to 10. b Treatment rate of dually infected individuals with primary syphilis ($r_{S1}$) is varied from 2 to 10