Abstract
Recently, hepatocyte–sinusoid alignment (HSA) has been identified as a mechanism that supports the coordination of hepatocytes during liver regeneration to reestablish a functional micro-architecture (Hoehme et al. in Proc Natl Acad Sci 107(23):10371–10376, 2010). HSA means that hepatocytes preferentially align along the closest micro-vessels. Here, we studied whether this mechanism is still active in early hepatocellular tumors. The same agent-based spatiotemporal model that previously correctly predicted HSA in liver regeneration was further developed to simulate scenarios in early tumor development, when individual initiated hepatocytes gain increased proliferation capacity. The model simulations were performed under conditions of realistic liver micro-architectures obtained from 3D reconstructions of confocal laser scanning micrographs. Interestingly, the established model predicted that initiated hepatocytes at first arrange in elongated patterns. Only when the tumor progresses to cell numbers of approximately 4000, does it adopt spherical structures. This prediction may have relevant consequences, since elongated tumors may reach critical structures faster, such as larger vessels, compared to a spherical tumor of similar cell number. Interestingly, this model prediction was confirmed by analysis of the spatial organization of initiated hepatocytes in a rat liver tumor initiation study using single doses of 250 mg/kg of the genotoxic carcinogen N-nitrosomorpholine (NNM). Indeed, small clusters of GST-P positive cells induced by NNM were elongated, almost columnar, while larger GDT-P positive foci of approximately the size of liver lobuli adopted spherical shapes. From simulations testing numerous possible mechanisms, only HSA could explain the experimentally observed initial deviation from spherical shape. The present study demonstrates that the architecture of small cell clusters of hepatocytes early after initiation is still controlled by physiological mechanisms. However, this coordinating influence is lost when the tumor grows to approximately 4000 cells, leading to further growth in spherical shape. Our findings stress the potential importance of organ micro-architecture in understanding tumor phenotypes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Phenotype and aggressiveness of a tumor may be influenced by its micro-architecture (Anderson et al. 2007; Hutchinson et al. 2016). For this reason, evaluation of histological analysis of the architecture of tumors is part of the standard clinical procedure serving as one aspect of staging and estimation of prognosis (Warth et al. 2012). Depending on the degree of dedifferentiation, malign tumors may still reflect features of the original tissue architecture.
In a recent communication, Hoehme et al. (2010) predicted an order principle in liver regeneration after drug-induced liver damage by quantitative simulations. The underlying mathematical model stated that in order to close the drug-induced peri-central necrotic lesion generated in the smallest functional and anatomical repetitive liver units, named lobules, hepatocytes orient their daughter cells after cell division along the closest micro-vessels (sinusoids). This mechanism, named hepatocyte–sinusoid alignment (HSA), could be validated by image analyses of regenerating mouse livers (see Fig. 12 in Appendix). We here ask the question whether signatures of HSA may still be present in early hepatocellular carcinoma. Liver cancer is the sixth most common cancer in the world, with increasing incidence (EASL 2012). The molecular mechanisms involved in the onset of liver cancer have been intensively studied (Perra et al. 2014; Petrelli et al. 2014), including the growth of preneoplastic cells (Kowalik et al. 2016; Satoh et al. 2012) and mechanisms of tumor promotion (Riegler et al. 2015; Rohr-Udilova et al. 2012; Braeuning et al. 2016). However, a study investigating early tumor shapes in liver cancer has not yet been performed.
A major path to hepatocellular carcinoma is through liver cirrhosis; in 10% of cases, cirrhosis turns into hepatocellular carcinoma (HCC), a primary cancer of the liver emerging from dedifferentiated hepatocytes, which forms the most frequent type of liver cancer. Liver cirrhosis is believed to finally emerge from an impaired balance between regeneration and degeneration; hence, it is interesting to study if signatures of HSA, that characterize regeneration of normal liver tissue, can still be found in early hepatocellular carcinoma.
As the addressed question is closely related to regeneration, we build upon our earlier regeneration model to gain a deeper understanding of the mechanisms controlling spatial organization of hepatocellular carcinoma at early stages after initiation (Hoehme et al. 2010). The model resulted from a pipeline consisting of experiments, image analysis and computational modeling established for that purpose (Hoehme et al. 2010). In a first step, the architecture of the liver lobule was reconstructed by image processing of confocal laser scanning micrographs (Hoehme et al. 2010; Drasdo et al. 2014a, b) (Fig. 1). The lobule, as the smallest repetitive functional and anatomical unit of the liver, has a diameter of about 25 cell diameters and exhibits a polygonal shape with a central vein and portal triads at its margin. A triad is composed of a vein, carrying blood from the intestine, the hepatic artery, leading blood from the aorta, and a biliary duct. Blood flows along rows of hepatocytes until it drains into the central vein. The complex spatial liver lobule architecture ensures an excellent exchange of molecules between the incoming blood and hepatocytes, the parenchymal cells of the liver.
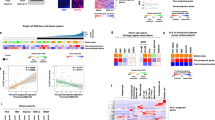
As initial spatial architecture of our model, statistically representative liver lobules obtained from reconstructed confocal laser scanning micrographs in Hoehme et al. (2010) were used, which had been constructed based on the following pipeline: (a) A stack of confocal laser scanning micrographs were transformed by image processing into a full 3D volume data set. (b) Lobule architecture parameters were defined to quantify the image information. (c) From this information, either a statistically representative lobule (e) was formed by sampling from the parameters, or simulations were directly performed on the 3D volume data set (d). In this study, (e) was used as the liver lobule architecture prior to tumor cell initiation. (f) Magnification of the confocal laser scanning micrograph indicating that hepatocytes resemble moderately deformed spheres. This justifies the choice of a center-based agent-based model for the simulation
In the next step, a statistically representative lobule was generated based on parameter distributions obtained by the image analysis of many lobules. In a further step, a computational spatiotemporal model was established to simulate the regeneration process within a virtual experiment on the computer. In this model, each hepatocyte and the lobular capillaries, called sinusoids, have been represented as model units. Using an agent-based approach, each model cell was parameterized by biophysical and bio-kinetic properties, was able to move, grow, divide and interact with other cells and sinusoids by forces within a so-called center-based model (Anderson et al. 2007), in which forces between cells were mimicked as forces between cell centers. The movement of each cell was calculated from all forces exerted on that cell including its own micro-motility using an equation of motion. Agent-based models in which an individual agent represents each cell have been extensively used to mimic the emergence of spatial tumor phenotypes in tumor development and evolution as they are perfectly suited to represent heterogeneity at cellular resolution (e.g., Anderson et al. 2006; Tang et al. 2011; Macklin et al. 2012). They are equally well able to display spatial tissue structures on scales of individual cells, as they occur on the level of liver micro-architecture, and permit the direct display and fate tracking of each individual cell and vessel at the scale of liver lobules. This is an advantage particularly if the micro-architecture is remodeled, as occurs, for example, as a consequence of interactions between the cells or molecular factors transported into the liver via the blood. The center-based modeling approach used in this paper permits modeling of arbitrary small cell displacements, and of small deformations or compressions. The approach is suited to run simulations directly in 3D volume data sets reconstructed from images. There is in the meanwhile a wide range of different single-cell-based models both on lattices and in lattice-free space. The pros and cons of different types of agent-based models have been discussed in-depth in Liedekerke et al. (2015). Simulations with single-cell-based models can be considered as experiments in silico, i.e., on the computer. Accordingly, in the presence of stochastic sources (e.g., randomness in the cell micro-motility, cell cycle duration, orientation of cell division) many simulations might be necessary to draw reliable conclusions. However, growth processes are often self-averaging, so that above a certain number of cells realizations are good representatives for the average over many simulations. Nevertheless, computing time can be significant, and sensitivity analyses can be performed only numerically (Jagiella et al. 2016; for a general discussion on the concept of self-averaging, see Landau and Binder 2000).
Fundamentally, the computational study of many processes in liver lobules may also be amenable to sophisticated continuum models (Ricken et al. 2010, 2014), whereby cells are not tracked individually, but local averages are performed usually approximating tissue pieces as a continuous body. However, if the tissue piece is only one cell thick, as is the case in the hepatic lobule for the hepatocyte sheets located between neighboring sinusoids, and at the same time cell growth, division and death of cells occur, then a continuous approach mimicking realistic growth or remodeling processes in liver lobules might be difficult to justify. In any case, such approaches would not be expected to be simpler if all interactions considered below would be taken into account. At spatial scales of a liver lobe or entire liver (depending on species, a liver can consist of up to five lobes), i.e., large compared to the organ microstructure, continuum models would be expected to be more efficient. Homogenization might be suited to obtain mechanical and flow properties given the statistically repetitive structure of liver in terms of liver lobules.
Here we pursue an agent-based model of tumor initiation, which we integrate into a model of liver regeneration (Hoehme et al. 2010), where we need to consider liver micro-architecture varying on the cell scale. In order to study regeneration, mechanisms that were hypothesized to potentially contribute to the closure of the peri-central liver lobule lesion and regeneration of micro-architecture after administration of the hepatotoxic drug \(\hbox {CCl}_{4}\) were stepwise implemented in Hoehme et al. (2010), and after each step simulation results were compared to spatiotemporal regeneration data. Carbon tetrachloride (\(\hbox {CCl}_{4}\)) is one of the most potent hepatotoxins (toxic to the liver), and for this reason it is widely used to evaluate hepatoprotective agents (Klaassen et al. 2013). It is also considered as a model drug for acetaminophen (paracetamol, APAP), as it causes a similar damage pattern as observed after APAP intoxication. It destroys the hepatocytes close to the central vein of each liver lobule. Even after more than 40% tissue damage, liver mass and architecture completely regenerate. In order to identify the best agreement at each stage between the model and experimental data, hundreds of simulations were performed within a simulated sensitivity analysis varying each model parameter over its physiological range. Hence, the effect of model parameters on the simulation outcome has extensively been studied, and parameters outside the considered ranges could be excluded as the model was parameterized by (in principle) measurable biophysical and bio-kinetic parameters. The final model included HSA (Fig. 2c) and active migration of hepatocytes toward the central necrotic lesion (Fig. 2e). This strategy ensures that even in complex models with many parameters clear conclusions can be drawn (Drasdo et al. 2014a, b). The finally predicted mechanism known as HSA has been validated by subsequent experiments. The model was later extended by integrating tissue regeneration and metabolism (Schliess et al. 2014; Drasdo et al. 2014a, b; Ghallab et al. 2016). In the study presented, the above described spatiotemporal model (Hoehme et al. 2010) served as a starting point and was further developed and extended to simulate early tumor development.
Model components. (a) Sketch of two interacting cells for the definition of the indention \({{\delta }}\) and cell radius \({R}_{{{i}}}\). (b) Implementation of cell growth in interphase by radius increase until cell volume has doubled, and division by splitting. In our study, we compared the spatial phenotype of early tumors if dividing tumor cells either (c) respect the order mechanism we could demonstrate for hepatocytes in regeneration of drug-induced peri-central liver lobule damage, namely that hepatocytes during division align along the closest sinusoid, a mechanism we had named ‘HSA’ (Hoehme et al. 2010), or (d) orient their axis of division uniformly and randomly (No HSA). (e) Consistent with (Hoehme et al. 2010) our model contained the mechanism that, in the case of necrosis, cells migrate actively into the necrotic region leading to stretching of cell-cell contacts as indicated schematically by the stretched spring. The sketch shows the lobule periphery after drug-induced liver damage (Hoehme et al. 2010). Even though necrotic lesions do not occur in the present study, we keep mechanism (e) as part of the model as a step toward a virtual liver model capable of explaining the response of liver to various perturbations on micro-architectural level. (f) Schematic of shear forces in the contact region (green) between a cell that moves to leave the column (red) and its neighbor cell (yellow)
The model developed in this paper simulates a scenario where initially one individual hepatocyte gains an increased proliferation rate, initiated as a consequence of genotoxic carcinogens. As our starting point is a thus far validated model, we can rely on parameters of the healthy hepatocytes and bypass extensive simulated parameter sensitivity analyses. To ensure that the emerging model is able to simulate both liver regeneration after drug-induced central liver lobule damage and early states of hepatocellular carcinoma, we maintained all mechanisms of the liver regeneration model and integrated mechanisms specific to cancer initiation. Prospectively, this shall permit us to construct a virtual liver model that can be used as a tool to perform virtual experiments and explore the consequence of various perturbations and malfunctions in liver (Holzhuetter et al. 2012; D’Alessandro et al. 2015).
Intuitively, it may be assumed that a tumor originating from a single initiated hepatocyte will grow with an approximately spherical shape. Surprisingly, our model predicted that this is not the case but that, instead, initially tumor growth in liver tissue should occur in longish, or extremely elongated (but clearly not in spherical) cell arrangements if HSA is still present. Only when the tumor reaches a cell number of approximately 4000 cells, do elongated cell arrangements progress to spherical structures. This model prediction stimulated us to revisit the tissue slides of previous liver tumor initiation studies in rats (Grasl-Kraupp et al. 2000). Importantly, the genotoxic carcinogen N-nitrosomorpholine (NNM)-induced elongated, almost columnar arrangements, of initiated hepatocytes after the first rounds of cell division, when the number of initiated cells was small, while larger foci adopted spherical shapes.
After these findings, simulation of numerous other possible mechanisms demonstrated that from all considered mechanisms, only hepatocyte–sinusoidal alignment (HSA), i.e., the mechanism involved in coordination of tissue organization (Drasdo et al. 2014a, b; Hoehme et al. 2010), could explain the initial deviation from spherical shape, suggesting that tumor cells early after initiation are still controlled by this order principle which in healthy liver tissue helps to coordinate the complex sheet-like tissue organization. The present study demonstrates that tumor cells at very early stages still obey physiological control mechanisms of tissue architecture but escape this regulation at sizes of approximately 4000 cells, which still represents a very small tumor. The findings presented here stress the important role of micro-architecture in early tumor development.
2 Model
As the model for liver regeneration in Hoehme et al. (2010) serves as a starting point for the present study of early hepatocellular cancer, we first enumerate the assumptions of that model before turning to the extension for hepatocellular cancer. With a view to developing a virtual liver model that is able to simulate the response on various types of perturbations (e.g. toxic damage of different type, aberrant states as steatosis, fibrosis, cirrhosis, cancer) at the level of micro-architecture, we also kept those model components from reference Hoehme et al. (2010) that may not be of importance for the present study of liver cancer modeling. However, in this paper we consider some model variations that we had not considered in Hoehme et al. (2010) for hepatocytes. These are marked below. Subsequently we address early hepatocellular cancer cells. Where applicable, we briefly summarize the assumptions. The details of the mathematical formulation are presented in Sect. 5.
The assumptions (A-number) of the simulation model in the healthy situation are:
(A-1) Hepatocyte cell shape and physical forces: Hepatocytes in 3D culture adopt an almost perfect spherical shape (cf. SI in Hoehme et al. 2010) and in confocal micrographs adopt shapes reminiscent of deformed spheres (Fig. 1). Therefore, we assumed that hepatocytes can be mimicked as homogeneous, isotropic elastic and adhesive, intrinsically spherical, objects capable of migration, growth, division and death. Hepatocyte–hepatocyte and hepatocyte–blood vessel interaction forces are mimicked by the Johnson–Kendall–Roberts (JKR) model, introduced in Drasdo and Hoehme (2005). The JKR model describes the force between homogeneous, isotropic, elastic sticky spheres, and was shown by Chu et al. (2005) to apply to cells if compression and pulling apart of one cell with respect to the other cell are sufficiently fast. It shows a hysteresis behavior depending on whether two objects approach each other or are pulled apart, i.e., cells adhere beyond the distance at which they came into contact. The hysteresis leads to a delay in cell–cell and cell–substrate detachment compared to models without hysteresis (Drasdo et al. 2007).
Healthy hepatocytes are polar, and the distribution of their cell adhesion molecules is not isotropic. We represent hepatocyte polarity by assuming that the contacts are constrained to a certain region of the hepatocyte surface. As a consequence, the force depends on the overlap of the cell surface region where adhesive molecules are located. In the case where the contact regions of two cells do not contain adhesive molecules, the adhesion force is zero.
(A-2) Equation of motion for cells: An equation of motion is used to calculate the change in position of an object (here a hepatocyte) with time. Knowing the velocity \({{{\underline{v}}}}_{i}\) and the current position \({{{\underline{r}}}}_{i}\) of an object i allows us to calculate its new position by integration of \(\hbox {d}{{{\underline{r}}}}_{i}/\hbox {d}t={{{\underline{v}}}}_{i}\) over time t. The equation of motion for a cell i (tumor cell or hepatocyte) results from:
The LHS denotes the inertia term with mass \(m_{i}\). For cells in tissues, the friction force dominates inertia forces (Reynolds numbers are sufficiently small) so inertia forces can be neglected. On the RHS, \({{\underline{F}}} _{{i}}^{{{f};{\text {C-ECM}}}}\) denotes the friction between cell and extracellular matrix, \({{\underline{F}}} _{{{ ij}}} ^{{{f};\mathrm{CC}}}\) the friction force between cells i and \(j,\,{{\underline{F}}} _{{{ ij}}}^{{{f};{\mathrm{CS}}}}\) the friction force between cell i and sinusoid \(j,\, {{\underline{F}}}_{{{ ij}}}^{{\text {adh-rep};\mathrm{CC}}} \) the adhesion and repulsion force between cells i and j (this is a central force), \({{\underline{F}}}_{{{ ij}}}^{{\text {adh-rep};\mathrm{CS}}}\) the cell–sinusoid adhesion–repulsion force (this is also a central force), \({{\underline{F}}}_{{i}}^{{\mathrm{act}}}\) the migration force, mimicking active cell motion. The detailed equation of motion can be found in Sect. 5, Eq. (4).
(A-3) Cell migration: Cells migrate actively. In absence of morphogen gradients, active cell micro-motility is assumed to be random and isotropic.
However, as our aim is to stepwise build a virtual liver model that can finally model regeneration and early cancer initiation within the same model, our model also contains a directed migration component toward a necrotic lesion in case there is a necrotic lesion formed (Fig. 2e). This migration component takes into account that in Hoehme et al. (2010) we demonstrated that random isotropic micro-motility of hepatocytes was insufficient to close the central tissue lesion that occurs in response to the drug \(\hbox {CCl}_{4}\).
In early hepatocellular cancer, as considered here, necrotic lesions do not occur; hence, directed migration would not be expected to play a role. This was verified by comparing the results of four tumor growth simulation cases, namely, (i) in presence of hepatocyte-sinusoid alignment (HSA) for both random uniform migration and directed migration, and (ii) in absence of HSA for both random uniform migration and directed migration (Fig. 13 in Appendix).
(A-4) Cell orientation changes: Cell orientation changes can be modeled by an optimization process based on the energy change occurring if the cell orientation changes (Drasdo et al. 2007), or an equation for the angular momentum (Drasdo 2005). The energy can be calculated from the forces by path integration of the energy. The energy-based method is much easier to evaluate and leads to equivalent results, which is why we used it here. Fundamentally, orientation changes were assumed to be driven by energy minimization for which we used the Metropolis algorithm (Drasdo and Hoehme 2005). In the Metropolis algorithm, a trial step (here: a small rotation) is performed, and subsequently it is evaluated whether this step is accepted, or rejected (in which case the trial step is taken back). The change in total energy of the whole cell configuration is used to evaluate the step. As the orientation change in a hepatocyte only affects the nearest and maybe next–nearest neighbors, only those neighbors need to be considered.
(A-5) Cell division: During \(\hbox {G}_{1}\), S, and \(\hbox {G}_{2}\)-phase (interphase) we assume that a cell doubles its volume and then deforms into a dumbbell at constant volume until division.
As a new variant of the model in Hoehme et al. (2010), we study the effect of pressure-inhibited cell cycle progression by assuming that a tumor cell i does not reenter the cell cycle if the pressure exerted on it overcomes a threshold value.
(A-6) Cell orientation during division: In Hoehme et al. (2010), we predicted that hepatocyte division occurs along the orientation of the closest sinusoid (micro-vessel), a mechanism we named HSA (Fig. 2c), while the absence of HSA (Fig. 2d) resulted in a failure in restoring liver lobule micro-architecture. The mechanism was subsequently experimentally validated. We implemented two alternative mechanisms of HSA. The first was a direct “restoring force”-like term, favoring orientation of a growing and dividing cell parallel to the closest sinusoid. Such a mechanism could be controlled by adhesion of cells to the ECM that fills the small space (space of Disse) between the basal cell membrane and the blood vessel, as well as by the (polar) cell–cell contacts at the lateral membranes. The second mechanism was cell division in a random direction in combination with attraction of hepatocyte cells by a sufficiently short-range morphogen secreted by the sinusoids. HSA was found to be a robust phenomenon. Even in the limit of immediate mitosis after volume doubling, oriented parallel to the closest sinusoid, we obtained the same results on the tissue scale. In this work, we only consider the first implementation of HSA.
(A-7) Cell cycle progression (normal hepatocytes): Unlike other epithelial tissues, as for example intestinal crypts (e.g., Drasdo and Loeffler 2001), the hepatocyte turnover is known to be slow (e.g., Malmgren 1956; Zou et al. 2012), so that we neglect it here.
(A-8) Sinusoids (blood micro-vessels): The model only considered sinusoids and hepatocytes, the main constituents in a liver lobule. Other cell types, such as hepatic stellate cells, Kupffer cells or externally invading macrophages, were neglected as these were not needed to explain the regeneration of liver mass and architecture after drug-induced liver damage. Sinusoids were mimicked as chains of spheres. Each sphere followed a similar equation of motion as each hepatocyte, however suppressing the active movement term.
(A-9) Reference parameters: All parameters in the model defined above have either a direct biophysical or bio-kinetic interpretation, and in principle, can be determined experimentally. Thus, the physiologically meaningful parameter range for each of the parameters could be estimated. As reference parameters (Table 2 in Appendix) for both normal hepatocytes as tumor cells, we used the parameter set for which we had found the best agreement between model simulations and experimental data in regeneration after drug-induced peri-central liver lobule damage in the mouse model (Hoehme et al. 2010). This set of parameters was found by extensive simulated parameter sensitivity analysis, varying each model parameter within its physiologically meaningful range, followed by direct comparison of the model simulation outcome and experimental findings. By this sensitivity analysis, which can be embedded in a general model identification strategy (Drasdo et al. 2014a, b), we were able to rule out model mechanisms that were insufficient in explaining the biological data and identify that model and its parameter range for which the experimental findings could be quantitatively explained. This final model required HSA.
The assumptions (AT-number) of the simulation model for tumor cells are:
AT-1: As initial state for the simulations, we labeled one cell as a tumor cell. For this cell, we assumed unlimited proliferation potential so that a monoclonal tumor emerges from one cancer precursor cell, which proliferates in contrast to the untransformed hepatocytes. When the transformed cell proliferates, it generates daughter cells that adopt the same phenotype as the precursor cell and enter the cell cycle again after division. We here assume HSA to hold for cancer cells.
In our reference simulation, all other parameters for both normal hepatocytes and transformed hepatocytes were taken from the original regeneration model in Hoehme et al. (2010).
AT-2: In the next step, we dropped the assumption of HSA for cancer cells made in AT-1, i.e., we allow dividing cancer cells to orient in a random direction. This should allow us to study the influence of HSA on early tumor initiation alone. Again, all other parameters for both normal hepatocytes and transformed hepatocytes were taken from the original regeneration model.
AT-3: In a further step, motivated by the comparison to data on early tumor initiation that will be performed below, we will define further specific parameter modifications for transformed cells in a step subsequent to AT-2. This will be motivated in the respective subsection.
For cancer cells, the same equation of motion as for normal hepatocytes is used (see Sect. 5). In those simulations where assumption (AT-3) applies, the parameters differ between normal hepatocytes and carcinoma cells.
The simulations have been carried out on a cluster of Linux-based workstations using the simulation software CellSys (Hoehme and Drasdo 2010). CellSys is a modular framework implemented in C\(++\) that utilizes SuperLU (Li 2005) for solving systems of equations, OpenMP for parallelization and OpenGL for visualization. CellSys is a tool for efficient off-lattice simulation of growth and tissue organization processes implementing the agent-based models described in section X. It uses real-time 3D visualization for the observation and assessment of simulation results.
3 Results
To simulate the earliest stages of tumor growth, we performed simulations in a liver lobule starting with one single tumor cell embedded in around 4000 hepatocytes. Simulations were performed until the tumor consisted of up to several thousand cells. The growth process was stochastic, since it contained several stochastic sources. These were micro-motility and cell cycle duration. As a consequence, each simulation (realization of the stochastic process) generated slightly different results. To exclude being misled in our conclusions by the stochastic variability within our simulations, different realizations of the stochastic process were compared by studying sufficiently high numbers of simulations. Accordingly, for a number of simulations, average and maximal/minimal values were displayed from several simulations. However, a single realization of the growth process was already a good representative of the expectation value reflecting that growth processes of this type are self-averaging, which could also be observed in other simulations (Jagiella et al. 2016).
Scenarios of tumor growth in a single liver lobule in (a, c) the presence of HSA, and (b) in the absence of HSA. In (c) the tangential friction impeding hepatocyte movement perpendicular to the formed columns along the sinusoids is elevated compared to (a). The images represent snapshots 3, 5 and 6.5 days after initiation, defined as the time point when a transformed hepatocyte adopts an increased proliferation rate. Notice that HSA (a, c) clearly causes early asymmetry of tumor cell assemblies (leftmost image column at 3 days), while with increasing tumor size this asymmetry is increasingly lost (right panel at 6.5 days). A one-cell-thick column could be found if movement perpendicular to the sinusoids was impeded by elevated shear forces, e.g., resulting from tight junctions between the apical poles of hepatocytes (compare (c) to Fig. 1a). (Fig. 10 shows the mechanical pressure in the three scenarios)
3.1 Hepatocyte–Sinusoid Alignment (HSA) Predicts an Elongated Shape of Tumor Nodules
To study the influence of HSA, simulations were performed with and without including this mechanism into the model (Fig. 3; see also model assumptions AT-1 and AT-2). All further model parameters were chosen as in the simulations of liver regeneration after drug-induced damage (Hoehme et al. 2010). We observed that simulations with HSA generate an elongated phenotype at a very early stage of their development (Fig. 3a). With increasing tumor size, elongation is lost, although the model still included HSA. At about 4000 cells, corresponding to a tumor diameter of about 370 \(\upmu \)m, the tumor has adopted an almost spherical shape.
In the next step, HSA was eliminated from the model and the cells were allowed to divide with random orientation (Fig. 3b). In this case, even at very early stages no elongation could be detected. To objectify the visual simulation result, we quantified the elongation of the tumor by the Karhunen–Loève transform (KLT, see Sect. 5), where the ratio R of longest versus shortest axis length of the tumor is clearly larger with than without HSA (Fig. 4). However, KLT reveals that even without HSA the ratio is slightly larger than one. The differences between the longest and shortest axis may be explained by the presence of blood vessels, which may favor tumor expansion in one direction within the lobule. In particular, blood vessels may constrain tumor expansion perpendicular to the portal triad-central vein axis, as this statistically represents the average vessel orientation.
Comparison of the ratio of the longest versus shortest tumor axis for simulations with HSA (black) and no HSA (red). Points represent averages over several simulations with the same parameters, lines the maximal/minimal values out of 10 realizations for tumor simulations with/without HSA (black/red lines) and 5 tumor simulations for a freely growing tumor (blue). The tumors grown in free liquid environment serve as reference. Tumors in which cells obey HSA show significant elongation compared to tumors in which tumor cells grew and divided in random directions (compare Fig. 3b, c). Note also that the degree of elongation for tumors growing in a liver lobule in the absence of HSA was not larger than for tumors grown in liquid environment despite the statistically approximately radial orientation of the sinusoids. The simulations demonstrate that the difference in tumor shape caused by HSA decreased with the size of the tumor and is no longer detectable for tumors with a size of approximately a liver lobule or larger. In total, 4000 cells correspond to a tumor diameter of about 370 \(\upmu \)m. The averages (models with and without HSA) have been formed over 10 realizations, for free tumors over 5 realizations. Figure 15 in Appendix shows individual realizations
In order to test these possibilities, we simulated tumor growth in free space. We found that as soon as tumor cells were allowed to proliferate without HSA they behaved similar to a tumor growing in free suspension. We concluded that possible differences in the axis lengths of the tumor caused by the orientation of the blood vessels were negligible compared to differences due to the stochasticity of the growth process (Fig. 4). Note also that at these tumor sizes, for both cases, HSA and no HSA, the growth of the tumor cell population size is exponential (Fig. 14 in Appendix).
3.2 Elongated Tumors Early After Initiation: Validation of the Model Prediction in a Rat Liver Tumor Initiation Study
The next step aimed at validation of the model predictions by experimental data. For this purpose, immunostained liver slices of a tumor initiation study in rats (Grasl-Kraupp et al. 2000) were reanalyzed. In those experiments, rats received a single dose of the genotoxic carcinogen N-nitrosomorpholine (NNM). Placental glutathione S-transferase (GST-P) was used as a marker of initiated hepatocytes. (Further details are explained in Sect. 5.) Representative images of GST-P positive foci with low (Fig. 5a) and high (Fig. 5b) numbers of initiated cells were taken. Altogether 26 tissue specimens have been analyzed at days 13.5, 17.5 or 24.5 after NNM administration whereby each animal could be analyzed only once (at one time point) as it had to be scarified for the analysis. In these samples, small groups of 2–6 GST-P positive cells have been found. Nine tissue specimens contained two GST-P positive cells, four could not be clearly evaluated. In 6 of 7 samples with 3 cells, the cells were aligned, in 2 of 3 samples with 4 cells the cells were aligned, and 2 of 3 samples of 5 or more cells the cells were aligned while in the third sample the cells were partially aligned. Assuming that cells can divide either in x, y or z directions with equal probability, each division orientation would have a chance of 1/3. If the division orientation were random, already at the 3 cells stage the chance of having all three cells aligned is about \(\sim \) 1/3, at 4 cells stage \(\sim \) 1/12, at 5 cells stage \(\sim \) 1/60. This statistical chance does not consider that formation of columns is energetically not favored as it requires that the growing column has to overcome mechanical compression at its tips to push aside the surrounding cells. A rough estimate of the relative elongation (\(R=\) longest axis/shortest axis) from the above values leads to an ‘average’ elongation of approximately longest axis = \([(6/7) \times 3 + (1/7) \times 2 + (2/3) \times 4 + (1/3) \times 3 + (2/3) \times 5 + (1/3) \times 3]/3 \approx 3.62\, \text {divided by shortest axis}\, = 1.38 \) at \(N=(3+4+5)/3=4\) cells stage from the 2D cross-sections leading to a ratio of 2.62. (The average of the 3, 4, 5 cell states was performed as for each individual case the number of values was small.) This value lies well within the error bars of the simulations with HSA in Fig. 4 but of course has to be taken with great caution as it was calculated from 2D image data. To statistically reliably quantify the elongation experimentally, a repetition of experiments with at least 3–4 animals per time point and analysis by confocal laser scanning microscopy to obtain 3D volume data sets of the early tumor cell populations would be desirable.
So we conclude that initially, the initiated cells tend to indeed form elongated arrangements and align along sinusoids, similarly as normal hepatocytes that also are arranged in sheets (Fig. 5a). At much larger population sizes, comparable to those of a liver lobule, nodules of GST-P positive cells adopt a compact, almost spherical shape (Fig. 5a). This occurs at a diameter of 280–420 \(\upmu \)m, which is in agreement with the model prediction, for which a spherical shape has been adopted at about 4000 cells, corresponding to a tumor diameter of about 370 \(\upmu \)m. Previously, strong evidence has been presented that these foci are of monoclonal origin (Grasl-Kraupp et al. 2000). Therefore, it seems plausible that the spherical nodules shown in Fig. 5b have evolved from the smaller, elongated GST-P positive cell arrangements as presented in Fig. 5a. Principally, it cannot be excluded that some nodules emerged from the fusion of different monoclonal foci, in which case they would not be monoclonal, but as the initial spatial density of elongated GST-positive cell clusters is relatively low, such cases should be rare.
Validation of the model prediction. Typical arrangements of GST-P positive, initiated cells in rat livers are shown after exposure to a single dose of the genotoxic carcinogen N-nitrosomorpholine (NNM) at very early (a) and later stages (b). Initiated cells express high levels of GST-P and appear in dark brown. Small cell populations of GST-P positive cells form elongated arrangements, turning to spherical tumor shape when the size of the GST-P positive foci increases. The inset in (a) shows a column of at least 5 GST-P positive cells mostly arranged in a row with the exception of at most 3 cells which escaped from the pure columnar structure (slides representing unpublished material from the experiments by Grasl-Kraupp et al. 2000). The scale bars denote twice the nucleus–nucleus distance corresponding to \(l\approx 2\times 23.3\, \upmu \mathrm{m}\). The diameter of the tumors in panel b is about \(6{-}9\times 46.6\,\upmu \mathrm{m} \approx 280{-}420\,\upmu \mathrm{m}.\) This is 50–75% of the average diameter of a liver lobule
Initially, it has been assumed that the observed elongated shapes in Grasl-Kraupp et al. (2000) occurred by chance. However, systematic formation of elongated shapes is very unlikely, and HSA can indeed explain such elongated shapes. In conclusion, the experimental findings validate our model predictions of early columnar tumor nodules that, as the nodules overcome a certain size, adopt a spherical shape.
However, the question arises if by variation of another model parameter, similar elongated early tumor shapes as predicted in the presence of HSA may be found. Moreover, in the experimental data, even one-cell-thick columns were observed (Fig. 5b), which we could not observe in any of the realizations with the reference parameter set and HSA. This leads to the question, if, in case no other mechanism can explain the elongated tumor shapes, any change in parameters could support elongation resulting in one-cell-thick columns.
3.3 Can Any Alternative Mechanism to Hepatocyte–Sinusoid Alignment (HSA) Explain Early Tumor Elongation?
In the next step we studied if alternative mechanisms to HSA could be responsible for the elongated arrangement of early transformed tumor cells that we observed in the presence of HSA. For this, we suppressed HSA (i.e., we assume isotropic cell division, Fig. 2d) and simultaneously changed another parameter for cancer cells.
We focused on parameter variations (denoted below as “No HSA-number”; number denoting a different parameter change), which we might have expected to potentially impact on the spatial tumor phenotype. The choice of parameter values throughout this paper serves to test values that are prospectively at, or close to, the border of physiological meaningful values. As reference (100%), we chose the values from Table 2 (Appendix, Hoehme et al. 2010). For example, for cells adhering to each other, (see under point “NO HSA-i” in the below enumeration), a corridor of about one order of magnitude has been reported for the adhesion strength (see Galle et al. 2005 and refs. therein). As the adhesion strength is largely controlled by the cell surface density of adhesion molecules, an increase by a factor of 5, for example, would mean that the adhesion molecule density is 5 times higher than the reference value denoted in Hoehme et al. (2010), 20% means 5 times lower. This captures even a bit more than the reported one order of magnitude in the cell-cell adhesion strength. The precise physiological borders of the physical and biological parameter values represented in the model are often not known, but if we did not find any changes within the range of values we tested, it seems unlikely that slightly larger or bigger values would have made a difference. For adhesion, the natural lower bound is absence of any adhesion, which we tested as well.
The particular parameters chosen, and the reasons why we thought they could have impacted the shape of the tumor, are explained below:
(No HSA-i) Decreased as well as increased cell–cell adhesion could perhaps modify the tumor spatial phenotype. For example, increased cell–cell adhesion of polar hepatocytes could favor formation of lengthy structures. To test this hypothesis, we considered a decreased cell–cell adhesion to 20% (Fig. 6, No HSA-i (A)) and zero (0%) (not shown), as well as an increased adhesion among tumors cells by a factor of 5 (Fig. 6, No HSA-i (B)).
(No HSA-ii) We have shown that for the reference parameter set the vessels had no impact on the early tumor shape (Fig. 4; compare curve without HSA with curve of a freely growing spheroid). However, at higher vessel stiffness the orientation of sinusoids might possibly enforce a preferred orientation of tumor growth. For this reason, simulations with increased stiffness of sinusoids were performed by increasing the sinusoid spring constant by 200% (Fig. 6, No HSA (C)) and by complete inhibition of sinusoid movement to mimic the limit of infinitely stiff vessels (Fig. 6, No HSA (D)).
(No HSA-iii) Increasing cell–matrix friction, or physically equivalently decreasing cell micro-motility might promote cells to stay longer in regions of high mechanical stress, which may form as a consequence of cell multiplication. As this could potentially impact on tumor shape, we considered a decreased tumor cell motility close to zero, by increasing the cell–matrix friction coefficient \(\xi _{i\mathrm{ECM}}^{\mathrm{CECM}}\) to a value much larger than the reference value, \(\xi _{i\mathrm{ECM}}^{\mathrm{CECM}} \gg \left( {\xi _{i\mathrm{ECM}}^{\mathrm{CECM}} } \right) _{\mathrm{REF}} \) (cf. Sect. 5) (Fig. 6, No HSA (E)). For completeness, we also considered the opposite case of increased micro-motility by decreasing the friction by a factor of three, \(\xi _{i\mathrm{ECM}}^{\mathrm{CECM}} =\left( {\xi _{i\mathrm{ECM}}^{\mathrm{CECM}} } \right) _{\mathrm{REF}}/3\) (result not shown).
Evaluation of alternative mechanisms to HSA, reflected in the figure legend by No HSA-i - No HSA-v, whereby “No HSA” stands for the absence of HSA, and i, ii, iii, iv, v each stand for a change in a particular model parameter or mechanisms according to their definitions in the text. No other mechanism than HSA was able to generate a significant elongation. (A) denotes the reference parameter set but a decreased cell–cell adhesion in cancer cells (to 20%), (B) an increased adhesion among tumors cells (by a factor of 5), (C) increased stiffness of sinusoids by increasing the sinusoid spring constant by a factor of 2 (D) complete inhibition of sinusoid movement to mimic the limit of infinitely stiff vessels, (E) an elevated friction of cell movement perpendicular to the orientation of the local sinusoid. In total, 4000 cells correspond to a tumor diameter of about 370 \(\upmu \)m. (F) denotes elevated cell–matrix friction, (G) increased cell vessel adhesion. (Black points represent averages over 10 realizations, black lines the maximal/minimal values out of the 10 realizations.)
(No HSA-iv) An increased cell–vessel adhesion might perhaps favor hepatocytes to stay close to the sinusoid. Therefore, the potential influence of an increased cell–vessel adhesion up to 300% was simulated (Fig. 6, No HSA (F)).
(No HSA-v) An elevated friction of cell movement perpendicular to the orientation of the local sinusoid may favor column formation (Fig. 5, No HSA (G)). This mechanism was simulated by increasing the respective friction coefficient \(\xi _\bot ^{\mathrm{CC}} \gg \left( {\xi _{ ij}^{\mathrm{CC}} } \right) _{\mathrm{REF}}\) (cf. Sect. 5, see sketch in Fig. 2f). If \(\alpha _{ ij}\) is the minimal angle between the axis connecting the centers of cell i and j, and the direction of movement of cell i, the additional friction generates a contribution to the friction force \(\propto |\underline{v}_i |\sin \left( {\alpha _{ ij} } \right) \), where \(\underline{v}_i\) is the velocity of cell i. Hence, a maximal increase in friction is obtained for \(\alpha _{ ij} =\pi /2\), while for \(\alpha _{ ij} =0\) the additional friction is zero. The physical justification for this parameter variation is that the shear forces are not quantitatively known (see A-2, Sect. 5). They at least partially originate from the adhesion forces. While the adhesion forces subject to pulling cells away from each other along the axis connecting their centers of mass have been reasonably well studied (e.g., Chu et al. 2005), the impact of adhesion forces on movement perpendicular to the orientation of the contact surface, reflecting shear forces, cannot readily be calculated from the central forces.
Surprisingly, for each of the parameter variations, the shape characteristics remain in the range of the curve found for the reference parameter set (Table 2) in the absence of HSA (compare Fig. 4 with Fig. 5). None of the above mechanisms generated an elongation of early tumor shape (Fig. 6; only selected parameter changes impacting on the mechanisms denoted in No HSA (i)–(v) are displayed).
(No HSA-vi) Finally a variant of (No HSA-ii) with sinusoidal spring constant of 200% was considered in which, in addition, cell cycle progression is inhibited if the pressure \(p_i\) overcomes a certain threshold P (A-7) (Fig. 7). We found that for small threshold values of \(P=1\) kPa the pressure inside the tissue quickly reached the threshold; hence, either tumor growth was inhibited completely or tumors grew only very slowly (Fig. 7). No elongation was observed. For thresholds \(P\gtrsim 1.8~\mathrm{kPa}\) cells proliferated in an unlimited fashion as for our reference parameter settings and cases No HSA-i to No HSA-v. However, in a small window of cell cycle reentrance pressures of \(1~\mathrm{kPa} \lesssim P\lesssim 1.8~\mathrm{kPa}\) elongated tumor shapes emerge. (We found a maximum elongation for \(P=1.5\) kPa.) In this window, the tumor cell proliferation was pressure-inhibited perpendicular to the sinusoids as growing against the mechanical resistance of the sinusoids elevated the pressure on the proliferating tumor cells. However, the pressure threshold was still big enough to permit proliferation between neighboring sinusoids, which approximately extended radially in the direction of the central vein–portal vein axis. As a consequence, the tumor expands preferentially into the central vein–portal vein axis as well. However, the elongation was significantly smaller as in the presence of HSA, where no pressure-dependent cell cycle progression inhibition had been considered. Interestingly, combining both HSA and the presence of a pressure-dependent cell cycle progression in the pressure threshold window \(1~\mathrm{kPa}\lesssim P\lesssim 1.8~\mathrm{kPa}\) did not promote early tumor elongation compared to HSA in the absence of a pressure-dependent cell cycle progression (Fig. 7).
As in the presence of HSA, beyond tumor population sizes of about 4000 cells, the curves for different mechanisms and parameters converge to a spherical tumor.
Tumor shape in case of pressure-inhibited tumor cell cycle progression above a threshold pressure P (assumption A7). For threshold values that were too small, the tumor did not grow or grew only very slowly (\(P=1\) kPa, violet curve). For \(P=1\) kPa, the time needed for the tumor to reach a population size of about 20 cells was the same as for \(P>1.8\,\mathrm{kPa}\) to reach a population size of 4000 cells. No elongation was observed. For large thresholds (\(P\gtrsim 1.8\,\mathrm{kPa}\), yellow curve) cells proliferated in an unlimited fashion. In a small window of \(1\,\mathrm{kPa} \lesssim P \lesssim 1.8\,\mathrm{kPa}\) elongated tumor shapes emerged (light blue, \(P=1.5\,\mathrm{kPa}\)) but the elongation was significantly smaller than for HSA. However, adding the pressure-inhibited cell cycle progression with a threshold value in the window \(1\,\mathrm{kPa}\lesssim P\lesssim 1.8\,\mathrm{kPa}\) to HSA does not yield a higher elongation than HSA alone (pink). The inset shows the pressure for this condition, which within the tumor exceeds 1.5 kPa (green). In total, 4000 cells correspond to a tumor diameter of about 370 \(\upmu \)m. (Black, blue and red points represent averages over several simulations with the same parameters, the black, blue and red lines maximal and minimal values)
3.4 Can Any Mechanism Amplify Hepatocyte–Sinusoid Alignment (HSA) Mediated Tumor Elongation?
Within numerous simulations using HSA alone, we could not observe the formation of the first five cells in one row as we could observe in the experiments (Fig. 5a). This motivated us to study whether a further mechanism or a parameter change for tumor cells could lead to an amplification of the column-forming capacity of HSA.
We considered as additional mechanisms some of those we had studied above (enumerated as No HSA-X, X=i, ii, \({\ldots }\), v) with regard to their column-forming-capacity in the absence of HSA (cf. Fig. 5):
-
(HSA-i) a decreased cell–cell adhesion in cancer cells of 20% and no adhesion at all (0%),
-
(HSA-ii) an increased adhesion among tumors cells by a factor of 5,
-
(HSA-iii) an increased stiffness of sinusoids by increasing the sinusoid spring constant by a factor of 2,
-
(HSA-iv) complete inhibition of sinusoid movement to mimic the limit of infinitely stiff vessels,
-
(HSA-v) increased tangential cell–cell friction leading to increased inhibition of movement perpendicular to the orientation of the closed sinusoids for cells that align along the sinusoids. As for our previous study of tumor shapes in the absence of HSA, we implemented this mechanism by choosing \(\xi _\bot ^\mathrm{CC} \gg \left( {\xi _{ ij}^\mathrm{CC}} \right) _\mathrm{REF}\).
Impeding tumor cell movement perpendicular to the cell–cell contacts can amply elongation (red curve at top, (E)) if HSA is present, all other mechanisms (see Fig. 7) have no significant impact on tumor elongation in the presence of HSA. Curve (A) denotes a decreased cell–cell adhesion in cancer cells (down to 20%), (B) an increased adhesion among tumors cells (by a factor of 5), (C) stiffness of sinusoids by the increase in the sinusoid spring constant by a factor of 2, (D) complete inhibition of sinusoid movement to mimic the limit of infinitely stiff vessels. (E) Increased perpendicular friction, (F) the effect of factors secreted by the cancer cells that destroy the closest vessel elements with a delay of 1 h. In total, 4000 cells correspond to a tumor diameter of about 370 \(\upmu \)m. (The dashed black and red lines represent the maximal and minimal values for the reference simulations presented in Fig. 4.)
The result of these complex simulations was that the parameter variations denoted under (HSA-i)–(HSA-iv) (stiff vessels, elevated sinusoid extensibility, elevated cell–vessel adhesion) did not promote tumor elongation (Fig. 8). However, impeding movement of hepatocyte transversal to the orientation of the sinusoid (HSA-v) amplified tumor elongation (Fig 8, dark blue curve; Fig. 3c). This can be understood as follows: the tumor cells located at the two tips (ends) of the growing column at the interface to normal hepatocytes have to push those hepatocytes away to gain space for further growth and division. As a consequence, the tumor cell column experiences an increasing mechanical pressure. If the column would not be constrained in its movement transversal to the force on its tips, it would undergo buckling in a collective movement of cells as soon as the growth-induced pressure overcomes a certain threshold (Drasdo 2000). As movement perpendicular to the tumor cell column is constrained by sinusoids and normal (non-transformed) hepatocytes, the column can release pressure only by individual cells moving out of the column causing the column to get thicker. (The same mechanism can explain piling up of cells in monolayers of cells that lost contact inhibition of growth (Galle et al. 2005)). However, an elevated perpendicular friction coefficient \(\xi _\bot ^\mathrm{CC} \gg \left( {\xi _{ ij}^\mathrm{CC} } \right) _\mathrm{REF}\) increases the friction force an individual cell has to overcome to leave the column, which in turn permits formation of longer columns. In this case, we observed initial column formation of a length of five cells (Fig. 3c). As the perpendicular friction coefficient can be largely attributed to shear forces due to tight junctions (see discussion in No HSA-v), sufficiently large contact forces between neighbor cells from impede cells from easily leaving the columnar formation and promote formation of relatively long cancer cell columns.
3.5 How Could the Elongation by Hepatocyte–Sinusoid Alignment (HSA) be Tested?
If HSA is responsible for early column formation, it should disappear if HCC cells also have the ability to destroy blood vessels they are in contact with. In order to model this, we tested destruction of vessels at different times after first contact with tumor cells (Fig. 16 in Appendix). When the delay time between contact and destruction was chosen smaller than 30 min, random fluctuations of cell positions were sufficient to destroy vessels. If the delay time went beyond 12 h, vessel destruction was found to have only little impact on the arrangement of the tumor cells in very early stages. For about 1 h delay between first contact and destruction, the effect of HSA was eliminated (Fig. 8, violet curve, Fig. 16 in Appendix). The same result was obtained if a drug was administered that destroys blood vessels.
3.6 Blood Vessel Fraction in Tumor Nodule
Finally we studied how far a growing tumor pushes blood vessels away from their original position in the presence or absence of HSA. Significant differences between cases, if they would occur, could provide a further experimentally testable prediction. For this purpose, the volume fraction of blood vessels inside the tumor was calculated (Fig. 9). The simulations showed that in the presence of HSA the volume fraction of vessel elements is slightly higher than in the absence of HSA (B vs. H, C vs. I, D vs. K, E vs. L, F vs. M). If sinusoid movement is completely inhibited (E, L), the vessel volume fraction equals the reference value without the tumor (A). Vessel destruction reduces the vessel volume fraction slightly as only the closest sinusoidal elements, representing pieces of sinusoids, are digested with a time delay. Elevated friction perpendicular to the sinusoid orientation increases the vessel fraction (G). However, at the studied tumor population size, for all values but complete inhibition of vessel movement a significant decrease in vessel volume fraction is observed, typically, by local deformation of the vessel network. This may be explained by the expanding tumor that pushing the vessel network aside. This effect is a bit stronger in the presence than in the absence of HSA because of the tendency of tumor cells to first grow along the sinusoids in the presence of HSA, but the difference is not sufficiently big to allow it to be used to distinguish between the presence and absence of HSA. For all cases, we studied in our simulations, only vessel stiffness has been found to have a strong impact on vessel density.
Blood vessel volume fraction inside the tumor. Here, (A) denotes the reference (without a tumor) of Hoehme et al. (2010). Adhesion among tumor cells being 20% of that between hepatocytes for HSA (B) and no HSA (C) adhesion among tumor cells 5 times as large as between hepatocytes for HSA (D) and no HSA (E), stiff vessels by elevation of the sinusoid element spring constant to a factor of 2 for HSA (F) and in the absence of HSA (G), infinitely stiff vessels mimicked by complete inhibition of sinusoid movement for HSA (H) and in the absence of HSA (I), elevated friction of cells perpendicular to orientation of closest sinusoid with HSA (K) and without HSA (L), (M) vessel destruction. Notice that each blue column and its right brown neighbor column differ only by the presence (blue) or absence (brown) of HSA, and otherwise share the same parameters, whereby (B,C), (D,E), (F,G), (H,I) and (K,L) differ by the parameters mentioned above and in the text of the paper (compare also assumption AT-3).
4 Discussion
In this study, we have shown that hepatocyte–sinusoidal alignment (HSA), a mechanism previously shown to be indispensable for restoration of liver micro-architecture during liver regeneration, predicts an elongation of early hepatocellular carcinoma. The model prediction was subsequently confirmed in a rat tumor initiation study using the genotoxic carcinogen N-nitrosomorpholine (NNM) and placental glutathione S-transferase as a marker for initiated cells. Further simulations demonstrated that none of the other potential mechanisms studied in this paper, neither a change in adhesion strength between cells, vessel stiffness, cell matrix friction, cell–vessel adhesion or shear forces between hepatocytes, could be responsible for the experimentally observed elongated arrangement of initiated cells in early HCC. The result strongly suggests that early after initiation, cells are still coordinated by HSA. The molecular mechanism responsible for HSA is not fully understood. In Hoehme et al. (2010) either direct orientation of dividing cells along the closest sinusoid or a mechanism that combines random orientation of cell division followed by short-range attraction by a morphogen have both been shown to fulfill the requirements of HSA. However, orientation may also emerge from a mechanical cause in case hepatocytes attach to their neighboring cells via their apical contacts and to extracellular matrix in the space of Disse, a small space between sinusoids and hepatocytes.
Our findings result from computer simulations with an agent-based model in a liver lobule that correctly represents the architectural features of real liver tissue (Hoehme et al. 2010). The liver lobule multicellular model that formed the starting point of the simulations in this paper had previously been experimentally validated for liver regeneration after drug-induced peri-central liver damage, occurring in each individual liver lobule as a consequence of exposure to hepatotoxic compounds. We used the same model with the same parameters as the starting point situation for our liver cancer development simulations in this paper, with the difference that we initially labeled one cell as a cancer cell, which then has an unlimited potential for cell division.
Testing possible alternative mechanisms to HSA and parameter settings different from the reference parameter set taken from Hoehme et al. (2010) (whereby the parameter changes caused different accentuations of the mechanisms at play, for example, an increase of the cell-cell adhesion strength increases relative weight of cell-cell adhesion in the simulation compared to the reference parameter set), we observed that neither a variation in the strength of cell–cell adhesion, of cell–vessel adhesion, an increased stiffness of vessels against extension, an elevated or reduced micro-motility or elevated shear forces between hepatocytes at their lateral sides could generate similar elongation effects. The latter mechanism was able to slightly enhance the effect of HSA, leading to an even higher degree of elongation of initiated cell foci. In absence of HSA, inhibition of cell cycle progression by mechanical compression was able to explain a moderate elongation of early hepatocellular carcinoma in a small window of mechanical pressures but the elongation found looks too small to explain the experimentally observed spatial tumor micro-patterns. Nevertheless cell cycle progression inhibition by mechanical cannot be completely excluded as potential mechanism underlying the elongated tumor shapes early after initiation.
The model was further able to predict the gradual loss of elongation of transformed cell foci with increasing tumor size. The loss of tumor elongation with increasing tumor size may be due to several reasons. Firstly, as a column grows it has to push normal hepatocytes aside in order to generate free space for its extension. This exerts forces on both normal hepatocytes and tumor cell columns, thereby elevating the compressive stress in the tumor, which increases with increasing size of the column. This interpretation is supported by visualization of the mechanical stress in the three scenarios of Fig. 3 (see Fig. 10). The more cells are forced to form columns (as in Fig. 10a, c), the higher becomes the mechanical stress that the cells in the column experience.
Scenarios of tumor growth in a single liver lobule from Fig. 3 together with pressure coloring (blue: low, green: high) in (a) the presence of HSA, (b) absence of HSA, and (c) the presence of HSA with elevated tangential friction impeding hepatocyte movement perpendicular to the formed columns along the sinusoids. The images represent snapshots at 3, 5 and 6.5 days after initiation, defined as the time point when a transformed hepatocyte adopts an increased proliferation rate. Notice that in the presence of HSA (a, c) the pressure in the early columns is elevated, as HSA forces cells into columnar order even if this leads to increased forces on the column
At a certain degree of compressive stress, the forces stabilizing the column formed by HSA are insufficient to ensure maintenance of the columnar shape. These are in particular polar cell–cell adhesion along the closest sinusoid, shear forces that hinder cell movement perpendicular to the orientation of the closest sinusoid (probably due to tight junctions), and repulsive forces if cells are pushed against sinusoids in their surroundings. Moreover, the sinusoidal network has many branching points, which perturb the growth of a column, firstly by representing mechanical obstacles, secondly by changing the local sinusoid orientation. They therefore constitute perturbation points that may trigger tumor cells to leave the columnar order. Finally, the sinusoidal network changes significantly, when the lobule borders are reached as the sinusoids are connected to the portal triads. Hence, when the tumor reaches the lobule border, the columnar order cannot be maintained. This explanation is in agreement with the experimental findings of tumors adopting a spherical shape at a diameter of about 50–75% of the liver lobule diameter.
The model simulations were performed in a statistically representative liver lobule obtained by statistical sampling from parameters that were used to quantitatively characterize liver lobule micro-architecture in 3D volume data sets reconstructed from confocal laser scanning micrographs. Normal hepatocytes and tumor cells were represented by individual agents within a biophysical model parameterizing each cell by biophysical and bio-kinetic quantities that are in principle accessible to experiments. This permitted the determination of physiologically meaningful parameter ranges within which the model parameters can be varied.
The parameters found to explain liver regeneration after drug-induced damage served as starting parameters. Within our model, each cell was able to move according to an equation of motion summarizing all forces on a cell including its own micro-motility.
The agent-based approach we used is also known as a “center-based model” as forces between cells are mimicked as forces between cell centers. Sinusoids were modeled as chains of spherical objects linked by linear springs, which permitted us to express movement of sinusoids as a collective movement of the spherical objects. This description allows us to formulate an equation of motion for each individual sphere of each vessel. Describing sinusoids as a chain of spheres is a natural choice that emerges from a medial axis transform of the blood vessel network, where the surfaces of the blood vessels have been experimentally labeled. The medial axis transform locally inscribes the sphere with maximum radius that touches the labeled vessel surface and then connects the centers of the sphere to obtain the vessel graph. This represents a direct, though abstracted, approach to model tumor cells, hepatocytes and vessels in a liver lobule. Simulations with the model can therefore be viewed as virtual experiments. The price of the relatively high degree of realism is many model parameters. However, as the model is almost fully parameterized by biomechanical or bio-kinetic parameters that can in principle be measured, the parameter ranges can be well estimated. In Hoehme et al. (2010), an extensive parameter sensitivity analysis comprising of hundreds of simulations has been performed to identify those parameters and mechanisms that were able to explain the restoration of liver mass and architecture in a regenerating lobule after drug-induced peri-central liver damage. The parameters thus identified served as the starting and reference parameter set in the present work. The emerging model can explain both, regeneration after drug-induced liver damage and growth of tumors after initiation. It may be viewed as a step toward a virtual liver lobule model that prospectively should be able to mimic numerous perturbations.
The model prediction of an initially elongated arrangement of initiated cell foci has been validated by reanalysis of liver slices from a tumor initiation study in rats (Grasl-Kraupp et al. 2000). Analysis of GST-P, which was used as a marker for initiation, demonstrated that relatively small clusters of 20 or less cells were always elongated or almost columnar, while larger foci of the size of lobules showed spherical shapes. A limitation of the experimental validation presented here is that the analysis of images was performed in a two-dimensional manner. In the past, we have reported that three-dimensional structures can easily be misinterpreted when only two-dimensional tissue slices are evaluated (Vartak et al. 2016; Drasdo et al. 2014a, b). For example, a column of initiated cells may appear as a single cell when the slice level is oriented perpendicular to the structure. To minimize misinterpretations, evaluation was performed only for images where the slice level was approximately parallel to the hepatocyte sheets and at least 4 cells could be seen. Under these conditions, almost all analyzed small foci with cell numbers smaller than about 10 cells showed the reported elongated shape. Therefore, it can be taken as demonstrated that at least a large fraction of early initiated cells arrange in elongated or column-like structures. However, the type of analysis performed here does not exclude the possibility that a small fraction of spherical, small, foci may also exist. Final validation might be possible from a three-dimensional analysis in future, where all cells of a confocal scan are considered (Hammad et al. 2014; Godoy et al. 2013). Nevertheless, the two-dimensional images presented here (Fig. 5a) give clear evidence that elongated small foci, as predicted by the simulation, indeed represent a predominant feature in NMN initiated rat livers.
In this study, we have shown an example of how computational tissue simulations are well suited to identify plausible candidate mechanisms, but also can be used to exclude mechanisms that despite looking plausible in the first place turn out to be incompatible with existing observations from direct comparison with the model simulations, and therefore do not have to be considered for further experimental validations anymore.
5 Materials and Methods
5.1 Model Details
Ad (A-1) The JKR-force \(F_{ ij}^\mathrm{JKR} =|\underline{F}_{ ij}^\mathrm{JKR} (d_{ ij})|\) where \({d}_{{ ij}}\) is the distance between the centers of two interacting spheres i and j that is calculated from two implicit equations (Fig. 2a):
where \(a_{ ij}\) is the contact radius. The effective radius \(\tilde{R}_{ ij}\) is defined by \(\tilde{R}_{ ij}^{-1}=R_{i}^{-1}+R_{j}^{-1}\), where \(R_{i}\) is the radius of cell i. \(d_{ ij} = R_{i}+R_{j} -\delta _{ij}\) is the distance between the centers of model cell i and cell j, where \(\delta _{\mathrm{ij}}=\delta _{\mathrm{i}}+\delta _{\mathrm{j}}\) is the sum of the deformations of each cell (upon compression it is the overlap of the two spheres) along the axis linking the centers of these cells. \(\tilde{E}_{ ij}\) is the composite Young’s modulus defined by \(\tilde{E}_{ ij}^{-1} =(1-\nu _i^2)E_i^{-1} +(1-\nu _j^2 )E_j^{-1}\). \(\nu _i\) is the Poisson ratio of cell i. We approximate \(\hat{\gamma }_{ ij}\thickapprox \rho _{ ij}^\mathrm{m} W_\mathrm{s}\) where \(\rho _{ ij}^\mathrm{m}\) is the density of surface adhesion molecules acting in the contact area and \(W_\mathrm{s}\) is the energy of a single bond. The second equation cannot be solved explicitly for \(F_{ ij}^\mathrm{JKR} (d_{ ij})\) if \(\hat{{\gamma }}>0\). It can be numerically solved first to obtain \(a_{ ij}(F_{ ij}^\mathrm{JKR})\). The value of \(a_{ ij}\) is then inserted into the first equation to give \(\delta _{ ij}(a_{ ij}), d_{ ij} = R_{i}+R_{j} -\delta _{ij}, d_{ ij}(a_{ ij})\). \(F_{ ij}^\mathrm{JKR} (d_{ ij})\) can be obtained by plotting \(F_{ ij}^\mathrm{JKR} (d_{ ij})\) versus \(d_{ ij}\).
The effect of polarity has been modeled by replacing the membrane density of adhesion molecules \(\rho _{ ij}^\mathrm{m} \rightarrow \rho _{ ij}^\mathrm{m} A_{ ij}^\mathrm{adh} (\psi _{ ij})/A_{ ij}\), in which case only adhesion is downscaled. Here, \(A_{ ij}^\mathrm{adh} (\psi _{ ij})\) is the area of the overlapping regions that are able to form the adhesive contact within the contact area \(A_{ ij}\approx \pi a_{ ij}\ge A_{ ij}^\mathrm{adh} (\psi _{ ij})\). This approximation results in a reduced adhesion force if the overlap area of the membrane regions of neighboring cells carrying the adhesion molecules is smaller than the physical contact area.
In general, the density of adhesion molecules on the surface of the two interacting cells differs (Ramis-Conde and Drasdo 2012, 2008), so that \(\rho _{ ij}^\mathrm{m}\) has to be calculated from the density of cell adhesion molecules on the surface of each individual cell (or, more generally, of a cell i and its interaction object X).
We assume that all surface adhesion molecules in the contact region of a cell and its interacting object (e.g., another cell or sinusoid) are saturated. In this case, the density of formed bonds behaves approximately as \(\rho _{{iX}}^\mathrm{m} \propto \min \left( {\rho _{i} , \rho _{X} } \right) \). Here \(\rho _{i}\) is the density of surface adhesion molecules of cell \(i,\rho _{X}\) the density of surface adhesion molecules of object X. We further assume that the density of adhesion molecules in the cell surface is the same for each cell. Reversible bond formation and bond release dynamics with mobile surface receptors in the contact zone between cell i and object X could be accounted for by \(\rho _{{iX}}^\mathrm{m} A_{{iX}}^\mathrm{adh} \approx (k^{ + }/k^{ - })\left( {A_{{iX}}^\mathrm{adh} } \right) ^{2} \rho _{i} \rho _{X}\), with \(k^{+},k^{-}\), being the bond formation and bond release rates, respectively. We here consider the simpler case \(\rho _{{iX}}^\mathrm{m} \propto \min \left( {\rho _{i},\,\rho _{X} } \right) \).
Ad (A-2) The equation of motion for the cell i sketched above (Eq. 1) reads:
Cell i can either be a hepatocyte or a cancer cell. Parameters for both may in principle be different, but as hepatocellular carcinoma originate from hepatocytes, it is reasonable to define, as a starting point, that the parameters of carcinoma cells are the same as for normal hepatocytes. \(\underline{\nu }_{i}(t)\) is the velocity of hepatocyte i. In the first sum, j denotes all neighbor cells of cell i: in the second sum, j denotes all sinusoidal elements interacting with cell i. Hereby, each sinusoid has been represented as a chain of small spheres connected by linear springs (see (A-8)). Within tissues the friction between cells and the extracellular matrix components, and between cells and the sinusoids, is large such that the inertia term, the first term in Eq. (3), can be neglected and be set to zero. \(\underline{\underline{\varsigma }}_{i\mathrm{ECM}}^{\mathrm{CECM}}\) denotes the friction tensor (here a \(3\times 3\) matrix) for cell-extracellular matrix friction, \(\underline{\underline{\varsigma }}_{ ij}^{\mathrm{CC}}\) describes the friction between cells i and \(j,\underline{\underline{\varsigma }}_{ ij}^{\mathrm{CS}}\) between cells i and sinusoids. The friction tensor may be decomposed into a perpendicular and a parallel component:
with \(k=\mathrm{CECM}, \mathrm{CC}, \mathrm{CS}, X=\mathrm{ECM}, j\). Here, \({{{\underline{u}}}}_{iX}=({{{\underline{r}}}}_{X}-{{{\underline{r}}}}_{i})/{\vert }{{{\underline{r}}}}_{X}-{{{\underline{r}}}}_{i} {\vert }\) with \({{{\underline{r}}}}_{i}\) denoting the position of cell i. “\(\otimes \)” denotes the dyadic product, \(\underline{F}_{iX}\) denotes the JKR-force between cells i and j (for \(X=j)\) as well as between cell i and substrate (for \(X=s\) enumerating sinusoidal elements), \(\underline{\underline{I}}\) is the unit matrix (here a \(3\times 3\) matrix with “1” on the diagonal and “0” on the off-diagonals). \(\gamma _{\bot }^{k,iX}, \gamma _{||}^{k,iX}\) are the perpendicular and parallel friction coefficients, respectively. The decomposition of the friction tensor in perpendicular and parallel components becomes more apparent when multiplying the friction tensor by the difference in velocity between cell i and object \(X, \Delta \underline{v}_{{iX}} = \underline{v}_{X} - \underline{v}_{i}\),
The first term on the RHS specifies the friction perpendicular to the direction of movement, the second and third terms on the RHS denote the tangential friction. For ECM (\(X=\mathrm{ECM}\)), \(\underline{v}_{\mathrm{ECM}} = 0\). In the case that the ECM was attached to an impermeable flat surface, the cell moves on the flat surface can be mimicked as a sphere with infinite radius by the settings, \({{{\underline{r}}}}_\mathrm{ECM}=-\infty {{{\underline{e}}}}_{z}, {{{\underline{u}}}}_{i\mathrm{ECM}}=-{{{\underline{e}}}}_{z}\). For cell movement purely tangential to the surface, the first and third term on the RHS of Eq. (5) become zero, and the second term determines the friction alone. \(\underline{F}_i^{\mathrm{active},H}\) denotes the active movement force by migration and is explained in assumption A-3.
The model assumes \(\underline{\underline{\varsigma }} _{i\mathrm{ECM}} ^{\mathrm{CECM}}=\gamma \underline{\underline{I}}\), i.e., isotropic friction with the extracellular matrix in the space of Disse.
Generally, the perpendicular and parallel friction coefficients, \(\gamma _{\bot }^{k}, \gamma _{\parallel }^{k}\), respectively, will be different for each type of interaction (\(k=\mathrm{CC}\), CS, ECM) and depend on the mechanisms of friction. For example, for adhesion controlled cell–cell friction one might expect \(\gamma _{{||}}^{k} = A_{ ij}^\mathrm{adh} \rho _{ ij}^\mathrm{m} \zeta _{\parallel }^{k}\) with \(k=\mathrm{CC}\). That is, friction will basically depend on the shared contact area decorated with adhesive bonds, the density of adhesive bonds formed, and an unknown coefficient that characterizes the strength of friction between two cells, \(\zeta _{\parallel }^{\mathrm{CC}}\).
If not stated otherwise, we lumped the density of surface adhesion molecules and friction coefficient together by setting \(\gamma _{\parallel }^{k} = A_{ ij}^\mathrm{adh} \xi _{\parallel }^{k}\) with \(\xi _{\parallel }^{k} = \rho _{ ij}^\mathrm{m} \zeta _{\parallel }^{k}\) and \(\gamma _{ \bot }^{k} = A_{ ij}^\mathrm{adh} \xi _{ \bot }^{k}\) with \( \xi _{ \bot }^{k} = \rho _{ ij}^\mathrm{m} \zeta _{ \bot }^{k}\). Moreover, for our reference data set, and if not otherwise stated, we chose \( \xi _{ \bot }^{k} = \xi _{\parallel }^{k} \equiv \xi ^{k}\) with \(k=\mathrm{CC}\), CS, CECM.
Remark
Note that the indices i, j take into account that the cells may be of different type, so automatically allow us to take into account transformed and non-transformed cells, or even the spherical elements that have been used to mimic the blood vessels. For the latter, however, no active migration terms have been considered.
Ad (A-3) Formally, active cell movement (migration) was mimicked by two alternative mechanisms which both produced an equivalent outcome (a) \(\underline{F}_i ^{\mathrm{active},H}=\chi \underline{\nabla }c+\sqrt{2D\gamma ^{2}}\underline{\eta }_i(t)\), (b) \(\underline{F}_i ^{\mathrm{active},H}=(1-\Theta [\underline{\nabla }\hat{{p}}_i \underline{\eta }_i ])\sqrt{2D\gamma ^{2}}\underline{\eta }{ }_i(t)\), respectively. Mechanism (a) mimics chemotaxis (first term) in combination with random isotropic movement (second term), (b) favors movement in the direction of small hepatocyte density.
\(\underline{\eta }_i (t)\) denotes a Gaussian-distributed random variable with average \(\left\langle {\underline{\eta }_i (t)} \right\rangle =0\) and autocorrelation \(\left\langle {\eta _{mi} (t^{\prime })\eta _{nj} (t)} \right\rangle =\delta _{ ij} \delta (t^{\prime }-t)({ m, n = x, y, z}\) denote the coordinate direction; i, j are the hepatocyte indices). Here, \(\left\langle {\underline{X}} \right\rangle \) denotes the expectation value obtained by averaging the random variable \({{{\underline{X}}}}\) over many of its realizations. As each component of \(\underline{\eta }\) is Gaussian distributed, each realization is sampled from a Gaussian distribution. D is the cell diffusion constant and assumed to be a scalar, \(\chi \) is the chemotaxis coefficient, \(c({{{\underline{r}}}},t)\) the morphogen concentration secreted by the cells dying from drug damage.
\(\hat{\rho }_{i}\) is a quantity by which the cell can sense the position of its neighbors. It is defined similar to a homeostatic pressure:
In the last equation, j is runs over all neighboring hepatocytes j of i, as well as over all sinusoidal elements. The index \(HX_{\varsigma m=0}\) means that only repulsive contributions to the interaction force were considered (formally by setting \(\rho _m=0\) in the equation for the central force).
Ad (A-4) To calculate the orientation change in a cell, within each time interval \(\Delta t\) for each hepatocyte a rotation trial around three space-fixed axes by angles \(\delta \beta _{{i}}\) with \(i=1, 2, 3, \delta \omega _{\mathrm{i}}\in [0, \delta \omega _{\max })\), with \(\delta \omega _{\max } \ll \uppi \)/2 was performed, using the algorithm of Barker and Watts (explained in Drasdo et al. 2007). The energy can be calculated by integration of the equation \(\underline{F}_{ ij} =-\frac{\partial V_{ ij} }{\partial \underline{r}_i }\) where only the JKR-force contributions were considered. The energy difference is then calculated from \(\Delta V_{ ij} (t)=V_{ ij} (t+\Delta t)-V{ }_{ ij}(t)\), and the probability that a step is accepted is calculated using \(p=\min (1, \mathrm{e}^{-\Delta V_{ ij}/F_T})\) where \(F_{T}\approx 10^{-16}\,\hbox {J}\) is a reference energy (comparable to the \(k_{\mathrm{B}} T\) in fluids or gases where \(k_{\mathrm{B}}\) is the Boltzmann factor, T the temperature).
Ad (A-5) During interphase, a cell increases its volume by increasing the radius R in small steps \(\Delta {R} \ll {R}\) until it has doubled its initial “intrinsic” volume to \(V_{\mathrm{DIV}}=2V_{\mathrm{INIT}}\), where \(V_{\mathrm{INIT}}\) was its volume immediately after cell division (Fig. 2b). Here, the intrinsic volume \(V_{i}\) of a model cell i is approximated by \(V_{i}(R_{i})=4\pi R_{i}^{3}/3\). If \(V_{i}=V_{\mathrm{DIV}}\) (hence \(R_{\mathrm{DIV}}\approx 1.26 R\)) then the model cell i deforms into a dumbbell at constant volume in mitosis (Fig. 2b). Subsequently, it divides into two daughter cells of radius R. The duration T of the cell cycle was stochastic, sampled from a Gaussian distribution with expectation value \(\tau \) and variance \(\Delta \tau =2h\) additionally cropping outside the interval \(T\in [\tau -\Delta \tau ,\tau +\Delta \tau ]\).
Pressure is defined by the simple measure \(p_{i} = \sum _{j} \frac{\underline{F}_{ ij}^{{CX}} \underline{u}_{ ij} }{{A_{ ij}}}\). Here, \(\underline{F}_{ ij}^{{CX}}\) denotes the interaction force between a cell i and object j (X denotes an object which can be a cell or a piece of the sinusoid, see A-8), \(\underline{u}_{ ij}\) the normal vector pointing from cell i to object j, \(A_{ ij}\) the interface between cell i and object j. An extension to tensors able to measure shear contributions is straightforward but not needed here (Liedekerke et al. 2015).
Ad (A-8) Sinusoids were represented as a graph. Along the graph, spheres were strung with a radius being equal to the radius of the sinusoid. The sinusoidal network of a whole liver lobule within the model consisted of approximately 50,000 spherical objects (agents).
Each of the sinusoidal spherical elements was assumed to interact with the hepatocytes by a JKR-force (\(\underline{F}_{ ij} =\underline{F}(d_{ ij},\psi _{ ij}))\). The forces among sinusoidal elements were approximated by linear elastic springs, \(\underline{F}_{{kl}}^{S} = - \frac{{kl_{0} }}{A} \times \left( {\frac{{l_{{kl}}^{S} }}{{l_{0} }} - 1} \right) \underline{u} _{{kl}}\), with k, l being spheres on the chain connected by a spring, \(A=\pi r_{kl}^S \) is the sinusoid element intersection area with \(r_{kl}^S\) being the radius of the sinusoid element connecting points k and l (In Hoehme et al. 2010, we used a constant sinusoid radius, see Table 1). \(l_{0}\) is the spring rest length, \(l_{kl}^S\) the actual length. The spring and geometrical parameters can be related to the (elastic) Young’s modulus by setting \(E^{S}=\frac{kl_0}{A}\). The Young’s modulus is one model parameter. \(\underline{u}_{kl}\) is the unit vector pointing from the center of sinusoidal object k to sinusoidal object l.
Movement of the sinusoids is modeled by an equation of motion for each of the sinusoidal spheroid elements using the same type of equation as for the hepatocytes except for the sinusoids we an active motion (migration) force.
Sinusoids in the model are anchored in the central vein and in the portal veins.
5.2 Characterization of Simulation Results
In order to quantify the tumor shape in our simulations, we perform an empirical Karhunen–Loève transform (KLT) at different tumor cell population sizes, conceptually closely related to a principle component analysis (Fig. 11). KLT minimizes the total mean square error and thus optimally spans three orthogonal eigenvectors and their associated eigenvalues, the latter giving information about tumor elongation: if all eigenvalues are similar, it indicates that there is no preferential direction of extension. On the contrary, if one eigenvalue results in significantly higher values than the others, then the tumor shape is elongated along the corresponding eigenvector. The ratio of the highest to third (lowest) eigenvalue provides a direct measure of tumor elongation, whereby the second and third eigenvalue have about the same magnitude. This measure turned out to be very robust in that different realizations of the stochastic growth process using the same parameters do not lead to any notable differences. In our figures, we displayed the ratio of the longest (extension along first eigenvector) to shortest (extension along second eigenvector) axis.
5.3 Liver Tumor Initiation and Tissue Analysis
Histological slides of a previously published study (Grasl-Kraupp et al. 2000) were reanalyzed. In this study, male Wistar rats received single doses of 250 mg of N-nitrosomorpholine (NNM)/10 ml solution/kg body weight by gavage. Livers of four animals were analyzed at days 0.5, 1.5, 2.5, 17.5, 20.5, 24.5, 27.5, 31.5 and 107.5 after NNM administration. Sections with 2 \(\upmu \)m thick were immunostained by anti-GST-P. The original study (Grasl-Kraupp et al. 2000) was designed to study the number of GST-P positive cells in relation to cell replication and cell death events. In the present study, the slides were reanalyzed to evaluate whether GST-P positive (initiated) hepatocytes are arranged in spherical or in elongated foci. For this purpose, slides were identified in which the slice level was oriented approximately in parallel to the hepatocyte sheets (allowing the identification of hepatocyte columns and sinusoids over at least 10 subsequent hepatocytes) and the shape of foci was photographically documented under a light microscope.
References
Alcaraz J, Buscemi L, Grabulosa M, Trepat X, Fabry B, Farre R, Navajas D (2003) Microrheology of human lung epithelial cells measured by atomic force. Biophys J 84:2071–2079
Anderson AR, Weaver AM, Cummings PT, Quaranta V (2006) Tumor morphology and phenotypic evolution driven by selective pressure from the microenvironment. Cell 127(5):905–915
Anderson AR, Chaplain MAJ, Rejniak KA (2007) Single-cell-based models in biology and medicine. Birkhäuser, Basel
Beysens D, Forgacs G, Glazier JA (2000) Cell sorting is analogous to phase ordering in fluids. Proc Natl Acad Sci USA 97(17):9467–9471
Braeuning A, Gavrilov A, Geissler M, Wenz C, Colnot S, Templin MF, Metzger U, Römer M, Zell A, Schwarz M (2016) Tumor promotion and inhibition by phenobarbital in livers of conditional Apc-deficient mice. Arch Toxicol 90(6):1481–1494
Casciari JJ, Sotirchos SV, Sutherland RM (1988) Glucose diffusivity in multicellular tumor spheroids. Cancer Res 48:3905–3909
Chesla SE, Selvaraj P, Zhu C (1998) Measuring two-dimensional receptor–ligand binding kinetics by micropipette. Biophys J 75:1553–1557
Chu Y-S, Dufour S, Paul Thiery J, Perez E, Pincet F (2005) Johnson–Kendall–Roberts theory applied to living cells. Phys Rev Lett 94:028102
D’Alessandro L, Höhme S, Drasdo* D, Klingmüller* U (2015) Unraveling liver complexity from molecular to organ level: challenges and perspectives. Prog Biophys Mol Biol 117(1):78–86
Davidson LA, Koehl MAR, Keller R, Oster GF (1995) How do sea urchins invaginate? Using bio-mechanics to distinguish between mechanisms of primary invagination. Development 121:2005–2018
Drasdo D (2000) Buckling Instabilities in one-layered growing tissues. Phys Rev Lett 84(18):4244–4247
Drasdo D (2005) Coarse graining in simulated cell populations. Adv Complex Syst 8(2&3):319–363
Drasdo D, Hoehme S (2005) A single-cell-based model of tumor growth in vitro: monolayers and spheroids. Phys Biol 2:133–147
Drasdo D, Loeffler M (2001) Individual-based models to growth and folding in one-layered tissues: intestinal crypts and early development. Nonlinear Anal Theory Methods Appl 47(1):245–256
Drasdo D, Hoehme S (2005) A single-cell-based model of tumor growth in vitro: monolayers and spheroids. Phys Biol 2:133–147
Drasdo D, Hoehme S, Block M (2007) On the role of physics in the growth and pattern formation of multi-cellular systems: what can we learn from individual-cell based models? J Stat Phys 128(1–2):287–345
Drasdo D, Hoehme S, Hengstler JG (2014a) How predictive quantitative modeling of tissue organization can inform liver disease pathogenesis. J Hepatol 61(4):951–956
Drasdo D, Bode J, Dahmen U, Dirsch O, Dooley S et al (2014b) The virtual liver: state of the art and future perspectives. Arch Toxicol 88(12):2071–2075
EASL (2012) EASL-EORTC clinical practice guidelines: management of hepatocellular carcinoma. J Hepat 56:908–943
Friebel A, Neitsch J, Johann T, Hammad S, Hengstler JG, Drasdo* D, Hoehme* S (2015) TiQuant: Software for tissue analysis, quantification and surface reconstruction. Bioinformatics. https://doi.org/10.1093/bioinformatics/btv346
Galle J, Loeffler M, Drasdo D (2005) Modelling the effect of deregulated proliferation and apoptosis on the growth dynamics of epithelial cell populations in vitro. Biophys J 88:62–75
Ghallab A, Cellière G, Henkel SG, Driesch D, Hoehme S, Hofmann U, Zellmer S, Godoy P, Sachinidis A, Blaszkewicz M, Reif R, Marchan R, Kuepfer L, Häussinger D, Drasdo* D, Gebhardt* R, Hengstler* JG (2016) Model guided identification and therapeutic implications of an ammonia sink mechanism. J Hepat 64:860–871
Godoy P, Hewitt NJ, Albrecht U, Andersen ME, Ansari N et al (2013) Recent advances in 2D and 3D in vitro systems using primary hepatocytes, alternative hepatocyte sources and non-parenchymal liver cells and their use in investigating mechanisms of hepatotoxicity, cell signaling and ADME. Arch Toxicol 87(8):1315–1530
Grasl-Kraupp B, Luebeck G, Wagner A, Löw-Baselli A, de Gunst M, Waldhör T, Moolgavkar S, Schulte-Hermann R (2000) Quantitative analysis of tumor initiation in rat liver: role of cell replication and cell death (apoptosis). Carcinogenesis 21(7):1411–1421
Hammad S, Hoehme S, Friebel A, von Recklinghausen I, Othman A, Begher-Tibbe B, Reif R, Godoy P, Johann T, Vartak A, Golka K, Bucur PO, Vibert E, Marchan R, Christ B, Dooley S, Meyer C, Ilkavets I, Dahmen U, Dirsch O, Böttger J, Gebhardt R, Drasdo D, Hengstler JG (2014) Protocols for staining of bile canalicular and sinusoidal networks of human, mouse and pig livers, three-dimensional reconstruction and quantification of tissue microarchitecture by image processing and analysis. Arch Toxicol 88(5):1161–1183
Hoehme S, Drasdo D (2010) A cell-based simulation software for multi-cellular systems. Bioinformatics 26(20):2641–2642
Hoehme S, Brulport M, Bauer A, Bedawy E, Schormann W, Gebhardt R, Zellmer S, Schwarz M, Bockamp E, Timmel TG, Hengstler JG, Drasdo D (2010) Prediction and validation of cell alignment along microvessels as order principle to restore tissue architecture in liver regeneration. Proc Natl Acad Sci 107(23):10371–10376
Holzhuetter H-G, Drasdo D, Preusser T, Lippert J, Henney AM (2012) The virtual liver: a multidisciplinary, multi-level challenge for systems biology. Wiley Interdiscipl Rev Syst Biol Med 4(3):221–235
Hutchinson LG, Gaffney EA, Maini PK, Wagg J, Phipps A, Byrne HM (2016) Vascular phenotype identification and anti-angiogenic treatment recommendation: a pseudo-multiscale mathematical model of angiogenesis. J Theor Biol 398:162–180. https://doi.org/10.1016/j.jtbi.2016.03.002
Jagiella N, Müller B, Müller M, Vignon-Clementel IE, Drasdo D (2016) Inferring growth control mechanisms in growing multi-cellular spheroids of NSCLC cells from spatial-temporal image data. PLoS Comput Biol 12(2):e1004412
Klaassen CD, Casarett LJ, Doull J (2013) Casarett and Doull’s toxicology: the basic science of Poisons, 8th edn. McGraw-Hill Education/Medical, New York
Kowalik MA, Perra A, Ledda-Columbano GM, Ippolito G, Piacentini M, Columbano A, Falasca L (2016) Induction of autophagy promotes the growth of early preneoplastic rat liver nodules. Oncotarget 7(5):5788–5799
Landau DP, Binder K (2000) Monte Carlo simulations in statistical physics. Cambridge University Press, Cambridge
Lekka M, Laidler P, Gil D, Lekki J, Stachura Z, Hrynkiewicz AZ (1999) Elasticity of normal and cancerous human bladder cells studied by scanning force microscopy. Eur Biophys J 28(4):312–316
Li XS (2005) An overview of SuperLU: algorithms, implementation, and user interface. ACM Trans Math Softw 31(3):302–325
Liedekerke P, Palm M, Jagiella N, Drasdo D (2015) Simulating tissue mechanics with agent-based models: concepts, perspectives and some novel results. Comput Particle Mech 26:401–444
Macklin P, Edgerton ME, Thompson AM, Cristini V (2012) Patient-calibrated agent-based modelling of ductal carcinoma in situ (DCIS): from microscopic measurements to macroscopic predictions of clinical progression. J Theor Biol 301:122–140
Mahaffy RE, Shih CK, MacKintosh FC, Käs J (2000) Scanning probe-based frequency-dependent microrheology of polymer gels and biological cells. Phys Rev Lett 85(4):880–883
Malmgren RA (1956) Observations on a liver mitotic stimulant present in tumor tissue. Cancer Res 16(3):232–236
Perra A, Kowalik MA, Ghiso E, Ledda-Columbano GM, Di Tommaso L, Angioni MM, Raschioni C, Testore E, Roncalli M, Giordano S, Columbano A (2014) YAP activation is an early event and a potential therapeutic target in liver cancer development. J Hepatol 61(5):1088–1096
Petrelli A, Perra A, Cora D, Sulas P, Menegon S, Manca C, Migliore C, Kowalik MA, Ledda-Columbano GM, Giordano S, Columbano A (2014) MicroRNA/gene profiling unveils early molecular changes and nuclear factor erythroid related factor 2 (NRF2) activation in a rat model recapitulating human hepatocellular carcinoma (HCC). Hepatology 59(1):228–241
Piper JW, Swerlick RA, Zhu C (1998) Determining force dependence of two-dimensional receptor–ligand binding affinity by centrifugation. Biophys J 74:492–513
Ramis-Conde* I, Drasdo D*, Anderson ARA, Chaplain MA J (2008) Modeling the influence of the E-cadherin-beta-catenin pathway in cancer cell invasion: a multiscale approach. Biophys J 95: 155–165
Ramis-Conde I, Drasdo D (2012) From genotypes to phenotypes: classification of the multi-cellular spatial–temporal tumour profiles for different variants of the cadherin adhesion pathway. Phys Biol 9(3):11
Ricken T, Dahmen U, Dirsch O (2010) A biphasic model for sinusoidal liver perfusion remodeling after outflow obstruction. Biomech Model Mechanobiol 9:435–450
Ricken T, Werner D, Holzhütter HG, König M, Dahmen U, Dirsch O (2014) Modeling function-perfusion behavior in liver lobules including tissue, blood, glucose, lactate and glycogen by use of a coupled two-scale PDE-ODE approach. Biomech Model Mechanobiol 14(3):515–536
Riegler T, Nejabat M, Eichner J, Stiebellehner M, Subosits S, Bilban M, Zell A, Huber WW, Schulte-Hermann R, Grasl-Kraupp B (2015) Proinflammatory mesenchymal effects of the non-genotoxic hepatocarcinogen phenobarbital: a novel mechanism of antiapoptosis and tumor promotion. Carcinogenesis 36(12):1521–1530
Robertson-Tessi M, Gillies RJ, Gatenby RA, Anderson AR (2015) Impact of metabolic heterogeneity on tumor growth, invasion, and treatment outcomes. Cancer Res 75(8):1567–1579. https://doi.org/10.1158/0008-5472.CAN-14-1428
Rohr-Udilova N, Sieghart W, Eferl R, Stoiber D, Björkhem-Bergman L, Eriksson LC, Stolze K, Hayden H, Keppler B, Sagmeister S, Grasl-Kraupp B, Schulte-Hermann R, Peck-Radosavljevic M (2012) Antagonistic effects of selenium and lipid peroxides on growth control in early hepatocellular carcinoma. Hepatology 55(4):1112–1121
Satoh K, Yamakawa D, Kasai K, Hayakari M, Uchida K, Miura T (2012) Nonclonal growth of preneoplastic cells positive for glutathione S-transferase P-form in the rat liver. Cancer Sci 103(8):1445–1450
Schienbein M, Franke M, Gruler H (1994) Random walk and directed movement: comparison between inert particles and self-organized molecular machines. Phys Rev E 49(6):5462–5471
Schliess F, Hoehme S, Henkel S, Ghallab A, Driesch D, Böttger J, Guthke R, Pfaff M, Hengstler JG, Gebhardt R, Häussinger D, Drasdo* D, Zellmer* S (2014) Integrated metabolic spatial-temporal model for the prediction of ammonia detoxification during liver damage and regeneration. Hepatology 60(6):2040–2051
Tang J, Enderling H, Becker-Weimann S, Pham C, Polyzos A, Chen CY, Costes SV (2011) Phenotypic transition maps of 3D breast acini obtained by imaging-guided agent-based modeling. Integr Biol 3(4):408–421
Vartak N, Damle-Vartak A, Richter B, Dirsch O, Dahmen U, Hammad S, Hengstler JG (2016) Cholestasis-induced adaptive remodeling of interlobular bile ducts. Hepatology 63(3):951–964
Vintermyr OK, Døskeland SO (1987) Cell cycle parameters of adult rat hepatocytes in a defined medium. A note on the timing of nucleolar DNA replication. J Cell Physiol 132:12–21
Warth A, Muley T, Meister M, Stenzinger A, Thomas M, Schirmacher P, Schnabel PA, Budczies J, Hoffmann H, Weichert W (2012) The novel histologic International Association for the Study of Lung Cancer/American Thoracic Society/European Respiratory Society classification system of lung adenocarcinoma is a stage-independent predictor of survival. J Clin Oncol 30(13):1438–1446
Xiaoye SL (2005) An overview of SuperLU: algorithms, implementation, and user interface. ACM Trans Math Softw (TOMS) 31(3):302–325
Zou Y, Bao Q, Kumar S, Hu M, Wang G-Y et al (2012) Four waves of hepatocyte proliferation linked with three waves of hepatic fat accumulation during partial hepatectomy-induced liver regeneration. PLoS ONE 7(2):e30675. https://doi.org/10.1371/journal.pone.0030675
Acknowledgements
DD gratefully acknowledges support by the projects EU-CancerSys, EU-PASSPORT, EU-NOTOX, BMBF-Virtual Liver Network, BMBF-LiSym and ANR-IFLOW, FB support by EU-CancerSys, SH by EU-CancerSys and BMBF-VLN, WW by project EU-CancerSys and EU NOTOX, JGH by EU CancerSys, BMBF-VLN, BMBF LiSym.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Parameter Tables
See Tables 1 and 2 and Figs. 12, 13, 14, 15 and 16.
Angle (probability) density (y-axis) versus angle (x-axis) for angle between orientation of hepatocyte division and the orientation of the closest sinusoid (x-axis) in experiment (red) and three models 1–3 during regeneration after drug-induced damage (Hoehme et al. 2010). Model 1 assumes uniform cell division direction (no HSA) and random uniform micro-motility, model 2 uniform cell division direction (no HSA) and directed cell movement toward the drug-induced necrotic tissue lesion, model 3 assumes cell division oriented along the closes sinusoid (HSA) and directed cell movement toward the drug-induced necrotic tissue lesion
Growth kinetics of tumors in case of HSA, no HSA and pure spheroids (i.e., in liquid suspension) (compare Fig. 4) show exponential growth with minor differences even for a single realization of the stochastic growth process
Individual realizations of the stochastic growth processes in Fig. 4. Notice that even the individual realizations are clearly separated, the size of the fluctuations decrease with the number of cells of the tumor. This is an effect of self-averaging that becomes stronger with the number of objects (here: cells)
Impact of delay between first tumor cell contact and vessel destruction on formation of early-elongated tumors. If destruction occurs 12 h after first contact with the tumor cell tumor elongation is not affected, while for earlier destruction of the vessel before 12 h after the first contact with tumor cells, the effect of HSA is reduced, or for a delay of less than or equal to 30 min, even eliminated
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hoehme, S., Bertaux, F., Weens, W. et al. Model Prediction and Validation of an Order Mechanism Controlling the Spatiotemporal Phenotype of Early Hepatocellular Carcinoma. Bull Math Biol 80, 1134–1171 (2018). https://doi.org/10.1007/s11538-017-0375-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11538-017-0375-1