1. Introduction

Absorption of orally administered drugs from the GI tract is an important determinant of the onset of the drug effect. Not surprisingly, the function describing absorption is a key component of a pharmacokinetic (PK) model. Models of systemic drug absorption are frequently based on a first-order rate process. Closed form solutions have been derived for the simultaneous differential equations describing first-order absorption and one and two compartmental disposition (Shargel and Yu, 1999; Gabrielson and Weiner, 2000). The first-order absorption model assumes instantaneous presence of the drug in the gut compartment and subsequently an exponential decrease of the absorption rate with time as dictated by the absorption rate constant, K a. The introduction of a lag time between oral administration and the onset of absorption accounts for delays due to passage through the GI tract. A limitation of this model is that it predicts an unrealistically sharp entrance front of the drug at the site of absorption.

In practice, the use of the first-order approach to predict plasma concentrations frequently yields a mismatch between predicted and measured plasma concentration versus time profiles (Weiss, 1996; Higaki et al., 2001; Ring, 2001). The first-order absorption model cannot describe sigmoid shapes in the upswing of the plasma concentration-time curve. This is related to its exponential decrease of the absorption rate with time, not allowing the presence of an inflection point (See Fig. 1, left panel). Fitting PK models with first-order absorption to data may thus hamper a sound interpretation of estimated absorption and disposition parameters. Various alternatives have been discussed for the first-order absorption model. A very extensive overview of different strategies to characterise drug absorption profiles is provided by Zhou (2003), discussing an array of different absorption models. One of these models is the Weibull distribution, which was suggested by Piotrovskii (1987) as an empirical absorption kinetics model in order to improve the description of the concentration-time curve. Recently, Higaki et al. (2001) developed a set of six different time-dependent absorption models as alternatives for the conventional first-order absorption model. These models, which include a time dependency in the absorption rate constant, are superior to the conventional first-order model with a lag time in predicting plasma concentration curves. However, all of the proposed models contain at least one additional parameter than the two parameters needed in the first-order absorption model.

Fig. 1
figure 1

Shape of the absorption rate-time relationship and the corresponding concentration-time curve in a 1-compartment model for (1) the first-order absorption model and (2) the inverse Gaussian density function.

Full size image

Weiss (1996) has proposed to use the Inverse Gaussian Density (IG)-input function as an alternative to the first-order absorption model to describe the absorption-time curve. Modelling exercises have shown that this type of absorption model can adequately describe an inflection point (Fig. 1, right panel) in the concentration-time curve when combined with a 1-compartment pharmacokinetic model (Weiss, 1996; Weiss et al., 1997; Ring, 2001). The appealing aspect of this input function is that it contains just two parameters. These parameters have a clear meaning in terms of the progress of the absorption process.

A possible mechanism that can explain the IG shape of the absorption-time curve is convective-dispersive transport from the site of administration to the gut. The drug has to pass the oesophagus, the stomach, and the duodenum, before arriving in the gut, which modulates the original input pulse. It is the purpose of this paper to clarify the theoretical background and rationale of the convective- dispersive transport equations in calculating absorption profiles. The application of the absorption model is illustrated by an example from the literature (Nimmo et al., 1973).

2. Theory

2.1. Mass balance

In pharmacokinetic models the mass balance at the absorption site, i.e. the gut compartment, is considered as the result of an incoming transport flux, N in, loss via excretion, N out, and loss via absorption, N abs:

$${{{\rm{d}}{A_G}} \over {{\rm{d}}t}} = {N_{{\rm<Subscript></Subscript>}}}(t) - {N_{{\rm{out}}}}(t) - {N_{{\rm{abs}}}}(t)$$
(1)

where A G is the amount of delivered drug at the site of absorption. The above mass balance equation thus considers a point mass balance at the absorption site, without specifying the local conditions that determine the terms on the right-hand side of the equation. A common assumption is that a constant fraction is unavailable for absorption and is consequently excreted:

$${N_{{\rm{out}}}} = (1 - F){N_{{\rm<Subscript></Subscript>}}}$$
(2)

where F is the bioavailability fraction. Assuming first-order absorption, this leads to the following equation (Shargel and Yu, 1999):

$${{d{A_G}} \over {{\rm{d}}t}} = F{N_{{\rm<Subscript></Subscript>}}}(t) - {K_a}{A_{\rm{G}}}$$
(3)

where K a is a rate constant, and N in(t) is considered as a series of instantaneous pulses, representing the dosages. Alternatively, it can be assumed that the absorption rate is not the limiting factor, but transport to the gut (N in), which leads to the following approximate equation:

$${N_{{\rm{abs}}}} = F{N_{{\rm<Subscript></Subscript>}}}$$
(4)

.

In order to model the absorption process according to Eq. (4), the transport term N in needs to be described as a function of time.

The theory for transport of tracer compounds, such as drugs, in bulk fluids that move along a transport direction to a certain site is based on two physical concepts:

  1. 1.

    The concept of mass balance of drug along the one-dimensional transport axis:

    $$\eqalign{ & {N_{{\rm{abs}}}} = F{N_{{\rm<Subscript></Subscript>}}} \cr & {{\partial C} \over {\partial t}} = - {{\partial J} \over {\partial z}} \cr} $$
    (5)

    where C is concentration, J is the mass flux, t is time and z is transport distance. whereby both C and J may vary with time and distance.

  2. 2.

    The assumption of a convective and a dispersive transport term to express the mass flux along the transport direction:

    $$J = vC - D{{\partial C} \over {\partial z}}$$
    (6)

    with the mass exchange rate, N

    $$N = \alpha J$$
    (7)

    where v is the transport velocity and D is the dispersion coefficient and α is the cross-sectional area of the flow field, i.e. the mean cross-sectional area of the GI tract. The convective term, vC, expresses the transport of drug with the movement of food and liquid suspensions through the GI tract to the gut. The dispersive term, D∂C/∂z, accounts for the dispersion in the transport pulse. The dispersion coefficient joins together variations in velocity and tortuous transport path within the GI tract, i.e. the flow lines are assumed to diverge and rejoin.

If no drug is eliminated during transport and if the dispersion coefficient and the transport velocity are adopted as constants, combination of Eqs. (5) and (6) yields:

$${{\partial C} \over {\partial t}} = D{{{\partial^2}C} \over {\partial {z^2}}} - v{{\partial C} \over {\partial z}}$$
(8)

which is known as the convection-dispersion equation (Carslaw and Jaeger, 1959; Kreft and Zuber, 1978). The above partial differential equation can be used to model the transport of drugs to the absorption site, by finding an expression for the flux, J, as a function of time at a certain distance from the entrance point (Eqs. (6) and (7)).

2.2. Initial and boundary conditions

To obtain the expression that gives the mass flux as a function of time and distance, Eq. (8) must be solved for the appropriate initial and boundary conditions.

If no drugs are present in the GI tract, the valid initial condition is:

$$C = 0,{\rm{ }}t = 0,{\rm{ }}z > 0$$
(9)

When drugs are taken orally in the form of soluble tablets or a solution, this can be considered as an instantaneous injection into the GI tract. Therefore, the following upper-boundary condition is pertinent:

$$C - {D \over v}{{\partial C} \over {\partial z}} = {{{A_{\rm{D}}}} \over {v\alpha }}\delta (t),{\rm{ }}t \ge 0,{\rm{ }}z = 0$$
(10)

where A D is the dose and δ(t) is the Dirac delta distribution. Eq. (10) incorporates continuity of flux at the upper boundary. This requirement for the mass balance in organs has been discussed previously in the case of liver distribution kinetics (Hisaka and Sugiyama, 1999; Roberts et al., 2000).

The lower-boundary condition concerns an assumption about the concentration and/or the concentration gradient at the outlet. The mass balance discussed in Eqs. (1)–(4) is of little use in formulating the lower-boundary conditions, since it represents a total mass balance without specifying the local condition needed to solve Eq. (8). The nature of the lower-boundary condition has been discussed in some detail (Parlange et al., 1992; Freijer et al., 1998; Hisaka and Sugiyama, 1999; Roberts et al., 2000). In the derivation of the IG-input function it is assumed that there is a negligible change of dispersion (mixing) when the food/liquid suspension leaves the duodenum and enters the gut, and the following lower-boundary condition is pertinent:

$$\eqalign{ & {{\partial C} \over {\partial z}} = 0,{\rm{ }}t \ge 0,{\rm{ }}z = \infty \cr & \cr} $$
(11)

2.3. Solution

The solution of differential equation (Eq. (8)) with the initial condition (Eq. (9)) and the boundary conditions (Eqs. (10) and (11)) is provided in Kreft and Zuber (1978). The following relationships and definitions are used:

$$\eqalign{ & {{\partial C} \over {\partial z}} = 0,{\rm{ }}t \ge 0,{\rm{ }}z = \infty \cr & {C_{\rm{F}}} = C - {D \over v}{{\partial C} \over {\partial z}} \cr} $$
(12)

where C F the “flux-averaged” concentration, which relates to J by

$$J = v{C_{\scriptstyle {\rm{F}} \hfill \atop \scriptstyle \hfill} }$$
(13)

The following dimensionless variables are used:

$$\xi = vz/D$$
(14)
$$\tau = {v^2}t/D$$
(15)

where ζ and τ are dimensionless distance and time, respectively.

Then, the solution for the concentration is (Kreft and Zuber, 1978; Veling, 1993):

$$C = {{{A_{\rm{D}}}{v^2}} \over {{v_\alpha }D}}\left( {{1 \over {\sqrt {\pi \tau } }}\exp \left( { - {{{{\left( {\zeta - \tau } \right)}^2}} \over {4\tau }}} \right) - {1 \over 2}\exp \left( \zeta \right){\rm{erfc }}\left( {{{\zeta + \tau } \over {2\sqrt \tau }}} \right)} \right)$$
(16)

where the complementary error function is defined as:

$${\rm{erfc}}(x) = {2 \over {\sqrt \pi }}\int\limits_x^\infty {\exp ( - {u^2}){\rm{d}}u} $$
(17)

.

See for an overview of approximations of the complementary error function Abramowitz and Stegun (1966). The solution for the flux-averaged concentration is (Kreft and Zuber, 1978; Veling, 1993)

$${C_{\rm{F}}} = {{{A_{\rm{D}}}{v^2}} \over {v\alpha D}}\left( {{1 \over {2\sqrt \pi }}{{\left[ {{1 \over \tau }} \right]}^{3/2}}\zeta \exp \left( { - {{{{(\xi - \tau )}^2}} \over {4\tau }}} \right)} \right)$$
(18)

.

Equation (18) is used to express the absorption rate, and not Eq. (16), as the latter expresses the resident concentration, and omits the concentration gradient required to calculate the total (convective and dispersive) flux (Hisaka and Sugiyama, 1999; Roberts et al., 2000).

Additionally, the following integral, giving the total mass that has passed distance z at time t is of interest (Veling, 1993):

$$M = \alpha \int\limits_z^\infty {C{\rm{d}}u = {A_{\rm{D}}}\left( {{1 \over 2}{\rm{erfc}}\left( {{{\left( {\xi - \tau } \right)} \over {\sqrt {4\tau } }}} \right) + {1 \over 2}\exp (\zeta ){\rm{erfc}}\left( {{{\zeta + \tau } \over {2\sqrt \tau }}} \right)} \right)} $$
(19)

.

Methods to arrive at these solutions are extensively discussed in Carslaw and Jaeger (1959).

2.4. Derivation of the Inverse Gaussian density function

The IG function, as proposed by Weiss (1996) utilises a statistical concept of absorption, where the probability of absorption changes with time. Weiss et al. (1997) point at the relationship of the density function with the solution presented above (Eq. (18)). In order to derive the IG function from Eq. (18), we have to rewrite Eq. (7). Using Eqs. (13)–(15), and (18) we can rewrite Eq. (7) as:

$$N = {A_{\rm{D}}}{{{v^2}} \over D}\left( {{1 \over {2\sqrt \pi }}{{\left[ {{1 \over \tau }} \right]}^{3/2}}\zeta \exp \left( { - {{{{\left( {\zeta - \tau } \right)}^2}} \over {4\tau }}} \right)} \right)$$
(20)

where the cross-sectional area, α, cancels from the equation. If we look at unity transport distance, i.e. velocity expressed in terms of the mean distance between the site of administration and the site of absorption, vz → v, then:

$${N_{{\rm<Subscript></Subscript>}}} = {A_{\rm{D}}}{\left[ {{1 \over {4\pi {t^3}D}}} \right]^{1/2}}\exp \left( { - {{{{(1/v - t)}^2}} \over {4tD/{v^2}}}} \right)$$
(21)

.

Now define the following two parameters:

$${\rm{MAT}} = {1 \over v}$$
(22)
$${\rm{C}}{{\rm{V}}^{\rm{2}}} = {{2D} \over v}$$
(23)

where MAT is the mean absorption time, and CV2 the term expressing the variation in absorption time. Substitution in Eq. (22) gives:

$${N_{{\rm<Subscript></Subscript>}}} = {A_{\rm{D}}}{\left[ {{{{\rm{MAT}}} \over {2\pi {\rm{C}}{{\rm{V}}^2}t3}}} \right]^{1/2}}\exp \left( { - {{{{(t - {\rm{MAT}})}^2}} \over {2{\rm{C}}{{\rm{V}}^2}{\rm{MAT}}t}}} \right)$$
(24)

. The above-derived equation is similar to the IG function and corresponds to Eq. (3) in Weiss (1996). Further, mathematical properties of Eq. (24) are discussed by Weiss (1996), Ring (2001), and Ring et al. (2000).

2.5. Absorption percentiles

Using Eq. (19), it is possible to calculate the time at which a certain fraction of drug has been absorbed. This can be achieved by iteratively solving Eq. (19) for a desired value of M for repeated estimates of time. Bisection methods are generally efficient enough to obtain rapid convergence.

3. Example

To illustrate the use of the convection-dispersion equation for oral absorption, we applied the IG-input function (Eq. (21)) to describe the absorption of paracetamol in a 22-year-old man (Nimmo et al., 1973). Data were taken from literature by digital processing of Fig. 2 in Nimmo et al. (1973) using the WinDIG program (Lovy, 1996). Dosage includes three consecutive single administrations of paracetamol (1500 mg) in the same individual, with enough washout in between administrations. This example covers a transport-related pharmacokinetic problem: paracetamol was administered alone, with metoclopramide, and with propantheline. Metaclopramide stimulates gastric emptying, while propantheline delays gastric emptying, thus influencing the mean-passage rate of the drug through the GI tract. This specific case therefore represents an example from literature where the feasibility of the transport-related absorption model can be verified. The model should be able to describe the concentration versus time curves, by using different transport velocities.

Fig. 2
figure 2

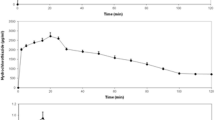
Model fit for paracetamol absorption in a 22-year-old man using a 1-compartment model with first-order elimination and first-order absorption without lag time. Corresponding parameter estimates and −2LL value are provided in Table 1.

Full size image

The PK model that was used to describe the data is a 1-compartment massbalance model with first-order elimination:

$$\eqalign{ & {N_{{\rm<Subscript></Subscript>}}} = {A_{\rm{D}}}{\left[ {{{{\rm{MAT}}} \over {2\pi {\rm{C}}{{\rm{V}}^2}t3}}} \right]^{1/2}}\exp ( - {{{{(t - {\rm{MAT}})}^2}} \over {2{\rm{C}}{{\rm{V}}^2}{\rm{MAT}}t}}) \cr & {{{\rm{d}}A} \over {{\rm{d}}t}}i = {N_{{\rm{abs}}}}(t) - kA \cr} $$
(25)

.

With the definition of plasma concentration and volumetric clearance as

$$C = A/V$$
(26)
$${\rm{CL}} = kV$$
(27)

.

Time series of plasma concentration after oral administration alone allows optimization of all the parameters in the absorption function, and of V/F and CL/F. The choice of a 1-compartment model was suggested by the fact that the concentration versus time data show only one exponential phase during washout.

The models’ differential equation for the mass balance of the plasma compartment and the three different functions describing the absorption rate were implemented in NONMEM V, a computer program for optimisation of non-linear mixed effects models (Boeckmann et al., 1994). This computer program estimates the model parameters by the maximum likelihood criterion. The model fits were compared using the minimum of −2×log likelihood (−2LL).Model fits were diagnosed by plots of the residuals (the normalised difference between observed and predicted concentrations). A numerical solution method was selected for solving the differential equation and the absorption function simultaneously.

Absorption was described in four different ways: (1) Using a common first-order absorption function. This function contains one absorption parameter, K a, which was allowed to vary between the three absorption cases (Eq. (3)). (2) Using a first-order absorption function with a lag time. This function contains two absorption parameters, K a and a lag time (t lag). Only K a was allowed to vary between the three absorption cases. (3) Absorption according to the IG function (Eqs. (4) and (21)). This function also contains two absorption parameters, v and D. Only v was allowed to vary between the three absorption cases. (4) Similar to case 3, but with D/v optimised instead of D. Alternative models, with inter-occasion differences also identified on lag time or dispersion coefficient did not result in a satisfactory −2LL minimisation. Neither could the model with a constant K a and t lag varied between the three absorption cases converge to a successful minimisation.

Results of the above-described exercise are provided in Figs. 2–6 and Tables 1 and 2. Figures 2–5 show the fits using the four different absorption models. All four models can describe differences in PK relating to the acceleration and delay of absorption when metoclopramide and propantheline are co-administrated. However, there are clear differences between the models for the fits of the concentration- time curves and the interpretation of the fitted parameters.

Fig. 3
figure 3

Model fit for paracetamol absorption in a 22-year-old man using a 1-compartment model with first-order elimination and first-order absorption with lag time. Corresponding parameter estimates and −2LL value are provided in Table 1.

Full size image
Fig. 4
figure 4

Model fit for paracetamol absorption in a 22-year-old man using a 1-compartment model with first-order elimination and IG-input function with D optimised. Corresponding parameter estimates and −2LL value are provided in Table 1.

Full size image
Fig. 5
figure 5

Model fit for paracetamol absorption in a 22-year-old man using a 1-compartment model with first-order elimination and IG-input function with D/v optimised. Corresponding parameter estimates and −2LL value are provided in Table 1.

Full size image
Fig. 6
figure 6

Residuals of the models fits for paracetamol absorption in a 22-year-old man using (1) 1-compartment model with first-order absorption (2) 1-compartment model with first-order absorption and an absorption lag time. (3) 1-compartment model with IG-absorption function (D optimised). (4) 1-compartment model with IG-absorption function (D/v optimised).

Full size image
Table 1 Parameter estimates and likelihood (−2×log likelihood) in the four different models for paracetamol absorption in a 22-year-old man.
Full size table

The first-order model (Fig. 2) shows a strong mismatch between the model predictions and the observations. The model cannot describe the maximum concentration, while the concentration upswing is overestimated. This also becomes clear in the plot of the residuals against time (Fig. 6, panel 1): The residuals are not evenly distributed along the origin. If a lag time is added to the first-order absorption model (Fig. 3) the model fit improves. Closer inspection of the residuals against time (Fig. 6, panel 2) however, indicates that some bias remains.

The fit of the models that employ the IG function are displayed in Figs. 4 and 5. Both models describe the data better than the first-order models. Remarkably, the fit where bias in the residuals is absent is when D/v is optimised and not D (Compare Fig. 6, panel 3 and 4). Optimisation of the dispersion coefficient scaled to the velocity suggests an increase of the dispersion coefficient with velocity. This correlation has also been observed in other disciplines that study transport processes, such as hydrology (Biggar and Nielsen, 1976), and indicates that variability in the transport velocity increases with velocity. This approach is in accordance with the reparameterisation that is used in the derivation of the IG function from the solution of the convection-dispersion equation (Eqs. (22)–(24)), and its original presentation as a statistical absorption function (Weiss, 1996).

Parametric results of the model fits are provided in Table 1. A comparison of the likelihood values and the residual error between the different models confirms that the IG function is superior to the first-order absorption models in describing the data (Table 1). The estimated clearance and distribution volumes are comparable for the various models. This suggests that the type of absorption model has no major impact on the estimates of the disposition parameters. The estimated absorption parameters all reflect the influence of co-administration of metoclopramide and propantheline, but quite differently. The first-order model explains the influence by different estimates of the absorption parameter, K a, which would suggest that metoclopramide and propantheline influence the actual uptake rate from the gut compartment. Identification of a variable lag time to explain the effect of these drugs was not successful for the first-order model. The transport-limited absorption model explains the influence of metoclopramide and propantheline through the transport velocity, which corresponds to the expected effect of these drugs on gastric emptying.

The uncertainty of the parameter estimates is low (coefficient of variation mostly less than 25%). For the model that fits the data best (IG absorption with D/v optimised) the coefficients of variation of all parameters, except CL/F are somewhat higher than for the other models (about 40%). This is accompanied by a strong correlation between these estimates (>0.95) that was not found for the other models. This is presumably caused by the scaling of the dispersion coefficient D to the transport velocity, v. While providing a better simultaneous description of the three PK curves, scaling results in an intrinsic correlation between the parameters.

The differences in the estimated absorption parameters (Table 1) have a distinct effect on the derived cumulative absorption profiles. Table 2 shows the times of the absorption percentiles for the four different models. There is a considerable difference in the computed moments in time at which a certain fraction was absorbed. In general, the first-order model without lag time shows a very early onset of the absorption, which is in correspondence with the observation that the model overestimates the concentrations before the maximum concentration is reached (Fig. 2). Additionally, for this model the 90 absorption percentile occurs much later than for the other three models: for the delayed absorption it occurs at an unrealistically long time of 13 h. The absorption percentile times of the first-order model with lag time and the two IG-absorption models correspond quite good for the upswing. However, for the first-order model with lag time, there is the limitation of the sudden start of absorption at the lag time (0.3 h), whereas for the IG-absorption model, cumulative absorption rises continuously from the time of administration, therefore providing a much more realistic estimate for the lower-absorption percentiles. The IG-absorption model with D/v optimised is the only model that predicts a relatively short absorption tail for the delayed absorption case (90 percentile at 7.3 h).

Table 2 Derived absorption percentiles, following four different models for paracetamol absorption in a 22-year-old man.
Full size table

4. Discussion and conclusions

There has been considerable debate on the derivation of the IG function from the underlying partial differential equation, the convection-dispersion equation (Hisaka and Sugiyama, 1999; Roberts et al., 2000). Hisaka and Sugiyama (1999) have pointed out the importance of the proper initial and boundary conditions. A concentration upper-boundary condition is incorrect, since it cannot adequately control the mass-exchange at the boundary. Instead, the proper upper-boundary condition should preserve continuity of mass. The lower-boundary condition relates to the local conditions at the receiving site. The total mass balance that is commonly used at the absorption site in PK models is, however, not very informative for specifying this lower-boundary condition. The commonly used IG function relates to the solution of the flux-averaged concentration with an instantaneous injection as the upper-boundary condition and the lower-boundary condition specified in Eq. (11). The upper-boundary condition therefore preserves continuity of mass (Weiss et al., 1997). The lower-boundary condition that relates to the IG function assumes that the resident concentration gradient is zero at infinite distance.

The application of the IG function to the paracetamol data show that the IG function can adequately describe the upswing of the concentration versus time curve. This confirms results obtained in earlier studies (Weiss, 1996; Weiss et al., 1997). The function is particularly interesting when abundant data is available before the occurrence of the inflection point in the measurements. In such cases the use of the first-order model frequently yields a mismatch between the model-fit and the observations. In drug development, the property of the IG-input function to describe an inflection point may be of crucial importance when quantifying and comparing moments of absorbed amount of drug derived from the concentration data. When deriving the absorption rate from concentration data, using the first-order model, the bias of the model fit inevitably propagates to the calculated fraction of absorption. This is particularly important for the development of drugs where the time of the intended effect is crucial, such as for analgesics, sleepinducing drugs and drugs used in the management of migraine attacks. In these cases one of the aims may be to optimise the onset of the effect by controlling the oral absorption rate. An accurate assessment of the absorption rate is then required to compare clinical trial results of new drugs with existing reference drugs.

Several alternative approaches for describing the absorption rate have been proposed (Piotrovskii, 1987; Tatsunami et al., 1998; Higaki et al., 2001; Lansky and Weiss, 2003; Zhou, 2003). In comparison with the other approaches, the IG function is of interest when transport through the GI tract limits the absorption rate. We have shown that the influence of metoclopramide and propantheline on paracetamol absorption could be modelled with the IG function by varying the transport velocity. This directly reflects the effect of metoclopramide and propantheline on gastric emptying. The convection-dispersion equation that forms the basis for the IG function has many other solutions for different types of boundary conditions and coordinate systems (Carslaw and Jaeger, 1959; Crank, 1975) that may be of future use in pharmacokinetic research.