Abstract
We show that the damping of plasmons in metallic nanoparticles highly exceeds that caused by scattering of electrons on defects, phonons, and other electrons and on boundaries of particles. The radiation losses in far-field zone due to the Lorentz friction is especially high at nanometre scale of metal confinement (e.g. attains the maximum at ca. 100 nm diameter of particle, Au in vacuum). This causes a different e-m response of such size structures in comparison to conventional solution of Maxwell-Fresnel equations using the bulk dielectric function for metal. The strong discrepancy occurs also if plasmons are coupled in near-field zone to nearby-located absorbing medium, e.g. semiconductor substrate. This coupling cannot be accounted for by classical electrodynamic treatment (e.g. by numerical solution of Maxwell equations by finite element method for differential equation solution) and needs the application of quantum Fermi golden rule to estimate plasmon damping and related modifications of dielectric functions both of metallic nanoparticles and of absorbing medium. Similarly, the perfect cancellation of radiative losses of plasmon-polaritons in metallic nano-chains is beyond classical Maxwell equation modelling, as it reveals the perfect vanishing of Lorentz friction losses in chain segments by radiative contribution from other segments in near-, medium- and far-field zones. This demonstrates that nano-plasmonic effects cannot be reliably numerically modelled using material parameters from conventional packets referred to optical constants measured in bulk.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Collective excitations of local charge density in conductors called plasmons were studied since the beginning of the XX century within the classical Maxwell electrodynamics. The Fresnel equation for the boundary problem between metal and dielectric allowed for the determination of light scattering and absorption in metal when photons incident from the dielectric side [1,2,3]. To solve such a problem the dielectric functions for both materials need to be known in advance, however. For a metal the dielectric function has been proposed by Drude upon the Lorentz model [1],
where \(\omega _p=\sqrt{\frac{e^2 n}{\varepsilon _0 m}}\) (e and m are the charge and mass of an electron, respectively, \(n=N/V\) is the concentration of free electrons in metal, \(\varepsilon _0\) is the dielectric constant) is the volume plasmon frequency in bulk metal and \(\gamma\) is the damping of this plasmon. In bulk metal \(\gamma \sim \frac{v_F}{2 \lambda _b}\), where \(v_F\) is the Fermi velocity of electrons and \(\lambda _b\) is the mean free path of electrons limited by scattering of them on admixtures and crystalline defects, on phonons and on other electrons [4]. Taking an advantage of the decomposition of plane wave of incident photons in the basis of spherical functions, it is possible to solve the Maxwell-Fresnel equation for metallic small spherical particles in an analytical manner (the so-called Mie solution in the form of series, generalised next to Gans solution for a spheroid) [5, 6]. For an arbitrary shape of the frontier between metal and dielectric the solution of differential Maxwell equations with boundary conditions by finite element method gives also a numerical effective solution (e.g. within the popular system Comsol Multiphysics®).
Nevertheless, in the case of metallic nanoparticles the damping in Drude-type formula (1) conventionally assumed as [4, 7,8,9]
where a is the nanoparticle radius and C is the constant of unity order to account type of electron scattering on nanoparticle boundary, occurs highly underestimated, as it neglects the radiation losses due to the Lorentz friction [10] in the case of a single particle in dielectric surroundings or losses due to the coupling of plasmons to absorbing nearby medium (like semiconductor substrate). The related corrections are especially large in the case of the nano-scale of metallic particles and cannot be accounted for by the modelling of the dielectric function (1) using experimental data for \(\gamma\) taken from measurements in bulk (or in thin layer geometry). In the present paper we emphasise the significant difference between damping of plasmons at nano-scale in comparison to bulk case [8, 9, 11, 12], which changes the dielectric function of Drude-type (1) and modifies the numerical classical simulations using dielectric functions as prerequisites. Especially large difference occurs between the simulation of photo-effect mediated by plasmons in metallic nanoparticles deposited on a semiconductor substrate without and with inclusion of the corrections to damping of plasmons [10]. In this case the modification concerns also the dielectric function of a semiconductor substrate, which is different if coupled to plasmons in metallic nanoparticles with respect to its form measured in bulk and separately [13]. In the following paragraphs we will address to the problem of damping of surface plasmons in metallic nanoparticles in the framework of random phase approximation (RPA) used to describe plasmons in bulk metal by Pines and Bohm [14,15,16], suitably generalised to confined nanoparticles.
Damping of Plasmons in Metallic Nanoparticles
Damping of Plasmons Due to the Lorentz Friction
To describe dynamics of plasmons in a metallic system of nanometre size one can adopt the RPA microscopic quantum approach to electron dynamics. This method has been originally proposed by Pines and Bohm in 1952 to describe a volume plasmon in bulk metal [16]. This quantum approach emphasises the role of electron repulsion in the creation of high energy collective excitation, \(\hbar\omega _p=\hbar\sqrt{\frac{e^2n}{\varepsilon _0 m}}\sim 10\) eV, called as volume plasmon in bulk metal (the large energy in the range of ultraviolet is estimated for typical free electron concentration in metals, being of order of the Avogadro number per cm\(^3\)). In infinite bulk system the positive jellium is perfectly cancelled by the zero \(\textbf{k}\) wave-vector (momentum if multiplied by Planck constant \(\hbar\)) mode of electron fluctuations, which simplifies Heisenberg dynamic equation for local charge fluctuations [16]. In a finite system, the momentum is not a good quantum number and Fourier components do not display charge fluctuation modes. For spherical symmetry one must use another basis of functions — spherical and Bessel functions. RPA is still possible, though it is much more complicated [10]. Instead of a single volume plasmon mode \(\omega _p\) in bulk, in a spherical nanoparticle there occur two branches of plasmonic excitations — the volume and surface ones. The volume modes correspond to charge density oscillations along the sphere radius \(r<a\) (a is the radius of a nanosphere),
whereas the surface oscillations at \(r=a\) can be represented by only locally 2D modes [10],
where n is the uniform equilibrium density of electrons, \(j_l(\xi )=\sqrt{\frac{\pi }{2\xi }}I_{l+1/2}(\xi )\) is the spherical Bessel function, \(Y_{lm}(\Omega )\) is the spherical function, \(\Omega\) is here the spherical angle, \(\omega _{li}= \omega _p\sqrt{1+\frac{x_{li}^2}{k^2_{TF}a^2}}\) are the frequencies of electron volume self-oscillations, \(k_{TF} = \sqrt{\frac{6 \Pi{ne}^2}{\epsilon_F}}\) is the reciprocal of the Thomas–Fermi radius (\(\epsilon_F\) is the Fermi energy), \(x_{li}\) are the nodes of the Bessel function \(j_l(\xi )\) numbered with \(i=1,2,3\dots\), \(k_{li}=x_{li}/a\), \(\omega _{l0}=\omega _p\sqrt{\frac{l}{2l+1}}\) are the frequencies of electron surface self-oscillations, \(A_{lmi}\) and \(B_{lm}\) are amplitudes of modes (constants), a is nanosphere radius (for more detail and the derivation cf. [10]). Remarkably, the volume plasmon frequencies in confined systems are larger than \(\omega _p\) in bulk, while the frequencies of surface plasmons are lower than \(\omega _p\). In noble metals these surface plasmon frequencies in nanoparticles fall onto a visible part of the e-m spectrum, which allows for optical applications.
The sketched above structure of plasmons displays only the ideal undamped case. Both electron scattering and their Lorentz friction contribute to plasmon damping. For a most important dipole mode \(l=1\) of surface plasmons in metallic nanosphere the full RPA dynamic equation including damping has the form [10],
where \(\omega _1=\frac{\omega _p}{\sqrt{3}}\) is the Mie frequency, c is the light velocity, \(\textbf{D}\) is the dipole of surface plasmon with \(l=1\), and \(\frac{1}{\tau _0}\) is given by Eq. (2). The last term with third order time derivative is the Lorentz friction term [2, 3] — this term causes an essential inharmonicity of plasmon oscillations. One can solve this equation analytically in the Fourier domain \(\sim e^{i\Omega t}\), and \(Re\Omega =\omega\) gives the self-frequency of dipole surface plasmon, whereas \(Im \Omega =\frac{1}{\tau }\) is its damping rate,
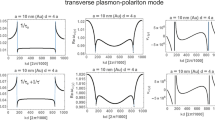
The functions \(\omega\) and \(\frac{1}{\tau }\) (in dimensionless units, i.e. divided by \(\omega _1\)) are plotted in Fig. 1 versus nanosphere radius a.
Real and imaginary parts of the solution of Eq. (5), i.e. the self-frequency and the damping rate of dipole mode of surface plasmon resonance in a metallic nanoparticle (Au), given by Eq. (6) versus radius of the nanosphere a (\(\frac{1}{\tau }\) and \(\omega\) in units of \(\omega _1\)). The resonances in vacuum (\(\varepsilon =1\)) and in dielectric surroundings with \(\varepsilon =2\) are compared. \(\frac{1}{\tau _0}\) lowering with a acc. to Eq. (2) is also plotted in the left panel
From Fig. 1 (and from the solution (6)) we see that the scattering of electrons (\(\frac{1}{\tau _0}\) which lowers with a) is important for plasmon damping for \(a<10\) nm, whereas for larger nanoparticles the damping of dipole surface plasmon is dominated by the giant Lorentz friction — it attains its maximum at ca. \(a\simeq 57\) nm (Au in vacuum) and lowers to the again small value at bulk.
Plasmons are not derived from Maxwell equations, they can be determined via the quantum RPA technique (originally developed for bulk metal by Pines and Bohm [14,15,16] and next generalised for nanoparticles [17]). Earlier, the single volume mode for plasmon in bulk metal occurs in the Lorentz-Drude dielectric function (1) [1] and the surface plasmons were identified for a spherical metallic particle by Mie and can be also found for irregular particle by numerical solution of Maxwell equations for a boundary problem, but with dielectric functions of both bordering media assumed as prerequisites. This makes room for phenomenology, in particular for modelling of Drude-type function [4, 7,8,9]. Knowing that the plasmon oscillations are not harmonic ones, as proved above (which does not satisfy assumptions for the oscillatory Lorentz model of dielectric function [1]) and that the imaginary part of this function is strongly different in nanoscale of confinement in comparison to bulk metal, one can use this information to improve the Drude-type function modelling. In the case of a metallic nanoparticle in a dielectric medium, the inclusion of Lorentz friction improves the agreement of Mie plasmon resonance (as well as of numerical solutions of Maxwell equations for plasmons) with the experimental observations, as is summarised in the Appendix.
Similar corrections to the dielectric functions of metallic nano-components with plasmons coupled to absorbing medium (e.g. a semiconductor substrate on which metallic nanoparticle is deposited) occur even stronger than that caused by the Lorentz friction and also cannot be accounted for via the solution of Maxwell equations for a boundary problem, unless microscopic quantum type corrections are taken into account with regard to plasmon damping change and simultaneous change of the dielectric function of absorbing subsystem (semiconductor). The significance of these corrections to numerical classical simulations of such system operation will be illustrated in the following paragraph.
Damping of Plasmons Due to Their Coupling in Near-Field Zone with Absorbing Substrate
In the case when plasmons from a metallic nanoparticle are coupled in the near-field zone with some nearby-located absorbing medium, then the damping of plasmons surpasses even the Lorentz friction. This effect is impossible to be accounted for by the solution of Maxwell-Fresnel equation and needs using quantum methods. Let us consider an example — the metallic nanosphere deposited on the semiconductor substrate. In the metallic nanoparticle the dipole surface plasmon oscillates as induced by external photons of light. The oscillating dipole induces in turn the electric and magnetic field around the particle in near-, medium- and far-field zones [2, 3]. The Fourier components of the electric \({\textbf{E}_{\omega }}\) and magnetic \({\textbf{B}_{\omega }}\) fields induced in the distance \(\textbf{R}\) from the centre of considered nanosphere with the dipole of surface plasmon oscillating with the frequency \(\omega\), have the form,
and
(\(\varepsilon\) is the dielectric permittivity, for simplicity sake assumed 1 here) where terms with denominators \(R^3\), \(R^2\) and R refer to near-, medium- and far-field zones, respectively. In the case of the spherical symmetry, the dipole of plasmon is considered as pinned to the centre of the nanosphere, \({\textbf{D}}={\textbf{D}}_0 e^{-i\omega t}\). In Eqs. (7) and (8) we used the notation for the retarded argument, \(i\omega \left( t-\frac{R}{c}\right) =i\omega t -i k R\), \(\hat{\textbf{n}}=\frac{\textbf{R}}{R}\), \(\omega =ck\), momentum \(\textbf{p}=\hbar \textbf{k}\), c is the light velocity. Because we consider the interaction with a closely adjacent layer of the substrate semiconductor, the terms with denominator \(R^3\) (near-field zone) are of importance (the magnetic field disappears and the electric field is of the form of a static dipole field in this zone [3]). Therefore the related perturbation potential added to the Hamiltonian of the semiconductor band electron system attains the form,
The term \(w^{+}=\left( w^{-}\right) ^{*}=\frac{e}{\varepsilon R^2} \frac{e^{i\alpha }}{2i}\hat{\textbf{n}}\cdot \textbf{D}_0\) describes emission, i.e. the case of our interest.
According to the Fermi golden rule scheme, the interband transition probability induced by plasmons from metallic nanoparticle is proportional to,
where the Bloch states in the conduction and valence bands are assumed as planar waves (for simplicity), \(\Psi _{\textbf{k}}=\frac{1}{(2\pi )^{3/2}}e^{i\textbf{k}\cdot \textbf{R}-i E_{n(p)}(\textbf{k})t/\hbar }\), \(E_p(\textbf{k})=-\frac{\hbar ^2 k^2}{2\,m^*_p}-E_g,\; E_n(\textbf{k})=\frac{\hbar ^2 k^2}{2\,m^*_n}\) (indices n, p refer to electrons from the conduction and valence bands, respectively, \(E_g\) is the forbidden gap).
The matrix element,
can be found analytically by a direct integration [10], which gives the formula (\(\textbf{q}=\textbf{k}_1-\textbf{k}_2\)),
Next we must sum up over all initial and final states in both bands. Thus, for the total interband transition probability we have,
where \(f_1,f_2\) assign the temperature dependent distribution functions (Fermi-Dirac distribution functions) for initial and final states, respectively. For room temperatures \(f_2\simeq 0\) and \(f_1 \simeq 1\), which leads to,
After some also analytical integration in the above formula, we arrive at the expression,
according to assumed band dispersions, \(m_n^*\) and \(m_p^*\) denote the effective masses of electrons and holes, \(\mu =\frac{m_n^* m_p^*}{m_n^* +m_p^*}\) is the reduced mass, the parameter \(\xi =\frac{\sqrt{2(\hbar \omega -E_g)(m_n^* +m_p^*)}}{\hbar }\). In limiting cases for a nanoparticle radius a, we finally obtain,
With regard to two limiting cases, \(a\xi \ll 1\) or \(a\xi \gg 1\), \(\xi =\frac{\sqrt{2(\hbar \omega -E_g)(m_n^* +m_p^*)}}{\hbar }\), one can notice that for larger nanospheres, e.g. with \(a>10\) nm, the second regime holds.
Assuming that the energy acquired by the semiconductor band system, \(\mathcal{{A}}\), is equal to the output of plasmon oscillation energy (resulting in plasmon damping), one can estimate the corresponding damping rate of plasmon oscillations. Namely, at the lowering in time plasmon amplitude \(D_0(t)=D_0 e^{-t/\tau '}\), one finds for a total transmitted energy,
where \(\tau '\) is the damping time-rate, \(\beta\) accounts for losses not included in the model, especially to reduce the energy transfer for a realistic deposition type on the top of the semiconductor layer instead of the fully embedded case. Comparing the value of \(\mathcal{{A}}\) given by the formula (17) with the energy loss of damping plasmon estimated in [17] (the initial energy of the plasmon oscillations which has been transferred step-by-step to the semiconductor, \(\mathcal{{A}}=\frac{D_0^2}{2\varepsilon a^3}\)), one can find,
By \(\frac{1}{\tau '}\) we denote here a large damping of plasmons due to energy transfer to the semiconductor, which highly exceeds the internal damping, characterised by \(\frac{1}{\tau _0}\), due to scattering of electrons inside the metallic nanoparticle [17] (\(\frac{1}{\tau _0}\ll \frac{1}{\tau '}\)).
For example, for nanospheres of Au deposited on the Si layer we obtain for Mie self-frequency \(\omega =\omega _1\),
for light(heavy) carriers in Si, \(m_n^*=0.19(0.98)\;m\), \(m_p^*=0.16(0.52)\;m\), m is the bare electron mass, \(\mu =\frac{m_n^* m_p^*}{m_n^*+m_p^*}\) and \(E_g=1.14\) eV, \(\hbar \omega _1=2.72\) eV. For these parameters and nanospheres with the radius a in the range of 5–50 nm, the lower case of Eq. (19) applies (at \(\omega =\omega _1\)). The parameter \(\beta\) fitted from the experimental data [17, 18] equals to ca 0.001.
Damping of plasmons given by Eq. (18) is greater than the damping caused by electron scattering and even by the Lorentz friction (radiation to far-field zone without absorbing medium presence). This is an exceptional situation when the absorbing medium (semiconductor in this case) in the near-field zone, in a quantum way takes the energy of plasmons and transfers it to its own electron system — hence, it changes not only the dielectric function of the metal nanoparticle, but also of semiconductor substrate, if they are mutually coupled. When one accounts both corrections, then the system simulations significantly change in comparison to conventional numerical modelling using dielectric functions for the metallic components and the semiconductor separately.
Some examples in Figs. 2 and 3 illustrate this discrepancy. The details of the numerical simulation which is illustrated in Figs. 2 and 3 are listed in [19] — in short, the elementary cell for solution of Maxwell equations for multi-boundary system by finite element method (using software of Comsol) is a square plaquette with a single spherical Au nanoparticle with radius a deposited on a thick Si layer in the centre of the cell with width \(\Lambda\), the periodic Floquet conditions are imposed to simulate distribution change of nanoparticles on semiconductor (Si) substrate with varying planar concentration (via changes of \(\Lambda\)) or change of total mass of metal (by changing a at \(\Lambda = 3a\)); mutual interaction of particles from distinct cells is neglected; simulation by finite element method of Maxwell equation solution for incident vertically from above e-m planar wave (for more detail of simulation and for complete results cf. [19]). The cell size is assumed to be \(\Lambda = 3a\) in the simulation shown in Fig. 2 (i.e., constant ratio of the cell size and of particle radius for varying particle radius). In Fig. 3 the size of metallic nanoparticles is constant and \(\Lambda\) is changing, which simulates varying nanoparticle concentration. The discrepancy caused by the negligence of the damping contribution (right panels in both figures) in comparison to the properly corrected dielectric functions by damping factors (left panels) is evident and reaches ca. 90 % of the total plasmonic effect. Thus, we can conclude that conventional numerical simulations of plasmonic photo-effect can be misleading if the damping effects of plasmons are neglected.
The periodic model in Comsol of metallic nanoparticles deposited on semiconductor substrate. (A, B) The absorption enhancement in the Si substrate as the function of the wavelength of incident electromagnetic wave for varying radius of metallic nanoparticles. (C, D) The efficiency rate growth as a function of the wavelength of incident electromagnetic wave for varying radius of nanoparticles. (A, C) The results obtained in the model using modified \(\varepsilon ^{''}(\omega )\) — the damping part of the dielectric functions of nanoparticle and semiconductor. (B, D) The results obtained in the model using non-modified dielectric functions taken from the measurement in bulk and separate subsystems [11, 13]. The calculation was made for metallic nanoparticle (MNP) arrays with the period equal \(\Lambda = 3a\) and the radius of MNPs \(a=20,\;25,\;30,\;35,\;40,\;45,\;50,\;55,\;60\) nm, the dashed line — without MNPs [10, 19]. in Fig. 3
The periodic model of metallic nanoparticles deposited on semiconductor substrate in COMSOL simulation. (A, B) The enhancement of the light absorption in the Si substrate as the function of the wavelength of incident electromagnetic wave for various size of the unite cell \(\Lambda\). (C, D) The efficiency enhancement of the system as a function of the wavelength of incident electromagnetic wave. (A, C) The results obtained in the model using the dielectric functions of the metal and semiconductor modified by plasmon damping contribution (the energy leaving plasmons incomes to the semiconductor substrate). (B, D) The results obtained in the model using non-modified dielectric functions measured in bulk [11, 13]. The calculations was made for MNPs of radii \(a=40\) nm and for the array period \(\Lambda =90,\;100,\;110,\;120,\;160,\;200,\;240\) nm describing the lowering of the nanoparticle concentration, the dashed line — without MNPs [10, 19]
Some quantum effects in metallic nanoparticles have been studied formerly, including the decay of plasmons into high energy hole-electron pairs (the so-called Landau damping of plasmons) [20,21,22]. This effect is, however, not large and is of some importance in ultra-small clusters, with \(a<5\) nm [22], and can be neglected for medium size nanoparticles with \(a\in (10,100)\) nm. Another approach to quantum corrections is linked with hydrodynamic meso-scale non-local formulation of the e-m response (for recent review cf. [23, 24]) — these effects cause some corrections (blueshift in surface plasmon resonance) with maximum at \(a\simeq 3\) nm [25] and opposite to redshift caused by electron spill-out at this scale of confinement. All these effects are low at higher size of nanoparticles with \(a>10\) nm and can be neglected in comparison to giant increase of plasmon damping induced by the Lorentz friction in nanoparticles in dielectric surroundings or by coupling of plasmons in their near-field zone with an absorbing medium (like in the case of a semiconductor substrate). The latter effect is purely quantum and can be accounted for by the Fermi golden rule and turns out even stronger than that due to the Lorentz friction [10].
Damping of Plasmon-Polaritons
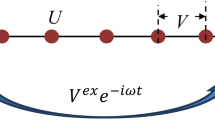
Let us consider collective surface plasmon oscillations synchronised along an equidistant chain of metallic nanospheres — as shown in Fig. 4.
The dipole of surface plasmon in a particular nanosphere induces the electric and magnetic field around the sphere according to Eqs. (7) and (8). These fields induce the oscillation of electrons in nearest and next-nearest neighbouring spheres in the chain. In the result the collective synchronised oscillations of dipoles in all segments of the chain can be organised in the form of a wave-type propagation due to the periodicity. Such a collective excitation is called plasmon-polariton [26,27,28,29,30]. Segments in the chain can be numbered by integers. The equation for the surface plasmon oscillations on the l-th sphere is as follows (instead of Eq. (5)),
where first term of the r.h.s. in Eq. (20) describes the dipole-type coupling between nanospheres (including time retardation, \(v=\frac{c}{\sqrt{\varepsilon }}\) is the light velocity in the surrounding medium), and the next one corresponds to the contribution to plasmon attenuation due to the Lorentz friction. The index \(\alpha\) denotes polarisations, longitudinal \(\alpha =z\) and transverse \(\alpha =x(y)\), with respect to the chain orientation (assumed in the z direction). According to Eq. (7), we have,
the magnetic field (8) is small and negligible here in comparison to the electric one [2, 3].
Due to the periodicity in the chain, the wave-type solution of Eq. (20) can be assumed,
This is equivalent to the Fourier picture of Eq. (20). As dipoles are localised on nanospheres in their centres, the system is discrete, similar to the case of phonons in a 1D crystal. One can thus apply the discrete Fourier transform (DFT) with respect to the positions, whereas the ordinary continuous Fourier transform (CFT) with respect to time. DFT is defined for a finite set of numbers, so we can consider the chain with \(2N+1\) nanospheres, i.e. the chain of length \(L= 2Nd\). Thus, for any discrete characteristics \(f(l),\;\;l=-N,...,0,...,N\) of the chain, like a selected polarisation of dipole distribution, one deals with the DFT picture,
where \(k=\frac{2\pi }{2Nd}n,\; n=0,...,2N\). This means that \(kd\in [0,2\pi ]\) due to the periodicity of the equidistant chain with the separation between nanosphere centres equal to d. On the whole system, the Born–Karman boundary condition is imposed, resulting in the above form of k. In order to account for the infinite length of the chain, one can take the limit \(N\rightarrow \infty\), which causes that the variable k is quasi-continuous, but still \(kd\in [0,2\pi ]\). Thus, one arrives at the Fourier picture of Eq. (20), DFT for positions and CFT for time,
with:
To solve Eq. (24) one must find \(Re\omega\) (\(\omega\) is complex, in general), which would give self-frequency of plasmon-polariton mode for each k, and \(Im \omega\), which would determine the damping of this k mode.
The direct calculation of the functions \(ImF_z(k,\omega )\) and \(Im F_{x(y)}(k,\omega )\), which correspond to the radiative damping for the longitudinal and transverse plasmon-polariton polarisations, respectively, gives,
for \(0<kd\pm \omega d/v<2\pi\). The property (26) means that plasmon-polariton does not lose energy via radiation — the strong Lorentz friction losses at each nanosphere (the first term in \(ImF_{\alpha }(k,\omega )\)) is perfectly balanced by energy influx from other spheres in the chain. The result is exact and can be verified analytically by application of the following sums to Eq. (25), [31],
The absence of the e-m signature of plasmon-polariton kinetic in the metallic nano-chain makes such metallic nanostructures ideal waveguides for signals for plasmon-opto-electronics [10, 30], when losses are only caused by scattering of electrons at oscillations in particular segments of the chain. Note, however, that the property (26) is out of reach for numerical simulations with predefined dielectric functions with optical constants from bulk, as it requires the inclusion of large plasmon damping due to the Lorentz friction in all nano-segments of the chain (taken into account in (25) by first terms in the imaginary parts for both polarisations).
If, however, the metallic nano-chain is embedded in or deposited on some absorbing medium (like a semiconductor substrate), then the coupling of plasmons in spheres of the chain in the near-field zone to the band electrons in the absorbing nearby-located system causes energy transfer (possible to be accounted for by Fermi golden rule), which increases plasmon-polariton non-radiative damping [32].
Conclusion
We demonstrated that the damping of plasmons in metallic nanoparticles highly exceeds that caused by only scattering of electrons in metal on admixtures, crystal lattice imperfections, on phonons and other electrons and on particle boundaries. The radiation in far-field zone due to the Lorentz friction of oscillating charges at the scale of nanometres for metal confinement occurs as the much more efficient channel for energy losses of plasmons. For dipole mode of surface plasmons the maximum of its damping including Lorentz friction losses is at ca. \(a= 57\) nm for nanosphere radius (Au in vacuum) and is at this particle size two orders of magnitude greater than that caused by electron scattering only. For ultra-small metallic clusters, with \(a<6\) the Lorentz friction damping practically disappears, because of a too small number of electrons in a cluster. For larger than the extremal size, the Lorentz friction losses also monotonically diminish with growth of a.
Similarly in the case when plasmons in metallic nanoparticles couple in near-field zone to some absorbing system (like semiconductor substrate), when the energy outflow to such a system highly increases damping of plasmons, which exceeds even the Lorentz fiction losses to far-field zone at dielectric surroundings of the metallic nanoparticles. For plasmon mediated photo-effect, the channel of energy transfer from incident photons to semiconductor band system via plasmons in metallic nanoparticles deposited on the semiconductor substrate, exceeds by more than 10 times the absorption strengthening due to electric field concentration in vicinity of nanoparticle curvature (the classical contribution to plasmon photo-effect possible to be assessed by solution of Maxwell-Fresnel problem). The damping of plasmons coupled to some absorber can be accounted for by the Fermi golden rule. This coupling is purely quantum behaviour, not accessible to Maxwell electrodynamics. Thus, the simulations of nano-plasmonic effects using conventional numerical finite element methods of solution of Maxwell equations for a boundary problem may be confusing if utilise the conventional packets with optical data for system components (for a metal antenna and absorber) referred to their bulk properties. To avoid errors the damping of plasmons and related changes of dielectric functions of nano-scale metallic antennas and absorbers must be accounted for as prerequisites before numerical classical modelling of nano-plasmonic phenomena. The discrepancy between simulations with and without radiative and quantum contributions to plasmon damping, may reach one order of the magnitude of the experimentally measured quantities, like plasmon induced efficiency growth in the case of nano-plasmonic photovoltaic effect. This concerns also various popular studies of nano-plasmonic improvement of sensors or catalysts, which also must be examined from the point of view of plasmon damping channels modifying the dielectric functions for components of coupled binary systems. The damping of plasmons in nano-scale must be taken into account in dielectric functions of coupled subsystems before classical simulations. The negligence of radiation and quantum induced damping of plasmons in the nano-scale of metal confinement, causes a significant discrepancy between classical simulations and experimental measurements of plasmon mediated effects. Thus classical simulations utilising as prerequisites optical data referred to measurements in bulk, must be treated with care. Typical antenna-reactor (absorber) configurations in plasmon assisted effects must be always examined with regard to the sensitivity of optical material parameters versus the nano-scale of confinement and plasmon damping contribution. To the class of such systems belong not only plasmonic photovoltaic solutions but also a broad range of by plasmon improved sensors, actuators or catalysts.
The same problem occurs for plasmon-polaritons — collective plasmon oscillations synchronised in metallic nanoparticle arrays. In the case of a linear equidistant chain of metallic nanoparticles such a synchronisation of plasmons in segments of the chain takes place via dipole coupling between segments, which results in the wave-type kinetics of the plasmon-polariton conditioned by the chain periodicity. Surprisingly, the strong Lorentz friction damping of plasmons in each metallic nanoparticle completely disappears in the chain, because at plasmon-polariton kinetics, exactly the same energy as is lost due to the Lorentz friction in a particular nanoparticle is perfectly balanced in it by the energy influx from other segments in the chain via dipole coupling. The result is exact and proved analytically, but is out of reach for numerical simulations of plasmon-polaritons if the dielectric function for metal components is taken in the form as in bulk without Lorentz friction damping of plasmon. This perfect cancellation of radiative losses for plasmon-polaritons in nano-chains agrees with experiments and can serve as the test for numerical studies of plasmon-polaritons.
Data Availability
All data are available within the article.
References
Bohren CF, Huffman DR (1983) Absorption and scattering of light by small particles. Wiley, New York
Jackson JD (1998) Classical electrodynamics. John Willey & Sons Inc., New York
Landau LD, Lifshitz EM (1973) Field theory. Nauka, Moscow
Vollmer M, Kreibig U (1995) Optical properties of metal clusters. Springer Ser Mat Sci 25
Mie G (1908) Beiträge zur optik trüber medien, speziell kolloidaler metallösungen. Ann Phys 330(3):377–445
Gans R (1912) Über die form ultramikroskopischer goldteilchen. Ann Phys 342(5):881–900
Kolwas K, Derkachova A (2013) Damping rates of surface plasmons for particles of size from nano-to micrometers; reduction of the nonradiative decay. J Quant Spectrosc Radiat Transf 114:45–55
Link S, El-Sayed MA (1999) Size and temperature dependence of the plasmon absorption of colloidal gold nanoparticles. J Phys Chem B 103:4212
Sönnichsen C, Franzl T, Wilk T, von Plessen G, Feldmann J (2002) Plasmon resonances in large noble-metal clusters. New J Phys 4:93
Jacak WA (2020) Quantum nano-plasmonics. Cambridge University Press, Cambridge, UK
Johnson PB, Christy R-W (1972) Optical constants of the noble metals. Phys Rev B 6(12):4370
Link S, El-Sayed MA (2000) Shape and size dependence of radiative, non-radiative and photothermal properties of gold nanocrystals. Int Rev Phys Chem 19:409
Aspnes D, Studna A (1982) Dielectric functions and optical parameters of Si, Ge, GaP, GaAs, GaSb, InP, InAs, and InSb from 1.5 to 6.0 eV. Phys Rev B 27:985
Pines D, Bohm D (1952) A collective description of electron interactions: II. Collective vs individual particle aspects of the interactions. Phys Rev 85:338
Pines D, Bohm D (1953) A collective description of electron interactions: III. Coulomb interactions in a degenerate electron gas. Phys Rev 92:609
Pines D (1999) Elementary excitations in solids. ABP Perseus Books, Massachusetts
Jacak J, Krasnyj J, Jacak W, Gonczarek R, Chepok A, Jacak L (2010) Surface and volume plasmons in metallic nanospheres in semiclassical RPA-type approach; near-field coupling of surface plasmons with semiconductor substrate. Phys Rev B 82:035418
Schaadt DM, Feng B, Yu ET (2005) Enhanced semiconductor optical absorption via surface plasmon excitation in metal nanoparticles. Appl Phys Lett 86:063106
Kluczyk K, David C, Jacak J, Jacak W (2019) On modeling of plasmon-induced enhancement of the efficiency of solar cells modified by metallic nano-particles. Nanomaterials 9:3
Brack M (1993) The physics of simple metal clusters: Self-consistent jellium model and semiclassical approaches. Rev Mod Phys 65:667
Ekardt W (1985) Size-dependent photoabsorption and photoemission of small metal particles. Phys Rev B 31:6360
Weick G, Ingold GL, Jalabert RA, Weinmann D (2006) Surface plasmon in metallic nanoparticles: Renormalization effects due to electron-hole excitations. Phys Rev B 74:165421
Stamatopoulou PE, Tserkezis CH (2022) Finite-size and quantum effects in plasmonics: Manifestations and theoretical modelling. Opt Mater Express 12:1869
Mortensen NA (2021) Mesoscopic electrodynamics at metal surfaces. Nanophotonics 10:2563
Kluczyk K, David C, Jacak W (2017) On quantum approach to modeling of plasmon photovoltaic effect. J Opt Soc Am B 34:2115
Pitarke JM, Silkin VM, Chulkov EV, Echenique PM (2007) Theory of surface plasmons and surface-plasmon polaritons. Rep Prog Phys 70:1
Citrin DS (2005) Plasmon polaritons in finite-length metal-nanoparticle chains: The role of chain length unravelled. Nano Lett 5:985
de Abajo FJG (2010) Optical excitations in electron microscopy. Rev Mod Phys 82:209
Brongersma ML, Hartman JW, Atwater HA (2000) Electromagnetic energy transfer and switching in nanoparticle chain arrays below the diffraction limit. Phys Rev B 62:16356
Maier SA (2007) Plasmonics: Fundamentals and applications. Springer, Berlin
Gradstein IS, Rizik IM (1962) Tables of integrals. Fizmatizdat, Moscow
Jacak W (2019) Nonradiative energy losses of plasmon-polariton in a metallic nano-chain deposited on a semiconductor substrate. Plasmonics 14:465
Jacak W, Krasnyj J, Jacak J, Gonczarek R, Chepok A, Jacak L, Hu D, Schaadt D (2010) Radius dependent shift of surface plasmon frequency in large metallic nanospheres: Theory and experiment. J Appl Phys 107:124317
Funding
The paper has been supported by Polish NCN project P.2018/31/B/ST3/03764.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to this work.
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix. Size Dependence of Mie Resonance
Appendix. Size Dependence of Mie Resonance
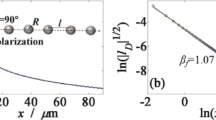
The original formulation [1, 5] gives the Mie frequency independent of the sphere size, \(\omega _1=\frac{\omega _p}{\sqrt{3}}\) in the simplest case, which does not meet with experimental observations. For ultra-small clusters some radius dependence can be introduced by the dependence of the volume plasmon frequency \(\omega _p\) on the electron density n (\(\omega _p\sim \sqrt{n}\)) and by the accounting for dilution of electrons caused by the spill-out. The resulting redshift of Mie resonance agrees with observations for extremely small nanoparticles, where the spill-out is important [20]. For larger nanospheres this correction disappears as spill-out starts to be unimportant for \(a>3\) nm. Nevertheless, for the range \(a\in (5,75)\) nm (for Au in vacuum) a strong size dependence of the surface plasmon resonance is observed clearly beyond the simplest version of the Mie approach. Moreover, at ca. \(a \sim 12\) nm (Au in vacuum) the cross-over in the size dependence of the resonance frequency is observed. To cope with this problem some artificial corrections to the Mie approach have been proposed. To explain the cross-over in the size dependence of the experimentally observed redshift of plasmon resonance in metallic nanoparticles with growing nanosphere radius, two regimes of the Mie theory were introduced [12]: the intrinsic size effect (for \(a<20\) nm, for Au) and the extrinsic one (for \(a>20\) nm). The intrinsic size effect is referred to the dipole approximation of the Mie response, when other multipole contributions are neglected. Simultaneously, the electron scattering energy dissipation has been included in the dielectric function (with the damping rate defined by Eq. (2)) which gives \(\sim \frac{1}{a}\) redshift of the dipole Mie resonance due to \(\sim \frac{1}{a}\) contribution of the scattering on nanoparticle boundary. For larger nanospheres (approximately for \(a>20\) nm, for Au) when in experiment it is observed the resonance redshift rising with a growth, the extrinsic mechanism is introduced in the Mie theory [8, 12]. The latter corresponds to the inclusion of the multipole response mixing and the corrections for the pole of dipole response component. To obtain a coincidence with the experimentally observed size effect in the redshift of plasmon resonance in larger nanospheres the radiation corrections to the dielectric function have been introduced proportional to the number of electrons, thus \(\sim a^3\) [7]. This overestimates, however, the radiative damping for radii \(>30\) nm (Au).
This phenomenological modelling upon the Mie approach gives the cross-over in the surface plasmon resonance from \(\frac{1}{a}\) to \(a^3\) upon the dipole approximation only (by modifying the metal dielectric function). The frontier between the dipole and multipole limits is not sharply defined and multipole corrections occur gradually with stronger intensity for larger nanoparticles. The Lorentz friction induced radiation losses strongly contribute to plasmon energy dissipation for \(a>12\) nm (for Au in vacuum). Thus for nanospheres with radii of order of 5–10 nm the Mie approach gives a reasonably intrinsic size effect neglecting the Lorentz friction losses. It is, however, not true at \(a\sim 15\)–25 nm or at larger scale for the radius. For such radii the radiation losses dominate plasmon damping. This was not included in the conventional Mie theory upon the intrinsic size effect. The accurate irregular size effect of plasmon damping caused by the Lorentz friction (cf. formula (6)) well explains the experimentally observed irregular (i.e. not proportional to \(a^3\)) size effect for the redshift. Therefore the Mie approach must be modified by (6) instead of the incorrect \(a^3\) contribution to the dielectric function. This strongly modifies the dipole contribution in the Mie response in consistency with observations up to \(a\sim 60\) nm (Au in vacuum) without any multipole contributions. The latter start to be important for radii \(a>60\) nm (Au) significantly exceeding the previously suggested limiting of 20 nm as the onset of the extrinsic regime [7, 8, 12]. This agrees better with the observations — the multipole contribution for \(a>60\) nm (Au) results in the deformation and larger broadening of the extinction features no longer allowing a Lorentzian form (the higher energy quadrupole assistant broad peak occurs first at smaller wavelength in association to the dipole peak broadened and redshifted by the Lorentz friction). In the experiment it is visible for Au (at 75 nm) [9, 33].
As was previously shown [10] the \(\sim a^3\) growth of the irradiation induced damping of plasmons, phenomenologically accounted for in the Mie theory, must quickly saturate. Thus, the inclusion of the exact form of the Lorentz friction damping rate (as given by Eq. (6)) into the modelled dielectric function for nano-systems (needed in Mie theory and especially important in its regime for the intrinsic size effect) is the significant correction of the Mie approach. The intrinsic Mie regime with inclusion of the Lorentz friction can be extended to larger radii (up to ca. 60 nm, for Au) where the extrinsic multipole effect starts to contribute with gradually growing intensity for higher radii, but up to 60 nm the extrinsic effect rather weakly mixes with the saturation and lowering of the damping rate due to the Lorentz friction.
The multipole corrections cannot be avoided for radii \(a>60\) nm. The deformation of the Lorentzian shape describing the extinction features is accompanied by their significant broadening, for Au observed at \(a> 70\) nm. However, in the radius window 10–60 nm (for Au) the dipole approximation is sufficient to explain the observed irregular size effect of plasmon resonance, provided the accurate Lorentz friction contribution (6) to dipole plasmon damping is included.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Krzemińska, Z., Jacak, J.E. & Jacak, W.A. On Damping of Plasmons and Plasmon-Polaritons in Metallic Nanostructures and Its Influence onto Numerical Simulations. Plasmonics 18, 1211–1222 (2023). https://doi.org/10.1007/s11468-023-01838-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11468-023-01838-5