Introduction

Magnetometers are the key elements for the measurement of magnetic fields and magnetic dipole moments of magnetic materials. The methods for measuring a sample's magnetic moment can be divided into two groups: those that use magnetic induction caused by stray fields in the sample and those whose optical properties are dependent on the sample's intrinsic magnetic moment. For the first category currently, the broadly used techniques with the highest sensitivity are vibrating sample magnetometry (VSM) [1] and the superconducting quantum interference device (SQUID) [2]. These measure the magnetic moment of bulk samples and thus depend on sample volume.

On the other hand, to directly examine the surface magnetic moment, the most commonly used technique is the magnetooptical Kerr effect (MOKE) [3], which uses light as a measuring probe. As opposed to the magnetic induction methods, the traditional MOKE setups include the possibility of imaging small magnetic regions at the micron and submicron scales. The sensitivity of this technique is limited to a very thin surface layer as a consequence of a narrow penetration depth of the incident light (few nanometers for most metals). Because of the low signal to noise ratio for weakly magnetic materials, this technique can only be used on a limited number of sample types.

Plasmon resonance comes as an interesting alternative to amplify the MOKE signal. The interaction of electromagnetic fields with electron charges at a metal–dielectric interface leads to surface plasmon polariton (SPPs) waves. These are the result of the coupling of the parallel component of the incident light wave vector to the frequency and linear momentum of electrons’ collective oscillations at the metal–dielectric interface.

This leads to giant electromagnetic plasmon fields in the surroundings. It has been widely demonstrated that these giant fields enhance the MOKE signal of nanostructures [4,5,6,7,8,9].

A common approach to accomplish this is by intercalating a ferromagnet between two metals in a metal/ferromagnet/metal trilayered structure.

Until today, most experimental work in this direction has been carried out exciting SPPs using a grating [10,11,12] or a prism in attenuated total reflection (ATR) condition in the so-called Kretschmann-Raether configuration [13, 14].

The enhancement of the magnetooptic signal is usually achieved in a prism/metal/ferromagnet/metal/dielectric (P/M/F/M/D) layered structure where the prism has a high refractive index while the dielectric has a low refractive index. Here, the ferromagnetic layer provides the magnetooptic activity while the noble metal delivers stronger resonant plasmonic properties facilitating plasmons to be excited at the M/D interface. This layer arrangement corresponds to the Kretschmann-Raether configuration [13, 14], in which the dielectric, usually air, is last in the structure. However, for versatile magnetometry and sensing applications, magnetic samples come as separate entities; therefore, a total separation of the sample from the plasmonic structure is required.

In the M/F/M structure, the fact that the ferromagnet is placed between two metals makes it physically impossible to separate it from the structure. Furthermore, the total thickness of the M/F/M structure is limited to the evanescent wave penetration depth (~ 100 nm for pure silver); otherwise, plasmons cannot be excited at the M/F interface. Consequently, the ferromagnet thickness is also constrained by this limitation. As a result, Kretschmann-Raether’s configuration is unsuitable for practical applications such as magnetometers.

In the present work, following a pending patent [16] where a P/D1/M/F/D2 structure is used instead, we demonstrate a separation between magnetic sample and plasmonic structure is in principle possible using the so-called Otto configuration [15]. Here, an air gap is used as first dielectric (D1) between the prism and the metal layer where the SPP´s are excited.

Nonetheless, in this scenario, the effective refractive index of the structure is modified with each sample. This can be overcome when the first dielectric thickness is variable. Indeed, employing air as a low refractive index dielectric (D1) permits an easy variation of the air gap distance and thus tunes the effective refractive index of the structure. This way, although different magnetic samples bring variations in the plasmon resonance and TMOKE signal, the optimum resonance of the structure can be found by slightly modifying the angle of incidence and the dielectric thickness of the device.

Device Architecture and Theory

In 1968, Otto described a method for exciting SPPs waves (later modified by Kretschmann). The basic Otto structure consists of a prism/air gap/metal structure, where the prism is used to couple light with a thin metallic layer beneath the air gap. Provided that the angle of incidence has reached the attenuated total reflection (ATR) condition and is greater than the critical angle, the evanescent wave travels across the air gap. Finally, when the evanescent wave, with exponential decay, reaches the metal/air interface SPPs waves get excited. The fact that the Otto configuration includes an air gap permits tunability of the resonance characteristics [17]. Given the practical difficulties that come with having an air gap to our knowledge, there are only a few works in the Otto configuration that deal with magneto plasmonics. The first one was a theoretical proposal of a double layer dielectric and ferromagnetic metal [18] and experimental proof [19]. Later on, using gratings the Otto configuration was employed in references [10, 11] to characterize an ultrathin magnetic film for applications in waveguides. In all these works [10, 11, 18, 19], the sample was always part of the structure and the dielectric thickness was fixed in each structure. On the other hand, in the current study, we tuned the dielectric thickness using air as the dielectric (D1) in order to improve the plasmon resonance.

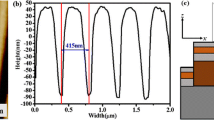
As the first step to demonstrate the usage of the Otto configuration and tunability of the plasmon resonance given a variable air gap, we studied the effective structure prism/Air (~ 255 nm)//Ag (20 nm)/Co (10 nm)/Si (substrate) as depicted in Fig. 1a. Here, the double backslash indicates the prism/Air (~ 255 nm) is physically separated from the Ag (20 nm)/Co (10 nm)/Si (substrate) structure, i.e., in the Otto configuration. As we explain in “Optical and magneto-optical characterization,” the air gap of ~ 255 nm is the result of adjusting the distance between the prism and Ag surfaces, to obtain the maximum TMOKE signal and thus tuning the plasmon resonance.

Fig. 1
figure 1

Enlarged schematic illustration (not-to-scale) of the studied structure, with prism and sample; a prior coupling the sample to the prism; b after the sample is coupled to the prism (prism diameter ~ 2.8 cm) in the Otto configuration where the effect of the press is exemplified; c direct TMOKE configuration (light shining directly on the sample); and d top view of the sample; Ti frame (inverted U shape) on top of Ag/Co bilayer, on a silicon substrate. The air gap between the Ag and prism surfaces is achieved by the Ti frame, which separates the prism and the Ag/Co bilayer. e Theoretical simulations illustrate the effect of changing the gap distance between the values of 400 nm, 255 nm and 200 nm. In the actual experiment, this is achieved by applying pressure on the sample using the press or screw exemplified in b

Full size image

For convenience, the air gap between the prism and the Ag is achieved by a standard optical lithography techniques to fabricating a U shape frame of Ti (thickness ~ 500 nm), on top of the Ag layer [Fig. 1d]. As explained in the next section, the air gap distance can be reduced by applying pressure. By experimenting with advanced lithographic techniques, it may be feasible to engineer a Ti frame/Ag (20 nm) structure directly on top of the prism, leaving the Co (10 nm)/Si (substrate) segregated from the plasmonic resonance device. However, to simply investigate the device architecture in the Otto configuration, such more complex fabrication process was not necessary.

The metallic layers were grown on silicon substrate deposited by e-gun evaporation under high vacuum (HV) conditions. The base pressure was better than 2 × 10−6 Torr, and the evaporation pressure was less than 7 × 10−6 Torr. Each layer thickness was monitored during growth, by quartz balance, with a resolution better than 0.1 Å.

To study the angular dependence of the reflectance of the system, the prism was mounted onto a central rotating automated stage (goniometer) with a high resolution of better than 1 mrad, allowing the variation of the angle of incidence with a P polarized laser (532 nm).

To enhance the magnetooptical signal of the samples, separated a distance from the plasmonic device, we use the transverse magnetooptic Kerr effect (TMOKE). In this configuration, the magnetic field is applied parallel to the plane of the structure and perpendicular to the plane of incidence. Details of the system can be found in reference [8].

When this configuration satisfies the total reflection condition at the Prism/Air interface; i.e., for angles greater than the critical angle, the evanescent field extends along the Air gap with exponential decay. The evanescent wave has an associated wave propagation constant parallel to the Prism/Air interface \({K}_{ev}=\frac{\omega }{c}\sqrt{{\varepsilon }_{p}}\mathrm{sin}\theta\), where \({\varepsilon }_{p}\) denotes the dielectric function of the prism. When evanescent field crosses the air gap and reaches the noble metal, at the resonance condition matching the propagation constant of surface plasmons, i.e., \({K}_{ev}={K}_{SP}\), surface plasmons are excited at the Air/metal interface [20,21,22]. This produces electric fields of three or four orders of magnitude higher that extend perpendicular to the metal surface and penetrate the thin noble metal layer to finally reach the magnetic Co sample, leading to the enhancement of the MOKE signal. Here, we observe a strong signal enhancement close to seven-folds with respect to the sample signal in the absence of plasmonic excitation.

The relation between frequency and wave vector (dispersion relation) is unique for the system configuration. For example, for an Air/Metal semi-infinite interface the dispersion relation is given by the expression \({K}_{SP}=\frac{\omega }{c}\sqrt{{\varepsilon }_{m}{\varepsilon }_{d}/{(\varepsilon }_{m}+{\varepsilon }_{d})}\) where \({\varepsilon }_{m}\) and \({\varepsilon }_{d}\) are the dielectric constants of the metal and dielectric medium respectively. For the case of magnetic samples, instead of having a dielectric constant, we have a dielectric tensor that describes the MO activity. This can be characterized by different geometries responsible for the magnetooptic Kerr effect (MOKE). For the present investigation, we have focused on the transversal configuration, i.e., the magnetization (along the y axis) perpendicular to the xz-plane of incidence or TMOKE. Here, the dielectric tensor of the ferromagnetic layer is described by

$${\varepsilon }_{m}=\left(\begin{array}{ccc}{\varepsilon }_{xx}& 0& {-g}_{y}{M}_{y}\\ 0& {\varepsilon }_{yy}& 0\\ {g}_{y}{M}_{y}& 0& {\varepsilon }_{zz}\end{array}\right)$$
(1)

This dielectric tensor depends on magnetization \(({M}_{y})\), the magnetooptical \({g}_{y}\) factor (that depends on the material, the incident frequency and temperature). For the present investigation, the magnitude for the off-diagonal terms used for Cobalt in the simulations is |\({g}_{y}{M}_{y}\)|= 0.28 + 0.14*i. The diagonal terms \({(\varepsilon }_{xx},{\varepsilon }_{yy},{\varepsilon }_{zz})\) consider the merely optic response of the system. Given that the dispersion relation \({K}_{SP}\) explicitly depends on the dielectric tensor \({\varepsilon }_{m}\), it is possible to obtain a connection between wave vector \({K}_{SP}\) and magnetization \({M}_{y}\) that permits control over the plasmonic properties of the structure employing an external magnetic field. In magnetic transversal geometry, the magnetooptic signal consists of a change in the reflected intensity as a function of magnetization. In this way, the T-MOKE signal is defined as

$$\frac{\Delta R}{R}=\frac{R\left(+M\right)-R\left(-M\right)}{R\left(0\right)}$$
(2)

where \(R\left(\pm M\right)\) is the reflectivity in the positive/negative saturated magnetization state, and \(R\left(0\right)\) the reflectivity in the absence of magnetization. However, we can define the T-MOKE signal as the change in reflectivity under magnetization inversion

$$\Delta R=R\left(+M\right)-R\left(-M\right)$$
(3)

This eliminates the artificial enhancement result of the minimum close to plasmon resonance [6,7,8]. For the theoretical analysis of the anisotropic layered structures, we used numerical calculations by the scattering matrix method [23] to compute the optical and magnetooptical response of the multilayer structures. The refractive index of the prism/glass–substrate system was experimentally measured by a Brewster-angle experiment giving a value of 1.448, while the air refractive index was taken as 1. Given that is very difficult to obtain experimentally the exact thickness of the native SiO2 oxide layer on top of Si substrate, right at the measurement spot, we obtained it by fitting our experimental data to theory. This way we found that an oxide thickness of roughly 215 nm on top of Si provides a better match of our experimental data.

As we will discuss in the next section, in the experiment (Fig. 1), we change the gap distance between the prism/air interface and the Ag surface, where plasmons will be excited, by applying pressure on the sample.

Using the transfer method approach, which is the product of transmission and propagation matrices in each of the mediums, we can analyze the effect of changing the gap distance (dielectric thickness). Once the evanescent wave propagates across the dielectric medium D1, the diagonal terms of the propagation matrix P1, contemplate the effect of changing the dielectric thickness \({d}_{1}\) and the propagating wave angle \({\theta }_{1}\) in that medium;

$${P}_{1}=\left[\begin{array}{cc}{e}^{-i{\varphi }_{1}}& 0\\ 0& {e}^{i{\varphi }_{1}}\end{array}\right]$$
(4)
$${\varphi }_{1}=\frac{2\pi }{\lambda }{n}_{1}{d}_{1}Cos({\theta }_{1})$$
(5)

Additionally, analyzing the transmission term of the transfer method, one finds that the effect of the variation in dielectric thickness is competing with propagating wave angle (which also depend on the index of refraction of adjacent mediums). Therefore, the reflected intensity depends in a nonlinear way on the angle of incidence and dielectric thickness.

Indeed, simulations (Fig. 1e) illustrate the effect of changing the gap distance between the values of 400, 255, and 200 nm on reflectivity and TMOKE signal. These clearly show the resonance quality as well as the momentum matching condition (angle of minimum reflectivity) strongly depends on the gap distance.

In other words, the spatial phase introduced by the air gap shifts the excitation condition of the evanescent wave impinging on the Ag surface. Because the spatial phase is proportional to the length of the air gap, changing the gap alters the quality characteristic of the plasmon mode excited on the Ag surface.

Optical and Magnetooptical Characterization

As shown in the schematic representation of the studied structure in Fig. 1a, using a mechanical press the Ag (20 nm)/Co(10 nm)/Si (substrate) multilayer is put in contact with the prism, in the Otto configuration, supported on the Ti frame. This leads to an initial air gap of ~ 500 nm, which corresponds to the Ti frame thickness. The pressure applied by the press slightly bends the sample reducing the air gap distance between the Ag layer and the prism. This way is possible to tune the resonance condition until the minimum reflectivity value is found. During the experimental procedure, we look for a minimum reflectivity and maximum TMOKE signal. This is achieved using a press or screw. A schematic representation of the device has been drawn “not-to-scale,” to exemplify the bending effect (Fig. 1b) that the press produces on the layered structure.

The structure was optically and magneto-optically (MO) characterized by angular spectral reflectivity and transverse magnetooptic Kerr effect (T-MOKE) between incident angles of 33° and 65°. This was achieved by adopting a goniometer for the acquisition of the angular spectra reflectivity. The sample was illuminated through a cylindrical glass lens (BK7) by a p-polarized coherent light source of 532 nm wavelength (2.33 eV), while a photodetector collected data from the reflected light. The magnetooptical characterization was done by an alternating magnetic field (B), with an amplitude ~ 15 mT, located in the plane of the sample normal to the plane of incidence. In this way, the magnetization of the sample was along the sample plane. This allows extracting the T-MOKE signal from the changes in the reflectivity of the incident light due to the magnetic state of the sample. We used two methods for extracting small variations in the reflectivity signal; the first one used a Lock-in amplifier in phase with an oscillatory magnetic field. The second method simply uses amplifiers to obtain directly the hysteresis loops. A detailed explanation of these two experimental methods can be found in [8].

During the experiment, we see that mechanically varying the air gap distance provides good tunability of the plasmon resonance where a minimum reflectivity and maximum TMOKE signal is found. Later, for the chosen Ag/Co/Si(substrate) structure, after fitting these data to the theory we found this optimum distance came to be around 255 nm.

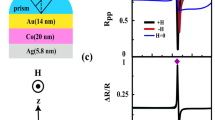
Figure 2 shows the theoretical fit (dash line) and data (solid spheres) obtained from the SPR experiments in the angular reflectivity. Here, the minimum of reflectance is found at around 43°, and the total internal reflection occurs at around 35°.

Fig. 2
figure 2

Angular reflectivity measurement (solid spheres) and theoretical prediction (dash line) for the sample in Otto configuration

Full size image

For the magnetooptical characterization, the first method uses a Lock-In amplifier where its voltage signal was referenced to an AC signal generator, responsible for the external magnetic field. This way the system analyzes just the light intensity variations that are in phase with changes in the magnetic field. The experimental TMOKE signal obtained this way can be found in Fig. 3 (solid spheres). The red dashed line in this graph corresponds to the signal predicted by the theory. Here, the maximum TMOKE signal of ~ 2 ‰, compared to the incident light intensity, is found around 46°.

Fig. 3
figure 3

Transverse magnetooptical measurement (solid spheres) and theoretical prediction (red dash line) for the sample in Otto configuration. For comparison, the black dashed line shows the experimental data using direct illumination in the traditional TMOKE configuration in Fig. 1c

Full size image

Finally, when the prism was completely removed (as in Fig. 1c) and the sample was directly illuminated by the light; i.e., in a traditional transversal MOKE configuration, the direct TMOKE signal was less than 0.1 ‰ as shown in Fig. 3 using black dashed lines.

When we compare this number to the TMOKE signal at 33° ~ 0.3 ‰ (below the total reflection condition in the absence of plasmon resonance), we can see that it is significantly higher. Indeed, this is about 7 times larger. This is comparable with previous works [6, 8, 24], different structures using the Kretschmann-Raether configuration.

Resonance Vs. Traditional MOKE Characterization

The amplification of the MOKE signal in the proposed architecture where the plasmon resonance can be tuned is unmistakably demonstrated by the data shown in Fig. 3.

This constitutes the practical implementation of a plasmon resonance magnetooptical Kerr effect (PRMOKE) in the transverse configuration. However, it is instructional to directly compare the PRMOKE enhancement with the actual hysteresis loops obtained with traditional MOKE. Instead of employing the Lock-In amplifier (first method), a set of electronic amplifiers were used to obtain the hysteresis loops [8]. The MOKE hysteresis loop was taken right after the measurements with the Lock-In amplifier, at the same angle. In the presence of surface plasmons, we observed an augmented hysteresis loop (Fig. 4, blue spheres), with a signal to noise ratio (SNR) ~ 11, in agreement with the previously observed enhancement with the TMOKE signal. Finally, the prism was removed and the light was directly irradiated towards the magnetic sample as shown in Fig. 1c. A smaller hysteresis loop (Fig. 4, red spheres), with a SNR ~ 2.5, was obtained. Given that, in this case, the angle of incidence does not play any role in the MOKE signal, we just took a few measurements at the angle where the maximum TMOKE signal is observed at ~ 46°. The hysteresis loops of these two experiments, shown in Fig. 4, reveal an eightfold increase in TMOKE in the presence of SPR compared to traditional MOKE without the prism. This is a little larger than the enhancement demonstrated with the first method using the Lock-In method; however, this minor increase could be explained by small light intensity losses by the thin Ag capping layer.

Fig. 4
figure 4

Hysteresis loops (TMOKE), taken at 46°, for the sample in presence of SPR (blue spheres) using the Otto configuration [Fig. 1b] and in the absence (red spheres) via direct illumination in traditional MOKE experiments [Fig. 1c]

Full size image

Summary and Conclusions

In this work, we have obtained enhancement of the TMOKE signal of the effective structure prism/Air (~ 255 nm)//Ag(20 nm)/Co(10 nm)/Si (substrate). This corresponds to the Otto configuration where surface plasmons have been excited in the Air/Ag interface across the air gap. In Otto configuration, the sample is irradiated with a plasmon field, which substitutes the direct laser illumination used in traditional MOKE. Here, the TMOKE signal shows an enhancement ~ 7 times larger, in the presence of surface plasmons, translating to an increase of the TMOKE signal of about ~ 2 ‰ with respect to the incident light. This is comparable with our previous work [6], but this time in Otto configuration.

The present work demonstrates the enhancement of the TMOKE signal of a magnetic sample that is physically separated from the plasmon resonance. The separation between the plasmon source and multilayered sample is achieved by an air gap.

Given that its principle of operation does not depend upon the magnetooptical (MO) geometry, this arrangement could be easily applied to other MO geometries such as polar or longitudinal MOKE, which generally can be implemented with greater sensitivity.

This development constitutes the practical implementation of a plasmon resonance magnetooptical Kerr effect (PRMOKE) in the transverse configuration with resonance tuning capabilities. Here, the Otto configuration allows magnetic samples to be separated by the plasmon resonance device, eliminating the necessity of optically coupling the samples to the prism, with the following advantages. Given that light could be absorbed by opaque samples or dispersed by rough or granular surfaces [22] away from the detector, one of the most significant advantages of PRMOKE over standard MOKE is that the plasmon field generated at the metal-air interface substitutes the laser light used in traditional MOKE. Consequently, a continuous and smooth sample is not required in the Otto configuration shown here. This envisages the possibility of using this technique in optically opaque samples, or with granular characteristics. Unlike a laser, the plasmon field is not restricted to a single spot, favouring dissipation in a larger area and thus reducing local heat production. Finally, the penetration depth of the plasmonic field into the sample may be tuned by controlling the distance between the plasmonic device and the sample. This provides a unique method of probing the magnetization’s depth profile. These characteristics make this development ideal to investigate different magnetic materials. This includes materials that cannot be deposited in transparent substrates. This could find applications in magnetic sensors and magnetometers.