Introduction

Metasurfaces, a type of ultrathin flat structured interface with varying profiles of subwavelength nanostructure, have attracted great attention for their enormous potential in the development of new planar optical devices [1,2,3,4,5]. The strong interaction of light with these nanostructures, which act as plasmonic scatterers (also called nanoantennas), leads to abrupt changes in phase, amplitude, and polarization of the light beam passing through the metasurface. Therefore, complete control over light propagation has been achieved through metasurfaces at the nanoscale. Meanwhile, the use of nanostructure materials makes the metasurfaces more versatile than conventional diffractive, refractive, and reflective optical components, because the shape, dimensions, materials, and mutual arrangement of the nanostructures are more artificially controllable in the desired way. Thus far, studies on metasurfaces have led to a variety of optical applications, such as ultrathin planar lenses [6,7,8], wave plates [9, 10], holograms [11,12,13], broadband optical filters [14], planar retroreflectors [15], vortex generators [16,17,18], and complex color routing [19]. Since the constituent materials of the metasurfaces are at the nanoscale level, the light-nanostructure interactions are closely related to their geometric features, including their shapes and configurations, in addition to their intrinsic optical properties [20]. Observing the near-field distribution around metasurfaces in nanoscopic resolution is the key route to understand the underlying physical mechanism of light-nanostructure interactions and is also crucial to the performance of these novel devices. Especially for specific arrangements of metallic nanostructures on metasurfaces, many novel optical phenomena, such as the photonic spin Hall effect [21,22,23,24,25], anomalous diffraction, and refraction [16, 26, 27], trace to the accurate knowledge of the near-field distribution. In this work, regularly arranged nanoslits (also called metamolecules) on Au films, forming a ring-shaped metasurface, generate different topological charges (q-values) that add a geometric phase in the surface plasmon polariton (SPP) near field under the illumination of circularly polarized light. The scanning near-field optical microscope (SNOM) measurements and theoretical simulations show that with an additional degree of freedom of geometric phases, the excited SPP field modes are tunable by q-values and have an electromagnetic structural character that coincides with the metasurface geometry. Meanwhile, planar chiral features of the nanoslits also greatly affect the SPP near field.

Design Considerations

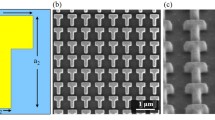
In our designed metasurfaces, two types of specific nanoslits (metamolecules) were perforated in a 150-nm thick gold film, as shown in Fig. 1. One of them has a rectangular shape, called a bar-type, which is 250 nm long and 100 nm wide (Fig. 1a). Others exhibit a Z or \( \overline{Z} \) shape (Fig. 1b), called Z- or \( \overline{Z} \)-type, respectively, which is two bar-type nanoslits (250 × 100 nm2) connected by a shorter nanoslit (50 × 100 nm2). From the point of view of planar structures, the bar-type nanoslit is achiral, while the Z- and \( \overline{Z} \)-type nanoslits are chiral enantiomers that are right-handed and left-handed and are also comparable to the right circularly polarized light (∣σ+⟩) and the left circularly polarized light (∣σ−⟩), respectively. These metamolecules were arranged in the form of a ring, to form a metasurface on a gold film with a certain radius, as shown in Fig. 1c. In this scheme, each metamolecule rotates by an angle θ, depending on the azimuthal angle α, which produces the topological charge (q) of the metasurface, defined as [7, 17]

$$ q=\frac{d\theta}{d\alpha} $$
(1)
Fig. 1
figure 1

a, b Scheme of bar-type and Z- and \( \overline{Z} \)-type nanoslits milled onto Au films, forming the achiral and chiral planar plasmonic metamolecules, respectively. The arrows in b represent the helicity of the corresponding Z- and \( \overline{Z} \)-type nanoslits and the incident light. c Ring-shaped metasurfaces constructed from the bar-type metamolecules (the same for Z- and \( \overline{Z} \)-type). For each metamolecule, the rotation angle is θ, and the azimuthal angle is α

Full size image

When circularly polarized light is incident on the nanoslit metamolecules, excited SPPs can be added to the geometric phase. The electric field of the SPPs can be written as [3]

$$ {E}_{\mathrm{spp}}=\frac{1}{\sqrt{2}}{E}_0\exp \left(\pm jq\upvarphi \right)\left[\begin{array}{c} cosq\varphi \\ {}\sin q\varphi \end{array}\right] $$
(2)

where ±denotes the right (or left) circularly polarized incident light (∣σ+⟩ or ∣σ−⟩), θ = qφ, E0 is the amplitude of the incident light, exp(±jqφ) is the added geometric phase, and \( \left[\begin{array}{c} cosq\varphi \\ {}\sin q\varphi \end{array}\right] \) indicates that the SPP propagation direction is perpendicular to the long axis of the nanoslit.

The bar-type nanoslits exhibit plasmonic resonance at approximately 670 nm in the transmission spectra, as shown in Fig. 2. Obviously, this resonance arises when the polarization of the incident light is perpendicular to the long axis of the slit. When the polarization is parallel to the long axis, the resonance peak occurs at a wavelength of 846 nm. Therefore, rectangular nanoslits are analogues of the polarizer of SPPs at a wavelength of 670 nm. Such anisotropic polarization excitation of SPPs is an establishment requirement for Eq. 2, which is the cause of the generation of geometric phases [3]. For maximum SPP excitation efficiency, the excited light wavelength of 671 nm was chosen in the following experiment.

Fig. 2
figure 2

Transmission spectra of a rectangular nanoslit under illumination of incident light with linear polarization. The angles are located between the long axis of the nanoslit and the polarization of the incident light

Full size image

Figure 3 shows the ring-shaped metasurface structures with a radius of 2.6 μm, constructed from different densities of the bar-type nanoslit metamolecules. At a higher density of 36 metamolecules around the ring circumference [Fig. 3(a1)], the out-of-plane electric field (I⊥) distribution [Fig. 3(a2)] in the SPP near field under illumination of ∣σ+⟩ is close to that of the circular slit (see Fig. S2) due to the strong near-field coupling between the metamolecules. At a lower density of 12 metamolecules [Fig. 3(b1)], they are so sparse that the near-field coupling is very weak, and each metamolecule functions as an individual SPP excitation source [Fig. 3(b2)]. In the SPP propagation, due to the SPP diffusion enlarging, interference occurs in the inner region of the rings. In theory [28], the in-plane component of the SPP electric field has a derivative relationship with the out-of-plane one. There is an obvious difference in the electric field distribution, as shown in Fig. 3(a2, a3, b2, b3); the frequency of the wave peak in the in-plane component of the SPP electric field corresponds to the valley of the out-of-plane one. For our aperture fiber-tip type SNOM detection, the acquired near-field signal is much more sensitive to the in-plane component, because this component corresponds to the conductivity mode in the detected optical fiber [20]. In the following, we offer only the simulation results of the in-plane component of the SPP electric field for comparison with SNOM measurements.

Fig. 3
figure 3

Calculated SPP coupling effects between bar-type metamolecules under illumination of ∣σ+⟩. (a1) The ring-shaped metasurface with a radius of 2.6 μm, composed of 36 nanoslit metamolecules. (a2) The calculated out-of-plane electric intensity (I⊥ = |E⊥|2). (a3) The calculated in-plane electric intensity (I|| = |E|||2). (b1) The ring-shaped metasurface with a radius of 2.6 μm, composed of 12 nanoslit metamolecules. (b2) The calculated out-of-plane electric intensity (I⊥ = |E⊥|2). (b3) The calculated in-plane electric intensity (I|| = |E|||2). The bar at the bottom-right corner of (a1) represents 1 μm, which is applicable to the rest of the frames

Full size image

Results and Discussion

The experimental results of bar-type metasurfaces with different q-values under the illumination of ∣σ+⟩ were presented in Fig. 4. The scanning electron microscope (SEM) images in Fig. 4(a1, b1, c1, d1) show the metasurface structures of q = 1, − 1, 2, − 2, corresponding to the exp(jα), exp(− jα), exp(2jα), and exp(− 2jα) geometric phases of SPP, respectively. Here, the ring radius of 2.6 μm and 36 metamolecules were chosen. Due to the rotation of each metamolecule, the metasurface structures changed from circular symmetry (q = 1) to square (q = − 1), line (q = 2), and hexagon symmetries (q = − 2). When analyzing the near-field intensity in Fig. 4(a2, b2, c2, d2), different SPP modes within the rings can be achieved. Specific near-field interference patterns are circular, square, line, and hexagonal symmetries, arising from the metasurface structural features induced by the q-values. The simulation results [Fig. 4(a3, b3, c3, d3)] are in good agreement with the SNOM measurements. Previous works [29] show that in the metasurface structure of circular slits, the appearance of the geometric phase of SPPs arises from the phase delay, when circularly polarized light rotates around the structure. This is similar to our case where q = 1. In contrast to the circular slit structure, we can obtain any topological charge q-values as the metamolecules rotate, so that the excited SPP geometric phase is tunable. Therefore, different SPP propagation modes can be artificially controlled. In Fig. S3, when the incident light was changed to ∣σ−⟩, the near-field interference patterns are exactly the same as for ∣σ+⟩ illumination, which indicates that the achiral structure of the bar-type nanoslits cannot distinguish the helicity of light.

Fig. 4
figure 4

(a1, b1, c1, d1) Scanning electron microscope images of ring-shaped metasurfaces made of bar-type metamolecules for topological charges q = 1, − 1, 2, − 2, respectively. The radius of the ring is 2.6 μm and the number of metamolecules within the circumference is 36. Under the illumination of ∣σ+⟩, the excited SPP distribution (I|| = |E|||2) for various topological charges was measured by SNOM (a2, b2, c2, d2) and simulated by FDTD (a3, b3, c3, d3). The bar at the bottom-right corner of (a1) represents 1 μm, which is applicable to the rest of the frames

Full size image

For the \( \overline{Z} \)-type metasurfaces, Fig. 5(a1, b1, c1, d1) shows SEM images of q = 1, − 1, 2, and − 2, respectively. Obviously, in comparison with Fig. 4, the symmetry of the metasurfaces was not changed by the replacement of metamolecules. The characteristics of circular, square, line, and hexagonal symmetries remained correspondent to q = 1, −1, 2, and − 2, respectively. Under ∣σ+⟩ illumination, specific near-field interference patterns, SNOM results [Fig. 5(a2, b2, c2, d2)], and the corresponding simulations [Fig. 5(a3, b3, c3, d3)] still maintain the same symmetry as the geometric structures, although the detailed fringes differ significantly from those for the bar-type metasurfaces. Especially notable is that in Fig. 5(a2), almost no SNOM signals can be detected for the q = 1 metasurface, and the corresponding calculated electric filed intensity of Fig. 5(a3) is very weak (quantitatively, approximately an order of magnitude smaller than for other metasurfaces). Referring to previous works [29], in asymmetrical metasurface structures, such as spiral structures, under the circularly polarized light illumination, the excited SPP field is a chiral vortex structure carrying an orbital angular momentum. These \( \overline{Z} \)-type metamolecules, which are planar chiral left-handed structures, can also create a chiral vortex SPP electromagnetic field with circulation around the ring. Because the helicity of \( \overline{Z} \) contradicts the right-handed circularly polarized incident light, near-field destructive interference occurs between the left-handed chiral vortex field and the field with geometric phases, produced by the right-handed circularly polarized light in the metasurface with q = 1. For non-circular symmetric metasurfaces, a complete vortex field could not be formed due to a symmetry effect; then, a complete weakening of the interference could not occur, which was more clearly observed in Fig. 5(b3, c3, d3), manifested in some fringe relics accompanied by main symmetric fringes. However, under ∣σ−⟩ illumination of the q = 1 metasurface, constructive interference occurs due to the identity of the incident light and metamolecules, as shown in Fig. 5(a4, a5), where clear fringes are observed. For other symmetric metasurfaces [Fig. 5(b, c, d)], the structures of the near field of SPPs are similar to those of the bar-type metasurfaces under ∣σ+⟩ illumination, but the detailed interference fringes have changed completely and are distinguished easily. This indicates that for metasurfaces with chiral metamolecules, it is possible to differentiate the helicity of the incident light, which is the appearance of the optical spin Hall effect. It is noted that the results of the Z-type metasurface are completely opposite to those of the \( \overline{Z} \)-type one and are not shown here.

Fig. 5
figure 5

(a1, b1, c1, d1) Scanning electron microscope images of ring-shaped metasurfaces made of \( \overline{Z} \)-type metamolecules for topological charges q = 1, − 1, 2, − 2, respectively. The radius of the ring is 2.6 μm and the number of metamolecules within the circumference is 36. Under the illumination of ∣σ+⟩, the excited SPP distribution (I|| = |E|||2) for various topological charges was measured by SNOM (a2, b2, c2, d2) and simulated by FDTD (a3, b3, c3, d3). When illuminated by ∣σ−⟩, an excited SPP distribution (I|| = |E|||2) for different topological charges was measured by SNOM (a4, b4, c4, d4) and simulated by FDTD (a5, b5, c5, d5). The bar at the bottom-right corner of (a1) represents 1 μm, which is applicable to the rest of the frames

Full size image

Conclusion

In this work, we have established a tunable topological charge on a ring-shaped metasurface, which facilitates significant control over the propagation modes of excited SPPs under the illumination of circularly polarized light. This is due to the fact that, at the nanoscale, regularly arranged metamolecules introduce additional geometric phases in the SPP field, which creates a field exhibiting apparent geometric structural character in accordance with metasurface structures. The exact details of the induced SPP field are also closely related to the planar chiral properties of metamolecules, since the excited source is circularly polarized light that causes geometric phases. Our results may help understand the physical mechanism of light-nanostructure interactions and can pave the way for active control of SPP propagation in near fields. It provides an approach to manipulating the optical field of SPPs in nanoscale and may have potential applications in highly integrated photonic devices and detection of light chirality.

Methods

Figure S1 presents an experimental setup for measuring the near field of surface plasmons. A laser beam of 671 nm was focused on the metasurface from the bottom under normal incidence. The linearly polarized incident light was converted into right-hand (or left-hand) circularly polarized light by using a linear polarizer (P1) and a quarter-wave plate (QWP1). The field distribution of surface plasmons above metasurfaces was carried out using a scanning near-field optical microscope (SNOM, Nanonics MV2000), in the collection mode. The surface plasmon near field was coupled to a Si APD by an optical fiber with an aperture width of 100 nm, in a tip coated with Al. The fiber tip was glued to a tuning fork with a resonant frequency of approximately 32 kHz. The sample-tip distance was kept constant at approximately 10 nm. The samples were perforated using a focusing ion beam in a 150-nm thick gold film evaporated onto a glass substrate. The theoretical simulations were performed using a finite-difference time-domain (FDTD) method. The boundary conditions used is PML (perfect matching layer), the mesh is cuboid, each side of which is smaller than λ/10, usually taken as 5 nm.