Abstract
We investigate the performance of a simple corrugated aperture scanning near-field optical microscope (SNOM) probe with various cladding metals. The probes have only one corrugation, however, they offer increased transmission over both uncorrugated probes and those with many grooves. Enhancement of light throughput results from excitation of surface plasmons at the corrugation at the core–cladding interface. We show how the choice of metal influences radiation properties of grooved probes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Current work on various plasmonic phenomena and nano-optical devices in the submicrometer scale requires characterization capable of analyzing samples at resolution better than a plasmon wavelength. This is achieved by various techniques and of them is the scanning optical near-field microscope (SNOM) [1], which employs probes of two kinds: apertured and apertureless. SNOM applications range from optical imaging of biological samples [2] to measurement of surface plasmon-polaritons (SPPs) [3], nano-scale Raman and IR spectroscopy for chemical analysis [4], optical trapping [5–7] and others. A transmission based SNOM combined with an atomic force microscope has also been employed to probe with single nanometer resolution the field inside an optical microcavity [8].
One significant drawback of high resolution aperture SNOM probes is their low energy throughput. Its origin lies in the fact that narrow cylindrical dielectric waveguides with a metallic coating have a cutoff beyond which only evanescent fields exists. Modern-day apertures are smaller than the cutoff diameter, hence such probes have low transmission, which limits further resolution improvement. Various ideas to improve light throughput of SNOM probes have been suggested. They include modification of the taper angle of probes [9], nanopatterning the aperture area into bow-ties [10] and I-shapes [11] or structuring the core–coating interface to facilitate plasmon excitation [12–14].
Localized nanosources of light may also take the form of apertureless probes in which their apex serves as a scattering and superfocusing center for light impinging onto the tip from the far field [15, 16]. Additionally, such tapered metallic rods focus plasmons on their ends, where the field enhancement increased with a decrease of the apex radius [17]. One solution to the still open question of how to efficiently generate surface waves in such geometries is milling grooves into the metal cones to facilitate conversion [18, 19]. It is also possible to form a standing wave on the nanowire facet to enhance conversion [20]. Other methods for achieving strongly enhanced spots have been proposed in fully metal coated tapered dielectric apertureless probes, where a radially polarized excitation signal couples from the inside of the probe to plasmons on the outside of the metal coating [21–23]. Recently, it has been shown that azimuthal grooves over an arc of 160° enable efficient nanofocusing of linearly polarized light [24]. Conically shaped probes made of nanoparticles have also been investigated for their focusing properties [25].
In this work we simplify our original corrugated probe design [12] by reducing the number of grooves to one. This results from the fact that focused ion beam technology provides one of the best ways of milling grooves into SNOM probes [14, 18] and a reduction in their number will speed up potential fabrication. The role of a groove is to couple light to plasmons on the inside of the probe to enhance energy throughput. Moreover, we carry out a thorough investigation of how transmission and resolution, defined as full-width at half-maximum (FWHM) of probe radiation, depend on various parameters of the groove and on the type of metal coating.
Method of Analysis
Results presented here are calculated using the Finite-Difference Time-Domain (FDTD) method [26]. The considered probes are of cylindrical symmetry, thus we use the Body of Revolution formalism [26] to simplify the computational burden to a two dimensional simulation in the longitudinal and radial directions, as the electromagnetic fields in the azimuthal direction are expanded in a Fourier series and this dependence is analytically expressed in the FDTD equations. We use an in-house code [23] with Drude and Drude–Lorentz dispersion models and a convolution Perfectly Matched Layer [26] to absorb scattered radiation. Use of the FDTD method allows for computation of the whole desired spectrum in one simulation as a result of using an ultrashort pulse as an excitation signal and utilization of the Fourier Transform (FT).
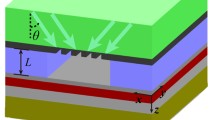
We consider aperture SNOM probes tapered at an angle of 20° with an aperture diameter 2r = 50 nm and made of a dispersionless dielectric with refractive index 1.457. A schematic view of a probe with dimensions not to scale is shown in Fig. 1. The metal coating is of uniform thickness equal to 100 nm, which is larger than for typical SNOM probes, however, this larger value is used to dampen tunneling of light though the coating for metals with smaller losses, e.g. gold. At the core–coating interface we introduce a single corrugation defined by three parameters: length l (not taking into account the rounded corners defined by circles), depth d, and position z defined as distance to the aperture plane. Both l and z are measured along the propagation axis OZ.
Scheme of the analyzed SNOM probe with one groove. The taper angle is 20°, aperture radius r = 25 nm, metal thickness h = 100 nm. The groove is defined by its length l, depth and radius of curvature on either end d, and position z. The metal coating is shown in red, core in blue, and part of the cladding in orange. An ultrashort pulse with a frequency spectrum centered at 599.58 THz with a Gaussian spatial profile is used as an excitation signal. Dimensions are not to scale
Aluminum, copper and gold are used as coating material. The Drude (for Al omitting the third term in Eq. 1) or Drude–Lorentz (for Cu and Au) model are employed to describe their dispersion
with parameters listed in Table 1. The parameters are fitted to data from Johnson and Christy [27] for copper and gold using the Drude–Lorentz model to take into account the change of permittivity due to interband absorption and from Ordal et al. [28] for aluminum using the Drude model for wavelengths λ in the range 400–700 nm. In Fig. 2 we present experimental data points taken from the two papers along with our calculated dispersion curves.
The input field is an ultrashort pulse with a frequency spectrum centered at 599.58 THz, has a Gaussian spatial profile, and is linearly polarized.
Optical Properties of the Probe
Energy throughput and FWHM are two key parameters of aperture SNOM probes that decide on their usefulness. They are evaluated in a plane 10 nm from the aperture where we record the temporal evolution of the fields and via the FT calculate radial profiles in the range of 400–700 nm. In this work we present normalized transmission (used interchangebly with transmission enhancement) \(\tilde{T}|_{\rm met}\) defined as
where \(\left.T_{0}(\lambda)\right|_{\rm met}\) is transmission through an uncorrugated probe, \(\left.T\left(\lambda;l,d,z\right)\right|_{\rm met}\)—transmission through a probe with one corrugation defined by parameters l, d, and z, and met = Al, Cu, Au.
First, we change the groove position z within the range from 300 to 1,400 nm while keeping the other two parameters, length and depth, fixed at 100 and 40 nm, respectively, and in Fig. 3 we present results of these simulations. The transmission enhancement shows high sensitivity to the position of the groove. As its distance z from the aperture plane increases, we observe several distinct transmission bands for all considered metals, however, the maximum amplitude and the wavelength for which it occurs depend on the metal. For aluminum the highest enhancement of 6 occurs for λ = 400 nm, while for copper a seven-fold enhancement at λ = 575 nm is observed and for gold a 33-fold at 555 nm. For Al, the imaginary part of permittivity is the lowest for the shortest wavelengths considered, while for Cu and Au the lowest absorption is for longer wavelengths in the considered wavelength range. The enhancement bands, clearly seen for aluminum coating in Fig. 3a, can be explained in terms of matching the plasmon wavelength to the distance between the groove and the aperture. However, as is for the case of Al, the bands consist of two distinct sub-bands, for example the first one has maxima at z = 400 and 550 nm. The wide bands are the result of the incident light scattering on a groove and converting into plasmons. However, this interaction can be dominant on either end of the groove. In the analyzed cases, the whole groove including its rounded edges is about 190 nm long taking into account the angle of the probe. The excitation efficiency of plasmons is approximately equal at either end of the groove due to groove symmetry. However, those generated closer to the apex will have a smaller distance to propagate towards the aperture than those generated at the far end of the groove and will be less attenuated.
Next, we choose a position for which large enhancement of transmission is observed, in this case z = 500 nm, and keep this value constant for all other simulations. In the second set of calculations, for which d = 40 nm, we assess the impact of groove length on probe transmittance properties. The smallest l is equal to 0 nm, what corresponds to a semicircular groove of radius 40 nm, and the longest groove is 300 nm long, not taking into account the circular edges and taper angle. In Fig. 4 we present the calculated transmission enhancement values. Changing the value of l does not shift the spectral position of the main peak, but affects its intensity. At the same time, for larger l, enhancement bands shift toward longer wavelengths, what is most clearly visible for the Al coating and less so for Cu. In the case of gold, due to the lowest losses the resonance peak is highest of all three metals and it dominates the spectrum. However, faint bands with a positive slope can be observed. Aside from the main enhancement peak, other bands have lower transmission which does not exceed three-fold the throughput of uncorrugated probes. This suggests that the wavelength for which maximum enhancement occurs is determined by the position of the groove and, of course, the dispersion of the metal coating.
The last parameter investigated in this work is the depth of the groove d, which determines how deep, relative to the core–coating interface, the grooves are. Moreover, d also directly determines the radius of the rounded ends of grooves, hence it slightly changes their length l. The results presented in Fig. 5 show how transmission enhancement depends on the wavelength of light and on the depth d. The plots in Fig. 5 are qualitatively similar to those in Fig. 4, suggesting similar physical properties. The maximum enhancement peaks are confined to the wavelengths for which the value of z determines maximum transmission. Changing the depth allows for some tuning of the enhancement value, but not the spectral position.
Increasing energy throughput via grooves will allow for a decrease of aperture diameter, thus resolution improvement, while keeping the energy throughput at levels assuring efficient measurements. However, modeled probes need to offer resolution which is comparable to that of probes without grooves. In Fig. 6 we present calculated FWHMs for probes with one groove as a function of wavelength, position, and, as reference, separated by a white line from the main part of the plot, FWHMs of probes without grooves. In Fig. 6b and c white pixels indicates FWHM values which considerably exceed the maximum value of the scale. In the case of aluminum coating, probes without grooves have an average FWHM (71.4±0.5) nm over the whole wavelength range, while for probes with grooves it is equal (71.5±0.4) nm. Variations from wavelength-to-wavelength of the plot visible in Fig. 6a result from a simple calculation of the FWHM in which it is equal to twice the distance from the axis of the first pixel with intensity half that at maximum. For the other two metal coatings it is not possible to calculate an average resolution, because such a value is without meaning, as FWHM changes considerably as a function of both wavelength, especially for λ > 550 nm, and position z. Moreover, for some parameters it exceeds 250 nm, what is the total extent of the probe in the plane of the aperture equal to twice the metal cladding thickness and aperture diameter. The reason behind slightly increased FWHMs are low dissipative losses in the coating. Because electromagnetic fields are weakly dissipated in both copper and gold in comparison to aluminum for λ > 550 nm, plasmons leak out of the aperture and propagate radially away from it, decreasing resolution for probes with Cu and Au coating, but only for λ > 550 nm. However, this increases the FWHM by about 15 nm, so nowhere near to the value of 300 nm observed for some other groove parameters. Let us note that a large FWHM, thus exceptionally poor resolution, results from higher intensity fields concentrated at the outer rim of the coating than being transmitted through the aperture [29]. The fields at the outside of the metal coating originate from coupling light from the inside of the core to plasmons across the metal. They propagate toward the plane of the aperture, where their amplitude may exceed the amplitude of fields in the aperture, what may happen under one of two conditions. The first is low transmission enhancement on the order of 10%, which is observed in probes with Cu and Au coatings between bands of high transmission for wavelengths larger than 550 nm. The second, which happens only for gold, is observed for λ from 450 to 550 nm for grooved probes with z > 700 nm and for a probe without a groove. In this wavelength range light coupling to plasmons is especially efficient due to momentum matching, so even though energy throughput enhancement is between 0.7 and 1, energy confined to the outside of the coating dominates. For z < 700 nm transmission enhancement is larger than unity and light leaving the clearance of the aperture has greater intensity than the outer plasmons. Hence, for these positions and wavelength range resolution is on the order of 80 nm.
FWHM in nanometers of single groove probes with a aluminum, b copper, and c gold coatings as functions of wavelength and groove position z. Just above the x-axis, separated from the main plot with a white line, is the FWHM of a probe without grooves. Groove depth d = 40 nm and length l = 100 nm. White pixels indicate FWHM exceeding 200 nm
Discussion
A propagating plasmon at a flat dielectric-metal interface cannot be excited by direct illumination, because the free space wavevector k 0 is shorter than that of a surface wave k spp. To overcome this mismatch various methods have been used, e.g. prism coupling or grating coupling. The second makes use of the reciprocal vector of the grating γ = 2π/Λ, where Λ is the lattice period, to shift the wavevector of impinging light to the value of
where ϕ is the angle of incidence, n is the index of refraction, and m is an integer. In the considered case we aim at exciting plasmons at the inner side of the dielectric-metal interface of the probe. Incident light propagates in glass and has a larger wavevector than in free space, but smaller than that of the surface plasmon at the glass-metal interface. The angle of incidence relative to the dielectric-metal interface is 70°. To fulfill Eq. 3 an additional factor coming from the lattice is required. Figure 7 shows the dispersion relation for the wavevector component of incident light k ∥ = nk 0cos(π/9) parallel to the coating and the real part of plasmon wavevectors on a slab of metal k met, where met is Al, Cu or Au. Wavevectors of plasmons at the metal–silica interfaces in the relevant spectral range (430–750 THz) have a similar magnitude for individual frequencies. The major difference results from the change of permittivity due to interband absorption in gold and copper modeled using the Drude–Lorentz model. In addition, Fig. 7 shows the differences between k met and k ∥ , which are a measure of spatial frequency mismatch and must be provided by the groove.
One groove can enable photon-plasmon coupling provided the structure is small enough, which means in terms of Fourier Optics that it has a wide spatial spectrum. This approach gives a way of calculating γ by applying the FT. The groove is modeled by an analytical function consisting of two quarter-circles and a rectangular function of width l = 0, 100, 200 and 300 nm as shown in Fig. 8. We use the Discrete FT to calculate numerically the spatial frequencies that constitute these functions and plot the results at the bottom of Fig. 8. For the missing range of frequencies 1.6 × 105–8 × 105 m − 1 shown in Fig. 7 with dashed lines, the spectra, especially for short grooves, are almost constant, and the only major decrease of 9% is observed for the longest groove l = 300 nm for the largest spatial frequencies. This means that in the whole analyzed wavelength range plasmon generation efficiency is almost uniform, what relaxes experimental accuracy of groove milling, and other effects are responsible for modulation of the transmission spectra. It needs to be stressed, that this conclusion is valid for the considered taper angle and in another probe geometry will need to be revised. In general, for smaller taper angles the Fourier spectra will be more uniform than in the considered case, while for larger taper angles the modulation of the |DFT| shown in Fig. 8b will be greater. In the latter cases plasmon excitation and transmission spectra will greatly depend on the groove geometry.
The groove acts as a scattering center enabling conversion of light to plasmons which increase energy throughput of SNOM probes and this conversion is most effective when the intensity of light at the groove is the greatest. The highest intensity of incident light, where it is squeezed into the narrowest envelope, is before the position of the cutoff diameter. Hence, for a given position of the groove a wavelength exists which has its cutoff in its vicinity. Moreover, the plasmon wavelength needs to match the distance between the groove and the aperture, what ensures that this volume acts as a resonator and can accumulate energy. However, this does not ensure maximum transmission in the whole analyzed parameter range, as with the increase of z the distance between the groove and the aperture increases and losses will rise. Naturally, to properly assess losses the dispersion relation of permittivity must be taken into account. Thus, aluminum coated probes with a groove work best for short wavelengths 410–470 nm and gold and copper coated ones for wavelengths on the longer-wavelength side of the interband absorption, i.e. about 550–600 nm.
The other two parameters of the groove, length l and depth d, are less crucial to spectral tuning of the transmission maximum, but allow for fine tuning its amplitude for selected wavelengths. It is because the groove acts not only as a scaterer, but also as a resonator. Changing its length and depth allows for matching the resonance frequency to that of the incident light, hence amplifying photon to plasmon conversion and increasing throughput.
Resolution offered by aperture SNOM probes, as expected, depends on the aperture diameter and skin depth of the coating, but only for metals which confine light to the core very efficiently. Aluminum, which has been used since the beginning of SNOM, is the best for this application and offers the best and most uniform FWHM of the three analyzed probes. Moreover, Al sticks readily and easily to silica, however, due to high losses, it allows only modest six-fold increase of transmission. Use of other metals for coating decreases resolution by a little, mostly due to an increased skin depth, but it also allows for greater light leakage through the side walls. In the case when light is resonantly coupled from the inside of the core to plasmons on the outside their signal can be comparable to that coming from the aperture clearance, what was observed for gold. However, those metals allow for a larger increase of energy enhancement, as well as overall increased transmission. The key point is that adding the groove does not decrease resolution when keeping the aperture diameter constant. Thus, to increase resolution it is enough to reduce the radius of the aperture. This is made possible by enhanced energy throughput assured by grooves so that this increase counteracts the decrease introduced by shrinking the aperture.
Conclusions
In conclusion, we have presented a thorough numerical investigation of the properties of an aperture SNOM probe coated with various metals and with a single groove to enhance plasmon excitation inside the probe and, by virtue of this, energy throughput. Analysis yielded a possible six-fold increase of transmission for Al coated probes and a larger for Cu and Au, what is in qualitative agreement with numerical and experimental investigations of more complicated probes with a large number of grooves [12–14]. However, the modified probe will be easier to fabricate using focused ion beam milling. The enhancement of energy throughput from adding the groove will counteract the decrease of transmission resulting from decreasing the aperture diameter, that is increasing resolution. We have identified the main mechanism governing increased transmission as matching the position z of the groove to the plasmon wavelength. Other mechanisms, which tune the amplitude of the enhancement, are the position of the groove with respect to the cutoff, groove length and depth.
References
Pohl DW, Denk W, Lanz M (1984) Optical stethoscopy: image recording with resolution λ/20. Appl Phys Lett 44:651–653
Whitesides GM (2003) The ‘right’ size in nanobiotechnology. Nature Biotechnol 21:1161–1165
Klar T, Perner M, Grosse S, von Plessen G, Spirkl W, Feldmann J (1998) Surface-plasmon resonances in single metallic nanoparticles. Phys Rev Lett 80:4249–4252
Stöckle RM, Suh YD, Deckert V, Zenobi R (2000) Nanoscale chemical analysis by tip-enchanced Raman spectroscopy. Chem Phys Lett 318:131–136
Ashkin A (1997) Optical trap and manupulation of neutral particles using lasers. PNAS 94:4853–4860
Klimov VV, Sekatskii SK, Dietler G (2006) Laser nanotraps and nanotweezers for cold atoms: 3D gradient dipole force trap in the vicinity of scanning near-field optical microscope tip. Opt Commun 259:883–887
Yang AHJ, Moore SD, Schmidt BS, Klug M, Lipson M, Erickson D (2009) Optical manupulation of nanoparticles and biomolecules in sub-wavelength slot waveguides. Nature 457:71–75
Hopman WCL, Stoffer R, de Ridder RM (2007) High-resolution measurement of resonant wave patterns by perturbing the evanescent field using a nanosized probe in a transmission scanning near-field optical microscopy configuration. J Lightwave Technol 25:1811–1818
Yatsui T, Kourogi M, Ohtsu M (1998) Increasing throughput of a near-field optical fiber probe over 1000 times by the use of a triple-tapered structure. Appl Phys Lett 73:2090–2092
Murphy-DuBay N, Wang L, Xu X (2008) Nanolithography using high transmission nanoscale ridge aperture probe. Appl Phys A 93:881–884
Tanaka K, Tanaka M, Sugiyama T (2006) Creation of strongly localized and strongly enhanced optical near-field on metallic probe-tip with surface plasmon polaritons. Opt Express 14:832–846
Antosiewicz TJ, Szoplik T (2007) Corrugated metal-coated tapered tip for scanning near-field optical microscope. Opt Express 15:10920–10928
Antosiewicz TJ, Szoplik T (2007) Corrugated SNOM probe with enhanced energy throughput. Opto-Electron Rev 16:451–457
Wang Y, Srituravanich W, Sun C, Zhang X (2008) Plasmonic nearfield scanning probe with high transmission. Nano Lett 8:3041–3045
Novotny L, Hecht B (2006) Principles of nano-optics. Cambridge University Press
Gramotnev DK, Vogel MV, Stockman MI (2008) Optimized nonadiabatic nanofocusing of plasmons by tapered metal rods. J Appl Phys 104:034311
Janunts NA, Baghdasaryan KS, Nerkararyan KhV, Hecht B (2005) Excitation and superfocusing of surface plasmon polaritons on a silver-coated optical fiber tip. Opt Commun 253:118–124
Ropers C, Neacsu CC, Elsaesser T, Albrecht M, Raschke MB, Lienau C (2007) Grating-coupling of surface plasmons onto metallic tips: a nanoconfined light source. Nano Lett 7:2784–2788
Baida FI, Belkhir A (2009) Superfocusing and light confinement by surface plasmon excitation through radially polarized beam. Plasmonics 4:51–59
Chen XW, Sandoghdar V, Agio M (2010) Nanofocusing radially-polarized beams for high-throughput funneling of optical energy to the near field. Opt Express 18:10878–10887
Bouhelier A, Renger J, Beversluis MR, Novotny L (2003) Plasmon-coupled tip-enhanced near-field optical microscopy. J Microsc 210:220–224
Vaccaro L, Aeschimann L, Staufer U, Herzig HP, Dändliker R (2003) Propagation of the electromagnetic field in fully coated near-field optical probes. Appl Phys Lett 83:584
Antosiewicz TJ, Wróbel P, Szoplik T (2009) Nanofocusing of radially polarized light with dielectric-metal-dielectric probe. Opt Express 17:9191–9196
Lotito V, Sennhauser U, Hafner C (2010) Effects of asymmetric surface corrugations on fully metal-coated scanning near field optical microscopy tips. Opt Express 18:8722–8734
Mühlig S, Rockstuhl C, Pniewski J, Simovski CR, Tretyakov SA, Lederer F (2010) Three-dimensional metamaterial nanotips. Phys Rev B 81:075317
Taflove A, Hagness SC (2005) Computational electrodynamics, 3rd edn. Artech House, Norwood
Johnson P, Christy R (1972) Optical constants of the noble metals. Phys Rev B 6:4370–4379
Ordal MA, Long LL, Bell RJ, Bell RR Jr, Alexander RW, Ward CA (1983) Optical properties of the metals Al, Co, Cu, Fe, Pb, Ni, Pd, Pt, Ag, Ti, and W in the infrared and far infrared. Appl Opt 22:1099–1119
Antosiewicz TJ, Szoplik T (2007) Description of near- and far-field light emitted from a metal-coated tapered fiber tip. Opt Express 15:7845–7852
Acknowledgements
This work was supported by the Polish Ministry of Science and Higher Education under the project N N507 445534 and the National Centre for R&D under the project N R15 0018 06. The authors are partners in COST Actions MP 0702 and MP 0803. Simulations were performed in the ICM, University of Warsaw, grant #G33-7.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Antosiewicz, T.J., Wróbel, P. & Szoplik, T. Performance of Scanning Near-Field Optical Microscope Probes with Single Groove and Various Metal Coatings. Plasmonics 6, 11–18 (2011). https://doi.org/10.1007/s11468-010-9163-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11468-010-9163-6