Experimental determination of hypoplastic parameters and cyclic numerical analysis for railway bridge backfills

Abstract

Long integral bridges experience an enhanced cyclic soil structure interaction with their granular backfills, especially due to seasonal thermal loading. For numerical modelling of this interaction behaviour under cyclic loading, it is important to employ a suitable constitutive model and calibrate it thoroughly. However, up to the present, experimental data and calibrated soil models for this purpose with focus on typical well-graded coarse-grained bridge backfill materials are rarely available in the literature. Therefore, one aim of this paper is to present results of a comprehensive cyclic laboratory testing programme on highly compacted gravel backfill material. Based on this, a hypoplastic constitutive model with intergranular strain extension for small strain and cyclic behaviour is calibrated and evaluated against the experimental test data. The soil model’s abilities and limitations are discussed at element test level. In addition, cyclic FE analyses of an integral bridge are conducted with several hypoplastic parameter sets from the literature and compared to the calibrated gravel backfill material. The investigation highlights that poorly-graded sands show significantly smaller cyclic earth pressures compared to well-graded gravels intended for the backfilling of a bridge. The soil structure interaction behaviour is clearly governed by the general soil model stiffness, including the small strain stiffness.

1 Introduction

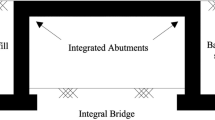
Integral railway bridges have no bearings and a rigid connection of the superstructure and its abutments (Fig. 1a). Consequently, and as illustrated in Fig. 1b, these structures interact strongly with their granular backfills, especially due to seasonal thermal loading and resulting horizontal deformation $\Delta u_x$ of the superstructure. This cyclic soil structure interaction (SSI) leads to a continuous passive mobilization and increase in earth pressure $\sigma _{\rm px,mob}$ during summer and settlement accumulations in the backfill over the bridge’s lifetime [19, 32]. The numerical simulation of this cyclic interaction is still challenging. In particular, the applied constitutive models need to be able to reproduce the cyclic behaviour of the backfill and its increasing densification realistically. This requires a thorough calibration of the soil models based on representative soils with additional consideration of their in situ state (i.e. stress and relative density) and loading conditions.

Granular railway bridge backfills in Germany must be designed with well-graded sand and gravel materials compacted to 100% of Proctor density [11]. Yet so far, experimental 1g- or ng-(centrifuge) tests on the cyclic SSI of integral bridges [19, 24, 32, 52, 57, 59] were exclusively conducted with poorly-graded materials, in most cases fine sands. Additionally, testing and calibration of advanced soil models mainly concentrates on well-known poorly-graded (fine) sands, e.g. in [16, 21, 22, 33, 63, 66]. Calibrated soil model parameter sets for well-graded coarse-grained materials, however, are hardly available, especially for problems of a cyclic nature. In Sect. 3, this lack of research will be demonstrated based on the hypoplastic soil model by von Wolffersdorff [64] with extension for intergranular strain IGS [45]–short Hypo+IGS.

Therefore, in this paper, results of a comprehensive experimental programme [55] on a representative highly densified gravel backfill material are summarized. The testing series consists of several monotonic and cyclic oedometric compression and triaxial tests on cylindrical specimens. Additionally, cyclic triaxial tests on prismatic specimens with Bender-Element and local strain measurements (LDTs) have been conducted to capture the behaviour under small strains. The test results allow a thorough calibration of advanced soil models with focus on cyclic loading, e.g. the cyclic SSI of integral bridge abutments with their granular backfills. In the following, the calibration of the Hypo+IGS soil model is shown in detail. Thereby, this research will contribute a first Hypo+IGS parameter set for a gravel backfill material with explicit focus on the cyclic behaviour. This allows a more realistic SSI analysis of integral bridges. The performance of the derived final parameter set will be discussed based on re-calculations of all executed monotonic and cyclic element tests.

In the end, additional numerical studies on the cyclic SSI of integral railway bridges with different Hypo+IGS parameter sets for the granular backfill will be presented. Several parameter sets from the literature are compared to the calibrated gravel backfill materials. The cyclic lateral stress development on the bridge abutment is evaluated and discussed for different initial densities and bridge lengths.

Fig. 1

(a) Illustration of an integral railway bridge abutment; (b) Cyclic soil-structure interaction mechanism of an integral abutment and its granular backfill [53]; (c) Measurement of the critical friction angle from the inclination of a pluviated cone of the tested gravel material

2 Hypoplastic model with intergranular strain

The hypoplastic model by von Wolffersdorff [64] is formulated in rates of strains and stresses (with no distinction of elastic and plastic strain) and considers soil nonlinearity as well as stress- (barotropy) and density-dependency (pyknotropy). In its general form, it can be expressed in a single tensorial equation, linking the effective stress rate $\varvec{\dot{{\varvec{\sigma }}}}$ with the strain rate $\varvec{\dot{{\varvec{\varepsilon }}}}$ (both second-order tensors):

$$\begin{aligned} \varvec{\dot{{\varvec{\sigma }}}} = \varvec{\textsf{M}}\left( \varvec{{\varvec{\sigma }}},e\right) :\varvec{\dot{{\varvec{\varepsilon }}}} = \left( \varvec{\textsf{L}} + \varvec{\rm{N}} \frac{\varvec{\dot{{\varvec{\varepsilon }}}}}{\Vert \varvec{\dot{{\varvec{\varepsilon }}}}\Vert } \right) : \varvec{\dot{{\varvec{\varepsilon }}}} \end{aligned}$$

(1)

Here, the stiffness tensors $\varvec{\textsf{M}}$, $\varvec{\textsf{L}}$ (fourth order) and N (second order) are functions of the state variables effective stress $\varvec{{\varvec{\sigma }}}$ and void ratio e. The equations for $\varvec{\textsf{L}}$ and N as well as all constitutive relations for the hypoplastic soil model (with IGS extension) are summarized together with the mathematical notations in Appendix A. In total, eight material parameters ($\varphi _{c},\ h_{s},\ n,\ e_{\rm c0},\ e_{\rm d0},\ e_{\rm i0},\ \alpha ,\ \beta$) are required. Herle and Gudehus [27] demonstrated the parameter determination based on standard laboratory tests, which will also be a focus in the following sections. While the model performs well on monotonic loading for granular materials, it shows severe deficiencies on cyclic loading, e.g. an exaggerate ratcheting behaviour and no stiffness increase upon reversal loading [16, 20, 34, 43].

Therefore, Niemunis and Herle [45] proposed an extension of the hypoplastic soil model to improve the small strain and cyclic loading behaviour. They introduced a strain-dependent state variable, the intergranular strain $\varvec{\rm{h}}$ (IGS) that evolves based on the recent strain history and increases the stiffness response in case of a change in the deformation direction. The basic equation of the extended Hypo+IGS soil model can be written as:

$$\begin{aligned} \varvec{\dot{{\varvec{\sigma }}}} = \varvec{\textsf{ M}}\left( \varvec{{\varvec{\sigma }}},\varvec{\rm{h}},e\right) :\varvec{\dot{{\varvec{\varepsilon }}}} \end{aligned}$$

(2)

The evolution law of the IGS rate $\varvec{\dot{\rm{h}}}$ follows [45]:

$$\begin{aligned} \varvec{\dot{\rm{h}}} = \left\{ \begin{array}{lll} \left( \varvec{\textsf{ I}} - \overrightarrow{\varvec{\rm{h}}} \otimes \overrightarrow{\varvec{\rm{h}}} \rho ^{\beta _r} \right) : \varvec{\dot{{\varvec{\varepsilon }}}} &{} &{} \rm{for}\ \overrightarrow{\varvec{\rm{h}}} : \varvec{\dot{{\varvec{\varepsilon }}}} > 0 \\ \varvec{\dot{{\varvec{\varepsilon }}}} &{} &{} {\rm{for}}\ \overrightarrow{\varvec{\rm{h}}} : \varvec{\dot{{\varvec{\varepsilon }}}} \le 0 \end{array} \right. \ \end{aligned}$$

(3)

where $\varvec{\textsf{ I}}$ is the unit tensor, $\overrightarrow{\varvec{\rm{h}}} = \varvec{\rm{h}} / \Vert \varvec{\rm{h}}\Vert$ is the IGS direction, and $\rho = \Vert \varvec{\rm{h}}\Vert / R$ describes the mobilization of the IGS corresponding to the elastic strain amplitude R. At large (monotonic) strains the IGS reaches a fully mobilized state with $\Vert \varvec{\rm{h}}\Vert = R$, while for cyclic loading $\Vert \varvec{\rm{h}}\Vert < R$. In the Hypo+IGS soil model, the stiffness tensor $\varvec{\textsf{M}}$ in Eq. (2) reads:

$$\begin{aligned}&\varvec{\textsf{M}} = \left[ \rho ^{\chi } m_T + \left( 1 - \rho ^{\chi } \right) m_R \right] \varvec{\textsf{L}} \nonumber \\&\qquad + \left\{ \begin{array}{ll} \rho ^{\chi } \left( 1 - m_T \right) \varvec{\textsf{L}} : \overrightarrow{\varvec{\rm{h}}} \otimes \overrightarrow{\varvec{\rm{h}}} + \rho ^{\chi } \varvec{\rm{N }} \otimes \overrightarrow{\varvec{\rm{h}}} &{} \rm{for}\ \overrightarrow{\varvec{\rm{h}}} : \varvec{\dot{{\varvec{\varepsilon }}}} > 0 \\ \rho ^{\chi } \left( m_R - m_T \right) \varvec{\textsf{L}} : \overrightarrow{\varvec{\rm{h}}} \otimes \overrightarrow{\varvec{\rm{h}}} &{} \rm{for}\ \overrightarrow{\varvec{\rm{h}}} : \varvec{\dot{{\varvec{\varepsilon }}}} \le 0 \end{array} \right. \end{aligned}$$

(4)

In this equation, the five additional IGS parameters ($R,\ m_R,\ m_T,\ \beta _r,\ \chi$) determine the influence of the intergranular strain: $m_R$ and $m_T$ are parameters that increase the stiffness for reversal ($\overrightarrow{\varvec{\rm{h}}}: \varvec{\dot{{\varvec{\varepsilon }}}} = -1$) or transversal ($\overrightarrow{\varvec{\rm{h}}}: \varvec{\dot{{\varvec{\varepsilon }}}} = 0$) strain loading, while $\beta _r$ and $\chi$ control the stiffness decay. The calibration of these parameters will be shown in the following sections. For large (monotonic) strains, the tangent stiffness $\varvec{\textsf{M}}$, i.e. the Hypo+IGS model response, corresponds to the one of the basic hypoplastic model according to von Wolffersdorff [64].

Detailed discussions on the general performance of the Hypo+IGS model for cyclic loading, especially in comparison with other advanced soil models, can be found, e.g. in [16, 17, 30, 33, 62, 63].

3 Existing experimental studies and Hypo+IGS parameter sets

In this section experimental studies on the cyclic SSI of integral bridges from literature will be briefly discussed. Additionally, published studies with calibrated Hypo+IGS parameter sets for sands and gravels will be summarized.

Experimental 1g- or ng-(centrifuge) tests have been used by several researcher [19, 24, 32, 52, 57, 59] to examine the cyclic SSI behaviour of integral railway bridges. Table 1 provides an overview of key test conditions of these test series. All test series on granular soils showed a consistent cyclic increase of lateral force $\Delta K_{\rm mob}$ in the abutment’s summer position, as can be seen from the results of 1g-tests in Fig. 2. The increase was most profound in the first 5–20 seasonal cycles, but generally continued at least for the first 100 seasonal cycles. Similarly, a continuous cyclic accumulation of settlements at the backfill surfaces has been reported, which corresponds to an increasing densification. Thus, the 1g- and ng-tests deliver valuable insights into the general cyclic SSI mechanisms of integral bridges. However, these tests also include some major limitations such as the inherent influence of boundary conditions due to the limited test box sizes. Additionally, all tests in Table 1 have been conducted on poorly-graded materials, mostly fine sands. These materials might not sufficiently represent real backfill materials, at least regarding railway backfills in Germany. According to DB Netz AG [11], a granular backfill for railway bridges must be designed with well-graded sands or gravels with less than 5% fine grains $d \le 0.063$ mm. In situ a compaction in layers of 30 cm to 100% of Proctor density $\rho _{\rm Pr}$ is required. By definition in [14], a well-graded material possesses a uniformity coefficient $C_{u}\ge$ 6. The reasons for this requirement in [11] are: Well-graded granular materials allow a higher and easier compaction compared to uniformly graded granular materials. Due to its heterogeneous grain sizes well-graded materials can be compacted to higher packing densities with smaller void ratios in relation to poorly-graded, mono-disperse materials [9, 31]. Empirical investigations, e.g. by Lauer [31], confirm, that the Proctor density $\rho _{\rm Pr}$ of granular soils increases greatly with increasing $C_{u}$. As a consequence well-graded coarse-grained materials are associated with significantly higher stiffness $E_{s}$ [9, 38, 51] and are less prone to settlements compared to uniformly graded materials. Therefore, these materials are more suitable for the design of persistent backfills with minimum deformations [14]. Due to the absence of $1$ $g$- or ng-test results the cyclic SSI behaviour of well-graded backfills will be investigated in the following based on an experimental test series with several monotonic and cyclic element tests. A typical well-graded gravel backfill material will be tested at loading conditions and initial densities similar to in situ conditions for backfills of integral bridges. The test results are a profound base for the calibration of the Hypo+IGS soil model and subsequent numerical analysis on the cyclic SSI of integral railway bridges.

Table 1 Overview of 1g- and ng-level tests from the literature

Fig. 2

Cyclic increase in normalized lateral forces $\Delta K_{\rm mob} = 2\Delta F_x / (\gamma \cdot h^2)$ on the test box front walls in 1g-tests [19, 24]

The calibration of the Hypo+IGS soil model for granular materials and the corresponding experimental testing requirements have been demonstrated by several authors, e.g. [27, 35, 40, 60]. In [27, 40, 48], numerous calibrated hypoplastic parameter sets (without IGS parameters) for granular soils are given. However, fewer fully calibrated Hypo+IGS parameter sets with focus on the calibration of the IGS parameters have been published. In fact, due to a lack of small strain and cyclic test results, in many academic as well as practical studies, e.g. [58, 65], "default" IGS parameters are assumed on the base of a few calibrated results from the literature [35, 40]. As the materials (grading curves and grain shape) and test conditions often differ from the original calibration subject, it remains unclear which influence the assumed IGS parameters might have on the calculation result of real boundary value problems.

Table 2 summarizes fully calibrated Hypo+IGS parameter sets for sands and gravels from the literature. So far, most research and consequently most Hypo+IGS calibrations have focused on finer sands with uniform grading (SP[2]), e.g. Hochstetten sand [25], Karlsruhe (fine) sand with different grading curves [33, 63], Dubai sand [40], Toyoura sand [42] or other fine quartz sands [8, 41]. The overview in Table 2 highlights that only a few studies and calibrated hypoplastic parameter sets exist for coarse-grained and well-graded materials. With exception of [50], none of these studies include cyclic laboratory tests and the calibration of IGS parameters. Herle [26] demonstrated the calibration of the basic hypoplastic model [64] for coarse-grained granular materials based on Hochstetten gravel ($C_u = 7.2$, $d_{50} = 2$ mm). Schünemann [50] investigated the long-term behaviour of railway ballast ($C_u$ $\le$ 2, $d_{50} = 40$ mm) due to crushing. He conducted several large-scale monotonic element tests to calibrate the hypoplastic parameters. Yet, only one cyclic oedometric test and no small strain tests were used to determine the IGS parameters. Railway ballast consists of uniformly graded angular gravels with grain sizes $\ge$ 31.5 mm [10], which are not intended for bridge backfills. Rondón et al. [48] conducted monotonic experimental tests on a well-graded and highly compacted unbound granular material (UGM) with $C_u = 100$ and $d_{50} = 6.3$ mm to derive hypoplastic material constants. This material is used for (sub)base layers of flexible (asphalt) pavements of traffic ways but could also serve as a backfill material for bridges in accordance with [11]. Although Rondón et al. [49] also presented high-cyclic drained triaxial tests on this material, their research did not focus on the calibration of the IGS parameters. In summary, it can be stated that up to the present no calibrated Hypo+IGS parameter set for a typical well-graded backfill material with explicit focus on the cyclic behaviour has been published. Therefore, in the following results of an experimental programme on a representative highly densified gravel backfill material as well as a thorough Hypo+IGS calibration for this material will be presented.

Table 2 Calibrated Hypo+IGS parameter sets for sands and gravel from the literature

4 Material and testing programme

4.1 Gravel backfill material

The tested gravel in this investigation represents a typical well-graded bridge backfill material. The grain size distribution curve of the material is shown in Fig. 3. Its mean and maximum grain size is $d_{50} = 4$ mm and $d_{100} = 16$ mm with a uniformity coefficient of $C_{u} = 24$. It was collected from a plant close to Rastatt (Germany) and originates from the Rhine river. Therefore, its grains have a smooth and subrounded shape, compare Fig. 1c. Standard index tests [13] gave a maximum void ratio $e_{\max } = 0.442$, a minimum void ratio $e_{\min } = 0.271$ and a grain density of $\rho _{s} = 2.636$ g/cm$^{3}$. A maximum dry density of $\rho _{\rm Pr} = 2.05$ g/cm$^{3}$ was determined by modified Proctor tests at a water content of $w_{\rm Pr} = 8\%$. This density corresponds to a void ratio of $e_{\rm Pr} = 0.286$ and a relative density of $D_{\rm r,Pr} = 91.8\%$. An average value for the critical friction angle of $\varphi _{c} = 34.4^\circ$ was determined from the inclination of five air-pluviated cone tests (Fig. 1c) with only a small scatter of ±0.6$^\circ$. Small segregation effects were observed in these tests. According to Herle [26], this effect should not significantly influence the measured $\varphi _{c}$. However, $\varphi _{c}$ in the presented tests is slightly smaller compared to findings for other coarse-grained materials, such as $\varphi _{c} = 36^\circ$ for Hochstetten gravel [25] or $\varphi _{c}$ = 38$^\circ$ for UGM [48]. Herle [25] points out that for granular material $\varphi _{c}$ mainly depends on the grain diameter, the uniformity and the grain shape. Thus, a rounded shape leads to a significantly smaller $\varphi _{c}$ compared to angular material. This might explain the smaller $\varphi _{c}$-value of the investigated subrounded gravel.

Fig. 3

Grain size distribution curve of the tested gravel

4.2 Testing programme

The experimental programme and the initial test conditions are summarized in Table 3. Three oedometric (OED) compression tests with two or 16 un- and reloading cycles on very loose and very dense samples (height $h = 16$ cm, diameter $d = 50$ cm) were conducted. Furthermore, three drained monotonic triaxial (DMT) tests were performed at initial mean stresses of $p_{0} = 50$, 100 and 300 kPa. The test at $p_{0} = 100$ kPa included three un- and reloading cycles at $\Delta \varepsilon _{1} = 0.5$, 1 and 1.5%. For the further investigation of the cyclic loading behaviour three undrained cyclic triaxial (UCT) tests were carried out. Two tests were conducted at initial mean pressures of $p_{0} = 50$ and 100 kPa with approx. 100 stress-controlled cycles of $q^{\text{ampl}} = \pm 25$ kPa at a frequency of $f = 1\cdot 10^{-3}$ Hz. The third UCT test was anisotropically consolidated with $p_{0} = 100$ kPa and $q_{0}$ = 75 kPa and afterwards also tested at $q^{\text{ampl}} = \pm 25$ kPa. Both triaxial test series (DMT and UCT) were performed on dense to very dense cylindrical specimens ($h = 10$ cm, $d = 10$ cm) with smeared end plates. Thus, a specimen-to-grain size ratio of $d / d_{100} = 6.25 > 6$ was reached, which is often considered an acceptable lower limit for a cylindrical specimen with well-graded material [3, 15]. The stress and loading conditions in the majority of tests were chosen in similar ranges to the in situ conditions for backfills of integral bridges. To further account for in situ conditions, all test series contained tests on highly compacted specimens with densities in the range of the modified Proctor density. All specimens in the triaxial tests were prepared in dry conditions by tamping in five layers as this represents best the in situ installation. Deviating from that, the oedometric samples were prepared by dry air pluviation and densified by vibration on a horizontally shaking table, due to the required specimen size.

Table 3 Summary of the triaxial and oedometric tests

At last, drained cyclic triaxial (DCT) tests on dry, dense to very dense specimens with a square cross section ($A = b\cdot b$ = 76 cm$^2$, $h = 18$ cm) were conducted, see Fig. 4. These tests at three isotropic consolidation pressures $p_{0}$ = 50, 100 and 300 kPa were performed with increasing cyclic shear stress amplitudes $q^{\text{ampl}}$ to capture the small strain behaviour. At each stress amplitude two cycles were applied with a frequency of $f = 1\cdot 10^{-3}$ Hz. Bender-Elements (BE) were placed in the end plates to measure the maximum shear stiffness $G_{0}$ (at $\gamma = 1\cdot 10^{-6}$) after the consolidation. Furthermore, local deformation transducers (LDTs), i.e. soft leaf spring-like strips of stainless steel equipped with strain gauges, were installed in horizontal and vertical alignment on the specimen (Fig. 4b). The LDTs allow local strain measurements during shearing and thus the evaluation of the (shear) stiffness degradation during the continuous cyclic loading with increasing shear stress amplitudes. The triaxial apparatus as well as the small strain measurement procedure is described in detail in [28, 29]. Regarding the square cross section: There is no necessity to use this specimen shape for triaxial tests with constant minor stress $\sigma _{3}$. The square shape was chosen due to the laboratory’s equipment and for a better applicability of the LDTs. Comparisons based on drained monotonic triaxial tests in [48, 61] showed that the shape of the cross section of a specimen has no significant influence on the test results. The ratio $b / d_{100} = 5.4$ of specimen edge length b to maximum grain size $d_{100}$ can be regarded as sufficiently high to ensure a homogeneous stress field in the specimen, especially due to the relatively small strain amplitudes in these tests.

Fig. 4

(a) Triaxial apparatus without cell for the tests on the dry prismatic specimens in black rubber membrane, that were equipped with Bender-Elements in both end plates; (b) LDTs for local strain measurements applied vertically and horizontally on the sample sites [29]

5 Calibration based on test results

The calibration procedure was chosen following the recommendations in [25, 27, 35, 40, 48, 60]. The consecutive calibration steps and the resulting Hypo+IGS parameters for the backfill gravel are summarized in Table 4. The results of the testing programme described above were used for every calibration step. While the experimental results of DCT tests are discussed in this section, the results of OED, DMT and UCT test are depicted in the following section together with a comparison to the final calibration results. For the simulation of all element tests in this investigation the Incremental Driver (ID) tool by Niemunis [44] and the Hypo+IGS UMAT by Mašín et al. [36] were used from [23].

First, the eight basic hypoplastic model parameters were calibrated based on [27]. (Step 1) As presented before, from the angle of repose an average critical friction angle of $\varphi _{c}$ = 34.4$^\circ$ was derived for (very) loose conditions. The results for $\varphi _{c}$ from the DMT tests were not considered as these tests were performed on very dense specimens which additionally showed shear band localization at large strains. (Step 2) The limit void ratios at zero pressure were determined from $e_{\rm d0} = e_{\min } = 0.271$, $e_{\rm c0} = e_{\max } = 0.442$ and $e_{\rm i0} = 1.1$ $e_{\max } = 0.486$. Herle [25] showed that the ratio $e_{\rm i0}/e_{\max }$ decreases with rising $C_{u}$ as well as an increasing roundness of the grain shape. For well-graded granular materials, he suggests choosing a low ratio, e.g. $e_{\rm i0}/e_{\max } = 1.15$. For the well-graded subrounded gravel in this study $e_{\rm i0}/e_{\max } = 1.1$ was chosen, similar to subrounded Hochstetten gravel discussed in [25].

(Step 3) The values for granulate hardness $h_{s} = 1.8$ MPa and the stiffness exponent $n = 0.26$ were first calculated by fitting Bauer’s [4] Eq. (5) on the results of the OED test with a dry, very loose sample (Fig. 12c):

$$\begin{aligned} \frac{e_i}{e_{\rm i0}} = \frac{e_c}{e_{\rm c0}} = \frac{e_d}{e_{\rm d0}} = \rm{exp} \left[ - \left( \frac{3p}{h_s} \right) ^{n} \right] \end{aligned}$$

(5)

using $p = -(\sigma _{1}+2\sigma _3)/3$ and an estimated effective lateral stress of $\sigma _{3} = K_{0}\ \sigma _{1}$ with $K_{0} = 1 - \rm{sin} \varphi _{c}$. The procedure is specified in detail in [27, 35]. Afterwards, the OED test was simulated with the element test programme (ID). Due to the weight of the top plate, the calculation started at an effective initial stress of $\sigma _{1} = 8.76$ kPa and $\sigma _{3} = K_{0}\ \sigma _{1} = 3.81$ kPa. The intergranular strain has been assumed to be initially fully mobilized in vertical direction ($h_{11} = -R$), which corresponds to similar approaches in the literature, e.g. in [33, 56, 61]. Thus, the simulation starts without increased (shear) stiffness. Consequently, the parameters $h_{s}$ and n were slightly adjusted to $h_{s} = 2$ MPa and n = 0.25 to match the initial loading path in the $e - \sigma _{1}$ curve.

Table 4 Calibration scheme and resulting Hypo+IGS parameters for the backfill gravel

(Step 4) The dilatancy parameter $\alpha$ was preliminarily calculated with a mean value of $\alpha = 0.19$ from Eqs. A15–A17 based on the three DMT test results with dry, highly compacted samples ($D_{\rm r0} = 95{-}98\%$) at initial mean stresses of $p_{0} = 50$, 100 and 300 kPa. The parameter $\beta$ that generally controls the stiffness of specimens with $e < e_{c}$, e.g. the stiffness in OED tests on (initially) very dense samples, was determined in the next step. A mean value of $\beta = 5.1$ was calculated first from Eqs. A18–A20. Thereby, the oedometric moduli of two OED tests at different initial densities ($D_{\rm r0} = 6.8$ and 91.3%) were compared for varying mean pressures $p = 40{-}400$ kPa, following the procedure described in [25] and [48]. The value of $\beta = 5.1$ is significantly larger than the range of $\beta = 1{-}3.5$ found in the literature, and hence, this preliminary result should be treated with caution. The high $\beta$-value indicates a very stiff soil behaviour for samples with $e < e_{c}$. Rondón et al. [48] reported values of $\beta = 3.2{-}3.8$ and a significant decrease of $\beta$ with p for UGM, which was not evident in this investigation.

(Step 5) In a consecutive step, the three DMT tests were simulated with ID [35, 40]. For the initialization of the intergranular strain tensor a full isotropic mobilization has been assumed ($h_{\rm ii,0} = -R /\sqrt{3}$, while all other components are set to zero) in order to simulate an isotropic compression prior to shearing in the tests [56, 61]. Both parameters $\alpha$ and $\beta$ had to be adjusted to $\alpha = 0.22$ and $\beta = 3$ to better fit the DMT results presented in Fig. 5. While $\alpha$ governs the peak friction angle (i.e. the peak deviatoric stress) and the dilatancy, $\beta$ controls the stiffness during first loading, and thus the position of the peak, in the $p - \varepsilon _{1}$ curve of the triaxial tests. Hence, Meier [40] suggests an iterative calibration of parameters $\alpha$ and $\beta$ (and $h_{s}$ as well as n) to achieve the best conformity in between DMT and OED test results. In the present study, the five IGS parameters also significantly influence the behaviour of the OED tests with un- and reloading cycles on highly densified samples ($D_{\rm r0} = 91.3$ and 93.1%). Therefore, these parameters were calibrated at next.

Fig. 5

Experimental results (solid lines) and simulations (dashed lines; final parameter set) of DMT tests on highly compacted samples ($D_{\rm r0} = 95{-}98\%$) at initial mean pressures $p_0 = 50$; 100 and 300 kPa: (a) $q - \varepsilon _1$ curve, (b) $\varepsilon _V - \varepsilon _1$ curve

(Step 6) In Fig. 6, the normalized shear modulus $G/G_{0} - \gamma ^{\text{ampl}}$ curves from three DCT tests with LDT measurements on dry, highly compacted specimens ($D_{\rm r0} = 95{-}98\%$) at confining pressures of $p_{0} = 50$, 100 and 300 kPa are displayed. The empty marker represents the single point test results of secant shear stiffness G in the first cycle of each shear stress amplitude $q^{\text{ampl}}$ and the full marker displays the measured results for the second shear stress cycle. The results for cycle 1 and 2 correspond fairly well. A certain scatter of the measurements can be seen at small strain amplitudes $\gamma ^{\text{ampl}}<3\cdot 10^{-5}$, as these values are close to the resolution limitation of the LDT sensors. The associated fitting curves in Fig. 6 were derived for the test results of the second stress cycle using the following modified hyperbolic equation by Oztoprak and Bolton [46]:

$$\begin{aligned} \left( \frac{G}{G_0}\right) = 1 \left[ 1 + \left( \frac{\gamma - \gamma _e}{\gamma _r} \right) ^{a} \right] \end{aligned}$$

(6)

where $G_{0}$ is the maximum shear stiffness, G is the secant shear modulus, $\gamma$ is the shear strain, $\gamma _{e}$ is the elastic threshold strain, $\gamma _{r}$ is the reference shear strain at $G/G_{0}$ = 0.5, and a is a curvature parameter. Equation (6) was iteratively adjusted and matches the LDT measurement points in Fig. 6 well. In general, the normalized degradation curves in Fig. 6 show a similar shape for the different consolidation pressures $p_{0}$. Wegener and Herle [60] propose to determine the IGS parameter R from the $G/G_{0} - \gamma$ curve as the shear strain $\gamma _{0.8}\approx R$ at $G/G_{0} = 0.8$. Based on this the constant $R = 1\cdot 10^{-4}$ is estimated from Fig. 6, which corresponds to the recommended value for non-cohesive soils in the literature, e.g. [35, 40].

Fig. 6

Degradation of normalized shear modulus $G/G_0$ with increasing shear strain amplitude $\gamma ^{\text{ampl}}$ from LDT measurements in DCT tests with increasing cyclic shear stress amplitudes $q^{\text{ampl}}$

Based on the final LDT fitting curves from Fig. 6 an estimation of $G_{0}$ at $\gamma ^{\text{ampl}} = 1\cdot 10^{-6}$ is possible, see results in Fig. 7. In this figure also the resulting $G_{0}$-values from the three BE measurements before every DCT test are displayed. Clearly, the results for $G_{0}$ from LDT and BE measurements partially deviate for the different initial mean pressures. Nevertheless, these results allow to calibrate the IGS parameter $m_{R}$ for the applied mean stress range of $p_{0} = 50{-}300$ kPa, following Mašín [35]. For this purpose, four triaxial tests with $p_{0} = 50$, 100, 200 and 300 kPa were simulated with a very small strain amplitude $\gamma ^{\text{ampl}} \le 1 \cdot 10^{-6}$. The initial state of the intergranular strain had to be set to $\Vert \varvec{\rm{h}}\Vert = R$ to simulate the shearing start with maximum (shear) stiffness after a 180$^{\circ }$ strain reversal. A value of $m_{R} = 5.2$ was found to fit best the BE- and LDT-results in Fig. 7. As illustrated in Fig. 7 also the parameter $\beta$ can influence the $G_{0}$ simulation, which should be kept in mind for the later iterative calibration of this constant. The parameter $m_{T}$ was estimated from $m_{T} = 0.7 m_{R} = 3.6$ as recommended in [35].

(Step 7) Based on the previous calibration, the DCT tests with increasing shear stress amplitude $q^{\text{ampl}}$ were simulated to reproduce the full stiffness degradation curves given in Fig. 6. Analogue to the procedure with the test data, single point results of the secant shear stiffness G were calculated for each cycle of shear stress amplitude $q^{\text{ampl}}$ (second cycle). The fitting curves based on the numerical results were then derived from Eq. (6). The comparison in Fig. 8 shows that a good agreement of experimental and computed data is achieved with a choice of the two remaining IGS parameters of $\beta _r = 0.1$ and $\chi = 0.7$. However, it has to be kept in mind that these preliminary parameters might have to be adjusted in the following step(s) to reproduce the test results with higher numbers of cycles N.

Fig. 7

Calibration of parameter $m_R$ based on Bender-Elements and LDT measurements of $G_0$

Fig. 8

Comparison of experimental results (diamond marker and solid lines based on fitting curve from Eq. (6)) with simulations (circle marker and dashed lines based on fitting curve from Eq. (6)): $G - \gamma ^{\text{ampl}}$ curve from LDT measurements in DCT tests with increasing cyclic shear stress amplitudes

(Step 8) The two IGS parameters $\beta _r = 0.1$ and $\chi = 1.3$ were further determined by simulating the two UCT tests at initial mean stresses of $p_{0} = 50$ and 100 kPa [35]. In order to simulate an isotropic compression prior to shearing in the tests, the IGS tensor was initialized with $h_{\rm ii,0} = -R /\sqrt{3}$, analogue to the DMT tests and literature [56, 61]. Figure 9 presents (besides results discussed in Sect. 6) the results of the UCT test with $p_{0} = 100$ kPa compared to the simulation result (with the final parameter set after the calibration). The iterative curve fitting of these test results can be rather subjective, especially for cases where only UCT tests are available and all five IGS parameters have to be fitted exclusively on these test data. This investigation focuses on the accurate simulation of the cyclic pore water pressure accumulation $\Delta u^\text{acc}(N)$. On the other hand, less emphasis was given on the simulation of the cyclic accumulation of axial strain $\varepsilon _{1}$ in Fig. 9b as these curves can generally not be reproduced well with the Hypo+IGS model, compare, e.g. [17, 62].

Fig. 9

Experimental results (grey line) and simulation (red line, final parameter set) of two UCT tests on highly compacted specimen ($D_{\rm r0} = 87$ and 84%) with 100 cycles and $q^{\text{ampl}} = \pm 25$ kPa: (a–c) isotropic consolidation of $p_{0} = 100$ kPa and (d–f) anisotropic consolidation $p_{0} = 100$ kPa, $q_{0} = 75$ kPa

(Step 9) In the last step, the calibration of the Hypo+IGS parameters can be iteratively optimized to reach the combined best simulation of OED, DMT and UCT element tests. The two OED tests with un- and reloading on highly densified samples ($D_{\rm r0}$ = 91.3 and 93.1%) are simulated with ID. The intergranular strain for the simulation has been set to $h_{\rm 11,0} = 0$, i.e. initially not mobilized in vertical direction. This assumption is based on the preparation method of the samples in these tests. Due to the strong vibration by the shaking table the specimen will experience multiple strong strain direction reversals. After the preparation of the samples the orientation of the intergranular contact forces resembles those of a non-preloaded grain skeleton. The assumption might partly also be justified with regard to the extraordinarily better fit of the simulation with the experimental data compared to re-calculations with an initialization of $h_{\rm 11,0} = -R$, see Fig. 10. Additionally, Buehler [6] and Prada Sarmiento [47] state that the assumption of $h_{\rm ii,0} = 0$ is more adequate for soils after a dynamic compaction. As a result of the simulation (with $h_{\rm ii,0} = 0$) the parameters $\beta$ and $\chi$ were slightly reduced to $\beta$ = 2.5 and $\chi = 1.2$ to account for the softer test behaviour.

Fig. 10

Comparison of ID simulations (with parameters from step 8 in Table 4 with initially fully mobilized ($h_{\rm 11,0} = -R$) and not mobilized ($h_{11,0} = 0$) intergranular strains in vertical direction to the experimental results of the OED test with $D_{\rm r0} = 93.1\%$

An even better fit could have been achieved for the very dense OED tests with a further reduction of $\beta$ and/or a reduction of $m_{R}$ (together with an adaptation of $\chi$ and $\beta _r$). However, this would have strongly diminished the reproduction of the DMT tests (in case of a reduction of $\beta$) as well as the $G_{0}(p_{0})$-values in Fig. 7 and 8. Thus, $\beta =2.5$ and $\chi = 1.2$ were chosen as a compromise to assure an evenly good agreement related to all conducted test re-calculations. The simulation of DMT and UCT tests was repeated and only $\alpha = 0.23$ was adjusted. Thus, no further iteration was necessary. The final parameter set is highlighted in Table 4.

6 Back-calculation of all element tests

In the following, the re-calculations of DMT, OED, DCT and UCT tests with the calibrated final parameter set from Table 4 are provided, compared and briefly discussed against the experimental data. The element tests have been numerically calculated as described in Sect. 5. In Fig. 5, the DMT test results are compared to the Hypo+IGS simulation. Overall, the peak strength and the shape of the $q - \varepsilon _1$ curve in Fig. 5a are well reproduced. The model displays a stiffer initial response. On the other hand, the measured initial stress–strain behaviour of the triaxial tests might also be slightly too soft due to (minor) bedding errors, which could be more pronounced in the current case due to the large grain size. These effects cannot be fully avoided unless a local strain measurement is conducted. Additionally, the model overpredicts the peak stress for the test with $p_{0} = 300$ kPa. Concerning the volumetric strain behaviour in Fig. 5b, the small initial compaction is underestimated, yet an overall good agreement with the following dilatancy effects is achieved for $\Delta \varepsilon _{1} < 5\%$. The numerical results of the DMT test at $p_{0} = 100$ kPa with un- and reloading cycles at $\Delta \varepsilon _{1}$ = 0.5, 1 and 1.5% are presented in Fig. 11. At the smallest un- and reloading amplitude (at $\varepsilon _{1}$ = 0.5) the model shows an unrealistically stiff response at the un- and reloading path which leads to an overestimation of the shear strength in the following reloading phase. For the largest un- and reloading amplitude (at $\varepsilon _{1}$ = 1.5), however, the model response at the reloading path is too soft and the shear strength is underestimated. These so called ”under-” or ”overshooting” effects are caused by an insufficient memory of the IGS formulation and can occur if a small unloading strain increment is followed by a larger reloading strain increment, compare, e.g. [1, 17, 39, 47]. In boundary value problems with drained conditions the overshooting effects could lead to an overestimation of the soil stiffness and an underestimation of ground (and structure) deformation [7, 18].

Fig. 11

Experimental results (solid line) and simulations (dashed lines; final parameter set) of the DMT test at $p_{0} = 100$ kPa with un- and reloading cycles at $\Delta \varepsilon _{1} = 0.5$, 1 and 1.5%

The results of all OED tests are presented in Fig. 12. Here, the model response for the very dense specimens in Fig. 12a,b is marginally too stiff for all (un)loading paths. The reason for this behaviour was already discussed in the previous section. Nevertheless, the prediction is quite satisfying considering the good reproduction of the axial strain accumulation during 16 consecutive un- and reloading cycles for the test in Fig. 12a as well as the good fit related to the very small void ratio changes at this high level of sample densification. The OED test on the very loose sample in Fig. 12c was simulated with and without the intermediate un- and reloading cycle at $\sigma _{1} = 500$ kPa, as this test mainly served to calibrate the stiffness parameters $h_{s}$ and n on the initial loading path (step 3 of the calibration). With the final parameter set the monotonic initial loading path is predicted almost perfectly, whereas the unloading paths show a slightly too soft response (especially for low stresses). The un- and reloading loop, which starts from $\sigma _{1}$ = 500 kPa, exhibits a "undershooting" behaviour at this large strain reversal amplitude. A similar under - or overshooting behaviour in un- and reloading paths of a oedometric test has also been reported for the Hypo+IGS model by Duque et al. [17] depending on the size of the un- and reloading cycles.

Fig. 12

Experimental results (solid lines) and simulations (dashed lines; final parameter set) of OED tests with un- and reloading on highly compacted (a, b) and very loose (c) specimens

Figure 9 provides the results of the UCT tests with isotropic and anisotropic compression at $p_{0} = 100$ kPa and $q_{0} = 75$ kPa compared to the simulation with the calibrated parameter set. Figure 9a,c and d,f shows a rather good agreement of experimental and numerical curves. Within the first cycle the model overpredicts the pore water pressure, which is mainly governed by the parameter $m_R$ and could be improved by its reduction. After that, the cyclic accumulation of normalized pore water pressure $\Delta u^\text{acc}(N)/p_{0}$ and thus the gradual cyclic decrease in effective mean pressure p is slightly overestimated in case of the test with isotropic compression (due to the reduction of parameter $\beta$ in the final iteration steps). The inability of the model to reach an effective stress of $p = 0$ during the cyclic mobility phase (butterfly shape of the stress path) is visible in Fig. 9a,c, which is a known Hypo+IGS shortcoming [62]. The simulation in Fig. 9b shows only a cyclic accumulation of axial strain to the extension side. This bias has also been reported in the literature for tests with isotropic consolidation, e.g. in [17, 62]. In both test re-calculations, the axial strain accumulation is noticeably underestimated, see Fig. 9b and 9e.

At last, in Fig. 8, the stiffness degradation curves from DCT tests with increasing shear stress amplitudes $q^{\text{ampl}}$ are compared to their numerical simulations. The simulations with the final parameter set show too low maximum shear moduli $G_{0}$, due to the reduction of $\beta = 2.5$ (as explained before regarding the numerical results in Fig. 7). This underestimation of $G_{0}$ can be accepted since in return a better reproduction of other test results, e.g. the OED and UCT tests is obtained. The consecutive stiffness degradation with increasing shear strain amplitude $\gamma ^{\text{ampl}}$ in Fig. 8 is matched fairly well with the calculations.

7 FE analysis of an integral bridge with various granular backfills

7.1 FE model

In this final section, a simplified numerical analysis on the cyclic SSI of an integral railway bridge is presented. Its goal is to compare the calibrated gravel backfill material to other calibrated Hypo+IGS parameter sets from the literature listed in Table 2. For the study a two-dimensional FE model of an integral bridge with a total length $l = 40$ and 160 m and an abutment height $h = 8$ m was used in Plaxis (version V22.2) [5], see Fig. 13. The FE mesh was discretized with 15 noded elements (using a shape function of $4^{th}$ order) and gradually refined towards the abutment. The abutment was simplified by a very stiff plate element with foot fixation, and the horizontal superstructure support was modelled with a prescribed displacement (which functions as a top fixation of the plate in the initial calculation phases). A zero thickness interface with linear elastic perfectly plastic properties was placed at the plate backside to account for the reduced strength ($R_\mathrm{{inter,\varphi }} = 0.7$) in the frictional contact zone and to allow relative displacements between the abutment and the adjacent soil. To avoid interpenetration effects, the interface normal stiffness was chosen significantly higher compared to the stiffness of the adjacent soil body following the recommendations in [54]. Additionally, the interface was vertically extended by 0.5 m underneath the plate foot point to reduce stress concentration in the interface at the foot point. For the backfill soil layer, the Hypo+IGS parameter sets from Table 2 were applied in consecutive calculations. The initial void ratio was chosen for an initial relative density of $D_{\rm r0} = 80\%$. The underground layer was modelled with a linear elastic perfectly plastic Mohr–Coulomb (MC) soil model ($\varphi = 40$°, $c=0$ kPa, $E = 45$ MPa, $\nu = 0.2$) for all performed analyses to reduce the cyclic influence of the underlying soil layer to a minimum. Drained conditions were assumed.

The initial stress state was generated by a $K_0$-procedure and the Hypo+IGS intergranular strains were assumed not mobilized ($h_{\rm ii,0} = 0$) to account for the increased small strain stiffness at the beginning of the calculation. In Fig. 14, the successive calculation phases are illustrated. In the phases 1)-5), a renewal of an old bridge and its adjacent backfill was simulated to create a more realistic stress state at the beginning of the cyclic loading phases. Vertical point loads at the top of the plate and line loads at the top of the backfill represent the permanent loads from superstructure and track (from phase 5 onward). In phases 6)–7)ff the seasonal temperature deformations of the superstructure into the summer and winter position were modelled by means of horizontal prescribed displacements $\Delta u_x = \pm 5$ or 20 mm at the top of the plate. Thus, the first and most important 20 seasonal cycles were simulated with an idealized foot point rotation of $\Delta u_x / h = \pm 0.06$ or 0.25%. The prescribed displacements were calculated by $\Delta u_x = \Delta l \cdot \Delta T \cdot \alpha _T = \pm 5$ or 20 mm assuming a free seasonal temperature deformation of an symmetrical integral bridge with a expansion length $\Delta l = 20$ or 80 m, a seasonal temperature difference $\Delta T = \pm 25$ K and a thermal expansion coefficient $\alpha _T = 1\cdot 10^{-5}$ 1/K. It must be emphasized that this constitutes a simplification of real conditions, i.e. because additional daily temperature cycles or creep and shrinkage deformation of the superstructure have not been superimposed. However, for the comparison of different Hypo+IGS parameter sets in this paper, these additional effects are not relevant.

Fig. 13

Simplified two-dimensional FE model with focus on the soil-structure interaction of an integral bridge

Fig. 14

Schematic illustration of the calculation phases

7.2 Results

At first, results of the FE analysis on the cyclic SSI of the shorter integral bridge ($l = 40$ m, $\Delta u_x / h = \pm 0.06\%$) with the calibrated railway gravel at different initial densities $D_{\rm r0}=60{-}80{-}95\%$ are presented in Fig. 15. In situ relative densities $D_{\rm r0} = 80{-}95\%$ can be expected after the compaction to a 100% of Proctor density, while $D_{\rm r0}$ = 60% might already be too low for practical purposes. As anticipated, higher initial densities will lead to higher earth pressure, i.e. lateral stresses $\sigma _x$ (Fig. 15b) behind the abutment and lower settlement accumulations $u_y$ (Fig. 15a) compared to calculations with lower densities (Fig. 15c,d). At higher $D_{\rm r0}$ a stronger mobilization of lateral stress occurs in the upper part of the backfill. The development of lateral earth pressure forces $F_x$ on the abutment with increasing number of cycles N (evaluated in summer position) is illustrated in Fig. 15e by the normalized lateral force $K_{\rm mob} = 2F_x~/~(\gamma ~\cdot ~h^2)$. A continuous cyclic increase of $K_{\rm mob}$ can be seen for all calculations over $N = 20$ cycles, while the increase is strongest for the first $N = 5$ cycles. This corresponds to the findings in the experimental studies from Table 1 and Fig. 2. Higher initial densities lead to higher $K_{\rm mob}$ and a stronger cyclic growth rate of $K_{\rm mob}$ for N > 10 cycles. This is consistent with the results for the lateral stresses in Fig. 15b,d.

Fig. 15

Results of cyclic FE calculations ($N = 20$ cycles) with the calibrated railway backfill gravel at $D_{\rm r0} = 60{-}80{-}95\%$ and $\Delta u_x / h = \pm 0.06\%$: (a) and (c) cyclic settlement accumulation $u_y$ at the backfill surface, (b) and (d) cyclic lateral stress distribution $\sigma _x$ over the abutment height h, (e) cyclic development of normalized lateral forces $K_{\rm mob} = 2F_x~/~(\gamma ~\cdot ~h^2)$–all results were evaluated in the abutment’s summer position

Fig. 16

Cyclic development of normalized lateral forces $K_{\rm mob}$ in FE calculations ($N = 20$ cycles, $D_{\rm r0} = 80\%$, $\Delta u_x / h=\pm 0.06\%$) with different calibrated Hypo+IGS parameter sets of poorly-graded sands and well-graded gravels from Table 2

In Fig. 16, the development of $K_{\rm mob}$ with increasing cycles N is displayed for different calibrated Hypo+IGS parameter sets from Table 2 for $D_{\rm r0} = 80\%$. For the Hochstetten and UGM gravel no IGS parameters exist. Therefore, two different IGS parameter sets with either $\beta _r = 0.1$ and $\chi =1$ (based on the recommendations in [35, 40] and similar to the here presented railway backfill gravel) or $\beta _r = 0.5$ and $\chi = 6$ (based on Hochstetten sand [45]) were assigned. The calculations for both gravels with the two different IGS parameter sets revealed only small differences regarding the cyclic development of $K_{\rm mob}$. For $\beta _r = 0.5$ and $\chi = 6$ a stronger $K_{\rm mob}$ increase occurs in the first $N = 5$ cycles, which gradually reverses to the opposite with increasing cycles. After $N = 20$ cycles rather similar $K_{\rm mob}$ values are obtained. The comparison is an indication that the IGS parameters $\beta _r$ and $\chi$, which are typically calibrated based on extensive laboratory tests as demonstrated in Sects. 4 and 5, do not have the most dominant influence in this boundary value problem. Therefore, the choice of default IGS parameters may be justified in studies of similar nature.

Two (other) major trends are visible from Fig. 16: Firstly, poorly-graded sands generally mobilize a significantly smaller lateral force (on the abutment in the summer position) due to the cyclic SSI compared to well-graded gravels. Secondly, the cyclic increase of $K_{\rm mob}$ for the well-graded gravels is noticeable stronger and more persistent for the first $N = 20$ cycles in comparison with the uniformly graded sands. The sand backfills show no relevant increase of $K_{\rm mob}$ for $N>5{-}10$ cycles at the considered temperature rotation amplitude of $\Delta u_x / h = \pm 0.06\%$. Similar results were observed in FE analysis on the cyclic SSI of integral bridges with $\Delta u_x / h = \pm 0.11\%$ by Deckert [12] with a Hypo+IGS parameter set of a fine sand.

The main reason for the first trend can be traced back to significantly different stiffnesses of the calibrated materials. To illustrate that, the OED tests at $D_{\rm r0} = 93.1\%$ with repeated un- and reloading cycles from Fig. 12a were repeated with each Hypo+IGS parameter set. The stress levels of $\sigma _1=50{-}200$ kPa in this test corresponds well to the stress level behind the abutment in the boundary value problem. For simplicity reasons the intergranular strain was assumed initially fully mobilized in vertical direction ($h_{\rm 11,0} = -R$). In Fig. 18, the tangential stiffnesses $E_\mathrm{tang.}$ at each loading step of these tests (with 2000 steps for each un- and reloading cycle) are provided. All well-graded gravels in Fig. 18a–d reach relative similar stiffnesses at the beginning of the un- and reloading phases. However, the gravels show several times higher stiffnesses during un- and reloading compared to all fine sands in Fig. 18e–h. Due to the relatively small strain amplitudes during the un- and reloading cycles the soil response is highly effected by the smalls strain stiffness of the material. This is especially true for the gravels, e.g. Hochstetten gravel (Fig. 18b) and UGM in Fig. 18d, but also for Karlsruhe fine sand (Fig. 18g), which all show an almost elastic response in the un- and reloading cycles. Thus, the small strain stiffness by the IGS parameters significantly influences the stiffness response over most parts of the un- and reloading cycles. This further increases the stiffness differences between fine sands and gravels. Similar strong differences between poorly-graded sands and well-graded gravels were observed for the shear stiffnesses in the simulations of cyclic simple shear tests. (Results are not explicitly presented here.)

Furthermore, a higher densification of larger backfill areas was detected for the present calculations with gravel backfills, which further contributes to the different cyclic stress increases observed in Fig. 16. An additional influence of potential overshooting effects, similar to the triaxial test results shown in Fig. 11, cannot be ruled out completely, but no evidence was found in several evaluated backfill stress paths over the abutment height.

Finally, also for longer integral bridges ($\Delta u_x / h$ = ±0.25%) profound differences can be seen. In Fig. 17, the cyclic increase of $K_{\rm mob}$ in relation to the second seasonal cycle (denoted as $\Delta K_{\rm mob}$, similar to Fig. 2) is presented for $\Delta u_x / h = \pm 0.06$ and 0.25%. On the one hand, at a higher rotation amplitude $\Delta u_x / h = \pm 0.25\%$ also the (Karlsruhe) fine sand backfill shows a noticeable and continuous cyclic stress increase. On the other hand, the cyclic increase of $\Delta K_{\rm mob}$ for the railway backfill gravel is still at least twice as big in relation to the fine sand. As a consequence the use of poorly-graded fine sands in numerical or experimental studies on the cyclic SSI of integral bridges could lead to an underestimation of the cyclic lateral earth pressures. This could also affect the structural bridge design. Future numerical and experimental studies should focus on representative well-graded backfill materials.

Fig. 17

Cyclic increase in normalized lateral forces $\Delta K_{\rm mob}$ with regard to the second seasonal cycle in FE calculations ($N = 20$ cycles, $D_{\rm r0} = 80\%$) with Karlsruhe fine sand and railway backfill gravel for different bridge lengths ($\Delta u_x / h$ = ±0.06 or 0.25%)

Fig. 18

Evaluation of the tangential stiffness $E_\mathrm{tang.}$ in numerical OED tests ($D_{\rm r0} = 93.1$, $h_{\rm 11,0} = -R$) with repeated un- and reloading cycles for different well-graded gravels (a–d) and uniformly graded sands (e–h) from Table 2

8 Conclusion

A comprehensive experimental programme on a highly densified, well-graded gravel, representative for bridge backfill material, has been presented. The test series include several oedometric compression tests with un- and reloading cycles as well as monotonic and cyclic triaxial tests under drained and undrained conditions. Additionally, cyclic triaxial tests on prismatic specimens with Bender-Element and local strain measurements (LDTs) have been conducted to investigate the small strain behaviour. The experimental data allow a profound calibration of advanced constitutive models with focus on cyclic loading for the typical backfill material.

In this study, the determination of the parameters for the Hypo+IGS soil model was demonstrated employing various calibration recommendations from the literature. Based on the test results, a new Hypo+IGS parameter set for the gravel material was derived. So far, parameter sets for such coarse-grained soils are barely documented in the literature, especially with a focus on the small strain and cyclic behaviour. The performance of the calibrated parameter sets was compared to the experimental data based on re-calculations of several monotonic and cyclic element tests. Overall, a very good agreement with the laboratory tests was achieved. Yet also inherent shortcomings of the Hypo+IGS model were pointed out.

Finally, a numerical study on the cyclic SSI of an integral bridge with different granular backfill materials was conducted. Here, the calibrated gravel backfill material was compared to several Hypo+IGS parameter sets from the literature. The results indicate that the IGS parameters $\beta _r$ and $\chi$, which require extensive laboratory testing for a thorough calibration, do not have the most dominant influence and thus the choice of default IGS parameters may be justified for similar boundary value problems. The SSI behaviour for all materials is clearly dominated by the general soil model stiffness, including the small strain (IGS) stiffness. For well-graded gravels, significantly higher cyclic earth pressures on the abutment (in summer position) resulted in comparison with analyses with poorly-graded sands, which are less suitable for bridge backfills. This might lead to an underestimation of the lateral forces on the abutment in the structural bridge design when results from numerical and/or experimental studies on the SSI of integral bridges with fine sands are being used. Thus, the numerical investigation highlights the practical relevance of the experimental programme and the calibrated gravel material set for bridge backfills.

Further research will use the experimental results to calibrate and evaluate other promising constitutive models for cyclic loading. The calibrated soil models will be employed for extensive numerical investigations on the cyclic soil structure interaction behaviour of railway bridges at various geometries.

Appendix: Notations and equations of the Hypo+IGS model

The following notations were used: scalars (e.g. e) in italic fonts, second-order tensors (e.g. $\varvec{\rm{N}}$, $\varvec{{\varvec{\sigma }}}$) in bold letters and fourth-order tensors (e.g. $\varvec{\textsf{M}}$) in sans-serif font. The operations were defined as: $\varvec{\rm{A}}: \varvec{\rm{B}} = A_{\rm ij} B_{\rm ij}, \varvec{\rm{A}} \otimes \varvec{\rm{B}} = A_{\rm ij} B_{\rm kl}, \Vert \varvec{\rm{A}}\Vert = \sqrt{A_{\rm ij}: A_{\rm ij}}, ~ \overrightarrow{\varvec{\rm{A}}} =\varvec{\rm{A}} / \Vert \varvec{\rm{A}}\Vert , \hat{\varvec{\rm{A}}} = \frac{\varvec{\rm{A}}}{\text{ tr }\,\varvec{\rm{A}}}, \varvec{\rm{A}}^* = \varvec{\rm{A}} - 1/3 (\text{ tr }\,\varvec{\rm{A}})$ 1 with the second-order unit tensor 1($\delta _{\rm ij}$). The unit tensor of fourth-order is defined as $\varvec{\textsf{I}} = 0.5 ( \delta _{\rm ik}\delta _{\rm jl} + \delta _{\rm il}\delta _{\rm jk}$), with the Kronecker symbol $\delta _{\rm ij}$. Stresses and strains are defined by the effective stress tensor $\varvec{{\varvec{\sigma }}}$ and the strain tensor $\varvec{{\varvec{\varepsilon }}}$ (negative in compression) or with the Roscoe variables p, q and $\varepsilon _V$. The equations of the Hypo+IGS model are summarized in Table 5.

Table 5 Functions of the Hypo+IGS model by von Wolffersdorff [64] and Niemunis and Herle [45]