Monotonic and cyclic triaxial testing of untreated and polyurethane-treated soil and soil–rubber mixtures

Abstract

The present research focuses on developing alternate sustainable base materials for a high-speed slab track. In this study, a series of monotonic triaxial, cyclic triaxial and permeability tests were conducted on four types of materials, viz. mix-A (gravel soil), mix-B (soil mixed with rubber), mix-C (polyurethane foam adhesive (PFA)-treated soil), and mix-D (PFA-treated soil–rubber mixture). The influence of cyclic loading frequency, effective confining pressure, drainage condition and relative density on the deformation, excess pore water pressure, resilient modulus and damping ratio of these different mixes is evaluated. The monotonic triaxial test results indicate that the PFA treatment of mix-A and mix-B increased their shear strength and critical state strength. In contrast, incorporating rubber into mix-A and mix-C helped enhance their ductility. The cyclic triaxial test results show that the PFA treatment of mix-A and mix-B significantly reduced the magnitude of deformation and generation of excess pore water pressure, which caused these untreated mixes to fail prematurely under lower confinement to which a typical base layer is subjected. The influence of cyclic loading frequency and effective confining pressure on the material's response differed for untreated and treated soil. The permeability test results indicate good drainage for mix-D comparable to mix-A.

1 Introduction

The increase in the construction pace worldwide has depleted natural resources, which has led to the exploration of alternative sustainable construction materials, viz. scrap tyres. These scrap tyres have shown tremendous potential in improving the vibration attenuation capability of railway tracks compared to other expensive alternatives, such as under-sleeper pads [48] and under-ballast mats [43]. On the other hand, the influence of scrap rubber incorporation on the settlement response of granular soil is not clear. Some studies [19, 47] report reduced settlement, while others [14] observed an increase in settlement due to scrap rubber addition. Recently, a rigorous laboratory investigation was performed by Farooq and Nimbalkar [15] to investigate the influence of scrap rubber on the performance of granular soil. They observed that at low rubber content (5–10%), a reduction in the settlement is observed, while the settlement increases at higher rubber dosages. The above-mentioned studies employed a ballast box or cyclic direct simple shear (CDSS) device wherein the influence of confining pressure, which mimics track confinement, cannot be studied. Moreover, as per the author’s knowledge, no studies have been performed on the use of scrap rubber with coarse granular material that resembles in situ base and subballast materials of a slab and ballasted tracks, respectively.

Various methods have been used by researchers to reinforce the track and reduce excessive settlement, viz. track reinforcement with geogrids [5, 25], under-sleeper pads [48] and under-ballast mats [43], fibres [21], and polyurethane [15, 16, 22]. According to Wu et al. [55, 56], the incorporation of rubber into sand has been observed to diminish its strength and modulus in comparison with host sand, which exhibits a deficiency in load-bearing capacity when used as a vibration isolation material. To address this issue, some scholars [11, 38, 55, 56] have suggested the placement of geosynthetics within sand–rubber mixtures to enhance the shear strength and overall stability of the system. These studies employed triaxial equipment [38, 55], cubical test chamber [11], and large-scale cyclic simple shear apparatus [56], and showed significant improvements in shear strength [38, 55] and dynamic shear modulus [56], and reduced settlement [11] compared to unreinforced soil–rubber mixture. Moreover, the placement of geosynthetics within soil–rubber mixtures facilitated an increase in the vertical confinement of the system [55, 56]. Extensive laboratory investigations were conducted to investigate the influence of polyurethane foam adhesive (PFA) and scrap rubber on the performance of coarse sand using CDSS device under drained conditions [15]. However, CDSS device offers limitations of scale effects due to sample size restrictions and insufficient stress transfer, which can be addressed using triaxial testing of the in situ material. In addition, very limited studies [e.g. 51, 32] have focussed on the influence of cyclic loading frequency, which replicates train speed, on the behaviour of the granular soil. Sun et al. [51] observed an increase in settlement, whereas Li et al. [32] observed a reduction in settlement with increasing cyclic loading frequency, suggesting a discrepancy in the influence of frequency on settlement of granular soil. Therefore, it is essential to conduct further study in this area to arrive at a unanimous outcome. Moreover, as per the author’s knowledge, no previous study shows a detailed comparison of the influence of cyclic loading frequency and effective confining pressure on the deformation, excess pore water pressure, resilient modulus, and damping ratio of untreated and PFA-treated soil and soil–rubber mixtures. The influence of loading frequency and confinement on the material’s response may differ for untreated and treated soils.

The present research is motivated by three main factors: (1) the economic and environmental benefits associated with using scrap rubber in railway tracks; (2) rubber, being a resilient material with excellent damping characteristics, will help to absorb energy and reduce settlement of the concrete slab, which often initiates cracking in the concrete slab and is the primary cause of slab track failure; (3) non-foaming PFA acts as a binder for granular material and scrap tyre and aids in improving the ductility of the base layer, and it also helps to maintain excellent drainage for the base layer. The aim of this paper is to understand the monotonic and cyclic behaviour of four different mixtures, viz. mix-A (soil), mix-B (soil mixed with rubber), mix-C (soil treated with PFA), and mix-D (PFA-treated soil mixed with rubber), for their prospective application as a base material in railway tracks. A total of sixty-six triaxial tests (sixteen monotonic and fifty cyclic) were conducted under varying effective confining pressure and cyclic loading frequency relevant to railway tracks. Permeability tests were also performed to compare the drainage performance of these different mixtures.

2 Materials and apparatus

2.1 Material description

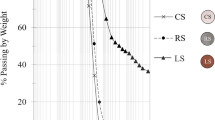
The materials, gravel, scrap rubber, and PFA, were procured from suppliers in Australia. The source of scrap rubber used in the present study comprised truck tyres and passenger car tyres, as per the supplier. The supplier processed the tyres through a Tana shark shredder, breaking down the tyres. The shredder removes the beading wire, which helps produce small crumb rubber. The produce from this shark shredder was passed through a secondary shredder, which produced metal-free crumb rubber. Next, the crumb rubber was processed through a series of granulators that removed nylon fibres using an air extraction system. Finally, the crumb rubber was graded into different sizes [9]. Eight different sizes of scrap rubber ranging from 19 to 0.075 mm were ordered and then graded as per the target PSD in this study. The particle size distribution (PSD) for base course material with 13.2 mm as nominal particle size as specified in TfNSW IC-QA-3051 [52] was adopted in this study. The PSD of the soil adopted in this study also conforms with the PSD of subballast material used in Australia, as shown in Fig. 1a. Figure 1a also shows the PSD of scrap rubber used in the present study, along with PSDs of base material/subballast adopted by previous studies [6, 20, 42, 58]. The various sizes of soil and GaR used in this study are shown in Fig. 1b and c, respectively. The compaction characteristics (maximum and minimum density) of the base material (soil) mixed with varying GaR were determined as described in AS 1289.5.5.1 [1].

Fig. 1

a Particle size distribution of materials used in the present study and comparison with previous studies, b components of soil and c GaR used in this study

2.2 Experimental setup

2.2.1 Sample preparation and testing procedure

A GDS advanced dynamic triaxial testing system (Fig. 2) was used to conduct drained monotonic and undrained cyclic triaxial tests. The cylindrical specimen [height (H) of 200 mm and diameter (D) of 100 mm, corresponding to an aspect ratio H/D = 2], were prepared with preferred gradation, as shown in Fig. 1. As shown in Fig. 1, the maximum particle size (d_max) of the soil was 13.2 mm, yielding a sample size ratio [SSR = D/d_max] of 7.6, which is higher than the minimum 6 specified in ASTM D7181 [2]. Similarly, the d_max of GaR was 9.5 mm, resulting in a SSR of 10.5. The testing plan is shown in Table 1. As shown in Table 1, sample preparation involved four mix types, viz. mix-A (soil), mix-B (soil mixed with GaR), mix-C (soil treated with PFA), and mix-D (soil mixed with GaR and PFA). In this study, most of the triaxial specimens were prepared at the optimum dosage of rubber [12, 15, 49] and PFA [15]. These optimum rubber and PFA contents were 10%. However, to compare and for more in-depth analysis, a few triaxial specimens were prepared at non-optimum GaR content, viz. 2.5 and 5% for untreated soil and 15, 20, and 25% for treated soil, and non-optimum PFA content, i.e. 15%. At PFA content of below 10%, the surface of soil and rubber particles was not sufficiently coated to bind them strongly. Hence, specimens were not prepared below 10% PFA content. The ingredients were mixed in a dry state and compacted in five different layers by adopting the undercompaction technique by Ladd [29]. More details of this technique are provided in Sect. 2.2.2. The untreated specimens (series-1) were also prepared in a dry state to enable a more accurate comparison with PFA-treated specimens because PFA-treated samples cannot be prepared with water due to their hydrophobic nature. The specimen was prepared in a loose-medium state (relative density = 40%) to ensure the dilatancy caused by the PFA improvement is directly attributed to adhesion offered by PFA. The sample preparation of the PFA-treated soil-rubber specimen is illustrated in Fig. 3; more details of the sample preparation of the PFA-treated specimen are provided in Farooq and Nimbalkar [16]. In order to prevent the sharp edges of the gravel particles from puncturing the membrane, the specimens were protected by two layers of 0.7-mm-thick latex rubber membranes. The unbound specimen was prepared on the base pedestal using a split mould, while the PFA-treated specimen was prepared and cured for 24 h and then set up on the pedestal.

Fig. 2

a Advanced dynamic triaxial equipment used in this study and b schematic diagram of experimental setup

Table 1 Testing plan for monotonic and cyclic triaxial testing

Fig. 3

Preparation of PFA-treated soil–rubber mixture

A vacuum pressure of 7 kPa was applied to the top of the specimen to remove the trapped air and ensure the airtightness of the membrane. The specimen was saturated by ramping both the cell and back pressures at 0.25 kPa/min until it reached 207 and 200 kPa, respectively. The specimen was left for 24 h at the target pressures. Before testing it was ensured that Skempton's B value of 0.95 or higher was obtained. After saturation, the specimen was isotropically consolidated under σ′₃ of 10, 50, and 150 kPa. The sensors (i.e. linear variable differential transducer and pore water pressure transducer) were calibrated before testing to ensure they capture data records correctly. The monotonic triaxial (MT) tests assisted in evaluating the soil's stress–strain response under varying σ′₃. These MT tests were carried out at steady and constant strain rate of 0.1 mm/min run till vertical strain ($\varepsilon_v$) reached 25%, which was the actuator displacement limit. The cyclic triaxial (CT) tests were carried out to evaluate the performance of different mixtures at varying effective confining pressures ($\sigma^{\prime}_3$ = 10–150 kPa) and cyclic loading frequencies (f_cyc = 1–4 Hz) to replicate the railway track environment and different train speeds, respectively. This range of $\sigma^{\prime}_3$ was based on typical values for the granular layer of a railway track [50]. In this study, the f_cyc was computed with respect to vehicle speed and bogie spacing ($f_{{\text{cyc}}} = V/3.6 \lambda_b$, where V is the train speed in km/h and $\lambda_b$ is the bogie spacing in m), as used by previous studies [e.g. 17]. For instance, f_cyc of 4 Hz resembles a $V$ of 260 km/h based on $\lambda_b$ of 18 m.

The cyclic deviatoric stress (q_cyc = 300 kPa) with q_max,cyc of 310 kPa (representing axle load of 200 kN) and q_min,cyc of 10 kPa (representing in situ stress on base layer of unloaded track) was applied. The $q_{{\text{cyc}}}$ of 300 kPa exists on the base layer of a slab track and was computed using the numerical model of a slab track, as detailed in Farooq et al. [17]. The CT tests were terminated at $\varepsilon_v$ of 20% or at 50,000 load cycles, whichever occurred earlier.

2.2.2 Undercompaction method

Soil specimens are usually compacted using the wet-pouring method or the application of constant compactive efforts to each layer. However, the segregation of soil particles occurs during sample preparation using wet pouring. Besides, the density of the specimen compacted using both these methods is non-uniform, with higher densities for the bottom layers and lower densities for the top layers of the specimen. A procedure was developed by Ladd [29] known as the undercompaction method to overcome these limitations. According to this method, each layer is compacted to a selected percentage of the target unit weight of the specimen, using Eq. (1) [29].

$$U_n = U_{ni} - \left[ {\frac{{\left( {U_{ni} - U_{nt} } \right)}}{n_t - 1} \times (n - 1)} \right]$$

(1)

where $U_{ni}$ is the percent undercompaction selected for the first layer; $U_{nt}$ is the percent undercompaction selected for the final layer (usually zero); n is the number of the layer being considered; $n_t$ is the total number of layers.

All specimens were prepared in five layers. In this study, an undercompaction of 6% was considered for the first layer. Hence, using Eq. (1), $U_n$ was computed for all specimens as 6, 4.5, 3, 1.5, and 0% for layer numbers 1, 2, 3, 4, and 5, respectively.

2.2.3 Drainage condition

Drainage condition during monotonic and cyclic loading depends on the purpose and prospective application. For instance, undrained conditions are adopted for liquefaction studies [59] and studies on railway subgrade [12]. Undrained conditions are also relevant to high-speed slab tracks where dissipation of excess pore pressure does not occur. On the other hand, drained conditions are suitable for studies on ballast and subballast material of ballasted tracks [50], where excess pore pressure gets quickly dissipated.

In this study, thirteen MT tests were performed under drained conditions to obtain the shear strength parameters, viz. cohesion and peak friction angle, the critical state parameters, viz. critical state friction angle, and volume change behaviour, viz. maximum compression or dilatancy of the different mixtures. Forty-six CT tests were performed under cyclic undrained conditions, representing the adverse in situ conditions relevant to a slab track. Three MT and four 4 CT tests were performed under undrained and drained conditions, respectively, for comparison purposes.

2.2.4 Choice of soil stabiliser and environmental implications of PFA

Chemical soil stabilisers are classified as inorganic or organic. Conventional cement or lime-based products are the inorganic soil stabiliser that can improve the strength but often have certain problems, viz. brittleness, alkalinity and environmental pollution [8, 31]. On the other hand, polyurethanes are inorganic compounds. The PFA used in this study was a hydrophobic polymer formed by combining isocyanate and polyol. PFA is a high-quality polymer with excellent material characteristics, viz. rapid strength gain, crack resistance, non-reactivity to moisture, and environmental protection [27, 53, 57]. In comparison with lime, isocyanate and polyol are relatively environmentally friendly and durable. Organic polymer materials have great potential to be ecologically safe for soil stabilisation [33]. Due to its water resistance, durability and environmental protection, Chen et al. [8] also recommended using PFA for maritime engineering projects. As a soil stabiliser, PFA prevents the permeation of any chemicals into the ground. PFA can thus be considered an eco-friendly soil stabiliser compared to an inorganic soil stabiliser.

Reducing the use of cement and switching to organic soil stabilisers, such as PFA, in geotechnical and transport applications is expected to reduce CO₂ emissions. For example, a previous study by Chang and Cho [7] showed a 192 times reduction in CO₂ emission with the use of an organic soil stabiliser (biopolymer). The use of inorganic chemical stabilisers, such as PFA, provides benefits of water resistance, durability and environmental protection. Nonetheless, using scrap rubber with PFA-treated soil in this research would further help reduce the additional cost associated with stockpiling of these scrap tyres and minimise harmful environmental impact.

2.2.5 Influence of curing time on unconfined compressive strength of PFA-treated soil

The influence of curing time on unconfined compressive strength (q_u) was studied for triaxial specimens, as shown in Fig. 4a. It can be seen that q_u increased with increasing curing period. In the present study, a curing period of one day was adopted to keep the peak strength of the PFA-treated soil below the maximum load capacity of the triaxial equipment. The maximum load capacity of the equipment was 25 kN. Considering the twenty-eight-day q_u of 4.8 MPa of the specimen, the peak load was 37.7 kN (peak load = q_u × area = 4.8 × 1000 × 0.00785), which was well beyond the maximum load capacity of the equipment. Although one MT test, performed under an effective confining pressure of 150 kPa, could not be completed due to the load limit of the equipment, all the other MT tests were completed, as indicated in Table 2.

Fig. 4

a Influence of curing time on the unconfined compressive strength of PFA-treated soil; b comparison of unconfined compressive strength of mixture prepared using different additives against the design criteria adopted for subbase of road by different countries

Table 2 Summary of monotonic triaxial test results at peak and critical state

2.2.6 Comparison of unconfined compressive strength of PFA-treated soil with other additives

Figure 4b shows the q_u of soil at 28 days treated with different stabilisers, viz. stabiliser-a (cement: fly ash = 80:20%), stabiliser-b (cement: fly ash = 60:40%), stabiliser-c (cement: fly ash: bottom ash = 56:14:30%), stabiliser-d (cement: fly ash: bottom ash = 42:28:30%), stabiliser-e (xanthum gum), and stabiliser-f (PFA). The stabilisers a, b, c, and d were used at 7% by weight of soil [30]. The content of xanthum gum and PFA used was 2 and 10%, respectively, by weight of soil. A comparison of q_u of soil treated with these stabilisers against design criteria mentioned in standards of different countries is shown in Fig. 4b (Australia [36], USA [28], India [26], and Korea [41]). It can be observed that the soil stabilised with PFA satisfied the design criteria of subbases recommended by different countries.

3 Experiment results and discussion of static triaxial testing

3.1 Stress–strain response

Figure 5 shows the drained stress–strain response of different mixtures, viz. mix-A, mix-B, mix-C, and mix-D, under various σ′₃ (i.e. 10, 50 and 150 kPa). It can be observed that the deviatoric stress [q] rises with $\varepsilon_v$ until peak deviatoric stress [$q_{{\text{peak}}}$] is reached (represented by a solid orange rhombus in Fig. 5a–d). There is little strain softening for untreated mixtures (mix-A and mix-B) due to their loose-medium state (RD = 40%). Asghari et al. [3] noted a similar strain softening tendency for gravelly sand compacted at RD of 50–60%. However, there is a noticeable strain softening when 10% PFA is added to mixes A and B. This complements the previous work of Xiao et al. [57], where the authors observed that the PFA-treated soil exhibits strain softening and dilatancy behaviour up to σ′₃ of 300 kPa. The q at the end of the test (i.e. $\varepsilon_v$ = 25%) is referred to as critical state deviatoric stress $[q_{{\text{cs}}} ]$ because the sample showed nearly constant $\varepsilon_{{\text{vol}}}$. The $q_{{\text{peak}}}$ and strain softening reduced with increasing σ′₃. However, under the same σ′₃, the addition of GaR reduced $q_{{\text{peak}}}$ and $q_{{\text{cs}}}$, while the addition of PFA increased both $q_{{\text{peak}}}$ and $q_{{\text{cs}}}$. Note that the $\varepsilon_{{\text{vol}}}$ of mix-B stabilised the least compared to the other mixes, especially under lower σ′₃ of 10 and 50 kPa. This is because the GaR particles continued to deform until the end of the test and prevented the attainment of constant $\varepsilon_{{\text{vol}}}$. The addition of PFA to mix-B helped to attain constant $\varepsilon_{{\text{vol}}}$ and achieve critical state.

Fig. 5

Static response of different mixtures: a–d deviatoric stress versus vertical strain and e–h volumetric strain versus vertical strain

All of the mixtures had minor volumetric contraction in comparison with dilation under σ′₃ of 10 and 50 kPa, as illustrated in Fig. 5e–h. At σ′₃ of 150, the volumetric contraction increased for all mixture types, with mix-B only exhibiting compressive behaviour. Therefore, utilising simply GaR may result in excessive track settlement, even with some damping enhancement. These excessive track settlements brought on by the introduction of GaR in the railway track can be reduced by PFA treatment of mix-B. As can be seen in Fig. 5h, when PFA was added to soil + 10% GaR (mix-B), the mix's behaviour transformed from contractive to dilative. The $q_{{\text{peak}}}$ and $q_{{\text{cs}}}$ are not reported for mix-C tested under σ′₃ of 150 kPa due to the termination of the test after reaching the maximum vertical load limit of the equipment, viz. 25 kN.

Referring to Fig. 6a, a comparison of the drained and undrained MT tests for mix-D illustrates that, for a specific σ′₃, $\varepsilon_v$ associated with the $q_{{\text{peak}}}$ was higher in the undrained specimen. Nevertheless, the softening was higher in the drained tests compared to the undrained tests indicating a more brittle behaviour for the drained specimen. This difference in the softening response of treated granular soil sheared under drained and undrained conditions agrees with the previous work of Haeri et al. [23] and Malandraki and Toll [37]. Figure 6b shows the variation of excess pore water pressure [$\Delta u$] with $\varepsilon_v$ for mix-D under the entire range of σ′₃ (i.e. σ′₃ = 10–150 kPa). It can be seen that mix-D at the beginning of loading showed a slight positive $\Delta u$ followed by a large negative $\Delta u$. This positive and negative $\Delta u$ represents the contractive and dilative behaviour of mix-D. The amount of positive $\Delta u$ increased with increasing σ′₃, and the negative $\Delta u$ reduced with an increase in σ′₃. After $\varepsilon_v$ = 14%, the $\Delta u$ stabilised to a constant value over the entire range of σ′₃ signifying the achievement of a critical state.

Fig. 6

a Comparison of deviatoric stress versus vertical strain for soil + 10% GaR + 10% PFA (mix-D) sheared under drained and undrained conditions and b change in pore water pressure versus vertical strain for mix-D tested under undrained conditions

3.2 Initial tangent modulus and brittleness index

The initial tangent modulus [E_i] represents the short-term static modulus of elasticity, which is used to assess the initial elastic deformation of the soil. E_i inversely correlates to the ductility of the soil; that is, the lower the E_i, the higher the ductility. E_i for different mixtures was determined by approximating stress–strain behaviour till $q_{{\text{peak}}}$ as hyperbolic, which is given by Eq. (2) [13].

$$q = \frac{\varepsilon_a }{{a + b\varepsilon_a }}$$

(2)

where a and b are the model parameters, which are obtained by curve fitting of the test data; 1/a represents the E_i.

Figure 7a illustrates a 3D representation of the variation of E_i sheared at different σ′₃ for mix-A, B, C and D. It can be seen that an increase in σ′₃ increased the E_i of all mixes. The addition of 10% GaR reduced the E_i of soil and PFA-treated soil, stipulating a reduction in stiffness and improved ductility of the mix. For instance, adding 10% GaR to soil (mix-A) and PFA-treated soil (mix-C) reduced E_i by 92 and 85.4%, respectively, sheared at σ′₃ of 10 kPa.

Fig. 7

a Variation of initial tangent modulus for different mixtures and b variation of brittleness index for different mixtures

Another measure of the ductility of soil is the brittleness index [I_B] given by Consoli et al. [10] and is represented by Eq. (3).

$$I_B = \frac{{q_{{\text{peak}}} }}{{q_{{\text{cs}}} }} - 1$$

(3)

where $q_{{\text{peak}}}$ is the peak deviatoric stress and $q_{{\text{cs}}}$ is the critical state or residual deviatoric stress.

Similar to E_i, I_B is inversely related to the ductility of the material. The cement treatment of soil can result in an increase in the strength but also increases its brittleness (i.e. reduces its ductility). This behaviour is reported by previous studies performed on Portland-cemented silty sand [45], Portland-cemented Ottawa sand [54], lime-treated gravelly sand [3], and gypsum-treated gravelly sand [23]. The ductility of soil is a major factor in the construction of railway tracks, and the comparison of $I_B$ of different mixtures considered in this study will help to evaluate the feasibility of using these mixtures in the field. Figure 7b shows the variation in the $I_B$ for different mixtures tested under varying σ′₃. Generally, an increase in σ′₃ reduces the $I_{\text{B}}$ of the soil. The reduction in $I_B$ on increasing σ′₃ from 10 to 150 kPa for mix-A, mix-B, mix-C, and mix-D was 72.2, 38.5, 94.8, and 87.8%, respectively. The smallest reduction in $I_B$ on increasing σ′₃ for mix-B indicates that GaR is more effective in improving the ductility of soil subjected to lower σ′₃. The treatment of soil (mix-A) with 10% PFA increases $I_B$ drastically from 0.54 to 38.9 at lower σ′₃ of 10 kPa. On the contrary, adding 10% GaR to soil and PFA-treated soil reduces the $I_B$ (at σ′₃ = 10 kPa) by 77.4 and 75.9%, respectively. Similarly, at σ′₃ of 150 kPa, a reduction in $I_B$ on GaR incorporation is more than 45% for soil. As shown in Fig. 7b, $I_B$ for mix-C tested under σ′₃ of 150 kPa is not reported due to the load limit of the equipment (i.e. 25 kN). Hence, an additional test was performed for mix-C at σ′₃ of 30 kPa. Although incorporation of GaR in both untreated and PFA-treated soil proved advantageous in improving ductility, a more pronounced benefit is realised for PFA-treated soil due to the substantial strength gain due to PFA treatment, as explained in Sect. 3.3.

One might argue that using PFA at lower dosages (i.e. PFA content < 10%) would reduce $I_B$, making the mix more ductile. However, due to the type of PFA used in our research, viz. non-foaming, it was not possible to entirely coat the soil and rubber particles at lower PFA contents. The rationale behind adopting non-foaming PFA was to avert the filling of voids, which prevented a reduction in the permeability of the mix and thus minimised the development of excess pore pressures. To support this argument further, the results of permeability and excess pore pressure are presented in the subsequent sections. On the other hand, with foaming PFA the mixes would be more ductile, but this foaming PFA would fill the voids, which may lead to the build-up of excess pore pressures.

3.3 Cohesion, peak and critical state friction angle, and maximum dilatancy

The cohesion [c], peak friction angle $[\emptyset_{{\text{peak}}} ]$, and critical state friction angle [$\emptyset_{{\text{cs}}}$] for different mixtures are illustrated in Fig. 8a. c and $\emptyset_{{\text{peak}}}$ were obtained from the peak envelopes for different mixtures, which were drawn using laboratory measured data of stresses. It can be seen that the addition of 10% PFA improved the shear strength of the soil, viz. c increased to 230 kPa and peak friction angle $[\emptyset_{{\text{peak}}} ]$ increased from 45° to 61.8°. Note that the peak envelopes were drawn using $q_{{\text{peak}}}$, and hence, the corresponding friction angle is designated as $\emptyset_{{\text{peak}}}$. The ultimate friction angle [$\emptyset_{{\text{ult}}}$] has not been reported. The $\emptyset_{{\text{ult}}}$ would be same as $\emptyset_{{\text{cs}}}$ as the tests were run till $\varepsilon_v$ of 25% and critical state was achieved before or at $\varepsilon_v$ of 25%. The attainment of a critical state is supported by the achievement of almost constant $\varepsilon_{{\text{vol}}}$. This is further verified later by the plot of dilatancy (Fig. 10). The dilatancy at the end of the test was zero signifying the attainment of a critical state. The $\emptyset_{{\text{cs}}}$ was computed from the slope of critical state line (M) in the $q - p^{\prime}$ plot, as shown in Fig. 9. The failure modes of untreated and PFA-treated soil–rubber mixtures are shown in Fig. 8b and c, respectively. It can be observed that both the untreated and PFA-treated soil–rubber mixtures exhibited a bulging failure mode.

Fig. 8

a Cohesion, peak and critical state friction angle of different mixes; sample before and after the static triaxial test: b soil + 10% GaR c Soil + 10% GaR + 10% PFA

Fig. 9

Comparison of stress paths for a drained and b undrained triaxial tests performed on soil + 10% PFA + 10% GaR (mix-D)

A comparison of stress paths of mix-D under drained and undrained conditions is shown in Fig. 9. The peak points of the stress path of an undrained specimen were higher than the drained specimens at lower σ′₃ of 10 and 50 kPa. The difference between the peak points of drained and undrained tests reduced with increasing σ′₃. At a higher σ′₃ of 150 kPa, the peak points of the stress paths for undrained specimen were slightly lower than the drained ones. The same behaviour was observed by Haeri et al. [23] on gypsum-treated gravely sands; however, a reduction in the peak points of the stress path in the undrained condition compared to drained ones occurred after σ′₃ of 300 kPa. This difference may be due to different chemicals used for treatment.

The $\emptyset_{{\text{cs}}}$ is computed using Eq. (4) [44].

$$\emptyset_{{\text{cs}}} = \sin^{ - 1} \frac{3M}{{6 + M}}$$

(4)

where M is the slope of critical state line.

A summary of the static triaxial test results (at peak and critical state), viz. deviatoric stress [q], mean effective stress [p′], vertical strain [$\varepsilon_v$], volumetric strain [$\varepsilon_{{\text{vol}}}$] for drained conditions and excess pore pressure [${\Delta }u$] for undrained conditions, is given in Table 2.

In this study, the stress–dilatancy relationship of different mixtures (mix-A, B, C, and D) is illustrated in Fig. 10. Figure 10a shows the experimental data of PFA-treated soil (mix-C) sheared under σ′₃ of 50 kPa. Note that the experimental data post maximum dilatancy are scattered (shown with blue triangles), and the average of the scattered data (shown with magenta dotted lines) was plotted. Similarly, this average was computed for different mixtures tested under σ′₃ of 10, 50 and 150 kPa, and is shown in Fig. 10b, c, and d, respectively. It can be observed that for all mixtures, the stress–dilatancy curves shifted from contraction to dilation before reaching maximum dilatancy and then reversed back towards zero dilatancy. The stress–dilatancy correlation tends to be most linear for PFA-treated soils, followed by PFA-treated soil–rubber mixture. The peak stress ratio and maximum dilatancy decreased with an increase of σ′₃. The reduction is maximum for PFA-treated soil and the lowest for soil + 10% GaR. Overall, after the curve is shifted on the right, the dilatancy of the PFA-treated soil (mix-C) was significantly higher than the other mixtures. The PFA-treated soil quickly reached the $q_{{\text{peak}}}$ and dilated, manifesting strain softening behaviour. This shows that dilatancy occurred after the rapid cementation breakage of the PFA-cemented soil, leading to brittle failure. On the contrary, for the PFA-treated soil–GaR mixture (mix-D), a gradual change in dilatancy with the increment of stress was observed, suggesting that GaR was effective in improving the brittle failure of PFA-treated soil. The plot of maximum dilatancy (Fig. 10e) shows that the addition of GaR reduced the maximum dilatancy of soil. In contrast, the incorporation of PFA significantly increased the dilatancy of the soil and soil–GaR mixture.

Fig. 10

a Experimental data of stress–dilatancy relationship for soil + 10% PFA (mix-C) tested at σ′₃ = 50 kPa; stress–dilatancy relationship of different mixtures at σ′₃: b 10 kPa c 50 kPa and d150 kPa; e maximum dilatancy of different mixtures under σ′₃ = 10, 50 and 150 kPa

Overall, an increase in σ′₃ led to a reduction in the maximum dilatancy. At lower σ′₃ of 10 kPa, the addition of 10% GaR to the soil reduced the maximum dilatancy by 3.6%. However, at σ′₃ of 50 and 150 kPa, the reduction in the maximum dilatancy after GaR addition increased to 27.8 and 26.2%, respectively. This shows that the maximum dilatancy reduced substantially beyond σ′₃ of 50 kPa, and GaR addition is more suitable for tracks subjected to very low lateral confinement, viz. σ′₃ of 10 kPa. This reduced dilatancy leads to the lower strength of the soil–GaR mixture. On the contrary, the PFA treatment of the soil and soil + GaR mixture increased the maximum dilatancy by 604 and 228%, respectively, at σ′₃ of 10 kPa. At a higher σ′₃ of 50 kPa, the percentage increase in the dilatancy of soil and soil + GaR mixture became comparable at 340 and 307%, respectively. This suggests that with an increase in σ′₃, there was a reduction in the maximum dilatancy of PFA-treated soil and an increase in the maximum dilatancy of the PFA-treated soil-GaR mixture. Hence, the mix-D showed a consistent maximum dilatancy (viz. consistent strength gain) over the wide range of σ′₃. This makes this mix-D very suitable for railway tracks, which are subjected to a wide range of confinement. Also, in the case of a slab track, it is deemed to have consistent material performance due to very high maintenance costs. Hence, this mix-D proves to be a suitable substitute for a conventional cement-treated base layer.

4 Experiment results and discussion of cyclic triaxial testing

The cyclic loading tests on mix-A, mix-B, mix-C, and mix-D were conducted stress-controlled at a loading frequency of 1, 2, and 4 Hz and σ′₃ of 10, 50 and 150 kPa. The specimen response was periodically recorded during the 50,000 load cycles. The linear variable differential transducer and pore water pressure transducer were calibrated before a new test to capture the readings correctly.

4.1 Influence of rubber content on the residual vertical strain, residual excess pore pressure, resilient modulus and damping ratio of soil

The response of soil (Mix-A), when subjected to cyclic loading under σ′₃ of 10 kPa, is shown in Fig. 11. Only an initial 100 load cycles are shown for better clarity as the same trend continues over the accumulated cycles. Figure 11 also shows the residual values of vertical strain (permanent deformation) and excess pore water pressure (indicated by half-shaded pink circles). These residual vertical strains [$\varepsilon_{{\text{vr}}}$] and residual pore water pressures [$\Delta u_r$] for different specimens subjected to varying σ′₃ and f_c are plotted in subsequent figures.

Fig. 11

Soil response with the number of load cycles: a vertical strain and b excess pore water pressure

The influence of rubber on $\varepsilon_{{\text{vr}}}$, shear modulus [G] and damping ratio [D_R] was evaluated under drained (constant normal load) conditions by Farooq and Nimbalkar [15]. In CDSS equipment, σ′₃ could not be applied. In cyclic triaxial testing, undrained conditions appropriate to high-speed slab track were adopted. Hence, to verify the results obtained through CDSS testing, two additional undrained cyclic triaxial tests of soil mixed with 2.5 and 5% GaR were performed under σ′₃ of 50 kPa and f_c of 1 Hz. Figure 12 shows the variation of $\varepsilon_{{\text{vr}}}$, $\Delta u_r$, resilient modulus [M_R], and D_R of soil mixed with 2.5, 5 and 10% GaR. It is observed that the results of $\varepsilon_{{\text{vr}}}$, M_R, and D_R are consistent with CDSS testing, viz. an increase in GaR content increased the $\varepsilon_{{\text{vr}}}$ and D_R and reduced the M_R of the soil. Specifically, an increase in granulated rubber (GaR) content has led to increase in $\varepsilon_{{\text{vr}}}$ and D_R and a decrease in M_R of the soil. For instance, the resilient modulus of soil mixed with 2.5, 5 and 10% GaR was 23.0, 11.1 and 5.8 MPa, respectively, measured at 100th load cycle. In comparison, the resilient modulus of soil without GaR was 45.4 MPa at the 100th load cycles. The 100th load cycle is selected for comparison purposes. The soil without GaR sustained 50,000 load cycles with $\varepsilon_{{\text{vr}}}$ of 4% at the end of the test. The addition of 2.5, 5 and 10% GaR to soil has caused the premature failure of specimen, with specimen reaching $\varepsilon_{{\text{vr}}}$ of 20% at 4000, 750 and 113 load cycles, respectively. The D_R of soil mixed with 2.5, 5 and 10% GaR was 10.0, 11.7 and 15.1%, respectively, measured at 100th load cycle. In contrast, the D_R of soil without GaR was 6.6 corresponding to 100th load cycle. From the aforementioned discussion, it is evident that the addition of GaR to soil has contributed to enhanced flexibility and energy absorption capacity, which was reflected via increase in D_R. However, it has also resulted in a reduction in M_R, indicating reduced strength and higher $\varepsilon_{{\text{vr}}}$ (settlement). Furthermore, the reduced strength of soil with incorporation of GaR is depicted through a reduction in peak and critical state friction angles, as shown previously in Fig. 8a. Therefore, it is recommended to adopt stabilising agent, such as PFA, to increase the strength of these soil–rubber mixtures. The influence of GaR addition on the $\Delta u_r$ of the soil was insignificant. A slight reduction in $\Delta u_r$ was observed with an increase in GaR content. In the next section, the influence of rubber content on $\varepsilon_{{\text{vr}}}$, $\Delta u_r$, M_R, and D_R of PFA-treated soil and PFA-treated soil–rubber mixtures is discussed.

Fig. 12

Influence of rubber content on a residual vertical strain, b residual excess pore water pressure, c resilient modulus, d damping ratio of soil, tested under σ′₃ = 50 kPa

4.2 Influence of rubber content on the residual vertical strain, residual excess pore pressure, resilient modulus and damping ratio of PFA-treated soil

Figure 13 illustrates the $\varepsilon_{{\text{vr}}}$, $\Delta u_r$, M_R, and D_R of PFA-treated soil (PFA = 10 and 15%) and PFA-treated soil–rubber mixtures (PFA = 10%, GaR = 10, 15, 20, and 25%). The specimens were tested under σ′₃ of 10 kPa and f_c of 1 Hz. PFA-treated soil showed similar behaviour in terms of $\varepsilon_{{\text{vr}}}$, M_R, and D_R as shown by untreated soil. Increase in PFA content above 10% led to a slight increase in $\varepsilon_{{\text{vr}}}$ of PFA-treated soil. This marginal increase in $\varepsilon_{{\text{vr}}}$ is due to disintegration of excessive PFA filling the voids. A significant reduction in $\Delta u_r$ with increasing GaR was observed for PFA-treated soil–rubber mixtures. It was observed that the average D_R increased by 120% on increasing GaR content from 10 to 25% for the PFA-treated soil–rubber mixture. However, the mix comprising soil + 10% PFA + 25% GaR failed prematurely with $\varepsilon_{{\text{vr}}}$ of 20% at 2240 load cycles. On the other hand, a substantial reduction in M_R was observed on increasing GaR content beyond 10%. For instance, on increasing GaR content from 10% to 15 and 20%, the average M_R reduced by 38.1 and 65.4%, respectively. Although higher D_R would benefit slab tracks in attenuating vibrations, strength and deformation should not be compromised. Figure 14 is plotted to compare $\varepsilon_{{\text{vr}}}$, M_R, and D_R of these different mixtures against base mixture (soil + 10% PFA). From Fig. 14, it is recommended to adopt soil + 10% PFA + 10% GaR mix as a base material for a slab track to achieve a balance between $\varepsilon_{{\text{vr}}}$, M_R, and D_R.

Fig. 13

Influence of PFA and rubber content on a residual vertical strain, b residual excess pore water pressure, c resilient modulus, d damping ratio of untreated and PFA-treated soil, tested under σ′₃ = 10 kPa

Fig. 14

Influence of GaR addition on the residual vertical strain, damping ratio and resilient modulus of PFA-treated soil normalised to base test

4.3 Cyclic drained-undrained triaxial comparison

Four consolidated-drained CT tests were performed on mix-A, mix-B, mix-C, and mix-D and compared with the consolidated-undrained CT tests. The triaxial tests were performed at a f_c of 4 Hz and under σ′₃ of 10 kPa. The $\varepsilon_{{\text{vr}}}$, volumetric strain [$\varepsilon_{{\text{vol}}}$], M_R, and D_R are presented in Fig. 15. It can be seen that $\varepsilon_{{\text{vr}}}$ of drained specimens was higher than undrained specimens. The $\varepsilon_{{\text{vol}}}$ of PFA-treated specimen was initially compressive but transited to dilative behaviour. The $\varepsilon_{{\text{vol}}}$ of soil was compressive, while $\varepsilon_{{\text{vol}}}$ of soil–rubber mixture was almost zero. M_R and D_R of untreated specimens (mix-A, mix-B) under drained conditions compared to undrained conditions were lower and higher, respectively. A reverse trend in M_R and D_R was observed for PFA-treated specimens (mix-C, mix-D).

Fig. 15

Comparison of a residual vertical strain versus number of load cycles for different mixtures sheared under drained and undrained conditions, b volumetric strain versus number of load cycles under drained conditions, c resilient modulus versus number of load cycles under drained and undrained conditions, d damping ratio versus number of load cycles under drained and undrained conditions

4.4 Cyclic undrained stress path

Figure 16 illustrates the stress paths of mix-A, B, C, and D tested cyclically under undrained conditions at a f_c of 4 Hz and under σ′₃ of 10 and 150 kPa. It can be observed from Fig. 16a that there is a drop in the q in the stress paths of mix-A and mix-B. This drop in q corresponds to excessive $\varepsilon_{{\text{vr}}}$ and specimens of mix-A and mix-B failed within 248 and 7 load cycles (i.e. $\varepsilon_{{\text{vr}}}$ = 20%), respectively, at σ′₃ of 10, shown in Fig. 17. The addition of 10% PFA to the soil (mix-A) and soil–rubber mixture (mix-B) reduced the $\varepsilon_{{\text{vr}}}$ considerably and both mixes (mix-C and mix-D) sustained 50,000 load cycles, which is depicted through stable stress paths for these mixes. On increasing the σ′₃ to 150 kPa, the stress path of mix-A also stabilised in addition to mix-C and mix-D (Fig. 16b). However, there is still a drop in q in the stress path of mix-B, and the specimen failed at 245 load cycles. This highlights the importance of PFA treatment of soil–rubber mixtures.

Fig. 16

Stress path of mix-A, B, C, and D tested cyclically under undrained conditions at effective confining pressure of a 10 kPa and b 150 kPa

Fig. 17

Influence of cyclic loading frequency on a–d residual vertical strain and e–h residual excess pore water pressure of different mixtures

4.5 Effect of cyclic loading frequency

4.5.1 Effect of cyclic loading frequency and confining pressure on vertical strain and excess pore water pressure

The effect of $f_c$ under σ′₃ of 10 kPa on the $\varepsilon_{{\text{vr}}}$ and $\Delta u_r$ of mix-A, mix-B, mix-C and mix-D is illustrated in Fig. 17. It was observed that $f_c$ has a significant influence on the development of $\varepsilon_{{\text{vr}}}$ of soil and soil + 10% GaR mixtures. An increase in $f_c$ substantially increased the $\varepsilon_{{\text{vr}}}$ of the soil. For instance, on increasing $f_c$ from 1 to 4 Hz, the number of load cycles [N] required to achieve $\varepsilon_{{\text{vr}}}$ of 20% reduced from 1300 to 260 under σ′₃ of 10 kPa. Similar behaviour of increased $\varepsilon_{{\text{vr}}}$ of railway ballast with an increase in $f_c$ was observed by previous studies [4, 51]. Likewise, in the case of soil + 10% GaR mixture, on increasing $f_c$ from 1 to 4 Hz, N required to achieve $\varepsilon_{{\text{vr}}}$ of 20% reduced from 18 to 8 under σ′₃ of 10 kPa, as shown in Fig. 17b. Similar behaviour of increasing $\varepsilon_{{\text{vr}}}$ with increased $f_c$ for soil and soil + 10% GaR was observed for σ′₃ of 50 and 150 kPa but with lower $\varepsilon_{{\text{vr}}}$, shown in Fig. 18. Figure 18 illustrates the accumulated vertical residual strain [$\varepsilon_{{\text{vra}}}$] and the accumulated residual excess porewater pressure [$\Delta u_{{\text{ra}}}$] of different mixtures. These $\varepsilon_{{\text{vra}}}$ and $\Delta u_{{\text{ra}}}$ have been reported for the end of test (N = 50,000) or $\varepsilon_{{\text{vr}}}$ of 20%, whichever occurred earlier, under varying σ′₃ and $f_c$. Likewise, an increase in $f_c$ and σ′₃ increased the $\Delta u_r$ for soil and soil–rubber mixture.

Fig. 18

a–d Accumulated residual vertical strain and e–h accumulated residual excess pore water pressure under varying effective confining pressure and cyclic loading frequency of different mixtures at the end of 50,000 load cycles or $\varepsilon_{{\text{vr}}}$ = 20%, whichever occurred earlier

Soil + 10% PFA (mix-C) showed a reverse trend for $\varepsilon_{{\text{vr}}}$, that is, with an increase in $f_c$, $\varepsilon_{{\text{vr}}}$ decreased or remained almost constant, as shown in Fig. 17c. This was due to a reduction in the time duration of dynamic stress to which the soil is subjected at a higher $f_c$. The amplification associated with a higher $f_c$ does not influence the mix-C. Due to PFA binding, the $\varepsilon_{{\text{vra}}}$ was negligible, viz. less than 0.2%. Also, the effect of σ′₃ on $\varepsilon_{{\text{vra}}}$ and $\Delta u_{{\text{ra}}}$ was marginal for mix-C. Similar behaviour of a reduction in $\varepsilon_{{\text{vra}}}$ with an increase in $f_c$ was observed for soil + 10% PFA + 10% GaR (mix-D) but with a slightly higher $\varepsilon_{{\text{vra}}}$ due to rubber incorporation (Fig. 17d). However, the $\varepsilon_{{\text{vra}}}$ was less than 1.2%, which was negligible. Compared to mix-C, the effect of σ′₃ on $\varepsilon_{{\text{vra}}}$ and $\Delta u_{{\text{ra}}}$ of mix-D was significant due to rubber incorporation, as shown in Fig. 18. Increasing $f_c$ led to increased $\Delta u_{{\text{ra}}}$ for both mix-C and mix-D due to a reduction in the time for the dissipation of excess pore water pressure.

4.5.2 Effect of frequency and effective confining pressure on resilient modulus and damping ratio

The effect of $f_{\text{c}}$ under σ′₃ of 10 kPa on the M_R and D_R of mix-A, mix-B, mix-C, and mix-D is illustrated in Fig. 19. M_R for untreated mixtures, viz. mix-A and mix-B, reduced with increasing $f_c$. This reduction in M_R signifies the reduced strength of mix-A at higher loading frequencies. On the contrary, D_R increased with increasing $f_c$ for mix-A and mix-B. Figure 20 shows the M_R and D_R of different mixtures under varying σ′₃ at the end of the test. An increase in σ′₃ up to 50 kPa increased the M_R of mix-A considerably, and after that, there was a marginal increase in M_R. On the other hand, the M_R of mix-B consistently increased with increasing confinement σ′₃ due to elastic nature of rubber. D_R of both untreated mixtures A and B reduced with an increase in σ′₃. The influence of $f_c$ on M_R and D_R of mix-A and B becomes insignificant at higher σ′₃ of 50 kPa. Hence, it is recommended that these untreated mixtures A and B are utilised in lower layers of the railway track, which are often subjected to higher σ′₃. Moreover, this mix-B will act as a damping layer and serve railway tracks subjected to a range of train speeds.

Fig. 19

Influence of cyclic loading frequency on: a–d resilient modulus and e–h damping ratio of different mixtures

Fig. 20

a–d Resilient modulus and e–h damping ratio under varying effective confining pressure and cyclic loading frequency of different mixtures at the end of 50,000 load cycles or $\varepsilon_{{\text{vr}}}$ = 20%, whichever occurred earlier

As shown in Fig. 19, $f_c$ has a negligible influence on the M_R of mix-C and mix-D under σ′₃ of 10 kPa. On the contrary, D_R reduced with increasing $f_c$ for mix-C across the range of σ′₃ (Fig. 20g), while for mix-D it reduced with increasing $f_c$ of up to 2 Hz and after this, D_R remained constant across the range of σ′₃ (Fig. 20h). This signifies that mix-D can act as a damping layer providing consistent damping that is marginally reduced at higher train speeds and higher confinement. Therefore, this mix-D is suitable for use as a base and subbase layers in high-speed slab tracks, which often are subjected to high vibrations and varying confinements.

4.6 Effect of relative density on the vertical strain, excess pore water pressure, resilient modulus and damping ratio

All the samples in the experiment were prepared at a relative density [RD] of 40. This lower RD was intended to help differentiate the influence of PFA cementation on dilatancy from that of grain packing configuration [54]. However, in the field, materials are usually compacted in a dense state. To study the impact of higher RD on the performance of mix-A, mix-B, mix-C, and mix-D in terms of $\varepsilon_{{\text{vra}}}$, $\Delta u_{{\text{ra}}}$, M_R, and D_R, one specimen of each mix type was prepared in a dense state (at RD of 90%). These mixtures were then tested cyclically at q_cyc of 300 kPa under σ′₃ of 10 kPa and $f_c$ of 4 Hz for 50,000 load cycles or 20% $\varepsilon_v$, whichever occurred first. Figure 20a, b, c, and d illustrates the $\varepsilon_{{\text{vra}}}$, $\Delta u_{{\text{ra}}}$, M_R, and D_R, respectively, of mix-A, mix-B, mix-C and mix-D prepared at RD of 40 and 90%. As shown in Fig. 21a, it can be observed that soil prepared at RD of 40% failed prematurely after application of 248 N; however, mix-A prepared at RD of 90% sustained 50,000 load cycles with $\varepsilon_v$ of 16.3% at the end of the test. The influence of higher compactness on $\varepsilon_v$ of mix-B was insignificant as the mix still failed prematurely despite being prepared at a higher RD, as shown in Fig. 21b. The mix-B specimen prepared at RD of 90% failed at N of 46 compared to N of 9 for a specimen prepared at RD of 40%. Hence, this mix-B is not recommended as a base layer in a slab track subjected to a lower σ′₃ of 10 kPa and a high q of 300 kPa. From Fig. 20c and d, it can be seen that although lower values of $\varepsilon_{{\text{vra}}}$ were recorded for mix-C and mix-D prepared in a dense state, the difference was marginal. Hence, producing mix-C and mix-D at lower RD in the field would translate to savings through lower material consumption and lower compaction effort.

Fig. 21

Influence of relative density on a residual vertical strain, b residual excess pore water pressure, c resilient modulus, d damping ratio of different mixtures at the end of 50,000 load cycles or $\varepsilon_{{\text{vr}}}$ = 20%, whichever occurred earlier, tested under effective confining pressure of 10 kPa and cyclic loading frequency of 4 Hz

In terms of $\Delta u_{{\text{ra}}}$ (Fig. 21b), the influence of RD was the least. The $\Delta u_{{\text{ra}}}$ of all mixtures prepared at RD of 90%, except mix-B, was the same or slightly lower than the mix compacted at RD of 40%. This higher initial negative $\Delta u$ of mix-B prepared at RD of 40% was due to the loose-medium state of the mixture and the compressible nature of GaR. Under lower σ′₃ and high $q_{{\text{cyc}}}$ of 300 kPa, the GaR is compressed instantaneously, leading to the creation of voids in the soil–GaR matrix. The pore water which develops in voids can flow into the spaces created by deformed particles leading to negative $\Delta u_r$. For the mix-B prepared at a higher RD of 90%, the compression of the rubber is lower due to the higher compactness of the mix, and there are fewer void spaces created in the soil–GaR matrix. Hence, there is less pore water migration, leading to higher values of $\Delta u_{{\text{ra}}}$.

Figure 21c shows that an increase in RD increased the M_R of all mix types, which is obvious. The higher the compactness, the higher will be the shear strength of the material. D_R, on the contrary, was reduced with an increase in RD for all mixtures except mix-D, as shown in Fig. 21d. It is important to note that an increase of 25% in D_R for mix-D was observed at a higher RD of 90% compared to RD of 40%. This finding signifies that a PFA-treated soil–rubber mixture compacted at higher RD showed higher modulus and damping and is better suited for use as a base layer for a slab track.

4.7 Permeability

The coefficient of permeability in the vertical direction [$k_v$] is calculated using Eq. (5).

$$k_v = \frac{\rho \times Q \times L}{{A \times \Delta p}}$$

(5)

where $\rho$ is the density of water (kg/m³), Q is the mean rate of flow through the soil specimen (m³/s), L is the height of the specimen (m), A is the cross-sectional area (m²), $\Delta p$ is the pressure difference between the pressure applied to the top and base back pressure lines (kPa).

Figure 22 compares the $k_v$ for mix-A, mix-B, mix-C, mix-C2 (soil + 15% PFA) and mix-D. The $k_v$ of the soil (mix-A) was $5.99 \times 10^{ - 5}$ m/s and reduced to $4.98 \times 10^{ - 5}$ m/s on the addition of 10% GaR to the soil. Similar observations of reduction in permeability on the increase in rubber content were observed by Madhusudhan et al. [34] and Masad et al. [39]. Shariatmadari et al. [46] assessed the permeability of gravel mixed with different sizes and contents of scrap rubber. Three types of tyre shreds were used, viz. large (19–9.5 mm), medium (9.5–4.75 mm) and fine (4.75–2 mm) at contents of 0–100%. It was observed that adding medium and fine rubber particles to gravel decreased the permeability of the mix due to a reduction in voids. Conversely, adding large tyre shreds increased the permeability of the soil–rubber mixture. In the present study, rubber particle size ranged between 9.5 and 0.075 mm; hence, a reduction in $k_v$ was observed. During the saturation phase, the finer rubber particle moved to void space offering resistance to the flow of water through the intricate paths, leading to reduction in $k_v$. The $k_v$ of mix-C and mix-D was comparable with mix-A at $5.83 \times 10^{ - 5}$ m/s and $5.94 \times 10^{ - 5}$ m/s, respectively. The addition of PFA to soil–rubber mixture binded the soil and rubber particles together, preventing their movement during saturation stage and creating paths for easy flow of water. Hence, a reduction in $k_v$ was not observed for mix-D. It is worth mentioning that non-foaming PFA was used in this study at an optimum dosage, which was sufficient to coat the particles but did not occupy the voids. On increasing the PFA dosage from 10 to 15%, a significant drop of 87.3% in $k_v$ was observed. This reduction in $k_v$ for mix-C2 is due to filling the void by PFA when used more than the optimum dosage.

Fig. 22

Comparison of coefficient of vertical permeability of different mixtures

4.8 Practical applications of different mixtures

Due to its high degree of rigidity, concrete is widely recognised for its minimal deformations. However, the placement of the concrete base and concrete slab in close proximity to one another results in excessive noise and vibration. One potential solution to this issue is to reduce the rigidity of the base layer. However, repeated train loads can cause the base layer with lower stiffness to crack, leading to excessive track settlement. Furthermore, the operation of high-speed rail can result in the accumulation of excess pore water pressure, which accelerates the breakdown of the impermeable concrete base layer. Ultimately, the concrete slab track fails due to the propagation of base layer cracks to the concrete slab through reflection cracking.

Undoubtedly, the GaR incorporation in mix-A improved the damping ratio [D_R] but significantly reduced the resilient modulus [M_R] signifying a reduction in strength and led to premature failure of specimen due to excessive settlement. This signifies that mix-B is not recommended to be used as a base layer subjected to lower confinement. PFA treatment of mix -A (soil) improved the strength and reduced the deformation of the base layer; however, the D_R reduced considerably. This reduced D_R relates to higher vibration levels of a track. PFA treatment of mix-B (soil–rubber mixture) helped to strike a balance between deformation, strength, and D_R. Moreover, the permeability test results, as shown in Sect. 4.7, indicated that the drainage was not impeded for mix-C (PFA-treated soil) and mix-D (PFA-treated soil rubber mixture) due to the use of non-foaming PFA. This non-foaming PFA coats the soil and rubber particles but does not fill the voids. Therefore, this non-foaming PFA helps to mitigate the formation of excess pore water pressure in high-speed railways. This argument is supported by reduced levels of excess pore water pressure of mix-C and mix-D, which were observed during undrained cyclic triaxial testing, as detailed in Sect. 4.5.1. Hence, both these PFA-treated mixtures have practical relevance to be used for high-speed railways providing excellent strength and reduced generation of excess pore pressures.

The evaluation of the effect of cyclic loading frequency [$f_c$] relates to the train speed. The results suggest an increase in deformation with increasing train speeds for untreated mixtures (mix-A and mix-B) and reduction in deformation with increasing train speeds for PFA-treated mixtures. The influence of $f_c$ on M_R and D_R of mix-A and B becomes insignificant at higher σ′₃ of 50 kPa. Hence, it is recommended that these untreated mixtures A and B are utilised in lower layers of the railway track, which are often subjected to higher σ′₃. The $f_c$ has negligible influence on the M_R of mix-C and mix-D under σ′₃ of 10 kPa. On the contrary, D_R for mix-D reduced with increasing $f_c$ of up to 2 Hz and after this, D_R remained constant across the range of σ′₃. This signifies that mix-D can act as a damping layer providing consistent damping that is marginally reduced at higher train speeds and higher confinement. Therefore, this mix-D is suitable for use as a base and subbase layers in high-speed slab tracks, which often are subjected to high vibrations and varying confinements. Evaluating the influence of relative density on performance of mixtures signified the importance of adopting mix-D at higher compactness for railway tracks, which require higher vibration reduction albeit slightly higher cost.

Finally, although the research was motivated towards developing a base/subbase layer for a high-speed slab track, this novel material (mix-D) can be applied to other areas, such as ballasted tracks and roads. The secondary applications of this novel material can be recommended as subbase and subballast layers. In ballasted track, if a more economical solution is sought, mix-B is also recommended as a subballast material.

4.9 Environmental implications of using TDA

Due to the benefits of preserving landfill space, producing useful products, preventing the spread of disease, as well as preventing fires and pollution, recycling scrap tyres into tyre-derived aggregates (TDA) is generally seen as a sustainable alternative [18]. But there are some environmental and health issues that need to be addressed with the use of TDA in construction purposes. Leachate studies on hazardous organic chemicals and other essential environmental testing can be used to evaluate these environmental consequences. As a result, recycling waste tyres would have the least amount of influence on the environment [40]. A few previous studies [e.g. 24, 35] evaluated the effect of scrap rubber leaching on the water quality. Humphrey and Swett [24] found that the amount of metal leaching was insignificant according to primary drinking water standards. Maeda and Finney [35] studied the potential water quality contaminants leach from TDA as a function of time using laboratory and field experiments. Based on the aforementioned findings, TDA can be utilised as a water-saturated fill material without running the danger of causing a short-term or long-term risks to the water quality of receiving water bodies. The aforementioned studies demonstrate that the use of TDA would have negligible impact on the environment. The present study employed metal-free TDA, which suggests that it is a suitable construction material due to its reduced leaching. The objective of the study is to employ TDA as the foundation layer of a railway track in a dry environment by ensuring efficient drainage. In addition, adding PFA to the soil–rubber mixture would prevent the rubber from deteriorating. The entire mixture (soil + GR + PFA) would have minimal impact on the ground water contamination owing to the PFA's hydrophobic properties.

5 Conclusions

The present study uses an experimental approach based on a series of monotonic triaxial and cyclic triaxial tests to assess the suitability of four types of mixes as a base and subballast layers in slab and ballasted tracks, respectively. These mixes include mix-A (soil), mix-B (rubber mixed soil), mix-C (PFA-treated soil), and mix-D (PFA-treated soil–rubber mixture). The monotonic response of the specimens was evaluated under effective confining pressure [σ′₃] of 10, 50, and 150 kPa. The cyclic response was investigated under varying cyclic loading frequencies [f_c] of 1, 2, and 4 Hz and under σ′₃ of 10, 50, and 150 kPa. The following conclusions are drawn from this study:

• The curing time had a significant impact on the unconfined compressive strength of the PFA-treated soil specimen. Nevertheless, the PFA-treated specimen exhibited significantly higher early strength gain than the concrete specimens.

• Incorporating granulated rubber (GaR) into mix-A and mix-C enhanced the ductility of the mix. This improved ductility was reflected through reduction in the initial tangent modulus and brittleness index of mix-A and mix-C. Mix-D showed a consistent maximum dilatancy (viz. consistent strength gain) over the wide range of σ′₃. This makes this mix-D very suitable for railway tracks.

• The PFA treatment of mix-A and mix-B increased their shear strength and critical state strength. Both the peak and critical state friction angles of mix-A and mix-B increased on PFA treatment.

• The addition of GaR improved the damping ratio [D_R] while reducing the resilient modulus [M_R] and increasing the residual vertical strain [ε_vr]. On the contrary, a reverse trend was observed with PFA treatment for D_R, M_R, and ε_vr. A drastic reduction in M_R of PFA-treated soil–rubber specimen was observed with a slight increase in D_R and ε_vr when GaR exceeded 10%. Therefore, the optimal GaR content for PFA-treated soil–rubber mixtures is recommended as 10% to attain a harmonious balance between ε_vr, M_R, and D_R.

• It was observed that an increase in f_c increased the ε_vr and reduced the M_R of untreated mixtures (mix-A and mix-B). On the contrary, the influence of f_c on ε_vr of PFA-treated mixtures, viz. mix-C and mix-D, had a reverse effect. The influence of $f_c$ on M_R and D_R of untreated mixtures become insignificant after σ′₃ of 50 and 150 kPa, respectively. On the contrary, $f_c$ has negligible and varied influence on the M_R and D_R, respectively, of PFA-treated mixtures.

• Overall, an increase in RD reduced the accumulated residual vertical strain [ε_vra] and accumulated residual excess pore water pressure $[\Delta u_{{\text{ra}}}$] and increased the M_R of all mixtures. The impact of RD was most influential for mix-A and insignificant for mix-B, as this mix-B still failed prematurely despite being prepared at a higher RD. A marginal difference in ε_vra was recorded for mix-C and mix-D prepared at different RD. Hence, it is recommended to use these PFA-treated mixtures at a lower degree of compaction in the field, which will translate to savings through lower material consumption and lower compaction effort.

• The reduction in vertical permeability [k_v] of soil due to rubber addition was higher compared to PFA treatment of soil due to use of non-foaming PFA. The k_v of mix-D was comparable to untreated soil. Adding PFA over the optimum content decreased the k_v drastically.

In summary, the novel mix-D (soil + 10% PFA + 10% GaR) provides a sustainable alternative to the conventional base and subballast material of slab and ballasted tracks, respectively. Alternate mix, soil + 10% PFA + 15% GaR may also be utilised in cases where greater energy dissipation is required. This is particularly relevant in scenarios where the passage of high-speed rail through urban areas may result in excessive noise and vibration, thereby posing a significant challenge.