An innovative design approach for anchored wire meshes

Abstract

Anchored wire meshes are commonly adopted to stabilize potentially unstable soil slopes. This reinforcement technique, employed either as an active or a passive anchoring system, is commonly designed according to ultimate limit state approaches. In this paper, an interaction model, useful for the design of anchored wire meshes, is proposed. The model is based on the results of a series of 3D large displacement finite element numerical analyses, in which the wire mesh mechanical behaviour is modelled as either an elastic or an elastic–plastic membrane. The model is inspired to standard load–displacement curves for shallow foundations, and the wire mesh presence is taken into account by suitably modifying the bearing capacity formula. The proposed model predictions are compared with experimental punching test results. The use of the model, only requiring the definition of geometry and soil–wire mesh mechanical properties, allows the pre-design of the reinforcement system without performing ad hoc finite element numerical analyses.

1 Introduction

Anchored wire meshes [9, 30] are often employed to stabilize shallow soil layer along inclined slopes. The connection between the wire mesh and the underlying stable bedrock is possible by using either tie rods or steel nails. To both inhibit local indentation of the wires in the soil and prevent superficial slope erosion, a geotextile membrane is usually combined with the wire mesh.

This stabilisation technique is also employed when slope profiles are cut for the construction of infrastructures along slopes [2, 3, 58] and can also be adopted in case of existing infrastructures due to the negligible traffic interference during installation. The success of this stabilizing system derives from its cost-effectiveness and versatility; in fact, (i) the system is ready-made, (ii) only installation of bars/ties is time consuming, (iii) elements can be put in place even if the slope profile is not planar and (iv) the visual impact is minimal. This system is usually conceived with the aim of both transmitting a stabilizing force to the potential failure mechanism and increasing the force acting normal to the potential sliding plane. Tie rods and steel nails can be designed to work as either active or passive anchoring systems [16].

These reinforcement structures are commonly designed by employing either ultimate limit state (ULS) approaches or “hybrid methods” [27]. In both cases, the reinforced slope factor of safety is obtained by following a “sub-structuring” approach, according to which slope and reinforcements are accounted for separately. In case ULS approaches are used, the retaining structure is substituted by a force, whereas, in case of hybrid methods, the mutual interaction is schematized by means of a “characteristic curve” relating the “far field” soil displacement to the stabilizing force. Both the ultimate value of the retaining force and the characteristic curve not only depend on the wire mesh tensile strength and stiffness, but also on its local deformed configuration, this latter severely affected by both geometry and local soil response. For this reason, to properly estimate the ultimate retaining force, the local soil-structure interaction problem has to be solved by taking into consideration the local yielding of the soil, the nonlinear mechanical behaviour of the wire mesh and second-order effects (geometrical nonlinearities).

At present, both the ultimate value of the interaction force and the characteristic curve are provided by the wire mesh producers on the basis of large-scale punching experimental test results. Unfortunately, the applicability of these results is questionable since experimental data depend not only on the mechanical properties of the wire mesh, but also on soil properties and geometry adopted for the experimental test, not necessarily representative for in situ conditions.

In this paper, the authors have numerically analysed this interaction problem by performing a series of nonlinear large-displacement three-dimensional finite element numerical analyses. Both geometrical and mechanical nonlinearities are accounted for and the wire mesh along with the geotextile is modelled as an equivalent membrane (either elastic or elastic–plastic). This numerical modelling strategy represents a significant improvement with respect to the works done by (i) di Prisco et al. [16] who considered axisymmetric conditions and simplified the local wire mesh/soil interaction by means of independent nonlinear springs and (ii) Blanco-Fernandez et al. [1] who considered a two-dimensional problem and disregarded wire mesh yielding.

The final goals of the herein presented numerical analyses are the comprehension of the complex mechanical interactions between anchored wire mesh and soil and the definition of a generalized constitutive relationship (a sort of meta-model) for a quick assessment of both ultimate interaction force and system characteristic curve. This meta-model, inspired to standard load–displacement curves [7] for shallow foundations suitably modified to account the wire mesh presence for, can be used during the early stages of the design to preliminarily choose the geometry of the reinforcing interventions (above all spacing) and the required wire mesh mechanical properties.

The paper is structured as follows: in Sect. 2, the numerical analysis results are presented, in Sect. 3, the simplified model is introduced and validated and, finally, in Sect. 4, a discussion of the practical application of the model is reported.

2 Numerical analyses

2.1 Numerical model

To analyse the mechanical response of the system, the authors performed nonlinear large displacements 3D FE numerical punching tests by employing the commercial finite element (FE) code ABAQUS 2017 (https://www.3ds.com/). Large displacement approach is fundamental to reproduce wire mesh membranal behaviour [34, 35, 43, 44].

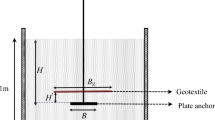
The adopted geometry is illustrated in Fig. 1a and 1b. Indeed, since the ground surface is assumed to be horizontal, the problem is symmetrical with respect to the vertical planes passing through the centre of the squared plate (Point M in Fig. 1c) and, therefore, only one quarter of the domain (S/2 × S/2 × H, where planar dimension S mimics the in situ spacing between adjacent plates and H the thickness of the unstable soil layer) is considered. As is schematised in Fig. 1a and b, the spatial domain is subdivided in soil, wire mesh and plate (subdomain P).

Fig. 1

Numerical model: a 3D geometry and imposed boundary conditions, b z–y view and c spatial discretization

To choose the most suitable spatial discretization for the domain (a good compromise between accuracy and computational times; Fig. 1c), a series of numerical analyses (hereafter omitted for brevity) was performed. Moreover, it is worth highlighting that mesh dependency problems related to strain localisation in the problem under exam are absent in the range of displacements analysed, since the wire mesh membranal behaviour promotes the spatial propagation of the yielded soil domain.

The wire mesh is numerically modelled as an equivalent isotropic membrane (the influence of its anisotropy is discussed in Appendix A), i.e. its flexural stiffness is assumed to be negligible. The authors have neglected the indentation phenomenon of mesh wires into the soil, since, in the current engineering practice, a geotextile is interposed between soil and wire mesh. The case of linear elastic membrane and elastic–plastic membranes is discussed in Sects. 2.2 and 2.3, respectively.

The soil stratum is assumed to be homogeneous and characterized by a constant unit weight value γ. Its mechanical behaviour is modelled by means of an elastic–perfectly plastic constitutive relationship with a non-associated flow rule. The elastic properties, that is Young modulus and Poisson’s ratio (E and ν, respectively), are assumed to be constant in the whole domain. The failure locus is given by the Mohr–Coulomb criterion, defined as a function of cohesion, internal friction angle and dilatancy angle (c’, ϕ’ and ψ, respectively). To improve numerical efficiency and to avoid the numerical instabilities associated with the edges of the yield function, the rounded version of the Mohr–Coulomb failure surface proposed by Panteghini and Lagioia [51, 52] and Lagioia and Panteghini [36, 37] is used. Despite its simplicity, this constitutive law can reproduce the main mechanical processes occurring in the soil domain. The results obtained by using more advanced constitutive relationships, for instance strain hardening elastic–plastic constitutive models [13, 14, 39, 40, 45, 47, 57], are expected to be very similar from a qualitative point of view. It is also worth noting that, in practice, sophisticated constitutive relationships very often cannot be properly calibrated owing to the lack of a sufficient number of laboratory/in situ tests data. For this reason, elastic–perfectly plastic constitutive relationships are still commonly adopted.

Along normal direction, the soil/membrane interface elements are perfectly fragile under tension and “quasi-rigid” under compression (interface stiffness is quite larger than the soil one). Along tangential direction, they are “quasi-rigid”-perfectly plastic: a Mohr–Coulomb failure criterion, with an interface friction angle equal to ϕ’ (in agreement with the experimental findings of [41, 42, 48] and a nil dilatancy, is assumed. The interface friction angle influence on the results was also analysed, but its role is negligible.

The steel plate, assumed to be rigid and in situ anchored by the nail, is modelled by imposing in the dark grey zone of Fig. 1 (subdomain P) nil displacements along x, y and z directions.

On the lateral boundary of the domain, normal displacements of both soil and wire mesh are not allowed. At the base of the model, the normal displacements (u_n) are controlled.

The numerical tests are subdivided in two phases: (i) imposition of gravity and (ii) displacement-controlled loading phase. In this latter phase, u_n is continuously increased. In fact, in contrast with what commonly done in the laboratory, the punching tests were performed by keeping fixed the plate and by imposing an upward normal displacement (u_n, in this case coinciding with the vertical component of the displacement) at the base of the domain ([4, 5]). This displacement field mimics the one expected to occur in real slopes. From a static perspective, imposing downward plate displacements (as in punching tests) and imposing upward far field displacements provide the same results.

2.2 Numerical results: the elastic membrane case

To highlight the mechanical response of the system, a reference case, concerning a linear elastic membrane, is discussed. In particular, the authors.

• i. analyse the response at the global scale (Sect. 2.2.1), by illustrating the evolution of retaining force F, calculated by integrating reaction forces in subdomain P, resultant force F_s of the normal/vertical stresses of the soil beneath subdomain P and resultant normal/vertical force F_w acting in the wire mesh with u_n,

• ii. discuss the mechanical processes taking place at the local scale (Sect. 2.2.2), in terms of displacement, strain and stress fields.

Geometrical dimensions, soil parameters (representative for medium–dense sand) and wire mesh properties are summarized in Table 1. The employed value of the equivalent membrane axial tensile stiffness J was derived from experimental one-dimensional tensile tests (Appendix B).

Table 1 Input data for elastic membrane case in the FE numerical model

2.2.1 Global scale response: characteristic curve determination

The characteristic curve (solid line of Fig. 2a) puts in relation u_n and F (Fig. 1). Initially, the F–u_n curve is characterized by a downward concavity, implying that irreversible strains develop in the soil domain, whereas, for larger u_n values, an upward concavity, mainly due to the progressive membrane stiffening (geometric nonlinearity; discussed in Sect. 2.2.2), is evident. To better understand the system response, in Fig. 2a, (i) F_s (dashed line) and (ii) F_w (dashed-dotted line) are also plotted. From O to A, F_s is practically equal to F and the wire mesh is practically unloaded; from A to B, most of the normal/vertical load is transferred to the soil (F_s > F_w); from B to D, the wire mesh contribution is dominant (F_w > F_s).

Fig. 2

Characteristic curves; a overall contribution (solid line), soil contribution (dashed line) and wire mesh contribution (dash-dotted line) in the reinforced reference case; b comparison between reinforced and unreinforced case

In Fig. 2b, to demonstrate the effectiveness of the reinforcing technique, the reinforced characteristic curve (solid line) is compared with the corresponding unreinforced one (i.e. J = 0): the two curves are initially superimposed, but in the unreinforced case concavity remains always negative. The comparison between the unreinforced curve of Fig. 2b and dashed curve of Fig. 2a allows us to capture the effect of the membrane on the soil mechanical response: at the very beginning, the presence of the membrane partially inhibits the development of normal/vertical stresses in the soil, for sufficiently large vertical displacements, the membrane presence, by affecting the failure mechanism in the soil, allows the soil to get progressively larger vertical stress values.

2.2.2 Local scale response

In this section, to better understand the interaction mechanisms governing the global response described in Sect. 2.2.1, (i) deviatoric plastic strains, (ii) surface settlement profile, (iii) vertical stress distribution on the ground surface and (iv) wire mesh tensile stresses are described.

Initially (Fig. 3a corresponds to point A of Fig. 2a), plastic strains do not develop, but for larger displacement values, irreversible strains (Fig. 3b–d refer to points B–D of Fig. 2a) accumulate next to the plate. The portion of the domain where irreversible strains accumulate progressively increases in size and reaches the domain boundaries, implying an interaction between adjacent plates. This plastic strain distribution significantly differs from the corresponding unreinforced ones (Fig. 3e–h refer to points A’–D’ of Fig. 2b, respectively), localized in a small subdomain next to the plate edge.

Fig. 3

Deviatoric plastic strains: a point A, b point B, c point C, d point D, e point A’, f point B’, g point C’ and h point D’ of Fig. 2b, respectively

In Fig. 4, the variation along x coordinate (Fig. 1) of u_n—u_gs, being u_gs (x, u_n) the ground surface displacements coinciding with the membrane ones, is plotted (Fig. 4a–d refer to points A–D of Fig. 2, respectively). The variable u_n − u_gs describes the displacement profile of an equivalent vertically loaded foundation, typically used when punching tests in the laboratory are performed. As is discussed in Appendix C, the presence of the soil beneath the membrane significantly increases the membrane local inclination and, consequently, its effectiveness.

Fig. 4

Ground surface and wire mesh settlement profile corresponding to a point A, b point B, c point C and d point D of Fig. 2a, respectively

Initially, irreversible strains do not accumulate (Fig. 3a) and u_n—u_gs is positive for any x value (Fig. 4a). Two zones are evident: the one where u_n—u_gs is constant and coincides with u_n (dark grey area for 0 < x < B/2, where u_gs is imposed to be nil) and the other one where u_n − u_gs is decreasing but still positive (light grey area for B/2 < x < S/2). For larger displacement values (Fig. 4b–d), when irreversible strains (Fig. 3b–d) accumulate next to the plate, negative u_n − u_gs values are observed for sufficiently large values of x. In this case, a third zone can be individuated: white area of Fig. 4b–d. The boundary between light grey and white areas of Fig. 4b–d is defined by condition x = x*(u_n), where u_n – u_gs (x*, u_n) = 0. The sub-domain for x < x*, being characterized by positive u_n − u_gs values, may be interpreted as a sort of equivalent deformable heterogeneous foundation of width B* = 2x*(u_n). B* can be defined only for u_n > $\overline{u}_{n} ,$ being $\overline{u}_{n}$ the first value of u_n for which negative u_n − u_gs values are observed.

The evolution of B* with u_n is illustrated in Fig. 5, where two branches can be identified: in the first one, B* remains practically constant with u_n (grey area), whereas, in the second one, B* linearly increases with u_n (light grey area). The first branch is got when plastic strains are still comparable with elastic strains, whereas the second one when plastic strains become predominant. In Fig. 5, the dashed line corresponds to the interpolating straight line of data belonging to the light grey area:

$${\mathcal{B}}\left( {\frac{{u_{n} }}{{{B}}}} \right) = b_{1} + b_{2} \frac{{u_{n} }}{B},$$

(1)

where b₁ and b₂ represent the intercept and the slope of the interpolating straight line, respectively. Both b₁ and b₂ are expected to be a function of soil/wire mesh properties and geometry. This is discussed in detail in Sect. 3.1.1.1.

Fig. 5

Evolution of deformable foundation dimension B^* (B, C, D points of Fig. 2a) and interpolating straight line of data belonging to the light grey area (maximum relative error equal to 3% for b₁ = 2 and b₂ = 4.1)

During the loading process, the membrane presence influences the vertical stress distribution even outside subdomain P (Fig. 1). As is shown in Fig. 6 (Fig. 6a–d refer to points A, B, C and D of Fig. 2a, respectively), the membrane outside subdomain P acts as a surcharge, but its effect is not negligible only in the B*-wide squared area. This, along with the displacement field reported in Fig. 4, suggests portion of ground surface within a square area of edge equal to B* to behave as a sort of an “equivalent deformable heterogeneous foundation”. This observation is one of the main ingredients of the model introduced in Sect. 3.

Fig. 6

Contours of vertical stresses in the soil domain corresponding to a point A, b point B, c point C and d point D of Fig. 2a

In Fig. 7 (Fig. 7a–d refer to points A, B, C and D of Fig. 2a, respectively), the contours of maximum principal (tensile) stresses in the elastic membrane are reported: tensile stresses develop in the surrounding of subdomain P (Fig. 1) but concentrate in the subdomain P corner.

Fig. 7

Contours of tensile stress in the wire mesh corresponding to a point A, b point B, c point C and d point D of Fig. 2b

The resultant force:

$$T = 2\mathop \int \limits_{0}^{{t_{m} }} \mathop \int \limits_{0}^{B/2} \sigma_{T} \left( x \right)dxdz$$

(2)

increases with u_n more than linearly (Fig. 8b) due to membrane stiffening (geometric nonlinearities), where t_m is the membrane thickness (assumed to coincide with the 2.7 mm wire diameter, Appendix B) and $\sigma_{T}$ the tensile stresses acting in the membrane along edge RS of Fig. 8a.

Fig. 8

a tensile stresses acting in the membrane along edge RS and b evolution of resultant tensile force T with u_n

2.3 Numerical results: the elastic–plastic membrane case

This section aims at validating the FE numerical model results against the experimental data reported in di Prisco et al. [16] and at highlighting the role of membrane yielding on the system response.

Indeed, in di Prisco et al. [16], experimentally performed punching tests [29] are reported, in particular two punching load-controlled tests employing a Tecco wire mesh. The experimental setup comprises a caisson filled with a compacted dry granular soil, a rigid frame at the top of the caisson to fix the wire mesh and a hollow vertical piston. The device is designed to allow the direct transmission of the pressure imposed by the piston to the steel plate. In Fig. 9, the derived range of variability of the experimental results, in terms of characteristic curve, is reported (grey zone).

Fig. 9

FE numerical characteristic curves, experimental results and ME model predictions: a characteristic curve, evolution of b tensile force and c equivalent deformable heterogeneous foundation width with u_n

The experimental data have been simulated by assuming the membrane to be isotropic and elastic–perfectly plastic (t_y (kN/m) stands for its average tensile strength). Geometry and wire mesh properties are taken from [4], whereas soil properties were calibrated on unreinforced punching tests (Table 2).

Table 2 Input data for elastic–plastic membrane case [4]

The agreement, in terms of characteristic curve, between FE simulations (crosses) and experimental test results, is qualitatively and quantitatively satisfactory (Fig. 9a). Both experimental and FE results are initially characterized by a locking trend due to the large membrane stiffness. Subsequently, both experimental and FE results present a change in concavity due to the membrane yielding. A slight discrepancy between the two curves is observed in the central part of the curves. This is likely to be due to the elastic–perfectly plastic constitutive relationship herein adopted for the membrane.

To underline the role of the membrane yielding, the FE results relative to elastic (circles) and elastic–plastic (crosses) membrane are compared in terms of evolution with u_n of F, T and B* (Fig. 9a, b and c, respectively). For sufficiently small values of u_n (before membrane yielding), elastic and elastic–plastic results are practically coincident in terms of both F and T (Fig. 9a and b). After wire mesh yielding, T remains constant (i.e. for u_n > u_y, being u_y the displacement corresponding to the complete membrane yielding T = T_y = t_yB) and the elastic and the elastic–plastic results significantly differ also in terms of B*: in the elastic–plastic case, B* stops increasing (B* = B^*_y; Fig. 9c).

3 Soil–wire mesh interaction model

In this section, a predictive model for the system mechanical response is introduced. The meta-model proposed by the authors starts from FE numerical simulation results and follows a procedure similar to that used according to machine learning (ML) approaches, but the functions used to define the model were chosen by critically analysing and mechanically interpreting the local interaction processes illustrated in the previous section.

The approach followed by the authors is inspired to the macro-element (ME) theory, commonly employed to analyse different soil structure interaction problems, e.g. shallow [11, 25, 31, 32, 49, 50, 54] and pile [38] foundations, offshore foundations and wind turbines [8, 10, 46, 53], piled embankments [18, 26], buried pipelines [12], rock boulders impacting on sheltering structures [15], tunnel cavities [20] and faces [17, 19, 24]. The ME theory stems from the idea of reproducing a complex system mechanical response via a low number of degrees of freedom and by defining a suitable incremental generalized/upscaled constitutive relationship between the static (in this case F and T) and kinematic (u_n) variables associated with the chosen degrees of freedom. In this sense, the ME approach is an upscaling procedure analogous to the ones commonly adopted in structural engineering.

The model is firstly defined and trained by assuming the membrane to be elastic (Sect. 3.1). Section 3.2 is devoted to extending the approach to the case of elastic–perfectly plastic membranes.

3.1 Elastic membrane case

The incremental generalized/upscaled constitutive relationship is formally expressed as:

$$\left[ {\begin{array}{*{20}c} {dF} \\ {dT} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {D_{F} \left( {B^{*} (u_{n} )} \right)} \\ { J \cdot D_{T} \left( {u_{n} } \right)} \\ \end{array} } \right]du_{n} ,$$

(3)

where $dF, dT$ and $du_{n}$ stand for increments of F, T and u_n, respectively, whereas D_F (Sect. 3.1.1) and D_T (in Sect. 3.1.2) are two generalized incremental stiffnesses depending on u_n.

3.1.1 Definition of D_F(u_n)

The expression employed for D_F is inspired to the well-known Butterfield’s formula [7] for rigid footings, where the foundation load-settlement curve is assumed to depend on two parameters: the initial curve stiffness (R₀) and the foundation bearing capacity (F_L):

$$D_{F} \left( F \right) = R_{0} \left( {1 - \frac{F}{{F_{L} }}} \right).$$

(4)

The initial response of the system is assumed to be elastic (Fig. 3a) and R₀ is calculated by employing the standard solution for shallow foundations resting on an elastic half-space:

$$R_{0} = \frac{E \cdot B}{{\left( {1 - \nu^{2} } \right)I_{\rho } }},$$

(5)

where $I_{\rho }$ is a non-dimensional coefficient taking into account the shape of the foundation [56]. Since the plate is rigid and squared, $I_{\rho } = 0.85$. In the following, the assumptions of both considering an initial elastic response and disregarding the soil layer thickness are shown not to compromise the capability of the model of reproducing the numerical results.

In contrast with what proposed by [7], in Eq. (4), F_L is assumed not to be constant. The authors suggest to calculate F_L(u_n) according to an extended Vesic’s formula [60]:

$$F_{L} \left( {u_{n} } \right) = \left( {\frac{1}{2}\gamma N_{\gamma } a_{\gamma } \left( {B^{*} } \right)s_{\gamma } B^{*} \left( {u_{n} } \right) + c^{\prime}N_{c} a_{c} \left( {B^{*} } \right)s_{c} + q\left( {u_{n} } \right)N_{q} a_{q} \left( {B^{*} } \right)s_{q} } \right)B^{*} \left( {u_{n} } \right)^{2} ,$$

(6)

where $N_{\gamma }$, $N_{c}$, $N_{q}$, $s_{\gamma }$, $s_{c}$ and $s_{q}$ [60] are the standard bearing capacity coefficients (in which $s_{\gamma }$, $s_{c}$ and $s_{q}$ account the foundation shape for), $a_{\gamma } \left( {B^{*} } \right)$, $a_{c} \left( {B^{*} } \right)$ and $a_{q} \left( {B^{*} } \right)$ are bearing capacity factors accounting for the interaction between adjacent plates [6]:

$$a_{c} \left( {B^{*} } \right) = a_{q} \left( {B^{*} } \right) = \frac{2.44}{{\left( {\frac{S}{{B^{*} }} - 1} \right)^{2.5} }} - e^{{ - 0.32\left( {\frac{S}{{B^{*} }} - 1} \right)}} + 1,$$

(7)

$$a_{\gamma } \left( {B^{*} } \right) = \frac{0.98}{{\left( {\frac{S}{{B^{*} }} - 1} \right)^{2.5} }} - e^{{ - 0.8\left( {\frac{S}{{B^{*} }} - 1} \right)}} + 1,$$

(8)

and q the lateral surcharge, linearly increasing with u_n due to the update of the current position of the soil around the plate,

$$q\left( {u_{n} } \right) = \gamma \cdot u_{n} .$$

(9)

To derive Eqs. (7) and (8), a series of small displacement numerical analyses, providing bearing capacity q_lim of square shallow foundations characterized by different S/B ratio values, was performed [6]. In the numerical code, an associated elastic–perfectly plastic constitutive relationship with a Mohr–Coulomb yield function is implemented. Two different sets of analyses were performed for different soil $\phi ^{\prime}$ values: the first one, aimed at the $a_{c}$ evaluation, was performed by imposing a nil soil unit weight, whereas the second one aimed at the $a_{\gamma }$ evaluation, by imposing the cohesion to be nil. In all the cases, a nil lateral surcharge was considered. Equations (7) and (8) are then reached by interpolating the numerical results. Analogously to what is done for shape footing bearing capacity coefficients [60], $a_{q}$ is assumed to be equal to $a_{c}$.

To take the non-associativity of the soil constitutive relationship into account, bearing capacity coefficients have been calculated by using friction angle and cohesion under simple shear conditions [18, 21, 22, 54, 59]:

$$\tan \phi_{ss}^{\prime} = \frac{{\sin \phi^{\prime}\mathrm {cos}\psi }}{{1 - \mathrm{sin}\phi^{\prime}\mathrm{sin}\psi }},$$

(10)

$$c_{ss}^{\prime} = c^{\prime}\frac{{\cos \phi^{\prime}\mathrm {cos}\psi }}{{1 - \mathrm {sin}\phi^{\prime}\mathrm {sin}\psi }}.$$

(11)

Equations (6), (7) and (8) depend on B*(u_n) which is a fundamental ingredient of the proposed model. The subsequent section is devoted to the definition of this function.

3.1.1.1 Definition of B*(u_n)—model training

To derive the function describing the evolution of B* with u_n, the authors performed a FE parametric study. The numerical results obtained by imposing different B, S, c’, ϕ’, ψ and relative membrane–soil stiffness (J/EB) and referring to Region 3 of Fig. 5 are plotted in Fig. 10. The results are influenced severely only by J/EB (Fig. 10f) and not negligibly by B, c’ and ψ (Fig. 10a, c and e).

Fig. 10

Evolution of deformable foundation dimension B*: FE numerical results and analytical calibration by varying a B, b S, c c’, d ϕ’, e ψ, f${ }J/\left( {BE} \right)$ ratio

To describe the dependency of B* on u_n, the authors propose the following expression:

$$\frac{{B^{*} \left( {u_{n} } \right)}}{{B}} = {\mathcal{B}} - \left( {{\mathcal{B}} - 1} \right) \cdot \exp \left({{ - \frac{{{\mathcalligra{b}}u_{n} /B}}{{{\mathcal{B}} - 1}}}}\right) .$$

(12)

Equation (12) is composed by the sum of two terms: the first describes the final linear response already discussed in Fig. 5 (Eq. 1), whereas the exponential branch, depending on the non-dimensional parameter $\mathcalligra{b}$, is introduced to impose an initial value equal to 1 (i.e. B* = B for u_n = 0) and ensure continuity. $\mathcalligra{b}$ is assumed to be constant equal to 45 and not influenced by geometry and mechanical properties.

In Eq. (1), ${\mathcal{B}}$ was defined with reference to a particular case, whereas in Fig. 10 its evolution is shown to be affected by geometry and material properties. To capture numerically such a dependence, coefficients b₁ and b₂ in Eq. 1 are assumed to depend on J/EB and c’_ss/γB, respectively (Fig. 11). The comparison between FE numerical results (symbols) and interpolating curves (dashed and solid lines, according to the case considered) obtained by employing Eqs. (1), (12) and functions reported in Fig. 11 is illustrated in Fig. 10 (maximum relative error slightly higher than 10% only in one case of Fig. 10c and e). The fitting is not satisfactory for J/BE < 0.1, but this range does not correspond to any practical application.

Fig. 11

a variation of b₁ with relative wire mesh—soil stiffness and b variation of b₂ with dimensionless cohesion

3.1.2 Definition of D_T(u_n)—model training

Analogously to what done in Sect. 3.1.1.1 for function B*(u_n), to derive the function describing the evolution of T with u_n, the authors employed the results of the previously mentioned FE parametric analyses. The numerical results obtained for different B, S, c’, ϕ’, ψ and J/EB values are plotted in Fig. 12. The numerical T–u_n curves are interpolated by using the following expression:

$$D_{T} \left( {u_{n} } \right) = 0.33\left( \frac{EB}{J} \right)^{0.33} \left( {\frac{{u_{n} }}{B}} \right)^{0.5} ,$$

(13)

where $D_{T}$ is assumed not to depend on S. This simplifying hypothesis, confirmed by the numerical data (Fig. 12), is due to the large values of S/B employed in the practise.

Fig. 12

Evolution of tensile force T: comparison between FE numerical results and ME model predictions

In this case, the model training only requires the determination of the three numerical constants allowing to best fit the FE results (Fig. 12). The agreement is satisfactory, and the maximum relative error is always lower than 7%.

3.1.3 Model use

The training procedure (Sects. 3.1.1.1 and 3.1.2) has only required the description of both functions B^*(u_n) and D_T(u_n). The results in terms of variation of F with u_n can be used to verify all the assumptions and functional dependencies introduced for this model. To this aim, the ME model blind predictions are compared with the FE results in Figs. 13 and 14. For all the cases, the agreement is very satisfactory. It is worth mentioning that:

• the characteristic curves obtained from FE simulations are practically unaffected by the soil stratum thickness (the maximum difference is lower than 3.5%, as is shown in Fig. 13c), justifying the choice of employing a R₀ value not depending on H/B;

• the agreement between ME predictions and FE results is satisfactory also for different dilatancy angle values (Fig. 14c), even if the dependency of B^* on ψ was disregarded;

• the maximum relative error does not exceed 15% for 0 < u_n < 4 cm, i.e. the actual range of practical interest in which the wire mesh behaviour is expected to be elastic. For higher u_n values, an elastic–plastic behaviour of the wire mesh has to be taken into account, as done in the next Section.

Fig. 13

Characteristic curve: comparison between FE results and ME predictions; influence of geometry

Fig. 14

Characteristic curve: comparison between FE results and ME predictions; influence of soil and membrane properties

From Eqs. (4)–(12), we derive that the model use requires the definition (i) of 9 input data (Table 3) concerning geometry (B and S), soil mechanical properties (E, ν, c', ϕ’, ψ and γ) and membrane stiffness (J) and (ii) an input variable (u_n). For this reason, the proposed model is “self-standing” since it does require neither additional FE numerical analyses nor model calibration.

Table 3 Input data for the elastic membrane case in the ME model

3.2 Elastic–plastic membrane case

In this section, the generalized constitutive relationship presented in Sect. 3.1 is extended to take the membrane yielding and an elastic–perfectly plastic membrane behaviour into account.

By integrating the second row of Eq. (3) in which Eq. (13) is introduced, the value of u_y, corresponding to condition T = T_y, can be calculated:

$$u_{y} = B\left( {0.5\frac{{T_{y} }}{{0.33JB\left( \frac{EB}{J} \right)^{0.33} }}} \right)^{2} .$$

(14)

As was previously mentioned, when the wire mesh is completely yielded (u = u_y; Fig. 9b), B^* stops increasing (Fig. 9c). To extend the validity domain of the model in case of u > u_y and by assuming an elastic–perfectly plastic response for the membrane, Eq. (12) is modified as it follows:

$$\frac{{B^{*} }}{B} = \left\{ {\begin{array}{*{20}l} {{\mathcal{B}} - \left( {{\mathcal{B}} - 1} \right)\left( {e^{{ - \frac{{{\mathcalligra{b}}u_{n} /B}}{{{\mathcal{B}} - 1}}}} } \right)} & {u_{n} < u_{y} } \\ {\frac{{B_{y}^{*} }}{B}} & {u_{n} > u_{y} } \\ \end{array} } \right. .$$

(15)

The elastic–plastic ME model predictions (solid lines) are compared against both FE (cross symbols) and experimental results (grey area) in Fig. 9. From a qualitative point of view, the agreement in terms of characteristic curve is satisfactory, but also quantitatively for u_n/B < 0.5. ME model seems to better capture the experimental data than the FE numerical data (Fig. 9a). This is likely to be due to the non-perfectly plastic behaviour of the steel threads constituting the mesh. In terms of evolution of T and B^* versus u_n (Fig. 9b and c, respectively), the agreement between ME and FE data is very satisfactory for any u_n value.

It is worth mentioning that, in the elastic case (Sect. 3.1), the two equations defining the ME model (Eq. 3) are uncoupled and can be solved separately. In contrast, in the elastic–plastic case, the membrane yielding introduces a coupling (Eqs. 14 and 15), since the B* evolution depends on membrane yielding.

4 Discussion

As was already mentioned, according to ULS approaches, the evaluation of retaining force is crucial for stability analysis calculations and is commonly estimated by performing laboratory punching tests. Alternatively, to this aim, large displacement soil–structure interaction numerical analyses can be performed to properly reproduce the in situ conditions (in terms of geometry and soil/membrane mechanical properties).

In the past, this second strategy was followed by di Prisco et al. [16] who proposed a simplified approach by studying the complex anchored wire mesh/soil interaction mechanism for evaluating the pressure exerted by the wire mesh upon the ground surface. These authors introduced a simplified displacement-based approach, but its practical applicability is not straightforward, since an ad hoc large-displacement wire mesh/soil interaction problem has to be numerically solved. However, within the actual range of practical interest, i.e. before wire mesh yielding (u_n < u_y), the maximum difference, in predicting the experimental results shown in Fig. 9, between F outputs coming from this approach and the one proposed in this paper is 5%.

An attempt in this direction was also done by Blanco-Fernandez et al. [1], who, however, did not consider the tridimensionality of the problem, the presence of the steel plate and the wire mesh failure. They also propose a formula for maximum wire mesh/soil interaction pressure not dependent on S, J/EB, c’, $\psi$ and t_y and not capable of simulating punching tests, conversely to the model proposed in this paper.

This latter is an alternative approach for calculating the interaction force, not requiring neither numerical FE simulations nor experimental punching tests. The model use only necessitates the definition of input data describing the geometry and basic wire mesh and soil mechanical properties and the employment of Eq. 3. A simplified example of the practical application of the method is discussed in Sect. 5.

For the sake of completeness, some additional practical remarks on the application of the model introduced in Sect. 3 and its limitations are reported here in below. In particular, (1) wire mesh anisotropy, (2) wire mesh fragility, (3) ground surface inclination and (4) plate deformability are discussed:

• (1) the wire meshes employed in practice are characterized by anisotropy in both stiffness and strength. The results of a series of numerical FE analyses (Appendix A) show that, for realistic anisotropy factor values, the characteristic curves obtained by considering either an anisotropic membrane or an isotropic membrane with average stiffness and strength values are practically coincident.

• (2) the comparison between predictions and experimental results seems to suggest that in both FE and ME models accounting for wire mesh fragility is not mandatory. The ductility of steel seems to ensure the yielding of a large number of threads under the plate edge, until T_y is reached.

• (3) inclined ground surfaces are not considered in the model presented in Sect. 3. To highlight the influence of in situ inclination on the system response, a series of additional numerical FE analyses was performed. The results (Appendix D) highlight that, for realistic inclination values (not larger than 40°), the ground surface inclination does not significantly affect the interaction problem in terms of characteristic curves. In Appendix D, an extension of the model for inclined ground surfaces is also presented.

• (4) for large F values, the plate is expected to bend. A simple method for designing the plate and thus avoiding excessive bending may be based on a sub-structuring approach: (i) the model of Sect. 3 for rigid plate may be employed to calculate the maximum values of both F and T; (ii) the structural problem of a plate, loaded by a normal stress uniformly distributed of resultant F plus normal uniform line loads of resultant T applied on the four edges, has to be solved. This approach, disregarding the inclination of T, provides a safe side estimation but not too unrealistic, since, as is shown in Fig. 4, the local inclination of the membrane and the normal component of T close to the plate edge becomes rapidly very large.

5 Practical application

In this paragraph, the practical use of the model with reference to a simplified case is illustrated. The considered slope geometry and planar failure mechanism (of inclination β) are described in Fig. 15a. Geometry, soil and wire mesh properties are reported in Table 4. Being $\beta > \phi ^{\prime}$, the factor of safety FS in the unreinforced case is lower than 1 (FS₀ = 0.82). Given wire mesh properties and plate dimension, the model is employed to assess S to obtain FS > 1.3.

Fig. 15

Practical application: a geometry, b T vs. u_n, c F vs. u_n, d F_y vs. S and f $FS/FS_{0}$ vs. S

Table 4 Input data for application case

To derive the variation of FS with S, the authors employ the model and the following equation:

$${\text{FS}}\left( {\text{S}} \right) = \frac{{W \cdot \cos \beta + F_{y} \left( S \right) \cdot \frac{\ell }{{S^{2} }} \cdot \cos \left( {\alpha - \beta } \right)}}{{W \cdot {\text{sin}}\beta + F_{y} \left( S \right) \cdot \frac{\ell }{{S^{2} }} \cdot {\text{sin}}\left( {\alpha - \beta } \right)}} \cdot \tan \phi^{\prime},$$

(16)

with $W$ the weight of the soil block per unit length along the out of plane direction and $F_{y}$ the stabilizing force at u_n = u_y. Due to the large number of plates considered in all the cases, the influence of the nails close to the bottom and the top of the block at failure is assumed to be negligible.

In Eq. (16), all the terms are known with the exception of $F_{y}$, depending on not only wire mesh properties but also geometry and soil properties. Once wire mesh and plate are chosen, by using Eq. (14) (Fig. 15b), u_y is calculated. As was mentioned in Sect. 3.1.2, T versus u_n does not depend on S. Thus, by integrating Eq. (3) for a certain number of S values (Table 4), curves of Fig. 15c are obtained and employed to calculate the F_y values corresponding to u_y. The obtained dependency of F_y on S is illustrated in Fig. 15d and the variation in FS with S in Fig. 15e. As is evident, FS > 1.3 for S $\le$ 2.5 m.

An optimization process could require the use of the model for individuating the maximum S values corresponding to different wire meshes: this is particularly useful during the pre-design stage to tune, according to the specific case, the reinforcing system.

6 Concluding remarks

In the design of slope stabilization measures, the assessment of the maximum value of the force provided by the retaining structure is commonly considered to be crucial. In case of deformable facing structures, as anchored wire meshes, such an assessment has been shown in this paper to be possible only by correctly accounting for (i) the local soil–structure interaction, (ii) the local yielding of the soil, (iii) the nonlinear mechanical behaviour of the wire mesh and (iv) second order effects (geometrical nonlinearities).

The results of the numerical analyses performed by the authors clearly show that both the stabilising force and the tension in the membrane increase with the imposed relative displacement and are not only functions of wire mesh properties, but also of geometry and soil mechanical properties. In other words, the knowledge of the wire mesh tensile strength, provided by the mesh manufacturer, is not sufficient to determine a priori the maximum stabilizing force of the system.

The numerical results also show that normal stresses develop in an area larger than the anchoring plate, involving a surrounding zone. The size of this zone progressively increases with the relative soil-plate displacement. In this perspective, the anchoring plate along with this portion of the surrounding wire mesh behaves like a sort of “deformable heterogeneous foundation”.

This observation is a fundamental “ingredient” of the simplified calculation tool introduced by the authors. This tool is intended to be an alternative to experimental punching test results, usually performed by the wire mesh producers, providing an estimation of the maximum stabilising force. The tool, conceived by following an innovative approach, is capable of reproducing the soil–structure interaction in terms of evolution of (i) retaining force (the so-called characteristic curve) and (ii) membrane tensile force with relative soil–structure displacements. The tool is self-standing, and its use only requires the definition of input data describing the geometry and basic wire mesh and soil mechanical properties.

The model is conceived for isotropic meshes, but, by using average stiffness and strength values, also anisotropic meshes can be considered. The wire mesh fragile failure is not accounted for, but this is not a severe limitation of the model since in practical applications even the yielding of the mesh, developing before its failure, is not acceptable. The calculation tool refers to horizontal ground surfaces, but ad hoc numerical results highlighted that the influence of slope inclination plays a minor role. Plate deformability is not accounted for, but a simplified approach to analyse its response is suggested.

The predictive tool is particularly useful during planning and preliminary design since it allows, with a negligible calculation effort, to sieve different possibilities and to give a cost estimation. In addition, such a tool is suitable for being employed by producers to optimize the use of their products and designers to reduce the costs of interventions and to increase the sustainability of the retaining system.

Appendices

Appendix A

The wire meshes commonly adopted for slope stabilization are characterized by an anisotropic structure. To investigate the influence of anisotropy here below, the results of a series of numerical analyses, performed on orthotropic elastic/elastic–plastic membranes, are discussed. The anisotropy is described in terms of two factors: the ratio between stiffnesses along principal directions (elastic anisotropy factor EAF) and the ratio between strength along principal directions (strength anisotropy factor SAF).

In Fig. 

Fig. 16

Influence of anisotropy on the characteristic curve (elastic wire mesh)

16, the numerical characteristic curves, obtained by considering elastic meshes and EAF = 1, 2, 10, but an equal average stiffness of 3920 kN/m, are illustrated. For all the cases considered, both geometry and soil mechanical properties correspond to the ones of the reference case (Tables 1,23). For u_n < 0.1 m, the influence of anisotropy on the characteristic curve is practically negligible, at least in case EAF < 10 [9, 16].

In the elastic–plastic case, the authors have chosen to consider a different wire mesh [16], for which experimental data are available and EAF and SAF are equal to 3 and 2.5, respectively. The curves plotted in Fig. 

Fig. 17

Influence of anisotropy on the characteristic curve (elastic–perfectly plastic wire mesh)

17, corresponding to the anisotropic elastic–plastic case and to the corresponding isotropic one (EAF = SAF = 1), are practically superimposed, putting in evidence again that anisotropy, given the imposed loading conditions, does not play a significant role.

Appendix B

The J value employed for the numerical reference case (Sect. 2.2) is obtained from the results of a series of one-dimensional tensile tests performed on squared wire mesh specimens of width l = 1 m, constituted of (i) rhomboidal unit cells (83 × 143 mm), (ii) 2.7 mm wire diameter and (iii) 34 × 31 cm spaced ropes with a diameter of 8 mm. The tests were performed along the two principal orthogonal directions (hereafter, named x and y).

In Fig. 

Fig. 18

Results of one-dimensional tensile tests along the two principal orthogonal directions (x and y)

18, the correspondent results, in terms of imposed force N versus measured displacement s, are shown (Fig. 18a and b refer to direction x and y, respectively). The initial branch of the curves is not linear and is associated with a progressively increasing stiffness. This geometrical nonlinearity is due to an initial non-planarity of the wire mesh. Subsequently, N seems to be linearly increasing with s up to the failure load N_y.

The value of wire mesh stiffness along direction x and y (J_x and J_y, respectively) is taken equal to the average slope of the N–s curves in their linear range (Table

Table 5 Wire mesh stiffnesses and yield strengths along the two principal orthogonal directions (x and y)

5). Yield strength t_y (t_y,x and t_y,y, respectively) is calculated as the ratio of N_y (N_y,x and N_y,y, respectively) and l (Table 5).

With the aim of modelling the wire mesh as an equivalent isotropic membrane, a stiffness J and a yield strength t_y equal to the average between the correspondent values along the two orthogonal directions are considered (J = 7415 kN/m and t_y = 170 kN/m).

Appendix C

Hereafter, the numerical results obtained by performing a punching test on a square (edge S = 1.8 m) elastic membrane (J = 7.4MN/m) without the underneath soil (Fig. 18) are discussed. The membrane is vertically free of moving, but on the lateral boundaries of the domain normal and vertical displacements are prevented, whereas on the axes of symmetry, only normal displacements are not allowed. On a square area (edge B = 25 cm), a uniform vertical displacement field u_n is imposed.

The results, in terms of (i) membrane deformed shape along the x-axis of Fig. 

Fig. 19

a Geometry and b spatial discretization

19 (Fig. 

Fig. 20

Membrane deformed shape

20, where u_m represents the membrane displacements), (ii) maximum (tensile) principal stress distribution (Fig. 

Fig. 21

Contours of maximum tensile stress

21) and (iii) variation in the integral of the tensile stress along one side of the zone in which displacements are imposed (Fig. 

Fig. 22

Variation of the resultant of tensile stresses with the imposed displacement

22), are compared with the corresponding ones of Figs. 4, 8 and 9.

The two membrane deformed shapes significantly differ (Figs. 4 and 20): when the soil is present, larger local membrane strains and curvatures in proximity of the plate are obtained, implying larger values of tensile stresses (Figs. 8 and 21) and tensile forces (Figs. 9 and 22).

These numerical results clearly put in evidence that punching tests performed upon wire meshes without the soil [23, 28, 33, 55] are not representative of the soil–structure interaction problem under exam.

Appendix D

To study the influence of ground surface inclination, a numerical model analogous to the one described in Sect. 2.2 is employed. The main differences with the previous numerical model consist in: (i) an α inclined ground surface; (ii) modelling half of the considered domain (shown in Fig. 1b), being the problem only symmetrical with respect to the vertical plane, passing through the centre of the plate and having normal along x direction; (iii) imposing periodic boundary conditions [61], according to which the displacements of the two domain boundaries having normal along the y direction coincide.

The contours of displacements along z direction obtained by imposing (i) the input data enlisted in Tables 1, 2 and 3, (ii) c’ = 10 kPa and (iii) α= 40° (considered an upper bound for the inclination of slopes reinforced with anchored wire meshes) are reported in Fig. 

Fig. 23

Contour of the displacement component in the z direction at a u_n = 0.5 mm and b u_n = 50 mm (input data of Tables 1, 2 and 3 with c’ = 10 kPa and α  = 40°)

23. For small imposed u_n values, the displacement field is not symmetrical but, for large u_n values, due to the presence of the membrane, the displacement field becomes almost symmetrical, suggesting the role of slope inclination to be marginal. This is also testified by comparing the characteristic curve with the corresponding ones for α  = 0° in the F–u_n plane (Fig. 

Fig. 24

Characteristic curve derived both numerically and by the just-proposed theoretical model: comparison between horizontal and α  = 40° inclined slopes

24).

For the sake of completeness, in Fig. 24, the numerical results obtained by imposing c’ = 25 kPa are also reported. In this case, the influence of α is even smaller, with respect to the previous case, suggesting that this effect decreases by increasing cohesion.

The influence of α on the characteristic curve (Fig. 24) is also negligible if in the calculation tool, proposed in Sect. 3, $\gamma$ is substituted in Eq. 4 with $\gamma^{*} = \gamma \cdot {\text{cos}}\left( \alpha \right)$, that is if the stabilizing component of the standard bearing capacity equation associated with the soil self-weight is projected in the direction normal to the ground surface.