Void size distribution and hydraulic conductivity of a binary granular soil mixture

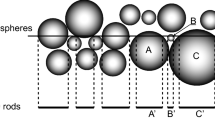
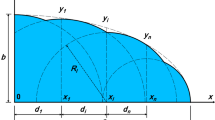
Abstract

Permeability of binary mixtures of soils is important for several industrial and engineering applications. Previous models for predicting the permeability of a binary mixture of soils were primarily developed from Kozeny–Carman equation with an empirical approach. The permeability is predicted based on an equivalent particle size of the two species. This study is aimed to develop a model using a more fundamental approach. Instead of an equivalent particle size, the permeability is predicted based on the bimodal void sizes of the binary mixture. Because the bimodal void sizes are not available as commonly measured physical properties. We first develop an analytical method that has the capability of predicting the bimodal void sizes of a binary mixture. A permeability model is then developed based on the bimodal void sizes of the binary mixture. The developed permeability model is evaluated by comparing the predicted and experimentally measured results for binary mixtures of glass beads, crush sand, and gravel sand. The findings can contribute to a better understanding of the important influence of pore structure on the prediction of permeability.

Appendix 1: A brief summary of a particle packing model by Chang and Deng [11]

In the model derivation for particle packing of binary mixtures, specific volume $\upsilon$ was used. By definition, specific volume $\upsilon$ is related to void ratio $e$ by $\upsilon =1+e$. Thus, the equations in the derivation for the specific volume of a binary packing mixture can be replaced by the void ratio, which is a function of the solid fractions of species (${y}_{1}$, ${y}_{2}$) and the partial void ratios, given by

$$e={e}_{1}{y}_{1}+{e}_{2}{y}_{2}$$

(18)

Based on the concept of excess particle volume-potential for each species in a mixture [11], the partial void ratios of the two species in a granular mixture were postulated to be:

$$e_{1} = e_{1}^{0} - \alpha_{1} \left( {e_{1}^{0} - 1} \right)$$

(19)

$$e_{2} = e_{2}^{0} - \alpha_{2} e_{2}^{0}$$

(20)

where ${e}_{1}^{0}$ and ${e}_{2}^{0}$ are respectively the mono-sized void ratios of the two species. The values of two activity coefficients ${\alpha }_{1}$, ${\alpha }_{2}$ are between 0 and 1. With Eqs. (18), (19), and (20), the void ratio of the mixture can be expressed as:

$$e=\left({e}_{1}^{0}-{\alpha }_{1}({e}_{1}^{0}-1)\right){y}_{1}+\left(1-{\alpha }_{2}\right){e}_{2}^{0}{y}_{2}$$

(21)

The activity coefficients ${\alpha }_{i}$ is hypothesized to be a function of the two characteristic lengths in the form of power law, given by

$${\alpha }_{1}={\left(1-\frac{x}{{d}_{1}}\right)}^{\eta }; {\alpha }_{2}={\left(1-\frac{{d}_{2}}{x}\right)}^{\eta }$$

(22)

where ${d}_{1}$ and ${d}_{2}$ are the particle size of the two species, x is the characteristic length of the packing and $\eta$ is a material coefficient.

Based on the thermodynamics second law, the excess volume potential must be minimized at equilibrium of the system, thus it leads to

$$\frac{{\partial \alpha }_{1}(x)}{\partial x}{(e}_{1}^{0}-1){y}_{1}+\frac{{\partial \alpha }_{2}(x)}{\partial x}{e}_{2}^{0}{y}_{2}=0$$

(23)

The unknown variables, ${\alpha }_{1}$, ${\alpha }_{2}$ and $x$ can be solved by Eqs. (22) and (23). Then, the void ratio $e$ of the binary mixture can be determined from Eq. (21). The partial void ratios can be determined from Eqs. (19) and (20).