A 3D image-based method to measure soil stiffness in triaxial tests

Abstract

This paper describes a new simple and inexpensive method for accurately measuring the three-dimensional deformation of soil specimens during triaxial tests. The method incorporates a cost-effective image capture system that can be applied to any triaxial apparatus as well as an automated post-image analysis approach for processing the images acquired during triaxial tests. Image capture is performed using multiple low-cost Raspberry Pi cameras and accessories placed outside the triaxial chamber. The system employs particle image velocimetry, camera calibration and stereophotogrammetry to determine the spatial variation in axial and radial sample strains as samples are loaded. It is demonstrated that axial and radial displacements can be measured with an accuracy of 1–2 μm, respectively, and it is verified by comparison with data from triaxial tests on sand samples that the full nonlinear stiffness–strain degradation of soil samples from fully elastic conditions can be determined without the need for any additional sensors.

1 Introduction

The nonlinear stress–strain behaviour of soils has been demonstrated in many field and laboratory studies (Jardine et al. [14]) while the importance of the measurement of soil stiffness at small and intermediate strain levels (less than about 0.3%) for ground movement predictions has been emphasized by Burland [7], and others. The nonlinear stiffness characteristic of soil is now a key input to constitutive models employed in finite element analyses for calculation of soil movements in geotechnical design.

The triaxial apparatus is the most popular laboratory testing device employed for measurement of the stress–strain behaviour of soil. However, conventional triaxial testing, which involves external measurement of strains, is not suitable for determination of soil stiffness at small strains due to a variety of inherent errors (Jardine et al. [15]). Consequently, strain measurement requires use of instruments, such as electro-levels, proximity transducers and local deformation transducers mounted locally on specimens (Goto et al. [10]; Hird & Yung [12]; Jardine et al. [15]). Such local instrumentation, often used together with bender elements installed at the sample ends to infer the elastic stiffness, is common for research and special industry projects. Local instrumentation is, however, rarely used outside of research because of the associated high additional costs and need for technical expertise.

The infrequent measurement of small strain stiffness in everyday engineering practice provided the motivation for the low-cost and user-friendly image-based system described in this paper. An image-based system uses remotely located, digital cameras and photogrammetry with corrections for refraction in both the cell fluid and cell wall. The image analysis approach has been adopted in a number of geotechnical studies to monitor soil deformation (Lehane [16]; Stanier & White [26]; White et al. [30]), shear band formation (Alshibli & Sture [2]; Gudehus & Nübel [11]; Liang et al. [18]; Rattez et al. [22]), volume change (Alshibli & Al-Hamdan [1]; Gachet et al. [9]; Hormdee et al. [13]; Ören et al. [21]; Uchaipichat et al. [27]) and liquefaction (Zhao et al. [32]).

Existing applications of image-based measurement systems relevant to triaxial testing involve two- and three-dimensional approaches. The 2D approaches use a single camera and derive measurements based on the observed 2D images (Bhandari et al. [5], Macari et al. [19]). It is necessary to make a number of geometric assumptions in order to convert the measurement results from 2D image coordinates to real-world units. The 3D approaches combine stereophotogrammetric techniques with 2D images to reconstruct the 3D coordinates of points observed by multiple cameras (Rechenmacher & Medina-Cetina [23]; Salazar [24]; Wang et al. [29]; Zhang et al. [31]). While all of these studies have contributed to the advancement of image-based measurement, they have been largely focused on volumetric strain measurements at relatively large strain levels. Based on a review of the literature, it became clear to the authors that there is currently no simple and cost-effective image analysis approach that can be applied directly to routine stiffness measurement in triaxial tests.

The system described in this paper was developed at The University of Western Australia (UWA) so that it could be easily and cheaply fitted to standard triaxial testing equipment used around the world. Particular attention was made to ensure that the hardware was both cost-effective and capable of resolving axial strains to an accuracy of 0.001% to 0.002%. A strain level of 0.001% corresponds approximately with the strain below which the soil behaves as a linear elastic medium (Atkinson [3]) implying that the system could dispense with the need to install bender elements to infer the elastic stiffness while also measuring the degradation of stiffness with axial strain and the variation in radial strain with axial strain.

This paper describes the components and features of the new UWA 3D image-based system, which followed on from a number of less successful versions of the system reported in Wang [28]. The accuracy and precision of the system are first demonstrated using dummy specimens before presenting the data measured in tests on isotropically and anisotropically consolidated sand samples.

2 The UWA 3-D image-based measurement system

2.1 Components of the system

The developed image-based approach contains two components: (i) a simple and cost-effective image capture system that facilitates photogrammetric measurements of the deformations of the triaxial sample and (ii) a 3D image analysis procedure to provide a simple, objective and accurate means of ongoing measurement of the spatial (x, y, z) coordinates of the surface of a near-cylindrical soil sample.

The UWA image-based measurement system used for triaxial compression tests is illustrated in Fig. 1. Raspberry Pi cameras and zero W boards are placed around the outside of the triaxial chamber. The Raspberry Pi Zero W board is a small single-board computer that controls a Raspberry Pi camera and stores images captured by the camera. Each Raspberry Pi camera has a lens with a focal length of 6 mm and a resolution of 12.3 MegaPixels and takes images at specified intervals during a test. The cameras' positions are controlled so that there is a sufficient overlap between any two adjacent cameras. As illustrated in Fig. 1, cameras and boards are connected to the chamber tie-rods by four stiff aluminium holders. Each Raspberry Pi combination (Raspberry Pi board + Raspberry Pi camera + lens) is connected to the power source by a USB-A cable. There are five lighting sources positioned in different directions to illuminate the sample. A number of trials indicated that the image capture was relatively insensitive to the lighting arrangement and a visual assessment of light uniformity is sufficient to check its adequacy.

Fig. 1

UWA Triaxial testing image capture system (a) View of complete system (b) View showing camera supports and layout with specked sample membrane (c) Schematic plan view showing the camera layout

The Raspberry Pi combinations and the triaxial device are both controlled by a desktop computer situated adjacent to the triaxial device. The triaxial device is connected to the computer via HDMI. The computer software controls all experimental procedures and records the results of the triaxial experiment. The Raspberry Pi boards are connected to the computer through a local wireless network. Upon initiation of the shearing stage, a computer script commands all cameras to begin capturing images simultaneously at specified times and intervals. The time at which the images are captured is recorded in order to correlate the results of the measurement with those obtained by the standard data recorded in standard triaxial testing (e.g. deviator load, cell pressure, pore pressure, volume change). A script was written to achieve synchronicity of the image capture, and tests that involved photographing of timers indicated that differences between all cameras were less than 50 ms.

2.2 Post-image analysis procedure

The image analysis procedure combines digital stereophotogrammetry and particle image velocimetry (PIV), referred to as 3DPIV. The 3DPIV analysis employs two adjacent cameras (labelled as the right camera and the left camera) that contain overlapped areas. Within the overlapped areas, a set of data points is defined on the specimen surface. A data point is representative of a group of unique coloured pixels on an image (patch of the image) and is referred to as an ‘image subset’ when performing PIV analysis. These data points are tracked using PIV employing the image coordinate system of each camera. Following PIV tracking, the 3D coordinates of the data points are first estimated based on the relative positions of the two cameras which are determined during the calibration process. As such, 3DPIV requires an additional step that involves placing a calibration target into the triaxial chamber and controlling all cameras to take calibration images at the end of the experiment. The calibration target is positioned on top of the triaxial pedestal, and the chamber is subsequently filled with water. All cameras are controlled to take ten images simultaneously while the calibration target is rotated with each set of images obtained at angular rotation increments of about 10 degrees. Although one calibration image is sufficient for a 3D calibration target, it is preferable to take more images as there is a risk of taking a poor-quality image. It is also beneficial to gather more observations to reduce errors in the calculation of the camera's parameters and distortion coefficients.

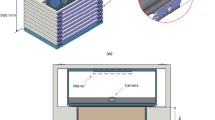
The calibration target is a cylindrical reference object whose surface has the calibration pattern shown in Fig. 2; this pattern was printed on paper with adhesive backing that was then placed on a steel cylinder. The pattern includes Aruco markers and a grid of circles. Each Aruco marker consists of a synthetic square marker with a black border that can be detected rapidly and an inner binary matrix that allows it to be identified. The markers are used to identify the circles surrounding them. The centroids of circles enclosing a marker are the ‘feature points’ used for calibration. Other calibration patterns (e.g. chessboard) were used and found to have lower accuracy because of unclear borders and high levels of noise. In contrast with the intersection of lines on a chessboard, the centroid of a circle is less affected by fuzzy borders and can be detected with greater accuracy.

Fig. 2

Calibration target

The post-image analysis process includes three primary procedures: camera calibration, tracking and correction, and 3D reconstruction. The length of time required for analysis depends on the specifications of the computers used. As an example, for the tests described in this paper, a complete triaxial test with samples tested to large strain with 16 cameras required 21 h of computational time using two standard laptops. Almost all of the computational time was associated with the 3DPIV analyses and much faster techniques using parallel processing are possible.

2.3 Camera calibration

The camera calibration determines the relationship between three coordinate systems by estimating the camera’s matrix and distortion parameters. Figure 3 shows the definition of each coordinate system. A camera's matrix consists of an intrinsic matrix and an extrinsic matrix. An extrinsic matrix corresponds to a transformation from the world's coordinate system to the camera's coordinate system, whereas an intrinsic matrix represents the conversion of points from the camera's coordinate system to the image's coordinate system. The distortion parameters act to correct for effects of distortion on the image caused by the camera lens, triaxial chamber and chamber fluid (water).

Fig. 3

Model for camera calibration

The image coordinates of feature points (centroids of circles) are first determined for each calibration image. A feature point can be represented as point A in Fig. 3. Point B is the world coordinate of the detected feature point on the calibration target, and its world coordinate is computed using the dimensions of the calibration target and the pattern.

The world coordinates of feature point B are calculated in two steps. As shown in Fig. 4, the coordinates of point B on the calibration pattern are (x, y) while its world coordinates are (X, Y, Z). Firstly, the cartesian coordinates of point B on the pattern are obtained. Due to the pattern being wrapped around the cylinder, the x-axis on the pattern corresponds with the circumference of the cylinder. The X, Y coordinate of point B in the world coordinate can therefore be calculated using Eq. (1), where D is the diameter of the cylinder:

$$\begin{array}{*{20}c} {X = \frac{D}{2}\cos \left( \frac{2x}{D} \right); Y = \frac{D}{2}\sin \left( \frac{2x}{D} \right); Z = y } \\ \end{array}$$

(1)

Fig. 4

Calculation of world coordinate for feature point

The OpenCV [20] computer vision library is used to compute the camera matrices and distortion parameters using the algorithms developed by Zhang [31] and Bouguet [6]. The parameters are determined from the many feature points with known image and world coordinates obtained in the calibration.

2.4 Tracking and correction

GeoPIV_RG (Stanier et al. [25]), which is a freely available PIV program, is used by the new system to detect the movement of selected data points (also referred to as subsets or patches) on the test images captured during the triaxial shearing of the soil samples. The circular patch (shown by red and green circles in Fig. 5) is referred to as an ‘image subset’, and its position and deformation are tracked in the GeoPIV_RG analysis. In each pair of horizontally adjacent cameras (i.e. the left and right cameras), a group of data points is defined within the overlapping fields of view of two cameras on the surface of the test specimen. The calibration parameters are used to map the data point onto the right and left image planes, as shown in Fig. 5. The mapping result is shown as the centroid of the red circle in the right and left images (Fig. 5).

Fig. 5

Data point (image subset) selection and correction

The world coordinates of data points are calculated assuming they are located on the surface of a perfect cylinder. However, triaxial soil specimens have irregular surfaces, resulting in mapped positions that are a few pixels off from the true positions. Hence, a correlation algorithm is applied to ensure that the same data point (image subset with the same texture) is tracked by GeoPIV_RG on the right and left images. As part of the correlation process, it is assumed that the red circled patch on the left image in Fig. 5 is the reference. On the right image, a search area (the rectangular dashed line in Fig. 5) is defined around the initial mapped position. This area is then searched until a circle patch (green circle) is found to be sufficiently correlated with the reference red circled patch.

The above steps define a group of data points and find their initial image subsets (circle patches) on the right and left images. GeoPIV_RG is then applied to track the deformation and movement of these image subsets as the triaxial test progresses. The outputs are the image coordinates (u,v) of the selected data points for each pair of cameras at any particular stage in a test.

2.5 3D reconstruction

PIV tracking results (i.e. the coordinates on the image plane) are corrected for distortion by using the distortion parameters prior to 3D reconstruction. The 3D reconstruction determines the 3D coordinates of all data points monitored by each pair of cameras using triangulation, as illustrated in Fig. 6. As illustrated in this figure, each projection ray (dash line) can be determined based on its corresponding image coordinate (u, v) and camera parameters. The output from this triangulation process is a point cloud in world coordinates at each time interval in a test; the term point cloud is used to denote the collection of data points in space that represent the 3D shape of the soil specimen.

Fig. 6

Geometry of 3D reconstruction

3 Assessment of precision and accuracy

Tests involving uniaxial compression of a plastic ‘dummy’ cylinder and vertical translation of the same cylinder were performed to assess the precision and accuracy of the developed image approach. These tests were performed in the same triaxial device shown in Fig. 7a. Figure 7c illustrates the positions of the eight cameras employed during the translation and compression tests. In the following analysis, each stereo camera pair (left camera A and right camera B) is referred to as "cam A&B". The 3DPIV method generates multiple meshes of data points around the surface of the test specimen. Measurement of local strain or displacement is based on the change in coordinates of data points.

Fig. 7

Setup of the translation test (a) schematic showing cylinder being supported by load cell (b) sprayed ‘dot’ pattern on cylinder and (c) camera arrangement

3.1 Vertical translation test

A dotted texture of black paint was sprayed onto the surface of the dummy cylinder to allow PIV analysis to be performed; see Fig. 7b. The cylinder, which had a diameter of 63 mm and a height of 140 mm, was subjected to a relative vertical displacement at a constant speed while images of the cylindrical surface were obtained using four camera pairs for PIV. The cylinder was attached to the frame through the cell ram and the chamber was filled with water. A LVDT displacement transducer positioned on top of the chamber was used to measure displacement of the system.

The translation speed was set at 0.005 mm/min upwards and images were captured every 20 s. Small differences in the displacement calculated using the translational speed and elapsed time with that measured using the LVDT indicated the potential for either a small degree of ‘stick–slip’ in the LVDT or minor variations in the driving motor of the triaxial machine. Figure 8 compares typical displacement results for the cameras with the external displacement transducer (LVDT) over a short displacement length of 0.01 mm at two stages of the test. In this instance, the displacement plotted for each camera pair was calculated by averaging the vertical displacement of the data points in their monitoring zone, as shown in Fig. 7c. There were typically 50 data points in each zone, and displacements indicated by each point at any given time were virtually identical. It is seen that the displacement measured by each camera pair varies linearly with the LVDT displacement. Near the beginning of the test (Fig. 8a), the average displacement is almost identical to the displacement indicated by the LVDT. There is, however, a difference of 0.006 mm at a later stage of the test (Fig. 8b) which may be due to minor errors associated with the experimental set-up. In all cases, the difference between a given camera measurement and the mean trend line differs by between 0.0005 mm and 0.002 mm from the mean trend line. Measurements of displacements by any given camera pair did not vary by more than about 0.0005 mm when the sample was stationary indicating a high level of precision of the system.

Fig. 8

Measurements obtained during vertical translation test of dummy cylinder a Displacement from 0.01 to 0.02 mm. b Displacement from 0.315 to 0.325 mm

3.2 Uniaxial compression test

Uniaxial compression tests were performed on a cylindrical acetal plastic sample to assess the suitability of the image analysis method. This cylinder was also wrapped with a dotted texture as for the translation test; see Fig. 7b. An axial displacement rate of 0.005 mm/min was employed with images captured every 20 s until the deviator reached 5000 kPa. The camera layout employed is shown in Fig. 7c and involved 4 camera pairs.

The measured variations in applied stress with axial strain are shown in Fig. 9a, where axial strains have been calculated using individual camera pairs and using the displacements measured by the external LVDT (as shown in Fig. 7a). It is evident that the stress–strain response is nonlinear in all cases plotted. The strain measurements obtained from camera pairs 3 & 4 and 7 & 8 on the one side of the sample were found to be closely comparable. On the opposite side of the sample (see Fig. 7c), the strain measurements obtained from camera pairs 1 & 2 and 5 & 6 were also observed to be highly comparable. This trend, including the registration by Cam 3&4 and Cam 5&6 of very small tensile strains at the start of the test, is indicative of sample bending induced by misalignment of the load cell with the top of the sample. The stress–strain relationship indicated by the LVDT measurements is highly nonlinear at the early stage of the test and displays a slightly concave upwards trend at larger strains.

Fig. 9

Measurements obtained during uniaxial compression test of dummy cylinder a results from different camera pairs. b average image analysis results vs LVDT

Effects of misalignment are anticipated in compression tests, and the normal procedure employed is to consider the average of the strains recorded by the ‘local’ gauges as representative of the sample. Figure 9b presents the stress–strain curve where the strains plotted are the average values of the 4 No. camera pairs.

It is seen that average of the four camera pairs leads to a stress–strain response closely comparable to the theoretical linear elastic characteristic for the acetal polymer cylinder (with a reported Young’s modulus, E of 2800 MPa). The trend is not perfectly linear possibly because of non-linearity in the load cell calibration or non-linearity in the material itself. However, strains derived from the average of four camera pairs in additional tests on dummy samples involving application of an initial bedding-in stress of 750 kPa matched the theoretical response exactly. It therefore appears that averaging of four camera pairs for the test presented in Fig. 9a was insufficient to completely remove the effect of poor alignment of the sample top with the load cell, i.e. simply averaging the measured results does not necessarily lead to the elemental response of the specimen.

4 Triaxial soil tests

Four consolidated drained triaxial tests were conducted using the current version of the UWA 3-D image-Based measurement system, which employs sixteen Raspberry Pi cameras (see Fig. 10a). Before testing, the texture required for the 3DPIV analysis was achieved by spray painting the sample membrane to achieve the ‘dot pattern’ shown in Fig. 7b. The tests were conducted using a subrounded silica sand with a mean effective particle size (d₅₀) of 0.18 mm and uniformity coefficient of 1.7. Bagbag et al. [4] present triaxial test results including local instrumentation and bender element data for the same sand and these results are used to check those obtained with the image-based system.

Fig. 10

a View of triaxial set-up with 16 No. cameras, b Point cloud on specimen's surface (test with Dr = 70%, σ′_a = 100 kPa, σ′_r = 100 kPa)

The wet pluviation method was used to prepare fully saturated triaxial specimens with a height of 140 mm and a diameter of 64 mm. Three of the samples tested had a relative density (D_r) of 70%, and the fourth sample had a D_r value of 36%. Two samples were consolidated anisotropically to axial stresses (σ′_a) of 100 kPa and 400 kPa with respective radial effective stresses (σ′_r) of 50 kPa and 200 kPa. The two other samples were consolidated isotropically to effective stresses of 100 kPa and 200 kPa.

The specimens were first sheared slowly at an axial strain rate of 0.0035% per minute with images captured at 0.001% intervals. The shearing rate was progressively increased (and the image capture frequency reduced) during the test to a constant value of 0.15% per minute after a strain of 0.7% was reached.

The positions of all cameras are shown in Fig. 10a. Each holder supports a camera viewing the bottom half and top half of the sample. The fields of view of the bottom and top halves correspond to sample elevations of 20–80 mm and 80–130 mm, respectively. Figure 10b depicts the positions of all data points on the surface of one of soil specimens tested.

4.1 Axial strain calculation

Typical examples of vertical displacement measurements obtained at various stages of drained shearing of an anisotropically consolidated sample are provided in Fig. 11. The three stages plotted correspond to nominal axial strains determined from the external LVDT measurements (given the symbol ε_g) of 0.004%, 0.033% and 0.4%. Given the variability of local strains indicated by the elastic sample in uniaxial compression (see Fig. 9b), regression analysis of the displacement data was considered the most appropriate and objective means of strain determination (noting that the slope of the vertical displacement vs. sample height, h, relationship equates to local axial strain). A number of features evident in Fig. 11 (with associated examples given in Figs. 12 and 13) and common to all 4 soil triaxial tests performed are summarized as follows:

Fig. 11

Typical example of vertical displacements indicated by datapoints on sample with D_r = 70%, consolidated to σ′_a = 400 kPa, σ′_r = 200 kPa

Fig. 12

Typical variation in normalized axial strain around sample periphery. a Results from top row of cameras. b Results from bottom row of cameras

Fig. 13

Vertical displacement observed at q = 150 kPa on a dense sand sample isotropically consolidated to 200 kPa

(i)There is a mismatch of about 0.0015mm between displacements recorded at the top and bottom half of the sample. This is evident under a very low applied stresses in Figure 11a which shows the offset of the best-fit regression lines for axial strain over the top and bottom half data points. This discrepancy is of fixed magnitude (i.e. it does not increase with increasing stress on the sample) and can be mitigated by assuming the average sample strain is the average of the upper and lower half strains.

(ii)Extrapolation of data for a perfect sample with no bedding or alignment issues should indicate zero displacement at h = 0. For example, Figure 11b shows that an extrapolated displacement at h = 0 of approximately 0.005mm when ε_g= 0.033%. This displacement can be attributed to a bedding error at the sample base and contributes to the unreliability of strain measurements inferred from external LVDTs.

(iii) Vertical displacements and axial strains determined by each camera pair vary with the angular co-ordinate of the triaxial sample; this is clear from the spread of displacements recorded at any given h value. Best-fit regression lines for displacement vs. height data at any given angular (polar) coordinate (θ) for camera pairs at the upper half of a sample are usually similar to those at the lower half of the sample. A typical example of what was observed is presented in Figure 12, which plots the magnitude of strains relative to the average and their dependence on θ. In this figure, the top row of cameras indicates some sample bending while the bottom row of cameras shows relatively uniform strains.

(iv) Displacements measured towards the top of soil samples often show significant variability. This variability is very pronounced in isotropically consolidated samples where misalignment and bedding errors have not been reduced during the anisotropic consolidation stage. An example of a particularly wide spread in displacement measurements for an isotropically consolidated sample is shown in Figure 13. Separate finite element analyses (Du [8]) predict this ‘flower’ type displacement pattern if the load cell is significantly misaligned with the top of a sample.

4.2 Vertical stiffness

The variation in the drained secant Young’s modulus (E′_v) determined from the four triaxial tests performed is plotted in Fig. 14. The axial strains used for calculation of these E′_v values were the average of those measured using all 16 camera pairs. E′_v values determined from the external LVDT measurements are also plotted.

Fig. 14

Variations in secant Young’s modulus (E′_v) with axial strain (ε_a) in four triaxial tests on sand samples

Bagbag et al. [4] report stiffness data for ten anisotropically consolidated samples of the same sand using bender elements (BE) and local strain instrumentation. Although these tests were not conducted on samples with the same densities and stress levels, their data are well represented by the following empirical format employed by Lehane & Cosgrove [17] using the fitting coefficients C_E and n given in Table 1:

$$E\prime_{{\text{v}}} \left( {{\text{at given }}\varepsilon_{{\text{a}}} } \right) \, = \, C_{{\text{E}}} F\left( e \right) \, \left( {\sigma \prime_{{{\text{vc}}}} /p_{{{\text{atm}}}} } \right)^{{\text{n}}}$$

(2a)

where

$$F\left( e \right) \, = \, \left( {{2}.{17} - e} \right)/\left( {{1} + e} \right)^{{2}} {\text{and }}e = {\text{void ratio}}$$

(2b)

Table 1 Empirical parameters, n & C_E, for use with Eq. 2

The degradation of stiffness with strain for isotropically consolidated samples differs from that of anisotropically consolidated samples. Therefore, corresponding C_E and n values for isotropic conditions provided in Table 1 were obtained directly from [17] based on regression analyses of triaxial tests on a variety of sands. The error bands for the C_E coefficients in this table are wider than for the anisotropic values as they are representative of a wider range of sands.

The E′_v values derived using the UWA image system are seen in Fig. 14 to be in very good agreement with those inferred from conventional local strain instrumentation. Exact agreement cannot be expected in view of the approximate nature of Eq. (2) but also because conventional local strain instrumentation only employs the average of two strain measurements to infer an average strain for a triaxial sample. As may be expected, the E′_v values inferred from external displacement measurement are significantly under-estimated at low strains in isotropic tests (e.g. often more than 5 times lower at ε_a = 0.01%) but are within 10 and 50% of stiffness values at ε_a = 0.01% in anisotropically consolidated samples due to the reduced effects of bedding and misalignment (as observed in the uniaxial compression tests on the plastic cylinder, discussed above). The stiffness determined at ε_a values of around 0.001 to 0.002% using the image-based approach matches those determined in BE tests indicating that the approach can dispense with the need for bender elements in addition to conventional local strain instrumentation.

4.3 Radial strain calculation

Radial strains at any given elevation on the sample are derived as:

$$\varepsilon_{r} = \frac{{\sqrt {\left( {X_{0} - X_{c0} } \right)^{2} + \left( {Y_{0} - Y_{c0} } \right)^{2} } - \sqrt {\left( {X_{i} - X_{ci} } \right)^{2} + \left( {Y_{i} - Y_{ci} } \right)^{2} } }}{{\sqrt {\left( {X_{0} - X_{c0} } \right)^{2} + \left( {Y_{0} - Y_{c0} } \right)^{2} } }}$$

(3)

where (X₀, Y₀, Z₀) and (X_i, Y_i, Z_i) refer to the initial and current world coordinates of data points, respectively. (X_c0, Y_c0) and (X_ci, Y_ci) refer to the initial and current centres of area at elevations of Z₀ and Z_i, respectively. These centres of area may differ due to rigid body rotation of the sample, and their values are determined using the x and y coordinates of all the datapoints monitored within a vertical distance of 5 mm from the vertical (z) co-ordinate. Lateral translation tests using a dummy cylinder, such as used for vertical translation tests (Fig. 7), indicated that the lateral movement of the surface of the cylinder using the current system can be confidently measured with an accuracy of about 2 μm.

A typical example of the radial displacements measured by the system is shown in Fig. 15 for a stage of a test where the axial strain is about 4%. The classic ‘barrelling’ sample shape is in evidence indicating no movement at the sample ends but a radial movement of about 2 mm at the centre of the sample. The measurements show that the deformation is not perfectly symmetrical, e.g. maximum radial displacements for camera pairs 2 & 3 and 10 & 11 are about 1.65 mm and for camera pairs 6 & 7 and 15 & 16, located at the opposite side of the sample, are about 2.2 mm. The maximum radial movements occur at h = 80 mm rather than at the mid-height of the sample at h = 70 mm. These observations and those for vertical displacements shown in Fig. 11 highlight the fact that the results from a triaxial test on a soil sample are an approximation of elemental soil response.

Fig. 15

Distribution of radial displacement at sample axial strain of about 4% (test performed on dense sample isotropically consolidated to 100 kPa)

The measured variations in deviator stress with radial strain (where tensile radial strain is taken as positive) are plotted for a typical test in Fig. 16. This shows strong similarity between the average strains measured by the average of the cameras monitoring the top and bottom halves of the sample. At larger strains, these averages were also closely comparable which is perhaps unexpected given the asymmetry shown in Fig. 15.

Fig. 16

Variation in deviator stress with radial strain; inset graph shows the variation at low strains (Test performed on dense sand sample anisotropically consolidated to σ′_a = 400 kPa & σ′_r = 200 kPa)

Research applications usually employ a radial strain belt, which only measures radial strain at one point at the mid-height of the triaxial sample. Such a measurement is clearly insufficient when one considers the actual deformation shape, such as shown in Fig. 15. For standard testing, the radial strain is determined from the volumetric strain measured using a volume gauge and the axial strain determined from the external LVDT. The radial strain determined in this manner is seen in Fig. 16 to match the image-based measurements (with an average difference between the data sets of 0.006% at low strains) and hence is a reasonable approximation for the average radial strain in the sample.

5 Conclusions

The key innovation of the system described in this paper is the development of a low-cost and simple 3D image analysis method for soil stiffness measurement in the triaxial test. The system has a resolution sufficient to avoid the need for bender elements as well as local strain gauges mounted on samples. The system can be fitted to any triaxial testing device and therefore has the potential to allow the non-linear stiffness characteristics of soil to be measured routinely in the many devices in use around the world. In contrast with the time and expertise required to fix local gauges to samples, use of the system requires no special technical skills. Calibration of the system is rapid as all the cameras can be calibrated simultaneously with the use of a cylindrical calibration target. Refraction effects are incorporated in the camera matrix and distortion parameters, which eliminates the need for complex calculations during post-image analysis.

The accuracy of the system was validated through a series of vertical translation tests, which over the beginning of the tests indicated a difference of 0.001 mm between measured and reference results. This high level of resolution explains the similarity of the Young’s moduli derived from the image measurement and those from bender elements in the very small strain region (strains less than 0.002%). Measured soil stiffness degradation curves are shown to compare well with previous triaxial test data and empirical formula while radial strains are consistent with average radial strains inferred from conventional external measurements. Additional testing will assist in refining and updating both the hardware and software employed to date. Future investigations with the system will explore shear band formation and will enable the development of recommendations for inference of elemental response from a triaxial test, which the image-based measurements have demonstrated is essentially a boundary value problem.