A zero-thickness interface element incorporating hydro-chemo-mechanical coupling and rate-dependency

Abstract

The interfaces play a key role in many engineering problems involving geologic materials. In particular, slope stability analyses of ancient landslides (that were subjected to large displacements along a slip surface) need the formulation of ad hoc interface elements. The mechanical response of slip surfaces in clays is affected by hydro-chemo-mechanical interactions and by rate effects and this paper presents the formulation of an innovative zero-thickness interface element for dealing with these kinds of effects. The proposed interface element is an extension of the modified zero-thickness element proposed by Goodman et al. (J Soil Mech Found Div ASCE 94:637–659, 1968). In addition to solid displacement, we consider the flow of water and the diffusion of a single salt in the fluid phase. Terzaghi’s effective stress principle is used leading to the usual hydro-mechanical coupling within the interface element. The fluxes of water and salt are considered in the longitudinal and in transversal directions of the interface element. For the constitutive relation, we propose an innovative nonlinear elastic energy that improves the numerical convergence in the occurrence of interface opening. The Mohr–Coulomb yield surface is used for the plastic regime in which we considered the effects of strain rate and salt concentration on the shearing behaviour of the interface element. The proposed element has been implemented in a user-defined subroutine of ABAQUS. The typical effects of salt concentration and displacement rate and the typical model responses for the longitudinal and transversal fluxes of salt and pore fluid are discussed in detail. Finally, the proposed interface element is validated through the comparison with experimental results.

1 Introduction

It is well-accepted that interfaces play a key role in many engineering problems related to geologic materials [29, 42, 52, 55, 56, 59, 61]. We can just recall the paramount importance of discontinuities in rock mechanics [29], in petroleum engineering [56], in CO$_2$ sequestration [42], and in geothermal energy exploitation [55]. In addition, the interfaces are very important for describing the boundary between soil and engineering structures, such as retaining walls, piles, and tunnels. Although the majority of these interface problems involve only hydro-mechanical coupling, due to the contemporary presence of the pore fluid and the solid skeleton, there are examples in which more complex formulations are needed, such as in geothermal piles in which the interface must account for the whole thermo-hydro-mechanical coupling [11].

Interfaces have also a special interest in slope stability analyses of ancient landslides, which underwent large displacements along a slip surface. As a result, these interfaces separate the same geologic material, namely the stable soil with respect to the failing mass, and their properties are the results of the large displacements that occurred in the previous geologic history. In clays, the main characteristic of these slip surfaces is that slope displacements are concentrated in narrow shear zones [57], where the shear strength reaches the minimum value that the soil can reach, due to the realignment of clay particles induced by the large displacements. This fact is well known and the minimum strength is denoted as residual strength and its properties have been fairly well investigated.

One important aspect of the residual shear strength that has been highlighted is the dependence of the residual strength on pore fluid composition: the variations of residual friction angles can be very large depending on the salt concentration of pore fluid and the activity of clay [15]. This fact is very important since it could be exploited for slope stabilization of ancient landslides [18, 19]. In addition, several results reported in the literature show a dependence of the residual shear strength on the displacement rate [16]. This is also very important for forecasting the landslide movements because many engineering structures suffer damages due to an interaction with a slowly moving landslide [18].

Finally, the interfaces may deeply affect the ground fluid flows, because they can constitute a preferential path along the longitudinal direction or, in contrast, can prevent the flux in their transversal direction. Di Maio et al. [19] have recently shown that the hydraulic conductivity along the slip surface in a clayey slope is more than two orders of magnitude higher than that of the landslide body.

Several types of interface elements have been proposed to model the discontinuities in geomaterials or soil-structure interfaces [14, 27]. The joint element proposed by Goodman et al. [27] is the earliest one in which two parallel surfaces with two nodes on each of them are considered and the interface is assumed to have virtually a zero thickness. In this interface element, a high value is assigned to the normal stiffness in order to prevent the penetration and overlapping of the two surfaces of the interface element with respect to each other. Reviews and applications of this element are available in various publications. Beer [6] has extended Goodman’s element to three-dimension. Yuan and Chua [60] and Amar Bouzid et al. [1] have presented the exact solution of an axisymmetric joint element when the applied load is axisymmetric or non-axisymmetric. Day and Potts [12] discussed the numerical instabilities of Goodman’s element such as high-stress gradient and ill-conditioning of the stiffness matrix. These numerical instabilities are due to the large aspect ratio (i.e. the ratio of length to thickness) of the joint element which can be reduced by decreasing the size of the element. Goodman’s element has been adapted to several applications such as in soil nailing [59], in concrete-faced rock-fill dams involving an interface between gravel cushion layers and concrete-face slabs [61], in soil-pile interaction [52], in frictional damping system [22]. Kaliakin and Li [30] developed a 6-node zero-thickness element as a solution for preventing the stress oscillation and ill-conditioning that occur in some applications of the joint element in finite element analysis. Coutinho et al. [10] modified Goodman’s element by adding a link element to eliminate kinematic inconsistencies.

Desai et al. [14] developed a thin solid element in order to simulate the interface behaviour under static and dynamic loading. The stiffness matrix of this element is computed as an isoparametric solid element but the constitutive matrix has only normal and shear components. In other words, the components related to the in-plain normal strain are assumed to be equal to zero. Experimental tests have been performed to investigate the effect of various factors such as normal stress, displacement amplitude, and the number of loading cycles on the behaviour of a sandy concrete interface [13]. Sharma and Desai [50] developed an interface element similar to a continuum (finite) element whereas its constitutive response has been defined differently from that of the neighbouring "solid" elements and a constant thickness was used in the definition of strain. It has been proposed that the constitutive matrix is transformed from a local to a global coordinate system.

Previous studies have considered only the mechanical behaviour of interface elements and the coupling between stresses with pore pressure was neglected. Ng and Small [38] proposed an interface element, based on Goodman’s element in which Biot’s consolidation theory was used to model the coupling of water pressure and displacement of solid interfaces or rock joints and the fluid flow through the discontinuity is a function of the pressure gradient. Nguyen and Selvadurai [39] have studied the coupled behaviour of rock joints and have considered that the longitudinal permeability of the rock joints changes with shearing and gouge material between the surfaces of the interface. Segura and Carol [46] proposed that the transversal flow must be included in addition to the longitudinal flow (Fig. 1). The formulation was developed for a single node, double node, and triple node in the element thickness, thus both transversal and longitudinal flows have been preserved [47]. The double nodded element has been extended to obtain a fully coupled hydro-mechanical model in terms of nodal displacement and pore pressure [48, 49]. Luo and Peng [34] further developed the formulation of Goodman’s element for considering the hydro-mechanical coupling based on Biot’s consolidation theory. Cerfontaine et al. [9] developed a 3D fully coupled hydro-mechanical formulation of triple nodded interface element. The coupling is created by the longitudinal fluid flow which depends on the gap size, whereas the effective stress was computed based on Terzaghi’s principle. A fully coupled thermo-hydro-mechanical formulation has been proposed for a 3D zero-thickness interface element by Cui et al. [11].

Fig. 1

Interface element between two continua with longitudinal and transversal fluxes

Concerning the constitutive model describing the interface response, in most cases, the Mohr–Coulomb yield criterion has been used for describing the irreversible behaviour of the interface element. The elastic behaviour was represented by linear or nonlinear functions in which normal and shear responses are decoupled. Samtani [43] and Samtani et al. [44] proposed a constitutive model for thin-layer interface elements in which the time-dependent behaviour of interface material has been considered in addition to the elastic and plastic behaviour. Gennaro and Frank [23] studied the interface behaviour between granular soil and structure. They proposed a constitutive relation based on the Mohr–Coulomb yield function which accounted for the dilatancy of soil during shearing. Karabatakis and Hatzigogos [31] studied the creep behaviour of interface elements with a constant thickness and concluded that the size and properties of the interface and neighbouring solid elements affect the creeping behaviour. Barton and Bandis [3,4,5] proposed a nonlinear, phenomenological model for rock joints based on the Mohr-Culoumb criterion and considering the joint roughness coefficient (JRC), and the joint compression strength (JCS). Wang et al. [58] developed a constitutive model for rock joints in which shear anisotropy is incorporated in the elastic deformation by introducing a shape function in the elastic shear stiffness. Finally it is worth mentioning the hypoplastic models that have been proposed to model the interface behaviour [51, 53, 54]. In particular, Stutz and Mašín [51] presented a hypoplastic model for 3D interfaces in fine-grained soils, whereas Stutz et. al [53] proposed a hypoplastic model including in-plane stresses within the interface.

Although the previous literature review is not probably exhaustive, we can conclude that just a minor part of the published works have considered the hydro-mechanical coupling, and even fewer of them have considered the rate dependency. In any case, to the best of the Authors’ knowledge, no formulation has been proposed for taking account of chemical and rate interaction at an interface. In this paper, such an interface element is proposed starting from the modified Goodman’s element [30], in which both the flow of water and salt diffusion are considered in addition to the mechanical response. This allows the simulation of discontinuities, cracks, pre-existing slip surfaces, and soil-structure interfaces. For the sake of simplicity, here it is assumed that a single salt may diffuse in the pore fluid and reference is made to the clay properties at the residual state. Anyway, the approach here presented can be easily extended to other applications in geotechnical engineering, just implementing suitable constitutive relationships.

The paper is organized as follows. The governing equations of the interface element consist of the momentum balance for the interface region and the mass balance of pore water and diffusing salt as explained in Sect. 2. The chemo-mechanical, rate-dependent constitutive response of the interface is described in Sect. 3. In particular, an innovative hyper-elasticity law is proposed in Sect. 3.1 for improving the numerical treatment when tensile displacements are applied. The finite element formulation is presented in Sect. 4. Solid displacements, pore pressure, and salt concentration have been selected as nodal unknowns. The interface element has been implemented in a user-defined subroutine (UEL) of ABAQUS [28] and typical simulations are presented in Sect. 5. Model validation and the comparisons with experimental results are presented in Sect. 6. Finally, the conclusions are drawn in Sect. 7.

In this work, vectors and matrices are denoted with bold characters, whereas scalar quantities are denoted with plain characters.

2 The balance equations

The proposed interface element is assumed to be composed of two phases: the solid and the fluid phase (denoted with the upper case subscript S or W), the latter including pore water and dissolved salt as water species (denoted with the lower case subscript s or w). From a geometrical point of view, this element consists of two parallel surfaces which can be considered even to be perfectly superposed for the mechanical response (in fact it can be considered a zero-thickness interface element) and are separated by a finite gap for the fluxes of water and salt. These two surfaces may have different pore pressures and salt concentrations with respect to each other. The following conservation laws must be considered: the conservation of momentum, the mass conservation of pore fluid, and the mass conservation of diffusing salt. Let us assume that the x- and y-coordinates are parallel and orthogonal to the discontinuity, respectively. Figure 2 shows the positive direction of the relevant quantities in the balance equations.

Fig. 2

Conventions for the interface region in (a) momentum balance, (b) mass balance of pore water, (c) mass balance of salt in the fluid phase

2.1 Momentum balance

From a mechanical point of view, the proposed interface can be visualized as a bed of non-linear, normal and shear (Winkler) springs, acting between the two (superposed) surfaces defining the interface. The mechanical response of these springs depends on salt concentration and displacement rate.

It is worth emphasizing that the two surfaces defining the interface have null in-plane (longitudinal, transversal, and bending) stiffnesses. Thus the mechanical contributions of the interface element consist only of the normal and shear stiffnesses of the springs. As a result, the conservation of momentum reduces to imposing the equilibrium of internal stresses with applied external pressures $f_n$ and $f_s$, in the normal and tangential directions to the interface,

$$\begin{aligned} \sigma _n = f_n^{\rm{top}} = -f_n^{\rm{bot}}, \qquad \sigma _s = f_s^{\rm{top}} = -f_s^{\rm{bot}}, \end{aligned}$$

(1)

where $\sigma _n$ and $\sigma _s$ are the total normal and shear stresses (positive when tensile), the superscripts $^{\rm{top}}$ and $^{\rm{bot}}$ denote the top and bottom surfaces of the interface element. The equalities $f_n^{\rm{top}} = -f_n^{\rm{bot}}$ and $f_s^{\rm{top}} = -f_s^{\rm{bot}}$ hold true for null body and inertial forces, as assumed herein.

2.2 Mass balance of pore water

For the fluid flow, the proposed interface consists of two parallel surfaces with a finite gap h and different permeabilities in the longitudinal and transversal directions [40]. The two surfaces of the interface may have different pore pressures when the discontinuity is filled with a low-permeable material.

As a result, there can be both a longitudinal and a transversal water flow between the interface surfaces. The transversal flow is induced by a pore pressure difference between the top and bottom surfaces of the interface element. Since all species (namely solid grains, pore fluid, and diffusing salt) are assumed incompressible and the interface element is perfectly saturated, the mass balance equation reduces to the continuity condition.

The longitudinal strain of the discontinuity may not be null, in general, and is defined as follows

$$\begin{aligned} \epsilon _l = \frac{\partial }{\partial x} \left( \frac{u^{\rm{top}}+u^{\rm{bot}}}{2} \right), \end{aligned}$$

(2)

where $u^{\rm{top}}$ and $u^{\rm{bot}}$ are the longitudinal displacements of the top and bottom surfaces. Let us introduce also the normal strain $\epsilon _n$, defined as follows [6, 11, 12, 30, 38]:

$$\begin{aligned} \epsilon _n=v^{\rm{top}}-v^{\rm{bot}}, \end{aligned}$$

(3)

with $v^{\rm{top}}-v^{\rm{bot}}$ the relative normal displacement of the two surfaces with $v^{\rm{top}}$ and $v^{\rm{bot}}$ the transversal displacements of the top and bottom surfaces, respectively. As a result, the normal strain has the units of a length L.

Through standard arguments, the mass balance equation for pore fluid contained in a volume element of dimension dx and dy can be written as

$$\begin{aligned}{} & {} \frac{1}{h} \frac{\partial \epsilon _n}{\partial t} + \frac{\partial \epsilon _l}{\partial t} + \frac{\partial J_W^l}{\partial x}+\frac{\partial J_W^t}{\partial y}=0, \end{aligned}$$

(4)

where $\epsilon _n$ is divided by h due to the definition given in Eq. (3).

It is worth noting that all quantities appearing in Eq. (4) depend only on the x variable (namely they are constant in the transversal direction). Thus, if Eq. (4) is integrated along y, we obtain

$$\begin{aligned}{} & {} \frac{\partial \epsilon _n}{\partial t} + h \frac{\partial \epsilon _l}{\partial t} + h \frac{\partial J_W^l}{\partial x}+ \int _h \frac{\partial J_W^t}{\partial y} {\rm{d}}y=0, \end{aligned}$$

(5)

where the last term obviously reduces to

$$\begin{aligned} \int _h \frac{\partial J_W^t}{\partial y} {\rm{d}}y = \left[ J_W^t \right] _0^h = J_{W}^{\rm{bot}}+J_{W}^{\rm{top}}, \end{aligned}$$

(6)

where $J_{W}^{\rm{bot}}$ and $J_{W}^{\rm{top}}$ are the outflow fluxes (with units L/T) through the bottom and top surfaces of the discontinuity, due to the leak-off from the discontinuity towards the neighbouring porous media. It is worth noting that Eq. (5) coincides in part with the analogous equation used by [47, 49]. The term $(\partial \epsilon _n/\partial t + h \partial \epsilon _l/\partial t )$ is the rate of volume change of the discontinuity (with units L/T) and $h J_W^l$ is the longitudinal flux of fluid (with units $L^2/T$) along the interface element. Equation (5) represents a continuity equation in the longitudinal direction of the discontinuity, in which the volume change of the solid skeleton is coupled with both the longitudinal and transversal fluxes of water. It is worth adding that the second term in Eq. (5) is often neglected in the literature.

Longitudinal water flux: The interface is assumed to have a finite, non-null thickness to allow water flux in the longitudinal direction of the interface. The longitudinal flux $J_W^l$ can be obtained from the generalized fluxes of water and salt in porous media as follows [37]:

$$\begin{aligned}{} & {} J_W^l=-\frac{K_{l}}{\rho _w g} \left( \frac{\partial p_{mW}}{\partial x} -\rho _w g_l \right) + \omega \frac{K_{l}}{\rho _w g} c_{msW} \nonumber \\{} & {} \quad \left( \frac{RT}{\text{ v}_s^{(M)}} \chi \frac{\partial ({\text{ Ln } \; c_{msW}})}{\partial x} \right), \end{aligned}$$

(7)

in which $K_{l}$ (with units L/T) is the hydraulic conductivity of the interface in the longitudinal direction, $g_l$ is the component of the gravity vector $\textbf{g}$ in the longitudinal direction, R is the ideal gas constant equal to 8.31451 J/(K mol), T is absolute temperature, $\omega$ is the osmotic efficiency of the infilled material at the discontinuity, $\chi$ is the ratio of molar volume of fluid phase to the molar volume of water, $\text{ v}_s^{(M)}$ is the molar volume of salt, $\rho _w$ is the density of water, and $c_{msW}$ is the salt concentration at the mid-plane of the discontinuity, namely $c_{msW}=(c_{sW}^{\rm{top}}+c_{sW}^{\rm{bot}})/2$, with $c_{sW}^{\rm{top}}$ and $c_{sW}^{\rm{bot}}$ the salt concentrations at the top and bottom surfaces of the discontinuity (see Sect. 2.3). Equivalently, $p_{mW}=(p_{W}^{\rm{top}}+p_{W}^{\rm{bot}})/2$ is the pore pressure at the mid-plane of the discontinuity, with $p_{W}^{\rm{top}}$ and $p_{W}^{\rm{bot}}$ the pore pressures of the top and bottom surfaces, respectively. Note that the longitudinal flux of water (and of salt) is based on the mean value of pore pressure (and of salt concentration) as proposed by Segura and Carol [46, 47, 49].

Transversal water flux: The transversal flux of water $J_W^t$ (with units L/T) between the two surfaces of the interface, is assumed to be defined by the generalized fluxes [37, 40, 49]:

$$\begin{aligned}{} & {} J_W^t=- \frac{K_t}{\rho _w g }\left( \dfrac{p_W^{\rm{top}}-p_W^{\rm{bot}}}{h} - \rho _w g_t \right) + \omega \frac{K_{t}}{\rho _w g} c_{msW} \nonumber \\{} & {} \quad \left( \frac{RT}{\text{ v}_s^{(M)}}\chi \frac{ \text{ Ln } \, \left( c_{sW}^{\rm{top}}/ c_{sW}^{\rm{bot}}\right) }{h} \right), \end{aligned}$$

(8)

where $K_t$ (with units L/T) is the hydraulic conductivity in the transversal direction to the discontinuity and $g_t$ is the component of the gravity vector $\textbf{g}$ in the transversal direction. If $K_t/h$ is very small, the discontinuity turns out to be a barrier to the flux of water in the orthogonal direction to the discontinuity, thus preventing the fluid flow in the transversal direction. In this case, the two surfaces of the discontinuity have different pore pressures with respect to each other. In contrast, if $K_t/h$ is very large, the two surfaces of the discontinuity have the same pore pressure.

2.3 Mass balance of salt in the fluid phase

In this work, a single salt is assumed to diffuse in the fluid phase for the sake of simplicity. Moreover, the solid particles are assumed to be not reactive, thus there is no mass transfer between the solid and fluid phases. This assumption is acceptable, due to the typically small amount of infilling material. In addition to the salt diffusion induced by a concentration gradient, there is an advective transport of salt due to the pore fluid flow.

Salt concentration $c_{sW}$ in the fluid phase is defined as a non-dimensional quantity equal to the ratio of the volume of the salt with respect to the volume of the fluid phase ($c_{sW}=V_{sW}/V_W$). Note that the sum of the concentrations of the species in the fluid phase (i.e. water and salt) is equal to one (i.e. $c_{sW}+c_{wW}=1$).

Similarly to the flow of water, salt may diffuse along both the longitudinal and transversal directions of the discontinuity. In analogy with Eq. (4), through standard arguments, the mass balance of salt for a volume element with dimensions dx and ${\rm{d}}y$ is

$$n_W \frac{\partial c_{sW}}{\partial t} + c_{sW} \left( \frac{1}{h} \frac{\partial \epsilon _n}{\partial t} + \frac{\partial \epsilon _l}{\partial t} \right) + \frac{\partial J_{sW}^l}{\partial x}+\frac{\partial J_{sW}^t}{\partial y}=0,$$

(9)

where $n_W$ is the porosity of the infilling material in the discontinuity ($n_W=1$ if the discontinuity is empty) and $J^l_{sW}$ and $J_{sW}^t$ are the longitudinal and transversal fluxes of salt along the discontinuity.

Similarly to Eq. (4), Eq. (9) can be integrated in the transversal direction (namely y axis), thus, taking into account that salt concentration varies linearly in the y direction, we obtain

$$\begin{aligned}{} & {} n_W h \frac{\partial c_{msW}}{\partial t} + c_{msW} \left( \frac{\partial \epsilon _n}{\partial t} + h \frac{\partial \epsilon _l}{\partial t} \right) \nonumber \\{} & {} \quad + h \frac{\partial J^l_{sW}}{\partial x} +J_{sW}^{\rm{top}}+J_{sW}^{\rm{bot}}=0, \end{aligned}$$

(10)

where $J_{sW}^{\rm{top}}$ and $J_{sW}^{\rm{bot}}$ are the salt leakages from the top and bottom surfaces of the discontinuity, respectively, due to the salt diffusion towards the neighbouring porous media, and $c_{msW}$ is the mean value of salt concentration, coinciding with the salt concentration at the intermediate plane of the discontinuity. It is worth remarking that a null transfer of water and salt has been assumed between the solid and fluid phases.

The longitudinal flux of salt is given by the sum of the advective flow of salt due to the fluid flow and the diffusion flux as:

$$\begin{aligned} J^l_{sW}=c_{msW} \text{ v}_{\rm{adv}}^l+J_{sW}^{dl}, \end{aligned}$$

(11)

where $\text{ v}_{\rm{adv}}^l$ is the longitudinal advective velocity due to the longitudinal water flow ($\text{ v}_{\rm{adv}}^l=\left( J_W^l-J_{sW}^{dl}\right) /n_W$ that is strictly valid for negligible osmotic efficiency) and $J_{sW}^{dl}$ is the longitudinal diffusion flux of salt.

In the balance equation of salt, the advective term is important for advection-dominated problems which have a value of Peclet number $Pe=|\text{ v}_{\rm{adv}}^l|l/D_{l}$ larger than 1, l is a characteristic length of the discontinuity element and $D_{l}$ is the diffusion coefficient along the longitudinal direction of the discontinuity.

Similar considerations hold true for the transversal flux of salt

$$\begin{aligned} J_{sW}^t=c_{msW}\text{ v}_{\rm{adv}}^t+J_{sW}^{dt}, \end{aligned}$$

(12)

where $\text{ v}_{\rm{adv}}^t$ is the transversal advective velocity ($\text{ v}_{\rm{adv}}^t=\left( J_W^t-J_{sW}^{dt}\right) /n_W$) and $J_{sW}^{dt}$ is the transversal diffusion flux of salt. It is worth noting that in the transversal direction, the Peclet number $Pe=|\text{ v}_{\rm{adv}}^t|h/D_{t}$ is typically very small, due to the small value of the thickness h, thus in most cases, no regularization is needed.

Longitudinal salt diffusion: The diffusion of salt in the longitudinal direction is given by the generalized fluxes of water and salt [37] applied to the 1D element.

$$\begin{aligned}{} & {} J_{sW}^{dl}=-n_W c_{msW} D_l \left( \frac{\partial ({\text{ Ln } \; c_{msW}})}{\partial x} \right) \nonumber \\{} & {} + \omega c_{msW} \frac{K_{l}}{\rho _w g} \left( \frac{\partial p_{mW}}{\partial x} -\rho _w g_l \right), \end{aligned}$$

(13)

where $D_l$ (with units L$^2$/T) is the effective diffusion coefficient for the transmission of salt in the longitudinal direction.

Transversal salt diffusion: Similarly to the transversal flow of water, the transversal flux of salt is related to the salt concentration at the top and the bottom surfaces of the interface element (Fig. 3):

$$\begin{aligned}{} & {} J_{sW}^{dt}=- n_W c_{msW} D_t \left( \frac{ \text{ Ln } \, \left( c_{sW}^{\rm{top}}/ c_{sW}^{\rm{bot}}\right) }{h} \right) \nonumber \\{} & {} + \omega c_{msW} \frac{K_{t}}{\rho _w g} \left( \dfrac{p_W^{\rm{top}}-p_W^{\rm{bot}}}{h} -\rho _w g_t \right), \end{aligned}$$

(14)

where $D_t$ (m/s) is the transversal diffusion coefficient. Equivalently to pore fluid flow, the discontinuity may be filled with a material having a very low diffusion coefficient (i.e. a low value of $D_t/h$), thus the discontinuity becomes an obstacle to the diffusion of salt in the normal direction to the discontinuity. In this case, the salt concentrations on the surfaces of the discontinuity are different with respect to each other. In contrast, for very high values of $D_t/h$, the salt concentrations on the surfaces of the discontinuity are equal to each other.

Fig. 3

Diffusion of salt in the normal direction based on the salt concentration gradient between the top and bottom plate of the interface element

3 Constitutive relationships

The proposed constitutive model for simulating the rate-dependency and the chemo-mechanical coupling of the interface was developed with special attention to the observed response of clayey soils at residual strength.

For the mechanical part, reference has been made to the modified Goodman’s element proposed by Kaliakin and Li [30] in order to prevent numerical instabilities. In the 2D version, this interface element is composed of two superposed surfaces (in fact the value of interface thickness is ineffective for the mechanical behaviour and a zero-thickness can be assumed) and the mechanical response is related to the relative normal and shear displacements of the two surfaces.

Following the notation proposed by others [11, 12, 30], in addition to the normal strain $\epsilon _n$ (see Eq. 3), we define the shear strain $\epsilon _s$ as follows:

$$\begin{aligned} \epsilon _s=u^{\rm{top}}-u^{\rm{bot}}, \end{aligned}$$

(15)

where $u^{\rm{top}}$ and $u^{\rm{bot}}$ have been defined with regards to Eq. (2). Thus the total strain is defined as ${ {\varvec{\epsilon }}}=\begin{bmatrix}\epsilon _n&\epsilon _s\end{bmatrix}^T$.

The quantities that are work-conjugated with these strains are the normal stress $\sigma _n$ and the shear stress $\sigma _s$ (having the dimension of a pressure).

Below, we assume that the usual strain decomposition holds true, namely, the strain increment is the sum of an elastic and a plastic fraction as follows

$$\begin{aligned} \delta { {\varvec{\epsilon }}}=\delta { {\varvec{\epsilon }}}^e+\delta { {\varvec{\epsilon }}}^p, \end{aligned}$$

(16)

where the superscripts e and p denote the elastic and plastic parts, respectively. Moreover, the plastic strain rate ${\dot{{ {\varvec{\epsilon }}}}}^p$ is defined as follows

$$\begin{aligned} {\dot{{ {\varvec{\epsilon }}}}}^p=\frac{\delta { {\varvec{\epsilon }}}^p}{\delta t}, \end{aligned}$$

(17)

where $\delta t$ is the time interval. We assume small strains and displacements, isothermal conditions, negligible inertial forces, and negligible body forces.

Hydromechanical coupling is due to the effects of the pore fluid pressure on the stress and strains of the solid skeleton and vice versa. In other words, the change of pore pressure generally leads to the opening/closing of the discontinuity and to a change of shear strength. The hydro-chemo-mechanical coupling is caused by the diffusion of salt inside the discontinuity and to the chemical reactivity of the soil. Since the quantity of infilling material is generally small and, in the case of empty discontinuities, salt effects are related only to the superficial effects occurring on the surfaces of the discontinuity, we have assumed that there is no mass exchange between the soil and fluid phases due to a change of salt concentration (in contrast with the assumptions by Loret et al. [33] for clayey soils as a continuum). Thus, the friction angle and the strains are directly affected by the variation of salt concentration in the pore fluid (and not by the amount of water adsorbed/desorbed from the solid phase).

The total stress ${{\varvec{\sigma }}}=\begin{bmatrix}\sigma _n&\sigma _s\end{bmatrix}^T$ (positive when tensile) is related to the effective stress ${{\varvec{\sigma }}}'=\begin{bmatrix}\sigma '_n&\sigma '_s\end{bmatrix}^T$ and to pore water pressure $p_W$ (positive in compression) through Terzaghi’s principle of effective stress [11, 38, 46,47,48,49], namely:

$$\begin{aligned} {{\varvec{\sigma }}}={{\varvec{\sigma }}}'- \textbf{m}\, p_W, \end{aligned}$$

(18)

where $\textbf{m}$ is the vector that takes into account the influence of pore fluid pressure in the normal direction of the discontinuity $\textbf{m}=\begin{bmatrix}1&0\end{bmatrix}^T$ and $p_W$ is the pore water pressure. In the case of an interface, $p_W$ is assumed to coincide with the pore pressure at the mid-plane (i.e. $p_W= p_{mW}$ in Eq. 18).

3.1 Elastic behaviour

In this work, we propose an innovative elastic strain energy function, which is inspired to the proposal by Argani and Gajo [2] for multiaxial stress states with the aim of improving the rate of convergence of Mohr–Coulomb models. For the sake of simplicity, we have assumed that the elastic properties do not depend on salt concentration, thus the elastic strain energy density function is proposed in the following form:

$$\Gamma [\epsilon _n^e,\epsilon _s^e]=\left\{ \begin{array}{ll} k_n(-\epsilon _n^e+\epsilon _0)^3+k_s(\epsilon _n^{e2}+\epsilon _s^{e2})^{3/2}\\ \quad \text {for} \quad \epsilon ^e_n\le 0,\\ k \; p_0 \exp (-\epsilon ^e_n/k)+k_s(\epsilon _s^{e2})^{3/2}\\ \quad \text {for} \quad \epsilon ^e_n>0, \end{array}\right.$$

(19)

where $k_n$ and $k_s$ are two stiffness parameters (with units $F/L^4$), $\epsilon _0$ is a small value selected by the user (e.g. equal to 0.0001), $k={\epsilon _0}/{2}$ and $p_0=3k_n\epsilon _0^2$. Since no experimental information about a possible dependency of $k_n$ and $k_s$ on $c_{sW}$ is available, this possibility is disregarded below.

The first derivative of the elastic strain energy function with respect to the normal and shear strains provides the normal and shear stresses (see Appendix A). The second derivative of the elastic energy with respect to the elastic normal and shear strains gives the components of the tangent elastic stiffness matrix as:

$$\textbf{D}_e =\left[\begin{array}{lll} \partial ^2\Gamma / \partial {\epsilon ^e_n}^2{} \partial ^2&\Gamma / \partial {\epsilon ^e_n}\partial {\epsilon ^e_s}\\ \partial ^2\Gamma / \partial {\epsilon ^e_n}\partial {\epsilon ^e_s} &{} \partial ^2\Gamma / \partial {\epsilon ^e_s}^2 \end{array}\right].$$

(20)

These terms are reported in Appendix A. Both $D_e(1,1)$ and $D_e(2,2)$ increase with $\epsilon ^e_n$ and $\epsilon ^e_s$, respectively. The non-null out-of-diagonal terms $D_e(1,2)=D_e(2,1)$ imply a coupling between shear and normal strains.

The main advantage of the proposed elastic energy is that the resulting stress state is C0, C1, and nearly C2 continuous in $\epsilon ^e_n=0$. Moreover, tensile stresses can not be obtained even for very large openings ($\epsilon ^e_n>0$) of the interface element, thus the elastic predictor (see Sect. 3.4) can never lay in a region in which the yield function is undefined.

3.2 The yield surface

Classical Perzyna’s approach [41] is used for modelling the visco-plastic response. Let us recall here that in Perzyna’s approach [41], two different yield surfaces can be identified: the static and the dynamic yield surface ($F_s=0$ and $F_d=0$) [32, 35, 36, 41]. The former refers to a vanishingly small plastic strain rate (${\dot{{ {\varvec{\epsilon }}}}}^p \rightarrow 0$), whereas the latter depends on a non-null plastic strain rate.

Figure 4 shows the static and dynamic yield surfaces and the plastic potential (G) in the shear stress vs. normal effective stress $\sigma '_s-\sigma '_n$ plot. If the elastic predictor lays inside the static yield surface ($F_s\le 0$), the material response is elastic and inviscid, with an elastic response that is defined in Sect. 3.1. The static yield surface has no hardening, because it is intended to simulate the residual strength along a slip surface at a vanishingly small displacement rate, and is defined as follows

$$\begin{aligned} F_s[{{\varvec{\sigma }}}', c_{msW}]=|\sigma '_s|+\sigma '_n\tan \left( \varphi [c_{msW}] \right) , \end{aligned}$$

(21)

where $\varphi [c_{msW}]$ is the friction angle depending on the mean salt concentration at the mid-plane of the discontinuity. Note that the proposed expression of $F_s$ implies perfect plasticity.

Fig. 4

The state of stress with respect to yield function and potential function. $F_s$ and $F_d$ are the static and dynamic yield functions, and G is the potential function

In this work, the friction angle is assumed to depend on salt concentration $c_{msW}$ through the same expression proposed by Loret et al. [33], namely

$$\begin{aligned} \varphi [c_{msW}]=c_1+c_2\,\rm{tanh}{\left( c_3\frac{c_{msW}-c_{sW}^{dw}}{c_{sW}^{\rm{sat}}-c_{sW}^{dw}}\right) } \end{aligned},$$

(22)

where

$$\begin{aligned} c_1=\varphi ^{dw} \qquad \text{ and } \qquad c_2=\varphi ^{\rm{sat}}-\varphi ^{dw}, \end{aligned}$$

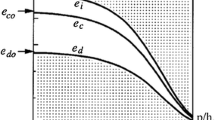
and $c_3$ is a constant value, selected by the user from experimental data. The values of $c_{sW}^{\rm{sat}}$ and $\varphi ^{\rm{sat}}$ are the salt concentration and the friction angle corresponding to a saturated salt solution. Equivalently, the $c_{sW}^{dw}$ and $\varphi ^{dw}$ are those of distilled water. This expression simulates the experimental observations [16, 45] showing that the friction angle changes very rapidly at the lowest salt concentrations and reaches a sort of saturation value at the highest concentrations (Fig. 5).

It is worth adding that a null cohesion has been assumed in Eq. (21), because this is the typical case of residual strength of clays. This limitation can however be easily removed by adding a cohesive contribution to Eq. (21).

Fig. 5

Change of friction angle with salt concentration: experimental results [16, 45] and model simulations for different values of $c_3$

The rate dependency is described according to Perzyna’s model [41], thus the stress state can lay outside the static yield surface only if the plastic strain rate is not null. According to Perzyna’s model [41], when the plastic deviatoric strain rate is not null ${\dot{\epsilon }}_s^p \ne 0$, then the dynamic yield surface does not coincide with the static one, namely

$$F_d[{{\varvec{\sigma }}}', c_{msW}, {\dot{\epsilon }}_s^p]=|\sigma '_s|+\sigma '_n\tan \left(\varphi [c_{msW}]\right) \left(1+ \Phi [{\dot{\epsilon }}_s^p] \right),$$

(23)

where $\Phi [{\dot{\epsilon }}_s^p]$ is the viscosity function that was inspired to the work of Madaschi and Gajo [36] on the creep behaviour of clays in oedometric compression. The viscosity function is assumed to consist of a logarithmic branch (for values of ${\dot{\epsilon }}_s^p$ larger than a minimum value, $\beta {\dot{\epsilon }}_{\rm{min}}$) and a polynomial branch close to the axis origin, namely

$$\Phi [{\dot{\epsilon }}_s^p] = {\left\{ \begin{array}{ll} \gamma \ln ({\dot{\epsilon }}_s^p/{\dot{\epsilon }}_{\rm{min}})\\ \quad \text{ for } \quad {\dot{\epsilon }}_s^p>\beta {\dot{\epsilon }}_{\rm{min}},\\ \gamma \left( A_1 {\dot{\epsilon }}_s^p+A_2({\dot{\epsilon }}_s^p)^2+A_3({\dot{\epsilon }}_s^p)^3 \right)\\ \quad \text{ for } \quad {\dot{\epsilon }}_s^p\le \beta {\dot{\epsilon }}_{\rm{min}}, \end{array}\right. }$$

(24)

where $\gamma$, ${\dot{\epsilon }}_{\rm{min}}$ and $\beta$ are constitutive parameters, whereas the polynomial coefficients $A_1$, $A_2$ and $A_3$ are deduced from ${\dot{\epsilon }}_{\rm{min}}$ and $\beta$ in such way that C0 and C1 continuity of the viscosity function $\Phi [{\dot{\epsilon }}_s^p]$ is ensured in the transition point ($\beta {\dot{\epsilon }}_{\rm{min}}$). These coefficients result equal to [36]:

$$\begin{aligned}A_1&=\frac{\alpha \text{ ln } \beta }{\beta {\dot{\epsilon }}_{\rm{min}}},\nonumber \\{} A_2&=\frac{3\text{ ln } \beta -2\alpha \text{ ln } \beta -1}{(\beta {\dot{\epsilon }}_{\rm{min}})^2},\nonumber \\ A_3&=\frac{\alpha \text{ ln } \beta +1-2 \text{ ln } \beta }{(\beta {\dot{\epsilon }}_{\rm{min}})^3}. \end{aligned}$$

(25)

where $\alpha$ is a fourth constitutive parameter defining the slope of the viscosity function $\Phi [{\dot{\epsilon }}_s^p]$ at the axis origin. Note that for a null plastic strain rate, the dynamic yield surface coincides with the static one.

As a result, the soil friction turns out to depend on the plastic shear strain rate ${\dot{\epsilon }}_s^p$ and on the salt concentration $c_{msW}$, namely: the greater ${\dot{\epsilon }}_s^p$ and $c_{msW}$, the larger the soil friction. Figure 6 shows the typical variation of the viscosity function with displacement rate plotted either with arithmetic or with a logarithm scale (for $\gamma$=0.01, $\alpha =1$, $\beta =10$, ${\dot{\epsilon }}_{\rm{min}}= 10^{-8}$ m/s).

Fig. 6

Change of viscosity function on (a) an arithmetic plot, and on (b) a semi-log plot of velocity

3.3 The plastic potential

The plastic potential G provides the plastic flow direction. In this work the flow rule is assumed to be non-associated, thus the plastic potential G is different with respect to the yield functions $F_s$ and $F_d$ and is defined as follows:

$$\begin{aligned} G[{{\varvec{\sigma }}}']=|\sigma '_s|+\sigma '_n\tan \psi, \end{aligned}$$

(26)

where $\psi$ is the dilation angle, which is generally smaller than the friction angle. Since the proposed interface element is intended to simulate mainly the residual strength, a null dilatancy angle $\psi =0$ will be assumed below, independently of salt concentration and strain rate.

The plastic strain increment is deduced as usual

$$\delta { {\varvec{\epsilon }}}^p=\delta \lambda \frac{\partial G}{\partial {{\varvec{\sigma }}}'}\qquad \text{ and }\; {\dot{{ {\varvec{\epsilon }}}}}^p=\frac{\delta { {\varvec{\epsilon }}}^p}{\delta t}=\frac{\delta \lambda }{\delta t}\frac{\partial G}{\partial {{\varvec{\sigma }}}'}, $$

(27)

where $\delta \lambda$ is the plastic multiplier.

3.4 The consistency condition and the calibration of constitutive parameters

The numerical integration of the constitutive model is performed using a general implicit, back-Euler method. Namely, at first, the strain increment is assumed to be purely elastic (thus obtaining the so-called elastic predictor). If the elastic predictor lays outside the static yield surface, then a visco-plastic strain increment occurs, otherwise, the strain increment is purely elastic.

The amplitude of the plastic strain increment is obtained from the consistency condition applied to the dynamic yield surface. This implies that the magnitudes of the plastic strain increment and of the plastic strain rate are evaluated in such a way that the updated stresses lay on the updated dynamic yield surface $F_d$. This automatically ensures also the consistency condition on the static yield surface for null plastic strain rate $F_s$. The resulting system of non-linear equations is solved numerically through a conventional Newton–Raphson scheme.

The tangent elastoplastic stiffness matrix can be deduced through a standard method [25] that will not be repeated here for the sake of brevity.

The key constitutive parameters that need to be calibrated are the residual friction angle $\varphi$ and its dependence on salt concentration (parameters $c_1$, $c_2$ and $c_3$ of Eq. 22). This task can be easily obtained from laboratory measurements of residual friction angle performed at different salt concentrations (e.g. see [45]). The dilatancy angle $\psi$ is typically null at the residual state. A further set of parameters that need to be calibrated are those describing the delayed behaviour ($\alpha$, $\gamma$, ${\dot{\epsilon }}_{\rm{min}}$ and $\beta$ in Eq. 24). Even in this case, laboratory measurements of residual strength at various displacement rates are needed (e.g. see [45]).

Finally, for the parameters describing the elastic behaviour, $k_n$ and $k_s$, the same approach used for soil and rock interfaces was followed.

4 FE formulation

The zero thickness element proposed by Goodman et al. [27] is widely used for the 2D modelling of discontinuities in rock masses. In soil-structure interaction problems, it is often assumed that the thickness of the interface element is equal to zero [14]. In this paper, we use the modified Goodman’s element proposed by Kaliakin and Li [30] to prevent numerical instabilities. For the solid skeleton, the interface element is composed of 6 nodes (Fig. 7), positioned on two parallel surfaces (i.e. three nodes on each surface), and, since its thickness is ineffective for the mechanical response, the thickness of the interface will be assumed to coincide with the real interface thickness needed for the water and salt fluxes. For the pore fluid flow and salt diffusion, the interface element is composed of 4 nodes positioned on the two parallel surfaces (i.e. two nodes on each surface), and the thickness of the interface h coincides with the real interface thickness that governs the longitudinal water and salt fluxes.

4.1 FE formulation for the mechanical analysis

In the local coordinate system, the displacements of the surfaces of the interface element can be expressed in terms of nodal displacements ${\tilde{u}}_i$ and interpolation functions $N_i^s$ as:

$$\begin{aligned} \textbf{u}=\sum {N_i^s {\tilde{u}}_i} = \textbf{N}^s {\tilde{\textbf{U}}} \end{aligned},$$

(28)

where $\textbf{u}=\begin{bmatrix} u&v \end{bmatrix}^T$ with u and v the longitudinal and the transversal displacements

$$\begin{aligned} {\tilde{\textbf{U}}} =\begin{bmatrix} {\tilde{u}}_1&{\tilde{v}}_1&{\tilde{u}}_2&{\tilde{v}}_2&...&{\tilde{u}}_6&{\tilde{v}}_6 \end{bmatrix}^T ,\end{aligned}$$

(29)

and $N_i^s$ are the shape functions for the solid skeleton written for the 6-node interface element (that is similar to a one-dimensional element with three nodes)

$$\begin{aligned}{} N_1^s&=N_4^s=\frac{1}{2}(\xi -1)\xi , \\ N_2^s&=N_3^s=\frac{1}{2}(\xi +1)\xi, \\ N_5^s&=N_6^s=(1-\xi ^2), \end{aligned}$$

(30)

where $-1\le \xi \le +1$ is the space variable in the natural coordinate system (Fig. 7).

Fig. 7

Relative displacement and degrees of freedom in zero thickness element with 6 nodes in the local coordinate system

Since the thickness of the interface element is vanishingly small as compared to its length, the interpolation functions of the nodes on the bottom surface of the element coincide with those of the adjacent nodes on the top surface. Considering Fig. 7, the horizontal and vertical displacements of the top and bottom surfaces of the interface element turn out to be

$$\begin{aligned}{} {} u^{\rm{top}}&=N_3^s{\tilde{u}}_3+N_4^s{\tilde{u}}_4+N_6^s{\tilde{u}}_6^s,\nonumber \\{} {} u^{\rm{bot}}&=N_1^s{\tilde{u}}_1+N_2^s{\tilde{u}}_2+N_5^s{\tilde{u}}_5, \end{aligned}$$

(31)

$$\begin{aligned}{} {} v^{\rm{top}}&=N_3^s{\tilde{v}}_3+N_4^s{\tilde{v}}_4+N_6^s{\tilde{v}}_6,\nonumber \\{} {} v^{\rm{bot}}&=N_1^s{\tilde{v}}_1+N_2^s{\tilde{v}}_2+N_5^s{\tilde{v}}_5, \end{aligned}$$

(32)

The strain at the interface can be deduced from nodal displacements by using the following relation:

$$\begin{aligned} { {\varvec{\epsilon }}}=\textbf{B}\,{\tilde{\textbf{U}}} \end{aligned},$$

(33)

where $\textbf{B}$ is the strain transformation matrix, given by [30, 38]

$$ \textbf{B}=\begin{bmatrix} 0&{}-N_1^s&{}...&0&N_6^s\\ -N_1^s&{}0&{}{}...&{}N_6^s&{}0 \end{bmatrix}.$$

(34)

Equation (34) holds true for an element with the longitudinal orientation coinciding with the global X-axis, namely when the local coordinate (x-axis) system coincides with the global one. In contrast, when the interface element has a different orientation, it is obviously necessary to consider a rotation matrix that leads to a strain transformation matrix $\textbf{B}_G$ (not be given here for the sake of brevity) that can be easily found through standard arguments [12, 38].

It is worth adding that from the expression of the total stress (Eq. 18), the nodal forces result equal to

$$\begin{aligned} \textbf{f}_S = \int _l{\textbf{B}_G^T \, {{\varvec{\sigma }}}{\rm{d}}l}=\int _l{\textbf{B}_G^T\,({{\varvec{\sigma }}}'- \textbf{m}\, p_{mW}) {\rm{d}}l }, \end{aligned}$$

(35)

thus the nodal forces are computed considering the total stress at the mid-section of the discontinuity. The tangent stiffness matrix reduces to

$$\delta \textbf{f}_S = \int _l{\textbf{B}_G^T \, \textbf{D}_{ep} \textbf{B}_G {\rm{d}}l} \; \delta {\tilde{\textbf{U}}} - \frac{1}{2} \int _l{\textbf{B}_G^T \textbf{m}\textbf{N}^p {\rm{d}}l } \; \delta {\tilde{\textbf{P}}}_W,$$

(36)

with $\textbf{D}_{ep}$ the tangent elastoplastic stiffness matrix relating stress to strain increments and $\textbf{N}^p$ are the interpolation functions for the pore pressure, which are defined in the next subsection (see Eqs. 38 and 39).

4.2 FE formulation for the fluid flow

For the pore pressure, the interface element can be considered as a four-nodded, 2D element, thus the pore water pressures within the interface can be expressed in terms of nodal values $\tilde{\text{p}}_i$ and interpolation functions ${\hat{N}}_i^p$ as:

$$\begin{aligned} \text{ p}_W=\sum {{\hat{N}}_i^p \tilde{\text{ p}}_i} = {\hat{\textbf{N}}}^p {\tilde{\textbf{P}}}_W, \end{aligned}$$

(37)

where ${\tilde{\textbf{P}}}_W^T=\begin{bmatrix} \tilde{\text{ p}}_1&\tilde{\text{ p}}_2&\tilde{\text{ p}}_3&\tilde{\text{ p}}_4 \end{bmatrix}$, ${\hat{\textbf{N}}}^p=\begin{bmatrix} {\hat{N}}_1^p&{\hat{N}}_2^p&{\hat{N}}_3^p&{\hat{N}}_4^p \end{bmatrix}$ and

$$\begin{aligned}{} & {} {\hat{N}}_{1}^p=\frac{1}{2}(1-\xi ) \frac{h-2y}{2h},\qquad {\hat{N}}_{2}^p=\frac{1}{2}(1+\xi ) \frac{h-2y}{2h},\nonumber \\& {\hat{N}}_{3}^p=\frac{1}{2}(1+\xi )\frac{h+2y}{2h},\qquad {\hat{N}}_{4}^p=\frac{1}{2}(1-\xi )\frac{h+2y}{2h}, \end{aligned}$$

(38)

with $-h/2 \le y \le h/2$. Note that the pore pressure varies linearly within the interface thickness.

Alternatively, the pore pressure can be defined only at the surfaces of the interface element (i.e. $y=-h/2$ and $y=h/2$). In this case the interpolation functions ${\hat{N}}_i^p$ reduce to $N_i^p$,

$$\begin{aligned} N_{1}^p=N_{4}^p=\frac{1}{2}(1-\xi ),\qquad N_{2}^p=N_{3}^p=\frac{1}{2}(1+\xi ), \end{aligned}$$

(39)

with $-1\le \xi \le +1$. The pore pressure at the mid-section of the discontinuity is the mean of the values at the surfaces of the discontinuity, namely [47, 49]

$$\begin{aligned} \text{ p}_{mW}=\frac{1}{2} \sum {N_i^p \tilde{\text{ p}}_i} = \frac{1}{2} \textbf{N}^p {\tilde{\textbf{P}}}_W . \end{aligned}$$

(40)

Let us define the $\textbf{B}$ matrices containing the derivatives of the shape functions

$${\hat{\textbf{B}}}_W^l = \left[ \frac{\partial {\hat{N}}_{1}^p}{\partial x} \;\; \frac{\partial {\hat{N}}_{2}^p}{\partial x} \;\; \frac{\partial {\hat{N}}_{3}^p}{\partial x} \;\; \frac{\partial {\hat{N}}_{4}^p}{\partial x} \right],$$

(41)

$$\begin{aligned}{\hat{\textbf{B}}}_W^t = \left[ \frac{\partial {\hat{N}}_{1}^p}{\partial y} \;\; \frac{\partial {\hat{N}}_{2}^p}{\partial y} \;\; \frac{\partial {\hat{N}}_{3}^p}{\partial y} \;\; \frac{\partial {\hat{N}}_{4}^p}{\partial y} \right] \nonumber \\{} & {} \quad = \frac{1}{h}\begin{bmatrix} -N_{1}^p&-N_{2}^p&N_{3}^p&N_{4}^p \end{bmatrix}.\end{aligned}$$

(42)

In order to obtain the weak form of the differential equations, the Galerkin method is first applied to Eq. (4), thus

$$\begin{aligned}&\int _l \left( \int _h ({\hat{\textbf{N}}}^{p})^T \frac{1}{h} \frac{\partial \epsilon _n}{\partial t} {\rm{d}}y \right) {\rm{d}}x + \int _l \left( \int _h ({\hat{\textbf{N}}}^{p})^T \frac{\partial \epsilon _l}{\partial t} {\rm{d}}y \right) {\rm{d}}x\\ + & \int _l \left( \int _h ( {\hat{\textbf{N}}}^{p})^T \frac{\partial J_W^l}{\partial x} {\rm{d}}y \right) {\rm{d}}x \\+& \int _l \left( \int _h ({\hat{\textbf{N}}}^{p})^T \frac{\partial J_W^t}{\partial y} {\rm{d}}y \right) {\rm{d}}x =0, \end{aligned}$$

(43)

then the resulting equation is integrated along the transversal direction (i.e. y direction). Note that in the transversal direction, the shape functions ${\hat{N}}_i^p$ vary linearly and their integral is equal to h/2. The integration by parts finally leads the mass balance equation of pore water to an expression that contains functions only varying in the longitudinal direction of the discontinuity, namely

$$\begin{aligned}&\frac{1}{2}\,\int _l{(\textbf{N}^{p})^T \,\textbf{m}^T \, \frac{\partial { {\varvec{\epsilon }}}}{\partial t} {\rm{d}}x}+\frac{h}{2} \,\int _l {(\textbf{N}^{p})^T \, \frac{\partial \epsilon _l}{\partial t} {\rm{d}}x} -\\& \frac{h}{2} \, \int _l{(\textbf{B}_W^l)^T \,J_W^l {\rm{d}}x}- h \, \int _l{(\textbf{B}_W^t)^T \,J_W^t {\rm{d}}x} = - \textbf{f}_W , \end{aligned}$$

(44)

where

$$\textbf{B}^l_W = \left[ \frac{\partial N_{1}^p}{\partial x} \;\; \frac{\partial N_{2}^p}{\partial x} \;\; \frac{\partial N_{3}^p}{\partial x} \;\; \frac{\partial N_{4}^p}{\partial x} \right],$$

(45)

$$\begin{aligned}{} & {} \textbf{B}^t_W = {\hat{\textbf{B}}}_W^t, \end{aligned}$$

(46)

$$\begin{aligned}{} & {} J_W^l=-\frac{K_{l}}{\rho _w g} \left( \frac{1}{2}\textbf{B}_W^l {\tilde{\textbf{P}}}_W - \rho _w g_l \right) \nonumber \\{} & +\omega \frac{K_{l}}{\rho _w g} \frac{RT}{\text{ v}_s^{(M)}}\chi \left( \frac{1}{2}\textbf{B}_W^l {\tilde{\textbf{C}}}_{sW} \right), \end{aligned}$$

(47)

$$\begin{aligned}{} & {} J_W^t=-\frac{K_{t}}{\rho _w g} \left( \textbf{B}_W^t {\tilde{\textbf{P}}}_W - \rho _w g_t \right) \nonumber \\{} & + \omega \frac{K_{t}}{\rho _w g} \frac{RT}{\text{ v}_s^{(M)}}\chi \left( \textbf{B}_W^t {\tilde{\textbf{C}}}_{sW} \right), \end{aligned}$$

(48)

$$\begin{aligned}{} & {} \epsilon _l = \frac{1}{2}\textbf{B}_l {\tilde{\textbf{U}}}, \end{aligned}$$

(49)

$$\textbf{B}_l =\left[ \frac{\partial N_1^s}{\partial x} \;\; 0 \;\;... \;\; \frac{\partial N_6^s}{\partial x} \;\; 0 \right],$$

(50)

whereas the boundary fluxes result equal to

$$\begin{aligned}{} & {} \textbf{f}_W^T = \frac{h}{2}\begin{bmatrix} (J^l_W)_{\rm{left}}&(J^l_W)_{\rm{right}}&(J^l_W)_{right}&(J^l_W)_{\rm{left}} \end{bmatrix} \\&+ \int _l{J_{W}^{\rm{bot}} \begin{bmatrix} N_{1}^p&N_{2}^p&0&0 \end{bmatrix} {\rm{d}}x} \\& +\int _l{J_{W}^{\rm{top}}\begin{bmatrix} 0&0&N_{3}^p&N_{4}^p \end{bmatrix} {\rm{d}}x}, \end{aligned}$$

(51)

with $(J^l_W)_{\rm{left}}$ and $(J^l_W)_{\rm{right}}$ the longitudinal pore water fluxes (with units L/T) at the left-hand side and at the right-hand side of the discontinuity, respectively, and $J_{W}^{\rm{top}}$ and $J_{W}^{\rm{bot}}$ are the outflow fluxes (with units L/T) at upper and lower surfaces of the discontinuity. The advantage of Eq. (44) is that 1D shape functions and $\textbf{B}$ matrices are considered. In this way, this finite element formulation coincides with that one proposed by [49], although a different method was used here for deducing it. Equation (50) is valid only in the case of alignment of local coordinate axes with global ones, otherwise, a suitable rotation matrix must be considered.

Finally, as compared with Eq. (8), we have assumed in the expression of $J^t_W$ that

$$c_{msW} \frac{\text{ Ln }(c_{sW}^{\rm{top}}/c_{sW}^{\rm{bot}})}{h} \approx \frac{c_{sW}^{\rm{top}}-c_{sW}^{\rm{bot}}}{h},$$

(52)

where $\text{ c}_{msW}$ is the salt concentration at the mid-section of the discontinuity, coinciding with the mean value of the salt concentrations at the surfaces of the discontinuity, namely

$${\text{c}}_{msW}=\frac{1}{2} \sum {N_i^p (\tilde{\text{c}}_{sW})_i} = \frac{1}{2} {\textbf{N}}^p \, {\tilde{\textbf{C}}}_{sW},$$

(53)

where $(\tilde{\text{c}}_{sW})_i$ are the nodal values of salt concentration, $\textbf{N}^p$ is defined in Eq. (39) and ${\tilde{\textbf{C}}}_{sW}^T=\begin{bmatrix} (\tilde{\text{c}}_{sW})_1&(\tilde{\text{c}}_{sW})_2&(\tilde{\text{c}}_{sW})_3&(\tilde{\text{c}}_{sW})_4. \end{bmatrix}$ It is worth emphasizing that the approximation of Eq. (52) is valid for values of $c_{sW}^{\rm{top}}$ and $c_{sW}^{\rm{bot}}$ sufficiently close to each other.

4.3 FE formulation for the salt diffusion

Similarly to pore pressures, salt concentrations at the surfaces of the interface element can be expressed in terms of nodal values $(\tilde{\text{c}}_{sW})_i$ and interpolation function ${\hat{N}}_i^p$ as:

$$\begin{aligned} \text{c}_{sW}=\sum {{\hat{N}}_i^p (\tilde{\text{c}}_{sW})_i} = {\hat{\textbf{N}}}^p \, {\tilde{\textbf{C}}}_{sW}, \end{aligned}$$

(54)

where ${\tilde{\textbf{C}}}_{sW}$ is given in Sect. 4.2 and $\textbf{N}^p$ is defined in Eq. (39).

Similarly to the method used for pore water, the method of Galerkin is first applied to Eq. (9), then the resulting equation is integrated along the transversal direction (i.e. y direction), taking into account also Eq. (10). The integration by parts finally leads the mass balance equation of salt to reduce to

$$\begin{aligned}&\frac{h}{2}\,\int _l{(\textbf{N}^{p})^T \,n_W \, \frac{\partial c_{msW}}{\partial t} {\rm{d}}l}+ \frac{1}{2}\,\int _l{(\textbf{N}^{p})^T \,c_{msW}\,\textbf{m}^T \, \frac{\partial { {\varvec{\epsilon }}}}{\partial t} {\rm{d}}l}+\\& \frac{h}{2} \, \int _l {(\textbf{N}^{p})^T \,c_{msW} \, \frac{\partial \epsilon _l}{\partial t} {\rm{d}}l} - \frac{h}{2} \, \int _l{(\textbf{B}_W^l)^T \,J^l_{sW} {\rm{d}}l} - \\& h \, \int _l{(\textbf{B}_W^t)^T \,J_{sW}^t {\rm{d}}l} = - \textbf{f}_{sW}, \end{aligned}$$

(55)

where $\textbf{B}_W^l$ and $\textbf{B}_W^t$ are defined in Eqs. (45) and (46), whereas $J^l_{sW}=c_{msW} (J_W^l-J_{sW}^{dl})/n_W+J_{sW}^{dl}$ and $J_{sW}^t=c_{msW} (J_W^t-J_{sW}^{dt})/n_W+J_{sW}^{dt}$, with the diffusion fluxes equal to

$$\begin{aligned}&J_{sW}^{dl}=-n_W D_l \frac{1}{2}\textbf{B}_W^l {\tilde{\textbf{C}}}_{sW} \\&+\omega c_{msW} \frac{K_{l}}{\rho _w g} \left( \frac{1}{2}\textbf{B}_W^l {\tilde{\textbf{P}}}_W -\rho _w g_l \right),\end{aligned}$$

(56)

$$\begin{aligned}&J_{sW}^{dt}=-n_W D_t \textbf{B}_W^t {\tilde{\textbf{C}}}_{sW}\\ &+\omega c_{msW} \frac{K_{t}}{\rho _w g} \left( \textbf{B}_W^t {\tilde{\textbf{P}}}_{W} -\rho _w g_t \right).\end{aligned}$$

(57)

Finally, the salt fluxes at the boundaries are equal to

$$\begin{aligned} \textbf{f}_{sW}^T &= \frac{h}{2}\begin{bmatrix} (J^l_{sW})_{\rm{left}}&(J^l_{sW})_{\rm{right}}&(J^l_{sW})_{\rm{right}}&(J^l_{sW})_{\rm{left}} \end{bmatrix} +\\ &\int _l{J_{sW}^{\rm{bot}} \begin{bmatrix} N_{1}^p&N_{2}^p&0&0 \end{bmatrix} {\rm{d}}l}+ \\ &\int _l{J_{sW}^{\rm{top}}\begin{bmatrix} 0&0&N_{3}^p&N_{4}^p \end{bmatrix} {\rm{d}}l}, \end{aligned}$$

(58)

with $(J^l_{sW})_{\rm{left}}$ and $(J^l_{sW})_{\rm{right}}$ the longitudinal salt fluxes (with units L/T) at the left-hand side and at the right-hand side of the discontinuity, respectively, and $J_{sW}^{\rm{top}}$ and $J_{sW}^{\rm{bot}}$ are the outflow fluxes (with units L/T) at upper and lower surfaces of the discontinuity.

In order to regularize the numerical solution, thus avoiding negative values of salt concentration when a sharp variation of salt concentration is applied at the boundaries, we have adopted the suggestion by Celia et al. [8] and a lumped salt storage matrix has been used. This approach coincides with the selection of integration points located at the nodes (instead of the Gauss points). In addition, for the mass balance of the pore fluid and diffused salt, the integration points are assumed to be distributed on the upper and lower surfaces of the interface element.

4.4 The Jacobian tangent matrices

The spatial discretization of the balance equations leads to the following tangent matrix in terms of increments of nodal solid displacements, pore pressures, and salt concentrations:

$$\begin{aligned}{} & {} \begin{bmatrix} \textbf{K}_{uu}^e&{}\textbf{K}_{up}^e&{}\textbf{K}_{uc}^e\\ 0&{}\textbf{K}_{pp}^e&{}\textbf{K}_{pc}^e \\ 0&{}\textbf{K}_{cp}^e &{}\textbf{K}_{cc}^e \end{bmatrix}\begin{bmatrix} \tilde{\delta \textbf{U}}\\ \tilde{\delta \textbf{P}}_W\\ \tilde{\delta \textbf{C}}_{sW} \end{bmatrix}+\begin{bmatrix} 0&{}0&{}0\\ \textbf{C}_{pu}^e&{}0&{}0\\ \textbf{C}_{cu}^e&{}0&{}\textbf{C}_{cc}^e \end{bmatrix}\begin{bmatrix} \partial {\tilde{\textbf{U}}}/\partial t\\ \partial {\tilde{\textbf{P}}}_W/\partial t\\ \partial {\tilde{\textbf{C}}}_{sW}/\partial t \end{bmatrix}=\begin{bmatrix} \delta \textbf{f}_S\\ \delta \textbf{f}_W\\ \delta \textbf{f}_{sW} \end{bmatrix}. \end{aligned}$$

(59)

The right-hand side vector contains the increments of external nodal forces. The block components in the matrices above are given in Appendix B.

5 Typical responses of the interface element

This section presents the typical chemo-hydro-mechanical responses of the proposed interface element. Either an isolated interface element or an interface element inserted within a soil mass are considered. In particular, the rate dependency and the chemo-mechanical interactions, the longitudinal pore fluid flow and salt diffusion along the discontinuity, and, finally, the transversal pore fluid flow and salt diffusion are considered separately.

5.1 The rate dependency and the chemo-mechanical interactions

The mechanical response of an isolated horizontal interface element with a length of 10 cm and a thickness of 1 mm was considered. In the numerical tests, the displacements of all nodes belonging to the lower surface of the interface were constrained whereas a horizontal displacement was applied to the upper surface of the interface element. The pore pressure of all nodes was set equal to zero.

Table 1 reports the values of the constitutive parameters used for the test which have been calibrated with the experimental results obtained with a Casagrande shear box and with a ring shear test on bentonite by [16] and [45]. The concentration of salt in the fluid phase is expressed in two units, namely kg/m$^3$ and in m$^3$/m$^3$ (that are obtained with a hydrated salt density of $\rho _s=2925$ kg/m$^3$). For the nonlinear elasticity law, the following values were considered: $k_s =k_n= 100$ N/cm$^4$.

Table 1 Values of the constitutive parameters describing the dependence of the residual friction angle in terms of salt concentration and displacement rate

The salt concentration was assumed to be equal either to distilled water (i.e. 0.000011 m$^3$/m$^3$) or to a saturated solution (i.e. 0.109743 m$^3$/m$^3$). Different normal stresses were applied to the upper surface of the interface element, whereas a low horizontal displacement rate was imposed on the upper surface. The computed shear stress-displacement response is shown in Fig. 8a for different normal stresses and for a salt concentration equal to saturated solution. Figure 8b shows the same quantities evaluated for distilled water.

Fig. 8

The effect of variation of normal stress on shearing behaviour of interface element in contact with (a) saturated solution, and with (b) distilled water (displacement rate ${\dot{\epsilon }}_s^p=0.0009$ mm/min)

The numerical results plotted in the $\sigma '_s-\sigma '_n$ diagram compare well with experimental results obtained by Di Maio and Scaringi [16] (Fig. 9). In particular, it can be noted the much higher shear strength of the interface element prepared with a saturated solution with respect to that one prepared with distilled water.

Fig. 9

The effect of variation of salt concentration on the shear strength for various normal stresses: comparison of model simulations with experimental results obtained by Di Maio and Scaringi [16] (displacement rate ${\dot{\epsilon }}_s^p=0.0009$ mm/min)

Finally, the effects of the displacement rate on the shearing strength were examined. The same geometry of the interface was considered. In this case, under a vertical stress of 100 kPa, a horizontal displacement with a velocity of 45 mm/min was initially applied to the upper surface of the discontinuity. Then, after a while, the velocity was sharply decreased to 0.018 mm/min. Figure 10 shows that the sudden reduction of the applied displacement rate leads to a sudden decrease of the residual shear strength in the samples exposed either to distilled water or to the saturated solution.

Fig. 10

The effect of variation of displacement rate on shear strength of interface element, for different salt concentrations and for $\sigma '_n$ = 100 kPa

5.2 The longitudinal water flow and salt diffusion

The longitudinal water flow and salt diffusion along the interface element are analyzed below. A very simple geometry has been considered: a column of interface elements having a total height of 10 cm and a thickness $h= 0.01$ mm. The longitudinal hydraulic conductivity was assumed constant and equal to $K_l=10^{-6}$ m/s (the transversal one is irrelevant). The mechanical behaviour of the interface was characterized by a normal stiffness equal to $k_n=10^{8}$ N/m$^4$ (whereas the shear stiffness is irrelevant). The mesh size is equal to 0.2 mm. Figure 11a shows the boundary conditions and the geometry of the model. At the bottom boundary, no water flux was assumed, whereas, at the upper boundary, the pore pressure was increased from 0 to 10 kPa, gradually (in 100 s). No gravity and a constant salt concentration were assumed.

The hydro-mechanical coupling within the interface element was evaluated considering the following constraints of the solid displacements: the transversal (i.e. the horizontal) displacements of the left-hand side surface of the interface elements were constrained (see Fig. 11a) whereas the transversal displacements of the right-hand side surface were left unconstrained. All longitudinal (i.e. the vertical) displacements were constrained. As a result, the discontinuity can open in the transversal direction if the pore pressure is increased. A normal compression stress equal to 20 kPa was applied to the right-hand side surface of the interface elements. Figure 11b shows the longitudinal distribution of pore pressure. Due to the transversal deformability of the interface, a consolidation process is induced in the longitudinal direction. Figure 11c shows the distribution of the horizontal displacements at various times. Similarly to pore pressure distribution (Fig. 11b), the transversal displacements gradually increase along the longitudinal direction from a null initial value to 1.7 mm (Fig. 11c).

Fig. 11

Longitudinal flow of water when the pore pressure is increased from 0 to 10 kPa at the top of the model: (a) boundary conditions, (b) pore pressure distribution by time, (c) horizontal displacement of the right-hand side surface of the interface elements at various times

For the analysis of the longitudinal salt diffusion we have considered longitudinal diffusion coefficients equal to $10^{-8}$ m$^2$/s (whereas the transversal one is irrelevant) and the boundary conditions were modified as shown in Fig. 12a. All nodal displacements were constrained in the two directions. The flux of salt is null at the bottom boundary, whereas salt concentration was increased in 100 s from 0.0325 kg/m$^3$ to 320 kg/m$^3$ at the upper boundary. Pore pressure was assumed null at all nodes. Figure 12b shows the distribution of salt concentration along the interface at various times. It can be observed that the salt concentration propagates inside the interface elements gradually and after 30 days, the salt concentration has almost reached the equilibrium value of 320 kg/m$^3$ along the whole interface.

Fig. 12

Diffusion of salt after an increase of salt concentration in 100 s at the top of the first element: (a) boundary conditions, (b) diffusion of salt inside the model

5.3 The transversal salt diffusion and water flow

The transversal salt diffusion has been examined on a horizontal interface element with a length of 10 cm and a thickness of 1 mm. All nodal displacements were constrained in the two directions. The pore pressure of all nodes was set equal to zero and the initial salt concentration was assumed equal to distilled water. Two different diffusion coefficients have been considered in the transversal direction, namely $D_t=10^{-11}$ m$^2$/s and $D_t=10^{-12}$ m$^2$/s. The following boundary conditions were considered: at the upper surface, the salt concentration was increased instantaneously from the value of distilled water to 58.5 kg/m$^3$ (1 M NaCl). At the bottom surface, null salt flux was assumed. The evolution of salt concentration in the nodes of the bottom surface of the interface element is shown in Fig. 13. It can be observed that the salt concentration increases gradually with time and, as expected, for $D_t=10^{-12}$ m$^2$/s, the increase of salt concentration is much slower with respect to $D_t=10^{-11}$ m$^2$/s.

Fig. 13

Validation of transversal salt flux: (a) boundary condition, (b) change of salt concentration at the bottom surface with time when salt concentration is increased instantaneously at the top surface

The evaluation of the transversal water flux was performed on a vertical soil column incorporating a horizontal interface element in the middle section, as shown in Fig. 14a. The soil above and below the interface element was simulated with the 2D finite elements proposed by Ghalamzan Esfahani et al. [24, 26]. Salt concentration in pore fluid was constrained at all nodes and no chemo-mechanical interaction was considered. This implies that the 2D elements have the same behaviour as the standard finite element in ABAQUS which is used for simulating soil behaviour. In addition, both horizontal and vertical nodal displacements were constrained. The hydraulic conductivity of the 2D continuous element was assumed equal to 10$^{-8}$ m/s. The mesh size ranges between 0.0125 mm at the top and bottom boundaries of the sample and 0.2 mm in the middle section. The thickness of the interface element is equal $h=$0.2 mm. The pore pressure was set equal to zero at the bottom boundary of the model and was slowly increased from 0 to 10 kPa at the upper boundary, as shown in Fig. 14a. The computed pore pressure distribution is shown in Fig. 14b for different values of the transversal hydraulic conductivity $K_t$ of the interface element when the stationary condition is reached. It can be observed that the pore pressure distribution is linear in the vertical direction if $K_t$ is equal to the permeability of the upper and lower soil (i.e. $K_t=10^{-8}$ m/s), whereas there is a pore pressure drop at the interface element, for $K_t<10^{-8}$ m/s. The amount of pore pressure drop is the larger, the smaller the value of the transversal hydraulic conductivity $K_t$.

Fig. 14

Effect of transversal hydraulic conductivity of interface element on pore pressure distribution in a clay sample with an interface element at the middle: (a) boundary condition and geometry, (b) distribution of pore pressure at steady state

The same trend is obtained for the salt diffusion in the vertical direction (not shown here for the sake of brevity).

6 Model validation with experimental results

In order to validate the proposed interface element, we have compared the simulated effects of salt concentration and displacement rate with the experimental results obtained from the shear tests on bentonite performed by Di Maio and Scaringi [16] and Scaringi and Di Maio [45]. These results deserve special attention due to their completeness and innovativeness. In fact, some experimental results were obtained following the standard procedures for evaluating the residual shear strength in direct shear tests, whereas other results were obtained with a more complex chemo-mechanical loading history in which the mechanical load was alternated with changes of salt concentration at the sample boundaries.

In our analyses, the first set of experimental data was used for calibrating the constitutive parameters, whereas the subsequent model simulations were used for validating the model forecast with the experimental results obtained with the more complex chemo-mechanical loading history.

Figure 15 shows the schematics of the Casagrande direct shear apparatus. Within the innovative experimental procedure proposed by Di Maio and Scaringi [16], the loading phase was split into 3 phases. Initially, the soil sample was reconstituted with 1 M NaCl solution (i.e. a salt concentration of 58.5 kg/m$^3$), was put in the apparatus between two porous plates, and was finally submerged in 1 M solution of NaCl. After consolidation under a vertical stress equal to 150 kPa, the first phase began. A horizontal displacement was applied (with a low velocity of v = 5 $\mu$m/min, under displacement-controlled conditions) to the upper part of the sample while the bottom part was constrained. The standard procedure for generating the residual strength along a slip surface was then adopted. Namely, the shearing was repeated several times with various forward/backward cycles in order to induce residual conditions.

Then, after the sample had reached its residual state (a cumulative displacement of 30 mm of forward cycles was needed), in the second phase, the shear stress was decreased (from nearly 50 kPa to 29 kPa) and kept constant (under load-controlled conditions). It is worth noting that the value of 29 kPa is smaller than the residual strength of bentonite prepared with 1 M NaCl solution and larger than the residual strength of bentonite prepared with distilled water. Subsequently, the salty water in the external reservoir was substituted with distilled water (that was renewed once per day). The diffusion of salt from inside the sample to the external reservoir led to a decrease in the shear strength and then to a creep response under constant shear stress. This phase lasted 16 days and led to a final displacement of about 3 mm.

Finally, in the third phase, the horizontal displacement was increased at a constant low rate (v = 5 $\upmu$m/min, under displacement-controlled conditions) while the salt concentration of the external reservoir was renewed with distilled water once per day. In this phase (equivalently to the first phase), a series of forward/backward cycles was applied and the shear strength of the soil decreased even further due to the salt diffusion out of the sample, while the cumulative displacement was increased. This phase lasted about 50 days and led to a final cumulative displacement of 160 mm.

Fig. 15

Schematic setup of the Casagrande shearing test apparatus

6.1 Test setup and simulation of the direct shear test

The horizontal size of the sample and porous plates in the Casagrande direct shear test is equal to 6 cm and the thicknesses of the top and bottom porous plates and soil sample are equal to 8 mm, 4 mm, and 28 mm, respectively. From Fig. 15, it can be observed that salt may diffuse through the porous plates and through the lateral edges of the interface. In particular, the upper surface of the top porous plate and the lower surface of the bottom porous plate are in contact with a thin layer of water. Thus salt must diffuse out of the porous plates through the thin layers of water before reaching the cell reservoir. In addition, the cell fluid was renewed about once per day with fresh water and was scarcely mixed in the cell reservoir [17]. In order to simulate properly the experimental test, the cell reservoir and the renewal process were carefully simulated in FEM analyses.

Taking account of the vertical and horizontal symmetries, only the lower quarter of the test setup was simulated. In the simulations, half of the value of the real interface thickness ($h/2$) was considered. The lower part of the sample was considered in the simulations due to the smaller thickness of the lower porous plate and the consequent faster diffusion process in the lower part of the sample. Figure 16a shows the size of the model and the boundary conditions. The relative vertical displacements of all nodes of the interface surfaces were constrained to be null in order to prevent any rotation of the upper surface of the interface region during the load-controlled phase. In addition, the upper surface of the interface, Fig. 16a, was ’clued’ to a truss element that approximately simulates the stiffness of the upper part of the soil sample (that was not considered in the simulations). The fictitious truss element provides some bending and shear stiffness in the transversal direction of the interface.

Figure 16b shows the FE mesh used for discretizing the model. Note that, for both the porous plate and soil sample, the mesh size is finer (0.2 mm) close to the boundaries, whereas it is coarser in the middle (0.4 mm) in order to prevent salt concentration oscillations close to the boundaries. The horizontal dimension was discretized with 15 finite elements having the same horizontal size. In order to simulate a drained test, the pore pressure of all nodes was constrained to be null.

The soil elements, porous plate, cell reservoir, and thin layer of water were simulated with the 2D finite element proposed by Ghalamzan Esfahani et al. [24, 26]. In this element, the salt diffusion and the mass exchange between solid particles and the fluid phase are considered in addition to the solid displacement and pore pressures. The constitutive parameters used for the soil are reported in Appendix C. The hydraulic conductivity and effective diffusion coefficient of the soil elements are equal to 5$\times$10$^{-11}$ m/s and 3.3$\times$10$^{-10}$ m$^2$/s, respectively (reported in [20]). The adsorption/desorption of water is assumed to be null for the porous plate, cell reservoir, and thin layer of water. The porosity of the cell reservoir and the thin layer of water is close to unit (0.9) and the displacements are constrained. A large diffusion coefficient equal to $10^{-6}$ m$^2$/s was selected for the cell reservoir in order to simulate some mixing. The thin layer of water at the lower surface of the porous plate has a thickness equal to 0.3 mm and a diffusion coefficient equal to pore water (1.5$\times 10^{-9}$ m$^2$/s). The porosity of the porous plate is equal to 0.046 and its effective diffusion coefficient is equal to $1.5\times 10^{-9}$ m$^2$/s.

Fig. 16

The Casagrande direct shear test: (a) size of the sample and porous stones and boundary conditions, (b) mesh size

Tables 1 and 2 report the selected constitutive parameters describing the chemo-mechanical interactions and those describing the fluid flow and salt diffusion within the interface element, respectively. It is worth noting that the hydraulic conductivity of the interface elements is assumed constant and the osmotic efficiency is assumed null. The preliminary, standard shear tests provided a residual friction angle equal to 6.5$^\circ$ for the clay mixed with distilled water and to 17$^\circ$ for the clay mixed with 1 M NaCl solution [16, 45] (Fig. 9).

Table 2 Transversal and longitudinal permeability and diffusion coefficient of the interface element.

Figure 17a shows the measured dependence of shear strength $\sigma '_s/\sigma '_n$ on displacement rate, for various salt concentrations. An alternative representation is shown in Fig. 18a, where the dependence of shear strength on salt concentration is shown for various displacement rates. Figures 17b and 18b show the corresponding model simulations. The good consistency of model simulations with experimental data confirms the proper selection of the interpolation functions describing the dependence of friction angle on salt concentration and displacement rate (through the viscosity function).

Fig. 17

Change of $\sigma '_s/\sigma '_n$ with displacement rate and molarity of pore solution with $\sigma '_n$ = 150 kPa: (a) experimental data [45], (b) proposed interpolation function

Fig. 18

Change of $\sigma '_s/\sigma '_n$ with pore solution molarity with $\sigma '_n$ = 150 kPa: (a) experimental data [45], (b) proposed interpolation function

6.1.1 Simulation of the displacement-controlled phases

This subsection presents the simulations of phases no. 1 and 3 of the loading history described in Sect. 6. In the simulations, all chemical-loading steps used in the experiments were carefully simulated. In particular, the renewal of cell fluid was simulated with a frequency of once per day by setting the salt concentration in the cell reservoir equal to distilled water and by restarting the transient analysis. Moreover, for the phases in which displacement-controlled conditions are applied, namely phases n. 1 and 3, the backward/forward cycles were not simulated and just a monotonous displacement was considered. This is acceptable because our analyses were performed within a small strain framework, thus all evaluations were performed with regard to the undeformed, initial configuration.

Figure 19 shows the comparison between experimental results and model simulations concerning the evolution of the shear strength in terms of cumulative horizontal displacement. It is worth noting in Fig. 19 that the results are represented in terms of displacements, thus the second phase (where the horizontal displacement increases from 30 to 33 mm) appears very short as compared with the first and third phases, although the second phase actually lasted 16 days.

From the experimental data shown in Fig. 19 it can be observed that the horizontal displacement of 30 mm in phase 1 has led the shear strength to reach the residual value. This is a progressive phenomenon because it is related to the reorientation of clay particles. In contrast, in the simulations, the residual state is assumed to be established from the real beginning of the simulation, thus a horizontal plot is obtained in Fig. 19. The key point is that the experimental curve is consistent with the simulations at the end of phase 1.

The subsequent exposure to distilled water in the third phase leads the shear strength to decrease as a result of the decrease of salt concentration along the slip surface. In particular, the decrease in salt concentration occurs partly as a result of the diffusion through the upper and lower part of the sample and partly as a result of diffusion along the slip surface. The latter starts from the edges of the interface and propagates toward the central part of the sample. Figure 19 shows that model simulations are in good agreement with the experiment.

Fig. 19

Comparison of model simulations with experimental results obtained with the Casagrande direct shear test by Di Maio and Scaringi [16]

6.1.2 Simulation of the load-controlled phase

In phase n. 2 of the loading history described in Sect. 6 (see Fig. 19), the specimen was exposed to distilled water, under constant shear stress equal to 29 kPa, which is lower than the residual strength of the sample prepared with 1 M NaCl solution and higher than the residual strength of the sample prepared with distilled water. In this phase, the cell fluid was renewed with distilled water once per day, thus leading to a decrease in shear strength and to the consequent increase of the horizontal displacement.

The comparison between computed and measured evolution of the horizontal displacements is shown in Fig. 20. From the experimental data, it can be observed that the horizontal displacement rate is initially null, then, after about 2 days, it starts to gradually increase and becoming very large after about 16 days. In the simulations, the displacement rate is initially negligible and abruptly becomes very large after 16 days (or after 20 days, depending on the assumed interface thickness). Thus, the simulated increase of displacement rate is too sharp with respect to the measured one. The instant of occurrence of the sharp increase in displacement rate depends mainly on the longitudinal diffusion coefficient along the interface and on the interface thickness. Comparatively, salt diffusion across the porous plate and the intact clay has a minor role.

Fig. 20

Comparison of experimental results with model simulations obtained with two different values of the interface thickness in Casagrande apparatus [16] for the phase 2 of Fig. 19

Figure 21 shows the computed distribution of salt concentration along the interface region at various times. In Fig. 21 we have assumed that the distribution of salt concentration is symmetric with respect to the vertical axis. The salt concentration is obviously lower at the external edges of the interface region while it is higher in the middle of the interface. After about 16 days, the average amount of salt concentration was lower than 0.4 M, thus the average shear strength became smaller than the applied shear stress thus leading to a sharp increase in the displacement rate.

Thus, the major inconsistency between experimental results and model simulations in Fig. 20 concerns the sharpness of the increase in displacement rate. Since all constitutive parameters have been calibrated on the specific experimental results discussed in Sect. 6.1, the discrepancy shown in Fig. 20 cannot be easily explained, because no constitutive parameter can be adjusted to make the increase of displacement rate more progressive without worsening the other simulations discussed so far.

Excluding possible inconsistencies in the simulation of the experimental test (e.g. the forward/backward cycles that did not lead to bad results in Fig. 19, however), the inconsistencies of Fig. 20 might come from one of our constitutive assumptions. For this reason, we have explored the possibility that the elastic shear stiffness $k_s$ might depend on salt concentration. To this aim, we have used the typical variations of elastic stiffness observed in oedometric tests on bentonite (in which the elastic stiffness decreases by about 100 times when the salt concentration is reduced from saturated solution to distilled water). This analysis is not shown here for the sake of brevity. Although the dependence of elastic shear stiffness on salt concentration leads to a more gradual increase of displacement rate with time, it is not sufficient for explaining the discrepancies observed in Fig. 20. Thus further effects might be involved in the experimental tests, such as for instance, a viscoelastic response in addition to the assumed visco-plastic one. Further experimental results and numerical tests are needed for a better understanding of this behaviour.

Fig. 21

Salt distribution along the interface in the load-controlled phase (the gray lines were obtained by exploiting the symmetry with respect to the vertical axis)

7 Conclusion

The formulation of a new zero-thickness interface element is presented in this work. This element is capable of taking into account the chemo-hydro-mechanical interactions and the rate dependency observed experimentally along slip surfaces at residual state in natural clays. The proposed interface element consists of a solid and a fluid phase, in which dissolved salt diffuses. Thus the fluid phase consists of pore water and a single diffusing salt. The proposed element consists of two parallel surfaces which may have relative normal and shearing displacements with respect to each other. We have considered the flow of water and the diffusion of salt both in the longitudinal and transversal directions of the interface (as Segura and Carol [49] did for pore water flow). Moreover, the effects of salt concentration and strain rate are considered on the shearing behaviour of the interface element. Finally, a novel nonlinear elastic energy is proposed which strongly improves the numerical convergence when interface opening occurs.

The mechanical behaviour and the response to water and salt fluxes of the new interface element are carefully evaluated. In particular, we have assessed: (1) the effects of shear strain rate and salt concentration on the shear strength of the interface, (2) the coupled flow of water in the longitudinal direction of the interface, (3) the longitudinal diffusion of salt and (4) the transversal flow of water and diffusion of salt.

Moreover, we have used the proposed interface element together with the 2D element proposed by Ghalamzan Esfahani et al. [24, 26] to simulate the direct shear tests performed on bentonite by Di Maio and Scaringi [16]. These experimental results are particularly challenging because a mixture of chemical and mechanical loadings was applied to a soil sample, under either load- or displacement-controlled conditions that involved also the delayed mechanical response of the solid skeleton. Whereas the agreement between the experimental results and model simulations is very good for the displacement-controlled phases, there are some discrepancies in the delayed behaviour of soil under the load-controlled conditions. Although the general picture of this chemo-mechanical response is correctly captured, further experimental results and simulations are needed for a better understanding of these phenomena and for improving model simulations.

Appendices

Appendix A: Elastic stiffness

Within the proposed elasticity framework, the normal and shear stresses result equal to

$$\sigma '_n=\frac{\partial \Gamma }{\partial {\epsilon ^e_n}} ={\left\{ \begin{array}{ll} -3k_n(-\epsilon ^e_n+\epsilon _0)^2\\+3k_s\epsilon ^e_n(\epsilon _n^{e2}+\epsilon _s^{e2})^{\frac{1}{2}}&\text {for} \quad \epsilon ^e_n\le 0,\\ -P_0 \exp (-\epsilon ^e_n/k)& \text {for} \quad \epsilon ^e_n>0, \end{array}\right. } $$

(A1)

$$\sigma '_s=\frac{\partial \Gamma }{\partial {\epsilon ^e_s}}={\left\{ \begin{array}{ll} 3k_s\epsilon ^e_s(\epsilon _n^{e2}+\epsilon _s^{e2})^{\frac{1}{2}}& {}\text {for} \quad \epsilon ^e_n\le 0,\\ 3k_s\epsilon _s^{e2}&{} \text {for} \quad \epsilon ^e_n>0, \end{array}\right. } $$

(A2)

where the nonlinearity of the stress–strain relationship can be easily noticed.

The diagonal components of nonlinear elastic stiffness are as follows:

$$D_e(1,1) ={\left\{ \begin{array}{ll} 6k_n(-\epsilon _n^e+\epsilon _0)\\+3k_s\epsilon _n^{e2}(\epsilon _n^{e2}+\epsilon _s^{e2})^{-\frac {1}{2}}\\ +3k_s(\epsilon _n^{e2}+\epsilon _s^{e2})^{\frac{1}{2}}&\text {for} \quad \epsilon _n^e\le 0,\\ \frac{P_0}{k} \exp (-\epsilon ^e_n/k)&{} \text {for} \quad \epsilon _n^e>0, \end{array}\right. } $$

(A3)

$$D_e(2,2) ={\left\{ \begin{array}{ll} 3k_s\epsilon _s^{e2}(\epsilon _n^{e2}+\epsilon _s^{e2})^{-\frac{1}{2}}\\+3k_s(\epsilon _n^{e2}+\epsilon _s^{e2})^{\frac{1}{2}}& \text {for} \quad \epsilon _n^e\le 0,\\ 6k_s\epsilon _s^e& \text {for} \quad \epsilon _n^e>0. \end{array}\right. } $$

(A4)

The out-of-diagonal components of the stiffness matrix are obviously equal to each other and their value represents the coupling between normal and shear behaviour.

$$D_e(1,2)=D_e(2,1) ={\left\{ \begin{array}{ll} 3k_s\epsilon _n^e\epsilon _s^e\\ (\epsilon _n^{e2}+\epsilon _s^{e2})^{-\frac{1}{2}}&{} \text {for} \quad \epsilon _n^e\le 0,\\ 0&{} \text {for} \quad \epsilon _n^e>0. \end{array}\right. }$$

(A5)

Appendix B: Element matrices

From the momentum balance equation, we have the following matrices:

$$\begin{aligned}&\textbf{K}_{uu}^e=\int _l{\textbf{B}_G^T \textbf{D}_{ep} \textbf{B}_G {\rm{d}}l},\nonumber \\& \textbf{K}_{up}^e=-\frac{1}{2}\int _l{\textbf{B}_G^T \textbf{m}\textbf{N}^p {\rm{d}}l},\nonumber \\& \textbf{K}_{uc}^e=-\frac{1}{2}\int _l{\textbf{B}_G^T \frac{\partial {{\varvec{\sigma }}}}{\partial c_{sW}}\textbf{N}^p {\rm{d}}l}, \end{aligned}$$

(B1)

$\textbf{B}_G$ is the strain transformation matrix, with respect to the reference coordinate system $\textbf{B}_G=\textbf{B}\textbf{R}$, and $\textbf{R}$ is the rotation matrix (see [12, 38] for more details). The element conductivity matrix ($K_{pp}$) is the sum of the conductivity matrices in the longitudinal and transversal direction of the interface element as:

$$\begin{aligned}\textbf{K}_{pp}^e&=\textbf{K}_{pp}^l+\textbf{K}_{pp}^t, \\ \textbf{K}_{pp}^l&=\frac{h}{4}\int _l{(\textbf{B}_W^l)^T \frac{K_{l}}{\rho _w g}\textbf{B}_W^l {\rm{d}}l},\nonumber \\ \textbf{K}_{pp}^t&= h \int _l{(\textbf{B}_W^t)^T \frac{K_t }{\rho _w g}{\textbf{B}_W^t {\rm{d}}l}}. \end{aligned}$$

(B2)

The coupling matrices of change of pore pressure with salt concentration and displacement are:

$$\begin{aligned}\textbf{K}_{pc}^e&=\textbf{K}_{pc}^l+\textbf{K}_{pc}^t,\nonumber \\ \textbf{K}_{pc}^l&=-\frac{h}{4}\int _l{(\textbf{B}_W^l)^T\omega \frac{K_{l}}{\rho _w g} \frac{RT}{\text{ v}_s^{(M)}} \chi \textbf{B}_W^l {\rm{d}}l},\nonumber \\ \textbf{K}_{pc}^t&=-h\int _l{(\textbf{B}_W^t)^T\omega \frac{K_{t}}{\rho _w g} \frac{RT}{\text{ v}_s^{(M)}} \chi \textbf{B}_W^t {\rm{d}}l},\nonumber \\ \textbf{C}_{pu}^e&=\frac{1}{2}\int _l{(\textbf{N}^p)^T \textbf{m}^T \textbf{B}_G {\rm{d}}l}+\frac{h}{2} \,\int _l {(\textbf{N}^p)^T \, \textbf{B}_l {\rm{d}}l}. \end{aligned}$$

(B3)

The mass balance of salt leads to the element matrices in the third row of Eq. 59. The coupling flows in which the change of pore pressure induces the diffusion of salt is:

$$\begin{aligned}\textbf{C}_{cu}^e&=\frac{1}{2}\int _l{(\textbf{N}^p)^T \textbf{m}^T c_{msW} \textbf{B}_G {\rm{d}}l}+\frac{h}{2}\int _l{(\textbf{N}^p)^T c_{msW} \textbf{B}_l {\rm{d}}l},\nonumber \\ \textbf{K}_{cp}^e&=\textbf{K}_{cp}^l+\textbf{K}_{cp}^t, \nonumber \\ \textbf{K}_{cp}^l&=-\frac{h}{4}\int _l{(\textbf{B}_W^l)^T \omega \frac{K_{l}}{\rho _w g} c_{msW} c_{mwW} \textbf{B}_W^l {\rm{d}}l},\nonumber \\ \textbf{K}_{cp}^t&=-h\int _l{(\textbf{B}_W^t)^T \omega \frac{K_{t}}{\rho _w g} c_{msW} c_{mwW} \textbf{B}_W^t {\rm{d}}l}. \end{aligned}$$

(B4)

In the mass balance equation of salt, we assume that salt diffuses along the interface element and in the direction of interface thickness. Thus the element stiffness matrix for the diffusion of salt ($K_{cc}$) is the sum of longitudinal and transversal diffusion matrices as:

$$\begin{aligned}\textbf{K}_{cc}^e&=\textbf{K}_{cc}^l+\textbf{K}_{cc}^t,\nonumber \\ \textbf{K}_{cc}^l&=\frac{h}{4}\int _l{(\textbf{B}_W^l)^T n_W D_{l} c_{mwW} \chi \textbf{B}_W^l {\rm{d}}l},\nonumber \\ \textbf{K}_{cc}^t&= h \int _l{(\textbf{B}_W^t)^T D_t \textbf{B}_W^t {\rm{d}}l}. \end{aligned}$$

(B5)

When the advective flow of salt is considered in the longitudinal direction of the interface element in addition to salt diffusion, spurious oscillations (wiggles) typically occur if the Peclet number is greater than 1. The SUPG method is used to stabilize the advective flow by modifying the weighting function for the convective term through the addition of an artificial diffusive flux. The weighting function for the advective term is modified as follows:

$$\begin{aligned} \textbf{K}_{cc}^l=\frac{h}{4}\int _l{((\textbf{N}^p)^T+(\textbf{R}^p)^T) \text{ v}_{\rm{adv}}^l \textbf{B}_W^l {\rm{d}}l},\qquad \end{aligned}$$

(B6)

where $\textbf{R}^p$ is the perturbation weighting function which can be obtained from the following relation [7]:

$$\begin{aligned} \textbf{R}^p=\tilde{d}\frac{ \text{ v}_{\rm{adv}}^l}{\Vert \text{ v}_{\rm{adv}}^l\Vert } \textbf{B}_W^l, \end{aligned}$$

(B7)

in which $\text{ v}_{\rm{adv}}^l$ is the advective velocity and $\tilde{d}$ is the artificial diffusion equal to $\tilde{d}=({\text{ v}_{\rm{adv}}^l l}/{2})\tilde{\zeta }$, l is the length of the interface element and $\tilde{\zeta }$ can be approximated based on the value of Peclet number $P_e$ as follows:

$$\tilde{\zeta } = {\left\{ \begin{array}{ll} {\rm{sgn}} P_e &{} |P_e|> 3 ,\\ P_e/3 &{} -3\le P_e\le 3 ,\end{array}\right. } \, {\text{with}}\, P_e=\frac{|\text{ v}_{\rm{adv}}^l|l}{D_{l}}.$$

(B8)

The diffusion matrix of salt concentration $\textbf{C}_{cc}$ is written in terms of the element shape functions as:

$$\begin{aligned} \textbf{C}_{cc}=\frac{h}{4}\int _l{(\textbf{N}^p)^T n_W \textbf{N}^p {\rm{d}}l}. \end{aligned}$$

(B9)

It can be noticed that the stabilization of advective flow is implemented only for the flux in the longitudinal direction.

The effectiveness of SUPG stabilization on the distribution of salt concentration can be evaluated by considering a 10 mm high column of interface elements (Fig. 22). In this model, the mesh size changes gradually from 0.2 mm at the bottom to 0.02 mm at the top. The longitudinal diffusion coefficient and hydraulic conductivity of the interface elements are equal to 10$^{-9}$ m$^2$/s and 10$^{-5}$ m/s, respectively. The displacements of all nodes are constrained and the osmotic efficiency is null. The pore pressure is set equal to 1 kPa at the top of the model and to 0 at the bottom. The salt concentration at the top of the model is increased to 0.3 kg/m$^3$ in one second. The distribution of salt concentration along the interface elements is shown in Fig. 22 for different cases. When advection is neglected, the salt concentration diffuses very slowly and the salt concentration increases only close to the top of the model after 100 s. When SUPG stabilization is not applied, there are wiggles in salt distribution at 100 s close to the bottom boundary. In contrast, Fig. 22 shows that the SUPG stabilization method is effective in eliminating the numerical wiggles.

Fig. 22

The effect of advection and SUPG on the distribution of salt concentration in the longitudinal direction of the interface element

Appendix C: Constitutive parameters of clay

For the simulation of the compression and swelling behaviour of the clay above and below the interface element, in Sect. 6, the chemo-mechanical constitutive model proposed by Loret et al. [33] was adopted. This model is basically an extension of the Cam-Clay model to chemically active clays. As a result, the slope of the virgin compression line $\lambda$ and the slope of the swelling line $\kappa$ (also known as the unloading/reloading line) are assumed to depend on salt concentration. More details of the mathematical model are available in [20, 21, 26, 33]. The constitutive parameters used in this work are reported in Table 3 for the sake of completeness.

Table 3 Material parameters for chemo-mechanical behaviour of bentonite.