1 Introduction

Long-term geologic disposal of large-sized nuclear waste canisters, originally designed for temporary storage and for transportation, is being examined in the US national nuclear waste disposal programs [19]. In fact, this direct disposal concept could be a safe, simple and cost-effective alternative to the repackaging of nuclear waste into conventional small-sized canisters for final disposal. However, it is associated with some technical challenges, the extent of which depends on the geologic host media [15]. Large-sized canisters release a high amount of decay heat inducing very high temperatures in the repository for thousands of years [30]. Their size and weight can result in construction and operation technical challenges as well as long-term movements [15].

In this paper, we address geologic disposal in rock salt formations which offer a good tolerance to high temperatures, because of their high thermal conductivity. They are also an excellent natural barrier to a possible long-term release of radionuclides due to their low permeability and self-healing properties. A concept of disposing of radioactive waste in a salt repository consists of emplacing the canisters inside horizontal drifts that are backfilled with crushed salt thereafter. The crushed salt backfill undergoes a reconsolidation process due to the creep of the host rock and the associated drift closure. Previous research on salt nuclear repositories focused mainly on backfill compaction and geomechanical healing of micro-fractures induced by thermal pressurization [5, 6]. The potential for heavy, heat-generating canisters to sink (vertical movement) into the salt host rock due to viscoplastic creep has been well-recognized [9, 16, 40] but less investigated. Indeed, the slow but continuous accumulative nature of this creep-induced process may lead, in the long-term, to an extensive vertical movement. Hardin et al. [16] estimated a sinking rate of 1 m per 10,000 years for solid steel canisters that did not generate heat.

Accurate short- and long-term predictions of the sinking magnitude require the use of a constitutive model able to reproduce the behavior of rock salt under thermal and mechanical loading conditions that are of relevance to salt repositories. Several constitutive models have been developed to characterize the behavior of rock salt. The first models captured transient creep only [35, Lemaitre] or steady-state creep only (Norton–Hoff) and sometimes included both of them, such as the multimechanism deformation (MD) model [27] and Lubby2 model [22]. Advances in laboratory rock testing and insights gained from field measurements led to the emergence of advanced constitutive models or the enhancement of old ones to include, in addition to transient and stationary creep, other mechanisms such as damage, dilatancy, extension and healing; for instance, the multimechanism deformation coupled fracture (MDCF) model [12], the Lux/Wolters model [42], the Günther–Salzer model [13] and other common models used nowadays [14].

While constitutive models for rock salt are numerous, most of them have been calibrated against laboratory experiments that were conducted at high deviatoric stresses, beyond 5 MPa. Indeed, creep laboratory tests at low stress are experimentally difficult to handle because they require a long duration (months to years), in order to reach steady-state creep, meticulous control of humidity and temperature conditions and high precision of strain measuring instruments. Consequently, constitutive models were usually extrapolated to the low stress range resulting in unrealistic strain rate predictions when used in the numerical modeling of the geomechanical behavior of structures located in a salt formation. In the particular case of radioactive waste disposal, this extrapolation led to negligible long-term vertical movement of the nuclear waste canister, as in Dawson and Tillerson [11] and Clayton et al. [9], where a version of the MD model was used [26]. The inaccuracy of this extrapolation has been pointed out several times, especially for the study of the long-term closure of salt caverns [1, 10, 23, 37]. Moreover, previous micro-scale investigations into the deformation mechanisms of polycrystalline halite have identified two main regimes [31, 34, 36]: (1) dislocation creep refers to the time-dependent movement, creation and recovery of dislocations within the crystal lattice and dominates under high shear stresses and temperatures, which makes it easy to measure in the laboratory, (2) pressure solution creep consists of salt dissolution and precipitation under low stress along grain boundaries, resulting in low creep strain rates that could be challenging to measure at the laboratory but necessary to know for an accurate evaluation of long-term deformations. While the dislocation creep mechanism can be well-represented by a power creep law, the pressure solution creep mechanism can presumably be described by a linear relation between stress and strain rate [8, 34]. However, there remains considerable uncertainty regarding salt creep rates under low deviatoric stresses. For instance, theoretical models of pressure solution suggest the existence of a threshold stress, between 0.09 and 0.9 MPa [38], below which rock salt healing at the grain boundaries becomes active, preventing thus pressure solution creep from happening.

Evidence for the low-stress regime was confirmed experimentally by recent 2-year multistage creep tests performed by Bérest et al. [2,3,4], inside a mine, to ensure small temperature and humidity fluctuations, under low deviatoric stresses ranging between 0.1 and 1 MPa on rock salt samples, which showed that steady-state strain rates can be 7–8 orders of magnitude higher than those extrapolated from creep tests under high deviatoric stresses [4]. In accordance with this experimental observation, Bérest [1] simply modified the standard Norton-Hoff model to add an additional creep strain rate term linearly related to deviatoric stress when the latter is below a stress threshold equal to 5 MPa, approximately. In this modified Norton–Hoff model a sharp transition between the two stress regimes was accepted. In light of Bérest test results, Hardin et al. [16, 18] rerun canister sinking simulations using a creep power law that integrates the low-stress low-strain rate regime with a 4 MPa threshold stress which resulted in a sinking magnitude that is much higher than the one obtained using the MD model. Nevertheless, temperature effect on viscoplastic strain rate was not considered, which might result in an underestimation of the creep strain rates, especially that temperature in a salt repository, more precisely, 25 m away from the emplacement drift, could be greater than 80\(~^{\circ }\hbox {C}\) for at least 10,000 years for small conventional waste packages [5]. Recent enhancements of the MD model have been implemented by Reedlunn et al. [29], among which the implementation of new transient and steady-state rate terms to capture rock salt behavior at low stress. These new terms were calibrated against low-stress creep tests but only for a 60\(~^{\circ }\hbox {C}\) temperature. An enhanced MD model with a low equivalent stress mechanism was used by Sobolik and Ross [33] to simulate salt cavern closure, allowing for a better agreement between simulation results and in situ convergence measurements.

In this paper, we explore further the impact of the rock salt constitutive model formulation and commonly used fitted values of models parameters on the magnitude of canister sinking. For this purpose, the widely used Norton model and WIPP model, developed by Herrmann et al. [20, 21] specifically for the analysis of rock salt creep at the Waste Isolation Pilot Plant, are compared with the combined law, described as the sum of a power creep law and a linear law [25], and with the newly developed Lux/Wolters/Lerche (LWL) model [24] (an enhanced version of the Lux/Wolters model [42]), which is an advanced constitutive model that accounts for shear and tensile-induced dilatancy and healing phenomena in addition to transient and stationary creep. The comparison is performed at the material point scale and at the repository scale in order to assess the strengths and weaknesses of the compared constitutive models and their effect on canister sinking predictions.

The paper is organized as follows. In Sect. 2, the evolution of temperature, porosity and stress in a generic salt repository due to the disposal of large nuclear waste canisters is described. In Sect. 3, the mathematical formulation of the three models is recalled, and the formulation of the LWL model is presented. The fitting of their parameters is discussed and compared against recent experimental low-stress creep data. In Sect. 4, the four constitutive models are compared using a numerical creep test and simplified mechanical simulations of the disposal of a large nuclear waste package. Moreover, the new LWL model is used to analyze the effects of the repository temperature, rock salt viscosity and canister density on the vertical movement of the waste canister.

2 Evolution of a generic salt repository for large nuclear waste packages

The objective of this paper is to obtain a quantitative understanding of how the viscoplastic constitutive model can influence the predictions of the vertical movement of heavy waste packages. It is well-known that the viscoplastic behavior of rock salt and crushed salt is highly affected by a change of temperature and stress. The compaction rate of the crushed salt also affects its creep behavior. Hence, in this section, the evolution of temperature, porosity, pore pressure and stress in a salt repository for large-sized nuclear waste canisters is investigated through the numerical modeling of coupled thermal–hydraulic–mechanical processes taking place in a generic salt repository over more than 10,000 years. This will help set up a simplified modeling approach for the comparison of the salt constitutive models (see Sect. 4).

The decay heat released from a nuclear waste package depends on the number of pressurized water reactor (PWR) fuel elements it contains. Large waste canisters may contain up to 37 PWR elements [17], whereas conventional canisters are usually expected to carry less than 10 PWR elements [5, 28, 30]. Even if the interim storage period for large-sized canisters is very long, about 100 years versus 20 years for conventional canisters, the amount of post-emplacement decay heat released, per unit length of the drift, from large-sized canisters is expected to be higher than conventional canisters for an identical canister spacing along the emplacement drift. Figure 1 shows time variation of decay heat power per unit length for a conventional canister and a large-sized canister, both scaled for a 20 m canister spacing. The former is derived from the decay heat power function used in Blanco-Martín et al. [5], corresponding to a 10-PWR elements waste package with a 20-year interim storage. The latter is calculated from the decay heat power function used in Rutqvist [30] for a 37-PWR elements canister with an interim storage period of 100 years. For comparison purposes, the decay heat power functions were both scaled for a 20 m canister spacing; a spacing of less than 10 m is usually considered in the case of conventional canisters [5]. Figure 1 shows that even though the interim storage for the 37-PWR canister is five times longer, the heat power per unit length it produces is still greater than that of the 10-PWR canister. At 100 years, the difference in heat power per meter drift between the two functions reaches more than 150 W/m, then drops to less than 50 W/m 1000 years later.

Fig. 1
figure 1

Comparison of decay heat power per meter drift for a 10-PWR canister with 20-year interim storage and a 37-PWR canister with 100-year interim storage (canister spacing is 20 m)

Full size image

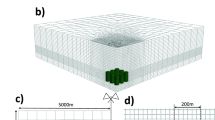
We simulate a generic salt repository for large waste packages using the TOUGH-FLAC simulator and the model geometry shown in Fig. 2, previously used by Blanco-Martín et al. [6] to simulate a generic salt repository for conventional canisters. The only modification was to apply to the steel canister elements the decay heat function that corresponds to the disposal of a 37-PWR element 100 years after it was taken out of the nuclear reactor (Fig. 1).

In this simulation, the repository is located in the middle of a 400-m-thick salt layer, at a depth of 600 m from the ground surface. Two 400-m-thick sandstone layers confine the rock salt. The drifts are 4.5 m wide, 3.5 m high, parallel and evenly spaced, and the cylindrical waste canisters have a diameter of 1.6 m. By using repetitive symmetry of the drifts, the geometry consists of half of one drift and the width of the model is equal to half the drift spacing.

A geothermal gradient of 0.03 K/m is initially applied to the model, with the ground surface temperature equal to 10\(~^{\circ }\hbox {C}\). The stress state is initially isotropic, equal to the lithostatic stress, and the water pressure is hydrostatic, with the water table located at the ground level. A no-flow (heat and fluid) boundary condition is assigned to the lateral boundaries and temperature and liquid pressure in the top and bottom boundaries are maintained equal to their initial values. Moreover, a roller boundary condition (i.e., displacement normal to the boundary fixed to zero) is assigned to the lateral and bottom boundaries.

The simulation starts with the excavation of the drift followed by the emplacement of the cylindrical waste canister and the drift backfilling with crushed salt. Note that the results shown in this section correspond to the post-backfilling phase.

Fig. 2
figure 2

Two-dimensional model geometry of the salt repository [6]

Full size image

To describe the behavior of rock salt, the Lux/Wolters constitutive model was used allowing to simulate salt creep, damage induced by high shear stresses and tensile stresses and healing induced by the closure of micro-fissures. Moreover, both thermo-mechanical damage and the increase in pore pressure beyond the lithostatic pressure level are assumed to result in the creation of a secondary permeability, and the Biot coefficient, initially very low, is assumed to increase with rock salt damage level [5, 42].

For crushed salt, a modified version of the CWIPP model is used [7]. During reconsolidation of the crushed salt backfill, both thermal conductivity and permeability change with the current porosity of the backfill. When full compaction is reached, the thermal conductivity of the backfill changes with temperature similarly to natural salt.

Elastic behavior is assumed for the waste package and the confining layers and their thermal and hydraulic properties are assumed constant.

The detailed mathematical formulation of all the used constitutive models and empirical laws as well as the fitted values of their parameters can be found in [5].

Figures 3 and 4 show the evolution of temperature and porosity in different locations of the repository for two values of canister spacing along the emplacement drift: 10 m and 20 m. The line heat load used for the 10-m canister spacing is two times higher than the one shown in Fig. 1 for a 20-m spacing.

Figure 3 shows an early local peak reached at the waste package (red point) after nearly one year due to the low initial thermal conductivity of the crushed salt backfill. Thereafter, temperature near the canister, at the drift wall and 25 m away in the host rock all converge to a maximum average that is around 110–120\(~^{\circ }\hbox {C}\) for a 20-m canister spacing and almost two times larger for a 10-m canister spacing. Moreover, temperature in the three locations remains nearly stabilized at this maximum average value before starting to decrease at 10,000 years.

For both spacing cases, and despite the differences in temperature, the porosity of the backfill, initially equal to 30%, becomes nearly equal to the porosity of natural salt, in less than 20 years. The compaction process is triggered by the creep and dilatant behavior of the host rock inducing drift closure, and accelerated by the temperature increase in the repository resulting in higher creep rates. The small increase in the porosity of rock salt (green point) near the drift is due to changes in temperature, in volumetric strain due to the closure of the drift and the compaction of the backfill, and in pressure due to temperature- and deformation-induced desaturation.

Furthermore, as compaction occurs, the crushed salt’s elastic moduli tend to those of intact salt, and the stress state, which is initially close to zero, evolves to the initial isotropic stress state, as shown in Fig. 5, which depicts the stress evolution in the crushed salt backfill and the drift wall.

Figure 6 shows the evolution of pore pressure. In the host rock, 25 m away from the drift, pore pressure is initially hydrostatic, whereas in the drift, pore pressure is set to atmospheric pressure during the waste package emplacement and backfilling stages. Thereafter, pore pressure increases due to the reconsolidation of the backfill and thermal pressurization and exceeds the lithostatic stress level, roughly equal to 13.5 MPa at the repository level, for both canister spacing cases. This triggers a small jump in the porosity of crushed salt that could be seen in Fig. 4, an increase in permeability and a fluid infiltration into the rock salt mass. Consequently, pore pressure starts to decrease immediately after the peak and stabilizes around the lithostatic stress level. As temperature decreases, pore pressure drops below the hydrostatic pressure level but begins to increase again at about 16,000 years, returning to the initial undisturbed pore pressure levels (Figs. 3b, 6b). Indeed, the cooling-induced depressurization leads to an increase in the effective stress which causes the rock to deform and the pore pressure to increase.

Regarding the shear stress component, Fig. 7 shows the distribution of the von Mises equivalent stress in the backfill at different dates, for the case of a 20-m canister spacing. In the first 10 years, during the reconsolidation of the backfill, the von Mises equivalent stress increases, especially in the vicinity of the waste canister, and in the right corner but it does not go beyond 2.4 MPa, except in the corner. As the crushed salt further strengthens, the maximum compressive stress tends toward an isotropic stress state (see Fig. 5b) and deviatoric stresses decrease; they go as low as 0.06 MPa at 20 years in most of the zones. After that, changes in pore pressure due to thermal pressurization (see Fig. 6b) lead to an increase in the maximum compressive stress and hence to an increase in shear stresses in all of the backfill volume; they reach an average value of 2 MPa at 40 years. When the stress state becomes isotropic again, the shear stresses decrease again, and at 10,062 years, their value is below 0.4 MPa in most of the backfill area. Moreover, as temperature starts decreasing, creep rates also decrease and the von Mises stress slowly rises reaching more than 0.6 MPa at 30,000 years.

As for the distribution of deviatoric stresses in the rock salt around the backfill, they may exceed 15 MPa during the excavation phase of the drift. As crushed salt strengthens, they decrease falling below 0.1 MPa level at 50 years.

In short, both in the backfill and in the host rock, the deviatoric stress in the vicinity of the waste package after 50 years remains below 1 MPa which represents a low value of deviatoric stress that traditional creep laws cannot capture accurately enough.

Fig. 3
figure 3

Simulated temperature at three different locations for a a 10-m canister spacing and b a 20-m canister spacing

Full size image
Fig. 4
figure 4

Simulated porosity at three different locations for a a 10-m canister spacing and b a 20-m canister spacing

Full size image
Fig. 5
figure 5

Simulated maximum compressive stress at two different locations for a a 10-m canister spacing and b a 20-m canister spacing

Full size image
Fig. 6
figure 6

Simulated pore pressure at three different locations for a a 10-m canister spacing and b a 20-m canister spacing

Full size image
Fig. 7
figure 7

Simulated 2D profiles of von Mises equivalent stress (MPa) in the crushed salt backfill at different dates for the 20-m canister spacing case

Full size image

3 Constitutive models for rock salt

In the literature, most of the constitutive models of rock salt are based on the partition of the total strain rate tensor \(\overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!\) into elastic \(\overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!^\text {e}\) and viscoplastic \(\overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!^{\text {vp}}\) components:

$$\begin{aligned} \overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!=\overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!^\text {e}+\overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!^{\text {vp}} \end{aligned}$$
(1)

For rock salt, the elastic strain rate tensor \(\overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!^\text {e}\) is usually described by the linear elastic Hooke’s law:

$$\begin{aligned} \overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!^\text {e}=\frac{1+\nu }{E}\overset{_{\,\text{. }}}{\varvec{\sigma }}\,\!-\frac{\nu }{E}\text {tr}\left( \overset{_{\,\text{. }}}{\varvec{\sigma }}\,\!\right) \varvec{1} \end{aligned}$$
(2)

where \(\varvec{\sigma }\) is the Cauchy stress tensor, E is the Young’s modulus, \(\nu\) is the Poisson’s coefficient, and \(\varvec{1}\) is the unit tensor.

However, these models differ in their definition of the viscoplastic strain tensor. In this section, we present its expression for the four constitutive models that are compared in this paper: Norton, WIPP, combined creep law (Norton + pressure solution creep law) and Lux/Wolters/Lerche.

3.1 The Norton, WIPP and combined creep laws

The three models agree that the viscoplastic strain rate is coaxial with the deviatoric stress tensor \(\varvec{\sigma }'=\varvec{\sigma }-\frac{1}{3} \text {tr}(\varvec{\sigma })\varvec{1}\), normalized by the von Mises equivalent stress \(\sigma _{\text {eq}}=\sqrt{\frac{3}{2}\varvec{\sigma }':\varvec{\sigma }'}\):

$$\begin{aligned} \overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!^{\text {vp}}=\frac{3}{2}\overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!^{\text {vp}}_{\text {eq}} \varvec{J}~;\quad \varvec{J}=\varvec{\sigma }'/\sigma _{\text {eq}} \end{aligned}$$
(3)

The difference between them lies in the definition of the viscoplastic equivalent strain rate \(\overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {vp}}_{\text {eq}}\).

In the Norton model, which is a purely steady-state flow law, the viscoplastic equivalent strain rate is expressed as follows:

$$\begin{aligned} \overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {vp}}_{\text {eq}}=A_{\text {N}}=A_1 \left( \frac{\sigma _{\text {eq}}}{\sigma _{\text {r}}}\right) ^n \text {exp}\left( -\frac{A_2}{T}\right) \end{aligned}$$
(4)

where T is temperature, \(\sigma _{\text {r}}\) is a reference stress (\(\sigma _{\text {r}}=1~\text {MPa}\)) and \(A_1\), \(A_2\) and n are material constants. \(A_2\) is commonly considered equal to Q/R, where R is the universal gas constant and Q is the activation energy.

The WIPP model, implemented in FLAC\(^\text {3D}\) based on the creep model described by Herrmann et al. [20, 21], partitions the viscoplastic equivalent strain rate into a steady-state flow component \(\overset{_{\,\text{. }}}{\varepsilon }\,\!_{\text {ss}}\) that is equal to the Norton’s viscoplastic equivalent strain rate \(A_{\text {N}}\), and a transient component \(\overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {tr}}_{\text {eq}}\) that is proportional to \(\overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {ss}}_{\text {eq}}\):

$$\begin{aligned} \overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {vp}}_{\text {eq}}=\overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {tr}}_{\text {eq}}+\overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {ss}}_{\text {eq}}=(1+H)\overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {ss}}_{\text {eq}}~;~\overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {ss}}_{\text {eq}}=A_{\text {N}} \end{aligned}$$
(5)

where H is defined as follows:

$$\begin{aligned} H=\left\{ \begin{array}{ll} B_1-B_2 \varepsilon ^{\text {tr}}_{\text {eq}},&{}\overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {ss}}_{\text {eq}}\ge \overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {ss}*}_{\text {eq}} \\ B_1-B_2 \left( \dfrac{\overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {ss}*}_{\text {eq}}}{\overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {ss}}_{\text {eq}}} \right) \varepsilon ^{\text {tr}}_{\text {eq}},&{}\overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {ss}}_{\text {eq}}< \overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {ss}*}_{\text {eq}}\\ \end{array}\right. \end{aligned}$$
(6)

where \(B_1\), \(B_2\) and \(\overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {ss}*}_{\text {eq}}\) are material constants.

The third creep law combines the Norton law with the linear creep law derived by Spiers et al. [34] to describe pressure solution behavior of dense rock salt which dominates at low stress and temperature, in the presence of brine in the rock pores:

$$\begin{aligned} \overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {vp}}_{\text {eq}}=A_{\text {N}}+\frac{A_3}{TD^3} ~ \frac{\sigma _{\text {eq}}}{\sigma _{\text {r}}} ~ \text {exp}\left( -\frac{A_4}{T}\right) \end{aligned}$$
(7)

Unlike Norton’s law, the pressure solution term depends on salt grain size D. The coarser the rock salt is the lower are the creep strain rates. The temperature dependency is also described differently: in addition to the Arrhenius term \(\text {exp}\left( -\frac{A_4}{T}\right)\), where \(A_4\) is the ratio of rock salt activation energy, under pressure solution regime, and of the universal gas constant, the pressure solution law is a function of the reciprocal of temperature. The coefficient \(A_3\) is a constant that depends on the grain shape and the molar volume of the solid phase.

3.2 The Lux/Wolters/Lerche constitutive model

The inelastic strain rate tensor in the Lux/Wolters/Lerche model is the sum of three main components: viscous strain rate \(\overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!^{\text {vp}}_{\text {v}}\) due to transient and steady-state creep, damage-induced strain rate \(\overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!^{\text {vp}}_{\text {d}}\) resulting from shear or tensile failure and healing-induced strain rate \(\overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!^{\text {vp}}_{\text {h}}\).

$$\begin{aligned} \overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!^{\text {vp}}=\overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!_{\text {v}}+\overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!_{\text {d}}+\overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!_{\text {h}} \end{aligned}$$
(8)

The viscous component is based on the constitutive model modLubby2 [23] and is described by the following equations:

$$\begin{aligned} \overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!_{\text {v}}=\overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!^{\text {tr}}+\overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!^{\text {ss}}=\frac{3}{2}\left[ \frac{1}{\bar{\eta }_\text {k}(\sigma _\text {eq})} \left\langle 1-\frac{\varepsilon ^{\text {tr}}_{\text {eq}}}{\text {max}~\varepsilon ^{\text {tr}}_{\text {eq}}} \right\rangle +\frac{1}{\bar{\eta }_{\text {m}}(\sigma _\text {eq},T)} \right] \varvec{\sigma }' \end{aligned}$$
(9)

The Maxwell and Kelvin viscosity moduli, \(\bar{\eta }_\text {m}\) and \(\bar{\eta }_\text {k}\), are expressed as follows:

$$\begin{aligned}{} & {} \bar{\eta }_\text {k}(\sigma _\text {eq})= \bar{\eta }_\text {k}^*~ \text {exp}(k_2\sigma _\text {eq}) \end{aligned}$$
(10)
$$\begin{aligned}{} & {} \bar{\eta }_\text {m}(\sigma _\text {eq},T)= \bar{\eta }_\text {m}^* \left( \frac{\sigma _\text {eq}}{\sigma _\text {r}} \right) ^a \text {exp}(m\sigma _\text {eq})~\text {exp}(lT) \end{aligned}$$
(11)

The Macauley Brackets \(\langle .\rangle\) are used because the transient creep saturates at the maximum equivalent Kelvin strain determined as follows:

$$\begin{aligned} \text {max}~\varepsilon ^{\text {tr}}_{\text {eq}}=\frac{\sigma _\text {eq}}{\bar{G}_\text {k}} \end{aligned}$$
(12)

with \(\bar{G}_k\) the Kelvin shear modulus, expressed as follows:

$$\begin{aligned} \bar{G}_\text {k}=\bar{G}_\text {k}^* \left( \frac{\sigma _\text {eq}}{\sigma _\text {r} }\right) ^b \text {exp}(k_1\sigma _\text {eq}) \end{aligned}$$
(13)

where \(\bar{\eta }_\text {k}^*\), \(\bar{\eta }_\text {m}^*\), \(\bar{G}_\text {k}^*\), m, l, a, b, \(k_1\) and \(k_2\) are material parameters. \(\sigma _\text {r}\) is a reference stress set equal to 1 MPa.

Expression of the damage strain rate component \(\overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!_{\text {d}}\) can be found in [24] and the expression of the healing component \(\overset{_{\,\text{. }}}{\varvec{\varepsilon }}\,\!_{\text {h}}\) in [23, 41].

3.3 Parameters determination and models comparison

Table 1 lists two sets of parameters for the four constitutive models. The first set, referred to as “Old Calibration,” is based on values reported in the literature and widely used in the salt mechanics community. The second set, designated as “New Calibration,” starts with the old calibration and modifies some parameters to fit newly available creep data.

The elastic properties apply to the four creep models. Parameters of Norton and WIPP creep laws in the Old Calibration set are traditionally used to characterize the creep of Permian Salado formation salt [5, 39]. Regarding the pressure solution component of the combined creep law, parameters determined by Spiers et al. [34] for synthetic dense poly-crystalline salt samples are used.

Parameters of the LWL model in the first set have been calibrated against creep tests and conventional triaxial compression tests conducted on different salt samples coming from different salt formations (US and Germany), in wide ranges of stress, strain rate and temperature, including the low deviatoric stress range, but not below 2 MPa [32]. The creep tests are carried out under a constant stress and allow to fit the damage-free viscoplastic component of the model, whereas in the conventional triaxial compression tests, a constant strain rate is applied allowing to characterize moderate as well as intense (up to residual strength) damage behavior. Additional long-term multistage creep tests with innovative boundary conditions are used to characterize damage development more exactly and to check transferability of the model from short-term conditions to long-term conditions (in situ relevant). These tests comprise unloading steps to investigate the healing process.

Some of the parameters of the old calibration set were recalibrated to fit new experimental data before using them in numerical simulations in Sect. 4. These data include two types of data points: (1) transient strain limit and steady-state strain rates from several long damage-free triaxial creep tests conducted by the Institute of Geomechanics GmbH (IfG) on argillaceous and clean WIPP salt at three different temperatures (25, 60 and 80\(~^{\circ }\hbox {C}\)) [29], (2) steady-state strain rates measured in multiple low-stress (from 0.1 to 1 MPa), low temperature (below 15\(~^{\circ }\hbox {C}\)) uniaxial creep tests carried out by Bérest et al. [4] on samples from different salt mines, Gorleben, Avery Island and Hauterives.

It should be emphasized that combining these two laboratory test data as a single dataset is arguable given the differences in testing conditions and rocksalt type. To begin, the specimens that were tested under unconfined conditions may have dilated, affecting the strain rate measurements at low deviatoric stresses. Moreover, while the grain size of the tested samples is comparable: an average of 10 mm for WIPP samples and an average of 4, 8, and 10 mm for Gorleben, Avery Island, and Hauterives samples, the moisture content of the latter is lower: 0.048, 0.005, and 0.0088%, respectively, versus 0.15% for clean WIPP salt and twice this value for argillaceous WIPP salt. In addition to that WIPP salt samples were tested under a broad range of temperature. Nevertheless, in the absence of data on WIPP salt in the very low stress range, results from the creep tests by Bérest et al. [4] provide an approximate magnitude of equivalent steady-state strain rate that one should expect for a low-stress state regime. Also, since the difference between the creep behavior of clean and argillaceous WIPP salt is minimal, they are viewed as one single material [29].

Table 1 Models’ parameters in the old and the new calibrations (any unchanged parameters from the Old Calibration are represented as blank cells in the New Calibration column)
Full size table

The first parameter that was recalibrated is the parameter \(A_2\) used in Norton and WIPP models and the combined creep law: \(A_2=6538\) K allows a better fit of IfG creep tests results on WIPP salt. Figure 8 shows in a log-log plot the evolution of the steady-state strain rate \(\overset{_{\,\text{. }}}{\varepsilon }\,\!_{\text {ss}}\) with the von Mises equivalent stress \(\sigma _{\text {eq}}\) in the Norton, WIPP and LWL models using the new recalibrated value of \(A_2\) and the values given in Table 1 for all the other models parameters, together with the WIPP salt data from Reedlunn et al. [29] and data from Bérest et al. [4]. As can be seen, data points corresponding to the creep tests performed under a \(60~^{\circ }\hbox {C}\) temperature (purple) suggest a change in slope around 8 MPa, which a Norton-type law (Norton and WIPP laws in this paper) will fail to reproduce. For a 1 MPa shear stress level, the steady-state strain rate predicted by the LWL model is higher by two orders of magnitude than Norton and WIPP laws’ strain rate and the gap between them increases at lower deviatoric stresses.

By adding the pressure solution term to the Norton law, the transition from strain rates driven by dislocation mechanisms to strain rates controlled by pressure solution creep behavior at low equivalent deviatoric stresses can be captured, as shown in Fig. 9, where the steady-state function of the combined law is plotted, using parameters from Table 1 and \(A_2=6538\) K, together with the experimental data points.

As can be seen in Figs. 8 and 9, both the LWL model and the combined law lead to steady-state creep rates that are smaller than the strain rates measured by Bérest et al. [4] for a deviatoric stress lower than 1 MPa. By reducing the grain size D from 1 cm to 3 mm in the combined creep law, a better agreement with experimental values of steady strain rates for deviatoric stresses below 4 MPa can be obtained (see Fig. 9). As for the LWL model, increasing the parameter a from \(-1\) to \(-0.3\) and slightly increasing the parameter l allowed to obtain a better agreement with experimental data for both stress regimes (see Fig. 10).

Fig. 8
figure 8

Stress dependence of the steady-state equivalent strain rate in Norton and LWL models. Data points are steady-state strain rates from IfG’s creep tests on WIPP salt [29] and low-stress creep tests on non-WIPP salt from Bérest et al. [4]

Full size image
Fig. 9
figure 9

Stress dependence of the steady-state equivalent strain rate in the combined law for two values of salt grain size. Data points are steady-state strain rates from IfG’s creep tests on WIPP salt [29] and low-stress creep tests on non-WIPP salt from Bérest et al. [4]

Full size image
Fig. 10
figure 10

Effect of the parameters of LWL model on the predictions of steady-state equivalent strain rate evolution with von Mises equivalent stress. Creep test results on WIPP salt from Reedlunn et al. [29] and on non-WIPP salt from Bérest et al. [4] are also plotted

Full size image

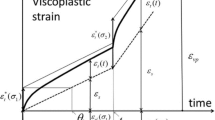
Regarding transient creep behavior, Fig. 11 illustrates in a log-log plot the stress dependence of the transient strain limit in the LWL and WIPP models. This limit is referred to by \(\text {max}~\varepsilon ^{\text {tr}}_{\text {eq}}\) in the LWL model and expressed by Eq. (12). In the WIPP model, its expression can be determined by resolving \(\overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {tr}}_{\text {eq}}=0\), which leads to:

$$\begin{aligned} \text {max}~\varepsilon ^{\text {tr}}_{\text {eq}}=\left\{ \begin{array}{ll} \dfrac{B_1}{B_2},&{}\overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {ss}}_{\text {eq}}\ge \overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {ss}*}_{\text {eq}} \\ \dfrac{B_1}{B_2} \left( \dfrac{ \overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {ss}}_{\text {eq}}}{\overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {ss}*}_{\text {eq}}} \right) ,&{}\overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {ss}}_{\text {eq}}< \overset{_{\,\text{. }}}{\varepsilon }\,\!^{\text {ss}*}_{\text {eq}}\\ \end{array} \right. \end{aligned}$$
(14)

Data points in Fig. 11 are deduced from strain measurements in the IfG creep tests on WIPP salt performed at three different temperatures (25, 60 and 80\(~^{\circ }\hbox {C}\)) [29]. They show that the sensitivity of the transient strain limit to temperature changes is not strong compared to steady-state creep rate. The choice of canceling the effect of temperature in the transient strain component of the LWL model is hence plausible, at least in this stress and temperature range. The effect of temperature is included in the WIPP model, since the transient strain rate component is a function of the steady-state strain rate which is itself a function of temperature. By using the set of parameters in Table 1, the blue dashed line representing the response of the WIPP law for \(T=80~^{\circ }\hbox {C}\) agrees fairly well with the measurements, but only for high stresses, above 8 MPa. The LWL model predicts similar behavior at high deviatoric stresses but greater transient strain limits at lower stresses (solid green line). The creep tests performed at \(T=80~^{\circ }\hbox {C}\) and relatively low stresses (below 8 MPa) confirm that extrapolating the transient strain limit from high to low stresses, as it is the case for WIPP law and many other widely used creep laws, can lead to wrong predictions of the transient behavior of rock salt. Furthermore, one of the key outputs of the creep tests performed by Bérest et al. [4] is the duration of the transient creep phase which turned out to be unexpectedly long at very low deviatoric stresses. An enhanced fit of the IfG WIPP tests using the LWL model is also provided in Fig. 11 (the dotted green curve) in which b and \(\bar{G}_\text {k}^*\) parameters were changed.

Fig. 11
figure 11

von Mises equivalent stress dependence of transient equivalent strain limit compared against creep experiments on WIPP salt from Reedlunn et al. [29]

Full size image

4 Numerical comparison of the constitutive models

In this section, the long-term predictions of the four models are compared, first using a numerical creep test and second through the simulation of the vertical movement of a heavy waste canister disposed in salt. We use for this the finite-volume geomechanical code FLAC\(^{\text {3D}}\), where all the studied models have been implemented. As for the material parameters, we use the New Calibration set given in Table 1.

4.1 Simulation of a creep test

Numerical creep tests are simulated using the four models and material parameters from the previous section. In these tests, a lateral (confining) pressure P and a vertical pressure Q are applied on the specimen (Fig. 12). Two deviator \(Q-P\) values are investigated: 10 and 1 MPa. Temperature is set equal to \(100~^{\circ }\hbox {C}\), in accordance with results of Sect. 2.

Among the four models studied in this paper, LWL model is the only one that is sensitive to the value of the confining pressure. (The yield strength of rock salt is a function of the minimum principal stress.) Hence, one confined creep test using LWL model, with \(P=12\)  MPa, is also simulated. We note that simulating the unconfined test is only relevant for the stress state in the first years, prior to the crushed salt backfill becoming completely reconsolidated. However, it is provided to highlight how it may influence the LWL model’s predictions.

Figure 13 shows the axial strain-time curves for both deviator cases. In the high deviator case, the LWL model response is similar to the response of the other models when the confining pressure was applied to the specimen. Otherwise, in the unconfined case, deviator and temperature conditions caused shear damage and accelerated creep within 150 days. In the low deviator case, as expected, the WIPP and Norton model predict significantly lower axial strain values compared to the LWL model and the combined law when a salt grain size of 3 mm is considered.

Furthermore, in both deviator cases, the axial strain quickly starts to increase linearly with time and the transient creep phase in WIPP and LWL model is rather very short.

Fig. 12
figure 12

Dimensions and boundary conditions for the numerical creep test

Full size image
Fig. 13
figure 13

Comparison of the strain-time behavior predicted by the compared creep models during numerical creep tests under \(100~^{\circ }\hbox {C}\) and two different deviators, 1 and 10 MPa. Figures are not in the same scale

Full size image

4.2 Simulation of long-term canister movement

Based on Sect. 2 results, the full reconsolidation of the backfill is a rather fast process compared to the 10,000 years period, and once the backfill is reconsolidated temperature in the drift and its vicinity does not change a lot. Hence, we assume in the following simulations that crushed salt is fully compacted and has the properties of the salt host rock, and that temperature within 30 m from the drift remains equal to 100\(~^{\circ }\hbox {C}\) during the 10,000 years period. Temperature elsewhere is equal to its initial undisturbed value and is not updated when the waste package moves. This allows us not to solve for the temperature, pore pressure and saturation fields and to use the simplified geometry and refined mesh shown in Fig. 14 instead of the one given in Fig. 2. Vertically, the geometry extends from a 550-m depth to 800-m depth, and an overburden pressure of 11.9 MPa is applied to the top boundary. A roller boundary condition is assigned to the lateral and bottom boundaries.

Fig. 14
figure 14

Simplified geometry of the salt repository

Full size image

In line with a worst-case scenario approach, the heavy waste package is assigned the parameters of steel. (Density is 7800 kg/m\(^3\), bulk modulus is 167 GPa, and shear modulus is 8 GPa.) The density of rock salt is 2200 kg/m\(^3\).

Fig. 15
figure 15

Evolution of the displacements at the top and bottom of the canister using: a Norton and WIPP laws, b LWL model and the Combined creep law (color figure online)

Full size image

Figure 15 shows the evolution of the vertical displacements at the top and bottom of the waste package during 10,000 years. Initially, the bottom moves upward and the top downward, as can be seen in Fig. 15a and the zoomed subfigure in Fig. 15b. Then, they both move downward indicating a sinking of the package. After 1000 years, the sinking rate predicted by the Norton and WIPP models is very low, approximating \(-4.4\times 10^{-7}\) mm/year. When using the LWL model and the combined creep law, the upward movement at the bottom becomes negligible, and both the top and the bottom move downward at the same rate and with nearly the same movement amplitude. The sinking rate is nearly constant after 20 years, equal to about \(-2.1\times 10^{-2}\) mm/year in the case of the LWL model and to about \(-3.1\times 10^{-2}\) mm/year in the case of the combined law creep. However, the simulated magnitude of vertical displacement remains less than 0.5 m in 10,000 years, even if the two models were calibrated to the recent low-stress creep data.

It is important to point out that even if the combined law led to less axial strain than the LWL model in the creep test presented in the previous subsection, it predicts here a sinking rate 1.5 times higher than the LWL model. Indeed, values of the von Mises equivalent stress around the waste package, after stress relaxation, are between \(2.4 \times 10^{-2}\) MPa and \(2 \times 10^{-3}\) MPa, as shown in Fig. 16a. In this stress range, the used calibrations of the LWL model and the combined law creep predict a higher steady-state strain rate for the latter (Sect. 3). This is an illustration of how the predictions of canister sinking are highly sensitive to the model’s parameters fitting. In fact, there is no unique best-fitting of a constitutive model against a data set. Added to this, the important uncertainties arising from the time, stress and temperature extrapolation of the model to ranges that are hard to investigate experimentally stress below 0.1 MPa for instance.

Furthermore, vertical movement of the package affects the surrounding rock salt domain within a diameter of about 30 m. The map of vertical displacements after 10,000 years shown in Fig. 16b and the deformed grid shown in Fig. 16c show that vertical displacements are the highest around the waste package and gradually decrease over 30 m above and below. Also, the downward movement of the waste package is expected to induce an upward movement, of smaller magnitude, at mid-spacing between two emplacement drifts, represented by the right vertical boundary in our model.

Fig. 16
figure 16

Distribution of a the von Mises equivalent stress (MPa) and b vertical displacements (m) 50 m above and 30 m below the waste package after 10,000 years and c deformed cropped grid (deformation increased by a factor of 7). Results are from the simulation using LWL model (blue curve in Fig. 15)

Full size image

Additional simulations were carried out to further investigate the influence of other parameters, namely the Maxwell viscosity \(\bar{\eta }_\text {m}^*\), the waste package density and the mean temperature, on the sinking predictions. The effect of the viscosity and temperature changes on the stress dependency of the steady-state equivalent strain rate is given in Fig. 17 for comparison purposes. The evolution with time of the displacement at the bottom of the canister in all these simulations is grouped in Fig. 18 and compared with the reference curve from Fig. 15.

Fig. 17
figure 17

Effect of the Maxwell viscosity parameter \(\bar{\eta }_\text {m}^*\) and the mean temperature in the repository on the steady-state strain rate evolution with the equivalent stress

Full size image
Fig. 18
figure 18

Effect of the Maxwell viscosity parameter \(\bar{\eta }_\text {m}^*\), the waste package density and the mean temperature in the repository on the vertical displacements at the bottom of the waste package

Full size image

4.2.1 Effect of rock salt viscosity

The viscosity of rock salt is strictly correlated with temperature, water content, stress level, salt grain size and the presence of impurities. Heterogeneity within a salt repository may lead to spatial heterogeneities in the viscosity values that cannot be predicted by typical creep tests because they are conducted on small specimens that are not necessarily representative of the natural material heterogeneity and under incomprehensive testing conditions. Hence, a new simulation was run with the LWL model, this time with a 10 times lower Maxwell viscosity by using \(0.1\bar{\eta }_\text {m}^*\) given in Table 1. The resulting long-term sinking rate is of \(-1.9\times 10^{-1}\) mm/year, which is 9 times higher than the sinking rate in the reference curve (see Fig. 18). After 10,000 years, the accumulated vertical displacement is about 1.8 m, which should be compared to the applicable safety regulations for a particular site.

4.2.2 Effect of the waste canister density

In all the previous simulations, the canister was assigned the density of steel. In this additional simulation, the average density of a large waste canister was used instead 5000 kg/m\(^3\) (1.56 times lower). As expected, the canister’s sinking decreases with a decreasing density. The new sinking rate is about \(-8.5\times 10^{-3}\) mm/year, 2.5 times lower than the reference value (Fig. 18).

4.2.3 Effect of near-field temperature

In all the previous simulations, a constant value of 100\(~^{\circ }\hbox {C}\) was assigned to temperature around the waste package, within 30 m. This value was based on temperature evolution in the repository when canisters are 20 m apart along emplacement tunnels (Fig. 3b). If canisters are less distant, temperature around the waste package will be higher (Fig. 3a).

For this reason, a new simulation was run with a higher temperature value 150\(~^{\circ }\hbox {C}\), that resulted, as expected, in a sinking rate that is higher than the sinking rate when temperature was equal to 100\(~^{\circ }\hbox {C}\) (Fig. 18); for a 1.5 times higher temperature, the sinking rate is 10 times higher approximately.

5 Conclusion

In this paper, the long-term movement of a nuclear waste package disposed in a salt formation is investigated through a comparative study of four different creep models. The strain rate predictions of these models were first confronted with measurements from recent creep tests conducted under high and low deviatoric stresses, which allowed a recalibration of some of these models’ parameters. Then, simulations of the vertical movement of a waste package were conducted under a high temperature that is representative of thermal conditions in a repository for large waste packages. It was found that both the absence of a low-stress mechanism in the rock salt creep model or the calibration of the model against large deviatoric stresses only would result in predictions of negligible long-term movement of waste packages.

While our study provides important insights into the long-term sinking of nuclear waste canisters in salt formations, it is important to note that several limitations exist that could alter the magnitude of the predicted sinking. Firstly, the data points for low-stress conditions do not correspond to salt samples from the WIPP site. Secondly, available experimental data points for the stress range between 0.7–4 MPa, in the transition between dislocation creep and pressure solution creep, are limited. Thirdly, the uniaxial tests used to calibrate the models in the low-stress range do not account for the potential effects of confining pressure. Fourthly, the effect of brine content on low-stress creep rates was not accounted for, due to a lack of available experimental data on this particular topic.

Finally, the sinking rate is highly sensitive to local heterogeneities translating into a spatial variability of rock salt grain-size and viscosity. Some precautions, such as limiting the density of the waste packages and reducing the temperature in the repository, can help mitigate this potential sinking problem.