1 Introduction

The growth in the number of construction projects worldwide has led to an increased use of natural resources, which has attracted the interest of researchers in the development of sustainable construction practices. One such approach involves using scrap tyres (also known as recycled tyres/ tyre-derived aggregates (TDA)) as a construction material. The stockpiling of these scrap tyres incurs high costs and acts as a hazard to human and environmental health [29]. The benefits of using scrap tyres as a construction material include low unit weight, free drainage, high thermal insulation, high compressibility, and superior vibration damping [2, 10]. These merits have led to the increased use of TDA for subgrade, embankment and trench fill material [1, 16, 45, 95]; a drainage layer in highway construction [52, 59]; vibration damping material in railway tracks [43, 91], the production of asphalt rubber [62, 70, 89], subgrade insulation in roads [47, 77], among others. Scrap tyres are believed to have the least influence on the quality of soil and groundwater as these are produced using inert chemicals.

Recently, scrap rubber has been used in railway engineering to attenuate environmental vibrations from moving trains [20, 85, 90]. Field trials of a ballasted track embedded with a TDA layer below ballast layers suggest that the efficacy of TDA to attenuate vibration is comparable to ballast mats [28]. In another field study, TDA was used as a replacement for subballast on a concrete railway bridge which aided the reduction of the maximum acceleration of sleeper by 63% [26]. Drop-weight impact loading tests showed that the addition of crumb rubber improved the damping properties of the ballast mixture [55]. An experimental study by Fathali et al. [32] suggested that on incorporating 10% TDA by weight (optimum content), particle breakage and settlement reduced by 47 and 6%, respectively. The addition of higher TDA content, viz. 20%, leads to a noticeable reduction in shear strength and higher ballast settlement. Another study by Sol-Sánchez et al. [79] also reported a decrease in track settlement on adding 10% of crumb rubber by volume of ballast. However, some studies, for example, Esmaeili et al. [25] reported an increase in the settlement of sand-fouled ballast by 142, 280, and 633% on the respective inclusion of 5, 10, and 15% of TDA (by weight), which suggests a need to perform in-depth research on the use of rubber with granular soil.

A study involving large-scale direct shear testing and the discrete element modelling of ballast–TDA mixture revealed that incorporating 10% TDA reduced the shear stress, dilation effect, and the ballast breakage index by 53% [40]. In another experiment by Song et al. [81], it was observed that the damping ratio was enhanced while resilient interface shear stiffness, peak shear stress, dilation effect, cohesion strength, and internal friction angle of ballast reduced on the addition of TDA to ballast. The study recommended 5% as the optimum TDA dosage. The use of scrap rubber has been shown to improve brittle behaviour, reduce dilation, and enhance the energy dissipation capability of bio-cemented sand [21]. The use of granulated rubber with sand was explored for use as a new railway subgrade filler material using static and cyclic triaxial apparatus. An optimum rubber content of 10% was recommended based on shear strength, dynamic pore water pressure, shear modulus, and damping ratio [23]. A recent study [3] on soil–clay mixtures also recommend 10% as optimum rubber dosage. This optimum percentage of granulated rubber was based on damping ratio [3] of the mix. The use of waste rubber has also shown ability to change the failure mode of clayey soil from brittle to ductile and has the potential to be used as a suitable filler for various geotechnical applications [24]. Recently, the application of lime with clay–rubber mixture was explored by Soltani et al. [80] and the soil–lime blend with 10% TDA content was recommended suitable in terms of reducing swelling potential and increasing the unconfined compressive strength of the soil.

Polyurethanes (PU) are a category of flexible materials used in various items, such as paints, insulation materials, foams, etc. PU is produced as a result of a chemical reaction between diisocyanate and polyester diol [4]. PU possesses unique characteristics of metals and rubber in terms of toughness and durability, respectively, which is responsible for their popularity [69]. Despite PU being used popularly in various industries in past decades, the application of PU in the railway industry is recent [50, 84]. Unfoamed PU has been used to stabilise railway ballast and create stiff bonding between aggregates [22]. Foamed PU was also utilised by Keene et al. [53] and the Chinese Academy of Railway Sciences (CARS) to strengthen the ballasted track [50]. CARS employs a spraying gun to spread PU uniformly over the ballast layer; the PU flows through the voids and coats the ballast particles. The initial strength enhancement starts within a half-hour. The curing time for PU can be adjusted using catalysts. The long-term strength gain could take up to a month [50]. Keene et al. [53] used rigid polyurethane to stabilise railway ballast. Cyclic triaxial tests revealed that plastic strain reduced by fourteen times with PU compared to clean ballast. However, the elastic modulus was reduced to 100 MPa compared to 275 MPa for clean ballast, which raised concern for the proper functioning of the reinforced track.

The present work aims to develop a novel material that can be used as a base layer in both ballasted and slab tracks. In this paper, firstly, the performance of scrap rubber in the form of ground rubber embedded in the sand is investigated. Secondly, the use of polyurethane with sand (treated sand), with and without ground rubber is also explored. The use of rubber in the base course could aid in alleviating the vibration, noise, and settlement problems associated with it. The use of scrap rubber would lead the way to sustainable construction practice. Furthermore, the polyurethane would act as adhesive and can reduce the deformation of the composite material.

There have been minimal studies on the use of scrap rubber and epoxy/polyurethane resin. Ho et al. [44] developed a new material, resilient bound ballast (RBB), comprising ballast mixed with TDA bonded together using a resilient epoxy binder. RBB showed improved strength over traditional ballast and can be used below concrete ties, which led to reduced abrasion and ballast fouling. Gómez et al. [39] developed an eco-friendly material consisting of rubber particles and single-component polyurethane resin, which acts as a vibration and noise attenuator in a railway track system with embedded rail. The use of crumb rubber mixed with short fibre reinforcement and epoxy-based resin was explored for railway sleeper application, and it was concluded that the strength properties of the sleeper decreased, but its flexibility improved [96]. Esmaeili and Namaei [27] used rubber-coated ballast glued using polyurethane-based adhesive and observed up to 77.5% reduction in Los Angeles abrasion and up to 60% enhancement in damping ratio. The short-term settlement increased by more than 24%, but the long-term settlement was less than the untreated ballast [27]. As per the authors’ knowledge, no previous study gives a detailed overview of performance comparisons of soil mixed with different proportions of polyurethane and scrap rubber. The novelty of the present study is rigorous laboratory investigation of performance verification of sand mixed with different proportions of polyurethane and scrap rubber. The same has been attempted using static and cyclic direct simple shear apparatus in the present study. The previous literature on cyclic response of sand–rubber and clay–rubber mixtures is shown in Table 1. It can be seen in Table 1 that all the previous cyclic studies on soil–rubber have been strain-controlled. In the present study, stress-controlled cyclic control was used in CDSS testing to better simulate traffic loading conditions.

Table 1 Summary of past studies involving the cyclic response of soil–rubber mixtures
Full size table

2 Direct simple shear apparatus

Triaxial and direct shear tests are extensively adopted to obtain shear strength parameters of the soil, but most of the geotechnical applications resemble simple shear states, which can be applied using equipment, viz. hollow cylinder (HC) and cyclic direct simple shear (CDSS). In addition, principal stress rotation occurs in these HC and CDSS tests due to the application of horizontal shear stress, which is not possible in triaxial tests. Of the HC and CDSS, the relative ease in sample preparation and simpler testing procedure makes CDSS an obvious choice.

The relevance of various geotechnical laboratory tests to field applications and the stress state of triaxial and direct simple shear is illustrated in Fig. 1. In the triaxial test, the Mohr’s circle can be drawn using the major principal stress [\(\it {\sigma }_{\mathrm{1}}\)] and minor principal stress [\(\it {\sigma }_{\mathrm{3}}\)] which are represented by axial and radial stress, respectively. The angle of internal friction [\(\phi\)] of soil can then be computed as shown in Fig. 1. In the DSS test, normal stress [\(\it {\sigma }_{\mathrm{x}}\)] and shear stress [\(\it {\tau }_{\mathrm{xn}}\)] on the vertical plane cannot be measured and only stress state on the horizontal plane (i.e., \(\it {\sigma }_{\mathrm{n}}, {\tau }_{\mathrm{nx}}\)) can be computed. Hence, assumptions are required for the construction of Mohr’s circle and the computation of the mobilised friction angle [\(\it {\phi }_{\mathrm{m}}\)] on the plane of maximum stress obliquity, defined in Eq. 1[69].

Fig. 1
figure 1

Relevance of various geotechnical laboratory tests to field application of slab tracks and stress states in triaxial and CDSS specimen

Full size image
$$\it {\phi }_{\mathrm{m}}={\mathrm{sin}}^{\mathrm{-1}}\left(\frac{{\sigma }_{\mathrm{1}}-{\sigma }_{\mathrm{3}}}{{\sigma }_{\mathrm{1}}+{\sigma }_{\mathrm{3}}}\right)$$
(1)

The following two assumptions are used to calculate the mobilised friction angle [13, 74]:

  1. (i)

    If the maximum shear stress is assumed to act on the horizontal plane, then mobilised friction angle [\({\phi }_{\alpha }]\) is given by Eq. 2

    $${\phi }_{\alpha }={\mathrm{sin}}^{-1}\left(\frac{{\tau }_{\mathrm{nx}}}{\it {\sigma }_{\mathrm{n}}}\right)$$
    (2)
  2. (ii)

    If the horizontal plane is assumed to be the plane of maximum stress obliquity, then mobilised friction angle [\({\phi }_{\beta }]\) is given by Eq. 3

    $${\phi }_{\beta }={\mathrm{tan}}^{-1}\left(\frac{{\tau }_{\mathrm{nx}}}{\it {\sigma }_{\mathrm{n}}}\right)$$
    (3)

Al Tarhouni et al. [5] showed that assumption (i) (Eq. 2) might overestimate the friction angle at low-stress levels. On the contrary, Atkinson et al. [13] showed that the friction angle calculated based on assumption (ii) (Eq. 3) is lower than the friction angle obtained from the triaxial test, and the difference depends on the ratio of horizontal to vertical stresses. Furthermore, assumption (ii) was validated for constant stress direct simple shear tests on loose to medium dense sand [54]. Hence, the mobilised friction angles reported for treated and untreated soil (with and without ground rubber), shown in Fig. 12, were based on assumption (ii) due to the loose-medium state of the sand chosen in the present study. However, for illustration, mobilised friction angles (i.e., \({\phi }_{m}, {\phi }_{\alpha }, {\phi }_{\beta }\)) calculated using different methods (Eqs. 1–3) for treated soil (soil + 10% PFA) are presented in the latter parts of the paper (Fig. 11d). The calculation of mobilised friction angle [\({\phi }_{m}\)] using Eq. 1 is shown in Fig. 12, assuming a horizontal plane as the failure plane. Half Mohr’s circles were drawn, and \(\it {\sigma }_{\mathrm{1}}\) and \(\it {\sigma }_{\mathrm{3}}\) were calculated from respective Mohr’s circles.

3 Experimental program

3.1 Test material

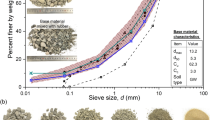
The material, sand, scrap rubber (in the form of ground rubber) and polyurethane foam adhesive (PFA) was procured from suppliers in Australia. The source of scrap rubber used in the present study comprises a truck tyre, off-the-road tyre, and passenger car tyre. The scrap rubber used in the present study is metal-free. All the tests on the materials were performed as per relevant standards (AS 1289.3.5.1, AS 1289.5.5.1 and ASTM D6270). The specimen size was 63.5 mm in diameter and 24 mm in height. The particle size distribution (PSD) of the track base course or subballast adopted by previous studies [14, 41, 68, 72, 75, 86] is shown in Fig. 2(a). The PSD for the base course material with 13.2 mm as the nominal particle size as specified in RMS-NSW specification [49] was adopted for the present study, as shown in Fig. 2. Considering the restriction of sample size ratio for SDSS and CDSS testing, 4.75 and 2.36 mm were adopted as maximum particle sizes for soil and ground rubber, respectively. PSD for the sand and GR was selected using the parallel gradation technique. The soil was classified as well-graded sand (SW) as per ASTM D2487 [9]. The sample size ratio of SDSS and CDSS testing was 13.4, larger than 6 as specified in ASTM D7181-11 [12]. The specific gravity of coarse sand (CS) and ground rubber (GR) was obtained as 2.74 and 1.165, respectively, according to AS 1289.3.5.1 [7]. The tensile strength and elongation at break of GR (with particle size less than 3.5 mm) are 0.6–1.1 MPa and 22–84%, respectively [34, 71]. GR was added in the proportion of 2.5, 5, 10, 15, 20, and 25% by mass of soil. This range for rubber was adopted in line with the recommended 5% optimum TDA dosage in previous studies [25, 81].

Fig. 2
figure 2

a PSD of base course/subballast adopted by previous studies b PSD adopted for the present study

Full size image

The maximum and minimum dry density of sand with varying GR content was determined as per AS 1289.5.5.1 [8], shown in Fig. 3. For the soil compaction test, a mould with a nominal capacity of 1000 cm3 and a surcharge weight of 5 kg was utilised. Loose pouring (dry placement method) and vibratory compaction (wet placement method) were performed on sand with varying GR to obtain the minimum and maximum dry densities, respectively. The dry densities of the test sample combined with different GR contents are also shown in Fig. 3. As evident from Fig. 3, the dry density decreased as the GR content increased. This is primarily because GR has a lower specific gravity (Gs = 1.165) than sand (Gs = 2.74). Other studies report similar reduction in density by increasing rubber content in sand [6, 37].

Fig. 3
figure 3

Variation of maximum and minimum dry density of sand with ground rubber content

Full size image

3.2 Loading conditions

In the CDSS test, two high-speed precision micro stepper motors control the loading mechanism for the vertical and horizontal load. The horizontal load can be applied as stress-controlled or strain-controlled. In the present study, stress-controlled cyclic control was used to simulate traffic loading. As per UIC [87], the axle load for train speeds up to 300 km/h is between 11 to 17 tonnes, and for the present study, an axle load of 20 tonnes has been considered. The numerical model of slab track previously developed by authors [30] was used to determine the vertical and shear stress on the top of the base layer (hydraulically bonded layer). The maximum vertical and shear stress due to axle load of 20 tonne on the top of the base layer was 300 and 60 kPa, respectively.

A shear stress of 16 kPa was deemed appropriate for the supporting layer of a slab track [83]. As per Yang et al. [94], the shear stress below ballast is approximately one-fifth of the vertical stress. Hence, considering the stress amplitude ratio (ratio of horizontal to vertical stress) of 1/5, the shear stress would be 60 kPa for vertical stress of 300 kPa. Hence, shear stresses of 50, 100, and 200 kPa were considered in the present study to cover a wide range of loading conditions. The constant normal stress of 300 kPa was adopted for the entire CDSS testing plan.

3.3 Sample preparation

The soil was sieved into individual size fractions of 4.75, 2.36, 1.18, 0.6, 0.3, and 0.075 mm. The ground rubber (GR) was sieved into individual size fractions of 2.36, 1.18, 0.6, 0.425, 0.3, and 0.15 mm. The proportion of each size fraction was determined to achieve the target particle size distribution of soil and GR. Sample preparation involved three series, as shown in Fig. 4. A total of 68 DSS tests under constant (normal) stress were conducted: 17 monotonic (SDSS) and 51 constant stress amplitude cyclic loading conditions (CDSS). Series-1 consisted of GR and coarse sand (CS) mixed in various proportions by weight (0, 2.5, 5, 10, 15, 20, and 25% GR by weight). Series-2 comprised CS and PFA mixed in various proportions by weight (5, 10, 15, and 20% PFA by weight). The optimum dosage of PFA was obtained from Series-2 testing, and this optimum PFA content was used in Series-3 testing. Series-3 involved CS, GR (0–25%), and PFA (10%).

Fig. 4
figure 4

Experimental plan for static direct simple shear (monotonic) and cyclic direct simple shear testing

Full size image

The latex membrane was placed on the bottom platen and a stack of Teflon coated aluminium rings were placed around the membrane. A split mould was then mounted on top of the stack of rings. A suction was applied to stretch the membrane against the inner surface of stack rings. The ingredients were mixed with utmost care so that the mixture would be as homogeneous as possible. The mixture was compacted in a dry state in three layers using undercompaction technique developed by Ladd [58] at a relative density of 40% using a vibratory compactor inside the split mould, as shown in Fig. 5.

Fig. 5
figure 5

Sample preparation for CDSS testing a untreated soil b treated soil c soil mixed with different PFA contents

Full size image

This nonlinear undercompaction criterion helps to achieve uniform density test specimens and ensures repeatability in the tests. The per cent undercompaction in the layer being considered was calculated using Eq. 4 [58]. In this study, undercompaction of 6% was considered for the first layer. The vibration method of compaction produced uniform soil–rubber mixtures and is recommended for cohesionless soils as per AS 1289.5.5.1 [8]. This uniform soil–rubber mixture was achieved by use of well-graded PSDs for soil and GR, with PSD of GR being finer. Due to the finer PSD, the rubber particles were entrapped in the void space of soil and according to ocular observation, segregation of the rubber particles during compaction did not occur. Owing to the hydrophobic nature of PFA, specimens were prepared in a dry state. During sample preparation, water was not added to the soil/soil–rubber mixture to allow for more accurate comparisons between untreated and treated specimens. Continuous height measurements were taken until the required density was achieved. The selection of relative density of 40% was based on the assessment by Wang and Leung [88] that loose state helps to minimise the variability in differentiating the influence of cementation on dilatancy from that due to grain packing. The top layer of specimen was levelled, and the top cap fixed with porous stone was placed. Split mould was removed, and the specimen was put on the CDSS apparatus and compressed for 1 h under constant normal stress of 300 kPa. This relative low time period for compression was considered as SDDS and CDSS tests were carried out in unsaturated condition. The specimen was then sheared (stress-controlled) for 50,000 cycles at a cyclic frequency of 1 Hz under constant normal load conditions with a cyclic shear stress amplitude (double amplitude) of 50, 100, and 200 kPa.

The PFA used in the study was a two-component, silicate modified, solvent-free, semi-flexible non-foaming polyurethane resin. The properties of components A and B as supplied by the manufacturer are shown in Table 2. The two components, A and B, were mixed in the volume ratio of 1:1 (100:82 by weight at 25 °C). After a few seconds of vigorous stirring at normal room temperature, the reaction between two components of PFA took place. The mixture was agitated for 30 s before being mixed with soil/soil–rubber mixture for 2 min. In case of PFA-treated specimens, the top surface of each layer was scrapped before placing the next layer to ensure proper bonding and specimen integrity. The compressive strength, bending strength, and flexural adhesive strength of PFA was greater than 40, 15, and 5 MPa, respectively.

$${U}_{\mathrm{n}}={U}_{\mathrm{ni}}-[\frac{\left({U}_{\mathrm{ni}}-{U}_{\mathrm{nt}}\right)}{{n}_{\mathrm{t}}-1}\times (n-1)]$$
(4)

where \({U}_{\mathrm{ni}}\) is the per cent undercompaction selected for first layer; \({U}_{\mathrm{nt}}\) is the per cent undercompaction selected for the final layer (usually zero); n is the number of layer being considered; \({n}_{\mathrm{t}}\) is the total number of layers (three in our case).

Table 2 Technical data of components A and B of PFA
Full size table

3.4 Equipment and testing details

The static and cyclic testing was performed using CDSS apparatus. Currently, there is no international standard related to consolidated drained cyclic direct simple testing. Hence, the appropriate approach outlined in ASTM D8296 [11] was used in this study. This study utilised CDSS equipment with horizontal and vertical loading capacities of 4.5 and 11 kN, respectively. The equipment has a maximum horizontal displacement limit of 25 and 10% for monotonic and cyclic peak-to-peak strain, respectively. The vertical displacement limit is 50 mm. The typical test range for cyclic frequency is 0.033 to 2 Hz [36]. Figure 6(a) and (b) illustrates some of the key parts of this apparatus. The CDSS test generates a fairly homogenous state of shear stress throughout the specimen, which provides the initial stress condition, stress path, and deformation configuration that models numerous field loading conditions more closely than any other test system, such as triaxial. The apparatus can be used to perform monotonic (SDSS) and cyclic (CDSS) tests on different soil types at drained and undrained conditions. Drained and undrained conditions are represented by constant normal stress and constant volume (also called constant height), respectively. The testing consists of two parts: static direct simple shear (SDSS) and CDSS test. SDSS tests were performed to evaluate the peak shear strength of the material in terms of cohesion [c] and friction angle [\(\phi\)]. CDSS tests were performed to assess the cyclic response (elastic and plastic strain [εae, εap]) of material for a large number of load cycles (50,000 cycles), and to assess the shear modulus [G] and damping ratio [DR] of the material. The selection of 50,000 load cycles in this study was based on logistical reasons (time/resources) and existing research on cyclic testing of railway track material. For instance, Brown [17] performed cyclic testing on granular railway material (that is, ballast) and found that the ballast reached a stable state after about 10,000 load cycles. Leshchinsky and Ling [61] investigated the effectiveness of geocell confinement on a ballasted track using 50,000 load cycles. Another study on cyclic performance of ballast and subballast employed 20,000 load cycles [15]. SDSS and CDSS testing was performed with horizontal control as strain and stress controlled, respectively. The strain rate of 0.01 mm/s was adopted for SDSS testing. Both SDSS and CDSS testing was performed under constant normal stress conditions. The frequency of 1 Hz was used for CDSS testing with frequency conditioning of 0.1 Hz for the first ten load cycles.

Fig. 6
figure 6

a Photograph of CDSS equipment b Schematic diagram of CDSS apparatus

Full size image

4 Results and discussion

4.1 SDSS (monotonic) test results

4.1.1 Stress–strain response

Figures 7, 8, and 9 show the variation of shear stress [\(\tau\)] with shear strain [\(\gamma\)] for Series-1, Series-2, and Series-3 of the experimental plan, respectively. The tests were performed under normal stress [\(\it {\sigma }_{\mathrm{n}}\)] of 50, 100, and 200 kPa. It can be seen from Fig. 7 that GR incorporation up to 5% shows a slight influence on the stress–strain response of the soil, with the highest \(\tau\) at 5% GR content. With an increase in GR content, \(\tau\) decreased for \(\it {\sigma }_{\mathrm{n}}\) of 50 and 100 kPa. At \(\it {\sigma }_{\mathrm{n}}\) of 200 kPa, the stress–strain behaviour of soil–GR mixtures with more than 10% GR content showed marginal variation.

Fig. 7
figure 7

Variation of shear stress with shear strain for soil mixed with varying GR content, sheared under normal stress a σn = 50 kPa b σn = 100 kPa c σn = 200 kPa

Full size image
Fig. 8
figure 8

Variation of shear stress with shear strain for soil mixed with varying PFA content, sheared under normal stress a \(\it {\sigma }_{\mathrm{n}}\)= 50 kPa b \(\it {\sigma }_{\mathrm{n}}\) = 100 kPa c \(\it {\sigma }_{\mathrm{n}}\)= 200 kPa

Full size image
Fig. 9
figure 9

Variation of shear stress with shear strain for treated soil mixed with varying GR, sheared under normal stress a \(\it {\sigma }_{\mathrm{n}}\)= 50 kPa b \(\it {\sigma }_{\mathrm{n}}\) = 100 kPa c \(\it {\sigma }_{\mathrm{n}}\)= 200 kPa

Full size image

From Fig. 8, it is evident that the addition of PFA increased the \(\tau\) of the soil, which was due to the enhancement of the cohesion of the soil. At a PFA content of 5%, \(\tau\) under \(\it {\sigma }_{\mathrm{n}}\) of 100 kPa was lower than untreated soil.

Figure 9 illustrates the shear stress variation with the shear strain of treated soil (soil mixed with optimum PFA content, viz. 10%) and varying GR content. This 10% optimum PFA content was based on shear strength parameters obtained from SDSS testing and cyclic response (elastic and plastic strain, shear modulus, and damping ratio) obtained from CDSS testing, explained in the latter part of the paper. Generally, it was observed that treated soil with 5% GR showed ultimate shear stress [\({\tau }_{\mathrm{ult}}]\) under the entire range of \(\it {\sigma }_{\mathrm{n}}\) (50–200 kPa). The \(\tau\) of treated soil with a GR content of up to 15% was higher than the treated soil without GR.

Figure 10(a) shows the \({\tau }_{\mathrm{ult}}\) values at different PFA content for \(\it {\sigma }_{\mathrm{n}}\) of 50–200 kPa. It is seen from Fig. 10 that there was a marginal increase in \({\tau }_{\mathrm{ult}}\) of soil on addition of 5% PFA. A sharp rise in \({\tau }_{\mathrm{ult}}\) was observed for PFA contents higher than 5%. Above 15% PFA content, the \({\tau }_{\mathrm{ult}}\) of soil either remained constant or reduced. For example, the \({\tau }_{\mathrm{ult}}\) of soil (under \(\it {\sigma }_{\mathrm{n}}\) of 50 kPa) reduced after reaching a maximum value of 51.5 kPa, advocating limiting the PFA content below 15%. Figure 10(b) compares \({\tau }_{\mathrm{ult}}\) at varying GR content for treated and untreated soil. It is seen that the highest \({\tau }_{\mathrm{ult}}\) for both treated and untreated soil was observed at 5% GR content and reduced with a further GR addition. The \({\tau }_{\mathrm{ult}}\) for treated soil was 218.7, 114.2, and 61.4 kPa under \(\it {\sigma }_{\mathrm{n}}\) of 50, 100, and 200 kPa, respectively, at 5% GR content. The maximum improvement in \({\tau }_{\mathrm{ult}}\) on addition of PFA to soil was observed with 10% GR content tested under \(\it {\sigma }_{\mathrm{n}}\) of 50 kPa. Overall, it is seen that at 10% GR content, there is a substantial increase in \({\tau }_{\mathrm{ult}}\) under the entire range of \(\it {\sigma }_{\mathrm{n}}\) for treated soil. Based on the above discussion, using up to 10% GR for untreated and treated soil is advisable.

Fig. 10
figure 10

Peak shear stress at varying a PFA content b GR content for PFA-treated and untreated soil

Full size image

4.1.2 Effect of normal stress on monotonic behaviour

Figure 11 shows the test results of the monotonic test performed on treated soil (soil + 10% PFA) compressed under a varying range of \(\it {\sigma }_{\mathrm{n}}\), viz. 50–300 kPa. The strain rate of 0.01 mm/s was used under constant \(\it {\sigma }_{\mathrm{n}}\) to shear the specimen. The shearing rate may significantly influence the drainage of saturated soil; nevertheless, the present study involved dry sand. The \(\tau\) increased with \(\gamma\) and reached a maximum value at \(\gamma\) = 15–25%. No peak or critical state was observed due to the loose-medium state of sand; hence, shear stress attained at the end of the test is referred to as ultimate shear stress in this paper. Also, this study could not report peak and critical state friction angles. Figure 11(b) shows a comparison of stress ratio with \(\gamma\). The maximum value of stress ratio reduced with an increase in \(\it {\sigma }_{\mathrm{n}}\). Al Tarhouni [5] reported a reduction in the maximum stress ratio from ~ 1.4 for \(\it {\sigma }_{\mathrm{n}}\) of 12.5 kPa to 0.62–0.65 for \(\it {\sigma }_{\mathrm{n}}\) of 100–400 kPa. Similarly, Stroud [82] reported a reduction in the maximum stress ratio from ~ 1.0 for \(\it {\sigma }_{\mathrm{n}}\) of 13.8 kPa to ~ 0.9 for \(\it {\sigma }_{\mathrm{n}}\) of 172 kPa. In the present study, the maximum stress ratio was reduced from 0.92 at \(\it {\sigma }_{\mathrm{n}}\) of 50 kPa to 0.55 at \(\it {\sigma }_{\mathrm{n}}\) of 300 kPa. It is important to note that similar values of stress ratio were observed for \(\it {\sigma }_{\mathrm{n}}\) of 50 kPa and 100 kPa till \(\gamma\) of 22.5%, which may be due to binding provided by PFA. Figure 11(c) illustrates the variation of axial strain \([{\upvarepsilon }_{\mathrm{a}}]\) with \(\gamma\) at different \(\it {\sigma }_{\mathrm{n}}\). It was observed that all the specimens showed dilation with initial compression occurring only at \(\it {\sigma }_{\mathrm{n}}\) of 50 kPa. At \(\it {\sigma }_{\mathrm{n}}\) of 300 kPa, the dilation started at \(\gamma\) of 10%. The rate of dilation started to reduce at \(\gamma \cong\) 20% for \(\it {\sigma }_{\mathrm{n}}\) of 50 and 100 kPa. The variation of mobilised friction angle [\({\phi }_{m},{\phi }_{\alpha },{\phi }_{\beta }\)] with \(\gamma\) under \(\it {\sigma }_{\mathrm{n}}\) of 50–300 kPa calculated using different methods is shown in Fig. 11(d). The \({\phi }_{m}\), \({\phi }_{\alpha },\) and \({\phi }_{\beta }\) were calculated using Eqs. 1, 2 and 3, respectively. Constant values of \({\phi }_{m}\) with varying \(\upgamma\) are shown as these were calculated at particular \(\it {\sigma }_{\mathrm{n}}\) and do not vary with \(\gamma\). The methodology for the calculation of \({\phi }_{m}\) is explained in Sect. 4.1.3. Almost similar values of \({\phi }_{\alpha }\) and \({\phi }_{\beta }\) were obtained under \(\it {\sigma }_{\mathrm{n}}\) of 50 and 100 kPa; however, lower values of \({\phi }_{\beta }\) were obtained at \(\it {\sigma }_{\mathrm{n}}\) of 300 kPa.

Fig. 11
figure 11

Influence of normal stress on monotonic tests (SDSS): a stress–strain b stress ratio c axial strain d mobilised friction angle

Full size image

4.1.3 Cohesion and friction angle

The \({\uptau }_{\mathrm{ult}}\) values at different \(\it {\sigma }_{\mathrm{n}}\) were used to calculate the ultimate friction angle [\({\phi }_{\mathrm{ult}}\)] and cohesion [c] of soil using the Mohr–Coulomb failure envelope. The friction angles are reported as \({\phi }_{\mathrm{ult}}\) as no peak behaviour was obtained for the soil due to its loose-medium state. Figure 12(a) shows a plot of a typical example for calculating \({\phi }_{\mathrm{ult}}\) and mobilised ultimate friction angle [\({\phi }_{\mathrm{m}}\)] of untreated soil mixed with 10% GR. Mohr’s circle was drawn to obtain the major principal stress [\(\it {\sigma }_{\mathrm{1}}\)] and minor principal stress [\(\it {\sigma }_{\mathrm{3}}\)], and the \({\phi }_{\mathrm{m}}\) of the soil was calculated. It is known that c for cohesionless soil (viz. sand) is zero. Hence, the fitting line was shifted to pass through the origin and was then used to calculate \({\phi }_{\mathrm{ult}}\) of the untreated soil. Similarly, Fig. 12(b) shows a typical example for the calculation of c, \({\phi }_{\mathrm{ult}}\), and \({\phi }_{\mathrm{m}}\) of the treated soil (soil mixed with 10% PFA).

Fig. 12
figure 12

a Calculation of ultimate friction angle and mobilised friction angle of sand mixed with 10% GR (untreated soil) b Calculation of cohesion, ultimate friction angle and mobilised friction angle of treated sand (sand mixed with 10% PFA)

Full size image

An asymptotic model (Eq. 5) and logistic model (Eq. 6) were proposed in this study for a nonlinear failure envelope of untreated soil (soil–rubber mixtures) and treated soil (soil–PFA or soil–PFA–rubber mixtures), respectively, as shown in Fig. 12(a) and (b). These equations can predict the \({\tau }_{\mathrm{ult}}\) under different \(\it {\sigma }_{\mathrm{n}}\).

$${\tau }_{\mathrm{ult}}=\mathrm{a}-\mathrm{b}\times {\mathrm{c}}^{\it {\sigma }_{\mathrm{n}}}$$
(5)

where \({\tau }_{\mathrm{ult}}\) is the ultimate shear stress, \(\it {\sigma }_{\mathrm{n}}\) is the normal stress.

The values of constants a, b, and c for untreated soil with 0% GR content were obtained by curve fitting as 235.48, 234.71, and 0.99641, respectively. Similarly, the values of constants a, b, and c for untreated soil with 25% GR content were 198.92, 199.53, and 0.99738, respectively.

$${\tau }_{\mathrm{ult}}=\mathrm{A}2+\frac{\mathrm{A}1-\mathrm{A}2}{\left(1+{\left(\frac{\it {\sigma }_{\mathrm{n}}}{\mathrm{x}0}\right)}^{p}\right)}$$
(6)

where \({\tau }_{\mathrm{ult}}\) is the ultimate shear stress, \(\it {\sigma }_{\mathrm{n}}\) is the normal stress, A1 = 30.4, and p = 3.

The values of constants A2 and x0 (logistic model) for treated soil with 5% PFA content were 180 and 150.4, respectively. Similarly, the values of constants A2 and x0 for treated soil with 20% PFA content were 215 and 115.4, respectively.

The values of constants A2 and x0 (logistic model) for treated soil–rubber mixture with 0% GR content (PFA = 10%) were 185 and 118.12, respectively. Similarly, the values of constants A2 and x0 for treated soil–rubber mixture with 25% GR content (PFA = 10%) were 155 and 108.31, respectively.

The maximum value of mobilised friction angle calculated using Eq. 3 is referred to as mobilised ultimate friction angle [\({\mathrm{\phi }}_{\upbeta ,\mathrm{ult}}\)] and is plotted in Fig. 13 to compare soil mixed with different GR and PFA contents. From Fig. 13(a), we can see that the addition of GR (up to 5%) to soil had less influence on both \({\phi }_{\mathrm{ult}}\) and \({\phi }_{\upbeta ,\mathrm{ult}}\) of the soil. The \({\mathrm{\phi }}_{\mathrm{ult}}\) of soil was 31.2° for up to 5% GR content and reduced to 26.9° on the addition of 10% GR. Above 15% GR content, the \({\phi }_{\mathrm{ult}}\) remained constant at approximately 22°. Similarly, the \({\phi }_{\upbeta ,\mathrm{ult}}\) of soil remained constant after 15% GR content. The \({\mathrm{\phi }}_{\upbeta ,\mathrm{ult}}\) of soil reduced with an increase in \(\it {\sigma }_{\mathrm{n}}\). Hence, it is recommended to use up to 5% GR (shown by the green shaded portion in Fig. 13a) based on the shear strength of soil (\({\phi }_{\mathrm{ult}}\) and \({\phi }_{\upbeta ,\mathrm{ult}}\)). Previous studies also recommend 5% TDA as optimum dosage based on breakage and stiffness [25] and based on peak shear stress, dilation, cohesion strength, and internal friction angle [81].

Fig. 13
figure 13figure 13

a Variation of friction angle with varying GR content for untreated soil; Variation of cohesion and friction angle with b PFA content c GR content for treated soil

Full size image

Figure 13(b) illustrates the variation of c, \({\phi }_{\mathrm{ult}}\) and \({\phi }_{\upbeta ,\mathrm{ult}}\) of soil mixed with varying dosage of PFA. It can be observed that the addition of 5% PFA increased the c of soil by 20 kPa but reduced the \({\phi }_{\mathrm{ult}}\) from 31.2° to 26.6°. This increase in cohesion without affecting friction angle on incorporation of PFA was also reported by Xiao et al. [92]. In this study sand was used wherein slight decrease in the friction angle was observed due to reduced relative mobility between particles and subsequent reduction in the frictional interlock of sand particles caused by the PFA treatment. Above 5% PFA, c and \({\phi }_{\mathrm{ult}}\) increased steadily with a maximum value of 32.3 kPa and 32.4°, respectively, at 15% PFA content. The \({\phi }_{\upbeta ,\mathrm{ult}}\) steadily increased from 27.4° to 34.1° with 0 to 20% PFA content, respectively, at \(\it {\sigma }_{\mathrm{n}}\) of 200 kPa. The reduction in \(\it {\sigma }_{\mathrm{n}}\) increased the \({\phi }_{\upbeta ,\mathrm{ult}}\), but the trend was similar to \(\it {\sigma }_{\mathrm{n}}\) of 200 kPa. Hence, the optimum PFA content can be recommended as 7.5–12.5% (shown as the green shaded area) based on c and friction angle (\({\phi }_{\mathrm{ult}}\) and \({\phi }_{\upbeta ,\mathrm{ult}}\)). Previous studies report optimum PFA dosages as 5–14% [60], 2–8% [93], 5–10% [46], 3–6% [18]. This variation in the optimum dosage of PFA was due to difference in the type of soil and PFA used. In the present study non-foaming type PFA was used that coated surface of soil/rubber sufficiently to bind them together improving integrity of the mix but did not fill the voids. In the present study, the optimum PFA content of 10% was adopted to prepare treated soil samples with varying GR content (0–25%).

Figure 13(c) shows the variation of c and friction angle (\({\phi }_{\mathrm{ult}}\) and \({\phi }_{\upbeta }\)) for soil mixed with varying GR content (0–25%) and mixed with 10% PFA. Both c and friction angle (\({\phi }_{\mathrm{ult}}\) and \({\phi }_{\upbeta ,\mathrm{ult}}\)) increased with the addition of GR up to 5% with maximum c and \({\phi }_{\mathrm{ult}}\) of 41.6 kPa and 34.3°, respectively. The maximum \({\mathrm{\phi }}_{\upbeta ,\mathrm{ult}}\) under \(\it {\sigma }_{\mathrm{n}}\) of 50, 100, and 200 kPa were 50.8°, 48.8° and 36.1°, respectively. The above 5% GR content, c, \({\mathrm{\phi }}_{\mathrm{ult}}\), and \({\phi }_{\upbeta }\) reduced with increasing GR content. The optimum GR content for treated soil–rubber mixtures is recommended in the range of 5–10% (shown as the green shaded area in Fig. 13c).

4.1.4 Dilation angle

The dilation angle \([\psi ]\) was calculated using Eq. 7 and was based on the assumption that the horizontal plane in the shear box is a zero extension line [78].

$$\mathrm{tan}\psi =-\frac{\mathrm{d}{\upvarepsilon }_{\mathrm{a}}}{\mathrm{d}\gamma }$$
(7)

where \({\upvarepsilon }_{\mathrm{a}}\) and \(\gamma\) are vertical compressive strain and shear strain, respectively. The negative sign is required to accommodate the anomalous convention that compressive strains are positive, while \(\psi\) is positive for volumetric increases.

No dilation was observed for soil–rubber mixtures due to the loose-medium state of the mix. Figure 14(a) illustrates the variation of \(\psi\) of soil mixed with varying PFA content. It can be seen that the \(\psi\) rose exponentially from 0° at 0% PFA to 8°, 5°, and 3° under \(\it {\sigma }_{\mathrm{n}}\) of 50, 100, and 300 kPa, respectively, at 10% PFA content; after this, it remained steady. This increase in \(\psi\) on the addition of 10% PFA justifies the gain in strength of soil due to dilation. Similar significant increase in dilatancy due to 8% PFA incorporation was observed by Xiao et al. [93]. In the present study, this strength gain is attributed to PFA cementation and not grain packing due to loose-medium state of the sample (relative density of 40%) which is similar to Xiao et al. [93], who used loose state specimens for triaxial testing (relative density of 25%). Similar recommendation to adopt loose state for cemented specimens was given by Wang and Leung [88]. Figure 14(b) shows the variation of \(\psi\) of soil mixed with 10% PFA and varying GR content. The addition of GR up to 10% reduced the \(\psi\) of treated soil considerably, and after this, it remained constant. The effect of \(\it {\sigma }_{\mathrm{n}}\) on the \(\psi\) of treated soil reduced remarkably after 20% GR content, and the \(\psi\) of treated soil with 25% GR was the same under the entire range of \(\it {\sigma }_{\mathrm{n}}\).

Fig. 14
figure 14

Variation of dilation angle at different normal stress for a soil mixed with different PFA content b treated soil mixed varying GR content

Full size image

4.2 CDSS test results

Mostly, liquefaction studies at constant stress amplitude cyclic DSS test are performed in undrained (or constant height/volume) conditions [5]. However, the present study involved a performance comparison of treated and untreated soil under a large number of load cycles and it was observed that limiting values of shear strain (\(\gamma\) = 15%) were reached within a few load cycles, especially at higher CSR. Hence, drained (or constant normal stress) conditions were chosen in the present study to evaluate the long-term performance of treated and untreated soil–rubber mixtures.

4.2.1 Cyclic stress–strain response

Figure 15 illustrates the cyclic stress ratio (CSR = \(\tau /\it {\sigma }_{\mathrm{n}}\)) versus shear strain [\(\gamma\)] plots for three CDSS tests performed on sand with cyclic shear stress amplitude [\({\tau }_{\mathrm{ cyc}}\)] varying between 50 and 200 kPa under constant \(\it {\sigma }_{\mathrm{n}}\) of 300 kPa. Generally, the size of the hysteresis loop increased with an increase in \({\tau }_{\mathrm{cyc}}\). The shear stress [\(\tau\)] increased with \(\gamma\) up to CSR (= 0.07, 0.15 and 0.27 for \({\tau }_{\mathrm{ cyc}}\) of 50, 100 and 300 kPa, respectively), reversed direction, and then switched direction again at CSR of −0.07, −0.15 and −0.27 for \({\tau }_{\mathrm{cyc}}\) of 50, 100 and 300 kPa, respectively. In addition, \(\gamma\) required to reach a particular CSR reduced with increasing load cycle; for instance, at \({\tau }_{\mathrm{cyc}}\) of 200 kPa, CSR was 0.27 at \(\gamma\) of 2.8% for the first load cycle, while the \(\gamma\) required to achieve the same CSR for the second and third load cycle was 2.2 and 2%, respectively.

Fig. 15
figure 15

Stress–strain response of sand for first 10 load cycles at different cyclic shear stress amplitude

Full size image

4.2.2 Axial elastic and plastic strain for untreated soil

Figure 16(a) represents the loading pattern that was adopted for the CDSS testing. All the CDSS tests were performed under \(\it {\sigma }_{\mathrm{n}}\) of 300 kPa. Soil samples were sheared under cyclic shear stress amplitude [\({\tau }_{\mathrm{cyc}}\)] of 50, 100, and 200 kPa for 50,000 load cycles. Frequency conditioning was used with 0.1 Hz for the first ten load cycles, followed by 1 Hz for the remaining load cycles.

Fig. 16
figure 16

a Application of load cycles in CDSS b Variation of axial strain with load cycles for soil subjected to different cyclic shear stress amplitude

Full size image

Figure 16(b) shows the variation of axial strain [\({\upvarepsilon }_{\mathrm{a}}\)] with time (and number of load cycles [N]) of the untreated soil when sheared at \({\tau }_{\mathrm{cyc}}\) of 50–200 kPa. It can be seen that with an increase in N, the elastic strain amplitude \([{\upvarepsilon }_{\mathrm{e}}]\) and plastic strain/irrecoverable plastic strain \([{\upvarepsilon }_{\mathrm{p}}]\) increased for the entire range of \({\tau }_{\mathrm{cyc}}\). At the end of 50,000 load cycles, the \({\upvarepsilon }_{\mathrm{p}}\) for \({\tau }_{\mathrm{cyc}}\) of 50, 100, and 200 kPa was 1.14, 2.48, and 5.51%, respectively. The same methodology was adopted for the entire CDSS testing plan and the calculation of \({\upvarepsilon }_{\mathrm{e}}\) and \({\upvarepsilon }_{\mathrm{p}}\) reported in this paper.

4.2.3 Axial strain of PFA-treated soil

The variation of \({\upvarepsilon }_{\mathrm{a}}\) with N of soil mixed with varying PFA content and sheared at \({\tau }_{\mathrm{cyc}}\) of 50–200 kPa is represented in Fig. 17(a)–(c). Overall, \({\upvarepsilon }_{\mathrm{a}}\) increased with N for soil mixed with varying PFA content. The initial rate of change of \({\upvarepsilon }_{\mathrm{a}}\) for untreated soil was significantly higher than treated soil. The \({\upvarepsilon }_{\mathrm{a}}\) of PFA-treated soil stabilised within 10,000 load cycles; however, the \({\upvarepsilon }_{\mathrm{a}}\) of untreated soil continued to rise. Across the range of \({\tau }_{\mathrm{cyc}}\), the minimum \({\varepsilon }_{a}\) was shown by soil treated with 10% PFA followed by soil treated with 5% PFA. At PFA content of 5%, the PFA was insufficient to completely coat the surface of soil/rubber particles leading to improper bonding between particles. This improper bonding led to lowered strength and higher \({\upvarepsilon }_{\mathrm{a}}\). Further addition of PFA above 10%, led to increased \({\upvarepsilon }_{\mathrm{a}}\). At lower \({\tau }_{\mathrm{cyc}}\) of 50–100 kPa, the progression of \({\upvarepsilon }_{\mathrm{a}}\) with N of soil treated with PFA content of 15 and 20% was almost similar. However, at higher \({\tau }_{\mathrm{cyc}}\) of 200 kPa, there was significant variation between \({\upvarepsilon }_{\mathrm{a}}\) of 15 and 20% PFA mix. The \({\upvarepsilon }_{\mathrm{p}}\) of soil mixed with different PFA content at the end of 50, 000 load cycles is shown in Fig. 18(a). It is seen that with the addition of 5% PFA, \({\upvarepsilon }_{\mathrm{p}}\) reduced from 1.14, 2.48, and 5.51% to 0.51, 1.00, and 1.92% at \({\tau }_{\mathrm{cyc}}\) of 50, 100, and 200 kPa, respectively. Chen et al. [18] recorded similar reduction in axial strain of PFA solidified calcareous sand when subjected to cyclic loading. In this study, the \({\upvarepsilon }_{\mathrm{p}}\) further reduced with an increase in PFA dosage of up to 10% and after this, \({\upvarepsilon }_{\mathrm{p}}\) either increased marginally or remained constant. The reason behind the increase in \({\upvarepsilon }_{\mathrm{p}}\) for PFA dosage above 10% was due to the cracking of PFA filling in the voids of the soil specimen when subjected to a large number of load cycles. However, the optimum PFA content provided a coating on soil particles which was sufficient to bind these soil particles together without filling the voids in the soil. The per cent reduction in \({\upvarepsilon }_{\mathrm{p}}\) of soil mixed with different PFA content at the end of cyclic loading (i.e., 50,000 load cycles) is shown in Fig. 18(b). It is observed that the maximum reduction in \({\upvarepsilon }_{\mathrm{p}}\) was 65.8, 63.4 and 68.3% at \({\tau }_{\mathrm{cyc}}\) of 50, 100, and 200 kPa, respectively, on the addition of 10% PFA to soil. Based on this analysis, the recommended optimum PFA content is 7.5–12.5%.

Fig. 17
figure 17

Variation of axial strain with load cycles of soil mixed with varying PFA, subjected to cyclic shear stress amplitude a \({\tau }_{\mathrm{cyc}}\)= 50 kPa b \({\tau }_{\mathrm{cyc}}\)= 100 kPa c \({\tau }_{\mathrm{cyc}}\)= 200 kPa

Full size image
Fig. 18
figure 18

a Total plastic strain at the end of 50,000 load cycles of soil mixed with varying PFA content sheared at different values of cyclic shear stress amplitude b Per cent reduction in plastic strain for different treated mixes at the end of 50,000 load cycles

Full size image

4.2.4 Axial strain of PFA-treated soil mixed with varying GR

Figure 19 illustrates the variation of \({\upvarepsilon }_{\mathrm{p}}\) with GR content for untreated and treated soil sheared under \({\tau }_{\mathrm{cyc}}\) of 50–200 kPa. The \({\upvarepsilon }_{\mathrm{p}}\) values are reported at the end of 50,000 load cycles. The \({\upvarepsilon }_{\mathrm{p}}\) of treated soil–GR mixtures was consistently lower compared to untreated soil–GR mixtures. It is seen that at \({\tau }_{\mathrm{cyc}}\) of 50, 100 and 200 kPa, \({\upvarepsilon }_{\mathrm{p}}\) kept on reducing for untreated soil with increasing GR content of up to 5% and then increased. The \({\upvarepsilon }_{\mathrm{p}}\) of treated soil at low \({\tau }_{\mathrm{cyc}}\) of 50 kPa increased continuously with an increase in GR, but low values of \({\upvarepsilon }_{\mathrm{p}}\) were recorded. However, at \({\tau }_{\mathrm{cyc}}\) of 100 and 200 kPa, \({\upvarepsilon }_{\mathrm{p}}\) of treated soil remained nearly constant till GR content of 15% and then started to rise. The maximum percentage reduction in \({\upvarepsilon }_{\mathrm{p}}\) after soil treatment was obtained at 0% GR content as 65.8, 63.4 and 68.3% at \({\tau }_{\mathrm{cyc}}\) of 50, 100, and 200 kPa, respectively. Conversely, the minimum percentage reduction in \({\upvarepsilon }_{\mathrm{p}}\) after soil treatment was obtained at 25% GR content as 17.8, 46.7 and 24.7% at \({\tau }_{\mathrm{cyc}}\) of 50, 100, and 200 kPa, respectively. Hence, it is concluded that the suitable GR content based on \({\upvarepsilon }_{\mathrm{p}}\) at the end of cyclic loading for untreated and treated soil is up to 5 and 15%, respectively.

Fig. 19
figure 19

Variation of \({\upvarepsilon }_{\mathrm{p}}\) at the end of 50,000 load cycles with GR content for treated and untreated soil sheared at cyclic shear stress amplitude a \({\tau }_{\mathrm{cyc}}\) = 50 kPa b \({\tau }_{\mathrm{cyc}}\) = 100 kPa c \({\tau }_{\mathrm{cyc}}\) = 200 kPa

Full size image

4.2.5 Shear modulus and damping ratio

The shear modulus [G] and damping ratio [DR] for each cycle were determined using Eqs. 8 and 9 [36], respectively, based on the hysteresis loop shown in Fig. 20. The G for each cycle was calculated by the ratio of the peak-to-peak shear stress and the peak-to-peak shear strain. The DR was calculated for each loading cycle using the hysteresis loop area and the area of the right triangle that forms under the maximum shear stress and maximum shear strain [56].

$$G= \frac{{\tau }_{\mathrm{cyc}}}{{\gamma }_{\mathrm{cyc}}}$$
(8)

where \({\tau }_{\mathrm{cyc}}\) is the cyclic shear stress amplitude (peak-to-peak shear stress for the cycle) and \({\gamma }_{\mathrm{cyc}}\) is the cyclic shear strain amplitude (peak-to-peak shear strain for the cycle).

$$\it{\text{D}_\mathrm{R}} = { }\frac{{\mathop \sum \nolimits_{{{\text{i}} = \mathrm{2}}}^{N} \mathrm{0.5} \times \left( {\tau_{{\text{i}}} + \tau_{{{\text{i}} - 1}} } \right) \times \left( {\gamma_{{\text{i}}} + \gamma_{{{\text{i}} - 1}} } \right)}}{{\mathrm{4} \times {\uppi } \times \mathrm{0.5} \times \tau_{{{\text{max}}}} \times \gamma_{{{\text{max}}}} }}$$
(9)

where N is the number of points per cycle.

Fig. 20
figure 20

Hysteresis loop for calculation of damping ratio and shear modulus

Full size image

Figure 21(a), (b) and (c) shows a three-dimensional representation of the variation of G with \({\tau }_{\mathrm{cyc}}\) and PFA content, \({\tau }_{\mathrm{cyc}}\) and GR content for untreated soil, and \({\tau }_{\mathrm{cyc}}\) and GR content for treated soil, respectively. Generally, G increased with an increase in \({\tau }_{\mathrm{cyc}}\). It is observed from Fig. 21(a) that G increased on the addition of PFA up to 5–10% and then started to reduce with the addition of further PFA. Similarly, increased soil modulus on addition of PFA was reported by Chen et al. [18]. In the present study the modulus reduction was observed when PFA content exceeded 10%. This reduction in modulus was triggered by the disintegration of excessive PFA filling the voids. The maximum G at \({\tau }_{\mathrm{cyc}}\) of 50, 100, and 200 kPa was 7418, 7340 and 7800 kPa, respectively. It can be seen from Fig. 21(b) that for untreated soil, G showed a fluctuating trend at \({\tau }_{\mathrm{cyc}}\) of 50 kPa. G increased from 5544 kPa at 0% GR to 8547 kPa at 15% GR and then started to reduce again and reached a value of 5267 kPa at 25% GR. At \({\tau }_{\mathrm{cyc}}\) of 100 and 200 kPa, G continuously reduced with an increase in GR content. The maximum G (soil + 0% GR) at \({\tau }_{\mathrm{cyc}}\) of 100 and 200 kPa was 6588 and 7242 kPa, respectively and the minimum G (soil + 25% GR) at \({\tau }_{\mathrm{cyc}}\) of 100 and 200 kPa was 4679 and 4980 kPa, respectively. From Fig. 21(c), it is seen that treated soil–rubber mixtures showed a similar trend for G at different \({\tau }_{\mathrm{cyc}}\) as untreated soil–rubber mixtures, although lower G values are recorded compared to untreated mixtures. The maximum G of soil at \({\tau }_{\mathrm{cyc}}\) of 50, 100, and 200 kPa was 7500 (with 15% GR), 6318 (with 2.5% GR) and 6300 kPa (with 0% GR), respectively.

Fig. 21
figure 21

Variation of shear modulus with cyclic shear stress amplitude and a PFA content b GR content for untreated c GR content for treated soil

Full size image

Hence, based on G, it was very difficult to fix an optimum dosage of PFA and GR due to the large variability of G at different \({\tau }_{\mathrm{cyc}}\). However, we can consider 5–10% PFA dosage as optimum that covers maximum G over wide range of \({\tau }_{\mathrm{cyc}}\). Similarly, GR content of 10% for untreated and treated soil can be regarded as optimum, covering maximum G over the entire range of \({\tau }_{\mathrm{cyc}}\).

Figure 22 shows a three-dimensional contour plot of the variation of DR with \({\tau }_{\mathrm{cyc}}\) and PFA content, \({\tau }_{\mathrm{cyc}}\) and GR content for untreated soil, and \({\tau }_{\mathrm{cyc}}\) and GR content for treated soil, respectively. Generally, the DR reduced with an increase in \({\tau }_{\mathrm{cyc}}\). It is observed from Fig. 22(a) that the DR reduced with an increase in PFA content for the entire range of \({\tau }_{\mathrm{cyc}}\). This was due to the increased stiffness of the soil. The maximum DR (soil + 0% PFA) at \({\tau }_{\mathrm{cyc}}\) of 50, 100 and 200 kPa was 23.7, 19.4, and 18.9%, respectively, and the minimum DR (soil + 20% PFA) at \({\tau }_{\mathrm{cyc}}\) of 50, 100 and 200 kPa was 19.4, 18.9, and 18.0%, respectively. Previous study by Chen et al. [18] also observed reduction in DR on PFA treatment of sand. Up to 32.8% reduction in DR was observed for PFA-treated calcareous sand (PFA = 6%) compared to virgin calcareous sand. Figure 22(b) represents the variation of DR at different \({\tau }_{\mathrm{cyc}}\) and GR content. It is seen that DR decreased with an increase in \({\tau }_{\mathrm{cyc}}\) and DR increased with increasing GR content. The maximum DR (soil + 25% GR) at \({\tau }_{\mathrm{cyc}}\) of 50, 100, and 200 kPa was 26, 23, and 21%, respectively. Similarly, from Fig. 22(c), a similar trend in terms of DR was observed for treated soil–rubber mixtures but with lower DR values compared to untreated mixtures. The maximum DR at \({\tau }_{\mathrm{cyc}}\) of 50, 100, and 200 kPa was 22% (soil + 20% GR), 21.2% (soil + 20% GR), and 20.7% (soil + 25% GR), respectively.

Fig. 22
figure 22

Variation of damping ratio with cyclic shear stress amplitude and a PFA content b GR content c GR content for PFA bound soil

Full size image

To conclude, although the DR continuously reduced with increasing PFA content, the optimum PFA dosage can be considered in the range of 5–10%. Similarly, the optimum GR content for treated soil can be considered in the range of 10–20%. At these PFA and GR contents, maximum advantages are obtained in terms of improved damping with least influence on other properties, viz. c, \(\mathrm{\phi }\), and G.

Figure 23 compares the maximum and minimum DR of soil and TDA reported by various studies. The DR for all the strain-controlled tests performed by various authors [19, 64, 66, 73, 76] was evaluated at shear strains of 0.1% as their studies focussed on earthquake engineering, and the dominant shear strains generated within soil due to seismic waves are relatively small. The present study was stress-controlled to replicate traffic loading, and the minimum and maximum DR correspond to maximum and minimum \({\tau }_{\mathrm{cyc}}\), respectively. It is shown that the highest DR is shown by soil + 10% GR mix followed by soil + 10% GR + 10% PFA mix. The addition of 10% PFA has a very insignificant influence on the DR of untreated soil.

Fig. 23
figure 23

Comparison of damping ratio of present study with previous studies

Full size image

5 Conclusions

An experimental study is presented to assess the performance of untreated soil (soil + GR mixture) and treated soil (soil + PFA and soil + GR + PFA) using SDSS and CDSS testing. SDSS (monotonic) tests were performed to evaluate the monotonic performance of all mixtures in terms of cohesion, ultimate friction angle, mobilised friction angle, and dilation angle. CDSS (cyclic) tests were performed to assess the long-term performance of these different mixes under repeated cyclic loading (50,000 load cycles) and varying cyclic shear stress amplitude [\({\tau }_{\mathrm{cyc}}]\). The following conclusions are drawn from the present study:

  • Empirical models were proposed in this study that can predict the ultimate shear strength of untreated and treated soil–rubber mixtures. These models, viz. asymptotic model (Eq. 5) and logistic model (Eq. 6), can predict the nonlinear failure envelopes of untreated soil and treated soil–rubber mixtures, respectively.

  • The strength of untreated soil was least impacted by addition of low amount of GR (up to 5%). A significant drop in strength was observed after that. On the contrary, the strength of the soil improved with PFA treatment. This strength gain was reflected through mobilisation of cohesion and increase in the friction angle (ultimate and mobilised) of the soil. The strength improvement was significant for PFA content of 7.5–12.5% and after that further PFA addition led to marginal strength improvement. The addition of GR up to 5% led to further improvement in the strength of treated soil. Above 10% GR content, the strength of treated soil started to reduce. The increase in normal stress reduced the mobilised friction angle of the soil.

  • Dilative behaviour was not observed for soil–rubber mixtures due to the loose-medium state of the soil. The PFA treatment of soil and soil–rubber mixture triggered dilative behaviour. Maximum dilation was observed at 10% PFA content, and after that further PFA addition showed insignificant changes in the dilative behaviour of the soil. The maximum dilation angle [\(\psi\)] of 8.7° under normal stress of 50 kPa was recorded. This maximum \(\psi\) was responsible for the highest shear strength of soil with 10% PFA content. But the incorporation of 10% GR to treated soil reduced the \(\psi\) to less than 3°.

  • The effect of normal stress [\(\it {\sigma }_{\mathrm{n}}\)] on strength of untreated and treated soil–rubber mixture was also studied. Overall, it was observed that increase in \(\it {\sigma }_{\mathrm{n}}\) reduced the cohesion, friction angles (ultimate and mobilised), and dilation in the soil. This reduction was more significant for untreated soil compared to treated soil.

  • Under cyclic loading, the performance of the untreated and treated soil with varying GR content was assessed based on the axial strain \([{\upvarepsilon }_{\mathrm{a}}]\), shear modulus [G] and damping ratio [DR] over range of \({\tau }_{\mathrm{cyc}}\). Generally, it was observed that with an increase in \({\tau }_{\mathrm{cyc}}\) (increase in CSR), the \({\upvarepsilon }_{\mathrm{a}}\) increased and the DR decreased. G showed non-uniform trend but mostly increased with increasing \({\tau }_{\mathrm{cyc}}\). The permanent axial strain (or plastic strain at the end of 50,000 load cycles) \([{\upvarepsilon }_{\mathrm{p}}]\) was calculated which relates to the irrecoverable settlement of the track.

    The addition of PFA up to a certain dosage (7.5–12.5%) reduced the \({\upvarepsilon }_{\mathrm{p}}\) of soil substantially across the range of \({\tau }_{\mathrm{cyc}}\). The addition of GR up to 5% showed a reduction in the \({\upvarepsilon }_{\mathrm{p}}\) of the untreated soil across the range of \({\tau }_{\mathrm{cyc}}\). For instance, at highest \({\tau }_{\mathrm{cyc}}\) = 200 kPa, the \({\upvarepsilon }_{\mathrm{p}}\) of untreated soil mixed with 5% GR content was 36.5% lower than the untreated soil (with 0% GR), signifying the importance of GR in reducing settlement at higher CSR. Although the same reduction in \({\upvarepsilon }_{\mathrm{p}}\) with GR incorporation was not observed for treated soil, the \({\upvarepsilon }_{\mathrm{p}}\) for treated soil with varying GR was significantly lower than untreated soil.

    For treated soil, at lower \({\tau }_{\mathrm{cyc}}\), \({\upvarepsilon }_{\mathrm{p}}\) rose with an increase in GR content of up to 20% but \({\upvarepsilon }_{\mathrm{p}}\) values were low at less than 1%. However, at \({\tau }_{\mathrm{cyc}}\) of 100 and 200 kPa, \({\upvarepsilon }_{\mathrm{p}}\) remained constant with the addition of up to 15% GR and then started to rise exponentially with further GR incorporation. Hence, it was concluded that the suitable GR content for untreated and treated soil is up to 5 and 15%, respectively.

  • Based on G, it was difficult to fix an optimum dosage of PFA and GR as G showed large variability at different \({\tau }_{\mathrm{cyc}}\). However, we can consider a PFA dosage of 5–10% and GR dosage of 10% for untreated and treated soil as optimum, which covers maximum G over the range of \({\tau }_{\mathrm{cyc}}\) considered in the present study.

    The addition of GR increased the DR and PFA treatment reduced the DR of the soil. This study recommends optimum PFA dosage of 5–10% and optimum GR content of 10–20% for treated soil to obtain desirable DR with least impact on other properties.

To conclude, based on output of detailed monotonic and cyclic testing, the PFA optimum dosage is recommended as 10% for soil. Furthermore, the optimum GR content for untreated and treated soil is recommended as 5 and 10%, respectively.

6 Limitations, future scope, and environmental implications

The scanning electron microscope (SEM) analysis was not performed in the present study. SEM could provide an additional insight in the microscopic analysis of PFA-treated soil–rubber mixtures and is recommended to be performed in the future studies. This study also recommends to evaluate the performance of untreated and treated soil–rubber mixtures at higher loading frequency and under confining pressure relevant to railway track.

The recycling of scrap tyre into tyre-derived aggregates (TDA) is frequently viewed as a sustainable solution due to the advantages of conservation of landfill space, creation of beneficial products, prevention of the spread of diseases as well as prevention of fires and pollution [31]. However, certain environmental and health implications must be addressed. These environmental effects can be assessed through vital environmental testing including leachate studies on toxic organic compounds. This would ensure that recycling of waste tyre has minimum environmental impact [65]. Humphrey and Swett [48] found that the amount of metal leaching was insignificant according to primary drinking water standards. In the present work, metal-free TDA was used implying its adequacy as a construction material in view of reduced leaching. The research aims to use TDA as a base layer of a railway track under dry (non-submerged) condition. In addition, the inclusion of PFA to the soil–rubber mixture would aid in preventing the rubber degradation. The hydrophobic nature of PFA would transform the entire mix (soil + GR + PFA) into hydrophobic, which would have the least impact on the contamination of ground water.