Optimal tip shape for minimum drag and lift during horizontal penetration in granular media

Abstract

Horizontal penetration in granular media is ubiquitous, from tunneling and geotechnical site investigation, to root growth and the locomotion of burrowing animals in nature. This contribution couples the discrete element method (DEM) with ant colony optimisation, a heuristic optimisation algorithm, to find the optimal tip shapes to minimise drag and lift forces during horizontal penetration. The tip which minimizes drag has a slender profile with a low tip curvature, to give a drag force that is $15.6\%$ lower compared to a conventional CPT intruder, however this shape induces a downwards force that increases with intruder depth. Conversely, the tip that minimizes lift is blunt, with a high tip curvature and short width, and reduces the drag and lift forces by $4.5\%$ and $30.8\%$ (respectively) compared to the CPT. The lift and drag forces are competing optimisation objectives, thus the tip shape with the optimal trade-off between drag and lift forces can be established using Pareto optimality. The Pareto optimal tip shape reduces the drag and lift forces by $10.7\%$ and $19.4\%$ respectively, and is strikingly similar to the profile of a sandfish. This contribution shows that when a common goal exists, bio-inspired solutions can offer an optimal solution to engineering applications. We also show the potential to integrate DEM simulations within an optimization framework to develop innovative design solutions.

1 Introduction

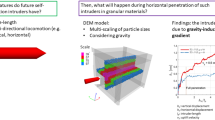
This study is motivated by the ever-growing need to explore, characterise and exploit the underground space. Recent developments in robotics, steering and data processing have enabled the development of autonomous devices for subterranean exploration. Still, our understanding of the physical mechanisms that underlie the horizontal penetration in granular media is limited. The prevalent methods of underground exploration (e.g. the CPT, and the pressuremeter test (PMT)) are limited to vertical penetration. Similarly, trenchless methods of underground construction, such as horizontal directional drilling (HDD) are adaptions of the methods developed for vertical drilling by the oil and gas industry.

In contrast, penetration and burrowing in granular media in nature are seldom limited to the vertical direction. A botanical example is root growth, where the changes in hydraulic availability, soil properties, and obstacles influence the direction of growth [14, 24]. In zoology, penetration is relevant to the the physiognomy and evolutionary traits of burrowing animals (e.g. earthworms, razor clams, moles and lizards), as the capacity to burrow and steer is related to key functions such as habitat exploration, escaping from predators and hunting for prey [2].

The concept of bio-inspired geotechnical engineering is now established [23] and it is clear there is scope to develop bio-inspired designs for penetrating devices [34]. To develop biologically inspired solutions one can mimic or copy the morphology of a well characterised animal. For example, [36] created a robotic probe inspired by the razor clams, that significantly reduced the energy costs associated with vertical digging. Similarly, [33] found a that cutter-blades with a shape inspired by the scale ribs found in sharks skin can reduce drag during sub-soiling. A contrasting, but well established approach in engineering is using mechanics and computational algorithms to optimize geometry. For example in aerodynamics, [15] found the maneuverability and accuracy of missiles depends on tip shape, and [39, 40] optimised the shape of the front nose of a high-speed train to reduce drag.

Here we adopt a hybrid approach. We use discrete element method (DEM), coupled with an optimisation algorithm to find the optimal tip shapes that minimise lift and drag forces during horizontal penetration. The discrete element method (DEM) enables simulation of penetration in granular materials, avoiding the challenges associated with large deformation continuum analyses. We show that the optimal morphology (obtained from the optimisation framework) matches the head shape of the sandfish (Snicus snicus), a lizard with an outstanding burrowing capacity. This study demonstrates that the optimal solution can indeed be a bio-inspired design. It also showcases the potential to use DEM coupled with optimisation algorithms to develop new design solutions in the geotechnical and particle science fields.

The optimisation described here sought to minimize both the lift force and the drag force because two of the challenges to overcome in developing horizontal penetration devices are exploration range and steerability. The exploration range is related to soil-type, depth and maximum distance that a intruder can explore for a finite energy source (e.g. a particular battery). The work (energy) needed for penetration in granular media is controlled by the resistive drag forces that develop around the intruder and oppose its movement. Steerability is the capacity of a intruder to keep, and change a given direction of movement. Previous studies show that symmetric intruders moving horizontally in granular media are diverted from their course by an upward force [12, 20, 30, 31]. This force, often termed the granular lift force, ‘pushes’ the intruder towards the free surface [8], and has been compared to the buoyancy force exerted on submerged bodies. However, the fundamental mechanisms behind granular lift and buoyancy are different, and granular lift is not completely understood [25].

Previous studies of intruders moving horizontally in granular media, established that the drag and lift forces acting on a cylindrical intruder increase with the intruder’s cross-sectional area [12]. The drag forces increase linearly with depth, while the lift force increases with depth up to a critical depth of $\sim 10$ times the device diameter, after which it remains constant [12, 30]. [41] compared 3D DEM simulations of horizontal penetration with and without gravity and showed that most, but not all, of the granular lift is force is induced by gravity. In the quasi-static range, the drag and lift forces are independent of intruder velocity, but beyond the quasi-static range, they increase non-linearly with penetration velocity [30, 31].

Previous sensitivity analysis using different tip shapes with similar cross-section have shown that while the tip shape does not significantly change the drag forces acting on the intruder, it has a significant effect on the lift forces [35]. Moreover, [20] developed a penetrating robot with different tip inclination angles, and found that by changing the shape of the intruder head, the granular lift force changes in direction, from positive (towards the free surface) to negative (in the direction of gravity). More recently, [25] developed a device that combines tip extension and airflow through the tip—to reduce penetration drag and vary the tip angle to control granular lift. These results show the complexity of the mechanical mechanisms behind penetration in granular media, and highlight the importance of tip shape for the drag and lift forces that control the penetration range and steerability of burrowing robots/intruders.

In the following we use discrete element method (DEM), coupled with an optimisation algorithm to find the optimal tip shapes to minimise drag and lift forces during horizontal penetration. In Sect. 2, we describe the DEM models used. Then, we study the drag/lift forces acting on a symmetric intruder of similar dimensions to the well established CPT profile, used as a baseline of comparison as described in Sect. 3. We outline the optimisation algorithm (Sect. 4) used to find the tip shapes that minimise the penetration forces. Then in Sect. 5 we analyse performance of the tip shape that minimises drag (MD), and in Sect. 6 we do the same with the shape that minimises lift forces (ML). Next, in Sect. 7 we use the principle of Pareto optimality to find the tip shape that yields the optimal trade-off between drag and lift forces. Lastly, in Sect. 8 we contrast the results of the different tip shapes, and compare them to the head shape of the sandfish (Snicus snicus), and in Sect. 9 we present the conclusions of the study.

2 DEM model

Two-dimensional discrete element method (DEM) simulations are carried out using the molecular dynamics software LAMMPS [29]. A simplified Hertz–Mindlin (SHM) contact model was used [13]; particles were assigned a shear modulus G = 29 GPa, a Poisson’s ratio $\nu = 0.12$, and a mass density of 2670 kg ${\text {m}^{-3}}$; consistent with the properties of quartz [32]. The critical time step of the DEM simulations was calculated from Eq. 1 according to [27].

$$\begin{aligned} \Delta t_{crit} = min \left( 2\sqrt{\frac{m_{min}}{8k_N +16k_T}}, 2\sqrt{\frac{m_{min}}{40k_T}}\right) \end{aligned}$$

(1)

where $m_{min}$ is the minimum particle mass (from the minimum particle diameter $d_{min}$ = 2 mm), and the normal ($k_N$) and tangential ($k_T$) contact stiffness values were calculated for the SHM model used here as: $k_N = \frac{G\sqrt{d_{min}\cdot \delta }}{1-\nu }$, and $k_T = k_N \frac{2(1-\nu )}{2-\nu }$, assuming a maximum overlap $\delta = 5\% \cdot d_{min}$. From the critical time step obtained $\Delta t_{crit} = {1.76\times {10^{-7}}}$s, a conservative time step $\Delta t = {1\times {10^{-7}}}$s was selected for all simulations.

Initially, the intruder follows the dimensions of a conventional cone penetrometer (CPT), with a diameter (height in 2D space) $D_p$ = 36 mm, and a triangular tip with an apex angle of $60^{\circ }$. The shape of the particle size distribution (PSD) is based on that of Toyoura sand, a fine, rounded and uniform sand with a coefficient of curvature $C_c = 0.96$, a coefficient of uniformity $C_u = 1.39$ and an original median grain size ($d_{50})$ of 0.22 mm [38]. In order to reduce computational cost and enable the 627 simulations required in the optimization study, the PSD was scaled by a factor of 17 to give a new $d_{50}$ = 3.7 mm and a total of 99,272 particles in the large model or 32,738 particles in the reduced model. The scaling factor used (17) was selected to achieve a ratio $D_p/d_{50}=10$, large enough to avoid particle size effects according to [16].

A large model was used to test the influence of intruder depth, while a reduced model was used for the tip shape optimisation. The large model has a width $W_m$ (dimension along the x-axis) of 1.44 mm, equivalent to a normalised width $W_n = W_m/D_p = 40$, and an overall height $H_m$ (dimension along the y-axis) of 0.97 m ($H_n = H_m/D_p = 27$). The reported height of the large model is measured after gravity settlement, reduced form an initial $H_n = 30$. Similarly, the dimensions of the reduced model, used for tip optimisation, are $W_n = 24$ and $H_n = 14$ (reduced form an initial value of 16 before particle settlement). The dimensions, number of particles, and maximum penetration distance ($X_p$) in the models are summarised in Table 1. The dimensions of the domain were chosen according to previous DEM studies on CPT penetration [16, 18, 37] to avoid border effects. Figure 1 shows a snapshot of the large and reduced domains.

Table 1 Dimensions and number of particles in the large and reduced DEM models

Fig. 1

Representative snapshot of DEM simulations. a Large model with a CPT-shaped intruder at a depth $H_p = 20 \times D_p$ and a penetration distance $X_p = 15 \times D_p$. b Reduced model with a intruder at a fixed depth $H_p = 5 \times D_p$ at a penetration distance $X_p= 10 \times D_p$

Samples were prepared by randomly placing particles in the domain, followed by a geostatic step during which particles settled under gravity (g = 9.81m ${\text {s}^{-2}}$) until equilibrium was reached. After gravity settlement the void ratio was $e=0.32$.

The intruder tips are parameterised using super-ellipse equations (as described on Sect. 4). Then, using the equation, equidistant points along the profile of the tip were computed, and their coordinates imported into the DEM software as the centers of the set of circular particles (referred as intruder particles herein) that form the given intruder shape. Intruder particles have a diameter $D_I$ = 2 mm, about $\sim 0.75 \cdot d_{min}$, where $d_{min}$ = 2.64 mm is the minimum particle diameter in the domain. The center-to-center spacing between neighboring intruder particles ($X_I$) controls the texture of the intruder. Figure 2 shows the drag and lift forces acting on the tip of four CPT-shaped intruders at a intruder depth $5 \cdot D_p$ with particle spacings $X_I: {0.34, 0.75, 1.0, 1.5} \times D_I$. Given the relatively small diameter of the intruder particles, spacings $X_I < D_I$ did not induce significant changes in the penetration forces. An intruder particle spacing $X_I = 0.75 \cdot D_I$ = 1.5 mm was selected for all the simulations.

During penetration, intruder particles were moved at a constant velocity $V_p$ = 25 mm$\text { s}^1$ in the right (positive x-axis) direction with no bonds or interactions between them, so that collectively they behave as a rigid body. The intruder was initially placed outside the domain, adjacent to the left wall.

Fig. 2

Effect of intruder particle spacing $X_I$ on the penetration forces for an intruder with a CPT-shaped tip. a Drag force on the tip ($D_{tip}$). b Lift force on the tip $L_{tip}$. Lines and shaded regions correspond to the moving average (with a window $D_p/2$) and the IQR of the drag forces respectively. Simulations performed using the reduced model

Each tip shape in the large model was tested at four different intruder depths $H_p: {5,10,15,20} \times D_p$, for normalised depths $H_n = H_p/D_p = {5, 10, 15, 20}$, each with a maximum penetration distance $X_p = 15 \times D_p$ (0.54 m). Reduced models, used for the large number of simulations created during tip shape optimisation, were at a fixed intruder depth $H_p = 5 \times D_p$, and a maximum penetration distance $X_p = 10 \times D_p$ (0.36 m). Figure 1 shows snapshots of: a) the large model with a CPT-shaped intruder at a depth of $20 \times D_p$ at a penetration distance $X_p = 15 \times D_p$, and b) the reduced model with a intruder depth $H_p = 5 \times D_p$ at a penetration distance $X_p = 10 \times D_p$.

The forces acting on the tip and on the complete intruder (tip + body) were recorded and exported every $5\times {10^{-4}}$ s, to give 80 sampling points per millimeter of intruder displacement. Particle and contact data were exported every 0.05 s, to give a snapshot of the system every 1.25 mm of penetration. In simulations using the large model, data were exported over the entire interval of penetration ($X_p = [0, 15] \times D_p$), while in the reduced model, data were only exported during the interval $X_p = [5, 10] \times D_p$, equivalent to the last $5 \times D_p$ (0.18 m) of penetration.

The Froude number Fr, used to define the regime of penetration (quasi-static or dynamic), is calculated as $Fr = V_p/ \sqrt{g \cdot H_p}$, where g and $H_p$ are the acceleration of gravity and the depth of the intruder (respectively)—according to [31]. The regime of penetration is quasi-static ($Fr \ll 1$), with Fr between 0.0188 and 0.0094 (for $H_n=5$ and $H_n=20$ respectively). Thus, the forces acting on the intruder tip are expected to be constant over the penetration interval, and independent of the penetration velocity $V_p$.

3 CPT-shaped intruder

The baseline analyses considered a conventional, conical (symmetric), CPT-shaped intruder tested at four depths: $H_p: {5,10,15,20} \times D_p$. The generated data indicate that the penetration had two stages: an initial stage when $0\le X_p\le 2 D_p$ during which the intruder tip is entering the domain and the influence of the left boundary is evident. When $2 D_p < X_p \le 15 D_p$ a steady-state stage of penetration is observed, representative of the penetration in a semi-infinite domain bounded only by the free surface. Preliminary simulations using the large model ($W_m = 40 D_p$) showed that for $X_p > 20\times D_p$, the region of influence around the intruder is affected by the sample boundaries (right wall).

3.1 Drag force

The penetration drag force is defined as the force acting in the direction opposite to the intruder movement. In the following, we adopt the convention of positive drag forces, calculated as the net force acting on the tip and body of the intruder in the negative x-direction. The drag force is equivalent to the rate of work (energy) during penetration, and it is a key metric for intruders that rely on an internal source of power.

The drag forces acting on the tip of the intruder, namely $D_{tip}$, and acting on the entire intruder (tip and body), namely $D_{int}$, are shown in Fig. 3a, b. Figure 3c shows the depth-normalised tip drag $DN_{tip} = D_{tip}/(H_n \cdot \gamma )$), while Fig. 3d shows the depth-normalised intruder drag ($DN_{int} =D_{int}/(H_n \cdot \gamma )$), where $\gamma$ = 2000kN ${m^{-3}}$ is the unit weight of the granular media. Solid lines in Fig. 3 correspond to the moving average (with a window $D_p/2$) of the force, and shaded regions correspond to the inter-quartile range (IQR) of the drag forces. The inter-quartile range (IQR), defined as the range between the 25^th and 75^th percentiles of the data, is used to quantify the amplitude of the fluctuations of the forces. These results are in agreement with (vertical) CPT tests [7, 19], with drag forces increasing linearly with intruder depth (Fig. 3a, b). Moreover, the tip drag remains relatively constant during penetration (after the initial penetration stage) (Fig. 3a), while the intruder depth increases linearly with the portion of the intruder body in contact with the media (Fig. 3b).

Fig. 3

Drag forces for an intruder with a conventional CPT-shaped tip. Lines and shaded regions correspond to the moving average (with a window $D_p/2$) and the IQR of the drag forces respectively. a Drag force on the tip ($D_{tip}$). b Drag force on the intruder ($D_{int}$). c Depth-normalised tip drag force ($DN_{tip}$). d Depth-normalised intruder drag force ($DN_{int}$). Quantities shown for the different intruder depths tested

The depth-normalised intruder drag force data ($DN_{int}$ in Fig. 3d) suggest that the total drag force $D_{int}$ can be described by a linear equation of the form:

$$\begin{aligned} D_{int}(X_p') = H_p \cdot (DN_{tip} + m_{int}(X_p')) \end{aligned}$$

(2)

where $X_p' = X_p - 2 \times D_p$, is the penetration length after the initial penetration stage, $DN_{tip} = 0.479$ is the average depth-normalized tip drag among the different tested depths, and $m_{int} = 0.0314$ is the slope of the best fit of the data in Fig. 3d.

The seemingly large range of fluctuation of the forces is a phenomenon attributed to particle size effects, [6] modeled CPT tests with scaled PSD (similar to this study) and found that the magnitude of the fluctuations of the soil response during penetration is related to the reduced in the number of particles in contact with the CPT surface. Moreover, for all the tip shapes tested, the amplitude of these fluctuations increases with intruder depth. This phenomenon may be attributed to force chain collapse/formation. With increasing depth, the magnitude of the contact forces along the force chains around the intruder increases, resulting in a larger amplitude of the fluctuations of the forces exerted on the intruder during penetration.

3.2 Granular lift force

The granular lift force is defined as the vertical (y) component of the net or resultant force acting on the tip ($L_{tip}$) and the entire intruder $L_{int}$ during penetration. Previous studies [1, 12, 25] have found that for symmetrical intruders, such as the CPT-shape tested in this section, the lift force tends to be positive, i.e., in the opposite direction of gravity and towards the free surface.

The lift forces during penetration are summarised in Fig. 4. The lines and shaded regions in Fig. 4a, c correspond to the moving mean and IQR of $L_{tip}$ and $L_{int}$ respectively. The box plots in Fig. 4b, d show the distributions of the lift forces. The boxes enclose the IQR of the data, the line inside the box corresponds to the median value (50th percentile), the whiskers (lines extending above and below each box) show the range of the data, and dots beyond the whiskers correspond to outliers. These data indicate that the lift force is mostly positive (towards the free surface) with small penetration intervals with negative lift forces (in the direction of gravity). The distribution of the lift forces (see Fig. 4b–d) shows a slight increase in the median $L_{int}$ and $L_{tip}$ with intruder depth. However the magnitude of the increase is within the range of fluctuations (IQR) of the values, suggesting that the depths tested are within the saturation range of the lift forces proposed by [12]. Similar to the case with the drag force data, the amplitude of fluctuations in the lift forces is large (IQR is up to 5 times the median $L_{tip}$), and increases with intruder depth.

Fig. 4

Lift forces—intruder with a conventional CPT-shaped tip, for the different intruder depths tested. Lines and shaded regions in a–c correspond to the moving average (with a window $D_p/2$) and the IQR of the drag forces respectively. Box plots in b–d show the distribution of the lift forces (before averaging) for the entire penetration range. a Lift force on the tip ($L_{tip}$). b Lift force on the intruder (tip+body) ($L_{int}$). c Distribution of $L_{tip}$. d Distribution of $L_{int}$

4 Tip shape optimisation

To find the tip shapes that minimise drag and lift forces during horizontal penetration, we coupled the DEM model with an implementation of ant colony optimisation (ACO), a heuristic algorithm inspired by the behavior of ant colonies. The decision to use ACO was not supported by a review of candidate genetic algorithms for optimization, rather it was based on knowledge that it would enable optimization based on the earlier study [28]. ACO is a genetic algorithm, which sequentially improves the knowledge of the optimisation domain, similar to the way ant colonies explore their habitat to find the best path to nearby resources [9]. Initially proposed for discrete combinatorial optimization problems, ACO has been modified to solve countless different optimisation problems, from common benchmark problems such as the traveling salesman problem [9], to problems with continuous domains, multi-objective optimisation, among many others [10]. In the following we describe the implementation adopted in this study, which is adapted from [28] and [42].

4.1 Optimisation algorithm

The optimisation algorithm seeks to sequentially improve the knowledge of the domain, to find the optimal combination of parameters (shape parameters in this case) that yields the best score (lowest drag and lift forces). The optimisation follows 4 stages: domain setup, initialization, evolution and termination. A schematic of the steps followed by the algorithm is shown in Fig. 5.

Key concepts that underpin the algorithm are defined as:

• Candidate solution (a): An intruder tip shape, defined by its set of shape parameters ($\eta$, $\zeta$, AR) and its score S; $\zeta$ is the apex height, $\eta$ is the tip curvature, and AR is the aspect ratio. Equivalent to an ant in the rationale of the algorithm.

• Score (S): A single numerical value that quantifies the performance of each candidate solution based on the current optimisation goal. In this study, S is either $S_D$ (mean drag force) or $S_L$ (mean absolute lift force), depending on the optimisation objective. Candidate solutions are ranked based on their score value.

• Generator function: Likelihood function used to sample sets of tip shape parameters: ($\eta$, $\zeta$, AR). Built as a sum of multivariate normal distributions from the candidate solutions with the lowest scores (S) in the colony.

• Generation ($G_i$): Group of candidate solutions sampled from the same generator function.

Fig. 5

Schematic of the steps followed by the ant colony optimisation (ACO) algorithm

4.1.1 Optimisation domain

The optimisation domain is the set of parameters that define the tip shapes tested. The tip shapes are parameterized as super-ellipse (or Lam$\acute{e}$ curve) segments, one for the top and one for t he bottom of the tip profile according to Eq. 3.

$$\begin{aligned} \begin{aligned} \left| \frac{2x}{AR \cdot D_p} \right| ^ \eta + \left| \frac{y}{(1-\zeta )\cdot D_p} \right| ^ \eta = 1 \qquad \left( \frac{y}{D_p}>\zeta \right) \\ \\ \left| \frac{2x}{AR \cdot D_p} \right| ^ \eta + \left| \frac{y}{\zeta \cdot D_p} \right| ^ \eta =1 \qquad \left( \frac{y}{D_p}\le \zeta \right) \end{aligned} \end{aligned}$$

(3)

From Eq. 3 the tip shape is controlled by three parameters: the apex height ($\zeta$), the tip curvature ($\eta$), and the aspect ratio (AR). The apex height $\zeta$ is the vertical distance from the bottom of the intruder to the tip apex, relative to $D_p$. A value of $\zeta = 0.5$ corresponds to a symmetrical tip, such as the CPT-shape in Sect. 3. The apex height was varied within the range $0.1 \le \zeta \le 0.9$. The tip curvature $\eta$ is the shape parameter of the super-ellipse and it is equal for the top and bottom sections of the tip. Values of $\eta < 1$ yield concave tips, $\eta = 1$ corresponds to straight lines (such as the CPT-shape), $\eta > 1$ gives a convex shape so that $\eta = 2$ gives elliptical profiles, and an ill-defined $\eta = \infty$ corresponds to a rectangular tip. Here the tip curvature was varied within the range $0.75 \le \eta \le 3.0$. The aspect ratio of the tip (AR) is the width of the tip (x-dimension length) relative to the height (y-dimension height) of the tip which was fixed to be $D_p$. The CPT intruder in Sect. 3 has $AR = 0.87$, while a circular tip would have $AR=1$. The aspect ratio of the tip was varied within the range $0.75 \le AR \le 2.0$.

4.1.2 Initialisation

Heuristic algorithms (such as ACO) are vulnerable to local minima that may compromise their robustness and lead to sub-optimal solutions. In order to prevent spurious convergence, the first set of candidate solutions, i.e. the first generation of the algorithm ($G_1$), is the only generation that was created without a generator function. Instead, it is designed to include more candidate solutions than the rest of the generations (27 vs 10), and cover the entire parameter domain with evenly-spaced values of $\zeta$, $\eta$ and AR over their range. The tip shape parameters of the 27 ($3^3$) candidate solutions result from the combination of the parameter values: $\zeta : 0.2, 0.5, 0.8$, $\eta : 1.0, 1.87, 2.75$, AR : 1.0, 1.37, 1.75.

4.1.3 Evolution and convergence

The optimisation goal uses a mathematical expression to assign a numerical score S to each candidate solution based on the forces exerted on the tip during the DEM-simulated penetration. Solutions are sorted according to their score, and the 10 candidate solutions with the best score used to create/update the generator function. The relatively high number of solutions in the generator function reduces the convergence rate of the algorithm, but improves it’s robustness.

Section 5 explores how to minimise the drag force on the intruder, thus $S_a = S_D$ the mean tip drag force $D_{tip}$ over the penetration interval $X_p = [5, 15] \times D_p$. Similarly, in Sect. 6 considers minimization of the lift force on the intruder, thus $S_a = S_L$ the mean absolute tip lift force $|L_{tip}|$ over the penetration interval $X_p = [5, 15] \times D_p$. In both cases, the candidate solutions with the lowest S are used to build the generator function.

The generator function is used to sample random vectors $a: [\eta , \zeta , AR]$, that represent different tip shapes. The generator function is defined within the range of the shape parameters and assigns a likelihood to each a. The likelihood of a is calculated as the sum of the probability density values of a from 10 multivariate normal distributions, one for each of the lowest scoring candidate solutions in the colony. The multivariate normal distribution of candidate solution i has mean ($\mu _i$) and covariance ($\Sigma _i$) values calculated from:

$$\begin{aligned} \mu _a = \begin{bmatrix} \zeta _i&\eta _i&AR_i \end{bmatrix} \end{aligned}$$

(4)

$$\begin{aligned} \Sigma _i = \begin{bmatrix} K_{\zeta ,\zeta } &{} \quad K_{\zeta , \eta } &{} \quad K_{\zeta , AR} \\ K_{\zeta , \eta } &{} \quad K_{\eta , \eta } &{} \quad K_{\eta , AR} \\ K_{\zeta , AR} &{}\quad K_{\eta , AR} &{}\quad K_{AR, AR} \\ \end{bmatrix} \end{aligned}$$

(5)

$$\begin{aligned} K_{X,Y} = \frac{1}{10}\sum _{j}^{10}(X_i-X_j)(Y_i-Y_j) \end{aligned}$$

(6)

The resulting generator function is a scalar multiple of a probability density function (as its integral is not equal to the unity). The generator function is computed from scratch at every generation as the solutions with the lowest score in the colony may change. We sampled random vectors from the generator function using slice sampling [26], which creates a Markov Chain with values that follow the distribution of the generator function. To reduce correlation between samples, we discarded the first 10000 values of the chain, and sample one of every 10 values in the chain. If a sampled vector is outside the range of $(\zeta , \eta , AR)$ it is discarded and re-sampled.

Ten random vectors $a: [\eta , \zeta , AR]$ were sampled from the generation function to form the next generation $G_i$ of the colony. For each, a reduced model was set up (as described in 2) and a DEM simulation was completed. At each generation, the coefficient of variability (COV) of the $\zeta$, $\eta$, AR and score (S) of the candidate solutions in the current generator function were calculated. $COV_x = std(x)/\bar{x}$, where std(x) is the standard deviation of the values x, and $\bar{x}$ is their mean value. Both instances of the optimisation algorithm (i.e., drag and lift minimisation) run over 30 generations, after which the algorithm converges, with $COV_{S}< 5\%$. Convergence profiles of the optimisation algorithm are shown in Figs. 6 and 10.

4.1.4 Algorithm implementation

The large number of simulations needed for the optimisation of the tip shape (607 in total) rendered it impractical to set up each simulation manually; a Python script was developed to execute and monitor the optimisation process automatically. The overall architecture of the script follow the steps shown in Fig. 5. For the first generation, the colony was initialised (see initialisation description above); for subsequent generations $G_i$, candidate solutions in the colony were sorted according to their score, and the 10 best scoring solutions were used to build the generator function considering the evolution and convergence concepts introduced above. Then 10 new candidate solutions were sampled from the generator function, and for each, a DEM simulation was set up. Here each simulation was submitted to the distributed memory HPC cluster used using an automatic secure shell (SSH) session.

Next, the script post-processed the output files for the finished simulations, assigning scores S, and adding the completed solutions to the colony. The colony is represented by a ledger file that keeps the name, location (path), shape parameters, scores, and status (prepared/running/completed) of each simulation at all times. Once each generation was completed, the scripts checked the convergence criteria of the algorithm. If convergence was not achieved, a new generation was started, repeating the process. Here the convergence criterion was the maximum number of generations to run (30), but other metrics may be used, e.g. $COV_{S}< 5\%$.

The optimisation algorithm was deployed using Imperial College’s distributed memory HPC cluster. For each generation, 10 computing jobs (one per candidate solution) were run concurrently. Each computing job ran a LAMMPS simulation (using MPI) using 12 cores, and took 5–6 h to complete. Thus, each optimisation (MD and ML) required about 21600 core hours over $\sim 9$ days.

5 Drag force minimisation

Fig. 6

Drag minimisation—convergence profile. Solid lines and shaded regions correspond to the median and inter-quartile range of the shape parameters (a–c), and score $S_D$ (d) of the solutions in the generator function

When seeking the tip shape that minimises the drag force during penetration, the score assigned to each tested shape, i.e., candidate solution a in the algorithm, was the drag score $(S_D)_a$, calculated following [31] as the mean tip drag force $D_{tip}$ over an arbitrary but representative distance during steady state penetration, in this case the interval $X_p = [5, 15] \times D_p$. The optimisation algorithm ran over 30 generations, for a total of 317 DEM simulations (27 in $G_1$ and 10 in every subsequent generation $G_i$). The generator function is built from the 10 candidate solutions with the lowest $S_D$ in the colony. The convergence profile of the algorithm is shown in Fig. 6, with lines and shaded regions corresponding to the median and IQR of the solutions in the generator function (respectively).

The dispersion of the shape parameters and $S_D$ in the generator function is measured in terms of the coefficient of variance COV, calculated as the ratio between the standard deviation and the mean value of the data. After 30 generations, the dispersion of the drag score of solutions in the generator function is $COV_{S} = 1.09\%$. The range of the parameters are: the tip location $0.13<\zeta < 0.18$ and $COV_\zeta = 17.9\%$, the shape parameter $1.05<\eta < 1.11$ and $COV_\eta = 3.8\%$, and the aspect ratio $1.41<AR<1.67$ and $COV_{AR} = 10.8\%$. The relative wide range of AR relative to $S_D$ and the other shape parameters indicates that it is a flexible parameter, as any tip shape within that range will yield similar drag force values. Conversely, the process is more sensitive to the curvature and apex location of the tip, with only a small range of values yielding values close to the minimum drag force.

The tip that minimises drag forces, denoted MD, is ‘sharp’ and slender, with shape parameters $\zeta = 0.16$, $\eta = 1.07$, $AR = 1.65$, and shown in Fig. 7. This shape was tested using the large model at intruder depths ($H_p = [5, 10, 15, 20] \times D_p$), similar to the CPT intruder in Sect. 3.

Fig. 7

Comparison of different profiles of the tip shapes tested. Values shown are normalised by tip height, equal to $D_p$ = 36 mm for CPT, MD, ML and PO, and equal to 17 mm for the sandfish head

Fig. 8

Drag forces—minimum drag intruder MD ($\zeta = 0.16$, $\eta = 1.07$, $AR = 1.65$). Lines and shaded regions correspond to the moving average (with a window $D_p/2$) and the IQR of the drag forces respectively. a Drag force on the tip ($D_{tip}$). b Drag force on the intruder ($D_{int}$). c Depth-normalised tip drag force ($DN_{tip}$). d Depth-normalised intruder drag force ($DN_{int}$). Quantities shown for the different intruder depths tested

It is informative to consider the forces acting on the drag-optimized intruder. Referring to Fig. 8, just as was in the case of the CPT intruder (see Fig. 3), the drag forces acting on the tip and entire intruder increase linearly with depth and, once normalized, they can be described by the simple linear relation in Eq. 2, with intercept $DN_{tip} = 0.405$, and slope $m_{int} = 0.0264$. For comparison, the linear relations for MD and CPT are shown in Fig. 8c, d. On average, the optimised shape MD reduces the tip drag ($D_{tip}$) by $12.5\%$, and the $D_{int}$ by $15.6\%$ (at $X_p = 15 \times D_p$), when compared to CPT. These results mean that MD not only reduces $D_{tip}$, but also reduces the drag forces in the body of the intruder, which is the same for CPT and MD.

Fig. 9

Lift forces—minimum drag intruder MD ($\zeta = 0.16$, $\eta = 1.07$, $AR = 1.65$) for the different intruder depths tested. Lines and shaded regions in a, c correspond to the moving average (with a window $D_p/2$) and the IQR of the drag forces respectively. Box plots in b, d show the distribution of the lift forces (before averaging) for the entire penetration range. a Lift force on the tip ($L_{tip}$). b Lift force on the intruder ($L_{int}$). c Distribution of $L_{tip}$. d Distribution of $L_{int}$

The lift forces data on Fig. 9 show that for MD, the lift forces are negative, i.e. they act to push the intruder downwards in the direction of gravity. The magnitude of the tip $L_{tip}$ and intruder $L_{int}$ lift forces significantly increase with intruder depth, in contrast to the results from CPT, where the lift forces had little dependence of the intruder depth. This unsought and undesirable change in the lift mechanisms shows that the reduction in drag forces comes at the cost of increased and depth-dependent lift forces, which may hinder the steerability of the intruder.

6 Granular lift minimization

Fig. 10

Lift minimisation—convergence profile. Solid lines and shaded regions correspond to the median and IQR (inter-quartile range) of the candidate solutions in the generator function

When seeking the tip shape that minimises the lift force during penetration, the score $S_L$ assigned to each candidate solution a, was the mean absolute value of the lift force at the tip ($|L_{tip}|$) over the penetration interval $X_p = [5, 10] \times D_p$. Similar to the drag force minimisation, the algorithm runs for 30 generations for a total of 317 simulations. The convergence profile for the minimisation of the lift forces is shown in Fig. 10.

After 30 generations, the dispersion of the $S_L$ among the solutions in the generator function is $COV_{S} = 4.64 \%$. The range of the parameters in the generator function are: for the tip location $0.14<\zeta < 0.19$ and $COV_\zeta = 13.0\%$, the shape parameter $2.28< \eta < 2.54]$ and $COV_\eta = 12.8 \%$, and for the aspect ratio $0.81<AR < 1.00]$ and $COV_{AR} = 12.2 \%$. As shown in Fig. 7 the tip shape that minimises the lift forces is blunt, with shape parameters $\zeta = 0.13$, $\eta = 2.56$, $AR = 0.81$.

Fig. 11

Drag forces—minimum lift force intruder ML ($\zeta = 0.13$, $\eta = 2.56$, $AR = 0.81$). Lines and shaded regions correspond to the moving average (with a window $D_p/2$) and the IQR of the drag forces respectively. a Drag force on the tip ($D_{tip}$). b Drag force on the intruder (tip+body) ($D_{int}$). c Normalised tip drag force ($Dn_{tip}$). d Normalised intruder drag force ($Dn_{int}$). Quantities shown for the different intruder depths tested

ML was tested using the large model at intruder depths ($H_p = [5, 10, 15, 20] \times D_p$). The drag forces acting on the intruder are shown in Fig. 11. Once more, the tip drag forces ($D_{tip}$, and $D_{int}$) increase linearly with depth, and the total drag force can be described by the linear relationship shown in Eq. 2, with intercept $DN_{tip} = 0.4852$, and slope $m_{int} = 0.0278$. These values, together with the values from CPT are shown in Fig. 11c, d. Surprisingly, even though the shape of ML and CPT are considerably different, the drag forces acting on them are similar, with tip (average $D_{tip}$) and intruder ($D_{int}$ at $X_p = 15 \times D_p$) drag forces of ML being $0.3\%$ and $4.5\%$ lower than that of CPT (respectively).

Fig. 12

Lift forces—minimum lift force intruder ML ($\zeta = 0.13$, $\eta = 2.56$, $AR = 0.81$). Lines and shaded regions in a, c correspond to the moving average (with a window $D_p/2$) and the IQR of the lift forces respectively. Box plots in b, d show the distribution of the lift forces (before averaging) for the entire penetration range. a Lift force on the tip ($L_{tip}$). b Lift force on the intruder (tip+body) ($L_{int}$). c Distribution of $L_{tip}$. d Distribution of $L_{int}$

The lift force data in Fig. 12 show that the shape of ML significantly reduces the lift forces, reducing (in average) the tip lift force $L_{tip}$ in $44.4\%$ and the intruder lift force $L_{int}$ in $30.8\%$. The lift forces acting on ML are small (close to zero), and therefore fluctuate in orientation. Still, the median lift forces are negative and their magnitude increases slightly with intruder depth. Then, ML shape not only achieves important reductions in lift force, but also small reductions in drag (relative to the CPT baseline). However, drag forces acting on MD are still $13\%$ lower than those on ML.

7 Pareto optimality

The tip shapes that minimise drag (MD) and lift (ML) are significantly different from each other, with fairly different tip curvatures $\eta$ (1.07 and 2.56 respectively) and aspect ratios AR (1.65 and 0.81 respectively), but a relatively similar apex height $\zeta$ (0.16 and 0.13 respectively). As expected, MD outperformed CPT and ML in terms of drag forces, while ML outperformed CPT and MD in terms of lift forces, see Fig. 16.

Minimising drag did not result in a significant reduction in lift (and vice-versa); this suggests that the minimisation of lift and drag are competing objectives, so that no shape can minimise simultaneously both lift and drag. However, it is desirable to find a tip shape that reduces both drag and lift forces to the maximum extent possible. Pareto optimality is a principle used in multi-objective optimisation to find the solution that offers the optimal trade-off between two (or more) competing goals, such as in this case. In the absence of a tip shape that reaches the minimum lift and drag forces at once, a Pareto-optimal solution is a tip shape for which no lower drag force can be obtained without it resulting in a higher lift force (and vice-versa).

To find the Pareto-optimal tip shape, we considered Pareto-normalised drag and lift scores, denoted $\widehat{S_D})$ and $(\widehat{S_L})$ respectively, and defined as:

$$\begin{aligned} \begin{aligned} \widehat{S_D} = \frac{S_D - (S_D)_{MD}}{(S_D)_{ML} - (S_D)_{MD}} \\ \widehat{S_L} = \frac{S_L - (S_L)_{ML}}{(S_L)_{MD} - (S_L)_{ML}} \\ PS = \sqrt{(\widehat{S_D})^2 + (\widehat{S_L})^2} \\ \end{aligned} \end{aligned}$$

(7)

By definition, the Pareto-normalised scores of MD are: $\widehat{S_D}=0$ and $\widehat{S_L}=1$, while the scores of ML are: $\widehat{S_D}=1$ and $\widehat{S_L}=0$. Candidate solutions with $\widehat{S_D}>1$ have drag forces larger than those for the ML case, and similarly, candidate solutions with $\widehat{S_L}>1$ have lift forces larger those experienced by the MD case. The Pareto-normalised scores, i.e. $\widehat{S_D}$ and $\widehat{S_L}]$ for the solutions in the range [0, 1] are shown in Fig. 13.

Fig. 13

Pareto-normalised candidate solution scores. Points include the solutions created during the lift and drag optimisation, the initial generation $G_1$, and the Pareto front that separated the non-attainable region, and the sub-optimal, dominated solutions. MD and ML are the data points for the optimal profiles for drag and lift respectively

The Pareto front, or Pareto frontier, shown in Fig. 13 is the convex boundary of the simulations in the Pareto-normalised score plot, and defines the set of Pareto-optimal solutions, all of which have an optimal trade-off between drag and lift forces. The Pareto front is also the boundary between the of the non-attainable region, i.e. the region of impossible solutions, and the region of sub-optimal or dominated solutions. Any solution along the Pareto front is a better trade-off between optimisation goals than any dominated solution.

Seven candidate solutions (tip shapes) define the Pareto front, these include the ML and MD topologies. These shapes can be ranked based on their Pareto score PS, i.e., the Euclidean distance from the solution to the origin in the Pareto-normalised score plot, according to Eq. 7. The tip shape with the minimum Pareto score ($PS=0.43$) is the Pareto Optimal (PO) tip shape, it is illustrated in Fig. 7 and has shape parameters $\zeta = 0.23$, $\eta = 1.18$, $AR = 1.29$.

Similar to the other optimal tip shapes, the penetration of the PO in the large domain was simulated using four different depths. The drag forces acting on the PO, illustrated in Fig. 14, follow a similar trend to those found for the other intruders, with the drag force increasing linearly with depth. The normalized values follow a linear relation described by Eq. 2 with intercept $DN_{tip} = 0.425$, and slope $m_{int} = 0.0282$. The linear relation for the CPT is shown in Fig. 14c, d for comparison. As illustrated on Fig. 15, the lift forces are small in magnitude and negative (i.e. pushing the intruder downwards). Interestingly, $L_{tip}$ increases with depth, while $L_{int}$ is relatively constant. For $X_p > 12 \times D_p$, the magnitude of $L_{int}$ starts to increase, which may indicate a boundary effect (see Fig. 9).

Fig. 14

Drag forces—Pareto optimal (PO) intruder ($\zeta = 0.23$, $\eta = 1.18$, $AR = 1.29$). Lines and shaded regions correspond to the moving average (with a window $D_p/2$) and the IQR of the drag forces respectively. a Drag force on the tip ($D_{tip}$). b Drag force on the intruder (tip+body) ($D_{int}$). c Depth-normalised tip drag force ($DN_{tip}$). d Depth-normalised intruder drag force ($DN_{int}$). All quantities shown for the different intruder depths tested

Fig. 15

Lift forces—Pareto optimal (PO) intruder ($\zeta = 0.23$, $\eta = 1.18$, $AR = 1.29$) for the different intruder depths tested. Lines and shaded regions in a–c correspond to the moving average (with a window $D_p/2$) and the IQR of the drag forces respectively. Box plots in b–d show the distribution of the lift forces (before averaging) for the entire penetration range. a Lift force on the tip ($L_{tip}$). b Lift force on the intruder (tip+body) ($L_{int}$). c Distribution of $L_{tip}$. d Distribution of $L_{int}$

8 Discussion

8.1 Comparison of optimal profiles

The three key profiles, i.e. MD, ML and PO are directly compared with the CPT profile in Fig. 7. Figure 16 compares the drag and lift forces for the four profiles and the four depths considered. The data are presented as the increase in force beyond the minimum drag/lift force for the depth considered. These results confirm that the PO profile is a trade-off solution that yields smaller lift forces than MD, and smaller drag forces than ML. The PO profile outperforms CPT both in terms of drag and lift forces, and the CPT is clearly a dominated (sub-optimal) tip shape.

Fig. 16

Comparison of drag and lift forces relative to MD (x-axis) and to ML (y-axis). Values plotted as the relative increase in drag/lift force relative to the minimum drag/lift force for the given depth

Table 2 Shape parameters for the different tip profiles studied, $\zeta$ is the apex height, $\eta$ is the curvature and AR is the aspect ratio

The combinations of shape parameters for the 10 profiles with the lowest drag and lift, the PO profile, the CPT profile and a circular profile are presented graphically in Fig. 17. The shape parameters for the optimal solutions are summarised in Table 2. The tip shape that minimises drag (MD), is ‘sharp’, with low curvature ($\eta$), and a slender (high) aspect ratio. In contrast, the tip shape that minimised lift forces (ML), is blunt, with high curvature and a low AR. The drag reduction achieved with a sharp tip is intuitive, and has been reported in previous studies [5, 20]. Still, results from MD show that optimising a single optimisation goal, i.e. minimising drag force, compromises the steerability of the intruder, as a consequence of the increased lift force.

Interestingly, the location of the tip shape ($\zeta$) is similar for MD and ML, with the tip apex at about $13\%$ to $16\%$ from the bottom of the profile. However the results suggest that AR is a relatively ‘flexible’ parameter, with a relatively wide range of values, $1.3< AR < 1.8$ for the solutions that minimize drag and $0.75< AR<1.05$ for the optimal lift solutions, all of which yield similar results. On the other hand, the tip shape curvature $\eta$ is significantly different for MD and ML (2.56 and 1.2 respectively), which indicates that it is the differentiating parameter that controls the transition from drag to lift minimisation (or vice-versa). The shape of the Pareto Optimal (PO) tip is similar to the minimum drag (MD) tip, but with a smaller aspect ratio and slightly increased curvature, which results in a less slender shape.

Fig. 17

Optimisation domain and results, axis limits correspond to the range of the shape parameters considered in the optimisation. a Curvature ($\eta$) versus AR. b Apex height ($\zeta$) versus AR. Data are for the 10 candidate solutions (tip shapes) with lowest drag and lift, the Pareto optimal (PO) tip shape, the baseline CPT shape, and the parameters of a circular tip (for reference)

8.2 Comparison with sandfish

It is noteworthy that the PO profile resembles the head of the sandfish (Scincus scincus), a lizard that has been extensively studied due to its remarkable ability to burrow through sand [4, 21]. This observation was verified with a 3D model of a sandfish available from [4]. The model was rotated to match the orientation of its principal directions. The principal directions were obtained applying principal component analysis (PCA) to the volume enclosed by the sandfish. The head width was measured from the tip of the snout to the approximate location of the back of the parietal bone, as proposed by [3, 17]. The head height was measured as the distance between the lowest and highest parts of the head; the aspect ratio was calculated as the ratio between the width and the height of the head, for $AR = 1.33$. The location parameter was calculated as the ratio between snout height (distance from the lowest part of the head to the height of the snout tip) and the head height, for a $\eta = 0.27$. The curvature parameter was found from the best fit of the profile of the head and Eq. 3, for a $\zeta = 1.20$ and a coefficient of determination of the fit $R^2 = 0.95$. To enable direct comparison with the optimized profiles, sandfish profile (from the 3D model) and the best fit of the sandfish profile to Eq. 3, namely SF, are shown in Fig. 7. A summary of the shape parameters for MD, ML, PO, and SF are shown in Table 2, and graphically in Fig. 17.

Previous studies have found that the evolution of the head shape of lizards is constrained by a set of different and potentially conflicting functions, such as locomotion, prey capture, display and defensive behaviours [17]. For instance, [17] studied Tropidurinae lizards, a family of species that climb vertical structures (trees/rocks), and found an adaptive co-variation between their head shape and the inclusion of hard prey into their diet; while habitat use did not drive head shape evolution. In contrast, locomotion performance is a key factor that drives the evolution of the head shape in burrowing lizards, playing an important role in predator escaping, foraging (exploration of their ecosystem) and defence of their territory [11]. For instance, [3] studied Gymnophthalmid lizards, a family that includes burrowing (fossorial) species, and species that live on the soil surface without burrowing (epigeal) - Results from this study showed that the head of burrowing (Gymnophthalmid) lizards is shaped under the influence of microhabitat use, independently of the prey consumed. This prevalence of locomotion performance over other competing goals in burrowing animals, may explain the striking similarity between the SF and PO, and highlights the potential of bio-inspiration and bio-mimicry in engineering design.

Fig. 18

Contact forces at a penetration distance $X_p = 10 \times D_p$ at a intruder depth $H_p = 10 \times D_p$ in the large model. Each view corresponds to a 0.5 m $\times$ 0.5 m window, and the cartesian position values given along both the horizontal and vertical axes are measured in metres from the bottom left corner of the model. Contact color and thickness proportional to force magnitude. a CPT intruder, b) minimum drag (MD) intruder, c minimum lift (ML) intruder, d Pareto optimal (PO) intruder

8.3 Contact forces and lift

The DEM simulations generated a wealth of detailed information on the mechanical response of the system during penetration. In a previous study, [20] proposed that in comparison with the symmetric case, asymmetric tip shapes change the balance between the number and magnitude of contact forces above and below the tip apex. As a result, asymmetric tip shapes can control the resulting magnitude and direction of lift. This observation is qualitatively assessed using Fig. 18, which shows the contact forces in the region around the tip shapes tested (CPT, MD, ML, PO).

The CPT tip-shape has the highest apex height ($\zeta = 0.50$) and the largest positive lift force among the optimal tips (see Figs. 17, 3). The gradient of stresses (induced by the geostatic conditions) causes an increase in the contact forces with depth, and explains the high density of strong contacts under the apex of the symmetric intruder in Fig. 18a. This imbalance in contact forces above/below the intruder supports previous studies [22, 25, 41] that propose that geostatic stress gradients are responsible for the development of granular lift forces that push symmetric intruder towards the free surface.

In contrast, the distribution of contacts above/below the intruder apex is relatively symmetrical for ML and PO, the tip shapes with lower (i.e. more balanced) lift forces. These results indicate that the asymmetric tip shapes can nearly balance the geostatic gradient of contact forces in the media, reducing the resulting lift forces. Furthermore, the minimum drag tip MD has the lowest apex height ($\zeta = 0.13$) and with it, the largest negative lift force. The concentration of strong contact forces right above the tip in Fig. 18b suggests that lowering the tip apex height further, creates a change in the direction of the force, pushing the intruder downwards in the direction of gravity.

Moreover, for all the tip shapes tested, the amplitude of the fluctuations of the drag and lift forces increases with intruder depth. This phenomenon may be attributed to force chain collapse/formation—combined with particle size effects. With increasing depth, the magnitude of the contact forces along the force chains around the intruder increases, and as these force chains collapse/form during penetration, larger fluctuations of the forces exerted on the intruder are observed.

9 Conclusions

A number of applications in geotechnical engineering require horizontal penetration into soil. This study has used 2D DEM simulations to explore the relationship between drag and lift forces, and the tip shape of an intruder moving horizontally in granular media. A heuristic optimisation algorithm (ACO) was used along with discrete element (DEM) simulations to find the tip shapes that minimise drag and lift during penetration. The tip shapes were described as super-ellipse sections of varying aspect ratio (AR), tip curvature ($\eta$), and apex height ($\zeta$).

At a high level the study makes two significant contributions:

• 1. The match between the optimal engineered intruder and the head shape of the sandfish is the result of a common objective that drives their evolution: to move underground more efficiently. These findings make a case for bio-inspired solutions when a common objective between nature and engineering applications exists.

• 2. We have demonstrated the scope for DEM simulations to be integrated within an optimization framework to develop innovative design solutions for systems that involve large deformations of granular materials.

The detailed findings relate both to an improved understanding of the forces acting on a horizontally orientated probe and the influence of probe morphology on these forces and they can be summarized as follows:

• 1. Drag force: Regardless of the tip shape, the drag force during horizontal penetration increases linearly with depth, in agreement with [12, 31, 35]. This force can be described as a linear relationship that includes the (relatively) constant drag at the intruder tip, plus the drag around the body of the intruder, which increases proportionally with intruder length. In addition, it was shown that optimising the tip shape not only reduced the tip-drag, but also the drag along the body of the intruder.

• 2. Lift force: The direction and magnitude of the lift forces depends heavily on the intruder tip shape. The direction of the lift force transitions from positive (opposite to the direction of gravity)—observed for symmetric intruders with a tip elevation $\zeta = 0.5$, to negative (in the direction of gravity) for asymmetric tip shapes with $\zeta < 0.5$. The relationship between the tip shape parameters and its relationship with the intruder depth is complex, and ranges from approximately independent from depth for CPT-shaped intruders, to negative and increasing with depth for the slender shape of the minimum drag tip (MD).

• 3. Optimal tip profile: The tip shape that minimised the drag forces, MD, has a sharp, slender profile with a low curvature and high aspect ratio. The ML tip profile that minimises lift forces has a blunt morphology with a low aspect ratio and a high curvature. The difference in the optimal tip shapes demonstrates that the minimisation of the drag and lift forces are competing optimisation goals; thus, no single tip shape can minimise lift and drag forces at once. With this in mind, the Pareto front of the optimisation goals was calculated, and the Pareto optimal tip shape PO evaluated. PO proved to be a trade-off solution that reduces both the drag and lift forces (compared to CPT), with drag and lift forces that are (in average) only $5\%$ and $20\%$ higher than their minimum values obtained with MD and ML (respectively).

• 4. Contact force network: Inspection of the contact network around the intruder tips suggests that different tip shapes change the balance between the orientation, number and magnitude of the contact forces around the intruder. Symmetric intruders experience (positive) lift forces due to the increased magnitude of the contacts below the tip, a consequence of geostatic stress conditions. For ML and PO, the asymmetry of the tip reduces the magnitude of the (positive) lift forces at the bottom section of the tip, and increases it on the top section; reaching a more symmetric distribution of contact forces around the intruder, and with it a lower resulting lift force.

• 5. Linking optimized profile to sandfish: The Pareto optimal profile, PO, has a striking similarity with the head shape of the sandfish (S. snicus), a burrowing lizard with a remarkable capacity to move through sand. This similarity, added to the fact that the head shape in burrowing lizards is tied to their capacity to burrow [3], further supports that the head shape of the sandfish has been optimised to move underground more efficiently (i.e. with less drag force), and with improved manoeuvrability (i.e. reduced lift forces). And at the same time, highlights the potential of bio-inspired solutions in engineering.

Future work in this area may include the extension of the numerical work to study the effect of particle size and shape, poly-dispersity; and the extension to three dimensions, and the experimental validation of the findings. Similarly, releasing the constraint of the fixed horizontal movement of the intruder may help quantify the deviations in the direction of the intruder that results from the non-zero lift forces. Furthermore, steering methods can draw upon the results from this study, and exploit the non-symmetry of the forces around the intruder induced by different intruder shapes to steer underground devices at will, and correct their course in real time.