1 Introduction

Abundant geothermal resources are trapped in the low-permeability hard rock underlying most continental regions, wherein the geothermal energy could be accessed through the well and artificial heat exchanger, i.e. enhanced geothermal system (EGS) [30]. Therefore, a suitable heat exchanger with high permeability is very important for economical heat mining in low-permeability rocks. Hydraulic fracturing is currently the most effective technique for enhancing the permeability and forming an artificial fracture for heat exchanging [1]. The performance of EGS is highly impacted by the features of created fractures, like permeability, geometry, stimulated reservoir volume and area, etc., which can be evaluated by the seismic events measured in field during hydraulic fracturing [12]. Additionally, due to the low cost and high visualization in comparison with field measurement, numerical modelling is considered an efficient alternative method. In general, the numerical modelling is more suitable for preliminary assessment and optimization design.

During hydraulic fracturing, the fracture propagates diversely in different rock types and reservoirs. Typical unconventional reservoirs, for instance tight and shale gas reservoirs, are mainly composed of sedimentary rocks [9, 23], in which usually a dominant fracture path is stimulated under high-pressure condition by fluid injection, if no natural fractures are present. The geothermal reservoir, especially the hot dry rock (HDR), is discovered mostly in the hard crystalline rocks with strong brittleness, where complex fracture networks are more likely to be stimulated, under the effect of higher Young’s modulus and pre-existing joints, which has been proven by many researchers [7, 32]. Two dominant mechanisms are involved for enhancing permeability during fracturing: (1) opening fracture triggered by tensile failure (Mode I) and (2) dilatation fracture triggered by shear failure (Mode II) [26, 34]. Therefore, a numerical model incorporating these mechanisms is required to precisely characterize the fracture propagation in hard crystalline rocks.

Enhancing permeability in hard brittle rocks is usually linked to the fracture network via damage. In the phenomenological models, the damage-induced permeability alteration has been formulated with the internal scalar variables, like the crack growth [29], compressive stress-induced crack opening [25], change in pore size distribution [3], viscoplastic strain in tension and compression [22] and crack density distribution [19, 20]. These phenomenological characteristics are macro-scale features of microstructure behaviour under different loadings. To measure the permeability alteration on microstructure explicitly, the micromechanical model has been introduced, in which the microstructure is described by the variables, e.g. crack volume fraction, direction, connectivity, density, etc. [5, 11] Apparently, the micromechanical model can predict the permeability more accurately, but requires much more computational capacity to represent the huge number of variables on the microstructure.

In recent years, several simulation tools have been introduced to characterize the hydraulic fracturing in hard rocks. Yoon et al. [33] used a 2D discrete element model (DEM) to study the stress shadow due to fluid injection in a naturally fractured geothermal reservoir. This discrete element model is represented by a collection of round particles. Pre-existing fractures are embedded using the smooth joint model. The mechanical response between microparticles is transferred by the assumed springs in both normal and tangential directions, which controls the tensile/compress and shear strength. The fluid can flow in the pores between particles even breaking the assumed springs, to create a hydraulic fracture. Although DEM is a useful method to demonstrate shear and tensile failure in fracture propagation, it raises the computational capacity requirement for small particles size, or even loss of the information of grain for large particles size in a field-scale reservoir. Wang et al. [31] introduced the extended finite element method (XFEM) to model the non-planar hydraulic fracture propagation in brittle and ductile rocks. The XEFM performs very well for re-orientation of fracture, as additional enrichment function is introduced to describe continuous and discontinuous deformation around fracture as well as fracture tip. Yet, it is limited for 3D problem and not suitable for fracture networks. More recently, Riahi et al. [21] applied a field-scale model based on discrete fracture network (DFN) to study hydraulic stimulation in FORGE EGS reservoir. In this model, the complex natural fracture is explicitly reconstructed in a DNF. The impermeable matrix out of the DFN cannot be stimulated. Hence, the leak off from stimulated fracture is not considered in this DFN model.

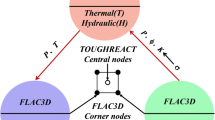
In this work, the aim is to create a continuum model for the hydraulic fracturing in low-permeability hard rock based on anisotropic damage–permeability model. The phenomenological damage model by means of tensile strain is used to estimate the anisotropic damage tensor [14]. The damage-induced permeability is interpreted in terms of cubic damage. Additionally, the isotropic effect of compressive stress on permeability is taken into consideration as well. Information of damage-induced permeability direction is derived from damage tensor, with the help of model developed by Maleki and Pouya [17]. To incorporate the influence of pre-existing joints, the ubiquitous joint model is used to simulate the potential plastic failure during fracturing. In comparison with aforementioned models, the developed model has advantages of high computational efficiency, simple implementation, modelling anisotropic equivalent permeability alteration in fracture network and containing joint information without generating complex DFN. The key contributions of this study to numerical modelling for hydraulic fracturing in hard rock can be summarized as follows: (i) establishing a complete correlation of deformation–damage–permeability involving anisotropic direction information; (ii) developing an anisotropic damage–permeability model in framework of TOUGH2MP-FLAC3D for hydraulic fracturing in hard rock; and (iii) validating the reliability of the developed model with triaxial compression test on four typical hard crystalline rocks and hydraulic fracturing test from the Äspö Hard Rock Laboratory.

2 Concept and model description

2.1 Basic concept

The basic concept of anisotropic damage–permeability model can be explained in Fig. 1. During loading, increasing deviatoric stress will cause some tensile deformation in a sample, because of tensile failure or shear dilation. In the present work, the tensile deformation (ɛ+) with corresponding direction information is contained in a damage tensor. Meanwhile, tensile deformation manifests as cracks at the macroscopic level. It is well known that the hydraulic conductivity is enhanced significantly along induced cracks. On this basis, the equivalent anisotropic permeability evolution during loading can be generated on the damage tensor, linking further to the tensile deformation (ɛ+). The tensile deformation–damage–permeability correlation in detail is introduced in the following subsection.

Fig. 1
figure 1

a stress–strain curve, b damaged sample and c local enlarged view of a triaxial test with the sample from the outcrop at Landau EGS Project, Germany

Full size image

2.2 Plastic–damage model

The anisotropic damage model is implemented in continuum mechanics code FLAC3D [8] as described in the work of Liao et al. [14]. As FLAC3D adopts the sign convention used in solid mechanics, i.e. compressions are negative and tensions positive (σ1 ≤ σ2 ≤ σ3), unless otherwise noted, we apply this convention in this work. On a representative element volume (REV), the fundamental equilibrium and geometry equations are formulated as shown below

$${\sigma }_{ij,j}+\rho {g}_{i}=\rho \frac{\partial {v}_{i}}{\partial t}$$
(1)
$$\Delta {{\varepsilon }^{e}}_{ij}=\frac{1}{2}\Delta t\left({v}_{i,j}+{v}_{j,i}\right)$$
(2)

The equilibrium equation is formulated in the term of stress \({\sigma }_{ij}\), body force \({g}_{i}\) and velocity \({v}_{i}\) on grid point of the element, which is solved by using finite difference method. And the strain at mechanical time step \(\Delta t\) is estimated explicitly from the grid point velocity. It should be mentioned that the mechanical time in Eqs. 1 and 2 is a virtual physical time, which is introduced for mechanical damping from a dynamic state to a quasi-static state. The mechanical calculation terminates when the maximum unbalance force from all the grid points meets a given error tolerance. More solution details can be found in the commercial software FLAC3D manual [8].

Several constitutive models for brittle materials have been proposed in the literatures [6, 13, 18, 24], which are often based on a thermodynamic process approach. The formulation of free elastic energy in the form of damage term D is taken after Chiareli et al. [6] and written in following

$${\psi }^{e}\left({{\varvec{\varepsilon}}}^{e},{\varvec{D}}\right)=\frac{{\lambda }_{0}}{2}{\left(\mathrm{tr}{{\varvec{\varepsilon}}}^{e}\right)}^{2}+{\mu }_{0}\mathrm{tr}\left({{\varvec{\varepsilon}}}^{e}{{\varvec{\varepsilon}}}^{e}\right)+{a}_{1}\mathrm{tr}\left({{\varvec{\varepsilon}}}^{e}\right)\mathrm{tr}\left({{\varvec{\varepsilon}}}^{e}{\varvec{D}}\right)+{a}_{2}\mathrm{tr}\left({{{\varvec{\varepsilon}}}^{e}{\varvec{\varepsilon}}}^{e}{\varvec{D}}\right)$$
(3)

Deriving Eq. 3 with respect to elastic strain tensor, the constitutive equation in the term of elastic strain and damage can be achieved in Eq. 4.

$${{\varvec{\sigma}}}^{\boldsymbol{^{\prime}}}={\frac{{\partial \psi }^{e}\left({{\varvec{\varepsilon}}}^{e},{\varvec{D}}\right)}{\partial {{\varvec{\varepsilon}}}^{e}}=\lambda }_{0}\mathrm{tr}{{\varvec{\varepsilon}}}^{e}{\varvec{I}}+2{\mu }_{0}{{\varvec{\varepsilon}}}^{{\varvec{e}}}+{a}_{1}\left(\mathrm{tr}\left({{\varvec{\varepsilon}}}^{e}{\varvec{D}}\right){\varvec{I}}+\mathrm{tr}\left({{\varvec{\varepsilon}}}^{e}\right){\varvec{D}}\right)+{a}_{2}({{\varvec{\varepsilon}}}^{e}{\varvec{D}}+{\varvec{D}}{{\varvec{\varepsilon}}}^{e}$$
(4)

Considering the effect of pore pressure on effective stress [28], the constitutive equation can be written as

$${\varvec{\sigma}}+{\alpha }_{hy}P{\varvec{I}}={{\varvec{\sigma}}}^{\boldsymbol{^{\prime}}}={\mathbb{C}}\left({\varvec{D}}\right):{\varepsilon }^{e}$$
(5)

where \({\mathbb{C}}\left({\varvec{D}}\right)\) is the fourth-order damaged elasticity tensor and is given in following [6, 17]

$${\mathbb{C}}_{ijkl}\left({D}_{ij}\right)={\lambda }_{0}{\delta }_{ij}{\delta }_{kl}+{\mu }_{0}\left({\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk}\right)+{a}_{1}\left({\delta }_{ij}{D}_{kl}+{\delta }_{kl}{D}_{ij}\right)+\frac{1}{2}{a}_{2}\left({\delta }_{ik}{D}_{jl}+{\delta }_{il}{D}_{jk}+{\delta }_{jl}{D}_{ik}+{\delta }_{ik}{D}_{il}\right)$$

Deriving Eq. 5 with respect to the elastic strain and damage, the stress–strain relation in the increment form becomes

$$\Delta {{\varvec{\sigma}}}^{\boldsymbol{^{\prime}}}={\mathbb{C}}\left({\varvec{D}}\right):\Delta {\varepsilon }^{e}+\Delta {\mathbb{C}}\left({\varvec{D}}\right):{\varepsilon }^{e}$$
(6)

The stiffness tensor increment is defined in Eq. 7.

$$\Delta {\mathbb{C}}\left({\varvec{D}}\right)=\frac{\partial {\mathbb{C}}\left({\varvec{D}}\right)}{\partial {\varvec{D}}}:\Delta {\varvec{D}}$$
(7)

The microcracks in rock sample are appearance of tensile strain at the macroscopic level. A second rank symmetric damage tensor D based on tensile strain is introduced to describe the extent and orientation of microcracks [6]. The generalized tensile strain \({{\varvec{\varepsilon}}}^{+}\) is defined as the positive cone of the total strain tensor (Eq. 8).

$$ {\varvec{\varepsilon}}^{ + } = \mathop {\sum \left\langle {\varepsilon_{i} } \right\rangle }\limits_{i = 1}^{3} u_{i} \otimes u_{i} $$
(8)
$$\langle \varepsilon _{i} \rangle = \left\{ {\begin{array}{*{20}c} {\varepsilon _{i} } & {{\text{if}}\,\varepsilon _{i} > 0} \\ 0 & {{\text{if}}\,\varepsilon _{i} \le 0} \\ \end{array} } \right.$$

Assuming the damage is conjugated with the generalized tensile strain, the simple expression of damage increment can be written in Eq. 9 [6, 17]. Meanwhile, the orientation information of tensile strain is transferred to damage increment in the second-order tensor.

$$\Delta {\varvec{D}}={d\lambda }_{d}\frac{{{\varvec{\varepsilon}}}^{+}}{\sqrt{{{\varvec{\varepsilon}}}^{+}:{{\varvec{\varepsilon}}}^{+}}}$$
(9)

A damage criterion in the form of generalized tensile strain \({{\varvec{\varepsilon}}}^{+}\) and damage is taken after Chiarelli et al. [6] and modified in Eq. 10, in which a maximum damage is introduced to limit the damage ceiling.

$${f}_{d}\left({{\varvec{\varepsilon}}}^{+},{\varvec{D}}\right)=\sqrt{{{\varvec{\varepsilon}}}^{+}:{{\varvec{\varepsilon}}}^{+}}-\left[{r}_{0}+\frac{{r}_{1}}{{\left(1-\frac{\mathrm{tr}{\varvec{D}}}{{D}_{\mathrm{max}}}\right)}^{{k}_{\mathrm{d}}}}\cdot \mathrm{tr}{\varvec{D}}\right]$$
(10)

The value of upper limit \({D}_{\mathrm{max}}\) could be larger than one, as it compares with the trace of damage tensor. Another constant \({k}_{\mathrm{d}}\) also controls the damage evolution rate. Figure 2 displays the damage envelopes for different values of material variables with set \({f}_{d}\left({{\varvec{\varepsilon}}}^{+},{\varvec{D}}\right)=0\). Figure 2a plots the damage envelope for different values of constant kd. The initial damage threshold, as it will be seen, determines the starting point for damage envelope. After that, the damage grows with increasing tensile strain \(\sqrt{{{\varvec{\varepsilon}}}^{+}:{{\varvec{\varepsilon}}}^{+}}\), and the growing rate gradually slows down with the value of damage approaching upper limit. Obviously, a higher value of kd means slower evolution rate for damage. The damage evolution rate r1 has a similar effect on damage evolution rate (Fig. 2b), which shows a negative correlation with tensile strain as well.

Fig. 2
figure 2

The damage envelope for different values of material parameters, a constant kd; b damage evolution rate r1

Full size image

The plastic loading–unloading conditions, often referred to as the Karush–Kuhn–Tucker conditions [27], are written as follows

$${f}_{d}\ge 0,\quad {d\lambda }_{d}\ge 0,\quad { d\lambda }_{d}{f}_{d}=0$$
(11)

For the consistency condition, the derivative of damage criterion should be zero.

$$\Delta {f}_{d}=\frac{\partial {f}_{d}}{\partial {\varepsilon }^{+}}:\Delta {\varepsilon }^{+}+\frac{\partial {f}_{d}}{\partial D}:\Delta D=0$$
(12)

Substituting Eq. 9 in Eq. 12 gives

$$\frac{\partial {f}_{d}}{\partial {\varepsilon }^{+}}:\Delta {\varepsilon }^{+}+{d\lambda }_{d}\frac{\partial {f}_{d}}{\partial {\varvec{D}}}:\frac{{{\varvec{\varepsilon}}}^{+}}{\sqrt{{{\varvec{\varepsilon}}}^{+}:{{\varvec{\varepsilon}}}^{+}}}=0$$
(13)

Thus, the damage multiple is derived in the following equation

$${d\lambda }_{d}=\frac{{\left({D}_{\mathrm{max}}-\mathrm{tr}{\varvec{D}}\right)}^{{k}_{\mathrm{d}}+1}}{{{D}_{max}}^{{k}_{\mathrm{d}}+1}+{{D}_{\mathrm{max}}}^{{k}_{\mathrm{d}}}\mathrm{tr}{\varvec{D}}\left({k}_{\mathrm{d}}-1\right)}\cdot \frac{{{\varvec{\varepsilon}}}^{+}:{\Delta{\varvec{\varepsilon}}}^{+}}{{r}_{1}\cdot \mathrm{tr}{{\varvec{\varepsilon}}}^{+}}$$
(14)

Apparently, the total strain increment is composed of elastic and plastic strain, if the plastic deformation takes place in the REV.

$$\Delta \varepsilon ={\Delta \varepsilon }^{\mathrm{e}}+\Delta {\varepsilon }^{\mathrm{p}}$$
(15)

Substituting Eq. 15 in Eq. 6, the stress increment can be reformulated as

$$ \Delta {\varvec{\sigma}}^{\prime} = {\mathbb{C}}\left( {\varvec{D}} \right):\left( {\Delta {\varvec{\varepsilon}} - \Delta {\varvec{\varepsilon}}^{p} } \right) + \Delta {\mathbb{C}}\left( {\varvec{D}} \right):{\varvec{\varepsilon}}^{e} $$
(16)

In this work, the rock mass is assumed as porous geo-material containing joint. As shown in Fig. 3, plane with a statistically dominant direction n is positioned in the matrix to represent the joint in this element. The corresponding plastic failure criterion in the current model is formulated based on the classic ubiquitous joint model [8], in which a hardening/softening parameter is considered. The shear and tensile failure criterions on matrix are formulated on the global coordinate system (Eq. 17 and 18).

$${f}_{m}^{s}\left(\sigma , {\varepsilon }_{p},D\right)={\sigma }_{1}-{\sigma }_{3}{N}_{\varphi }\eta +2c\sqrt{{N}_{\varphi }}\eta $$
(17)
$${f}_{m}^{t}\left(\sigma \right)={\sigma }_{3}-{\sigma }^{t}\eta $$
(18)

where \({N}_{\varphi }=\frac{1+\mathrm{sin}\varphi }{1-\mathrm{sin}\varphi }\)

Fig. 3
figure 3

Jointed rock mass with the joints dominant in n direction

Full size image

For the shear and tensile failure criterions on joint, Eqs. 19 and 20 are formulated on a local coordinate system, which is generated on the joint plane.

$${f}_{j}^{s}\left(\sigma , {\varepsilon }_{p},D\right)=\tau +{\sigma }_{{z}^{^{\prime}}}\,\,\mathrm{tan}{\varphi }_{j}\eta -{c}_{j}\eta $$
(19)
$${f}_{j}^{t}\left(\sigma \right)={\sigma }_{{z}^{^{\prime}}}-{\sigma }_{j}^{t}\eta $$
(20)

The hardening/softening parameter is given in the form of damage and plastic strain.

$$\eta \left({k}_{m}\right)={\left(1-\mathrm{tr}{\varvec{D}}\right)}^{R}\left[1+\left({\eta }_{m}-1\right)\frac{{k}_{m}}{{b}_{1}+{k}_{m}}\right]$$
(21)
$${k}_{m}=\frac{1}{3}\sqrt{{\left({\varepsilon }_{1}^{p}\right)}^{2}+{\left({\varepsilon }_{2}^{p}\right)}^{2}+{\left({\varepsilon }_{3}^{p}\right)}^{2}}$$
(22)

The plastic strains (\({\varepsilon }_{1}^{\mathrm{p}}\),\({\varepsilon }_{2}^{\mathrm{p}}\),\({\varepsilon }_{3}^{\mathrm{p}}\)) are three plastic strains corresponding to the principal direction. The hardening/softening behaviours with respect to damage and plastic deformation are illustrated in Fig. 4, respectively. Generally, the hardening parameter \({\eta }_{m}\) has a value over one, as the yield surface in common is higher than plastic onset surface. The final yield surface declines with smaller value of parameters \({\eta }_{m}\), and an ideal plastic behaviour is observed at \({\eta }_{m}=1\), where the yield surface and plastic surface are coincident (Fig. 4a). The damage-dependent softening behaviour is plotted in Fig. 4b. The parameter R confers a curvature of softening behaviour, which degenerates into in liner correlation at R = 1.

Fig. 4
figure 4

Correlation of hardening/softening parameters \({\eta }\) with a the plastic deformation Km and b the damage trD

Full size image

The plastic increment can be obtained by solving the following equation.

$$\Delta {{\varvec{\upvarepsilon}}}^{\mathrm{p}}=\mathrm{d}{\lambda }_{p}\frac{\partial {g}_{p}}{\partial{\varvec{\sigma}}}$$
(23)

Non-associated potential functions are adopted in this work. Corresponding shear and tensile potential functions on matrix are presented in Eqs. 24 and 25, respectively.

$${g}_{m}^{s}={\sigma }_{1}-{\sigma }_{3}{N}_{\theta }\eta $$
(24)
$${g}_{m}^{t}={\sigma }_{3}$$
(25)

Similarly, the shear and tensile potential functions on joint are written in the following equations

$${g}_{j}^{s}=\tau +{\sigma }_{{z}^{^{\prime}}}\mathrm{tan}{\varphi }_{j}\eta $$
(26)
$${g}_{j}^{t}={\sigma }_{{z}^{^{\prime}}}$$
(27)

The corresponding loading–unloading conditions for plastic evolution are given as follows

$${f}_{p}\le 0,\quad {d\lambda }_{p}\le 0,\quad { d\lambda }_{p}{f}_{p}=0$$
(28)

As the damage has been determined according to known total strain tensor, only the plastic strain and stress are left as unknown. Likewise, considering the consistency condition, the derivative of failure criterion with respect to plastic strain and stress should be zero.

$$\Delta {f}_{p}=\frac{\partial {f}_{p}}{\partial{\varvec{\sigma}}}:\Delta{\varvec{\sigma}}+\frac{\partial {f}_{p}}{\partial \eta }\Delta \eta =0$$
(29)
$$\Delta \eta =\frac{\partial \eta }{\partial {{\varvec{\varepsilon}}}^{{\varvec{p}}}}:\Delta {{\varvec{\varepsilon}}}^{{\varvec{p}}}$$
(30)

Substituting Eqs. 30 and 16 in Eq. 29, then the current plastic multiple can be archived as

$${d\lambda }_{p}=\frac{\frac{\partial {f}_{p}}{\partial{\varvec{\sigma}}}:\left[{\mathbb{C}}\left({\varvec{D}}\right):\Delta{\varvec{\varepsilon}}+\Delta {\mathbb{C}}\left({\varvec{D}}\right):{\varepsilon }^{e}\right]}{\frac{\partial {f}_{p}}{\partial{\varvec{\sigma}}}:{\mathbb{C}}\left({\varvec{D}}\right):\frac{\partial g}{\partial{\varvec{\sigma}}}-\frac{\partial {f}_{p}}{\partial \eta }\left(\frac{\partial \eta }{\partial {{\varvec{\varepsilon}}}^{{\varvec{p}}}}:\frac{\partial g}{\partial{\varvec{\sigma}}}\right)}$$
(31)

2.3 Permeability model

The permeability change during fracturing consists of two parts. One is caused by effective compression stress and the other one by damage. Considering the permeability change under varying effective stress, the pore, pre-existing cracks or even induced cracks can be compressed with an increasing effective stress, resulting in decreasing the permeability, and vice versa. As damage in this work is converted from crack characteristic namely tensile strain, the damage-induced permeability can be approximated by cubic law of damage, which is widely used to characterize flow behaviour between fracture apertures [15]. Here, an isotropic impact of compression stress is taken after Zhang [36] and modified in terms of effective mean stress in Eq. 35.

$${K}_{D}={{K}_{0}c}_{2}{\left(\mathrm{tr}{\varvec{D}}\right)}^{3}$$
(32)
$${f}_{\mathrm{es}}={c}_{1}+\left(1-{c}_{1}\right)\mathrm{exp}\left(-\gamma \langle {-\sigma }_{m}^{^{\prime}}\rangle \right)$$
(33)

The impact of compression stress for different values of parameters is illustrated in Fig. 5a, b. The parameter c1 determines the lower limit that can be compressed. The parameter γ, which confers a curvature to the evolution curve, determines the difficulty for compressing. Apparently, a higher value of parameter γ means that the rock is much easier to be compressed. Figure 5c illustrates the damage-induced permeability with an initial permeability at k0 = 1 × 10−20m2. The parameter c2 controls the maximum induced permeability as well as growing rate after failure, which is related to rock type.

Fig. 5
figure 5

Evolution of permeability and the impact of compression stress for different values of parameters a c1 and b γ, c the damage-induced permeability for different values of parameter c2

Full size image

Considering the impact of compression stress, the induced permeability can be written as

$$K={{f}_{\mathrm{es}}({K}_{0}+K}_{D})=\left[{c}_{1}+\left(1-{c}_{1}\right)\mathrm{exp}\left(-\gamma \langle {-\sigma }_{m}^{^{\prime}}\rangle \right)\right]{K}_{0}\left[1+{c}_{2}{\left(\mathrm{tr}{\varvec{D}}\right)}^{3}\right]$$
(34)

In this model, the equivalent permeability of failure rock is anisotropic, whose anisotropy is dependent on the induced cracks at microscopic scale. Furthermore, cracks’ direction is strongly correlated with different loading types. As illustrated in Fig. 6, Maleki and Pouya [17] used an ellipsoid to explain the normalized permeability distribution under different loading types. The induced permeability was evaluated based on indicator of crack density in a radial rotating cut plane. Thirty-six cut planes, each with 10° rotation angle, were evaluated. Radial axis is the normalized permeability that equals the ratio of obtained permeability to the maximum permeability. The normalized permeability distributes itself symmetrically with respect to the cut plane having 0°, which corresponds to axial direction of sample cylinder. The maximum induced permeability in compression case (Fig. 6a), observed from crack density, distributes in vertical direction. Yet, in Fig. 6b, most of cracks are measured in horizontal direction under extension case. The permeability in case of isotropic loading is assumed isotropic. In this work, with the help of a linear interpolation, the permeability direction of a general case can be interpreted by a combination of forementioned loading types. The expression of anisotropic permeability tensor relating to damage and loading types can be written as

$$ {\varvec{K}}_{{\varvec{D}}} = \frac{{K_{D} }}{{tr{\varvec{D}}}}\left\{ {\left[ {\alpha_{e} \left( {d_{1} - d_{2} } \right) + 2\alpha_{c} \left( {d_{2} - d_{3} } \right) + d_{3} } \right]\delta + \left( {d_{1} - d_{2} } \right)\left( {1 - 3\alpha_{e} } \right)e_{1} \otimes e_{1} + 2\left( {d_{2} - d_{3} } \right)\left( {1 - 3\alpha_{c} } \right)e_{3} \otimes e_{3} } \right\} $$
(35)

where \({\alpha }_{c}=\frac{1}{4}\) and \({\alpha }_{e}=\frac{5}{12}\) refers to [17].

Fig. 6
figure 6

Normalized permeability ellipsoid in radial plane along vertical direction of different types [17]

Full size image

Then, the total permeability tensor can be written as follows

$${\varvec{K}}={{f}_{\mathrm{es}}({\varvec{K}}}_{{\varvec{D}}}+K_{0}{\varvec{I}})$$
(36)

2.4 Fluid and heat flow

In this work, the fluid and heat flow are solved with the help of popular code TOUGH2MP [37], in which the fracture network is also treated as a “porous medium”, for which the equivalent permeability in anisotropy is updated according to damage component (Eq. 36). Local thermal equilibrium condition is assumed to describe the fluid transfer in pore. The flow of all mobile phases obeys Darcy’s law in pore space. Only aqueous phase is considered in this work.

2.5 Coupling process

As shown in Fig. 7(a), the coupling cyclical is realized on the fundament of TOUGH2MP-FLAC3D coupling framework. The above-mentioned anisotropic damage and permeability are implemented and integrated in the mechanical code FLAC3D using dll file (dynamic link library) (M). With known strain, the corresponding damage, stress and permeability tensor can be determined by solving Eqs. 10, 16 and 35 in succession. Then the updated permeability is sent to TOUGH2MP for fluid calculations, involving hydraulic process (H), in which the newly computed pressure will be sent back to FLAC3D for updating new strain. The multi-models are coupled through coupling parameters marked in red. The specific parameters transferred among different models and time steps are illustrated in Fig. 7(b).

Fig. 7
figure 7

a computing schema and coupling principle of the coupled simulator, b data flow between different models and time steps

Full size image

3 Model calibration and validation

In this section, several triaxial test examples for calibration of plastic deformation, damage, permeability and its anisotropy on hard rock are discussed separately. To calibrate the elastoplastic and damage model, complete knowledge of stress–strain curve and damage measurement in a triaxial configuration are necessary. Fortunately, some test data measured under isothermal condition with a confining pressure of 10 MPa on the Beishan granite from China were reported in the work of Chen et al. [4]. Available material parameters of intact rock including the elastic parameters from Chen et al. [4] and friction angle from Chen et al. [5] are listed in Table 1. As shown in Fig. 8a, the simulated axial stress of intact rock is plotted against the simulated axial strain to compare the simulated results from Chen et al. [4]. The parameter \({\eta }_{m}\) is measured from the plastic onset and yield point. However, the onset of plasticity is not always trivial to detect. In this case, the onset of plasticity is determined as the deviation from linearity of elastic behaviour in stress–strain curve, and the yield surface is determined as the peak value. The rest of the plastic parameters R, b1 and damage parameter \({a}_{1}\), \({a}_{2}\) are archived by stress–strain curve matching of measured strain–stress curve. The damage parameters r0, Dmax are determined from the tensile strain at damage initiation and maximum value, respectively (see in Fig. 8b). As the simulated damage of the present model is averaged from three principal components in damage tensor, the damage upper limit is set as 1.2. Likewise, parameters r1, kd are determined by strain–damage curve matching. The calibration parameters that achieve a good agreement between simulated and existing data are summarized in Table 1.

Table 1 Calibration parameters of different granite
Full size table
Fig. 8
figure 8

Comparing a the stress–strain curve and b simulated damage of Beishan granite

Full size image

The permeability function in Eq. 34 involving parameters c1, c2, γ is calibrated by the data from a triaxial test on the intact granite from Lac du Bonnet [29]. The testing condition and sample quality are the same as the first example. The damage was evaluated in previous simulation work of Jiang et al. [11]. The plastic parameter and damage parameters are calibrated in the same procedure as the first example. To calibrate the permeability, the parameter k0 is the initial permeability, which is determined directly at the point with zero deviatoric stress. And parameter c1 is detected from the lowest value. As shown in Fig. 9, parameter γis achieved by nonlinear regression on the first curve of measured permeability. However, the lack of data in the post-peak makes it difficult to detect the maximum permeability directly from the measured data. In this case, the parameter c2 is thus determined through nonlinear regression on the second curve after damage initiation. All the calibration parameters are summarized in Table 1.

Fig. 9
figure 9

Comparing a the stress–strain curve and b simulated damage and permeability of Lac du Bonnet granite

Full size image

To check the feasibility of anisotropic permeability model, two triaxial tests on the intact granodiorite from Cerro Cristale and the intact granite from Westerly are simulated under a confining pressure of 10 MPa and compared with the measured permeability. Likewise, an isothermal condition and a dry condition were used in this example. All used parameters are summarized in Table 1. The simulated results are shown in Figs. 10 and 11. The axial and radial stress–strain curve of the present model matches the measured data well, except for the radial-strain curve of Westerly granite, because the unexpected nonlinear behaviour at the beginning of test is difficult to be captured (Figs. 10a and 11a). As shown in Figs. 10b and 11b, the simulated and measured permeability has a slight decline at the beginning of loading, under the effect of increasing compression stress. Then, the permeability stays at a constant level. With continuous loading, the permeability increases gradually into two different values relating to axial and radial directions. The permeability in axial direction shows a good agreement with measured permeability detected in the axial direction while the permeability in radial direction is relatively low, within twice the difference, as the cracks mostly activated in vertical direction significantly enhance the permeability in axial direction in a compression test [17].

Fig. 10
figure 10

Comparing a the stress–strain curve and b simulated anisotropic permeability of Cerro Cristale granodiorite

Full size image
Fig. 11
figure 11

Comparing a the stress–strain curve and b simulated anisotropic permeability of Westerly granite

Full size image

4 Field experiment and geological model

The field hydraulic fracturing test was implemented at 410 m depth at Aspö Hard Rock Laboratory, Sweden, attempting to optimize the geothermal heat exchange in crystalline rock mass by cyclic injection with minimal impact on the environment, namely seismic events. As shown in Fig. 12, the fracturing was conducted in a borehole drilled from tunnel. Many sensors were installed to record the seismic events during fracturing. Overall, 6 fracturing stages were carried out. More information for the fracturing test can be found in references [16, 35, 40]. In this work, the second stage (HF2 in black rectangle) is selected to conduct the simulation. A brick model with a declination angle of 28° from the North is generated in the dimensions of 60 m × 40 m × 40 m. In the light of measured seismic events trace, a target fracture plane with dip angle of 60° is inserted in this model. And the injection point is placed at the intersection of fracture plane and injection well, which is drilled along y-direction in this model. Referring to [35], the initial stress with known orientation is illustrated in the stereographic projection with fracture plane, in which the minimum initial stress (σ3) of 8.6 MPa is estimated from the instantaneous shut-in pressure, while the other two initial stresses of 10 MPa and 22.6 MPa are taken from the experimental near field.

Fig. 12
figure 12

Model generation and stress information

Full size image

The dominant rock type is Ävrö granodiorite. Its intact rock’s Young’s modulus of 76 MPa and Poisson ratio of 0.25 is taken from the laboratory test by Andersson and Martin [2]. Tensile strength of 4.2 MPa is detected from pressure curve during cyclic fracturing [35]. Considering the possible pre-existing natural fractures or joints, a much sensitive damage evolution rate with parameter r1 = 1 × 10–4, r0 = 1 × 10–3 and low damage ceiling are adopted, so does a low friction angle of 43°. Generally, pre-existing natural fractures or joint reduce the peak strength, a low ratio ηm = 1.4 is thus considered. Other plastic and damage parameters adopt the same values as of Cerro Cristale granodiorite in Table 1. The joints in matrix are parallel to the potential fracture plane. Corresponding plastic parameter on joint has 20% reduction, in comparison with the one on intact rock. The permeability parameter is also taken from Cerro Cristale granodiorite, except for a higher initial permeability of 1 × 10–18 m2 and maximum damage-induced permeability, for compatibility with the measured data. All the applied parameters are summarized in Table 2.

Table 2 Applied parameters for the simulation
Full size table

In this model, the normal displacement on the bottom and four sides is fixed, while on the top side is free. The initial stress of −22.6 MPa, −8.8 MPa and −9.5 MPa is applied in x-, y- and z-directions. Initial pore pressure is converted from the hydrostatic pressure. In this model, the changed stress state due to water injection will trigger the damage. Once damage is initiated, the original element is converted into fractured element. The anisotropic permeability in fractured element largely determines the flow direction and fracture propagation direction. The final cluster of fractured elements is used to represent the stimulated fracture.

5 Results and discussion

The second stage, including one pre-fracturing, one main fracturing (MF) and 5 re-fracturing (RF), was carried out by water injection according to the injection scheme (see the blue line in Fig. 13). Except the pre-fracturing, other fracturing and inter-flow back (MFB and FB) are simulated one by one, using this anisotropic damage–permeability model. Figure 13 shows the simulated and measured injection pressure recorded in the injection well under the cyclic injection treatment. A good agreement is observed between measured and simulated results, except for the peak pressure in main fracturing. As the pre-fracturing is not considered in this model, the breakdown pressure in virgin rock causes a significant high value in main fracturing.

Fig. 13
figure 13

Injection pressure during fracturing, PF: pre-fracturing; MF: main fracturing; 1 ~ 5.RF: 1 ~ 5 re-fracturing; MFB: flow back after main fracturing; 1 ~ 5.FB: flow back after 1 ~ 5 re-fracturing

Full size image

The fracture geometry in cyclic fracturing is compared in Fig. 14, respectively. A quasi-circle fracture with radius of about 3 m is created after the main fracturing, and the fracture propagate continuously with re-injection. Finally, the fracture grows into a circular shape with a radius of about 6 m. The fracture in second and fourth re-fracturing (2.RF and 4.RF) has only a slight or even no growth, because the injection duration is too short to completely re-activate the closed fracture from previous flow back. This phenomenon could be observed also from individual SRV increment (stimulated reservoir volume), which is the accumulated volume of fractured element (see in Fig. 15). During re-fracturing, the declined pressure due to flow back should be built up firstly inside the closed fracture. Only when the built pressure front reaches the fracture tip, fracture propagation can be re-activated again. Therefore, prolonged injection can promote the fracture propagation, as compared in second–third and fourth–fifth re-fracturing pairs. Additionally, the SRV in fifth re-fracturing is significantly higher than the one in third re-fracturing, which indicates that the injection rate is another important factor affecting the fracture propagation in re-fracturing.

Fig. 14
figure 14

Stimulated fracture after different fracturing stages

Full size image
Fig. 15
figure 15

Illustration of accumulated stimulated reservoir volume and simulated reservoir volume increment in each fracturing and re-fracturing

Full size image

The flow back between every adjacent fracturing and re-fracturing is carried out under a fixed injection pressure at atmosphere pressure (see in Fig. 13). Then, the fluid contents accumulated in the period of flow back are compared with the measured results in Fig. 16a. Obviously, the value of simulated and measured results is very close, which is confirmed by the linear coefficient over 0.98 in Fig. 16b. Yet, a significant underestimation of simulated results is observed in second flow back, for the simulated reservoir pressure in second flow back is lower than measured, which can be observed from the mismatched injection pressure in second re-fracturing in Fig. 13.

Fig. 16
figure 16

Comparing the simulated and measured flow-back content

Full size image

The anisotropic permeability of created fracture after main fracturing is illustrated in x-, y- and z-directions, respectively, in Fig. 17. The maximum permeability of about 4 × 10–14 m2 is enhanced around injection well and the permeability in x- and z-direction is relatively higher than in y-direction. The direction of maximum permeability is parallel to the fracture plane. Hou et al. [10] suggested an average permeability weighted based on the distance from injection well to characterize the conductivity of hydraulic fracture (Eq. 37). The average permeability in fracture plane is compared with the experimental results in Fig. 18. The simulated permeability increases gradually with fracturing process while a slight degradation of measured permeability after first re-fracturing is not captured in the simulation results, as the irreversible damage is considered in this model. However, the simulated results having a difference less than twice are still acceptable. The permeability greatly varies ranging from 1 × 10–18 to 4 × 10–14.

Fig. 17
figure 17

Directional permeability after main fracturing

Full size image
Fig. 18
figure 18

Distance-weighted average permeability after different fracturing stages

Full size image
$$k=\frac{{\sum }_{i=1}^{n}\frac{{V}_{i}}{{l}_{i}}{K}_{i}}{{\sum }_{i=1}^{n}\frac{{V}_{i}}{{l}_{i}}}$$
(37)

The damage data acquired in simulation are displayed by the beach balls in the software ParaView. In the damage tensor, the three components (dx, dy, dz) as well as mean value (dm = (dx + dy + dz)/3) are illustrated in Fig. 19, respectively. The maximum damage is found in y-direction, which is consistent with the direction of the minimum principal stress. And a negligible damage is induced in x-direction. As the damage conjugates with tensile strain (see in the Eq. 10), the damage dominant in y- and z-direction indicates that the fracture propagation is mostly triggered by tensile failure. The maximum approximate value of mean damage of 0.22 is found around injection well, which decreases with increasing distance from injection well. The mean damage distribution is shown in Fig. 20 by each fracturing and re-fracturing. The damage evolution is consistent with fracture propagation, and the maximum value increases gradually with fracturing, because, even in created fracture from previous fracturing, some new damage will be produced during re-fracturing, due to the re-activation of closed fracture.

Fig. 19
figure 19

Demonstration of directional damage component and mean damage at main fracturing stage

Full size image
Fig. 20
figure 20

The mean damage at different fracturing and re-fracturing

Full size image

After fifth re-fracturing, the induced stress shadow, namely compression stress and created fracture, is shown in a side view in Fig. 21. The maximum induced compression stress of about -5 MPa distributes in the middle of fracture and decreases gradually towards fracture tip. Indeed, a tensile stress (negative value) is induced around the fracture tip. After fifth re-fracturing, both tensile and shear plastic strain with fracture framework are exhibited in Fig. 22a, b, respectively. The tensile plastic strain of3.3 × 10–3 is obviously higher than the shear plastic strain, which means that mostly tensile failure occurs during fracturing. This phenomenon coincides with the observations in the work of López-Comino et al. [16].

Fig. 21
figure 21

The stress shadow after fifth re-fracturing

Full size image
Fig. 22
figure 22

Comparing the a tensile strain and b shear strain on the fracture plane after fifth re-fracturing

Full size image

The created fracture profiles are compared with the measured seismic events in Fig. 23. In the top view, the measured seismic events are located within the boundary of fracture, but concentrate only on one side of injection well, because the pre-existing fractures or damage induced by drilling are not considered in this model. From the side view, the measured seismic events are highly coincident with the fracture trace beyond injection well. Similarly, the measured seismic events along the injection well are not captured by the simulated fracture, because the hydraulic fracture is arrested by the drilling triggered damage and turns the direction to injection well. In spite of this, the simulated fracture captures the main characteristics of measured seismic events.

Fig. 23
figure 23

Comparing the scope of created fracture with measured seismic events in different perspectives, a top view and b front view

Full size image

6 Conclusion

In this work, an anisotropic damage–permeability model is developed on the fundament of continuum theory, in which the plastic–damage is a direct extension and improvement of the model previously developed in the work of Chiarelli et al. [6]. In this plastic–damage model, a maximum damage is introduced for controlling the damage ceiling, and plasticity-hardening and damage-softening behaviours are considered by a function with the variables of plastic strain and damage. The permeability enhanced by damage is approximated by a cubic law, and an impact factor is adopted to characterize the isotropic effect of compression stress on permeability. The stress-induced permeability is isotropic, while the damage-induced permeability is anisotropic, whose directional information is converted from damage tensor. Then, the corresponding variables of this model are calibrated by the measured damage, axial permeability and stress–strain curve from two triaxial tests on granite. And the feasibility of the anisotropic permeability is checked through comparing with the measured permeability from additional two triaxial tests on granodiorite and granite.

The newly developed model has been applied to study the cyclic fracturing test at Aspö Hard Rock Laboratory, and the simulated injection pressure, flow-back content and averaged permeability are compared to the experimentally measured data. Good agreement between experimental and numerical predictions shows that the developed model is suitable to simulate the hydraulic fracturing in hard rock, e.g. granite. In analysis of the fracture propagation, the fracture will be closed during flow back and re-activated in subsequent re-fracturing. If the created fracture in previous fracturing is not re-activated completely, no new fracture will be created in current re-fracturing. And the damage accumulated continuously due to repeated re-activation of closed fracture during re-fracturing. The significant plastic tensile strain indicates that the created fracture is mostly triggered by tensile failure in this case. The simulated fracture can capture the domain features of measured seismic events. However, still some measured seismic events locate out of the fracture profile as a result of the pre-existing microcracks, and drilling-induced damage is not considered in this model.

The main limitation of this approach is that the adopted phenomenological damage model by means of tensile strain cannot explicityly descreibe the growth and deformation beahviour of microcracks at microscropic scale, which will be addressed by introducing the friction-damage model [38, 39] in our future work.