Hydromechanical state of soil fluidisation: a microscale perspective

Abstract

This paper investigates soil fluidisation at the microscale using the discrete element method (DEM) in combination with the lattice Boltzmann method (LBM). Numerical simulations were carried out at varying hydraulic gradients across the granular assembly of soil. The development of local hydraulic gradients, the contact distribution, and the associated fabric changes were investigated. Microscale findings suggest that a critical hydromechanical state inducing fluid-like instability of a granular assembly can be defined by a substantial increase in grain slip associated with a rapid reduction in interparticle contacts. Based on these results, a new micromechanical criterion is proposed to characterise the transformation of granular soil from a hydromechanically stable to an unstable state. The constraint ratio (ratio of the number of constraints to the number of degrees of freedom) is introduced to portray the relative slippage between particles and the loss of interparticle contacts within the granular fabric. Its magnitude of unity corresponds to the condition of zero effective stress, representing the critical hydromechanical state. In practical terms, the results of this study reflect the phenomenon of subgrade mud pumping that occurs in railways when heavy-haul trains pass through at certain axle loads and speeds.

1 Introduction

A major problem leading to railroad instability that creates immense maintenance costs is related to the degradation of the soft subgrade and its potential for fluidisation or mud-pumping [7, 13, 24, 30, 40]. In this context, fluidisation is defined as when saturated soils are exposed to excessive hydraulic gradients and lose their intergranular contacts to transform into a fluid-like state. As a result, this slurry of fine particles migrates (pumps) into the overlying coarser ballast layer, hence the commonly used term mud-pumping, as investigated experimentally [2, 13, 27, 30]. These laboratory tests enable a better understanding of the hydromechanical behaviour of the subgrade soils, but primarily at the macroscale. From a micromechanical perspective, i.e. at the grain level, slippage and/or breakage of the interparticle contacts and the resulting fabric evolution may initiate the transition from a hydromechanically stable to an unstable state that is still not fully understood. Hydromechanically stable state means that the effective stresses are still present in the soil layer to resist fluidisation. The unstable state means that there are no effective stresses in the layer, and the soil has fluidised after experiencing a higher number of broken contacts and zero shear resistance.

The discrete element method (DEM) is a useful tool for assessing the micromechanics of a granular medium [11, 42] that has been effectively used to study the evolution of interparticle contacts and fabric during shear using the scalar and directional parameters [3, 15, 16, 50]. In this study, the scalar parameters are chosen for the purpose of analysis since the fluidisation behaviour is closely related to scalar measurements of the fabric. The coordination number (number of contacts per particle in the granular assembly) is a fundamental microscale fabric descriptor for characterising granular medium [15, 50]. Nonetheless, the state of interparticle contacts and fabric during fluid flow has rarely been considered. In addition, the constraint ratio, defined by the ratio of the number of constraints to the number of degrees of freedom within the particle system [12], can be used to represent the relative slip and loss of interparticle contacts during instability.

The primary scope of this paper includes an attempt to describe and quantify the critical hydromechanical conditions corresponding to the fluidisation phenomenon with special attention to granular soil at the microscale, adopting the concepts of the coordination number and the constraint ratio, as mentioned above. In this context, the DEM can be combined with unresolved and resolved computational fluid dynamics (CFD) to study fluid-particle interaction in detail [6, 38, 39, 54]. Neither of these studies could accurately quantify the critical hydromechanical conditions leading to potential fluidisation from a microscale perspective, so a more insightful microscale study of this instability process is needed.

In view of the above, this study uses a combined LBM-DEM approach that is becoming increasingly popular to investigate fluid-particle interactions [4, 17, 18, 21, 29, 36, 55]. The advantages of fully resolved approaches (using LBM) over unresolved approaches include (a) the ability to generate a much finer mesh size, i.e. finer than the particles that can simulate true experimental conditions, (b) a higher computational speed when executed on parallel computers and, (c) the relative feasibility of implementation in complex geometries of porous media [19, 44]. In addition, the LBM is based on the kinetic theory of gases and represents a fluid through an assembly of particles that go through successive collision and propagation processes. This enables the calculation of the macroscopic fluid velocity and the pressure as a function of the momentum of these particles [44, 46].

2 Lattice Boltzmann method (LBM) combined with discrete element method (DEM)

The theoretical formulations of the LBM-DEM approach are described as follows:

2.1 Fluid equations

The governing Boltzmann equation is written as [8]:

$$ \frac{{\partial f_{\alpha } \left( {x, t} \right)}}{\partial t} + e_{\alpha }^{v} \nabla f_{\alpha } \left( {x, t} \right) = \Omega_{\alpha } \quad \left( {\alpha = 1,2, \ldots \ldots \ldots ..,N } \right) $$

(1)

where $f_{\alpha } \left( {x, t} \right)$ is the particle distribution function in the $\alpha$ direction, $e_{\alpha }^{v}$ is the microscopic fluid velocity and $\Omega_{\alpha }$ is the collision operator, and $t$ is the time. Equation (1) can be discretised on a regular lattice using a unique finite difference method, and the lattice Boltzmann equation with the Bhatnagar–Gross–Krook (BGK) collision operator for a Newtonian fluid is written as [5, 8]:

$$ f_{\alpha } \left( {x + e_{\alpha }^{v} \Delta t, t + \Delta t} \right) - f_{\alpha } \left( {x, t} \right) = \Omega_{\alpha }^{{{\text{BGK}}}} $$

(2)

where $\Omega_{\alpha }^{{\text{BGK}}}$ is the BGK collision operator, and $\Delta t$ is the time step.

Each time step is divided into two sub-steps, i.e. the collision and streaming step, and the collision step is written as:

$$ f_{\alpha } \left( {x,t^{*} } \right) = f_{\alpha } \left( {x, t} \right) + \Omega_{\alpha }^{{\text{BGK}}} $$

(3)

$f_{\alpha } \left( {x,t^{*} } \right)$ and $f_{\alpha } \left( {x, t} \right)$ are the particle distribution functions after and before the collision, respectively, and $t^{*}$ is the time after the collision. In the streaming step, the $f_{\alpha } \left( {x,t^{*} } \right)$ is propagated over the lattice grid as follows:

$$ f_{\alpha } \left( {x + e_{\alpha }^{v} \Delta t, t + \Delta t} \right) = f_{\alpha } \left( {x, t^{*} } \right) $$

(4)

2.2 Fluid-particle interaction

The participation of solid particles in the fluid is achieved by introducing an additional collision term ($\Omega_{\alpha }^{s}$) in Eq. (3) [41]:

$$ f_{\alpha } \left( {x,t^{*} } \right) = f_{\alpha } \left( {x, t} \right) + \left[ {1 - B } \right]\Omega_{\alpha }^{{\text{BGK}}} + B\Omega_{\alpha }^{s} $$

(5)

$$ B = \frac{{\varepsilon_{s} \left( {{\raise0.7ex\hbox{$\tau $} \!\mathord{\left/ {\vphantom {\tau {\Delta t}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\Delta t}$}} - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right)}}{{\left( {1 - \varepsilon_{s} } \right) + \left( {{\raise0.7ex\hbox{$\tau $} \!\mathord{\left/ {\vphantom {\tau {\Delta t}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\Delta t}$}} - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right)}} = \left( {0,1} \right) $$

(5)

where $\varepsilon_{s}$ is the solid fraction in the fluid cell volume, $B$ is a weighting function for correcting the collision phase of the lattice-BGK equation due to the presence of solid particles, and $\tau$ is the relaxation time (Appendix 1). The method for calculating the solid fraction for the moving particles is described by Seil [45].

The non-equilibrium part of the particle distribution function is bounced back and $\Omega_{\alpha }^{s}$ is computed using:

$$ \Omega_{\alpha }^{s} = f_{ - \alpha } \left( {x, t} \right) - f_{\alpha } \left( {x, t} \right) + f_{\alpha }^{{\text{eq}}} \left( {\rho_{f}, v^{p} } \right) - f_{ - \alpha }^{{\text{eq}}} \left( {\rho_{f}, u} \right) $$

(7)

where $v^{p}$ is the velocity of solid particle $p$ at time $t + \Delta t$ at the node, $u$ is the macroscopic fluid velocity, and the notation $f_{ - \alpha }$ is the rebound state obtained by reversing all microscopic fluid velocities, i.e. $e_{\alpha }^{v}$ to $e_{ - \alpha }^{v}$. Further details on the fluid equations and the fluid-particle interaction are described in Appendix 1.

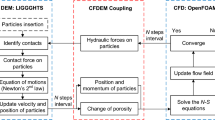
Figure 1 shows the flow chart of the LBM-DEM approach described above. The DEM calculation cycles are within the LBM cycles. A suitable interval for the information transfer was chosen so that the accuracy of the simulation could not be impaired. The DEM code Lammps Improved for General Granular, and Granular Heat Transfer Simulations (LIGGGHTS) was coupled with LBM code PALABOS [33, 45].

Fig. 1

Flow chart of the lattice Boltzmann method (LBM) combined with the discrete element method (DEM)

3 Simulating soil specimen fluidisation

3.1 Simulation approach

Three-dimensional LBM-DEM simulations were carried out using the Hertz-Mindlin contact model (Appendix 2) with the Young's modulus and the Poisson's ratio of the particles as 70 GPa and 0.3, respectively [26, 50]. The particle density was set to 2650 kg/m³, and the rigid boundary walls were used. The most widely employed boundary type includes rigid boundaries with frictional walls (O’Sullivan [42]) and they have been used in the past to simulate fluidisation and internal instability (e.g. Thornton et al. [52], Nguyen and Indraratna [38], Kawano et al. [32]). Based on these past studies, frictional walls as boundary conditions have been adopted in this study. In a real soil column, the use of frictional walls considers the presence of lateral grains. Although periodic boundaries could have been used instead (e.g. Thornton [50]). Rigid frictional boundaries are often more straightforward to implement than periodic boundaries. Not examining the influence of different boundary conditions on the micromechanics of the soil sample is a limitation of the current study. The gravitational deposition method was used for sample preparation [1], whereby the acceleration due to the force of gravity of the particles was set to 9.81 m/s². The particles were initially created in a larger volume with no overlap and then dropped under gravity. The particles were allowed to settle until equilibrium was reached, thereby ensuring that the coordination number remained constant for a sufficient number of numerical cycles. The sample was prepared in a dense state by setting the coefficient of friction (µ_s) to 0 [1, 9, 26]. Subsequently, µ_s was changed to 0.30, and the particles were re-equilibrated with a sufficient number of numerical cycles before the particles became saturated with the fluid [9, 50]. The µ_s value used in this study is in the range of real quartz particle values that can be determined experimentally with a micromechanical interparticle loading apparatus (e.g. [47]). It is assumed that the particle–wall contact parameters correspond to the particle–particle contact parameters [22].

The fluid density was set to 1000 kg/m³ with a kinematic viscosity of 1 × 10^–6 m²/s according to pure water properties at 20 °C and 1 atmosphere (101 kPa). The resolution of the fluid lattice was chosen with at least five lattices in each particle, i.e. the smallest particle diameter corresponds to at least five fluid cells with regard to the validation of the single particle displaced downwards into the fluid as described previously. A relaxation parameter close to but greater than 0.50 was chosen, and the Mach number was kept below 0.1, inspired by the need for improved accuracy, as explained elsewhere by Han et al. [19]. The fluid flow was initiated with the relevant inlet and outlet pressure boundary conditions, and no-slip conditions were imposed on the boundaries perpendicular to the flow. For each hydraulic gradient applied, the flow was continued over a sufficient period of time until a steady-state condition was attained. The flow was initiated in the upward direction with the gravity of the particles on.

3.2 Particle size distribution and homogeneity of the sample

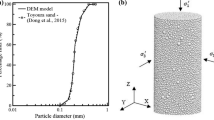
Figure 2a shows the particle size distribution of the selected sample from an experimental study carried out by Indraratna et al. [28]. Figure 2b shows the three-dimensional DEM-based sample with 17,607 particles, and the direction of flow of the fluid is also shown, i.e. the z-direction. Mud pumping and fluidisation occur owing to the upward flow induced by the excessive hydraulic gradient (e.g. Indraratna et al. [27, 28]), which is why the authors have chosen the z-direction (upward direction) for simulation purposes. Figure 2c shows the division of the sample into ten different inner layers. The ratio of the lateral dimension of the simulation domain to the maximum particle diameter was kept greater than 12 in order to obtain a representative elementary volume (REV) and avoid the boundary effects. A local increase in the void ratio occurs near the rigid boundaries [42]; hence, the bottom boundary layer (besides the rigid bottom boundary) was neglected in order to nullify the boundary effects [23]. The thickness of each layer was chosen to be more than twice the maximum particle diameter to define a REV [23]. The stresses at the boundaries do not reflect the actual material response; therefore, the interaction of the particles in each layer with the lateral boundaries was not taken into account.

Fig. 2

a Particle size distribution of the sample selected for modelling in DEM; b three-dimensional sample modelled in DEM; c division of the sample into different layers with the mentioned layer numbers and initial void ratios (e_oi); d a close-up view of the particles modelled in the fluid mesh using the LBM-DEM approach

Figure 2c shows the similar initial void ratios of all layers, indicating the REV in each layer, and the initial homogeneity of the sample was further confirmed by considering the variances in the void ratios as reported by Jiang et al. [31]:

$$ S^{2} = \frac{1}{{n_{L} - 1}} \mathop \sum \limits_{k = 1}^{{n_{L} }} \left( {e_{oi}^{k} - e_{oi}^{{\text{avg}}} } \right)^{2} { } $$

(8)

where $S$ is the variance of the void ratios, $n_{L}$ is the total number of layers, $e_{oi}^{k}$ is the initial void ratio of the kth layer, and $e_{oi}^{{\text{avg}}}$ is the initial void ratio of the entire sample. The $S^{2}$ value for the sample in Fig. 2c is 2.72 × 10^–5, which is sufficiently low to classify the sample as homogenous with respect to the REV in each layer. The overall void ratio of the numerical sample is the same as that of the experimental sample. Note that the void ratio does not take into account the particulate structure of the granular medium. Figure 2d shows a close-up view of the particles modelled in the fluid mesh. It can be seen that the mesh size is much smaller than the particle and pore size, in contrast to the conventional unresolved approach with the Navier–Stokes equation.

3.3 Calibration

Fluid and grain densities were determined from previous experimental investigations carried out earlier by the authors (Indraratna et al. [28]), and the contact friction angle was chosen from previous DEM studies on similar granular materials (e.g. Sufian et al. [48]). Since the above parameters were determined at the initial stage, the relaxation time (τ) was then obtained during the calibration process. Figure 3a shows the calibration of the relaxation time (τ) for soil fluidisation by comparing the pressure drops obtained from the LBM-DEM approach and an analytical solution (Ergun [14]). For further analysis, a relaxation time (τ) = 0.56 was chosen, and this is in-line with the appropriate value of the kinematic viscosity of the water as used in the experiments. Figure 3b compares the flow curves obtained from the LBM-DEM approach and an earlier experimental study [28]. The flow curves obtained from the LBM-DEM approach and experimental methods agree. The overall critical hydraulic gradient (i_o,cr) refers to the gradient at which the effective stresses drop to zero, and the soil becomes fluidised. i_o,cr predicted by the LBM-DEM approach was 1.050, while the experimental value of i_o,cr was 1.180. These values are in reasonable agreement with each other. This acceptable agreement with the experimental results implies that the lattice resolution of five fluid cells per particle is sufficient to capture the fluidisation behaviour of the particle size distribution considered in this study. Nevertheless, in complex LBM-DEM modelling such as this, where a huge number of particles of different sizes and shapes cannot be accommodated to represent an ideal real-life pore structure or void distribution due to the obvious computational challenges, one cannot guarantee perfect accuracy; this is recognised as a current limitation to be further improved in the future.

Fig. 3

a Calibration of the relaxation parameter by comparing the pressure drops obtained from the LBM-DEM and an analytical solution, b comparison of the flow curves obtained from the LBM-DEM and the documented experimental work

4 Results and discussion

4.1 Stress-hydraulic gradient evolution

Figure 4a shows the evolution of overall hydraulic gradient over time. Figure 4b shows the stress-hydraulic gradient space where the local hydraulic gradients (i_hyd) are plotted against the normalised Cauchy effective stresses ($\sigma_{zz}^{^{\prime}} /\sigma_{zzo}^{^{\prime}}$) of particles in a given layer in the fluid flow direction (vertical direction) at any time, where $\sigma_{zz}^{^{\prime}}$ is the Cauchy effective stresses of the particles in a layer at any time, and $\sigma_{zzo}^{^{\prime}}$ is the initial Cauchy effective stresses of the particles in that particular layer. The $\sigma_{zz}^{^{\prime}}$ is obtained using the particle-based stresses via the following second-order stress tensor equation [43].

$$ \sigma_{ij}^{^{\prime}} = \frac{1}{V} \mathop \sum \limits_{p = 1}^{{N_{p} }} \sigma_{ij}^{p^{\prime}} V^{p} { } $$

(9)

where $V$ is the volume of the layer or the selected region, $V^{p}$ is the volume of particle $p$ in the region, $N_{p}$ is the number of particles in the layer, and $\sigma_{ij}^{p^{\prime}}$ is the average stress tensor within a particle $p$ and is given by:

$$ \sigma_{ij}^{p^{\prime}} = \frac{1}{{V^{p} }} \mathop \sum \limits_{c = 1}^{{N_{c}^{p} }} \left| {x_{i}^{c} - x_{i}^{p} } \right|n_{i}^{c,p} f_{j}^{c} { } $$

(10)

where $f_{j}^{c}$ is the force vector in the jth direction at contact c with the location $x_{i}^{c}$, $x_{i}^{p}$ is the location of the particle's centroid, $n_{i}^{c,p}$ is the unit normal vector from the particle's centroid to the contact location and $N_{c}^{p}$ is the number of contacts on the particle p. Note that Eqs. (9) and (10) compute the effective stresses directly from the contact moments and not according to Terzaghi's concept used in the macroscale laboratory studies. Reynold's stresses are negligible and are not taken into account.

Fig. 4

a Evolution of overall hydraulic gradient with time; b evolution of the increasing local hydraulic gradient (i_hyd) and the decreasing normalised effective stresses (${\sigma }_{zz}^{^{\prime}}/{\sigma }_{zzo}^{^{\prime}}$) (for each layer, the eight symbols correspond to the initial state and the seven increase in the overall hydraulic gradient (a))

Figure 4b shows that the onset of fluidisation of the soil is associated with hydraulic and stress conditions, i.e. hydromechanical conditions. The effective stresses decrease with increasing local hydraulic gradients in each layer. The onset occurs at a critical hydraulic gradient when the effective stresses drop to zero. The evolution of the stress-gradient of each layer is not the same. The stress-gradient paths of Layers 1–6 are approximately linear with a slope of − 1. In contrast to the theoretical linear stress-gradient paths presented by Li and Fannin [35], the stress-gradient paths of Layers 7–10 (lower layers) are nonlinear until failure. The failure initiates when the effective stress of Layer 10 approaches zero. At the same time, Layers 1–9 show residual stresses due to the motion of the particles in the form of clusters. These residual stresses decrease as the particles in the cluster would lose further contacts over time after onset until complete fluidisation occurs.

Lateral (horizontal) stresses did not affect fluidisation in the current study, as the ratio between the horizontal and vertical stresses was always less than 1 at the hydrostatic state and before fluidisation (see Fig. 5a, b). The effective horizontal stresses (due to increased water pressure) decrease to zero, so it is the vertical stresses that predominantly control the onset of fluidisation (Fig. 5b). In this respect, there is no possibility of any arching effect when approaching the state of fluidisation, and only the vertical stresses should be considered when quantifying soil fluidisation. In real-life situations, the observed instability of shallow soil deposits (e.g. mud pumping under cyclic train loading) has also proven that the ratio of effective lateral to vertical stresses in the field is smaller than unity.

Fig. 5

a Division of the sample into different layers with the indicated layer numbers and coefficient of earth pressure (K) values at the hydrostatic state, b development of the normalised horizontal and vertical effective stress with hydraulic gradient

4.2 Broken contacts

Figure 6 shows the development of the broken contacts (B_R) compared to the normalised effective stresses ($\sigma_{zz}^{^{\prime}} /\sigma_{zzo}^{^{\prime}}$). B_R is the percentage of interparticle contact losses in the initial number of contacts in the corresponding layer. The value of B_R increases with increasing hydraulic gradient and decreasing effective stresses. Contact is lost when the normal contact force due to hydrodynamic forces becomes zero. When the fluid flows, the contacts break off, and new contacts are also formed in the layer. The sharp turn in B_R represents the critical hydromechanical state where the contacts are notably lost. The granular assembly would become a fully fluid-like material when the number of unconnected particles increases to the maximum due to the breakage of the contacts, i.e. most of the particles would simply float without any contact. It can also be seen that the contact losses in the lower layers are greater than in the upper layers, which shows that more particles lose contact at the bottom and migrate upwards with the fluid flow if the constrictions are wide enough. The B_R at the critical hydraulic gradient is about 5% in Layer 1 and 17% in Layer 10 and increases considerably with a further slight increase in the hydraulic gradient applied across the soil specimen. The bottom layer has a higher percentage of broken contacts because the local hydraulic gradient is higher in the bottom layer than in the top layer. This difference in local hydraulic gradients is attributed to anisotropy in the contact and pore networks due to gravity deposition. The microscale parameters considered in this study can be determined in the field where the variations in hydraulic gradients, effective stresses and void ratios can be predicted, and then used to back-calculate these microscale parameters.

Fig. 6

Evolution of increasing broken contacts (B_R) with the decreasing normalised effective stresses (${\sigma }_{zz}^{^{\prime}}/{\sigma }_{zzo}^{^{\prime}}$) (for each layer, the eight symbols correspond to the initial state and the seven increase in the overall hydraulic gradient (Fig. 4a))

4.3 Mechanically stable particles

Figure 7 shows the evolution of the fraction of mechanically stable particles (M_s) with normalised effective stresses ($\sigma_{zz}^{^{\prime}} /\sigma_{zzo}^{^{\prime}}$) under increasing hydraulic gradients. The mechanically stable particles are those that participate in the stable network of force transmission. The value of M_s is defined by [25]:

$$ M_{s} = \frac{{N_{p}^{ \ge 4} }}{{N_{p} }} $$

(11)

where $N_{p}^{ \ge 4}$ is the number of particles with at least 4 or more contacts. Particles with zero contacts that do not participate in the stable network of force transmission are called rattlers or unconnected particles; hence, they are excluded. The particles with 1, 2, and 3 contacts are temporarily stable for a limited time, so they are also neglected in the above equation.

Fig. 7

Development of the decreasing fraction of mechanically stable particles (M_s) with decreasing normalised effective stresses (${\sigma }_{zz}^{^{\prime}}/{\sigma }_{zzo}^{^{\prime}}$) (For each layer, the eight symbols correspond to the initial state and the seven increase in the overall hydraulic gradient (Fig. 4a))

It should be noted that the values of M_s are always smaller than 1 across all layers since the temporarily stable particles are also present at the hydrostatic state. The initial values of M_s are higher in the lower layers than in the upper layers. The values of M_s decrease across all layers with a decrease in the values of the effective stresses. This reduction becomes significant at the critical hydraulic and stress conditions that indicate the break-up of the clusters of mechanically stable particles. The results show that a critical value of M_s ≈ 0.75 is found for all layers, below which the fluid-like behaviour of the soil is observed.

4.4 Evolution of the soil fabric

Figure 8 shows a conceptual model that describes the differences in the fabrics of two-particle systems where particles with two different geometrical arrangements are placed. Note that the void ratios of both arrangements are the same. However, the number of interparticle contacts is different due to the dissimilarity of the fabrics of the particulate systems. It is noteworthy that the geometric arrangement of the particles is more important than the void ratio when it comes to the strength of the granular assembly [12]. Similar initial void ratios of all layers indicate that the number of particles in each layer is the same. However, the number of interparticle contacts can vary due to the different geometrical configurations of the particles. During fluid flow, the number of particles in each layer remains unchanged until fluidisation begins, while the geometrical re-arrangement of the particles can occur, mainly due to the fact that the interparticle contacts within the layer slip and/or break.

Fig. 8

Conceptual model showing the differences in the fabrics of particles with the same void ratios

To assess the evolution of soil fabric under fluid flow, this study uses a scalar approach (e.g. Fonseca et al., 2013) to quantify the fabric with a scalar fabric descriptor called the coordination number (Z) and is computed as follows [50].

$$ Z = \frac{{2N_{c} }}{{N_{p} }} $$

(12)

where $N_{c}$ is the number of contacts and is multiplied by 2 since each contact is shared by two different particles. The coordination number is a basic descriptor to quantify the fabric, and the non-application of more advanced approaches is a limitation of this study.

Figure 9 shows the distribution of the Z at the hydrostatic state and the onset of soil fluidisation, taking into account three distinct cases:

• (a) all particles

• (b) particles with diameters (d_p) ≥ d₅₀ (where d₅₀ is the particle size that is 50% finer by mass), and

• (c) particles with d_p ≥ d₈₅ (where d₈₅ is the particle size that is 85% finer by mass).

Fig. 9

Cumulative distributions of the coordination number (Z) at the hydrostatic state and the onset of fluidisation of soil specimen

Despite the narrow range in the particle size distribution curve, the difference in the coordination number distribution becomes clearer when the conditions d_p > d₅₀ and d_p > d₈₅ are applied. Therefore, it is essential to consider all cases.

Figure 9a shows that the distribution of the coordination numbers at the hydrostatic state across different layers is somewhat dissimilar when all particles are considered. This difference is enhanced when the larger particle sizes are taken into consideration (Fig. 9c, e), which shows a dissimilarity in the fabric of all layers despite the similar void ratios. This fabric dissimilarity is ascribed to the influence of gravity during the sample preparation phase. The curves of the lower layers are on the right-hand side and show higher values of the coordination numbers than those of the upper layers. The slight difference in the evolution of local hydraulic gradients and effective stresses through each layer, as previously described, is due to this slight dissimilarity of the particles' fabric in the layers. It is appealing to note that at the onset of fluidisation, the distributions of the coordination numbers of all layers converge and become similar (Fig. 9b, d, f). The median value of the coordination number (Z₅₀) is 4 when all particles in the granular medium of the layer are taken into account (Fig. 8b). Thus, at the onset of fluidisation, the distributions of the interparticle contacts are uniform and show a similar fabric for all soil layers.

Figure 10 shows average coordination numbers (Z_avg) versus normalised effective stresses ($\sigma_{zz}^{^{\prime}} /\sigma_{zzo}^{^{\prime}}$), where the initial (at the hydrostatic state) average coordination of Layer 10 is the highest (i.e. Z_avg = 5.405), while Layer 1 has the lowest (i.e. Z_avg = 4.811). As the normalised effective stresses decrease, the values of Z_avg decrease across all layers, and so does the difference between them. Although each layer initially had a different fabric, the Z_avg of all layers has evolved to become the same, i.e. 4.6 at critical hydromechanical state.

Fig. 10

Development of the decreasing average coordination number (Z_avg) with decreasing normalised effective stresses (${\sigma }_{zz}^{^{\prime}}/{\sigma }_{zzo}^{^{\prime}}$) (For each layer, the eight symbols correspond to the initial state and the seven increase in the overall hydraulic gradient (Fig. 4a))

4.5 Sliding index

Figure 11 shows the distribution of the sliding index ($S_{i}$) of the selected Layer 10. Note that all layers show an almost similar development in the sliding index as the local hydraulic gradient increases. The sliding index ($S_{i}$) is defined by [25]:

$$ S_{i} = \frac{{f^{T} }}{{\mu_{s} f^{N} }} $$

(13)

Sliding or the plastic contacts occur when the tangential contact force ($f^{T}$) has fully mobilised the friction, i.e. $S_{i}$ = 1. The contacts with $S_{i}$ < 1 are the elastic contacts and $f^{T}$ is independent of $f^{N}$ in such contacts. Note that contacts that have already been lost are not taken into account when calculating $S_{i}$.

Fig. 11

Distribution of the sliding index (S_i) of the selected Layer 10 with different local hydraulic gradients (i_hyd)

The results show that a small proportion of the contacts slide even at the hydrostatic state since the static buoyancy forces would be acting on the particles when they are saturated with the fluid. As the local hydraulic gradients increase, the elastic contacts decrease, and the sliding contacts increase. The hydrodynamic forces from the seepage flow tend to move the particles, causing a change in the magnitudes of the resisting tangential contact force and the normal contact force. As a result, a slip is caused when the elastic tangential contact force reaches the Coulomb cut-off, i.e. $f^{T} = \mu_{s} f^{N}$. Two types of contact networks are present, strong and weak contacts. Strong and weak contact forces are defined for each layer with respect to the mean contact force in each corresponding layer. The strong contacts that carry the primary load are those with above-average normal contact forces; otherwise, they correspond to weak contacts (Thornton and Antony [51]), and this sliding of the particles occurs in the weak contacts [10]. At i_hyd ≤ 1, the proportion of sliding contacts in the total number of contacts in the layer is ≤ 10%, while it is around 17% at the critical i_hyd = 1.251 (Fig. 11g). Thereafter, this proportion of sliding contacts increases steeply with a further, albeit slight, increase in the hydraulic gradient. It is noteworthy that the maximum tangential force is controlled by the value of $\mu_{s}$. Therefore, the value of $\mu_{s}$ has a profound influence on the proportion of sliding contacts and consequently on the macroscale behaviour of the granular assembly.

4.6 Constraint ratio

Figure 12 shows a three-dimensional representation of the constraint ratio (R) versus local hydraulic gradients (i_hyd) and normalised effective stresses ($\sigma_{zz}^{^{\prime}} /\sigma_{zzo}^{^{\prime}}$). The constraint ratio for a three-dimensional particle system that only takes the sliding resistance into account is given by [12]:

$$ R = \frac{{N_{ct} }}{{N_{d} }} = \frac{{N_{c} \left( {3 - 2S_{c} } \right)}}{{6N_{p} }}{ } $$

(14)

where $N_{ct}$ is the number of constraints, $N_{d}$ is the number of degrees of freedom, and $S_{c}$ is the fraction of slipping contacts in the total number of contacts at a given point in time. For an idealised granular medium with $\mu_{s} = \infty$, $N_{ct} = 3N_{c}$ and $N_{d} = 6N_{p}$. The realistic granular medium, however, would have a finite value of $\mu_{s}$; therefore, the two tangential force constraints on contacts subject to slipping vanish and are excluded from the total number of constraints given in Eq. (14). Theoretically, if $N_{ct} > N_{d}$ > $N_{d}$, the granular assembly is considered to be over-constrained or mechanically stable, and if $N_{ct} = N_{d}$, it is considered to be in a critical or transitional state; otherwise, it is unstable. Note that R represents both slipping and loss of contacts in the particle systems, whereas the coordination number [50] does not take into account the slipping of particles.

Fig. 12

(a) Three-dimensional representation of the hydraulic gradient (i_hyd), the normalised effective stresses (${\sigma }_{zz}^{^{\prime}}/{\sigma }_{zzo}^{^{\prime}}$), and the constraint ratio (R); (b) projections of the three-dimensional plot of i_hdy, ${\sigma }_{zz}^{^{\prime}}/{\sigma }_{zzo}^{^{\prime}}$, and R (for each layer, the eight symbols correspond to the initial state and the seven increase in the overall hydraulic gradient (Fig. 4a))

The constraint ratio in each layer decreases according to the nonlinear power laws when the normalised effective stresses decrease, and it decays exponentially after the onset of the soil fluidisation (Fig. 12). The initial mild slope shows that at the relatively low i_hyd values, i.e. i_hyd < 1, the particles slip less and have minimal loss of contacts. The abrupt change in slope after onset is triggered by substantial slipping and the associated rapid loss of interparticle contacts. The point at which the slope value changes represents the critical microscale hydromechanical state or the onset of soil fluidisation. This point is marked as a transition line from a hydromechanically stable to a fluid-like state, as shown in Fig. 12b. This critical hydromechanical state corresponds to R ≈ 1, with effective stresses ≈ 0 at the critical hydraulic gradient. Therefore, the soil is hydromechanically stable when R is greater than 1. It is in a transition state from a hydromechanically stable to a fluid-like state when R is 1; otherwise, it corresponds to a slurry or fluid-like state. Complete fluidisation of the soil specimen occurs when almost all interparticle contacts are lost, with a constraint ratio well below 1.

5 Conclusions

This study assessed the hydromechanical state of soil fluidisation from a micromechanical perspective using the LBM-DEM approach. The good agreement between the model predictions and the experimental observations in relation to particle motion, fluid flow curves, and the critical hydraulic gradients confirms the capability and reliability of this hybrid numerical method. Based on the findings of this study, the following salient outcomes can be drawn:

• At comparatively low values of the local hydraulic gradient (i_hyd), i.e. i_hyd ≤ 1, the proportion of slipping contacts in the total number of contacts of the selected Layer 10 (bottom of the specimen) was ≤ 10%, while it was approximately 17% at the critical i_hyd = 1.251. The extent of slipping contacts increased with a further increase in the hydraulic gradient applied across the soil specimen.

• The fraction of mechanically stable particles was generally larger at the deeper layers but decreased with the reduction in normalised effective stress during the corresponding increase in hydraulic gradient. The fluid-like state of soil was triggered when this fraction of mechanically stable particles dropped below 0.75.

• The hydrodynamic forces induced by the seepage flow inevitably destabilize and move the particles within the granular assembly, resulting in reduced contact forces, thus creating critical conditions to facilitate particle slipping. The loss of interparticle contacts was not uniform across the depth of the soil specimen, as this was more pronounced in the deeper layers when subjected to an upward flow from the base of the specimen.

• At the critical hydraulic gradient, the percentage of interparticle contact losses relative to the initial number of contacts was non-uniform and varied between 5 and 17% across the specimen depth. After that, even with a slight increase in the hydraulic gradients, the breakage of the interparticle contacts appeared to exacerbate.

• At the onset of fluidisation, the distributions of the coordination numbers across all layers of the soil specimen became more uniform, with a median value of 4 and an average value of 4.6, thus representing a more uniform granular fabric across the soil layers.

• The constraint ratio (ratio of the number of constraints to the number of degrees of freedom in the particle system) was used to distinguish hydromechanically stable and unstable states. A value of the constraint ratio greater than 1 represented the hydromechanically stable state and less than 1 the unstable state. The critical hydromechanical state was found at a constraint ratio of unity. Constraint ratio represented the slippage and loss of contacts in the particle system, and its value decreased with the increase in the hydraulic gradient. The slipping and the associated loss of contact between the soil particles would cause the effective stresses to drop. This implies from a microscale perspective that soil fluidisation could be triggered by excessive slippage and the inevitable loss of contacts between particles.

Appendices

Appendix 1: LBM-DEM approach

The $\Omega_{\alpha }^{{\text{BGK}}}$, through which the momentum transfer occurs between the fluid particles when they collide, is given by [5]:

$$ \Omega_{\alpha }^{{\text{BGK}}} = - \frac{\Delta t}{\tau }\left( {f_{\alpha } \left( {x, t} \right) - f_{\alpha }^{{\text{eq}}} \left( {x,t} \right)} \right) $$

(15)

where $f_{\alpha }^{{\text{eq}}} \left( {x,t} \right)$ is the equilibrium distribution function, $\tau$ is the relaxation time, and is related to the kinematic viscosity ($\nu_{f}$) of the fluid, the lattice spacing ($\Delta x$), and the time step ($\Delta t$) by the following relationship:

$$ \nu_{f} = \frac{1}{3}\left( {\tau - \frac{1}{2}} \right)\frac{{\Delta x^{2} }}{\Delta t} $$

(16)

Equation (16) implies that the $\tau$ value should be greater than 0.5. For a given value of $\nu_{f}$ and $\tau$, the $\Delta t$ is defined according to the chosen $\Delta x$ by:

$$ \Delta t = \frac{1}{{3\nu_{f} }}\left( {\tau - \frac{1}{2}} \right)\Delta x^{2} $$

(17)

The $f_{\alpha }^{{\text{eq}}} \left( {x,t} \right)$ for the BGK model is given by [5]:

$$ f_{\alpha }^{{\text{eq}}} \left( {x,t} \right) = \omega_{\alpha } \rho_{f} \left( {1 + \frac{3}{{c_{L}^{2} }}e_{\alpha }^{v} u + \frac{9}{{2c_{L}^{4} }}\left( {e_{\alpha }^{v} u} \right)^{2} - \frac{3}{{2c_{L}^{2} }}u^{2} } \right) $$

(18)

where $\omega_{\alpha }$ is the weighting factor for the velocity vectors, $\rho_{f}$ is the fluid density, $e_{\alpha }^{v}$ is the microscopic fluid velocity, u is the macroscopic fluid velocity, and c_L $\mathrm{c}= \frac{\Delta \mathrm{z}}{\Delta \mathrm{t}}$ $\mathrm{c}=\frac{\Delta \mathrm{z}}{\Delta \mathrm{t}}$ is the lattice speed given by:

$$ c_{L} = \frac{\Delta x}{{\Delta t}} $$

(19)

In lattice Boltzmann computations, $c_{L} = \Delta x = \Delta t = 1$, and the discretisation schemes in LBM are labelled as DdQq, where d is the number of dimensions, and q represents the number of velocity vectors. This study used the D3Q19, a three-dimensional scheme with 19 velocity vectors, including one at rest. Figure 

Fig. 13

Directions of the 19 (0–18) velocity vectors of the D3Q19 discretisation scheme used in this study

13 shows the directions of the velocity vectors ($e_{\alpha }^{v}$) for the D3Q19 scheme and, for the sake of simplicity, their magnitudes are already defined by:

$$ e_{\alpha }^{v} = \left\{ {\begin{array}{*{20}l} {\left( {0,0,0} \right) } \hfill & {i = 0} \hfill \\ {\left( { \pm c_{L},0,0} \right), \left( {0, \pm c_{L},0} \right), \left( {0,0, \pm c_{L} } \right)} \hfill & { i = 1,2,3,4,5,6} \hfill \\ {\left( { \pm c_{L}, \pm c_{L},0} \right), \left( { \pm c_{L},0, \pm c_{L} } \right), \left( {0, \pm c_{L}, \pm c_{L} } \right)} \hfill & { i = 7,8,9,10,11, \ldots,18} \hfill \\ \end{array} } \right. $$

(20)

and the weighing factors are $\omega_{0} = 1/3$, $\omega_{1,2,3,4,5,6} = 1/18$ and $\omega_{7,8, \ldots,18} = 1/36$.

The macroscopic fluid properties, i.e. fluid density ($\rho_{f}$) and velocity ($u$), can be retrieved at each node and given by [18, 46]:

$$ \rho_{f} \left( {x, t} \right) = \mathop \sum \limits_{\alpha = 0}^{q - 1} f_{\alpha } \left( {x,t} \right) $$

(21)

$$ u{ }\left( {x, t} \right) = \frac{1}{{\rho_{f} }} \mathop \sum \limits_{\alpha = 0}^{q - 1} f_{\alpha } \left( {x,t} \right)e_{\alpha }^{v} $$

(22)

To determine the fluid pressure $p_{f}$, it is assumed that the fluid is slightly compressible, and the following state equation is used:

$$ p_{f} = c_{s}^{2} \rho_{f} { } $$

(23)

where $c_{s}$ is the sound celerity and is defined by:

$$ c_{s} = \frac{{c_{L} }}{\sqrt 3 } $$

(24)

Fluid modelled with LBM requires a slight variation in spatial density. An approximate incompressibility situation can only be achieved under the condition that the Mach number ($M$) is small; is therefore kept below 0.1 [19], and is defined by:

$$ M = \frac{{u_{\max } }}{{c_{L} }} $$

(25)

$u_{\max }$ is the maximum velocity in the fluid flow in physical units. Fluids with lower viscosity and turbulent flows can also be simulated with LBM using the Smagorinsky Large Eddy Simulation approach [20, 46]. Unit conversion between physical and lattice units is explained elsewhere by Latt [34].

For the fluid-particle interaction, the force ($f_{f}$) (without the static buoyancy force) and the torque ($T_{f}$) acting on a particle through the fluid can then be computed by [41, 46]:

$$ f_{f} = \frac{{\Delta x^{3} }}{\Delta t}\left[ {\mathop \sum \limits_{n} B_{n} \mathop \sum \limits_{\alpha } \Omega_{\alpha }^{s} e_{\alpha }^{v} } \right] $$

(26)

$$ T_{f} = \frac{{\Delta x^{3} }}{\Delta t}\left[ {\mathop \sum \limits_{n} B_{n} (x^{n} - x^{p} )\mathop \sum \limits_{\alpha } \Omega_{\alpha }^{s} e_{\alpha }^{v} } \right] $$

(27)

$B_{n}$ is the weighting function in the cell, $x^{n}$ is the coordinate of the lattice cell, and $x^{p}$ is the centre of mass of the particle. Equation (27) does not include the static buoyancy forces; therefore, they are applied separately to the particles and the total hydrodynamic force ($f_{hyd}$) on the particle, including the static buoyancy force ($f_{bu}$) is given by:

$$ f_{hyd} = f_{f} + f_{bu} $$

(28)

The governing equations of motion of solid particles given by Cundall and Strack (1979), with the additional fluid-particle interaction force and the torque, are as follows:

$$ m^{p} \frac{{{\text{d}}v^{p} }}{{{\text{d}}t}} = f_{g}^{p} + f_{hyd}^{p} + \mathop \sum \limits_{c = 1}^{{N_{c}^{p} }} f_{j}^{c} $$

(29)

$$ I^{p} \frac{{{\text{d}}w^{p} }}{{{\text{d}}t}} = T_{f}^{p} + \mathop \sum \limits_{c = 1}^{{N_{c}^{p} }} T_{j}^{c} $$

(30)

where $m^{p}$ and $I^{p}$ are the mass and the moment of inertia of the particle $p$, $v^{p}$ and $w^{p}$ are the translational and angular velocities of the particle $p$,$N_{c}^{p}$ is the total number of contacts on the particle p, $f_{j}^{c}$ is the contact force vector in the jth direction at contact c on the particle p, $T_{j}^{c}$ is the torque that acts on the particle p due to the tangential contact force at contact c, and $f_{g}^{p}$ is the gravitational force on the particle p.

1.1 Validation

Although LBM-DEM was previously validated by Indraratna et al. [29] with experimental observations of fluidisation, the transient motion of the particles in the fluid could not be quantified. In this regard, an attempt is made in this study to validate the motion of a single particle falling into the fluid with different particle Reynold's numbers (Re_p). This validation is carried out by comparing the numerical results with the experimental observations by Ten Cate et al. [49]. Figure 

Fig. 14

a Schematic representation of a single sphere falling into the fluid with a diameter (d_p) = 15 mm; b the modelled particle in the fluid mesh using LBM-DEM; c comparison of the numerical and experimental results of particle position over time; d comparison of experimental and numerical results of particle velocity over time

14a, b shows the schematic sketch and the modelled problem using the LBM-DEM approach, respectively. Table

Table 1 Fluid properties for simulating the single-particle falling into the fluid using the LBM-DEM approach (after Ten Cate et al. [49])

1 shows the fluid properties used with lattice resolution (N) = 5 (particle diameter corresponds to 5 fluid cells) and the relaxation time ($\tau$) = 0.53. It is noteworthy that N = 5 was chosen after a preliminary sensitivity analysis in which the simulation was run with N = 5, 7 and 10. The results showed insignificant difference in the numerical output when N > 5. Figure 14c, d shows an excellent agreement between the numerical and experimental results of the position and velocity of the falling particle over time at different Reynold's numbers. Hence, it could be justified with confidence that the LBM-DEM approach would reasonably predict the transient motion of the particles in the fluid with these selected numerical parameters, i.e. N = 5 and $\tau$ = 0.53.

Appendix 2: Hertz-Mindlin contact model

Figure 

Fig. 15

a Rheological scheme and b schematic sketch of the Hertz-Mindlin contact model used in this study to simulate fluidisation of soil specimen

15 shows the rheological scheme and schematic sketch of the Hertz-Mindlin contact model used in this study to simulate the fluidisation of the soil. The normal contact force ($f^{N}$) is based on Hertzian contact theory and the tangential contact force ($f^{T}$) is based on the work of Mindlin and Deresiewicz [37]. The $f^{N}$ and $f^{T}$ have the nonlinear spring and damping components. The normal and tangential damping coefficients (c_n and c_t) are related to the restitution coefficient as reported by Tsuji et al. [53]. The tangential frictional force follows Coulomb's law of friction (e.g. [11]).

$$ f^{N} = k_{n} \delta_{n} - c_{n} v_{n}^{rel} { } $$

(31)

where $k_{n}$ is the elastic constant for normal contact, $c_{n}$ is the viscoelastic damping constant for normal contact, $\delta_{n}$ is the normal component of the displacement at the contact as represented by the overlap distance, $v_{n}^{rel}$ is the normal component of the relative velocity of two spherical particles, and $k_{n}$ is given by:

$$ k_{n} = \frac{4}{3}E^{*} \sqrt {R^{*} \delta_{n} } { } $$

(32)

where $E^{*}$ is the equivalent Young's modulus and $R^{*}$ is the equivalent radius which can be written as follows:

$$ \frac{1}{{R^{*} }} = \frac{1}{{R_{i} }} + \frac{1}{{R_{j} }}{ } $$

(33)

$$ \frac{1}{{E^{*} }} = \frac{{1 - \nu_{i}^{2} }}{{E_{{y}_{i}} }} + \frac{{1 - \nu_{j}^{2} }}{{E_{{y}_{j}} }} $$

(34)

where $R_{i}$ and $R_{j}$ are the radius, $E_{{y}_{i}}$ and $E_{{y}_{j}}$ are Young's modulus, and $\nu_{i}$ and $\nu_{j}$ are the Poisson's ratio of each neighbouring spheres in contact. The viscoelastic damping constant ($c_{n}$) is given by:

$$ c_{n} = - 2\sqrt{\frac{5}{6}}\beta \sqrt {S_{n} m^{*} } \ge 0{ } $$

(35)

where $m^{*}$ is the equivalent mass and is given by:

$$ \frac{1}{{m^{*} }} = \frac{1}{{m_{i} }} + \frac{1}{{m_{j} }}{ } $$

(36)

$\beta$ and $S_{n}$ are given by:

$$ \beta = \frac{{\ln e_{r} }}{{\sqrt {ln^{2} e_{r} + \pi^{2} } }}{ } $$

(37)

$$ S_{n} = 2E^{*} \sqrt {R^{*} \delta_{n} } { } $$

(38)

where $e_{r}$ is the coefficient of restitution. The tangential contact force ($f^{T}$) is given by:

$$ f^{T} = k_{t} \delta_{t} - c_{t} v_{t}^{rel} $$

(39)

where $k_{t}$ is the elastic constant for tangential contact, $c_{t}$ is the viscoelastic damping constant for tangential contact, $\delta_{t}$ is the tangential overlap, and $v_{t}^{rel}$ is the tangential component of the relative velocity of two spherical particles, and $k_{t}$ is given by:

$$ k_{t} = 8G^{*} \sqrt {R^{*} \delta_{n} } $$

(40)

with $G^{*}$ as the equivalent shear modulus, and $c_{t}$ is written as follows:

$$ c_{t} = - 2\sqrt{\frac{5}{6}}\beta \sqrt {k_{t} m^{*} } \ge 0{ } $$

(41)

The $f^{T}$ is limited by:

$$ f^{T} = \mu_{s} f^{N} $$

(42)

where $\mu_{s}$ is the coefficient of sliding friction.