Numerical investigation of laboratory hydraulic fracturing tests in Pocheon granite

Abstract

This study investigates numerically several hydraulic fracturing experiments that were performed on intact cubic Pocheon granite samples applying different injection protocols. The goal of the laboratory experiments is to test the concept of cyclic soft stimulation which aims to increase permeability sustainably among others. The Irazu 2D numerical code is used to simulate explicitly coupled hydraulic diffusion and fracturing processes under bi-axial stress conditions. Using the hybrid finite-discrete element modelling approach, we test two injection schemes, constant-rate continuous injection and cyclic progressive injection on homogeneous and heterogeneous samples. Our study focuses on the connection between the geometry of hydraulic fractures, fracturing mechanisms and the permeability increase after injection. The models capture several characteristics of the hydraulic fracturing tests using a time-scaling approach. The numerical simulation results show good agreement with the laboratory experiments in terms of pressure evolution characteristics and fracture pattern. Based on the simulation results, the constant-rate continuous and cyclic progressive injection schemes applied to heterogeneous rock sample with pre-existing fractures show the highest hydraulic aperture increase, and thus permeability enhancement.

1 Introduction

Hydraulic fracturing is used in several engineering applications, such as increasing production in unconventional oil and gas reservoirs, enhancing the permeability of geothermal systems by hydraulic stimulation as well as injecting large amounts of waste water [50]. Although the method is applied routinely, the quantitative characterization of the underlying process is still subject of research due to its physical complexity and uncertainties. These include nonlinear, complex hydro-mechanical processes at different spatiotemporal scales [13].

One major technological challenge associated with productivity enhancement in geothermal reservoirs is the unsolicited induced seismicity. Thus, in the framework of the European Union’s Horizon 2020 project DESTRESS, i.e. Demonstration of Soft Stimulation Treatments of Geothermal Reservoirs, optimal stimulation techniques were investigated which allow increasing reservoir transmissivity, maintaining the productivity while mitigating environmental impacts [22].

Zang et al. [51] introduced the concept of cyclic injection which may allow enhancing permeability and reducing the magnitude of seismic events. The concept has been demonstrated experimentally at different scales in crystalline rock in the recent years. At field (km) scale, demonstration at the Pohang enhanced geothermal system (EGS) site in South Korea is presented by Hofmann et al. [21]. At mine (dm) scale, progressive cyclic and pulse stimulation underground tests in crystalline rock mass are reported by Zang et al. [52]. The concept has been tested at laboratory (cm) scale in South Korean Pocheon granite samples in several studies (e.g. [53,54,55]. These studies focus on testing various injection schemes, the resulting hydraulic and acoustic emission (AE) responses as well as fracturing characteristics. The investigations were conducted on intact samples at constant room temperature and exhibited tensile dominated fracturing.

In order to extend and optimize the testing of the concept, one should gain a better understanding of the underlying processes during hydraulic fracturing. For optimization processes, numerical tools are used since these allow systematic investigations at relatively low costs compared to laboratory or field experiments. However, the modelling of these phenomena, especially at laboratory scale has been challenging [29]. Concepts not implemented in the respective code can play a key role in the natural hydraulic fracturing process like cohesive crack tip zones as compared with stress singularity at crack tips modelled in linear elastic fracture mechanics (LEFM). Deviations from LEFM predictions have been reported at the laboratory and field scales in some cases, notably a larger fluid pressure and a shorter fracture length [13]. Liu [30] contributes the additional energy dissipation compared with LEFM to the impact of the rough fracture process zone on viscous fluid flow. Second, these challenges include extensive computational requirements to reproduce the hydro-mechanical characteristics during pressurization and fracture propagation at the same time.

In the past decades, several numerical tools have been developed by the petroleum industry. Chen et al. [11] give an in-depth review on numerical methods that are capable of solving coupled hydraulic and geomechanical processes. Farkas [17] presents evaluation of codes to explore which methods are the most suitable for simulating hydraulic fracturing in hard rock at various scales including grain scale. The evaluation considers the availability of two- or three-dimensional simulation, employed numerical method and solver, fracture growth (failure criterion, failure mode and fracture geometry), available coupling as well as hydraulic aperture versus normal stress relationship. According to that, discontinuum or hybrid continuum/discontinuum-based methods, such as Particle Flow Code 2D/3D [40], UDEC/3DEC [12], TOUGH-FLAC [47] as well as Irazu 2D/3D [4], [19]). These codes can handle fluid with low compressibility in a way so that incompressibility condition can be assumed [43]. Given that Irazu 2D is a promising tool to model fluid pressure induced fracturing processes in porous brittle rocks at laboratory scale using the concept of LEFM, we favor to use this hybrid finite-discrete element method in this study.

It must be pointed out that generally two strategies are employed for the simulation of coupled multi-physics [3]. One may either pursue fully implicit or fully-coupled strategy (strong coupling), where the full system (all equations) are solved at once. For example, Finite Element Method (FEM, [45] and Phase Field Model (PFM, [31] are widely used hydraulic fracturing simulators with strong coupling.

One may solve each physical process separately and sequentially. In this way, modular approach is employed where each module is dedicated to one physical process. The latter method is referred to as weak coupling. The codes mentioned above are well-known examples for hydraulic fracturing simulation using weak coupling.

Although weak coupling is supposed to provide similar results to the fully coupled one, however, weak coupling introduces operator splitting errors and restrictions on time step size to ensure mass conservation and numerical stability. Ahusborde et al. [3] point out that no comparative study exists yet to quantify the accuracy loss of weak coupling compared to fully implicit approach. However, due to easy model implementation, more realistic fracture patterns as well as reasonable computation costs, weakly coupled hydraulic fracturing simulators, such as discrete element method [40, 48] or hybrid finite-discrete element codes [5, 20] are widely used for simulating hydraulic fracturing processes [11].

The goal of this study is to develop a numerical model that enables studying the processes that may lead to the observations of the laboratory tests reported in Zhuang et al. [53]. We characterize the injection pressure history, the failure mechanisms, the fracture pattern including hydraulic apertures. The numerical model can be used to study the effect of different injection schemes on the fracturing processes and hydraulic aperture enhancement. Results can be used to make implications for the best injection strategy and selecting optimal rock fabric to induce a wide hydraulic fracture network with the possible highest hydraulic apertures, referred to as aperture fold of increase, suggested by Hofmann et al. [20].

The paper is structured as follows. First, we give an overview of the laboratory tests. Second, we present the numerical model and the computational implementation of the fluid injection experiments. After that, we summarize the results for homogeneous and heterogeneous materials as well as for two injection schemes, the conventional constant-rate continuous injection and the novel cyclic progressive injection scheme. In the discussion section, we compare the simulation results between the modelling cases and against the laboratory experiments. Finally, we make implications for field injection strategies and point out the limitations of the numerical model.

2 Overview of laboratory tests

In this section, we briefly summarize the concept, methodology and the key results of the laboratory hydraulic fracturing (HF) experiments including the testing conditions, the tested samples as well as pre- and post-test measures as reported by Zhuang et al. [53].

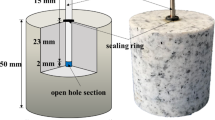
The laboratory test conditions are summarized in Fig. 1. For the experiments, a true triaxial hydraulic fracturing test setup with cubic specimens is used. The testing apparatus allows a maximum applied stress of 10 MPa. The maximum injection pressure allowed by the servo-control hydraulic pump is 35 MPa. Possible AE events during the hydraulic fracturing tests are monitored using eight Nano30 sensors that are directly installed on the corners of the specimens. Two sensors were attached close to the corners of each lateral face of the sample, and none on the top or bottom.

Fig. 1

Schematic illustration of the laboratory hydraulic fracturing test and the horizontal cross-section representing the 2D numerical modelling domain where hydraulic fracture (HF) propagates (modified from [53]

The tested Pocheon granite is prepared as cubic specimen with an edge length of 100 mm. A concentric, cylindrical vertical borehole is drilled at the top of the specimen with a diameter of 5 mm and length of 70 mm. For details on the mechanical properties of the granite, we refer to Table 1 and Zhuang et al. [54].

Table 1 Material and hydraulic parameters of the numerical model and the Pocheon granite samples. Discrete fracture network properties are based on Zhuang et al. [54] as well as Park et al. [35] and Park [36], respectively. The number of laboratory tests are indicated as N

The cubic specimens are subjected to three principal stresses (Fig. 1): 6 MPa representing the maximum horizontal stress (S_x), 4 MPa in vertical direction as intermediate principal stress (S_z) and 3 MPa as the minimum horizontal stress (S_y). Consequently, hydraulic fractures open up in the direction of minimum horizontal stress, and propagate in the plane spanned out by maximum horizontal stress and intermediate vertical stress.

In order to test the concept of cyclic soft stimulation, several different injection schemes were used in Zhuang et al. [53]. Among these tests, hydraulic fracturing tests denoted as “CCI1” and “CPI3” are the subject of this paper as these experiments are used for creating the reference numerical model. In the “CCI1” experiment (Fig. 2a), water is injected at 100 mm³/s (10⁻⁷ m³/s) flow rate for 65 s until shut-in. Due to injection, pressure in the borehole increases until a peak level is reached known as the formation breakdown pressure (FBP). At this point a hydraulic fracture is induced which is followed by a pressure drop. The injection pressure decreased from the peak value of approx. 15 MPa to 10 MPa, interpreted as the pressure required for propagating the HF, the fracture propagation pressure (FPP). As the pumping is stopped, the pressure decreases from the FPP to the initial, static level of 0 MPa. AE time clusters were first detected before and after observing the FBP. The maximum AE amplitude of 84 dB was detected about 5 s after reaching the peak pressure (not shown in Fig. 2a). More AE clusters were observed during the shut-in period. The recorded injection pressure and cumulative number of acoustic emission events are shown in Fig. 2a.

Fig. 2

Injection pressure record (blue) with flow rate (grey) and cumulative number of AE events before (green) and after (red) breakdown during a constant injection rate test “CCI1” and b cyclic progressive injection rate test “CPI3” (modified from [53]

For the cyclic progressive injection case “CPI3” (Fig. 2b), injection rates are increased stepwise from 20 to 100 mm³/s (“high” rate) with fixed injection rate of 10 mm³/s (“low rate”) between these steps. Based on the AE activity and pressure evolution, a hydraulic fracture is generated between the injection steps of 70 and 80 mm³/s. However, the maximum AE amplitude of 74 dB was observed ahead of these steps, at the 50 mm³/s step, before the failure inferred from the injection pressure curve (not shown in Fig. 2b).

Both constant-rate continuous injection and cyclic progressive injection schemes show a significant increase in the AE curve after shut-in, Fig. 2a and b, respectively. Based on Bunger et al. [10] and [44] this can be interpreted as hint for further microcrack generation. Furthermore, the number of cumulative AE events after shut-in is ten times higher than before if cyclic progressive injection is applied. This can be associated with the concept of cyclic hydraulic fracturing where the generation of a more complex fracture pattern, and the replacement of larger seismic events by a cloud of several smaller events compared to constant-rate, continuous fluid injection (the magnitude of AE events for respective experiments are shown in Zhuang et al. [53]. Furthermore, Song et al. [41] demonstrate in their experimental work that during cyclic loading, preferentially more grain boundary cracks, i.e. low-energy events are generated compared to inter and intra-granular cracks associated with monotonic loading.

3 Numerical model

3.1 Irazu 2D code

In this study, we use Irazu 2D version 4.0 [19] that allows simulating hydro-mechanically coupled processes in low-porosity rock samples using discrete, triangular elements. In this section, the principles of the numerical code are briefly presented based on [19] and Lisjak et al. [29]. Since laboratory experiments were conducted at constant room temperature, thermal effects are not considered and solely hydro-mechanically coupled processes are simulated. The simulation of hydraulic fracturing experiment is validated by comparing it against analytical solutions in terms of fracture aperture, fracture length and injection pressure in Lisjak et al. [29].

As for the mechanical part of the simulation, the discrete bodies can deform elastically, translate, rotate, interact, and fracture upon satisfying a given fracture criterion, hence producing new discrete bodies. The newly generated elements can further move, interact, deform, and crack. The code uses a combination of Finite Element Method (FEM) to calculate the deformation and to assess the failure criterion for fracturing and Discrete Element Method (DEM) for detecting new contacts and realizing translation, rotation, and interaction of discrete bodies. The method is referred to as Finite-Discrete Element Method (FDEM).

In the simulation loop, first connected triangular elements are identified for the mechanical calculations. Then, the nodal forces associated with interaction, deformation, and fracturing, due to internal or external loading are calculated. Using these forces, the equation of motion is integrated to update the new nodal coordinates. This loop is repeated until a pre-defined number of mechanical time integration steps.

The generation and propagation of explicit fractures are simulated in Irazu using the theory of nonlinear fracture mechanics (NLFM) [6, 14]. According to this concept, at the tip of a crack, an area characterized by nonlinear behavior, called the fracture process zone (FPZ), begins to form [49]. In brittle rock materials, the FPZ is affected by interlocking and microcracking. In Irazu, an analogous FPZ behavior is simulated ahead of crack tips subjected to loading. The load carrying capacity of the FPZ is approximated by triangular cohesive crack elements. Whether process zone cracks are mode I, mode II or mixed mode, depends on the boundary conditions of fracture growth [29].

The constitutive behavior of a crack element is defined in terms of the evolution of the bonding stresses. The relative displacement in the normal direction, o, depends on the effective normal stress, σ, and that in the tangential direction, s, is the function of shear stress, τ (Fig. 3).

Fig. 3

Numerical constitutive behavior of the crack elements. a Normal bonding stress versus crack opening for pure compressive/tensile loading and failure (Mode I); b shear bonding stress versus crack slip for pure shear loading and failure (Mode II); c elliptical coupling relationship between fracture opening and slip for mixed-Mode fracturing. Arrows denote loading, unloading, and reloading paths. The area under the curves in (a) and (b) is defined by G_I and G_II, respectively (modified from [29]

Under Mode I loading (Fig. 3a), the failure of a crack element is a function of its tensile strength, f_t, and the Mode I fracture energy, G_I. The dependence of f_t on G_I is implemented as a heuristic function defined below. At Mode I loading, the accumulating stress is calculated as:

$$ \sigma = \left[ {\frac{2o}{{o_{{\text{p}}} }} - \left( {\frac{o}{{o_{{\text{p}}} }}} \right)^{2} } \right]f_{t} $$

(1)

$$ o_{{\text{p}}} = \frac{{2hf_{t} }}{{p_{f} }} $$

(2)

where, o_p is the peak crack element opening, h is the edge length of the triangular element and p_f is the fracture penalty. The penalty term approximates the repulsive forces between contacting elements, which are calculated using a distributed contact force penalty function method [33]. This affects frictional forces between contacting elements, using intact crack element contact penalty, p_f, normal and tangential contact penalties, p_n and p_t, respectively, and it controls microcracking. The numerical implementation of p_f, p_n and p_t are described in greater detail in Lisjak et al. [29].

Under Mode II loading (Fig. 3b), the constitutive response is governed by the shear strength, f_s, and the Mode II fracture energy, G_II. The dependence of f_s on G_II is implemented as a heuristic function defined below. At Mode II loading, the accumulating stress is calculated as:

$$ \tau = \left[ {\frac{2s}{{s_{{\text{p}}} }} - \left( {\frac{s}{{s_{{\text{p}}} }}} \right)^{2} } \right]f_{s} $$

(3)

$$ s_{{\text{p}}} = \frac{{2hf_{s} }}{{p_{f} }} $$

(4)

where, s_p is the peak crack element slip. The shear strength, f_s, is defined in terms of the Mohr–Coulomb failure criterion:

$$ f_{s} = C + \sigma_{{\text{n}}} \tan \varphi $$

(5)

where, C is the cohesion, σ_n is the normal stress acting across the crack element and φ is the internal friction angle.

The softening behavior, i.e. post-peak gradual reduction of σ and τ, acting on crack elements are governed by the general form proposed by Munjiza et al. [32]:

$$ {\upsigma } = f\left( D \right)f_{t} $$

(6)

$$ {\uptau } = f\left( D \right)f_{s} $$

(7)

where f(D) is a heuristic function approximating the shape of the experimental stress-displacement curves of Evans and Marathe [16]:

$$ f\left( D \right) = \left[ {1 - \frac{a + b - 1}{{a + b}}e^{{D\frac{a + cb}{{\left( {a + b} \right)\left( {1 - a - b} \right)}}}} } \right]\left[ {a\left( {1 - D} \right) + b\left( {1 - D} \right)^{c} } \right] $$

(8)

where, a = 0.63, b = 1.8 and c = 6.0 are empirical curve fitting parameters, and D is the damage coefficient with a value between 0 for intact and 1 for damaged crack element. The value of D for a given crack element is defined as depending on the mode of displacement. For mode I displacement, D is calculated as

$$ {\text{Mode I}}:D = \frac{{o - o_{p} }}{{o_{{\text{r}}} - o_{p} }} $$

(9)

$$ o_{{\text{r}}} = o_{p} + \frac{{3G_{I} }}{{f_{t} }} $$

(10)

where, o_r is the residual crack element opening.

For mode II displacement, D is defined as

$$ {\text{Mode II}}:D = \frac{{s - s_{p} }}{{s_{{\text{r}}} - s_{p} }} $$

(11)

$$ s_{{\text{r}}} = s_{p} + \frac{{3G_{II} }}{{f_{s} }} $$

(12)

where, s_r is the residual crack element slip. Based on this analogy, the residual shear strength of a crack element, f_r, is calculated as

$$ f_{r} = \sigma_{{\text{n}}} \tan \varphi_{{\text{r}}} $$

(13)

where, φ_r is the residual friction angle.

For mixed Mode I-II fracturing (Fig. 3c), an elliptical coupling relationship is employed between crack opening and slip:

$$ {\text{Mode I}} - {\text{II}}:D = \sqrt {\left( {\frac{{o - o_{p} }}{{o_{{\text{r}}} - o_{p} }}} \right)^{2} + \left( {\frac{{s - s_{p} }}{{s_{{\text{r}}} - s_{p} }}} \right)^{2} } $$

(14)

There are two rate-dependent phenomena implemented in Irazu. The first one is related to the viscous damping formulation: viscous damping tensor is computed based on the strain rate tensor of an element. Since quasi-static process with critical viscous damping is modelled (viscous damping factor is equal to one in Table 1), thus its effect can be neglected. The second one is the strain-rate dependency that emerges from fracturing simulations. Even though the fracture model itself does not have any rate dependency, it can be shown that in general the emergent strength of the rock increases with higher loading/strain rate [42].

For more details on the implementation of the mechanical processes, the reader is referred to [19].

The hydraulic part of the simulation employs a hydraulic solver which assumes that fluid flows through a channel network generated from the same triangular mesh used for the mechanical calculations (Fig. 4a). The channels are defined at the interfaces of connected triangular finite elements. These flow channels connect virtual cavities or pores corresponding to the nodes of the original triangular mesh (blue dots in Fig. 4a). Each cavity behaves as a fluid reservoir with uniform pressure and volume.

Fig. 4

Computational framework adopted in the fluid flow solver using finite element mesh. Initial hydraulic aperture, a_i, are assigned to virtual cavities. a: network of rectangular flow channels connecting two virtual cavities before rock deformation. b: illustration of hydro-mechanical coupling in terms of linearly-varying hydraulic aperture at two end-points of the flow channel, a₀ and a₁ due to mechanical deformation, o₀ and o₁ (modified from [19])

The volume of the jth flow channel is defined as

$$ V_{j} = L_{j} \frac{{a_{0} + a_{1} }}{2} $$

(15)

where L_j is the length of the flow channel, and a₀, and a₁ are the hydraulic apertures at two end-points of the channel (Fig. 4b).

Fluid volume is stored at cavity, V_c, that is derived from the volume of the surrounding flow channels as

$$ V_{{\text{c}}} = \mathop \sum \limits_{j} \frac{{V_{j} }}{2} $$

(16)

Consequently, each cavity act as storage term in the hydraulic part of the equations. It must be noted that fluid flow and fluid pressure dissipation can occur only through the network of flow channels.

The explicit formulation of fluid flow allows straightforward coupling with the mechanical solver and parallelization. During each hydraulic time step, the following main steps are sequentially performed:

• 1. Channel hydraulic aperture and cavity volume are computed;

• 2. Darcy’s law and parallel-plate flow model at each channel are applied;

• 3. The hydraulic continuity equation at each cavity is applied; and

• 4. Fluid pressure field is calculated.

During the last step, the fluid pressure in a cavity is determined by considering the change in pressure using a linear fluid compressibility model:

$$ P_{t} = P_{t - 1} + K_{f} \frac{\Delta m}{{\rho_{f} V_{t} }} $$

(17)

where P_t and P_t−1 are the fluid pressure at time step t and t-1, respectively, V_t is the cavity volume at time step t, Δm is the change in fluid mass, K_f is the fluid bulk modulus and ρ_f is the fluid density.

The hydro-mechanical coupling is realized via a two-way explicit coupling approach, i.e. alternation between the mechanical and the hydraulic solvers while stepping forward in time (Fig. 5a). Consequently, the mechanical calculations are affected by inter-element fluid pressure; and the flow calculations are affected by the variation of hydraulic aperture between finite elements due to the rock deformation and fracturing process.

Fig. 5

a Explicit two-way hydro-mechanical coupling in the Irazu 2D model. b Relationship between hydraulic aperture and normal stress acting across the flow channel. Hydraulic aperture parameters are threshold (a_t), initial (a_i) and residual aperture (a_r) (modified from [19])

Figure 5b illustrates the hydraulic aperture as a function of effective normal stress acting on the flow channel. The hydraulic aperture is assumed to have lower (residual) and upper bounds (threshold), a_r and a_t, beyond which additional mechanical closing (compression) and opening (tension) have no effect. A linear relationship between aperture and normal stress is implemented. These definitions are applied for the sake of calculation simplicity. The initial hydraulic aperture, a_i, represents the aperture before any mechanical deformation [19].

Two time-discretization schemes are defined in the Irazu 2D code to maintain numerical stability during mechanical and hydraulic time-stepping. The coupling frequencies are defined in terms of the number of mechanical and hydraulic time steps for which each solver is run before switching to the other one.

Stability of the mechanical solver is controlled by the mechanical time step size for the integration of equations of motion of the discretized system. We refer to [29] for more details on the time marching approach of the explicit time integration scheme. The stability of the hydraulic solver is secured by controlling the size of the hydraulic time step (Δt_h) as [19],

$$ \Delta t_{h} \le min_{c} \left( {\frac{{V_{c} }}{{\frac{{K_{f} }}{{\rho_{f} }}\mathop \sum \nolimits_{j} \left( {\frac{{\left( {a_{0} a_{1} } \right)^{2} }}{{6\nu_{{\text{f}}} { }\left( {a_{0} + a_{1} } \right){\text{L}}_{j} }}} \right)}}} \right) = min_{c} \left( {\frac{{V_{c} }}{{\frac{{K_{f} }}{{\rho_{f} }}\mathop \sum \nolimits_{j} \left( {\frac{1}{{R_{j} }}} \right)}}} \right) $$

(18)

With c and j indexing over all the cavities and flow channels, respectively. K_f is the fluid bulk modulus, ρ_f is fluid density. υ_f is fluid kinematic viscosity and R is the flow resistance. Since mechanical time step is generally smaller than the hydraulic time step (nanoseconds versus milliseconds), thus, computational time is governed by the mechanical time step size. For the same reason, 15 mechanical cycles are calculated for each hydraulic step.

3.2 Numerical simulation of constant-rate injection test in Pocheon granite sample

3.2.1 Geometry and boundary conditions

Pocheon granite rock samples are represented as a set of discrete triangular mesh elements in a horizontal cross-section spanned by the minimum and maximum principal stress with a side length of 100 mm. The distinct bodies are generated using the Delaunay triangulation method in the open-source mesh generation software, Gmsh version 4.4.1. Two mesh generation areas are defined at the center of the rectangular modelling domain, where the inner one has an edge length of 60 mm parallel to the y-axis. (Fig. 6a). In the inner mesh generation domain, the average mesh edge length is 1 mm; in the outer one, that length is 1.5 mm. The inner, finer mesh aims at capturing hydraulic fracture initiation and fluid flow at the center of the model (Fig. 6b). This edge length corresponds to the average grain size of 1 mm reported by Zhuang et al. [54]. The outer, coarse mesh network serves as gradual size transition from finer to coarse mesh to maintain calculation times within practical limits. The numerical model contains 35,614 elements with 17,981 nodes.

Fig. 6

a Geometry and boundary conditions of the laboratory-scale hydraulic fracturing numerical model. The average mesh element size in the refined zone is 1 mm, in the outer zone that equals 1.5 mm. b: illustration of the hydraulic fracture along the edges of the triangular mesh elements

Fluid injection is modelled by applying a prescribed flow (mass) rate condition, i.e. hydraulic boundary condition, in a cavity located at the center of the model. The cavity itself is a node of the mesh. We note that borehole geometry, in terms of dedicated mesh elements, is not explicitly included in the model and, therefore, near-wellbore effects are not considered. In order to deal with potential singularity, injection node is located in refined mesh area as well as mechanical and hydraulic integration time step sizes are as low as possible.

Two types of mechanical boundary conditions are defined in the numerical model. First, the maximum and minimum principal stresses act perpendicular to the sample boundaries, i.e. S_x = S_H = 6 MPa, and S_y = S_h = 3 MPa. The stresses are acting upon the boundary elements in the respective directions. The second, mechanical boundary condition pins the boundary nodes, i.e. no displacement of those is allowed. The combination of the two boundary conditions mimics the 2D section of the true-triaxial stress loading conditions and thus allows simplification of the numerical model.

3.2.2 Material parameters and injection schemes

Two types of mechanical models and injection schemes are defined resulting in four modelling cases in total (Fig. 7). The model A is a homogeneous model from a mechanical point of view, and in model B a discrete fracture network (DFN) is added. In model B, the DFN is defined as a set of pre-existing joints with a length of 2.80 mm, fracture spacing of 1.85 mm as well as orientation of − 39°, − 11° and 86° measured counter-clockwise from the horizontal axis based on measured parameters reported by Park [36]. In this paper, joints share the same initial hydraulic properties as the rock mass and zero tensile strength is assigned to them. Thus, these joints can only sustain shear stresses characterized by residual friction. Consequently, joints are defined to explore shear-slip induced failure in the rock sample. It must be noted that no joints are generated in an area of 10 × 10 mm² around the injection point to enable distinction between pure hydraulic fracturing and shear-slip induced failure of pre-existing joints at the beginning of the injection.

Fig. 7

Mechanical models (left column) and injection cases (right column) tested in the numerical study. Injection point is represented by solid purple circle

As for the injection schemes, in case 1, pumping water at constant flow rate of 100 mm³/s is simulated as fluid injection into a single cavity (point) located at the center of the model based on the laboratory test “CCI1” reported by Zhuang et al. [53]. The second hydraulic injection scheme is based on the concept of cyclic soft stimulation (CSS). A cyclic progressive injection (CPI) scheme is applied with an injection rate increased by a given flow rate in each step until a target value of 100 mm³/s is reached based on the laboratory test “CPI3” reported by Zhuang et al. [53]. The duration of each step is determined using the approach described below.

The modelling time scale of the base case numerical model, A1, is determined via the laboratory scaling approach proposed by Bunger et al. [9] in order to ensure comparison of numerical models against experimental results at reasonable computational costs. According to them, there are several time scales during a laboratory hydraulic fracturing experiment that characterize the induction and propagation of hydraulic fractures referred to as limiting fracture behaviors [13]. These limiting regimes are associated with concurring energy dissipation mechanisms, that is, toughness and viscosity, as well as fluid volume conservation, i.e. storage and leak-off. Another time scale can be also applied for early time processes associated with fluid and pumping system compressibility and phenomena involving interaction of the crack with the wellbore. An additional timescale is associated with the finite lengths of experimental specimens meaning that at some point in time the fracture has no space to extend.

Due to practical reasons, we neglect the period linked with early wellbore compressibility and fracturing effects. Thus, we focus on the time scale that approximates the duration of the fracturing experiment. The estimated maximum time expected for the hydraulic fracturing test, t_e, can be defined using the plain strain modulus, E′, and stress intensity factor, K′ [9]:

$$ t_{e} = \frac{{H^{\frac{5}{2}} K^{\prime}}}{{Q_{0} E^{\prime}}} $$

(19)

$$ K^{\prime} = 4\left( {\frac{2}{\pi }} \right)^{\frac{1}{2}} K_{Ic} $$

(20)

$$ E^{\prime} = \frac{E}{{1 - \upsilon^{2} }} $$

(21)

where H is the distance to the critical specimen boundary, i.e. where interaction between the induced fracture and the specimen is expected, Q₀ is the (constant) injection rate, K_Ic is the mode I (tensional) fracture toughness, E is the Young’s modulus, and υ is the Poisson’s ratio. Note that H here equals to the sample length since a bi-wing hydraulic fracture is simulated in the numerical model.

Using the boundary conditions presented above, for injection rate Q₀ = 100 mm³/s and mechanical parameters listed in Table 1, t_e gives approx. 1500 ms. This agrees with the recorded characteristics of the lab test “CCI1”, where instantaneous pressure drop and associated increased acoustic emission activity are observed within few seconds (Fig. 2a). Thus, in the homogeneous model and heterogeneous model cases with constant-rate continuous injection (CCI), cases A1 and B1, respectively, fluid is injected at 100 mm³/s for 2000 ms.

Based on Detournay [13], one can calculate the characteristic time scale for given limiting regimes, i.e. for toughness- and viscosity-dominated fracture propagation, here referred to as MK- and OM-transitions, respectively. For this, we use the parameters listed in Table 1 and t_e ~ 1500 ms. The timescale for the MK-transition is t_mk < 1 ms and that for OM-transition is t_om ~ 1500 ms for this set of parameters. Thus, the hydraulic fracture should propagate in the toughness-dominated regime. Consequently, we assume toughness-dominated hydraulic fracture propagation with neglectable leak-off due to the very low intrinsic permeability of the granite samples.

The simulated duration of the CPI tests is determined based on the characteristic fracturing time of the “CCI” lab test and the step-wise manner of increasing the injection flow rate from lower levels to the desired flow rate of 100 mm³/s. The low steps, as base loading steps, are kept at 1 mm³/s, while the high steps are first increased from 2 to 10 in 1 mm³/s incremental steps, then from 10 to 100 mm³/s in 10 mm³/s increments. Each step lasts for 200 ms. Such scheme ensures keeping the injection pressure below the formation breakdown pressure in the initial injection steps. Consequently, modelling cases A2 and B2 last for 7000 ms.

Prior to simulating fluid-injection into the rock sample, the mechanical and hydraulic microscopic properties of the numerical model are calibrated following the procedures described in Tatone and Grasselli [42] and Lisjak et al. [29], respectively. The mechanical calibration is a trial-and-error approach where a combination of uniaxial compression and Brazilian tensile strength tests are conducted to match the mesh tensile and shear fracture penalty, energy as well as toughness parameters against the laboratory elastic and strength parameters. The desired macroscopic permeability is obtained by assigning an initial hydraulic aperture to the flow channels (a_i) and calibrating it via simple permeability test simulations. The calibrated rock material parameters, including elastic, strength and hydraulic properties are summarized in Table 1. The cavities are initially saturated to mimic laboratory conditions. The treatment begins at the onset of injection and the computation ends at the time of injection stop.

The numerical model parameters give a mechanical time step of 1.7 × 10⁻⁹ s. First, 200,000 mechanical time steps are repeated to initialize the anisotropic stress field. Since the time scale between mechanical and hydraulic processes are different, e.g. nanoseconds versus milliseconds, respectively, 20 mechanical steps are performed for each hydraulic step in the simulation. Model runtime lasts approx. three weeks on a workstation equipped with Intel Xeon CPU E5 processor unit, 128 GB of RAM and Nvidia Quadro P4000 GPU using parallel computation.

We must point out that no fluid-induced microseismicity is modelled. Instead, we directly analyze the failure mechanism and the spatial distribution of the microcracks.

4 Results

4.1 Summary of main simulation results

The four modelling cases and the respective results are summarized in Table 2. In each simulation case, the effects of fluid injection on hydro-mechanical fracturing processes is investigated. These processes are characterized via the formation breakdown pressure (FBP), the average pressure during fracture propagation (fracture propagation pressure, FPP), the maximum hydraulic aperture and the respective aperture fold of increase as well as the macroscopic total crack length. The aperture fold of increase is the ratio of maximum hydraulic aperture of the microcracks versus the initial crack aperture. Based on the hydraulic calibration procedure described in [29], this corresponds to the permeability increase of the rock sample. The effect of injected volume is investigated as well. This is an advantage compared to the laboratory experiments, where the injected fluid did not accumulate in the saturated sample due to drainage along the sample boundary surfaces [53]. The total crack length is defined as the temporal sum of microcrack lengths in the sample.

Table 2 Summary of modelling cases, injection parameters and test results and their comparison against laboratory experimental results reported by Zhuang et al. [53] and [55]

The presentation of the simulation results is structured in the following way. The points of interest are discussed separately for homogeneous and heterogeneous rock samples. For each sample, the effect of injection schemes is investigated. First, the evolution of fluid injection pressure and the cumulative injected volume at the injection point as well as the cumulative crack length of the rock sample are discussed. This is followed by the characterization of the hydraulic fracture initiation and propagation as well as its interaction with pre-existing fractures in the case of heterogeneous samples. Lastly, elastic stress transfer effects due to direct pore pressure effect and stress transfer across the triangular elements are analyzed in two ways. In one way, the principal stress trajectories (orientations) are compared against the hydraulic fracture pattern and fluid pressure distribution across the sample at the end of the simulation. In another way, the principal stress magnitudes and fluid pressure profiles are analyzed in two directions: in the direction of anticipated hydraulic fracture propagation, i.e. parallel to maximum principal stress, denoted as X-axis and perpendicular to that, termed as Y-axis. The two profiles intersect at the injection point, and they are studied shortly after hydraulic fracture initiation and at the end of simulation. We note that fluid pressure has positive value, while tensional and compressional stresses are positive and negative, respectively.

4.2 Investigation of injection schemes on homogeneous samples

The evolution of fluid injection pressure at the injection point, the cumulative injected volume as well as cumulative crack length due to constant-rate continuous injection in homogeneous rock sample are shown in Fig. 8. In this modelling case A1, the fluid pressure reaches the fracture breakdown pressure (FBP) of approx. 15 MPa within milliseconds during the initial pressurization phase. The pressurization phase is followed by a pressure drop to 5 MPa after 150 ms (shortly after state “a” in Fig. 8). This pressure level corresponds to the fracture propagation pressure (FPP) around which the pressure undulates until the injection stops at 2000 ms (state “b” in Fig. 8). The chainsaw type of simulated pressure curve is the combination of the high brittleness and the mesh resolution applied. Once an element undergoes failure, the stress drops instantaneously and the additional stress is transferred to the element ahead of the crack tip. The pressure increases until an additional element fails, and the cycle is repeated. It is important to mention that similar behavior can be seen in Figs. 11, 14 and 17. This numerical effect is reported in several numerical studies, e.g. Farkas et al. [18] and Parisio [34].

Fig. 8

Evolution of fluid pressure, cumulative crack length and injected volume at the injection point due to constant-rate continuous fluid injection in homogeneous rock sample. Pointers a and b refer to distinct states of the simulation shown in Figs. 9 and 10

The cumulative crack length, here the macroscopic length of the hydraulic fracture evolves initially at the same rate as the cumulative injected volume until approx. 800 ms. This is associated with the symmetrical propagation of the hydraulic fracture. Due to intrinsic mesh directional effect, asymmetric fracture propagation is sustained from this point until 1650 ms. Moreover, the injection pressure and the number of cracks remain constant from 1300 ms for 350 ms. This can be explained by fluid pressure accumulation within the hydrofrac until fluid pressure is high enough for extension in the shorter fracture direction.

At the end of the simulation, a symmetrical hydraulic fracture of 70 mm is generated after injection of 200 mm³ fluid (Figs. 8 and 9 and Table 2). The aperture fold of increase is 2.4 with a maximum hydraulic aperture of 8 µm.

Fig. 9

Hydraulic fracture pattern (black line), fluid pressure distribution (color bar) and principal stress trajectories (white lines) in the granitic rock sample at the end of constant-rate continuous fluid injection in the homogeneous rock sample (Base case model A1)

The generated fracture pattern, fluid pressure distribution and principal stress directions are shown in Fig. 9. Due to the homogeneous nature of the rock sample, only microcracks with mode I are induced that are oriented parallel to the direction of the maximum principal stress. According to Fig. 9, the fluid pressure accumulates only in the hydraulic fracture. This is associated with the low permeability of the rock mass which limits leak-off into intact rock. As for the principal stress trajectories, the orientation of the maximum principal stress is deviated by 25° around the fracture tips. The deviation angle decreases with increasing distance from the hydraulic fracture towards sample boundaries in the direction of the minimum principal stress. Around the injection point, the principal stress trajectories are rotated back to the directions acting at the sample boundaries.

The relationship between fracture pattern, fluid pressure distribution and principal stress magnitudes for the base case model A1 at two stages of the simulated injection experiment is illustrated in Fig. 10. Shortly after reaching the FBP, the principal stress magnitudes and fluid pressure distribution reveal the extent of newly induced hydraulic fracture (Fig. 10a). The minimum and maximum principal stresses are both compressive within the hydraulic fracture with a length of 10 mm along the X-axis, parallel to the direction of maximum principal stress. At both fracture tips, concentration of tensional minimum principal stress is observed preceding the generation of new microcracks and so the extension of the hydraulic fracture. Few millimeters away from the fracture tips, the magnitudes of the principal stresses agree with the boundary conditions, i.e. S_x = S_H = 6 MPa, and S_y = S_h = 3 MPa. Consequently, both the direct pore pressure effect and the elastic stress transfer are limited in this direction. In the Y-axis, parallel to the acting minimum principal stress, elevation of principal stresses in compression due to fluid pressure increase is observed. The stress alteration effect continuously diminishes with increasing distance from the injection point over 20 mm, which corresponds to the double distance of the hydraulic fracture length. Elevated fluid pressure dissipates a few mm away from the injection point due to lack of leak-off into the intact rock mass.

Fig. 10

Hydro-mechanical characterization of induced hydraulic fracture propagation due to constant-rate continuous injection into homogeneous rock sample at its center (magenta dot) at early phase (a) and end of the experiment (b). Left panel: fluid pressure distribution and hydraulic fracture evolution. Right panel: fluid pressure and principal stress profiles across the hydraulic fracture (X-axis) and perpendicular to that (Y-axis). Note that fluid pressure is only positive, while tensional and compressional stresses have positive and negative values, respectively

At the end of the fluid injection experiment (Fig. 10b), the fluid pressure along the hydraulic fracture shows a perturbation around 5 MPa which can be explained by the random orientation of the triangular element edges. However, the principal stress magnitudes as well as the minimum principal stress concentrations show the symmetrical location of the hydraulic fracture tips. Although the hydraulic fracture tips are relatively close to the sample boundaries, the maximum principal stress magnitudes are slightly affected there. In the perpendicular direction, however, both principal stress magnitudes are elevated along the profile. This is an indication for elastic stress transfer through the sample perpendicular to the hydraulic fracture caused by hydraulic fracture opening.

Figure 11 shows the evolution of fluid injection pressure at the injection point, the cumulative injected volume as well as cumulative crack length due to cyclic progressive injection in the same rock sample (simulation case A2). The initial pressurization phase is characterized by linear pressure increase in the first “low” and “high” injection steps. At the end of first “high” injection step with 2 mm³/s injection rate, first crack is initiated at FBP equal to 15.4 MPa. This is followed by moderate pressure drop and further pressure increase, which is associated with stress singularity due to loading and unloading cycles with low flow-rates and without any significant leak-off into the microcrack and rock mass. Thus, the apparent peak pressure is interpreted as unsolicited artefact. Subsequently, pressure drops, undulates and sequentially reaches an average FPP of 5.6 MPa at decreasing amplitudes. Comparing the fluid pressure evolution against cumulative crack length, it is evident that it takes several injection steps to increase the fluid pressure so that new microcracks can be generated (state “a” in Fig. 11a). The total length of the hydraulic fracture equals 75 mm as a result of fluid injection of 120 mm³ (state “b” in Fig. 11). The resulting aperture fold of increase is 2.1 (Table 2).

Fig. 11

Evolution of fluid pressure, cumulative crack length and injected volume at the injection point due to cyclic progressive fluid injection in homogeneous rock sample. Pointers a and b refer to distinct states of the simulation shown in Figs. 12 and 13

In Fig. 12, the fracture pattern, fluid pressure distribution and principal stress directions at the end of simulation case A2 are illustrated. The figure shows that the fluid pressure is limited in the asymmetric hydraulic fracture composed of mode I microcracks. The asymmetric nature of the hydraulic fracture is associated with the random orientation of the mesh edges. Furthermore, around the fracture tips, the orientation of maximum principal stress trajectories is deviated by 25° from that defined at the boundaries. As in modelling case A1, the deviation angle decreases with increasing distance from the hydraulic fracture tips towards sample boundaries in the direction of the minimum principal stress. Interestingly, in contrast to case A1, the minimum principal stress orientations are not altered at the end of simulation, which is a hint towards stress orientation redistribution after injection is stopped.

Fig. 12

Asymmetric hydraulic fracture pattern (black line), fluid pressure distribution (colour bar) and principal stress trajectories in the granitic rock sample (white orthogonal lines) at the end of cyclic progressive fluid injection in homogeneous rock sample (model case A2)

As for the extent of elastic stress transfer (Fig. 13), at the time of hydraulic fracture initiation (Fig. 13a), both direct pore pressure and elastic stress effects are concentrated around the injection point. At the end of the fluid injection experiment (Fig. 13b), the extent of the perturbation of the principal stress magnitudes due to elastic stress transfer, i.e. deviation from the magnitudes defined at the boundaries shows an asymmetric pattern which is linked to the macroscopic fracture geometry.

Fig. 13

Hydro-mechanical characterization of induced hydraulic fracture propagation due to cyclic progressive injection into homogeneous rock sample at its center (magenta dot) at early phase (a) and end of the experiment (b). Left panel: fluid pressure distribution and hydraulic fracture evolution. Right panel: fluid pressure and principal stress profiles across the hydraulic fracture (X-axis) and perpendicular to that (Y-axis). Note that fluid pressure is only positive, while tensional and compressional stresses have positive and negative values, respectively

4.3 Investigation of injection schemes on heterogeneous samples

The fluid injection pressure due to injection at a constant rate of 100 mm³/s into a fractured rock sample and the resulting cumulative crack length and injected volume are summarized in Fig. 14. In the modelling case B1, the FBP of 14.5 MPa is reached within few 10 ms. After that, pressure decreases rapidly within few 100 ms to an average FPP level of approx. 6 MPa (state “a” in Fig. 14). Pressure fluctuates around FPP as the hydraulic fracture extends until the end of the treatment (state “b” in Fig. 14). As for the crack length evolution during the experiment, it increases directly proportional to increasing injected volume from the onset of injection until fluctuation of the fluid pressure around average FPP begins (state “a” in Fig. 14). From that point on, the extension of the growing hydraulic fracture requires more fluid, thus the fracture propagation holds sequentially.

Fig. 14

Evolution of fluid pressure, cumulative crack length and injected volume at the injection point due to constant-rate continuous fluid injection in a heterogeneous rock sample. Pointers a and b refer to distinct states of the simulation shown in Figs. 15 and 16

At the end of the simulation, a complex hydraulic fracture composed of microcracks with a total length of 162 mm is generated after 200 mm³ of fluid injection (Fig. 15). The aperture fold of increase is equal to a factor of 6 with a maximum hydraulic aperture of 20 µm.

Fig. 15

Principal stress trajectories and fluid pressure distribution in the induced hydraulic fracture at the end of constant-rate continuous fluid injection in heterogeneous rock sample. Microcracks induced in tension in rock matrix are shown as black elements; hydro-sheared pre-existing fractures are dark purple elements as well as softened pre-existing fractures are illustrated as light pink elements. Pre-existing discrete fracture network is not shown for enhanced visibility (model case B1)

In Fig. 15, the principal stress trajectories, fluid pressure distribution and the microcrack pattern at the end of the injection experiment are shown. First, symmetrical mode I microcracks are induced in the intact rock mass around the injection point that are parallel to the direction of the maximum principal stress (black elements in Fig. 15). As the propagating hydraulic fracture approaches the pre-existing joints, those encounter first softening, then failure in mode II, referred to as hydro-shearing (light pink and dark purple elements, respectively, in Fig. 15). Due to hydraulic aperture increase associated with that, the joints are infiltrated and fluid pressure builds up due to ongoing injection. As pumping continues, new joints soften and fail as well as new mode I microcracks are generated that establish connection between two hydro-sheared joint elements. Mode I microcracks are only oriented parallel to the maximum principal stress. Interestingly, mode II fractures have various failure angles, i.e. failure angles that are not associated with optimally oriented for hydro-shearing. This can be explained by the fluid pressure build up and the limited leak-off into the rock mass. Since pressure accumulation is restricted to the fractured elements, fracture propagation requires less energy towards a not optimally oriented pre-existing joint (e.g. parallel to the minimum principal stress) than to induce a new mode I microcrack.

Comparing the distribution of pressurized elements against the location of microcracks, it is evident that the generated fractures are not restricted to pressurized regions. Thus, mode II cracks and softened elements due to elastic stress transfer are observed. Mode II microcracks are up to 10 mm away from the tip of the hydraulic fracture, i.e. farthest pressurized element from the injection point. In the case of mode II softened elements these can be as far as several 10 mm.

The complex fracture network has a clear influence on the stress trajectories. At the tips of the hydraulic fracture, the minimum stress orientations are diverted by up to 30° and the maximum principal stress orientations are slightly deviated. With increasing distance away from the hydraulic fracture tips in the direction of the minimum stress, horizontal stress directions show increasing deviation from the principal direction as well. Interestingly, around the injection point, where no pre-existing fractures were present, both principal stress directions agree with the boundary conditions. Possible explanation for this observation is that the high pressurized fracture elements close to the injection point act as free surface with principal stresses parallel and perpendicular.

Figure 16 summarizes the hydraulic fracture propagation as well as fluid pressure distribution and principal stress profiles due to constant-rate continuous injection into heterogeneous rock sample (model case B1) at early (a) and later stage of the experiment (b). At the early stage of the injection experiment, i.e. shortly after first mode II microcracks are generated during hydraulic fracture propagation, an approximately symmetrical fracture pattern is observed with a larger right wing due to interconnected joint elements. The symmetrical bi-wing fracture pattern is also apparent in both principal stress profiles where the minimum stress concentrations reveal a fracture half-length of 10 mm along the X-axis profile from the injection point. 10 mm away from the minimum stress concentrations, i.e. fracture tips in both profiles, the principal stresses agree with the magnitudes defined at the boundaries. This shows that the elastic stress transfer has a radius of ~ 20 mm which is about four times the hydraulic fracture half length. In contrast to the elastic effects, the direct pore pressure effect is limited to the extent of the hydraulic fracture and that is negligible perpendicular to the fracture as a result of lack of fluid leak-off into the intact rock mass.

Fig. 16

Hydro-mechanical characterization of induced bi-wing hydraulic fracture propagation due to constant-rate continuous injection into heterogeneous rock sample at its center (magenta dot) at early phase (a) and end of the experiment (b). Left panel: fluid pressure distribution and hydraulic fracture evolution. Right panel: fluid pressure and principal stress profiles across the hydraulic fracture (X-axis) and perpendicular to that (Y-axis). Note that fluid pressure is only positive, while tensional and compressional stresses have positive and negative values, respectively

At the end of the treatment (Fig. 16b), the half-distance of the pressurized farthest fracture tips is located 25 mm from the injection point parallel to the maximum principal stress. Around the fracture tips, elevated minimum stresses are visible in the X-axis profile, which diminishes to the pressure level defined at the boundaries within few 10 mm. Perpendicular to the hydraulic fracture, around the injection point, the principal stresses are slightly more compressional. Towards the boundaries, the maximum principal stress reduces to the level defined at the boundaries, whereas the minimum stress remains slightly more compressional, i.e. 4 MPa, at the boundaries.

Figure 17 exhibits the fluid pressure evolution due to cyclic progressive injection and the resulting cumulative crack lengths and injected volume in fractured rock sample (model case B2). Fluid pressure shows steady increase until FBP at a value of 15.5 MPa is reached during “high” injection step with a flow rate of 4 mm³/s where first crack is generated. Subsequently, pressure increases further until 22 MPa which is followed by large drop. The apparent peak pressure is associated with unsolicited numerical instability, as also observed for modelling case A2. Thus, the peak pressure is interpreted as numerical artefact. The pressure drop after reaching artefact is followed by pressure undulation with decreasing amplitudes as the propagating hydraulic fracture requires less pressure build up to extend. At this stage of the experiment, cumulative crack length and injected volume show similar evolution characteristics (state “a” in Fig. 17). After the hydraulic fracture reaches pre-existing joints, i.e. from the “high” step of 40 mm³/s, extension of the hydraulic fracture requires more fluid pressure due to the higher volume of the pressurized system. Thus, hydraulic fracture propagates at an average FPP of 5.8 MPa until the end of the treatment (state “b” in Fig. 17).

Fig. 17

Evolution of fluid pressure, cumulative crack length and injected volume at the injection point due to cyclic progressive fluid injection in heterogeneous rock sample. Pointers a and b refer to distinct states of the simulation shown in Figs. 18 and 19

At the end of the simulation, a complex hydraulic fracture composed of microcracks with a total length of 96 mm is generated after 120 mm³ of fluid injection (Fig. 18). The aperture fold of increase is equal to a factor of 6 with a maximum hydraulic aperture of 20 µm.

Fig. 18

Principal stress trajectories and fluid pressure distribution in the induced hydraulic fracture at the end of cyclic progressive fluid injection in heterogeneous rock sample. Microcracks induced in tension in rock matrix are shown as black lines; hydro-sheared pre-existing fractures are dark purple elements as well as softened pre-existing fractures are illustrated as light pink elements. Pre-existing discrete fracture network is not shown for enhanced visibility (model case B2)

In Fig. 18, the principal stress trajectories, the fluid pressure distribution and the generated microcracks are illustrated at the end of the treatment. The complex fracture network is the result of the hydraulic fracture induced at the injection point that propagates away parallel to the maximum principal stress and interferes with the pre-existing joints. It is evident in Fig. 18 that microcracks are generated both due to direct pore pressure, i.e. characterized by pressurized newly induced mode I fractures and hydro-sheared pre-existing joints, and as a consequence of elastic stress transfer effect. Interestingly, the minimum principal stress orientations are not deviated, however, the maximum principal stress trajectories are distorted around the hydraulic fracture tips and away from that perpendicular to the hydraulic fracture. Around the injection point, the trajectories agree with the boundary conditions.

The main hydro-mechanical characteristics of the cyclic progressive injection treatment in heterogeneous rock are summarized in Fig. 19. The characteristics, such as the extent of perturbed minimum and maximum principal stresses during hydraulic fracture propagation and at the end of injection are similar to model case B1.

Fig. 19

Hydro-mechanical characterization of induced hydraulic fracture propagation due to cyclic progressive injection into heterogeneous rock sample at its center (magenta dot) at early (a) and end of the experiment (b). Left panel: fluid pressure distribution and hydraulic fracture evolution. Right panel: fluid pressure and principal stress profiles across the hydraulic fracture (X-axis) and perpendicular to that (Y-axis). Note that fluid pressure is only positive, while tensional and compressional stresses have positive and negative values, respectively

5 Discussion

5.1 Comparison of hydro-mechanical indicators due to different injection schemes

By comparing the hydraulic and mechanical results of the different injection schemes in Table 2, following points can be discussed.

First, the FBP is slightly higher using the CPI scheme, between 0.5 and 1 MPa, regardless of rock fabric. Although this agrees with the laboratory experiments of Zhuang et al. [53], this is in contrast to laboratory studies such as Patel et al. [38] and Kang et al. [25] where FBP drops with number of injection cycles. Considering the laboratory tests of Zhuang et al. [53], there are mainly two reasons for the variation of FBP. First, sample heterogeneity can cause 1–2 MPa variance in BTS,and second, limitation in the test equipment that is likely to cause 1–2 MPa error. In the numerical model, the discrepancy can be explained by the limited leak-off into rock mass, random properties of pre-existing fractures, how the fluid volume is injected in the modelled rock sample as well as numerical effects. Considering numerical effects, cyclic loading would require more mechanical time steps for a given hydraulic time step to enable more effective relaxation, and hence unsolicited stress concentration leading to higher FBP and unsolicited apparent peak pressures. However, this would result in impractical lengthy computational times. Thus, it can be hypothesized that an improved numerical definition of the calculation scheme would result in reduced FBP for both schemes.

Second, the FPP is interestingly approx. the same in all modelling cases. Thus, that is neither influenced by the injection scheme nor the rock fabric. This is even more striking given that the pressurized joints have a larger aperture than the intact rock mass and the induced mode I microcracks. This is associated with the presence of only mode I microcracks around the injection point that control initial FBP and subsequent pressure drop during the injection experiment.

The comparison of the microcrack patterns, stress magnitude profiles and trajectories merits further discussion.

The fracture patterns in the homogeneous modelling cases (A1 in Fig. 10 and A2 in Fig. 13) show that the hydraulic fracture propagation is driven by classical fracture tip lubrication. Thus, at the end of the simulation, fluid pressure and the principal stresses are uniform parallel to the direction of propagation. Slight variations in fluid pressure are attributed to the irregular orientations of the mesh edges that connect virtual pores storing injected fluid. No microcrack is generated ahead of the fracture tip or away from the hydraulic fracture, i.e. no fracture process zone (FPZ) develops. The principal stress trajectories at the end of the homogeneous modelling cases (A1 in Fig. 9 and A2 in Fig. 12) show that the perturbation area, where the trajectories are oriented from the boundary condition, is around the fracture tip injection points (case A2) which propagates as the hydraulic fracture extends (case A1). Thus, at the time scale of the experiment, stress orientation redistribution can be observed around the injection point.

In contrast to the homogeneous modelling cases, more complex fracture patterns are generated in the heterogeneous modelling cases (B1 in Fig. 15 and Fig. 16 as well as B2 in Fig. 18 and Fig. 19). Initially, hydraulic fracture propagation is analogous to the homogeneous modelling cases, A1 and A2, as only mode I microcracks are generated in the intact portion of the heterogeneous rock sample. As soon as the propagating hydraulic fracture reaches the jointed rock mass, the main driving mechanism becomes the hydraulic pressurization of the jointed elements. These hydro-sheared pre-existing elements have various orientations regardless of optimal orientation for hydro-shearing. Only few mode I microcracks are generated in intact rock that connect two jointed elements. Moreover, joints soften and fail as mode II elements away from the tips of the hydraulic fracture. This is an indication that a mode II fracture process zone develops instead of mode I FPZ. The most distant softened or sheared elements are located 10–15 mm away from the tips with orientation of − 39° measured counter-clockwise from the direction of maximum principal stress. Furthermore, more indirect microcracks are generated around the pressurized fracture elements in the CCI scheme than in the CPI scheme. The complex fracture pattern including microcracks away from the hydraulic fracture is therefore the result of both fracturing due to direct pore effects and indirect elastic stress transfer. Thus, we demonstrate that locally the fracture follows the rock fabric (pre-existing fractures) and on a larger scale it follows overall the stress field directions.

The stress magnitude profiles in the heterogeneous cases exhibit asymmetric variation at the profile parallel to the fracture propagation, since that propagates rather through the hydro-sheared joints with different orientations. In both injection schemes, the stress magnitude profiles show asymmetric stress concentrations. This observation agrees with in-plane shear mechanism described in classical theory of linear elastic fracture mechanics [50], their Chapter 3). As for the principal stress trajectories, those at the end of the heterogeneous modelling cases (B1 in Fig. 15 and B2 in Fig. 17) show that the perturbation area, where the trajectories are oriented from the boundary condition, is not only around the fracture tips but around the indirectly hydro-sheared microcracks as well. However, analogously to the homogeneous modelling cases, at the time scale of the experiment, stress orientation redistribution can be observed around the injection point.

Although the effect of both natural and injection parameters is investigated in this study, it would be beneficial to extend the parametric study on investigating the effect of injection parameters, i.e. constant injection rate and cyclic injected volume on induced fracture geometry. Given the model complexity and large computational costs, future study should consider this option.

5.2 Comparison of simulation treatments against laboratory experiments

The simulation cases allow comparing the results with observations from laboratory experiments reported by Zhuang et al. [53].

First of all, test duration as well as time required for complete fracturing of the sample in the lab and the numerical simulation can be compared. As for the laboratory experiments, this can be determined indirectly via the evolution of the cumulative recorded AE curves while in the numerical model, this is simulated directly. Similarly, the permeability (aperture) fold of increase of the injection experiments due to the lab experiments are determined directly from the pressure curves and post-fracturing permeability test, whereas, in the numerical model, this is inferred from increase in hydraulic apertures.

In the case of CCI injection scheme with 100 mm³/s injection rate (Fig. 2a), the cumulative AE evolution indicates fracturing within few seconds, i.e. hydraulic fracture is induced instantaneously compared to the time of shut-in at approx. 65 s. Thus, the simulated duration of approx. two seconds for cross fracturing of the rock sample agrees with the proposed duration in Eq. 20 and in the lab (simulation cases A1 in Fig. 8 and case B1 in Fig. 14).

For the CPI injection scheme from 20 to 100 mm³/s in 10 mm³/s steps (Fig. 2b), the time required for complete fracturing of the sample cannot be determined unambiguously. Based on model cases A2 and B2, the fracturing of the sample using the CPI injection scheme requires at least seven seconds. This is much shorter, and thus, computationally beneficial compared to the laboratory experiment, where fracturing of the sample with the same injection scheme requires 250 s after initial pressurization and before shut-in.

Second, several hydro-mechanical process indicators can serve as comparison between the simulated and laboratory experiments. These include the FBP, the FPP, the comparison of characteristics of cumulative AE with simulated crack length curves as well as permeability increase (aperture fold of increase).

The reported FBP for CCI injection scheme with injection rates of 100 mm³/s is approx. 15 MPa which agrees with the simulated one. The reported FPP, however, is higher than the simulated one, i.e. 10 MPa versus 5.6 MPa (average FBPs of cases A1 and B1 in Table 2). Another possible explanation can be the lack of installed packers in the borehole, resulting in a hydraulic fracture with a height smaller than the length of the open hole section. Since the fluid-filled hydraulic fracture in the laboratory sample cross-cuts the sample as FBP is recorded, the higher FPP is likely associated with boundary effects in the laboratory. Similar observation is reported by Parisio [34], where fluid is injected at cubic granitic rock samples and such experiment is modelled using numerical code OpenGeoSys.

The simulated FBP for the CPI injection scheme shows good agreement with that reported in Zhuang et al. [53]. Considering the heterogeneity of the laboratory samples, and mesh sensitivity, the difference is insignificant. Thus, the larger FBP for the CPI injection scheme compared to CCI shows good agreement with the laboratory experiments and the simulation results. The FPP cannot be unambiguously determined for the laboratory experiments. Thus, no direct comparison is possible.

As for the characteristics of the AE curves, in the case of CCI injection scheme, the instantaneous rise of the cumulative AE curve stops and remains flat until shut-in as shown in Fig. 2a. As discussed above, this is a hint towards rapid hydraulic fracture generation that reaches sample boundaries. Therefore, this evolution agrees with that of the cumulative crack length of numerical model cases A1 and B1 as shown in Fig. 8 and Fig. 14, respectively.

The simulated permeability increment of the injection tests show that higher aperture fold of increase can be reached via using the CPI injection scheme compared to CCI, i.e. approx. 6 versus 2. However, in the lab, the injectivity increase for the CPI scheme and the maximum hydraulic aperture are lower than that for CCI. We can explain this discrepancy in that fracture aperture measured after cyclic injection in the lab is smaller compared with the maximum value during fracture propagation, i.e. during injection. This is due to fracture closure after injection is stopped.

5.3 Implications for EGS field injection strategies

The simulation results allow making implications for field injection strategies regarding natural and engineering factors for developing an optimal fracture network for EGS utilization. The natural factors considered here are the fracture pattern, stress field, and driving mechanisms of crack generation. Regarding the driving failure mechanisms, here we discuss the proposed phenomena underlying field-scale seismicity which is referred to either as induced or triggered [15]. Although the analysis of microseismicity is not the subject of this study, the hydraulic and mechanical controlling factors on the spatial extent of microcrack generation from the injection point can be discussed. The discussed engineering factor is the injection scheme.

A complex fracture network is a prerequisite for potential good hydraulic and thermal performance of an EGS system. Hofmann et al. [20] demonstrate that this is more favorable compared to the presence of a dominant single fracture path. Apart from that, hard and brittle rock with low permeability, a complex pre-existing fracture network with at least two intersecting natural fracture sets and with sets characterized by favorable orientation to the in-situ stress field are favorable. Our numerical results confirm that heterogeneous models (model cases B1 and B2) not only show agreement with these properties of hard and brittle rock but these models also exhibit higher maximum hydraulic apertures. Therefore, heterogeneous models imply potentially better hydraulic conductivity, compared to the homogeneous modelling cases (model cases A1 and A2) where single hydraulic fracture path with lower hydraulic aperture dominates the failure mechanism. Moreover, the heterogeneous models can be used in a future study to test their thermal performance as well. For field scale application, it is inferred that pre-fractured and heterogeneous formations lead to more complex fracture growth.

Regarding fracture geometry, the simulated fracture patterns show stair stepping which resembles observations in tunnel scale experiments ([23]; [52] and the multiple subparallel fractures in core-trough laboratory experiments [8, 37], [39]). Although the in-depth analysis of the interaction between hydraulic and natural fractures is beyond the scope of this study, future analysis may consider analyzing factors affecting stair-stepping size and the spacing between the offset fractures, e.g. Kresse et al. [27].

Considering the changes in stress field discussed in Sect. 5.1, the magnitude changes observed in the principal stress profiles show that the shearing of pre-existing fractures exerts additional compressive stress in the direction normal to the fracture as proposed by Warpinski and Branagan [46]. Thus, the numerical models demonstrate stress shadow effect as a result of both propagation of newly induced fracture and hydro-shearing of discrete fracture elements. This changes the local stress magnitudes and orientations around the injection point and the stimulated area. Consequently, if in one well a frac is generated which alters the stress field at a relatively close location, hydraulic fracture can propagate irrespective of local S_Hmax direction. Similar behavior has been demonstrated in laboratory and numerical experiments recently by Abe et al. [2] and Abe and Horne [1].

Regarding direct pore pressure effect and elastic stress transfer, the numerical model can be used for making implications towards hydro-mechanical controlling mechanisms during injection. The modelling results reveal that the microcrack generation is dominated by direct pore pressure effect. Fracturing due to elastic stressing occurs only in the heterogeneous model cases and those fractures are generated close to the directly pressurized fractures. However, such indirectly induced cracks are observed ahead of directly pressurized pre-existing microcracks. This demonstrates that a rupture front propagates faster than the fluid pressure front as shown by Bhattacharya and Viesca [7]. The directly reactivated fractures are mainly aligned close to the direction of the maximum principal stress direction, i.e.-11° measured counter-clockwise from the horizontal axis, whereas the indirectly reactivated ones are oriented at an angle of -39° from the same direction. The various orientations of the reactivated fractures are the consequence of an interplay of stress alteration and rotation effects. As a result, the factors controlling critical stress for hydro-shearing of pre-existing fractures are modified locally.

Injection scheme, i.e. flow rate, duration as well as injected volume are significant engineering factors of stimulation strategies, apart from rock mass properties. Our numerical investigations show that with the right strategy permeability can be increased by more than factor five if naturally fractured rock is stimulated instead of intact rock. However, this self-propping mechanism is not maintained if the injection is stopped. This leads to apparently lower maximum hydraulic aperture and aperture fold of increase in the CPI case as reported in the post-fracturing laboratory injectivity experiments (Table 2).

Lastly, it must be noted that, although thermal effects are not considered in this study, they may influence the hydro-mechanical properties of rock, especially rock strength properties and permeability [24, 28], and are worth future experimental research.

5.4 Numerical limitations

The limitations of the numerical experiments are the consequence of the algorithmic solutions used to simulate the hydro-mechanical processes described in this paper. The explicit temporal integration scheme solving the motion and flow equations in the mechanical and hydraulic solver, respectively, are well suited for nonlinear, dynamic problems. However, in order to avoid numerical instabilities, sufficiently small integration time steps for both solvers must be defined. That requires setting a trade-off between the number of mesh elements, mesh size as well as upper limit of hydraulic aperture according to Eq. 19. Therefore, a sub-mm scale simulation of the hydro-mechanical processes underlying laboratory fluid-injection experiments can only be conducted using the time scaling approach of the fracturing processes proposed by Bunger et al. [9]. Otherwise, the attempt to match the injection time in simulation with that of an experiment is practically impossible. The same limitation has been reported in numerical studies where explicit time-integration scheme is adopted for hydro-mechanically coupled simulations, e.g. Bai et al. [5] and Kong et al. [26].

Another deficiency of the approach is that the induced hydraulic fracture does not fully reach the draining sample boundaries for the sake of numerical stability. Hence, the injected fluid volume accumulates within the interconnected fracture elements. Since the rock matrix elements have very low permeability, the fluid is trapped in the fractured elements. Consequently, fluid cannot leak into the rock matrix or out of the sample along the boundaries, therefore, no pressure drop is observed during shut-in or reduced injection rate periods in the numerical model as compared to the laboratory experiments.

Moreover, microcracks can only propagate along the mesh edges mimicking intergranular fracturing, i.e. cracking along mineral grain boundaries. In the laboratory, both intragranular, where mineral grains are cut through, and intergranular fracturing occur during fluid injection into granitic rock samples [53, 55]. Furthermore, this unintentionally leads to asymmetric hydraulic fracture propagation in the case of CPI injection schemes regardless of rock fabric (Fig. 13 and Fig. 18). These may be solved by introducing a set of closed-loop polygons. The loop segments can be defined as joint elements that encompass several intact mesh elements representing the inner part of distinct mineral grains. An example for application of this approach is demonstrated by Yoon et al. [48], where blocky structures are simulated using discrete element modelling technique.

6 Conclusions

In this paper, we report on numerical simulation of laboratory fluid-injection experiments of Pocheon granite under two injection schemes and rock sample representations. The hydro-mechanical processes during the experiments are investigated. The research outcomes are summarized as follows:

• 1. The hybrid finite-discrete element simulation of pressurization and fracturing periods of laboratory fluid injection experiments can provide insights into hydro-mechanically coupled fracturing processes at reasonable computational costs using a time-scaling approach.

• 2. Stress rotation effect and elevated compressional stresses are observed around the fracture tips where elements are not infiltrated. This indirect elastic stress transfer leads to microcrack generation around the propagating tips of the macroscopic hydraulic fracture in heterogeneous samples. In these samples, the microcracks are located in an “off-fault” damage zone approximately perpendicular to the direction of hydraulic fracture propagation.

• 3. Constant-rate continuous injection and cyclic progressive injection schemes in heterogeneous rock sample with pre-existing fractures shows the highest hydraulic aperture increase compared to intact samples. Our numerical investigations show that hydraulic aperture can be increased by more than factor five if naturally fractured rock is stimulated instead of intact rock until shut-in. However, laboratory experiments show higher aperture fold of increase, consequently permeability enhancement after constant-rate injection. This shows that the self-proppant mechanism of cyclic progressive injection is not sustained if injection is stopped.

• 4. The least aperture fold of increase is produced by the same cyclic progressive injection scheme into homogeneous rock sample where the aperture increase is approx. factor two. This observation highlights the need and the potential for adjusted injection schemes for different geological conditions in order to optimize hydraulic stimulation treatments.

• 5. The numerical simulation results show good agreement with the laboratory experiments in terms of pressure evolution characteristics and fracture pattern. Furthermore, rock fabric has a significant on the simulated aperture fold of increase, and consequently on permeability increase. On the other hand, hydraulic fracture geometry is influenced by mineral grains in the laboratory experiments. Therefore, future numerical model should incorporate grain strength for improved simulations. Furthermore, the lack of explicit wellbore model and limited leak-off into the intact rock mass hinders simulation of coupled hydro-mechanical processes during early pressurization and shut-in periods, respectively.