Abstract
Traditionally, Biot’s formulation is employed to model the behavior of saturated soils. The \(u-p_w\) (solid displacement–pore water pressure) formulation can be considered as the standard one, since involves a good computational performance together with excellent accuracy for slow and moderate speed phenomena. Dynamic processes can be studied even if the acceleration of the water is neglected, what occurs in the undrained limit. It is well-known that \(u-p_w\) formulation might display instabilities in the undrained-incompressible limit. Several techniques have been proposed to overcome this issue, principally within an implicit time integration scheme for small strains. In this paper, a robust implementation of the divergence of the momentum equation technique is presented for an explicit \(u-p_w\) approach within the framework of optimal transportation meshfree scheme at finite strain. Several examples are provided in order to assess the good performance of the proposed methodology.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
Porous media dynamics at large strain is a cutting-edge issue in the field of computational geomechanics. In this respect, the \({\varvec{u}}-{\varvec{w}}-p_w\) and \({\varvec{u}}-{\varvec{w}}\) Biot formulations, where no dynamic terms are suppressed, are of paramount significant [27]. However, these formulations are computationally expensive compared with the \({\varvec{u}}-p_w\) formulation, since the latter requires, for each node, fewer degrees of freedom than the former ones. Although there are several problems where it is necessary to employ a complete formulation, since every dynamic term becomes important, the majority of the dynamic problems in saturated soils can be covered by the \({\varvec{u}}-p_w\) formulation without loss of accuracy, as most of them fall within its range of application [64].
Nevertheless, these formulations are not exempted from numerical drawbacks depending on the spatial discretization of the numerical method, even for the meshfree approach herein presented. An unstable behavior in numerical solutions of saturated porous media is usually manifested by an over-stiffening of the mechanical solution and a great and fictitious space variability of the water pressure field, occasionally leading to non-uniqueness and mesh dependence of the solutions as well as some instabilities. The occurrence of this kind of pathologies is connected with the undrained-incompressible limit of the coupled problem. While this type of pathology in the \({\varvec{u}}-{\varvec{w}}-p_w\) and the \({\varvec{u}}-p_w\) formulations is connected with the undrained-incompressible limit, that is, analogous to the incompressible limit in solid mechanics problems [46], in the \({\varvec{u}}-{\varvec{w}}\), the pathology appears when the compressibility of the fluid is some orders of magnitude higher than the compressibility of the mixture [40]. In order to overcome this numerical issue in the hydromechanical response of a saturated porous media, several alternatives have been proposed in the specialized literature.
The first approach aims to stabilize the pore pressure term by the inclusion of new terms in the formulation. Monforte et al. [34] assessed two of these techniques: Divergence of the momentum equation (DME) and polynomial projection technique (PPP). The DME was proposed for water problems by Hafez and Soliman [18] and later improved for the \({\varvec{u}}-p_w\) formulation by Pastor [45]. On the other hand, the PPP [14] was applied to the \({\varvec{u}}-p_w\) first by White and Borja [59] and extended by Sun et al. [57] and by Gavagnin et al. [17], being the first one for small strain and the latter for finite strain.
A different approach relies on an average pressure projection. The intrinsic idea is inspired by the work of Hughes [22] and the recent developments of the B-bar method [16]. Furthermore, the strategy behind is analogous to the diamond elements one (Hauret, Kuhl and Ortiz [19]). This approach has been extended to large strain formulations by Simo et al. [54, 55] and De Souza Neto and co-workers [11, 12], considering the F-Bar technique as a volume averaging procedure, changing the volumetric part of the strain tensor by a non-local one. More recently, Sun and coworkers [56, 57] have proposed a novel alternative, starting from the work of Moran et al. [35]. Related techniques have been extended to multiphase formulations for small and large strains in the context of the Optimal Transportation Meshfree method [36, 37, 40,41,42,43]. Also in the finite volume field exist several approaches that stabilize the poromechanical instabilities through macroelement techniques (see the work of Camargo et al. [8, 9]).
Furthermore, stable formulations can be also achieved by tuning the time discretization, as the split-operator [23, 68]. Some of these implementations employ fractional steps techniques that provides a stabilization which allows the employment of the same order of interpolation in mixed formulations. This was first noticed by Schneider et al. [52] and Kawahara and Ohmiya [25]. Zienkiewicz and coworkers [66] explained the reasons why the fractional step technique provides stabilization for computational fluid dynamic problems. This technique was also applied by Pastor et al. [46] for coupled analysis in saturated soil problems, and extended later by Li et al. [31], being worth mentioning the works of White and Borja [59] and Mira et al. [33]. In the geotechnical field, fractional step techniques have been proposed within several meshfree techniques such as the SPH formulations proposed by Blanc and Pastor [4] and the MPM ones proposed by Kularathna et al. [26].
Finally, different order of interpolation for pore pressure and displacement has been the main technique to obtain smooth results, although it requires a stronger computational effort as requires larger number of nodes for the solid phase than for the pore water pressure. Mira et al. [33] in the \({\varvec{u}}-p_w\) formulation and Jeremić et al [24] within \({\varvec{u}}-{\varvec{U}}-p_w\) formulation employed different order of interpolation for the different variables.
A summary of the different stabilization techniques in the context of small strain regime can be found in Markert et al. [32].
In this research, the explicit \({\varvec{u}}-p_w\) is employed due to its computational benefits, which come from both the explicit Newmark predictor-corrector scheme, which was first developed by Navas et al. [40] for the explicit \({\varvec{u}}-p_w\) formulation, and the intrinsic computational saving benefits of the employment of the \(u-p_w\) against the complete formulations. Regarding the application of this formulation in a finite deformation approach, the first works were tested simulating the constitutive behavior of the solid phases with linear elastic (Diebels and Ehlers [13]), Cam-Clay (Borja et al. [5, 6]) and Drucker–Prager theories (Armero [1]) as well as with anisotropic materials [62]. At the same time, Ehlers and Eipper [15] applied a new elastic nonlinear constitutive model to reproduce the compaction of the soil. Implicit schemes were employed in these works, being necessary the linearization of the derivatives of the \(u-p_w\) equations. Furthermore, Sanavia et al. [49] considered several neglected terms in the linearization of the previous works and extended the methodology to unsaturated soils [51]. Moreover, with meshfree schemes, we find excellent contributions to the explicit \({\varvec{u}}-p_w\) approach (see [60, 63]) in the small strain approach. The recent work of Navas et al. [40] shows excellent results within an explicit scheme at large strain.
In the present research, a novel robust stabilized predictor-corrector explicit algorithm for the \({\varvec{u}}-p_w\) formulation at large strain is proposed. The numerical framework considered in order to implement this new stabilized formulation is the optimal transportation meshfree (OTM) scheme [2, 28]. The door is opened to any extension to traditional or novel computational techniques, which can be easily made by adapting the spatial discretization.
The rest of the paper is structured as follows. The problem formulation is summarized in Sect. 2. The explicit methodology, as well as the constitutive models of the solid response, is drawn in Sect. 3. The stabilization technique is detailed in Sect. 4. Applications to several problems are illustrated in Sect. 5. Relevant conclusions are depicted in Sect. 6. The definitions of all symbols used in the equations are provided in the nomenclature appendix.
2 Biot’s equations: u-\(p_w\) formulation
The \(u-p_w\) formulation is one of the most common forms of the Biot’s equations [3]. This theory is based on three statements: the mechanical response of a solid-fluid mixture, the continuity of flux through a differential domain of saturated porous media and the coupling between the aforementioned phases. The derivation of the formulation is widely encountered in the literature. All the equations presented hereinafter are derived from those presented by Lewis and Schrefler [27], later proposed for the finite strain setting by Sanavia and Navas [42, 50, 51].
Respecting the notation, bold symbols has been employed herein for vectors and matrices as well as letters of the Latin alphabet for scalar variables. Let \({\varvec{u}}\) represents the displacement vector of the solid skeleton, \({\varvec{w}}\) the displacement vector of the fluid phase with respect to the solid and \(p_w\) the pore water pressure, which is assumed positive for compression. Terzaghi’s effective stress [58] is considered being defined for incompressible solid constituents as:
where \(\varvec{ \sigma '}\) is the effective Cauchy stress tensor, \(\varvec{ \sigma }\) is the total Cauchy stress tensor (both positive in tension) and \({\textbf {I}}\) is the second order unit tensor. Furthermore, \(D^s/Dt\) is the material time derivative following the movement of the solid particles, also defined as \(\dot{\Box }\).
The main assumption with respect to the full Biot’s formulation lies on neglecting the accelerations of the fluid phase. Thus, the linear balance equation of the mixture reads:
The continuity equation, also known as mass balance equation, is employed as well:
Moreover, both linear momentum balance equation of the fluid phase, defined through the Darcy’s theory, and the equilibrium of the mass, can be written together in order to reduce the number of degrees of freedom of our problem:
In equations (2) and (4), \(\rho\) is the density of the mixture, while \(\rho _{w}\) and \(\rho _{s}\) are the fluid and solid particle densities, respectively. These three densities are related to each other through the expression:
where n is the porosity defined by the ratio of volume of voids, \(V_v\), with respect to the total volume, \(V_T=V_v+V_s\), where \(V_s\) is the volume of the solid grains:
The soil is considered totally saturated. Thus, \(V_v\) is equal to the water volume. Furthermore, the volumetric compressibility of the mixture, Q [64], has been calculated considering incompressible solid constituents as
where \(K_w\) is the bulk modulus of the fluid phase, usually considered as water.
On the other hand, \({\varvec{g}}\) represents the gravity acceleration vector and \(\mathbf {\varkappa }\) the permeability matrix. This matrix can be written in terms of \(k^{rw}\), the hydraulic conductivity, \(\kappa\) [m/s], and the specific weight of the water through the following equation:
\(k^{rw}\) is set as 1 when full saturation is to be considered.
3 Implementation tools
In this section, spatial and time discretization, as well as the constitutive models employed in this research, are briefly explained.
3.1 Spatial discretization
The optimal transportation meshfree [21, 28, 29], as one of the most trending meshfree methods, is employed in the present research. Its fulfillment within geotechnical multiphase problems [38] makes this methodology a robust alternative to material point method or Smoothed Particle Hydrodynamics, among others. Similarly to the first one, OTM is based on a particle-to-node interpolation, where the shape functions that relates both sets are based on the work of Arroyo and Ortiz [2], who defined the Local Max-Ent shape function (LME) of the material point with respect to the nodal neighborhood. For the readers’ knowledge, the equation of the shape function and the achievement of the first derivatives of the shape function, as well as the details of every parameter, are depicted in [2, 28].
Applying the standard Galerkin procedure to the weak counterpart of Eqs. (2) and (4) (See [48, 51] for details), the following equations are obtained:
where:
while the mass and damping matrices, are written as follows:
In these expressions \(V_p\) is the volume associated with the material point P while \(N_p\) range from the neighborhood points associated with P. The matrix \({\mathbf {B}}\) is the symmetric shape function gradient operator while \({\mathbf {m}}\) the identity matrix in Voigt notation. Thus, \({\mathbf {B}}{\mathbf {m}}\) reproduces the divergence operation.
3.2 Explicit integration
The coupled problem in the time domain is solved in this research through the explicit central difference Newmark time integration scheme. Let the current step \(k+1\), and assuming the solution in the previous step, k, has been already obtained, the relationship between displacement, velocity and acceleration, \({\textbf {u}}_{k+1}\), \(\dot{{\textbf {u}}}_{k+1}\) and \(\ddot{{\textbf {u}}}_{k+1}\), follows the Newmark scheme for each phase:
By considering \(\theta =\gamma =0.5\) and \(\beta =0\), the Predictor and Corrector terms are read as follows:
where the underlined terms are the predictor ones, denoted as \(\dot{u}_{k+*}\) and \(p_{w_{k+*}}\), respectively.
On the other hand, the stability of this method is assured through the Courant–Friedrichs–Lewy (CFL) condition, being the time step, \(\varDelta t\), smaller than \(\frac{h}{V_c}\), where h represents the discretization size and \(V_c\) is the velocity of the p-wave (see [65]), defined by:
It bears to emphasize several aspects about the predicted step. About the stress, it has to be calculated in this predicted step through the predicted displacement as follows:
The logarithmic strain, as the strain measure to be employed in the deformed configuration, has to be calculated from the tensor \({\mathbf {b}}\), the Left Cauchy–Green strain tensor (\({\mathbf {b}}={\mathbf {F}}{\mathbf {F}}^T\)), which depends on the displacement on the predicted step as well:
Moreover, solid velocities and water internal forces must be evaluated in the predicted step, \(k+*\). In Section 4, all these premises will be considered in a pseudo-algorithm, written once the stabilization is taken into account.
3.3 Constitutive models for the solid phase
A brief note of the employed constitutive models is outlined in this Section: a hyper-elastic model for soils and another one that involves plastic deformation which follows the Drucker–Prager failure criterion, both developed in a finite strain approach.
As mentioned before, for elastic materials, a nonlinear law, considering the influence of the Jacobian calculation, the initial porosity \(n_0\) and the compaction point of the soil, is employed (see Ehlers and Eipper [15]). This law follows the subsequent definition of the Kirkchoff stress tensor:
In order to reproduce elasto-plastic behavior at large strain, the Drucker–Prager yield criterion proposed by Sanavia and coworkers for large strain is employed [48, 51]. The relationship between left Cauchy–Green strain tensor \({\mathbf {b}}\), calculated at the current configuration, and the small strain tensor \(\varvec{\varepsilon }\) is made through Ortiz, Simo and coworkers’ research [10, 44, 53]:
Trial stress measures are also computed from the elastic trial strain as:
where G and K represent the shear and bulk moduli of the solid, respectively. The yield conditions for the classical and apex regions are calculated in a different manner for the proposed yield criterion.
Once known which algorithm to employ, one of the following expressions applies:
where \(\varDelta \gamma _1=\frac{\Vert {\textbf {s}}^{trial}_{k+1}\Vert }{2G}\), \(\varDelta \gamma\) and \(\varDelta \gamma _2\) are the objective functions in the Newton–Raphson scheme for the classical or apex regions accordingly. In Eqs. 20) and (21), H is the hardening parameter of the material, \(c_k\) represents the cohesion, and \(\alpha _F\),\(\alpha _Q\) and \(\beta\) depend on the friction and dilatancy angles as well as the shape of the yield surface. For details of the calculation of the equivalent plastic strain, see [48, 51].
4 Stabilization of the water phase
The necessity of stabilization in the developed \({\varvec{u}}-p_w\) formulation lies on the work of Zienkiewicz and Taylor [67]. Assuming incompressible constituents, the Biot modulus Q is larger than the compressibility of the solid skeleton. Traditionally, the usual condition required for the \({\varvec{u}}-p_w\) problem is given by \(n_u \ge n_{p_w}\) (see, for instance, Pastor et al [45]). However, this condition, although necessary, must be fulfilled in any assembly of elements of the mesh [45, 67]. See [20] for a detailed study of the stability conditions of the three-field formulation.
The pore pressure term in the algebraic equation has been traditionally the one which suffers the aforementioned oscillations. Thus, the majority of the available techniques have this term as the target one, departing from the stabilization techniques employed in the context of Computational Fluid Dynamics. Brezzi and Pitkaranta [7] proposed to add to the pressure term, the so-called \({\varvec{K}}_{pp}\) position in the implicit mixed solid \({\varvec{u}}-p\) formulation, the stabilizing term:
which is equivalent to the one proposed by Hughes et al [23]. This term, when working with the \({\varvec{u}}-p_w\) implicit saturated formulation, is analogous to the \({\varvec{K}}_{p_{w}p_{w}}\) term, i.e., the pore pressure position of the continuity equation, Eq. (4) (see Pastor et. al. [45] for details).
Based on Petrov-Galerkin theory; the added term is proportional to the product of the linear momentum equation by \(\dfrac{h^2}{2 \, \mu } \nabla {\varvec{N}}\). Indeed, both techniques are proportional to h, the mesh size in Finite Element approaches or the nodal distance in meshfree methodologies. This fact leads to an interesting issue when the mesh is refined: the proposed term tends to zero and, thus, the consistency is preserved.
The methodology to be explained hereinafter is inheritor of the work of Hafez and Soliman [18] proposed to stabilize the Navier–Stokes equations and the one proposed by Pastor et. al. [45], which adapted the former one to the hydromechanical problem in quasi-static conditions (\({\varvec{u}}-p_w\) formulation). That work was later extended to a formulation valid for the full Biot equations by Monforte et. al. [34]. All these works are based on adding the divergence of the momentum equation to the mass balance equation.
In our case, in the explicit scheme, Eq. (10) may suffer numerical instabilities in the undrained limit. If \(\varkappa\) tends to zero, \({\varvec{M}}^{w}\), \({\varvec{f}}^{ext, \, w}\), and \({\varvec{R}}^{w*}\) tend to be much smaller than \({\varvec{C}} \dot{{\varvec{u}}}\). It leads to the situation that the pore pressure velocity depends only on the solid velocity, what means that no influence of the pore water phase affects the results. Due to this fact, spurious pore pressure oscillations are obtained. Moreover, in the incompressible limit, the increase in the compressibility of the mixture, Q, aggravates this situation since tends to increase the obtained result.
Thus, the objective is to add a new term, which is equal to zero in order to avoid nonphysical results, but avoids leaving the pore pressure value just in the hands of the velocity of the solid phase. Following the aforementioned works ( [34, 45]), in our proposal, the divergence of the linear momentum balance equation of the mixture, Eq. (2), will be employed. This equation, multiplied by the parameter \(\alpha\)= \(\alpha\)(h), yields:
taking into account the divergence of the volumetric forces is equal to zero. If the solid skeleton behavior is elastic, which can be perfectly assumed even if the material plasticizes, the divergence of the solid displacement can be expressed in terms of the volumetric stress invariant, \(p'\), and the bulk modulus, K, as:
From the same assumption, the divergence of the internal forces can be expressed as (see Pastor et. al. [45] for details):
where \(\lambda\) and G are the Lamé constant and shear modulus of the soil skeleton.
On the other hand, the displacement of the water is negligible if small permeability is employed, which is the case of the undrained limit, the goal of the proposed stabilization technique. Thus, from the integration on time of the equation (3) and plugging definition (24), we can obtain:
Thus, considering Eq. (25), the divergence of the internal forces of both fluid and solid phases yields:
Taking into account Eqs. (23) and (27), the divergence of momentum of the mixture can be rewritten as:
We have considered the incompressible limit, where \(\lambda\) and G are much smaller than the bulk modulus of the water phase, Q.
Pastor and coworkers proposed that the parameter \(\alpha\) may depend on the density of the mixture and the critical time step, which is the time step that is able to capture the P wave of the saturated media. The main components of this reference time step are the characteristic P-wave velocity, \(V_c\), and the element size, h:
Finally, as Eq. (28) is equal to zero, we can add directly to Eq. (4) without losing physical meaning:
Rewriting Eq. (30) in a matrix form, the stabilized system of equations yields:
where the \(^*\) terms are the stabilized terms that are built as:
4.1 Explicit stabilized pseudo-algorithm
The explicit scheme is similar to the one proposed by Navas et al. [39] with the introduction of the stabilization terms. Following, the pseudo-algorithm of the whole model is proposed, being the superscript p employed for material point calculations.
-
1.
Explicit Newmark Predictor (\(\gamma =0.5\), \(\beta =0\))
$$\begin{aligned} u_{k+1}= & {} u_k+\varDelta t \dot{u}_{k}+0.5\varDelta t^2 \, \ddot{u}_k, \\ \dot{u}_{k+*}= & {} \dot{u}_{k}+(1-\gamma )\varDelta t \, \ddot{u}_{k}, \\ p_{w_{k+*}}= & {} p_{w_k}+(1-\gamma )\varDelta t \, \dot{p}_{w_k}. \end{aligned}$$ -
2.
Update position of Nodes and Material points
$$\begin{aligned} x_{k+1}=&x_{k}+\varDelta u_{k+1}, \\ x_{k+1}^p=&x_{k}^p+\sum _{a=1}^{Nb}\varDelta u_{k+1}^a N^a(x^p_{k}). \end{aligned}$$ -
3.
Calculation of the deformation gradient and related parameters
$$\begin{aligned} \varDelta {\mathbf {F}}_{k+1}= & {} I+\sum _{a=1}^{Nb}\varDelta u_{k+1}^a \otimes \nabla N^a(x_{k}^p), \\ {\mathbf {F}}_{k+1}= & {} \varDelta {\mathbf {F}}_{k+1} {\mathbf {F}}_{k}, \\ V= & {} JV_0=\det {\mathbf {F}} \, V_0,\\ n= & {} 1-\frac{1-n_0}{J}. \end{aligned}$$ -
4.
Update density and mass. Construct lumped mass
$$\begin{aligned} \rho _{k+1}=n_{k+1}\rho _{w}+(1-n_{k+1})\rho _s. \end{aligned}$$ -
5.
Remapping nodes and material neighbors.
-
6.
Calculation of stresses \(\varvec{\sigma '}_{k+*}\) and internal forces, \({\varvec{R}}^s_{k+*}\) and \({\varvec{R}}^w_{k+*}\), through the constitutive model.
-
7.
Computing \(\ddot{\varvec{u}}_{k+1}\) from Eq. (31):
$$\begin{aligned} \ddot{{\varvec{u}}}_{k+1} = \left[ {\varvec{M}}^s \right] ^{-1}\left[ {\varvec{R}}^s_{k+*}- {\varvec{R}}^w_{k+*} + {\varvec{f}}^{ext, \, s}_{k+1}\right] \end{aligned}$$ -
8.
Calculate \(\dot{p_w}_{k+1}\) from Eq. (32):
$$\begin{aligned} \dot{p_w}_{k+1}=- {\varvec{C}} \dot{{\varvec{u}}}_{k+*} + {\varvec{M}}^{w*} \ddot{{\varvec{u}}}_{k+1} + {\varvec{f}}^{ext, \, w}_{k+1}-{\varvec{R}}^{w*}_{k+*} \end{aligned}$$ -
9.
Explicit Newmark Corrector
$$\begin{aligned} \dot{u}_{k+1}=\dot{u}_{k+*}+\gamma \varDelta t \, \ddot{u}_{k+1}, \\ {p}_{w_{k+1}}={p}_{w_{k+*}}+\gamma \varDelta t \, \dot{p}_{w_{k+1}}. \end{aligned}$$
5 Verification examples
Three different verification examples are considered in this section. The first verification case deals with a consolidation process in a saturated column of soil subjected to a bilinear loading at the surface The second one allows us to verify also the 2D component behavior, analyzing the behavior of the pore water pressure distribution along a 2D stratum when it is loaded by a strip footing. Finally, the third verification case assesses the failure of a vertical wall of saturated soil, aiming to analyze the performance of the proposed stabilization technique in a traditional geotechnical problem.
5.1 Consolidation of a column of soil
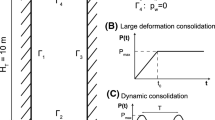
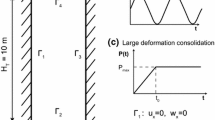
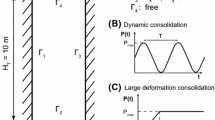
In this problem, an idealization of a semi-infinite stratum of soil through a 2D column is employed. The height and width of the column are \(H_T=10m\) and \(L=1m\), respectively. Horizontal displacement is forbidden in the vertical boundaries, while vertical displacement is blocked in the rigid base. In addition, the top boundary is considered perfectly drained (\(p_w=0\)). This geometry and boundary conditions are depicted in Fig. 1. Also, the load ramp considered is presented.
Sabetamal et al. [47] proposed a particular mesh in order to be able of a proper capturing of the wave provoked by the load. The upper meter of the stratum is discretized with a 0.25 m.; meanwhile, a discretization of 0.5 m. size is employed for the rest of the stratum. A similar discretization is employed in this research within the OTM configuration.
The objective of the present section is the verification of the methodology in the undrained-incompressible limit. A stratum of soil suffers the application of a pressure which follows the curve of Fig. 1B. The load is applied gradually until reaching \(P_{max}\) at \(t_0=7.5\) s. Following, the l when the load is kept constant until 7.5 s. The water and solid parameters are presented in Tab. 1, being the nonlinear elastic material of Eq. (15) employed for the solid model of the problem.
The solutions obtained, with and without the stabilization technique, are shown in Fig. 2 for the two cases. In this figure, the pore pressure distribution, when the whole load is applied (7.5 s), is plotted. The typical positive–negative pattern of an unstable pore pressure distribution is observed for the unstabilized case. Also, spurious maximum values, close to 500 Pa, are observed in this case; meanwhile, the maximum value of the stabilized case is close to the total amount of load, 100 Pa. Also, in Fig. 2, the pore pressure distribution obtained with a quadratic finite element scheme can be observed. A similar pattern can be appreciated between the proposed approach and the quadratic finite element one. However, oscillations close to the top of the column appear in the distribution obtained with the finite element approach. These oscillations are not present in the results obtained with the proposed approach.
If this pore pressure is plotted along the depth, Fig. 3, the oscillations are seen for the unstabilized case in the 3 first meters of the stratum of the column. The stabilization technique allows to mitigate this unrealistic behavior, smoothing out the solution without losing physical information. Although the pore pressure distribution obtained with the quadratic finite element approach improves the unstabilized result, it still presents some oscillations close to the top of the column.
5.2 Strip footing load
The following example is based on a saturated stratum loaded by a vibrating strip footing. Fig. 4 presents the geometry, boundary conditions as well as the history load of the aforementioned footing. This verification case was firstly studied by Li et al. [30] through the finite element method and later with the Material Point Method by Zhao and Choo [61]. The permeability of the soil stratum in the present work is similar to the one considered by Zhao an Choo, which is lower than the original one. The traditional Neo-Hookean model is employed. The material parameters are depicted in Fig. 4. It is worth mention that comparison against these works is not possible since no damping parameter is employed in the present research. However, it is possible to capture similar trends that were observed in the previous works. Moreover, they considered an incompressible pore water phase, whereas compressibility of the pore water is taken as 1e10 Pa in the present work.
First, the spatial distribution of the pore pressure shows oscillations, since it lies on the incompressible-undrained limit (Fig. 5). The values are not so severer than in the previous example, since no negative values are achieved. It can be due to the 2D configuration of the problem or the dynamic behavior of the load. However, unrealistic peak values are obtained.
The phenomenon is studied at t=0.1 s. In Fig. 5, the distribution of the pore pressure is depicted for the unstabilized and stabilized solutions and also the quadratic finite element scheme. The unstabilized profile shows a spurious oscillation, which is alleviated in the stabilized and the finite element solutions. The difference between the stabilized and the finite element solutions lies in the peak, which is more pronounced for the finite element one. This peak is quickly alleviated along the depth in both cases, being quicker in the finite element approach than in the stabilized solution. The value of the peak can be observed in Fig. 6. In this figure, the distribution of the pore pressure along the depth is depicted, located under the edge of the strip footing. While the stabilized solution and the quadratic one show a smooth transition, with a peak of around 3 MPa, the unstabilized solution oscillates around the correct solution providing unreal values, with a peak of 4 MPa.
Next, the time evolution of the pore water pressure at two different locations (A and B in Fig. 4, i.e., a shallow and a deep location) is analyzed.
As it can be appreciated in Fig. 7, the main difference can be encountered in the location at point A, shallow zone. Effectively, in Fig. 7A, there is an important overestimation of the peak values that is mitigated along the depth, as it can be observed in Fig. 7B. Although the overall trend is not greatly affected with depth, several peaks appear. In the present case, as the material is Neo-Hookean, these peaks scarcely affect the final result. However, with different constitutive materials, as in the following application case, the found peaks would alter the final result.
The differences between the quadratic and the stabilized solutions are depicted clearer in point B, where the quadratic one is able to dissipate pore pressure more efficiently than the proposed solution.
Pore pressure evolution at locations A and B of the Fig. 4 along the time
5.3 Vertical cut
In this final application, the proposed stabilization technique is applied to model a drainage process induced by a strip rigid footing over a square domain of a hyper-elastoplastic saturated soil. The failure of the material, leaded by the applied load, takes the shape of a typical vertical cut with an inclined shear band. A similar problem was previously assessed by Sanavia et al. [49, 50] in a quasi-static regime and by Navas et al. [41, 42] for a dynamic approach, considering different dilatancy angles in order to see the performance of the soil depending on the properties. In this case, only the case of friction angle 20\(^\circ\) and dilatancy 0\(^\circ\) is studied. The geometry and material properties are shown in Fig. 8A gradual displacement of 1 m at the boundary \(\Gamma _4\) is applied along the 10 s of the simulation, being the employed time step 1 ms. A nodal spacing of 0.833 m., forming a regular 12\(\times\)12 nodal discretization, is considered.
Pore pressure results are depicted, at the final stage, in Fig. 9. For the stabilized simulation, it was reached the final time of 10 s. However, for the non-stabilized case, the simulation breaks out at 1 s due to the influence of the spurious pore water pressure distribution over the solution process. In the third row, the solution obtained with a T6-P3 finite element technology, without stabilizing, is also shown. The results are similar to the stabilized one. In the referred bibliography, we found distributions of pore pressure similar to the stabilized one, taking into account that, in this case, the permeability was lowered to reach undrained conditions. Despite this fact, the trend of the behavior of the soil is well captured. Contrary, the unstabilized one presents the typical oscillations that become bigger due to the plastic behavior of the soil.
Regarding the relation with the development of the shear band, the three solutions are shown in Fig. 10. It can be observed how the stabilized one and the quadratic one are similar to those reached by Sanavia and coworkers for the case \(\phi =20^\circ\) and \(\psi =0^\circ\). Nevertheless, as we mentioned before, the spurious pore water pressure spatial distribution affects the spatial distribution of plastic zones and the subsequent development of the shear band mechanism.
6 Conclusions
The stabilization of the explicit Newmark predictor–corrector solution of the Biot’s \(u-p_w\) formulation is provided in this manuscript. This formulation has been at large strain within the optimal transportation meshfree method, although it can be extended to some other well-known meshfree schemes, such as smooth particle hydrodynamics or material point method. The stabilization is achieved through the addition of a stabilization term, which comes from the divergence of the momentum equation.
The proposed methodology was previously demonstrated to work in a robust way in dynamic problems of saturated soils, mainly under drained conditions, but in this research, it has been extended to the undrained-incompressible limit. Furthermore, the methodology accounts with the potential strength of an explicit scheme. Elastic and plastic materials have been tested, showing excellent results, mainly with the second one, since the spurious peak values are catastrophic by means of unreal plasticizing of the material.
The first example has demonstrated the performance of the proposed methodology in the traditional Terzaghi’s scheme. The second one extends this elastic scheme to 2D conditions in order to visualize the propagation of the waves along the domain. Harmonic loading has been employed to assess the behavior of the pore pressure along the time. Finally, a typical plastic problem has been analyzed. Under the light of the proposed stabilization technique, the expected shear band is attained. However, without stabilizing the problem, the plastic zone dissipates creating spurious plastic zones along the domain, being impossible the formation of the shear band. The wide range of applications allows us to validate the proposed methodology under dynamic conditions.
The present research opens the door of the explicit simulations of saturated soils by some other meshfree methods. Next steps will present this formulation in the material point method. Moreover, this methodology is feasibly transferable to unsaturated conditions by adding the influence of the degree of saturation and the air phase. Because of the nature of the explicit scheme, this formulation arises easily from the proposed in this paper.
Abbreviations
- \({\varvec{b}}={\varvec{F}}{\varvec{F}}^{T}\)::
-
Left Cauchy–Green tensor
- \(\varvec{\overline{b}}\)::
-
Body forces vector
- c::
-
Cohesion (equivalent to the yield stress, \(\sigma _Y\))
- \({\varvec{C}}\) :
-
(Time integration scheme): damping matrix
- \(\frac{D^s\Box }{Dt}\) \(\equiv \dot{\Box }\)::
-
Material time derivative of \(\square\) with respect to the solid
- \({\varvec{F}}=\frac{\partial {\varvec{x}}}{\partial {\varvec{X}}}\)::
-
Deformation gradient
- \({\varvec{g}}\)::
-
Gravity acceleration vector
- G::
-
Shear modulus
- h::
-
Nodal spacing
- H::
-
Hardening modulus, derivative of the cohesion against time.
- \({\varvec{I}}\)::
-
Second-order unit tensor
- \(J=\text{ det }{\varvec{F}}\)::
-
Jacobian determinant
- k::
-
Intrinsic permeability
- \({\varvec{k}}\)::
-
Permeability tensor
- K::
-
Bulk modulus
- \(K_s\)::
-
Bulk modulus of the solid grains
- \(K_w\)::
-
Bulk modulus of the fluid
- \({\varvec{M}}\) ::
-
Mass matrix
- n::
-
Porosity
- \(N({\varvec{x}})\), \(\nabla N({\varvec{x}})\)::
-
Shape function and its derivatives
- p::
-
solid pressure
- \(p_w\)::
-
Pore pressure
- \({\varvec{P}}\) :
-
(Time integration scheme): external forces vector
- Q::
-
Volumetric compressibility of the mixture
- \({\varvec{R}}\)::
-
Internal forces vector
- \({\varvec{s}}=\varvec{\sigma }^{dev}\)::
-
Deviatoric stress tensor
- t::
-
time
- \({\varvec{u}}\)::
-
Displacement vector of the solid
- \({\varvec{U}}\)::
-
Displacement vector of the water
- \({\varvec{v}}^s=\varvec{\dot{u}}\)::
-
Velocity vector of the solid
- \({\varvec{v}}^{ws}\)::
-
Relative velocity vector of the water with respect to the solid
- \({\varvec{w}}\)::
-
Relative displacement vector of the water with respect to the solid
- \(Z({\varvec{x}},\varvec{\lambda })\)::
-
Denominator of the exponential shape function
- \(\alpha _{_F}\), \(\alpha _{_Q}\) and \(\beta\)::
-
Drucker–Prager parameters
- \(\beta\), \(\gamma\): :
-
Time integration schemes parameters
- \(\beta\), \(\gamma\)::
-
LME parameters related with the shape of the neighborhood
- \(\varDelta \gamma\)::
-
Increment in equivalent plastic strain
- \(\overline{\varepsilon }^p\)::
-
Equivalent plastic strain
- \(\varvec{\varepsilon }\)::
-
Small strain tensor
- \(\varepsilon _0\)::
-
Reference plastic strain
- \(\kappa\)::
-
Hydraulic conductivity
- \(\lambda\)::
-
Lamé constant
- \(\varvec{\lambda }\)::
-
Minimizer of log\(Z({\varvec{x}},\varvec{\lambda })\)
- \(\mu _w\)::
-
Viscosity of the water
- \(\nu\)::
-
Poisson’s ratio
- \(\rho\)::
-
Current mixture density
- \(\rho _w\)::
-
Water density
- \(\rho _s\)::
-
Density of the solid particles
- \(\varvec{\sigma }\)::
-
Cauchy stress tensor
- \(\varvec{\sigma '}\)::
-
Effective Cauchy stress tensor
- \(\varvec{\tau }\)::
-
Kirchhoff stress tensor
- \(\varvec{\tau '}\)::
-
Effective Kirchhoff stress tensor
- \(\Phi\)::
-
Plastic yield surface
- \(\phi\)::
-
Friction angle
- \(\psi\)::
-
Dilatancy angle
- \(^{dev}\)::
-
Superscript for deviatoric part
- \(^{e}\)::
-
Superscript for elastic part
- \(_{k}\)::
-
Subscript for the previous step
- \(_{k+1}\)::
-
Subscript for the current step
- \(^{p}\)::
-
Superscript for plastic part
- \(^{s}\)::
-
Superscript for the solid part
- \(^{trial}\)::
-
Superscript for trial state in the plastic calculation
- \(^{vol}\)::
-
Superscript for volumetric part
- \(^{w}\)::
-
C superscript for the fluid part relative to the solid one
References
Armero F (1999) Formulation and finite element implementation of a multiplicative model of coupled poro-plasticity at finite strains under fully saturated conditions. Comput Methods Appl Mech Eng 171(3–4):205–241. https://doi.org/10.1016/S0045-7825(98)00211-4
Arroyo M, Ortiz M (2006) Local maximum-entropy approximation schemes: a seamless bridge between finite elements and meshfree methods. Int J Numer Meth Eng 65(13):2167–2202. https://doi.org/10.1002/nme.1534
Biot MA (1956) Theory of propagation of elastic waves in a fluid-saturated porous solid. I. low-frequency range. J Acoust Soc Am 28(2):168–178. https://doi.org/10.1121/1.1908239
Blanc T, Pastor M (2012) A stablized Runge-Kutta, Taylor smoothed particle hydrodynamics algorithm for large deformation problems in dynamics. Int J Numer Meth Eng 91(June):1427–1458. https://doi.org/10.1002/nme
Borja RI, Alarcón E (1995) A mathematical framework for finite strain elastoplastic consolidation. Part1: balance laws, variational formulation, and linearization. Comput Methods Appl Mech Eng 122(94):145–171
Borja RI, Tamagnini C, Alarcón E (1998) Elastoplastic consolidation at finite strain. Part 2: finite element implementation and numerical examples. Comput Methods Appl Mech Eng 159:103–122
Brezzi F, Pitkaranta J (1984) On the stabilization of finite element approximation of the Stokes problem. In: efficient solitions of elliptic problems, notes on numerical fluid mechanics, vol 10, pp 11–19
Camargo J, White J, Castelletto N, Borja RI (2021) Preconditioners for multiphase poromechanics with strong capillarity. Int J Numer Anal Meth Geomech 45:1141–1168. https://doi.org/10.1002/nag.3192
Camargo J, White J, Borja RI (2021) A macroelement stabilization for mixed finite element/finite volume discretizations of multiphase poromechanics. Comput Geosci 25:775–792. https://doi.org/10.1007/s10596-020-09964-3
Cuitiño A, Ortiz M (1992) A material-independent method for extending stress update algotithms from small-strain plasticity to finite plasticity with multiplicative kinematics. Eng Comput 9:437–451
De Souza Neto EA, Perić D, Dutko M, Owen DRJ (1996) Design of simple low order finite elements for large strain analysis of nearly incompressible solids. Int J Solids Struct 33(20–22):3277–3296. https://doi.org/10.1016/0020-7683(95)00259-6
de Souza Neto EA, Pires FM, Owen DRJ, Andrade Pires FM (2005) F-bar-based linear triangles and tetrahedra for finte strain analysis of nearly incompressible solids. Part I: formulation and benchmarking. Int J Numer Meth Eng 62(3):353–383. https://doi.org/10.1002/nme.1187
Diebels S, Ehlers W (1996) Dynamic analysis of a fully saturated porous medium accounting for geometrical and material non-linearities. Int J Numer Meth Eng 39(1):81–97. https://onlinelibrary.wiley.com/doi/10.1002/(SICI)1097-0207(19960115)39:1%3C81::AID-NME840%3E3.0.CO;2-B
Dohrmann CR, Bochev PB (2004) A stabilized finite element method for the Stokes problem based on polynomial pressure projections. Int J Numer Meth Fluids 46(2):183–201
Ehlers W, Eipper G (1999) Finite elastic deformations in liquid-saturated and empty porous solids. Transp Porous Media 34(1986):179–191. https://doi.org/10.1007/978-94-011-4579-4_11
Elguedj T, Bazilevs Y, Calo VMM, Hughes TJR (2008) B-bar and f-bar projection methods for nearly incompressible linear and non-linear elasticity and plasticity using higher-order nurbs elements. Comput Methods Appl Mech Eng 197(33–40):2732–2762
Gavagnin C, Sanavia L, De Lorenzis L (2020) Stabilized mixed formulation for phase-field computation of deviatoric fracture in elastic and poroelastic materials. Comput Mech. https://doi.org/10.1007/s00466-020-01829-x
Hafez M, Soliman M (1991) Numerical solution of the incompressible Navier-Stokes equations in primitive variables on unstaggered grids. In: 10th computational fluid dynamics conference, pp. 368–379. American Institute of Aeronautics and Astronautics
Hauret P, Kuhl E, Ortiz M (2007) Diamond elements: a finite element/discrete-mechanics approximation scheme with guaranteed optimal convergene in incompressible elasticity. Int J Numer Meth Eng 73(February):253–294. https://doi.org/10.1002/nme
Hong, Q, Kraus J (2017) Parameter-robust stability of classical three-field formulation of Biot’s consolidation model. arXiv preprint arXiv:1706.00724 (2017)
Huang D, Weißenfels C, Wriggers P (2019) Modelling of serrated chip formation processes using the stabilized optimal transportation meshfree method. Int J Mech Sci 155(March):323–333. https://doi.org/10.1016/j.ijmecsci.2019.03.005
Hughes TJR (1980) Generalization of selective integration procedures to anisotropic and nonlinear media. Int J Numer Meth Eng 15:1413–1418
Hughes TJR, Franca LP, Balestra M (1986) A new finite element formulation for fluid dynamics, V. Circumventing the Babuška-Brezzi condition: a stable Petrov-Galerkin formulation of the Stokes problem accomodating equal order interpolation. Comput Methods Appl Mech Eng 59(1):85–99
Jeremić B, Cheng Z, Taiebat M, Dafalias YF (2008) Numerical simulation of fully saturated porous materials. Int J Numer Anal Meth Geomech 32:1635–1660. https://doi.org/10.1002/nag.2347
Kawahara M, Ohmiya K (1985) Finite element analysis of density flow using velocity correction. Int J Numer Meth Fluids 5:981–993
Kularathna S, Liang W, Zhao T, Chandra B, Zhao J, Soga K (2021) A semi-implicit material point method based on fractional-step method for saturated soil. Int J Numer Anal Meth Geomech 45(10):1405–1436. https://doi.org/10.1002/nag.3207
Lewis RW, Schrefler BA (1998) The finite element method in the static and dynamic deformation and consolidation of porous media. John Wiley & Sons Ltd
Li B, Habbal F, Ortiz M (2010) Optimal transportation meshfree approximation schemes for fluid and plastic flows. Int J Numer Meth Eng 83(June):1541–1579. https://doi.org/10.1002/nme
Li B, Stalzer M, Ortiz M (2014) A massively parallel implementation of the optimal transportation meshfree (pOTM) method for explicit solid dynamics. Int J Numer Meth Eng 100:40–61
Li C, Borja RI, Regueiro RA (2004) Dynamics of porous media at finite strain. Comput Methods Appl Mech Eng 193(36–38):3837–3870. https://doi.org/10.1016/j.cma.2004.02.014
Li X, Han X, Pastor M (2003) An iterative stabilized fractional step algorithm for finite element analysis in saturated soil dynamics. Comput Methods Appl Mech Eng 192:3845–3859
Markert B, Heider Y, Ehlers W (2010) Comparison of monolithic and splitting solution schemes for dynamic porous media problems. Int J Numer Meth Eng 82(11):1341–1383. https://doi.org/10.1002/nme
Mira P, Pastor M, Li T, Liu X (2003) A new stabilized enhanced strain element with equal order of interpolation for soil consolidation problems. Comput Methods Appl Mech Eng 192(37–38):4257–4277. https://doi.org/10.1016/S0045-7825(03)00416-X
Monforte L, Navas P, Carbonell JM, Arroyo M, Gens A (2019) Low order stabilized finite element for the full Biot formulation in Soil Mechanics at Finite Strain. Int J Numer Anal Meth Geomech 43:1488–1515. https://doi.org/10.1002/nag.2923
Moran B, Ortiz M, Shih C (1990) Formulation of implicit finite element methods for multipicative finite deformation plasticity. Int J Numer Meth Eng 29:483–514
Navas P, López-Querol S, Yu RC, Li B (2016) B-bar based algorithm applied to meshfree numerical schemes to solve unconfined seepage problems through porous media. Int J Numer Anal Meth Geomech 40(6):962–984. https://doi.org/10.1002/nag.2472
Navas P, López-Querol S, Yu RC, Pastor M (2018) Optimal transportation meshfree method in geotechnical engineering problems under large deformation regime. Int J Numer Meth Eng 115(10):1217–1240. https://doi.org/10.1002/nme.5841
Navas P, Manzanal D, Martín Stickle M, Pastor M, Molinos M (2020) Meshfree modeling of cyclic behavior of sands within large strain generalized plasticity framework. Comput Geotech 122:103538. https://doi.org/10.1016/j.compgeo.2020.103538
Navas P, Molinos M, Martín Stickle M, Manzanal D, Yagüe A, Pastor M (2021) Explicit meshfree \(u-p_w\) solution of the dynamic Biot formulation at large strain. Comput Part Mech. https://doi.org/10.1007/s40571-021-00436-8
Navas P, Pastor M, Yagüe A, Martín Stickle M, Manzanal D, Molinos M (2021) Fluid stabilization of the u-w biot’s formulation at large strain. Int J Numer Anal Meth Geomech 45(3):336–352. https://doi.org/10.1002/nag.3158
Navas P, Sanavia L, López-Querol S, Yu RC (2018) Explicit meshfree solution for large deformation dynamic problems in saturated porous media. Acta Geotech 13:227–242. https://doi.org/10.1007/s11440-017-0612-7
Navas P, Sanavia L, López-Querol S, Yu RC (2018) u-w formulation for dynamic problems in large deformation regime solved through an implicit meshfree scheme. Comput Mech 62:745–760. https://doi.org/10.1007/s00466-017-1524-y
Navas P, Yu RC, López-Querol S, Li B (2016) Dynamic consolidation problems in saturated soils solved through u-w formulation in a LME meshfree framework. Comput Geotech 79:55–72. https://doi.org/10.1016/j.compgeo.2016.05.021
Ortiz M, Simo JC (1985) A unified approach to finite deformation elastoplastic analysis based on the use of hyperelastic constitutive equations. Comput Methods Appl Mech Eng 49(2):221–245. https://doi.org/10.1016/0045-7825(85)90061-1
Pastor M, Li T, Liu X, Zienkiewicz OC (1999) Stabilized low-order finite elements for failure and localization problems in undrained soils and foundations. Comput Methods Appl Mech Eng 174(1–2):219–234. https://doi.org/10.1016/S0045-7825(98)00316-8
Pastor M, Li T, Liu X, Zienkiewicz OC, Quecedo M (2000) A fractional step algorithm allowing equal order of interpolation for coupled analysis of saturated soil problems. Mech Cohesive-frictional Mater 5(7):511–534
Sabetamal H, Nazem M, Sloan SW, Carter JP (2016) Frictionless contact formulation for dynamic analysis of nonlinear saturated porous media based on the mortar method. Int J Numer Anal Meth Geomech 40(1):25–61. https://doi.org/10.1002/nag.2347
Sanavia L, Pesavento F, Schrefler BA (2006) Finite element analysis of non-isothermal multiphase geomaterials with application to strain localization simulation. Comput Mech 37(4):331–348. https://doi.org/10.1007/s00466-005-0673-6
Sanavia L, Schrefler BA, Stein E, Steinmann P (2001) Modelling of localisation at finite inelastic strain in fluid saturated porous media. Proc. In: Ehlers W (eds.), IUTAM symposium on theoretical and numerical methods in continuum mechanics of porous materials, Kluwer Academic Publishers pp. 239–244
Sanavia L, Schrefler BA, Steinmann P (2001) A Mathematical and numerical model for finite elastoplastic deformations in fluid saturated porous media. In: Capriz G, Ghionna V, Giovine P (eds.) Modeling and mechanics of granular and porous materials. Engineering and technology, series of modeling and simulation in science, pp 297–346
Sanavia L, Schrefler BA, Steinmann P (2002) A formulation for an unsaturated porous medium undergoing large inelastic strains. Comput Mech 28(2):137–151. https://doi.org/10.1007/s00466-001-0277-8
Schneider GE, Raithby GD, Yovanovich MM (1978) Finite element analysis of incompressible flow incorporating equal order pressure and velocity interpolation. Numerical Methods for Laminar and Turbulent Flow. Pentech Press, Plymouth
Simo JC. Hughes TJR (2004) Interdisciplinary applied mathematics, Volume 7. Computational Inelasticity, vol. 79. https://doi.org/10.1086/425848
Simo JC, Taylor RL (1991) Quasi-incompressible finite elasticity in principal stretches. Continuum basis and numerical algorithms. Comput Methods Appl Mech Eng 85(3):273–310. https://doi.org/10.1016/0045-7825(91)90100-K
Simo JC, Taylor RL, Pister KS (1985) Variational and projection methods for the volume contraint in finite deformation elasto-plasticity. Comput Methods Appl Mech Eng 51:177–208
Sun W, Chen Q, Ostien Jakob T (2014) Modeling the hydro-mechanical responses of strip and circular punch loadings on water-saturated collapsible geomaterials. Acta Geotech 9(5):903–934
Sun W, Ostien Jakob T, Salinger AG (2013) A stabilized assumed deformation gradient finite element formulation for strongly coupled poromechanical simulations at finite strain. Int J Numer Anal Meth Geomech 37(16):2755–2788. https://doi.org/10.1002/nag.2161
Terzaghi KV (1925) Principles of soil mechanics. Eng News Rec 95:19–27
White JA, Borja RI (2008) Stabilized low-order finite elements for coupled solid-deformation/fluid-diffusion and their application to fault zone transients. Comput Methods Appl Mech Eng 197(49):4353–4366. https://doi.org/10.1016/j.cma.2008.05.015
Zhang HW, Wang K, Chen Z (2009) Material point method for dynamic analysis of saturated porous media under external contact/impact of solid bodies. Comput Methods Appl Mech Eng 198(17–20):1456–1472. https://doi.org/10.1016/J.CMA.2008.12.006
Zhao Y, Choo J (2020) Stabilized material point methods for coupled large deformation and fluid flow in porous materials. Comput Methods Appl Mech Eng 362:112742
Zhao Y, Borja RI (2020) A continuum framework for coupled solid deformation-fluid flow through anisotropic elastoplastic porous media. Comput Methods Appl Mech Eng 369:113225. https://doi.org/10.1016/j.cma.2020.113225
Zheng Y, Gao F, Zhang HW, Lu M (2013) Improved convected particle domain interpolation method for coupled dynamic analysis of fully saturated porous media involving large deformation. Comput Methods Appl Mech Eng 257:150–163. https://doi.org/10.1016/j.cma.2013.02.001
Zienkiewicz OC, Chan AHC, Pastor M, Schrefler BA, Shiomi T (1999) Computational geomechanics with special reference to earthquake engineering. John Wiley
Zienkiewicz OC, Chang CT, Bettes P (1980) Drained, undrained, consolidating and dynamic behaviour assumptions in soils. Géotechnique 30(4):385–395. https://doi.org/10.1016/j.ocecoaman.2012.02.008
Zienkiewicz OC, Codina R (1995) A general algorithm for compressible and incompressible flow. part i: the split characteristic based scheme. Int J Numer Meth Fluids 20:869–885
Zienkiewicz OC, Taylor RL (1994) The finite element method. Volume 1: basic formulation and linear problems, vol. 3. McGraw-Hill, London
Zienkiewicz OC, Wu J (1991) Incompressibility without tears-how to avoid restrictions of mixed formulations. Int J Numer Meth Eng 32:1184–1203
Acknowledgements
This research was funded by the Ministerio de Ciencia e Innovación, under Grant Number, PID2019-105630GB-I00, and the European Research Council-H2020 MSCA-RISE, Grant Agreement No 101007851 (DISCO2-STORE), being both greatly appreciated. Authors would like to thank the administrative and technical support of the ETSI Caminos, Canales y Puertos, from the Universidad Politécnica de Madrid, as well. Additionally, the fifth author really appreciates the Entrecanales Ibarra Foundation for his undergraduate scholarship.
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Contributions
Conceptualization and mathematical methodology were carried out by PN and MMS Implementation was done by MM and PN Validation was done by AY and DM Meanwhile, supervision, project administration and funding acquisition belong to MP. All authors have contributed to the writing and original draft preparation, and they read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Navas, P., Stickle, M.M., Yagüe, A. et al. Stabilized explicit \(u-p_w\) solution in soil dynamic problems near the undrained-incompressible limit. Acta Geotech. 18, 1199–1213 (2023). https://doi.org/10.1007/s11440-022-01642-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11440-022-01642-1